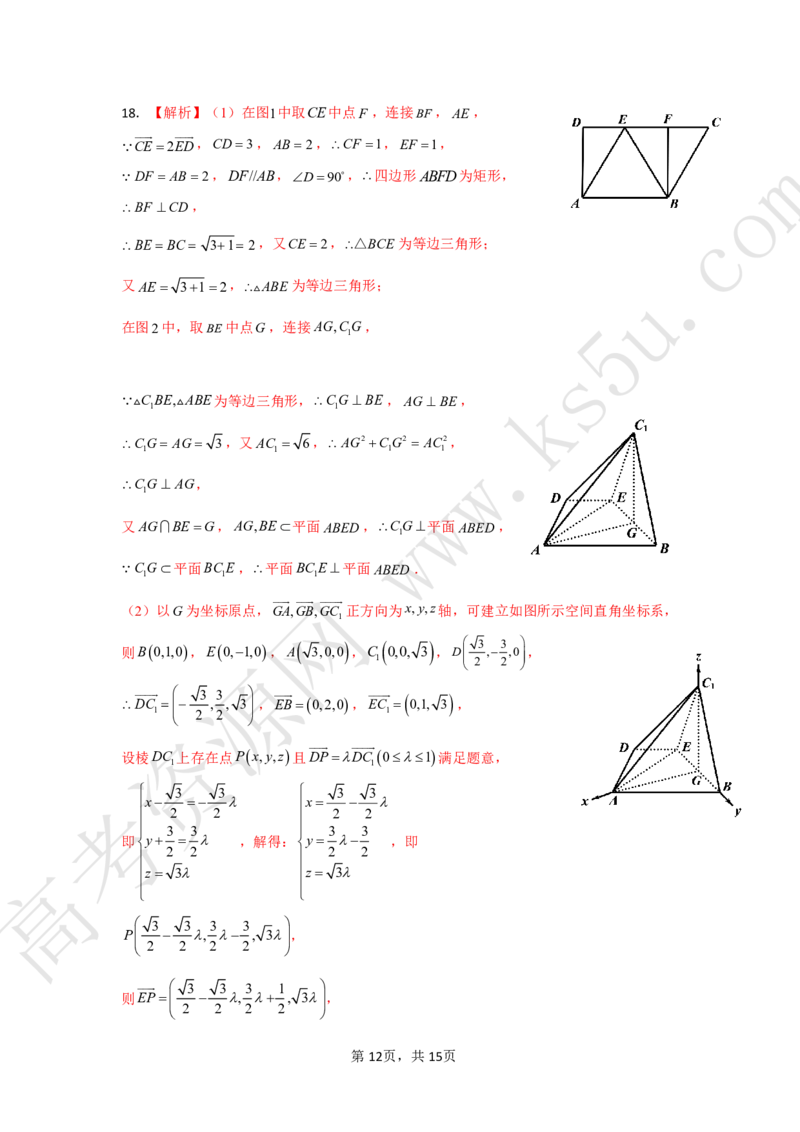2024学年第一学期质量检测高二数学参考答案_2024-2025高二（7-7月题库）_2024年11月试卷_1107浙江省宁波市余姚中学2024-2025学年高二上学期10月月考

余姚中学 2024 学年第一学期质量检测高二数学学科参考答案
1． 开口向下，故选C
1
p  m
4
o
2．B
c
【分析】由题意先求出l l 的充要条件，然后根据充分不必要条件的定义判断即可.
1 2
.
【详解】由题设l l a3a12a30，
1 2 u
5
解得a0或a . 5
3
5 5 s
故a l l ，l l  a .
3 1 2 1 2 3
k
5
所以“a ”是“l l ”的充分不必要条件.
1 2
3
.
故选：B.
w
3．A
w
【分析】结合几何图形，利用向量的线性运算公式，即可求解.
    3 w
【详解】AP AA AP AA  AC，
1 1 1 4 1
 3     3    
 AA  ACAA  AA  ABADAA ，
1 4 1 网 1 4 1
3 3 1 3  3  1 
 AB AD AA  a b c.
4 4 4 1 4 4 4
故选：A
源
资
考
4．D
高
【分析】设Ax,y,Bx,y，由椭圆性质和已知条件得2 x2，由两点间的距离公式得
AF  BF  x12y2  x12y2 ，然后化简、换元结合二次函数单调性可求
1 2
【详解】由题意，设Ax,y,Bx,y，
由于A，B是椭圆C上关于x轴对称的不同的两点，
第1页，共15页所以2 x2，又F 1,0,F1,0 ,
1
m
AF  BF  x12y2  x12y2
1 2
o
3 3
 x2 2x13 x2  x2 2x13 x2
4 4 c
1 1
 x22x4 x22x4
.
4 4
1  2 1 u
  x24 2x2 x42x216
4  16
5
令t  x2，因为2 x2，所以0t4，
s
1 1
所以 f t t22t16 t162，
16 16 k
由于对称轴为t16，所以 f t在0,4单调递减， .
所以 f 4 f t f 0，又 f 016, f 4 1  w 4162 9，
16
w
即9 f t16，所以3 AF  BF 4
1 2
w
故选：D
网
5．[解析] 连接AC',∵正方体的棱长为1,∴AC'= .∵PA+PC'=2,∴点P在以A,C'为焦点的
椭圆绕AC'旋转得到的椭球上.∵P在正方体的棱上3,∴P应是椭球与正方体的棱的交点,结合
源
正方体的性质可知,满足条件的点应该在棱B'C',C'D',CC',AA',AB,AD上各有一点满足条件,故
选C
资6．A
【详解】抛物线的焦点 ，圆M :(x2)2(y2)2 4，其圆心M2,2，半径r 2．
F(3,0) 1
考
设点Nx,y是满足NO2NF的任意一点，则x2 y2 4

x2(y3)2

，
化简得 x4 2  y2 4 ，结合AO2AF,BO2BF ，所以AB是圆M 与圆N 的公共弦，
高
将圆M 与圆N 的方程相减得，直线AB的方程为
x y20
，
则 PE  22, PE 2 2，
max min
故选：A．
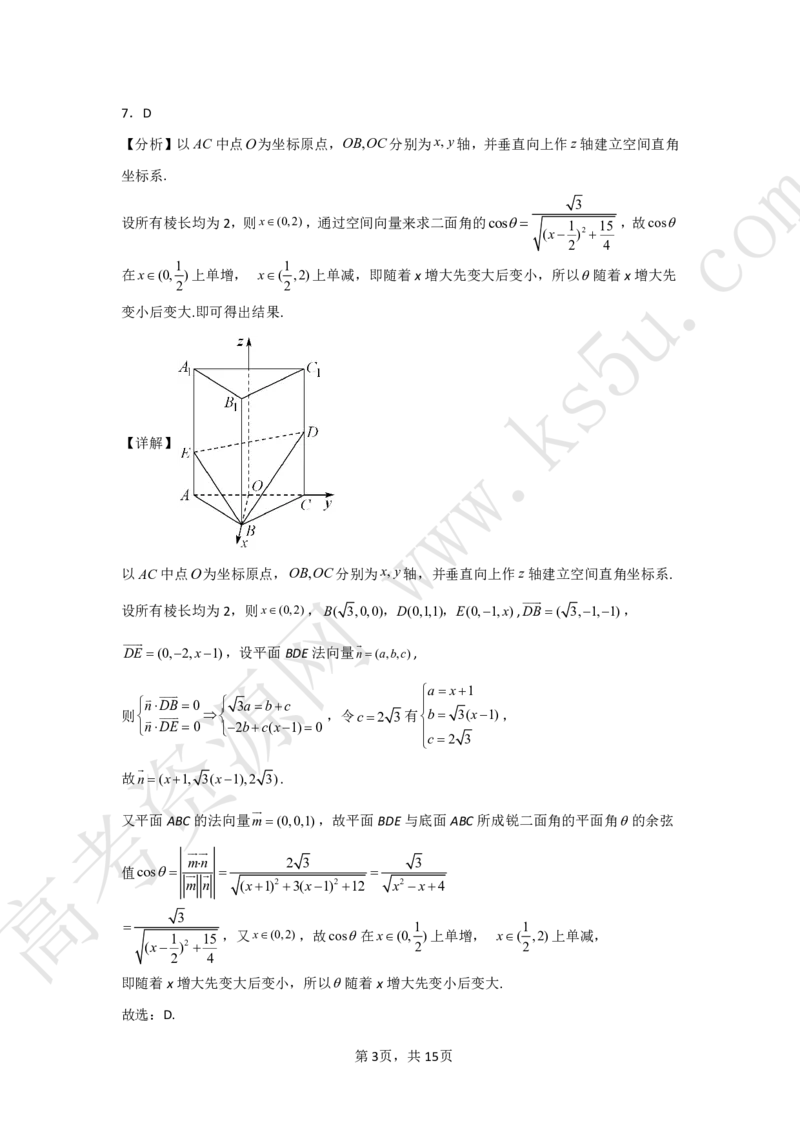
第2页，共15页7．D
【分析】以AC中点O为坐标原点，OB,OC分别为x,y轴，并垂直向上作z轴建立空间直角
m
坐标系.
o
3
c
设所有棱长均为2，则x(0,2)，通过空间向量来求二面角的cos
1 15
，故cos
(x )2
2 4
.
1 1
在x(0, )上单增， x( ,2)上单减，即随着x增大先变大后变小，所以随着x增大先
2 2 u
变小后变大.即可得出结果.
5
s
k
.
【详解】
w
w
w
以AC中点O为坐标原点，OB,OC分别为x,y轴，并垂直向上作z轴建立空间直角坐标系.
网

设所有棱长均为2，则x(0,2)，B( 3,0,0)，D(0,1,1)，E(0,1,x),DB( 3,1,1)，
 
DE (0,2,x1)，设平面BDE法向量n(a,b,c),
源
 
ax1
nDB0  3abc 
则   ，令c2 3有b 3(x1)，
资nDE 0 2bc(x1)0 
c2 3

故n(x1, 3(x1),2 3).
考

又平面ABC的法向量m(0,0,1)，故平面BDE与底面ABC所成锐二面角的平面角的余弦

高 mn 2 3 3
值cos    
m n (x1)23(x1)212 x2x4
3
 1 1
1 15
，又x(0,2)，故cos在x(0, )上单增， x( ,2)上单减，
(x )2  2 2
2 4
即随着x增大先变大后变小，所以随着x增大先变小后变大.
故选：D.
第3页，共15页m
o
c
.
u
8．B
5
【分析】连接AF ，BF ，设|BP|x则|FA||AB|2x，由题意可知|AF |2a2x，
2 2 1 2
s
6
|BF |4x2a，即|PF |2(4x2a)2x2 (2a2x)2(3x)2 (2c)2(5x)2，即x a， 则
2 2 k 5
53
a2 c2，求解离心率即可. .
5
w
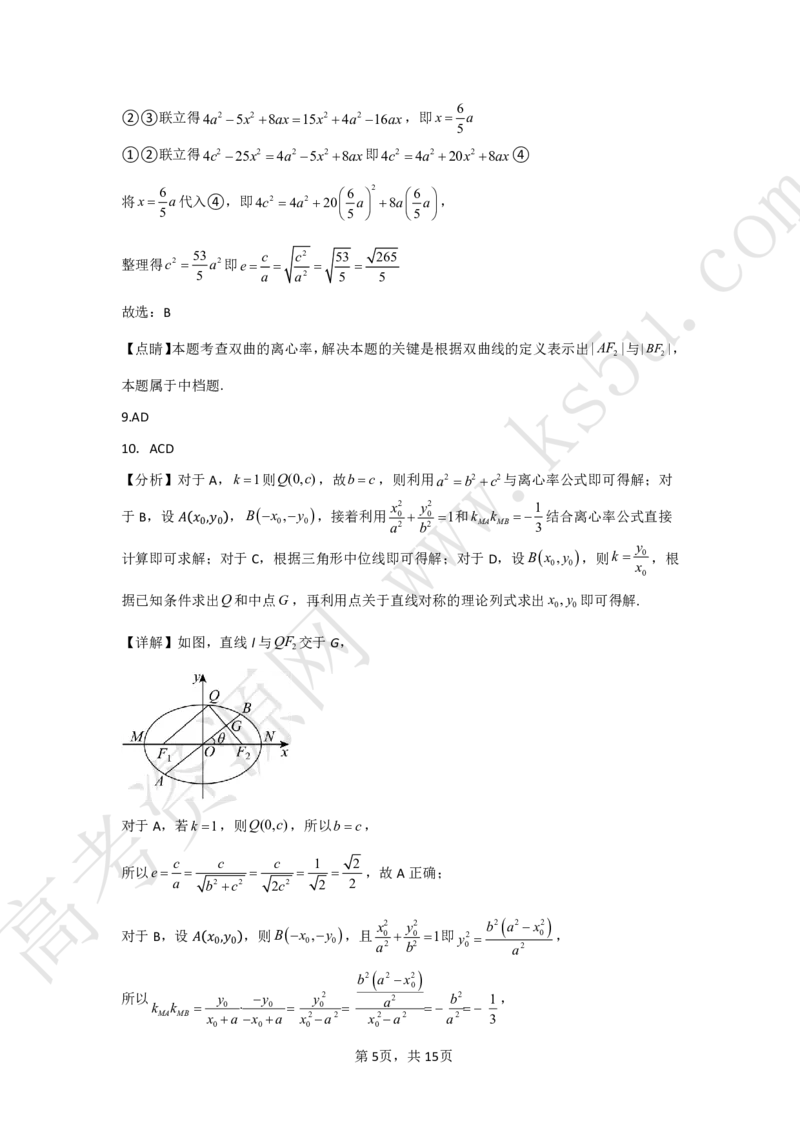
【详解】连接AF ，BF ，设|BP|x则|FA||AB|2x，即|PF |5x，|PA|3x，
2 2 1 1
w
w
网
源
根据双曲线定义可知，
资
|BF ||BF |2a即|BF ||BF |2a4x2a
1 2 2 1
|AF ||FA|2a即|AF |2a|FA|2a2x
考2 1 2 1
直线l与圆(xc)2y2 r2相切于点P
高
PF  PF
2 1
在RtFPF 中|PF |2|FF |2 |PF |2(2c)2(5x)2 4c225x2①
1 2 2 1 2 1
在RtAPF 中|PF |2|AF |2 |PA|2(2a2x)2(3x)2 4a25x28ax②
2 2 2
在RtBPF 中|PF |2|BF |2 |PB|2(4x2a)2(x)2 15x24a216ax③
2 2 2
第4页，共15页6
②③联立得4a25x28ax15x24a216ax，即x a
5
m
①②联立得4c225x2 4a25x28ax即4c2 4a220x28ax④
o
6 6  2 6 
将x a代入④，即4c2 4a220 a 8a a ，
5 5  5  c
.
53 c c2 53 265
整理得c2  a2即e   
5 a a2 5 5
u
故选：B
5
【点睛】本题考查双曲的离心率，解决本题的关键是根据双曲线的定义表示出|AF |与|BF |，
s2 2
本题属于中档题. k
9.AD
.
10．ACD
w
【分析】对于A，k 1则Q(0,c)，故bc，则利用a2 b2c2与离心率公式即可得解；对
w
于B，设 ，Bx ,y ，接着利用 x 0 2  y 0 2 1和k k  1 结合离心率公式直接
0 0 w a2 b2 MA MB 3
  y
计算即可求解；对于C，根据三角 形中位线即可得解；对于D，设Bx ,y ，则k  0 ，根
0 0 x
0
网
据已知条件求出Q和中点G，再利用点关于直线对称的理论列式求出x ,y 即可得解.
0 0
【详解】如图，直线l与QF 交于G，
2
源
资
考
对于A，若k 1，则Q(0,c)，所以bc，
高 c c c 1 2
所以e     ，故A正确；
a b2c2 2c2 2 2
对于B，设 ，则Bx 0 ,y 0 ，且 a x 0 2 2  b y 0 2 2 1即 y 0 2  b2 a a 2 2 x 0 2 ，
 
b2 a2 x2
0
所以 y y y2 a2 b2 1，
k k  0 · 0  0   
MA MB x a x a x2a2 x2a2 a2 3
0 0 0 0
第5页，共15页b2 a2 c2 c2 1 6
所以  1 1 e2  e ，故B错误；
a2 a2 a2 3 3
m
对于C，由题意可知OG是中位线，故l//FQ，故C正确；
1
o
y
对于D，设点Bx ,y ，则直线l:y 0 x，
0 0 x
0 c
cx y 
因为直线BQ平行于x轴，所以点Qx ,y ,FQ的中点G 0 , 0 ，
0 0 2  2 2  .
y y cx u
0  0· 0

 2 x 2
所以由点G在直线l上且k k 1得 0 ， 5
F2G l  y 0 · y 0 1
 x
0
c x
0 s
解得x  1 c，y2  3c 即y  3 c， k
0 2 0 4 0 2
.
3
 c
因此k  y 0  2  3，故D正确. w
x 1
0 c
2
w
故选：ACD．
w
【点睛】方法点睛：点关于直线对称的点的计算求解步骤：
（1）设所求点坐标，
网
（2）利用中点坐标公式求出中点坐标，
（3）利用中点坐标在直线上和两点所在直线与已知直线垂直则斜率乘积为1这两个条件建
源
立关于所求点坐标的方程组，利用该方程组即可求解.
（4）遇特殊直线如xm或yn一般直接得解.
资11．BCD
【分析】
考A选项，如图建立以A为原点的空间直角坐标系，利用空间向量可判断选项；做出截面求得
截面面积可判断B；利用线线平行可得线面平行判断C，求得P的轨迹方程可求得三棱锥
PBCD的体积最大值判断D.
高
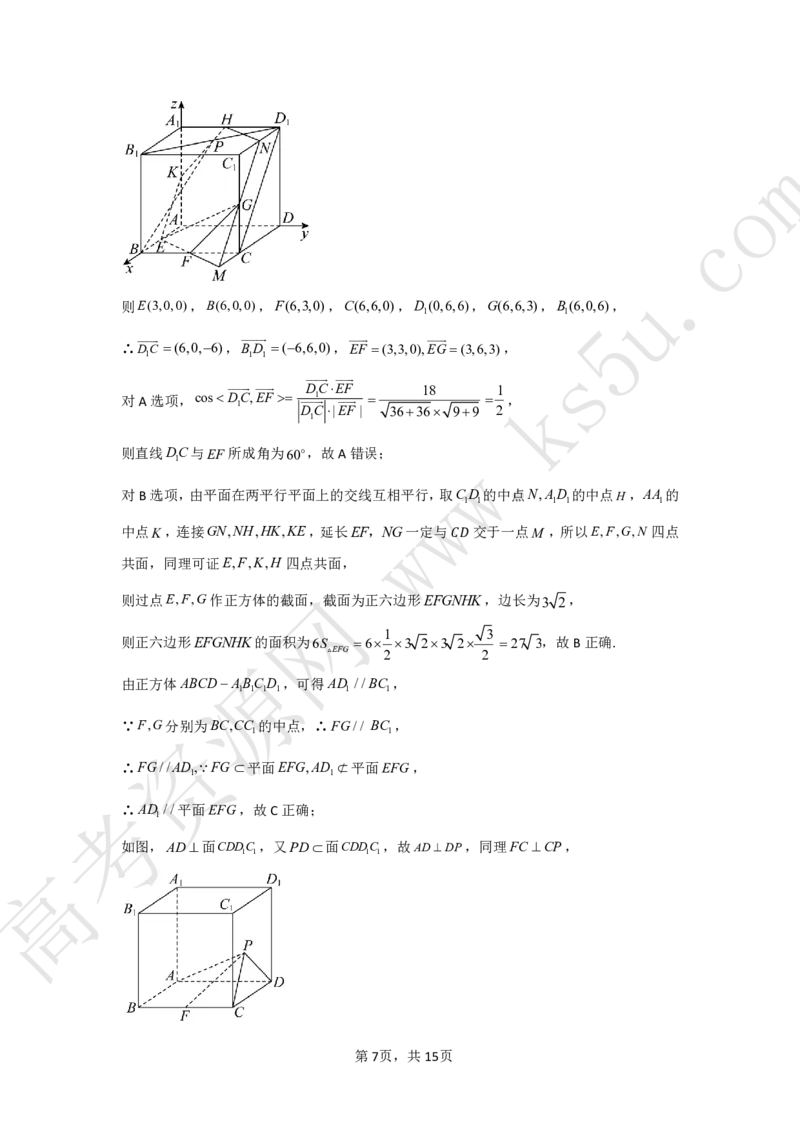
【详解】以A为坐标原点，以AB,AD,AA所在直线分别为x轴，y轴，z轴，建立如图所示
1
的空间直角坐标系，
第6页，共15页m
o
c
.
u
则E(3,0,0)，B(6,0,0)，F(6,3,0)，C(6,6,0)，D(0,6,6)，G(6,6,3)，B(6,0,6)，
1 1
5
   
∴D 1 C (6,0,6)，B 1 D 1 (6,6,0)，EF (3,3,0),EG(3,6,3)， s
 
  DCEF 18 k1
对A选项，cosD
1
C,EF  1    ，
DC |EF | 3636 99 2
1 .
则直线DC与EF所成角为60o，故A错误；
w
1
对B选项，由平面在两平行平面上的交线互相w平行，取CD的中点N,AD 的中点H，AA 的
1 1 1 1 1
w
中点K，连接GN,NH,HK,KE，延长EF，NG一定与 交于一点M ，所以E,F,G,N 四点
共面，同理可证E,F,K,H 四点共 面， 
网
则过点E,F,G作正方体的截面，截面为正六边形EFGNHK，边长为3 2，
1 3
则正六边形EFGNHK的面积为6S 6 3 23 2  27 3，故B正确.
EFG 2 2
源
由正方体ABCDABCD ，可得AD //BC ，
1 1 1 1 1 1
资
∵F,G分别为BC,CC
1
的中点，∴FG// BC
1
，
∴FG//AD,FG 平面EFG,AD  平面EFG，
1 1
考
∴AD //平面EFG，故C正确；
1
如图，AD面CDDC ，又PD面CDDC ，故ADDP，同理FC CP，
1 1 1 1
高
第7页，共15页AD 6 FC 3
tanAPD  ,tanFPC   ,
DP DP CP CP
6 3 DP m
又APDFPC,  , 2，
DP CP CP
o
根据题意可得D(0,6,0),C(6,6,0)，设P(x,6,z)，
c
DP DP2
又 2, 4，
CP CP2
.
x2z2
∴ 4，整理得(x8)2z2 16，
(x6)2 z2 u
∴在正方形CDDC 面内(包括边界)，P是以Q(8,6,0)为圆心，半径r4的圆上的点，
1 1 5
s
k
.
w
令x6，可得| y|2 3，
w
∴当P为圆Q与线段CC 的交点时，P到底面ABCD的距离最大，最大距离为2 3，
1 w
1 1 1
∴三棱锥PBCD的体积最大值是 S 2 3  662 312 3，故D正确.
3 BCD 3 2
故选:BCD. 网
【点睛】关键点点睛：本题解题关键是建立空间直角坐标系，用向量的方法研究点线面的位
置关系及数
源
量计算.
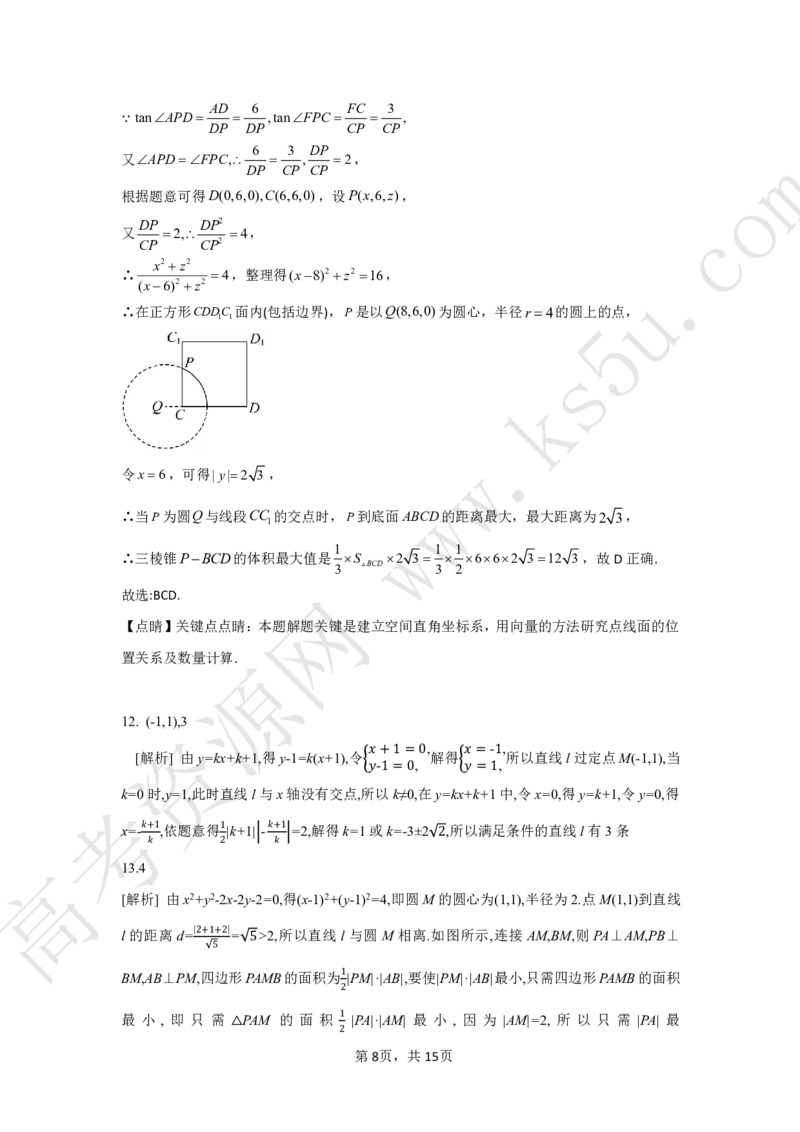
12. (-1,1),3
资
, - ,
[解析] 由y=kx+k+1,得y-1=k(x+1),令 解得 所以直线l过定点M(-1,1),当
- , ,
+1= = 1
考k=0时,y=1,此时直线l与x轴没有交点,所以1=k≠0,在y=kx+k=+11中,令x=0,得y=k+1,令y=0,得
x=- ,依题意得 |k+1| - =2,解得k=1或k=-3±2 ,所以满足条件的直线l有3条
+1 1 +1
高 13.4  2  2
[解析] 由x2+y2-2x-2y-2=0,得(x-1)2+(y-1)2=4,即圆M的圆心为(1,1),半径为2.点M(1,1)到直线
l 的距离 d= | | = >2,所以直线 l 与圆 M 相离.如图所示,连接 AM,BM,则 PA⊥AM,PB⊥
2+1+2
5 5
BM,AB⊥PM,四边形PAMB的面积为 |PM|·|AB|,要使|PM|·|AB|最小,只需四边形PAMB的面积
1
2
最 小 , 即 只 需 PAM 的 面 积 |PA|·|AM| 最 小 , 因 为 |AM|=2, 所 以 只 需 |PA| 最
1
△ 2 第8页，共15页小.|PA|= | | -| | = | | - ,所以只需直线 2x+y+2=0 上的动点 P 到点 M 的距离最
2 2 2
小,|PM|
min
=t,此时tPM⊥l,|PtA|=41,所以此时四边形PAMB的面积为2,即|PM|·|AB|的最小值为
m
4. 5
o
c
.
u
5
s
14.
k
.
w
w
w
网
源
资
考
高
15．（1）x50或5x12y370；
（2）
2
 7 4
x  

y1
2
 .
 3 9
第9页，共15页16．
【详解】（1）因为在梯形ABCD中，AB∥CD，ADDCCB1，ABC 60，如图：
m
过C作CF∥AD交AB于G，可得AB2，
o
c
.
u
5
则AC2  AB2BC22ABBCcos60o 3，
s
所以AB2 AC2BC2，得BC  AC，
k
又平面ACFE 平面ABCD，平面ACFE平面ABCDAC，BC面ABCD，
.
所以BC 平面ACFE；
因为四边形ACFE为矩形 w
所以ACCF ， w
又平面ACFE 平面ABCD，又平面AwCFE平面ABCDAC，CF平面ACFE，
所以CF 平面ABCD，
则CA,CB,CF两两垂直，如图建立空间直角坐标系，
网
则A  3,0,0  ,B0,1,0,M   3 ,0,1  ,E  3,0,1  ,D   3 , 1 ,0  ，
   
 2   2 2 
源
所以  A  M     3 ,0,1  ,  A  B     3,1,0  ,  E  A   0,0,1,  A  D     3 , 1 ,0   ，
   
 2   2 2 
资

设平面MAB的法向量为nx,y,z ，
1 1 1
   3
考nAM  x z 0   
则 2 1 1 ，取x 2可得n 2,2 3, 3 ，
  1
nAB 3x y 0
1 1
高 设平面EAD的法向量为m  x ,y ,z ，
2 2 2
 
mEAz 0
 2   
则   3 1 ，取x 2 2可得m 2,2 3,0 ，
mAD x  y 0
 2 2 2 2
 
  n,m 412 2 19
所以cosn,m     .
n m 4123 412 19
第10页，共15页2 19
所以平面MAB与平面EAD所成夹角的余弦值为 .
19
m
o
c
.
u
5
（2）
2 57 s
d 
19
k
y y 1
17．【分析】（1）设P(x,y)(x2)，根据条件建立等式   ，化简即可求出
.2x 2x 4
结果；
w
x2
（2）设l:y kxb，联立方程 y2 1，消y得到(14k2)x28kbx4b240 ，由韦达
w
4
8kb 4b2 4 1
定理得x x  ,xx  ，w利用条件k k  ，即可得到b2k或bk，
1 2 14k2 1 2 14k2 AM AN 12
即可证明结果；
网y y 1 x2
【详解】（1）设P(x,y)(x2)，由题有   ，化简得到 y2 1，
2x 2x 4 4
x2
所以曲线C的轨迹方程为 y2 1(y0).
4
源
1
（2）因为直线AM 和AN的斜率之积为 ，所以直线l的斜率存在，设l:y kxb，M(x,y)，
12 1 1
N(x ,y )，
资2 2
x2
由   4 y2 1 ，消y得到  14k2 x2 8kbx4b2 40   k  1 ，
  2
ykxb
考
8kb 4b2 4
则64k2b24(4b24)(14k2)0 ，x x  ,xx  ，
1 2 14k2 1 2 14k2
高 y y (kx b)(kx b) k2(4b24)8k2b2b24b2k2 1
k k  1  2  1 2   ，
AM AN x 2 x 2 xx 2(x x )4 4b2416kb416k2 12
1 2 1 2 1 2
化简整理得到2k2kbb2 0，得到b2k或bk，
当b2k时，ykx2k k(x2)，直线过定点(2,0)与A重合，不合题意，
当bk，ykxk k(x1)，直线过定点(1,0)，所以直线l过定点.
第11页，共15页18．【解析】（1）在图1中取CE中点F ，连接BF，AE，
 
CE2ED，CD3，AB2，CF 1，EF 1，
m
DF AB2，DF//AB，D90，四边形ABFD为矩形，
o
BF CD，
c
BEBC 31 2，又CE2，△BCE为等边三角形；
.
又AE 312，ABE为等边三角形； u
5
在图2中，取BE中点G，连接AG,CG，
1
s
k
CBE,ABE为等边三角形，CGBE，AGBE，
1 1
.
CG AG 3，又AC  6，AG2CG2  AC2，
1 1 1 1
w
CG AG，
1 w
又AGBEG，AG,BE平面ABEDw，CG平面ABED，
1
CG平面BCE，平面BCE平面ABED．
1 1 1
网
  
（2）以G为坐标原点，GA,GB,GC 正方向为x,y,z轴，可建立如图所示空间直角坐标系，
1
则B0,1,0，E0,1,0，A  3,0,0  ，C  0,0, 3  ，D   3 , 3 ,0  ，
源 1   2 2  
  D  C     3 , 3 , 3   ，  E  B  0,2,0，  E  C    0,1, 3  ，
1   2 2   1
资
 
设棱DC 上存在点Px,y,z且DPDC 01满足题意，
1 1
 3 3  3 3
考 x   x  
 2 2  2 2
 3 3  3 3
即y   ，解得：y  ，即
 2 2  2 2
高 z 3 z 3
 
 
 3 3 3 3 
P  ,  , 3，
 
 2 2 2 2 
  3 3 3 1 
则EP  ,  , 3，
 
 2 2 2 2 
第12页，共15页
设平面PBE的法向量na,b,c，
m
   3 3  3 1 b0
则   EPn   2  2    a 2  2   b 3c0 ，令a2，则   1， o
   E  B  n  2b0   c 
c
  1
n2,0, ，
   .
3 3 u
 
EC 1 n  6 1
C 到平面PBE的距离为d     ，解得： 5，
1 n 1 2 2 3
4 
   s

n2,0,2， k
 .
又平面ABE的一个法向量m0,0,1，
w
 
  mn 2 2
cosm,n     ，
m  n 2 2 2 w
w 
又二面角PBEA为锐二面角，二面角PBEA的大小为 ．
4
网
x2 y2
19．(1)  1
4 3
5 3
(2)
源
8
【分析】（1）根据焦距和椭圆所过点可构造方程求得结果；
资
（2）设直线DF :xty1，与椭圆方程联立可得韦达定理的结论，结合中点坐标公式可整
1
15y
考理得到y  0 ，结合三角形面积公式和基本不等式可求得最值.
M 4x225
0
【详解】（1）椭圆C的焦距2c2，c1；
高  3 1 9
椭圆C过点1, ，  1，又a2 b2c2 b21，
 2 a2 4b2
3 x2 y2
b2  （舍）或b2 3，a2  4，椭圆C的方程为：  1.
4 4 3
（2）
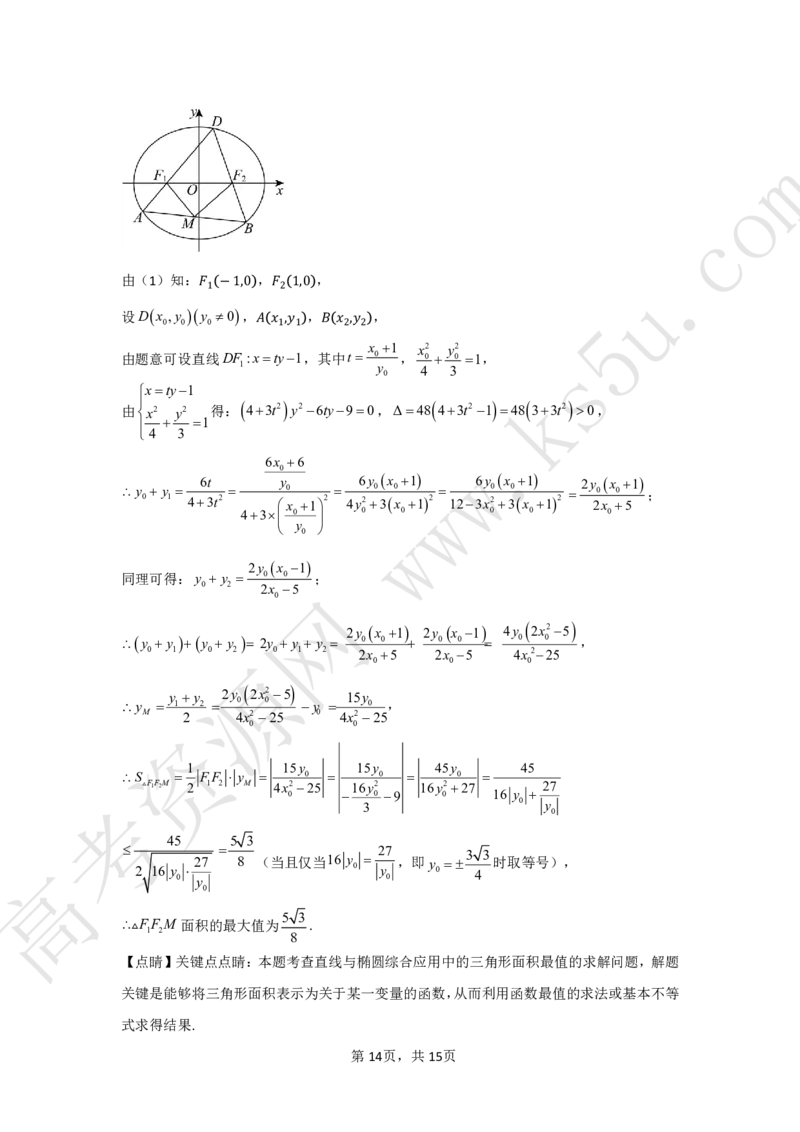
第13页，共15页m
o
c
.
由（1）知： ， ，
u
设Dx ,y  y 1  0 1 ，  2 1 ， ， 5
0 0 0
由题意可设直线DF :x    ty 1   1 1 ，其  中 2 t   2x 0 1 ， x 0 2  y 0 2 1， s
1 y 4 3
0
xty1 k
由  x2 y2 得：  43t2 y26ty90，Δ48  43t21  48  33t2 0，
  1 .
 4 3
w
6x 6
0
6t y 6y x 1 6y x 1 2y x 1
y  y   0  0 w0  0 0  0 0 ；
0 1 43t2 x 1 2 4y23x 12 123x23x 12 2x 5
43 0  0 0 0 0 0
 y  w
0
2y x 1
同理可得：y  y  0 0 ；
0 2 网2x 5
0
2y x 1 2y x 1 4y  2x25 
y  y y  y  2y  y  y  0 0  0 0  0 0 ，
0 1 0 2 0 1 2 2x 5 2x 5 4x225
源 0 0 0
y  y 2y  2x25  15y
y  1 2  0 0 y  0 ，
M 2 4x225 0 4x225
资0 0
1 15y 15y 45y 45
S  FF  y  0  0  0 
F1F2M 2 1 2 M 4x225 16y2 16y227 27
考 0  0 9 0 16 y 
3 0 y
0
45 5 3
高  2 16 y 0  2 y 7  8 （当且仅当16 y 0  2 y 7 0 ，即y 0  3 4 3 时取等号），
0
5 3
FF M 面积的最大值为 .
1 2
8
【点睛】关键点点睛：本题考查直线与椭圆综合应用中的三角形面积最值的求解问题，解题
关键是能够将三角形面积表示为关于某一变量的函数，从而利用函数最值的求法或基本不等
式求得结果.
第14页，共15页m
o
c
.
u
5
s
k
.
w
w
w
网
源
资
考
高
第15页，共15页