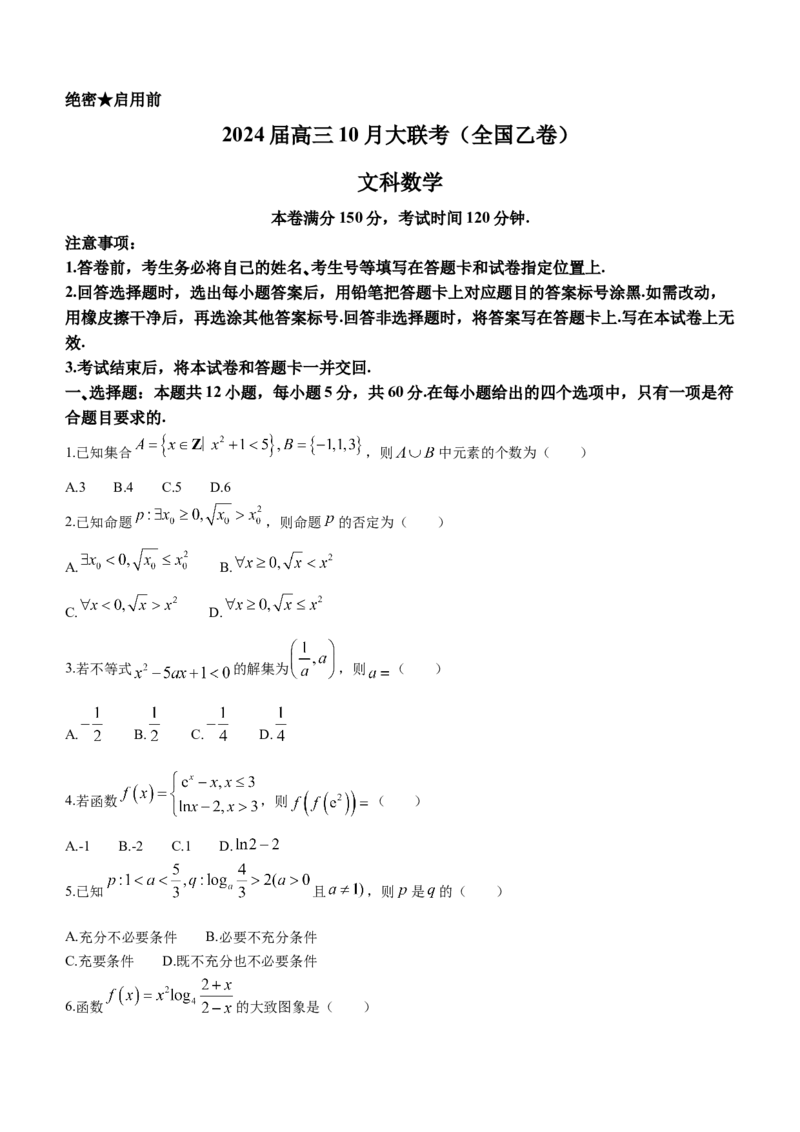文档内容
绝密★启用前
2024 届高三 10 月大联考(全国乙卷)
文科数学
本卷满分150分,考试时间120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无
效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合 ,则 中元素的个数为( )
A.3 B.4 C.5 D.6
2.已知命题 ,则命题 的否定为( )
A. B.
C. D.
3.若不等式 的解集为 ,则 ( )
A. B. C. D.
4.若函数 ,则 ( )
A.-1 B.-2 C.1 D.
5.已知 且 ,则 是 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.函数 的大致图象是( )
学科网(北京)股份有限公司A. B.
C. D.
7.白色污染是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓,经过长期研究,一种
全生物可降解塑料(简称PBAT)逐渐被应用于超市购物袋、外卖包装盒等产品.研究表明,在微生物的作用下,
PBAT最终可被完全分解为二氧化碳和水进入大自然,当其分解率( )超
过60%时,就会成为对环境无害的物质.为研究总质量为 的PBAT的已分解质量 (单位: )与时间
(单位:月)之间的关系,某研究所人员每隔1个月测量1次PBAT的已分解质量,对通过实验获取的数
据做计算处理,研究得出已分解质量 与时间 的函数关系式为 .据此研究结果可以推测,
总质量为 的PBAT被分解为对环境无害的物质的时间至少为( )(参考数据: )
A.8个月 B.9个月 C.10个月 D.11个月
8.已知 ,且 ,则
( )
A. B. C. D.
9.已知 是 所在平面内一点,若 均为
正数,则 的最小值为( )
A. B. C.1 D.
学科网(北京)股份有限公司10.若函数 的部分图象如图所示,则下列说法正确的个数为(
)
① ;② ;③ 在 上单调递减;④ .
A.1 B.2 C.3 D.4
11.已知函数 是偶函数,当 时, ,则不等式 的解集是(
)
A. B.
C. D.
12.已知函数 ,则 的大小关系为( )
A. .
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分.
学科网(北京)股份有限公司13.已知向量 ,若 ,则实数 __________.
14.请写出一个满足对任意的 ;都有 的函数__________.
15.《海岛算经》是魏晋时期数学家刘徽所著的测量学著作,书中有一道测量山上松树高度的题目,受此题启
发,小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度.如图,把塔底与塔顶分别看作
点C,D,CD与地面垂直,小李先在地面上选取点A,B(点 在建筑物的同一侧,且点 位于
同一个平面内),测得 ,在点 处测得点 的仰角分别为 ,在点 处测得点 的
仰角为 ,则塔高 为__________ .(参考数据: )
16.已知函数 在定义域上单调递增,则实数 的取值范围为__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知向量 ,函数 ,将函数 的图象向右平移 个单位
长度,得到函数 的图象.
(1)求函数 的最小正周期和单调递增区间;
(2)解方程 .
18.(12分)
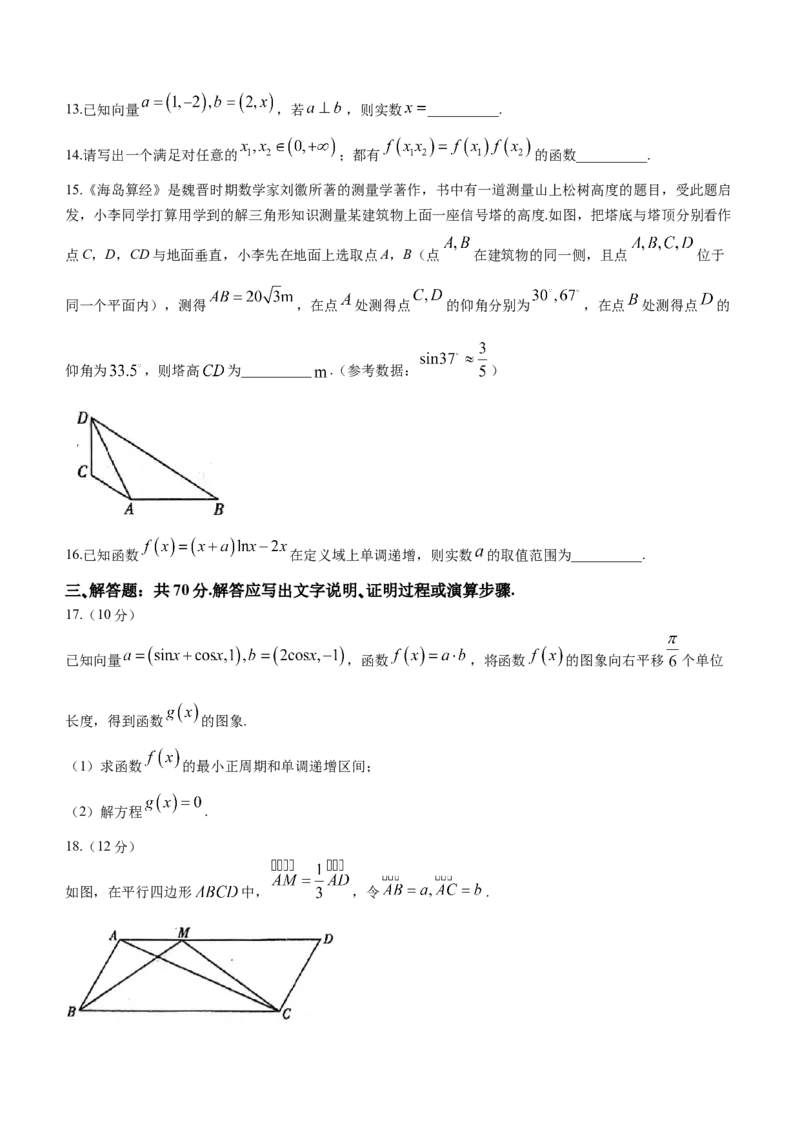
如图,在平行四边形 中, ,令 .
学科网(北京)股份有限公司(1)用 表示 ;
(2)若 ,且 ,求 .
19.(12分)
某公园池塘里浮萍的面积 (单位: )与时间 (单位:月)的关系如下表所示:
时间 月 1 2 3 4
浮萍的面积 3 5 9 17
现有以下三种函数模型可供选择:① ,② ,③ ,其中
均为常数, 且 .
(1)直接选出你认为最符合题意的函数模型,并求出 关于 的函数解析式;
(2)若该公园池塘里浮萍的面积蔓延到 所经过的时间分别为 ,写出一种
满足的等量关系式,并说明理由.
20.(12分)
在 中,内角 所对的边分别为 ,且__________.
在① ;② 两个条件中任选一个,填入上面横线处,并解决下列
问题.
(1)求 ;
(2)若 外接圆的半径为 的面积为 ,求 的周长.
注:若选择不同的条件分别解答,则按第一个解答计分.
21.(12分)
已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若 有两个不等的实根,求实数 的取值范围.
22.(12分)
已知函数 .
学科网(北京)股份有限公司(1)讨论函数 的单调性;
(2)当 时,令 ,若 为 的极大值点,证明: .
2024 届高三 10 月大联考(全国乙卷)
文科数学•全解全析及评分标准
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
B D A C B D C A B C D B
1.B 【解析】因为 ,所以
,有4个元素,故选B.
2.D 【解析】根据特称命题的否定为全称命题,知命题“ ”的否定是“
”,故选D.
3.A 【解析】因为不等式 的解集为 ,所以 ,解得 .又 ,所
以 或 ,所以 ( 不满足题意,舍去),当 时, ,故选A.
4.C 【解析】因为 ,所以 ,所以 ,故选C.
5.B 【解析】对于 ,若 ,则 .当 时, ,无解.当 时,
,得 ,即不等式 的解集为 .因为 ⫋ ,所以 是 的
必要不充分条件,故选B.
6.D 【解析】方法一:由题意,知函数 的定义域为 ,关于原点对称,且
,所以函数 是奇函数,其图象关于原点对称,故排除 ;当
学科网(北京)股份有限公司时, ,即 ,因此 ,故排除A.故选D.
方法二:由方法一,知函数 是奇函数,其图象关于原点对称,故排除 ;
又 ,所以排除A.故选D.
7.C 【解析】令 ,得 ,解得 ,故至少需要10个月,总
质量为 的PBAT才会被分解为对环境无害的物质.故选C.
8.A 【解析】因为 ,所以 ,
所以 .因为 ,所以 ,所以 ,所以
.
又 ,所以 ,所以 .故选A.
9.B 【解析】因为 ,所以点 是 的重心,所以
.
因为 ,所以 ,所以 .
因为 ,所以 三点共线,所以 ,即 .
因为 均为正数,所以 ,所以 ,所以 (当且仅当 ,即
时取等号),所以 的最小值为 .故选B.
学科网(北京)股份有限公司10.C 【解析】由题图,得 ,最小正周期 .又 ,所以 ,故①
正确;
,又 的图象过点 ,所以 ,所以
.又 ,所以 ,故②错误;
,令 ,当 时, ,函数 在 上
单调递减,故③正确;
,故④正确.故选C.
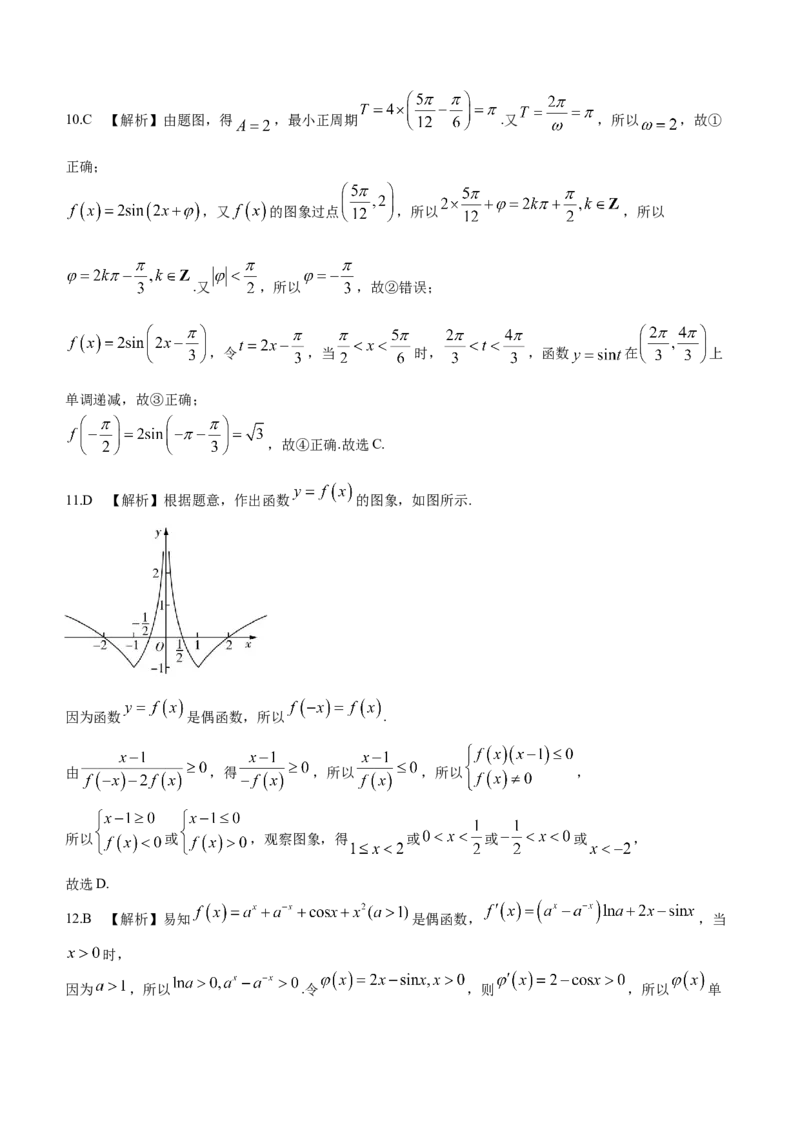
11.D 【解析】根据题意,作出函数 的图象,如图所示.
因为函数 是偶函数,所以 .
由 ,得 ,所以 ,所以 ,
所以 或 ,观察图象,得 或 或 或 ,
故选D.
12.B 【解析】易知 是偶函数, ,当
时,
因为 ,所以 .令 ,则 ,所以 单
学科网(北京)股份有限公司调递增,所以 ,所以 在 上单调递增.构造函数 ,则
.令 ,得 ,令 ,得 ,所以 在区间 上单调递增,
在区间 上单调递减.又 ,所以 ,所以 ,所以
,所以 ,即 .故选 .
二、填空题:本题共4小题,每小题5分,共20分.
13.1 【解析】因为 ,所以 ,解得 .故填1.
14. (答案不唯一) 【解析】任意定义域为 的幂函数均可,例如 ,
,即 成立.故可填
.
15.24 【解析】如图,延长 与 的延长线交于点 ,则 ,
所以 ,
所以 .在 中, ,由正弦定理,得
.故填24.
16. 【解析】 的定义域为 ,由 在定义域上
学科网(北京)股份有限公司单调递增,得 在 上恒成立,即 在 上恒成立.设
,所以只需 ,当 时, ,当 时,
,所以 在 上单调递增,在 上单调递减,所以 ,所以 ,
所以实数 的取值范围为 .故填 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
【解析】(1)由已知,得
所以函数 的最小正周期 .
由 ,解得 ,
所以函数 的单调递增区间为 .
(2)将函数 的图象向右平移 个单位长度,得到函数
的图象.
令 ,得 ,解得 ,
所以方程 的解集为 .
18.(12分)
学科网(北京)股份有限公司【解析】(1)因为 ,所以 ,
所以
所以 ,
所以 .
(2)方法一:由(1)知 .
又 ,
所以 ,
即 ,
解得 ,
所以 .
方法二:因为 ,所以 ,所以 .
因为 ,且 ,
所以 ,
解得 ,
所以 .
又 ,
学科网(北京)股份有限公司所以 .
19.(12分)
【解析】(1)应选择函数模型② .
依题意,得
解得
所以 关于 的函数解析式为 .
(2) .
理由:依题意,得 ,
所以 ,
所以
所以 ,
所以 .
20.(12分)
【解析】(1)若选①:由 及正弦定理,得 .
,
.
又 ,
学科网(北京)股份有限公司.
若选②:由 ,得 .
由正弦定理,得 .
由余弦定理,得 .
因为 ,所以 .
(2)设 外接圆的半径为 ,由正弦定理,得 .
又 ,所以 .
由 ,
可得 ,解得 ,
所以 的周长为 .
21.(12分)
【解析】(1)当 时, ,
所以曲线 在 处的切线方程为 ,即 .
(2)显然 ,要使方程 有两个不等的实根,
只需当 时, 有且仅有一个实根,
当 时,由方程 ,得 .
学科网(北京)股份有限公司令 ,则直线 与 的图象有且仅有一个交点.
.
又当 时, 单调递减,
当 时, 单调递减,
当 时, 单调递增,
所以当 时, 取得极小值 ,
又当 时, ,所以 ,即 ,
当 时, ,即 ,
所以作出 的大致图象如图所示.
由图象,知要使直线 与 的图象有且仅有一个交点,只需 或 .
综上,若 有两个不等的实根,则 的取值范围为 .
22.(12分)
【解析】(1)函数 的定义域为 ,
①当 时, ,函数 在 上单调递增;
②当 时,由 ,得 ,由 ,得 ,
学科网(北京)股份有限公司所以,函数 在 上单调递增,在 上单调递减.
综上,当 时,函数 在 上单调递增;当 时,函数 在 上单调递增,在
上单调递减.
(2)当 时, ,
设 ,则 ,当 时, ,所以 在 上单调递增,
又 ,所以存在 ,使得 ,
所以当 时, ,当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,在 上单调递增,
所以当 时, 取得极大值,且 ,所以 ,
.
因为 ,所以 .
学科网(北京)股份有限公司