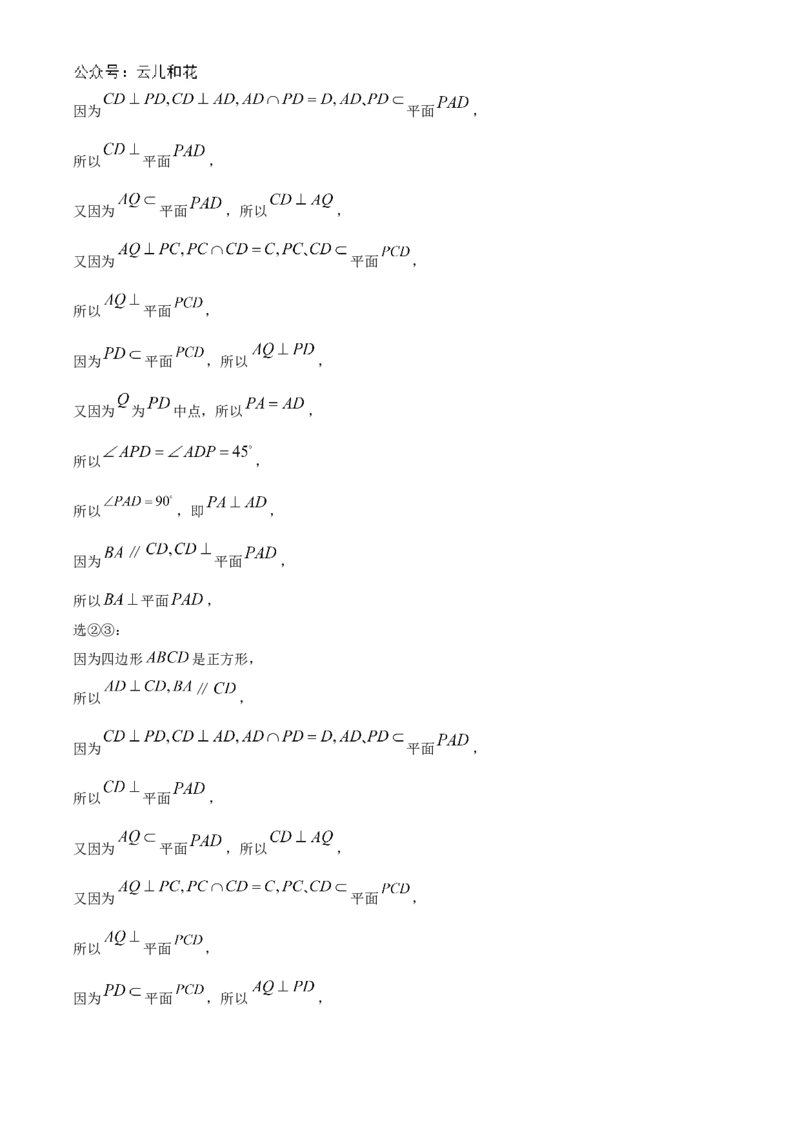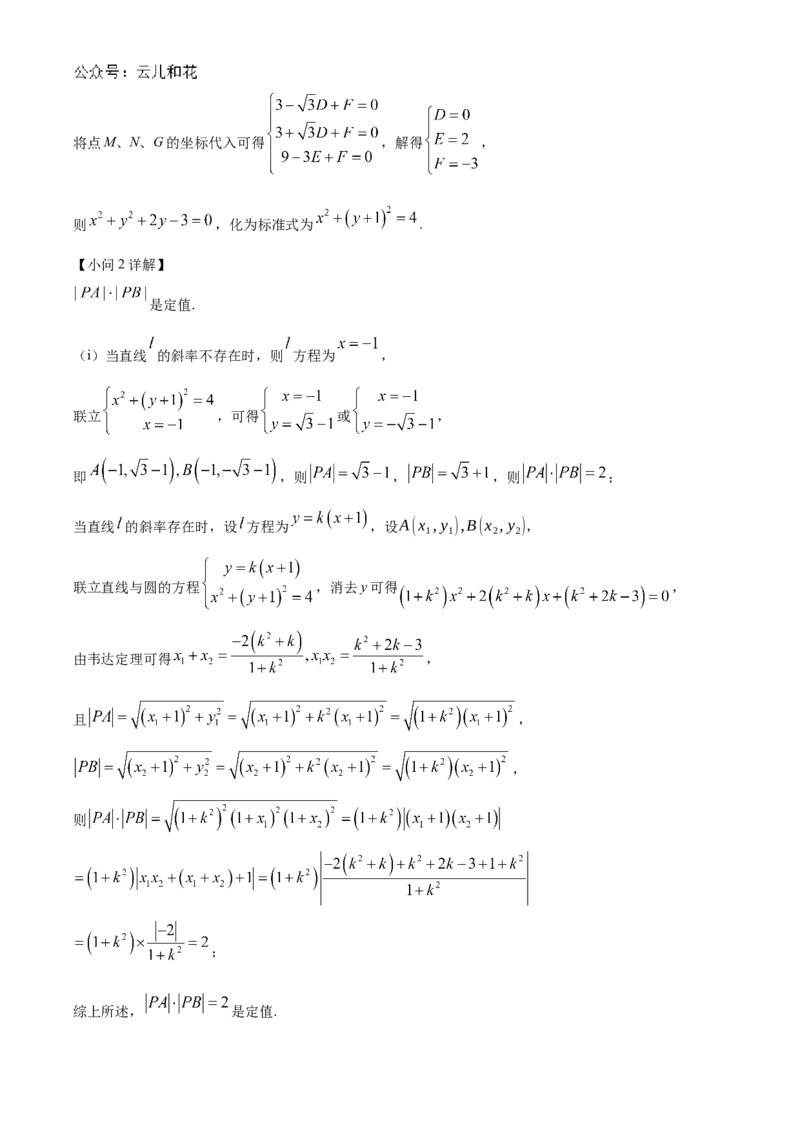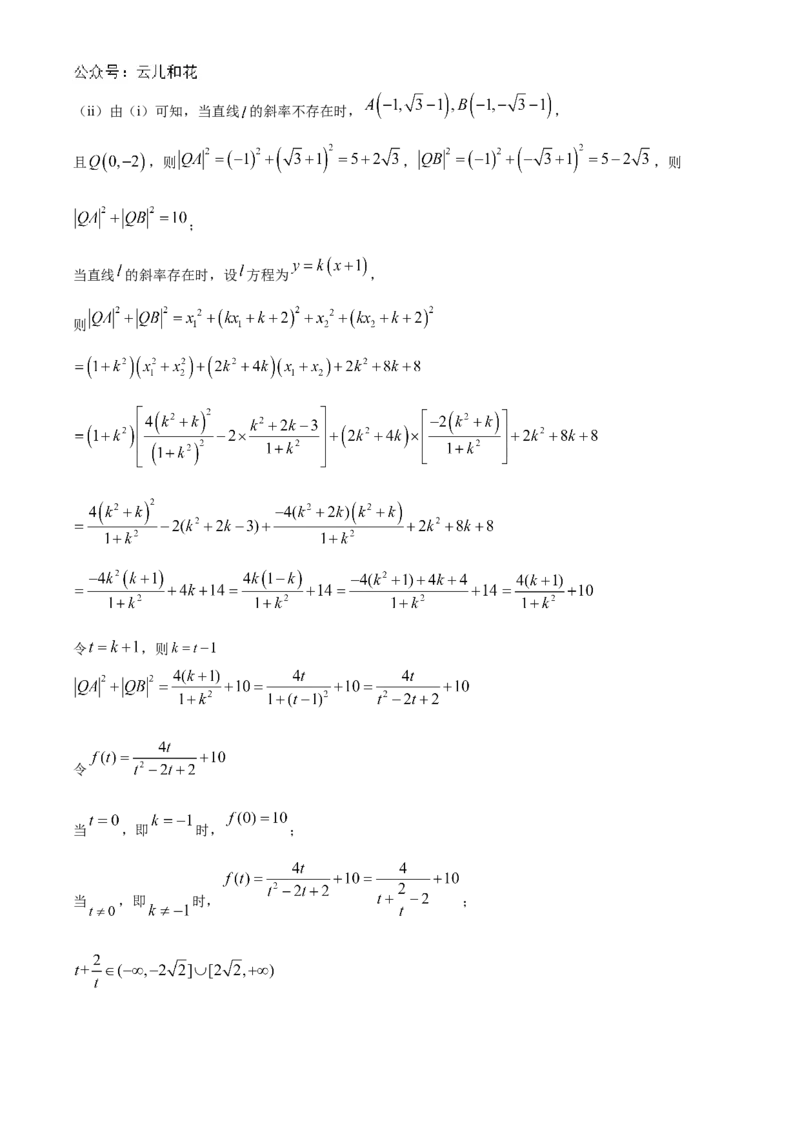文档内容
2024—2025 学年度第一学期高二年级数学期中练习
一、选择题,共10小题,每小题4分,共40分.
1. 直线 的倾斜角为( )
A. B. C. D.
【答案】B
【解析】
【分析】先由直线的一般式得到其斜率,再利用直线斜率与倾斜角的关系即可得解.
【详解】因为直线 可化为 ,
则其斜率为 ,设其倾斜角为 ,
则 ,所以 .
故选:B.
2. 正方体 的棱长为a,则棱 到面 的距离为( )
A. B. a C. D.
【答案】C
【解析】
【分析】连接 ,它们交于点 ,证明 平面 ,得 的长即为棱 到面
的距离,
【详解】如图,连接 ,它们交于点 ,正方形中 ,
又 平面 , 平面 ,所以 ,
平面 ,所以 平面 ,所以 的长即为棱 到面 的距离,而 ,
所以所求距离为 .
故选:C.
3. 如图所示,在平行六面体ABCD﹣ABC D 中, ( )
1 1 1 1
A. B. C. D.
【答案】B
【解析】
【分析】通过所给平行六面体 ,并结合相等向量、向量的加减运算,即可求解.
【详解】由题中所给平行六面体 可知, , ,
故 .
故选:B4. 已知直线 ,若 ,则 ( )
A. 或 B. C. 或 D.
【答案】B
【解析】
【
分析】由条件结合直线平行结论列方程求 ,并对所得结果进行检验.
【详解】因为 , ,
所以 ,所以 ,解得 或 ,
当 时, , ,直线 重合,不满足要求,
当 时, , ,直线 平行,满足要求,
故选:B.
5. 已知 为两条不同的直线, 为两个不同的平面,则下列结论正确的是( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
D. 若 ,则
【答案】D
【解析】
【分析】根据空间里面直线与平面、平面与平面位置关系的相关定理逐项判断即可.
【详解】A,若 ,则 或异面,故该选项错误;
B,若 ,则 或相交,故该选项错误;
C,若 ,则α,β不一定垂直,故该选项错误;D,若 ,则利用面面垂直的性质可得 ,故该选项正确.
故选:D.
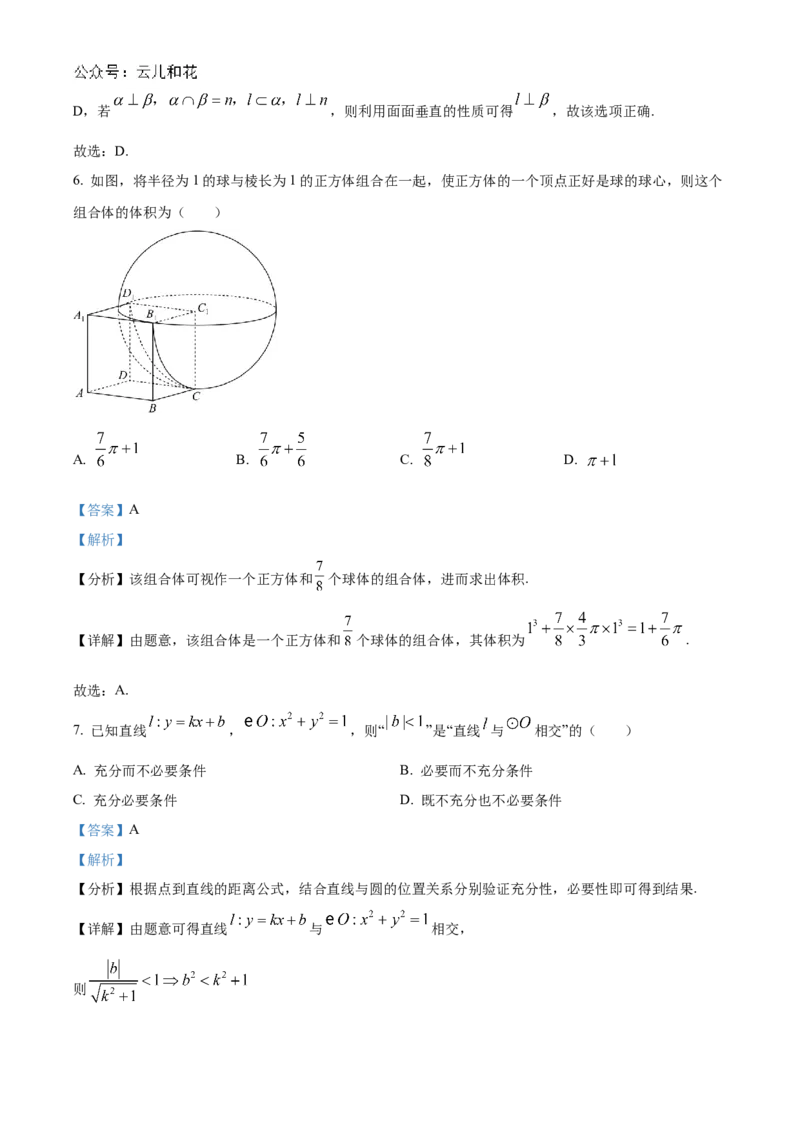
6. 如图,将半径为1的球与棱长为1的正方体组合在一起,使正方体的一个顶点正好是球的球心,则这个
组合体的体积为( )
A. B. C. D.
【答案】A
【解析】
【分析】该组合体可视作一个正方体和 个球体的组合体,进而求出体积.
【详解】由题意,该组合体是一个正方体和 个球体的组合体,其体积为 .
故选:A.
7. 已知直线 , ,则“ ”是“直线 与 相交”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】根据点到直线的距离公式,结合直线与圆的位置关系分别验证充分性,必要性即可得到结果.
【详解】由题意可得直线 与 相交,
则当 时,满足 ,即“ ”是“直线 与 相交”的充分条件;
当直线 与 相交时,不一定有 ,比如 也满足,所以“
”是“直线 与 相交”的充分不必要条件.
故选:A.
8. 已知直线 : 和点 , ,若l与线段 相交,则实数a的取值范围是(
)
A. B. 或 C. D. 或
【答案】D
【解析】
【分析】结合已知条件作图并求出直线 的定点 ,然后分别求出直线 和直线 的斜率,结合图像
求解即可.
【详解】由直线 : 可知直线 必过定点 ,且直线 的斜率为 ,如下图所示:
由斜率公式可知,直线 的斜率为 ,
直线 的斜率为 ,
若 与线段 相交,只需要 或 ,故实数a的取值范围是 或 .
故选:D.
9. 当曲线 与直线 有两个相异的交点时,实数 的取值范围是
A. B. C. D.
【答案】D
【解析】
【分析】根据图像计算直线过 时和相切时的斜率,计算得到答案.
【详解】如图所示:
∵曲线 ,直线 ,
∴ , , ,
圆心 ,直线过定点 ,
直线过 时,有两个交点,此时 , ,
直线与下半圆相切时, , ,
.
∴
故答案选D.【点睛】本题考查了直线的半圆的交点问题,忽略掉 的取值范围是容易犯的错误.
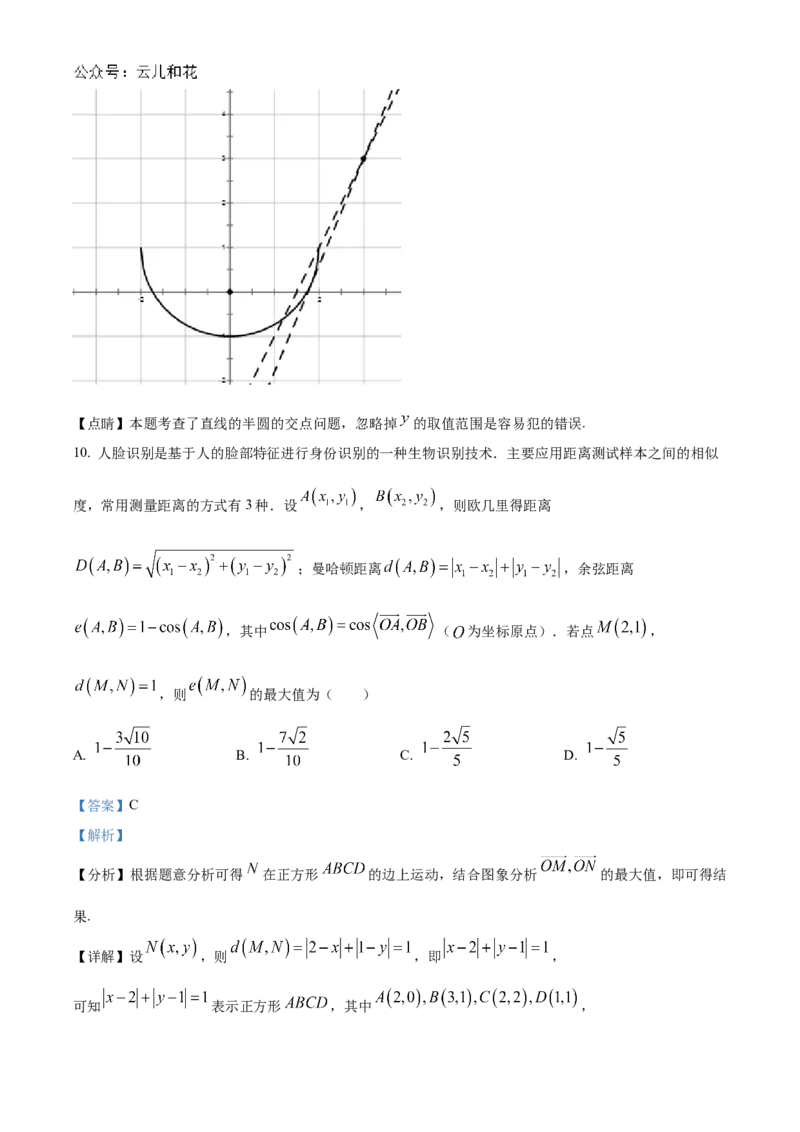
10. 人脸识别是基于人的脸部特征进行身份识别的一种生物识别技术.主要应用距离测试样本之间的相似
度,常用测量距离的方式有3种.设 , ,则欧几里得距离
;曼哈顿距离 ,余弦距离
,其中 ( 为坐标原点).若点 ,
,则 的最大值为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据题意分析可得 在正方形 的边上运动,结合图象分析 的最大值,即可得结
果.
【详解】设 ,则 ,即 ,
可知 表示正方形 ,其中 ,即点 在正方形 的边上运动,
因为 ,由图可知:
当 取到最小值,即 最大,
点 有如下两种可能:
①点 为点 ,则 ,可得 ;
②点 在线段 上运动时,此时 与 同向,不妨取 ,
则 ;
因为 ,所以 的最大值为 .
故选:C.
二、填空题,共5小题,每小题4分,共20分.
11. 两平行直线 : 与 : 之间的距离是_____.
【答案】 ##
【解析】
【分析】借助两平行线间距离公式计算即可得.
【详解】 .故答案为: .
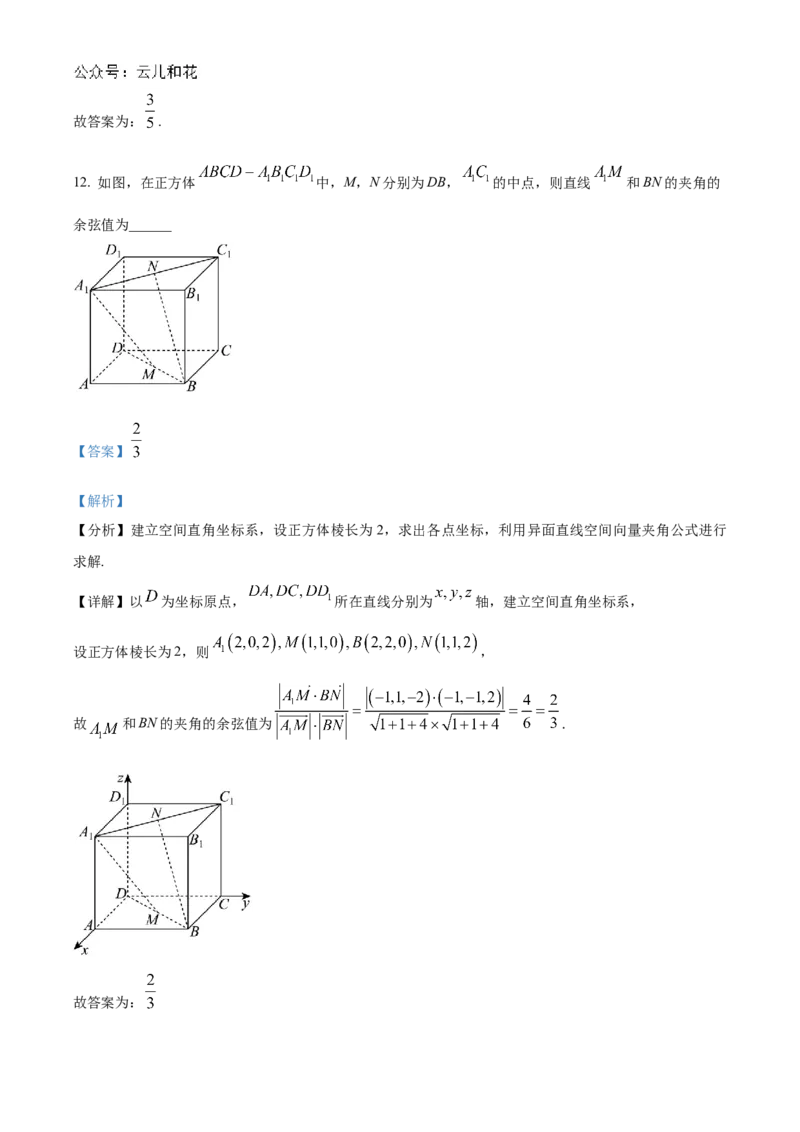
12. 如图,在正方体 中,M,N分别为DB, 的中点,则直线 和BN的夹角的
余弦值为______
【答案】
【解析】
【分析】建立空间直角坐标系,设正方体棱长为2,求出各点坐标,利用异面直线空间向量夹角公式进行
求解.
【详解】以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,
设正方体棱长为2,则 ,
故 和BN的夹角的余弦值为 .
故答案为:13. 已知圆 ,过点 作圆的切线,则切线方程为________.
【答案】
【解析】
【分析】先判断点P在圆上,再由垂直关系得出切线方程.
【详解】因为 ,所以点 在圆上,
设切线的斜率为 ,则 , .
则切线方程为 .
故答案为:
14. 已知直线 过点 且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点,当三角形
面积取最小值时直线 的斜率为_____.
【答案】 ##
【解析】
【分析】设出直线的截距式方程,由基本不等式得到三角形 面积取最小值时的直线方程,从而得到
直线的斜率.
【详解】设A(a,0), ,其中 ,设直线 的方程为 ,
因为直线 过点 ,所以 ,
由基本不等式可得 ,
所以 , ,当且仅当 ,即 , 时取等号,
的
所以 最小值为16,此时 的面积取最小值8,
直线 的斜率为 .
故答案为: .
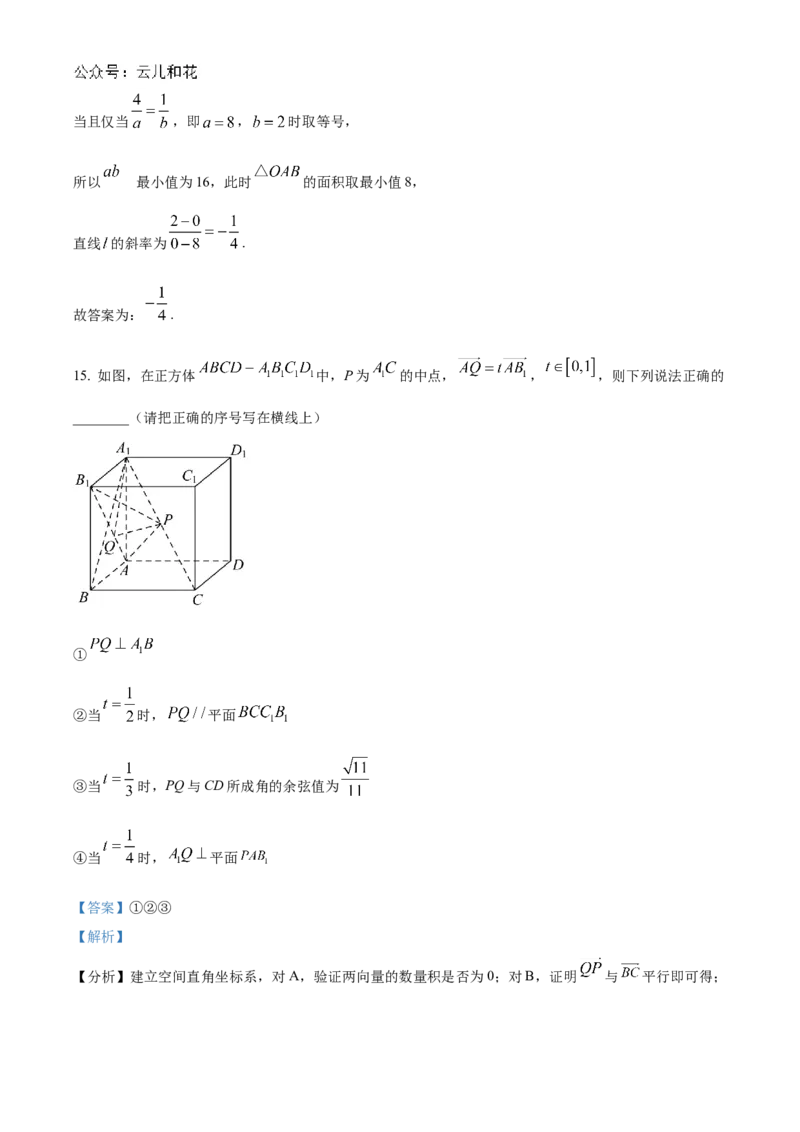
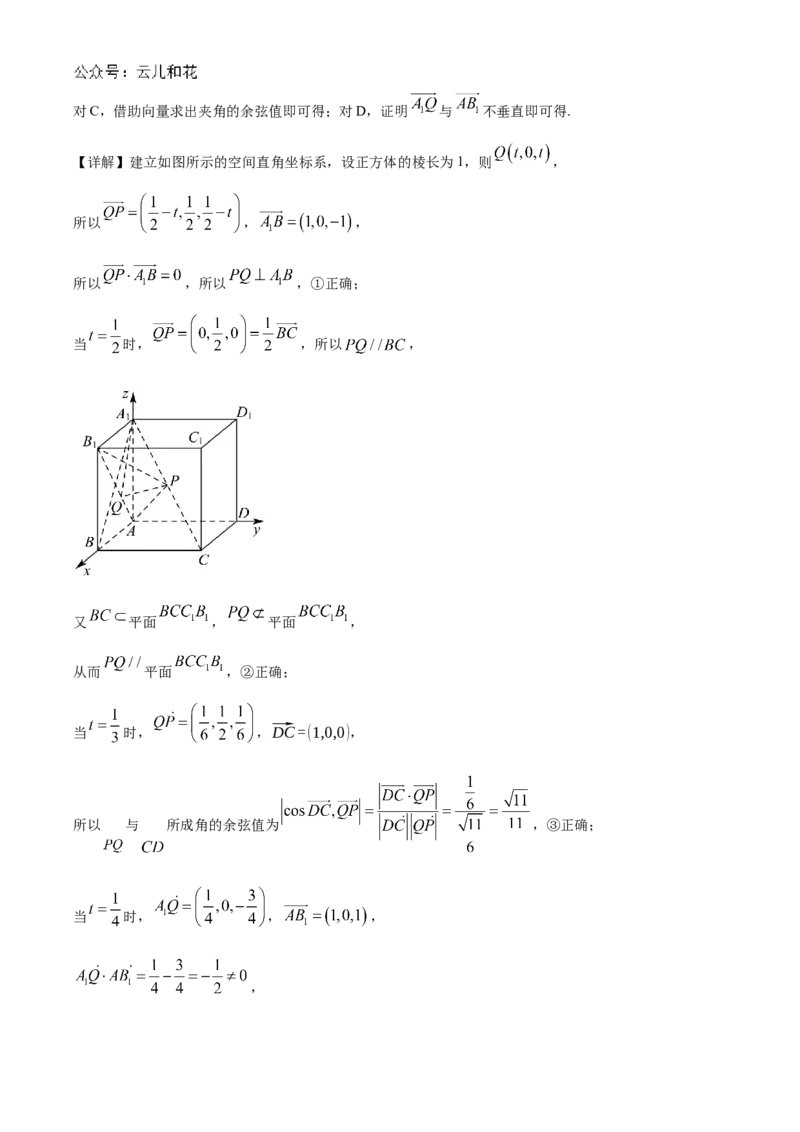
15. 如图,在正方体 中,P为 的中点, , ,则下列说法正确的
________(请把正确的序号写在横线上)
①
②当 时, 平面
③当 时,PQ与CD所成角的余弦值为
④当 时, 平面
【答案】①②③
【解析】
【分析】建立空间直角坐标系,对A,验证两向量的数量积是否为0;对B,证明 与 平行即可得;对C,借助向量求出夹角的余弦值即可得;对D,证明 与 不垂直即可得.
【详解】建立如图所示的空间直角坐标系,设正方体的棱长为1,则 ,
所以 , ,
所以 ,所以 ,①正确;
当 时, ,所以 ,
又 平面 , 平面 ,
从而 平面 ,②正确;
当 时, ,⃗DC=(1,0,0),
所以 与 所成角的余弦值为 ,③正确;
当 时, , ,
,所以 不垂直于 ,所以 不垂直于平面 ,④错误.
故答案为:①②③.
三、解答题,共4小题,每小题10分,共40分.解答应写出文字说明,演算步骤或证明过程.
16. 已知 的顶点 , , .
(1)求边 上的高 所在直线的方程;
(2)求边 上的中线 所在直线的方程;
(3)求 的面积.
【答案】(1)
(2)
(3)
【解析】
【分析】(1)利用直线垂直的性质求得高 的斜率,再利用直线的点斜式即可得解;
(2)利用中位坐标公式求得点 的坐标,再利用直线的两点式即可得解;
(3)利用直线的两点式求得直线 的方程,再利用点线距离公式与两点距离公式即可得解.
【小问1详解】
因为 , , ,
所以 ,所以 ,
则边 上的高 所在直线的方程为 ,即 ;
【小问2详解】
由题意可知 是 的中点,所以 ,
从而边 上的中线 所在直线的方程为 ,即 ;【小问3详解】
由题意知,边 所在直线的方程为 ,即 ,
所以点A到直线 的距离 ,
又 ,
所以 的面积为 .
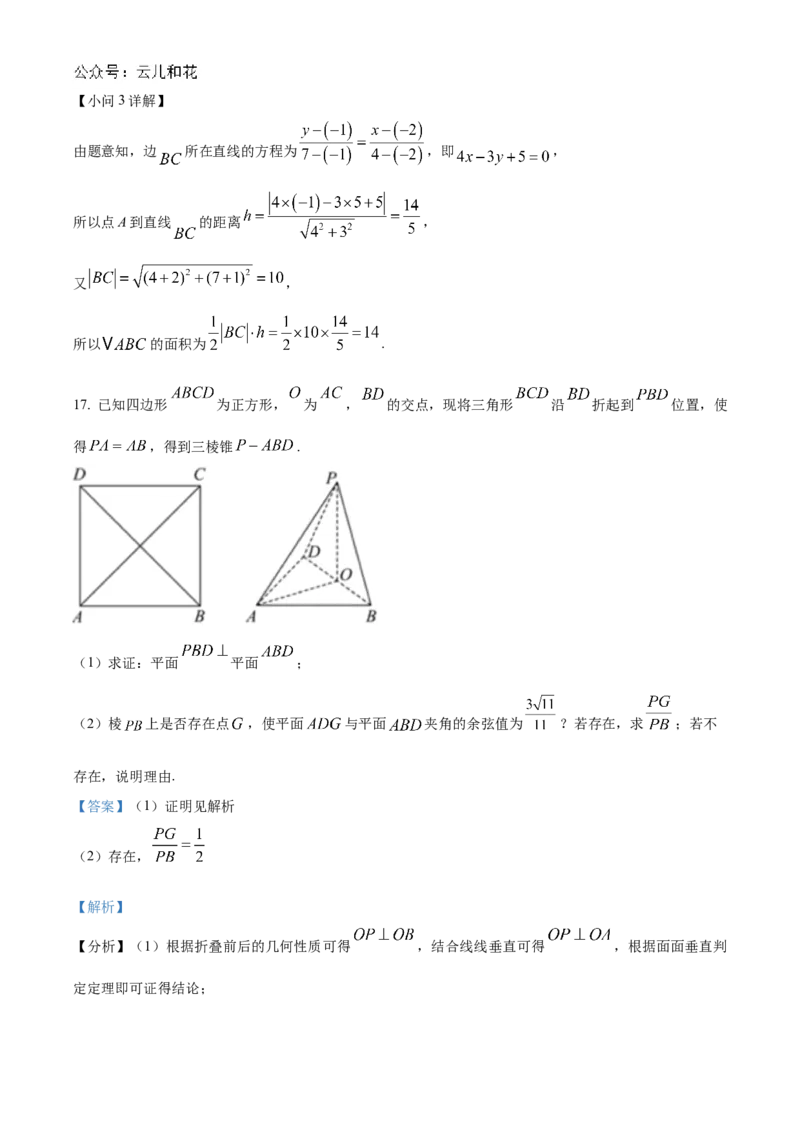
17. 已知四边形 为正方形, 为 , 的交点,现将三角形 沿 折起到 位置,使
得 ,得到三棱锥 .
(1)求证:平面 平面 ;
(2)棱 上是否存在点 ,使平面 与平面 夹角的余弦值为 ?若存在,求 ;若不
存在,说明理由.
【答案】(1)证明见解析
(2)存在,
【解析】
【分析】(1)根据折叠前后的几何性质可得 ,结合线线垂直可得 ,根据面面垂直判
定定理即可证得结论;(2)以 为原点,以 为 轴,以 为 轴,以 为 轴建立空间直角坐标系,根据空间向量的坐
标运算,设 ,分别求平面 与平面 的法向量,根据面面夹角
余弦值公式列方程求解 即可得结论.
【小问1详解】
因为四边形 为正方形,所以 , ,
所以折起后, , ,
由于折起前有 ,且折起后 ,
所以折起后有 ,即 ,
又 , , 平面 ,
所以 平面 ,
又 平面 ,所以平面 平面 .
【小问2详解】
存在,理由如下:
由(1)知 , , ,
所以以 为原点,以 为 轴,以 为 轴,以 为 轴建立空间直角坐标系,
设 ,则 , , , ,则 , , ,
假设存在满足题意的点 ,设 ,
则 ,
设平面 的法向量为 ,
则 ,即 ,
令 ,得 , ,即 ,
易知平面 的一个法向量为 ,
因为平面 与平面 夹角的余弦值为 ,
所以 ,
整理得
解得 或 (舍),
所以在棱 上存在点 ,使平面 与平面 夹角的余弦值为 ,且 .
的
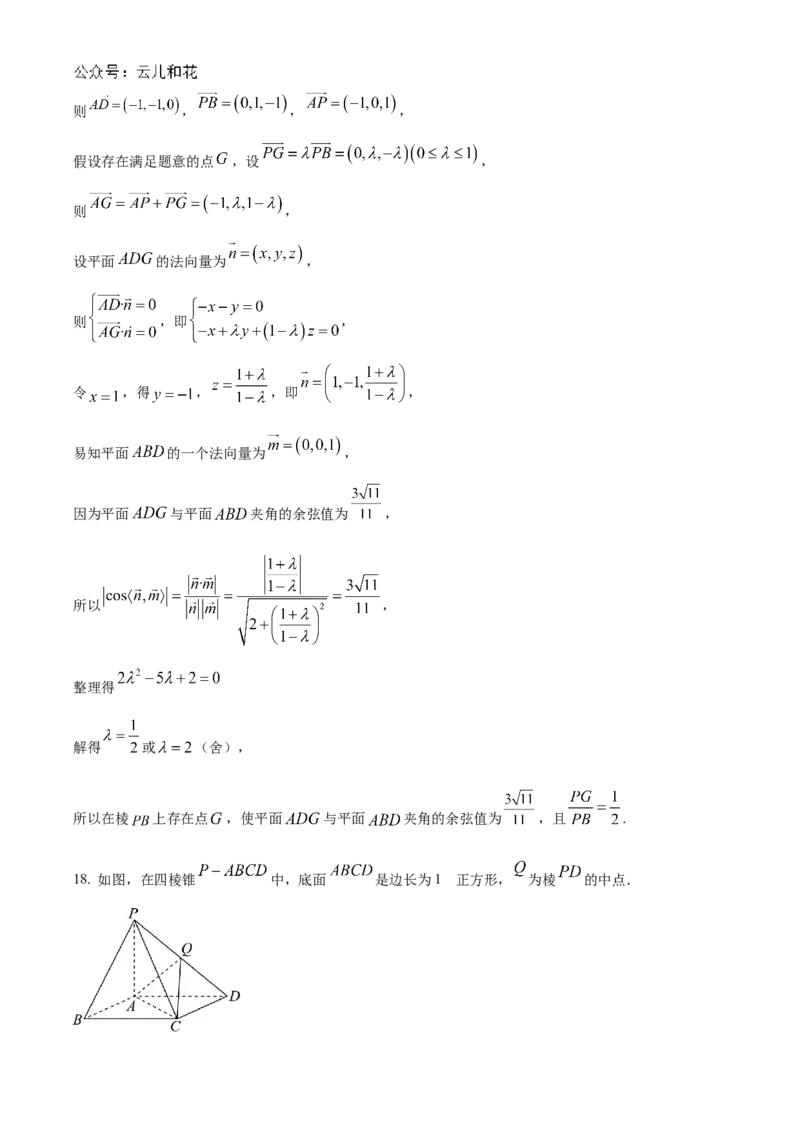
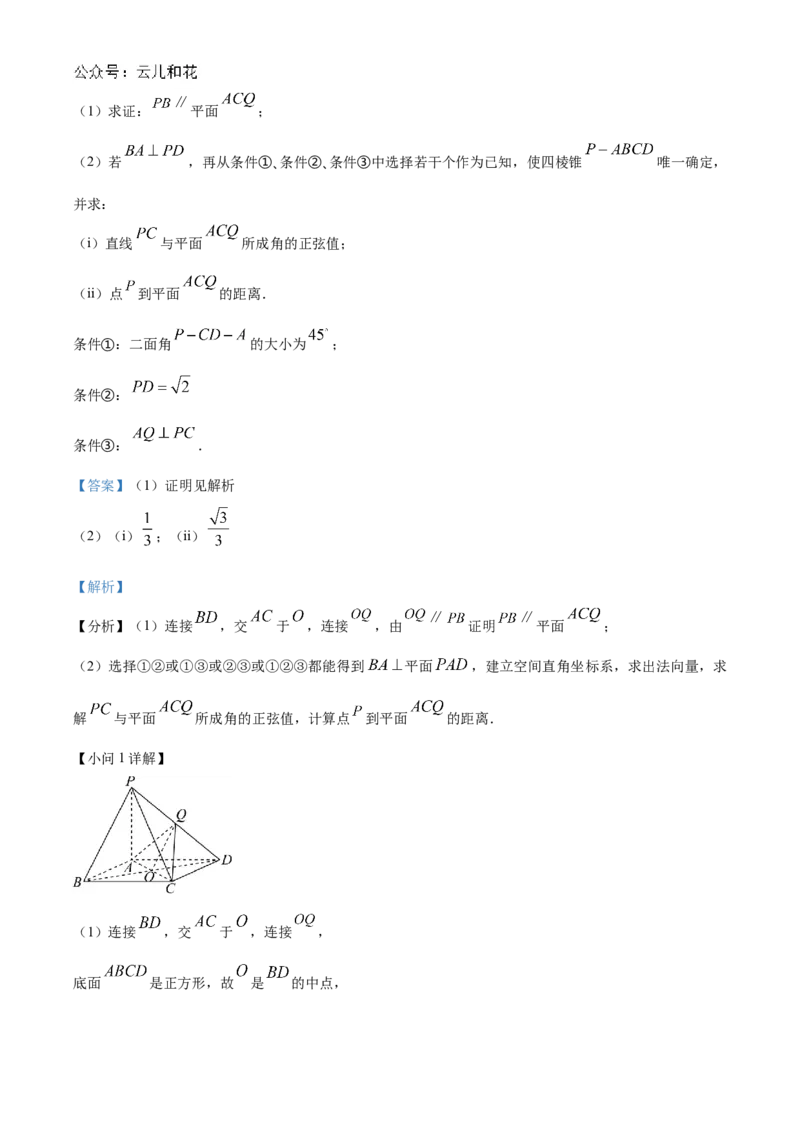
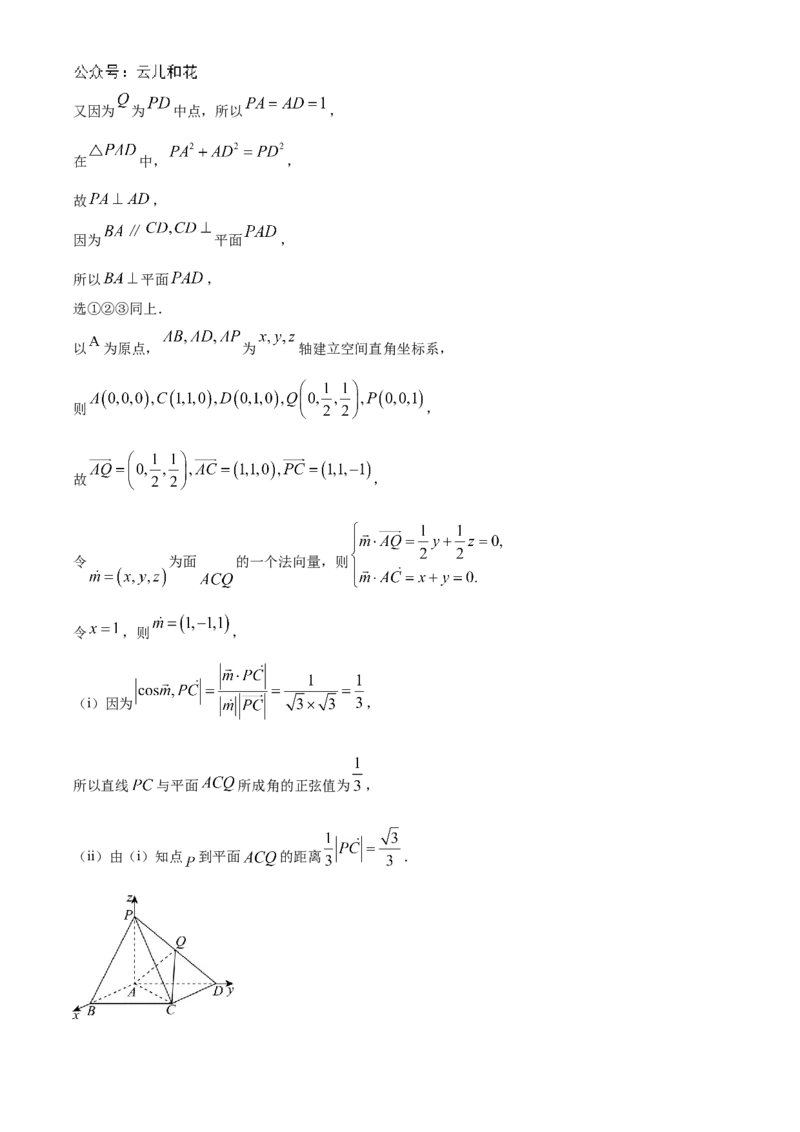
18. 如图,在四棱锥 中,底面 是边长为1 正方形, 为棱 的中点.(1)求证: 平面 ;
(2)若 ,再从条件①、条件②、条件③中选择若干个作为已知,使四棱锥 唯一确定,
并求:
(i)直线 与平面 所成角的正弦值;
(ii)点 到平面 的距离.
条件①:二面角 的大小为 ;
条件②:
条件③: .
【答案】(1)证明见解析
(2)(i) ;(ii)
【解析】
【分析】(1)连接 ,交 于 ,连接 ,由 证明 平面 ;
(2)选择①②或①③或②③或①②③都能得到 平面 ,建立空间直角坐标系,求出法向量,求
解 与平面 所成角的正弦值,计算点 到平面 的距离.
【小问1详解】
(1)连接 ,交 于 ,连接 ,
底面 是正方形,故 是 的中点,的
又因为 为棱 中点,
所以,在 中 ,
而 平面 平面 ,
所以 平面 .
【小问2详解】
选①②:
因为四边形 是正方形,
所以 ,
又因为 ,所以 ,
因为二面角 的大小为 ,平面 平面 ,所以
,
在 中, ,
所以 ,
故 ,
又因为 平面 ,
所以 平面 ,
选①③:
因为四边形 是正方形,
所以 ,
又因为 ,所以 ,
因为二面角 的大小为 ,平面 平面 ,
所以 ,因为 平面 ,
所以 平面 ,
又因为 平面 ,所以 ,
又因为 平面 ,
所以 平面 ,
因为 平面 ,所以 ,
又因为 为 中点,所以 ,
所以 ,
所以 ,即 ,
因为 平面 ,
所以 平面 ,
选②③:
因为四边形 是正方形,
所以 ,
因为 平面 ,
所以 平面 ,
又因为 平面 ,所以 ,
又因为 平面 ,
所以 平面 ,
因为 平面 ,所以 ,又因为 为 中点,所以 ,
在 中, ,
故 ,
因为 平面 ,
所以 平面 ,
选①②③同上.
以 为原点, 为 轴建立空间直角坐标系,
则 ,
故 ,
令 为面 的一个法向量,则
令 ,则 ,
(i)因为 ,
所以直线 与平面 所成角的正弦值为 ,
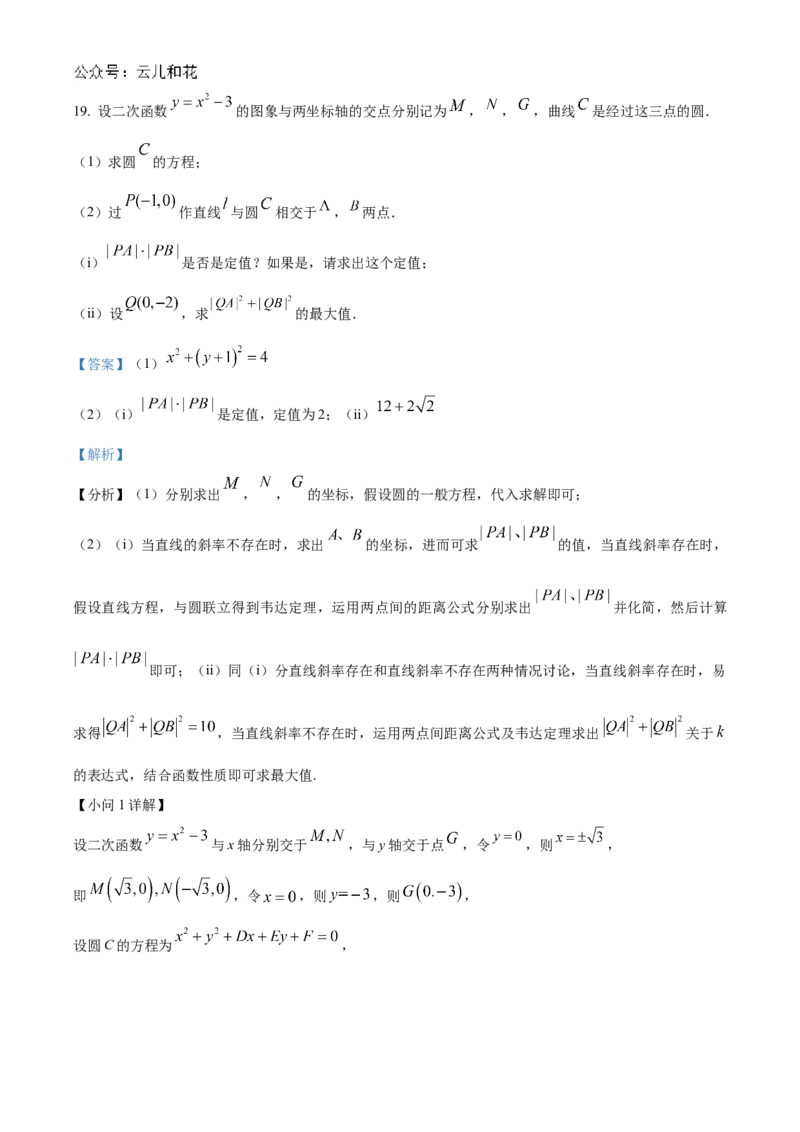
(ii)由(i)知点 到平面 的距离 .19. 设二次函数 的图象与两坐标轴的交点分别记为 , , ,曲线 是经过这三点的圆.
(1)求圆 的方程;
(2)过 作直线 与圆 相交于 , 两点.
(i) 是否是定值?如果是,请求出这个定值;
(ii)设 ,求 的最大值.
【答案】(1)
(2)(i) 是定值,定值为2;(ii)
【解析】
【分析】(1)分别求出 , , 的坐标,假设圆的一般方程,代入求解即可;
(2)(i)当直线的斜率不存在时,求出 的坐标,进而可求 的值,当直线斜率存在时,
假设直线方程,与圆联立得到韦达定理,运用两点间的距离公式分别求出 并化简,然后计算
即可;(ii)同(i)分直线斜率存在和直线斜率不存在两种情况讨论,当直线斜率存在时,易
求得 ,当直线斜率不存在时,运用两点间距离公式及韦达定理求出 关于
的表达式,结合函数性质即可求最大值.
【小问1详解】
设二次函数 与x轴分别交于 ,与y轴交于点 ,令 ,则 ,
即 ,令 ,则 ,则 ,
设圆C的方程为 ,将点M、N、G的坐标代入可得 ,解得 ,
则 ,化为标准式为 .
【小问2详解】
是定值.
(i)当直线 的斜率不存在时,则 方程为 ,
联立 ,可得 或 ,
即 ,则 , ,则 ;
当直线 的斜率存在时,设 方程为 ,设A(x ,y ),B(x ,y ),
1 1 2 2
联立直线与圆的方程 ,消去y可得 ,
由韦达定理可得 ,
且 ,
,
则
;
综上所述, 是定值.(ii)由(i)可知,当直线 的斜率不存在时, ,
且 ,则 , ,则
;
当直线 的斜率存在时,设 方程为 ,
则
令 ,则
令
当 ,即 时, ;
当 ,即 时, ;当 ,即 , 时,
取最大值 .所以 .