文档内容
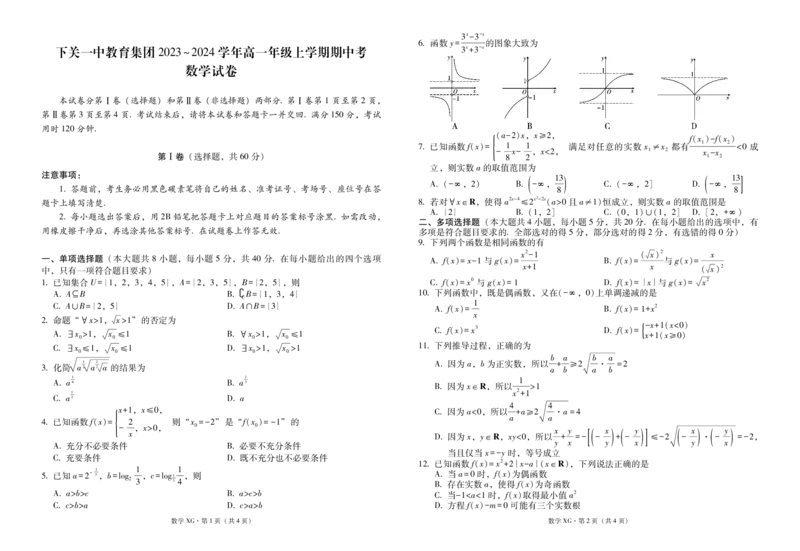
函数 3x-3-x的图象大致为
6. y=
下关一中教育集团 2023~2024 学年高一年级上学期期中考
3x+3-x
数学试卷
本试卷分第卷(选择题)和第卷(非选择题)两部分第卷第页至第页,
Ⅰ Ⅱ . Ⅰ 1 2
第卷第页至第页考试结束后,请将本试卷和答题卡一并交回满分 分,考试
Ⅱ 3 4 . . 150
用时 分钟
120 . ( ), ,
( ) ( )
已知函数() { a-2 x x≥2 满足对任意的实数 都有f x -f x 成
7. f x = 1 1, , x ≠x 1 2 <0
第卷(选择题,共 分) - x- x<2 1 2 x -x
Ⅰ 60 8 2 1 2
立,则实数的取值范围为
注意事项: a
( , ) ( ,13) ( , ] ( ,13]
答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答 A. -∞ 2 B. -∞ C. -∞ 2 D. -∞
1. 8 8
题卡上填写清楚 若对 ,使得 ( 且 )恒成立,则实数的取值范围是
. 8. { } x∈R a2x-4≤ ( 2x2 , -2x ] a>0 a≠1 (, ) (, a ] [, )
每小题选出答案后,用 铅笔把答题卡上对应题目的答案标号涂黑如需改动, A. 2 B. 1 2 C. 0 1 ∪ 1 2 D. 2 +∞
2. 2B . 二、多项选择题(本大题共小题,每小题分,共 分在每小题给出的选项中,有
用橡皮擦干净后,再选涂其他答案标号在试题卷上作答无效 多项是符合题目要求的全部 4 选对的得分, 5 部分选对 20 的得 . 分,有选错的得分)
. . . 5 2 0
下列两个函数是相同函数的有
9.
一、单项选择题(本大题共小题,每小题分,共 分在每小题给出的四个选项 () 与() x2-1 ()
(槡
x
)
2与() x
中,只有一项符合题目要求) 8 5 40 . A. f x = x-1 g x = B. f x = g x = (槡)
x+1 x x 2
已知集合 {, , , , }, {, , }, {, },则 () 与() () 与() 槡
1. U= 1 2 3 4 5 A= 2 3 5 B= 2 5 C. f x = x0 g x = 1 D. f x = x g x = x2
{, , } 下列函数中,既是偶函数,又在( , )上单调递减的是
A. AB B. 瓓B= 1 3 4 10. -∞ 0
{, } U {}
() 1 ()
C. A∪B= 2 5 D. A∩B= 3 A. f x = B. f x = 1+x2
命题“ ,槡”的否定为 x
2. x>1 x>1 ( )
,槡 ,槡 C. f ( x ) = x3 D. f ( x ) = {-x+ ( 1 x<0 )
A. x >1 x ≤1 B. x >1 x ≤1 x+1 x≥0
0 0 0 0 下列推导过程,正确的为
,槡 ,槡
11.
C. x ≤1 x ≤1 D. x >1 x >1
槡0
槡
0 0 0
因为, 为正实数,所以b a 槡b·a
化简
1
1槡的结果为
A. a b + ≥2 =2
3. a2 a2 a a b a b
1 1 因为 ,所以1
A. a4 B. a3
B. x∈R >1
1
x2+1
C. a2 D. a
, , 因为 ,所以4 槡4·
{x+1 x≤0 C. a<0 +a≥2 a =4
已知函数() 则“ ”是“( ) ”的
a a
4. f x = 2, , x =-2 f x = -1
- x>0 0 0 因为, , ,所以x y [( x) ( y)] 槡 ( x)·( y) ,
充分不必要条件
x
必要不充分条件
D. x y∈R xy<0 + =- - + - ≤-2 - - =-2
y x y x y x
A. B. 当且仅当 时,等号成立
充要条件 既不充分也不必要条件 x=-y
C. D. 已知函数() ( ),下列说法正确的是
12. f x = x2+2 x-a x∈R
5.
已知
a=2- 3 1
,
b=log
1,
c=log1
1,则
A. 存
当
在 a= 实 0 数
时,
, f
(
使 x 得
)为
(
偶函
)为
数
奇函数
2 3 3 4 B. a f x
当 时, ()取得最小值
A. a>b>c B. a>c>b C. -1<a<1 f x a2
方程() 可能有三个实数根
C. c>b>a D. c>a>b D. f x -m=0
数学 ·第页(共页) 数学 ·第页(共页)
XG 1 4 XG 2 4
{#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}
书书书第卷(非选择题,共 分) (本小题满分 分)
Ⅱ 90 20. 12
注意事项: 第 届世界杯足球赛将于 年开赛 年月 日,在莫斯科举行的国际足
23 2026 . 2018 6 13
第卷用黑色碳素笔在答题卡上各题的答题区域内作答,在试题卷上作答无效 联第 届大会上宣布,加拿大、墨西哥、美国三国联合申办 年世界杯足球赛
Ⅱ . 68 2026
成功这是世界杯第四次在北美举办,也是世界杯历史上第一次三国联合举办世界
. .
三、填空题(本大题共小题,每小题分,共 分) 杯,是球员们圆梦的舞台,是球迷们情怀的归宿,也是商人们角逐的竞技场某足
4 5 20 .
球运动装备生产企业, 年的固定成本为 万元,每生产千件装备,需另投
函数() 2x+1,且() ,则实数 2023 1000 x
13. f x = f p = 4 p= . , ,
x-1 {x2+ax 0≤x<80
入资金()(万元) 经计算与市场评估得() 调查
若 , ,且 ,则1 4的最小值为 R x . R x = 301x2-2750x+10000,
14. x>0 y>0 x+y=1 + . x≥80.
x y x
发现,当生产 千件装备时需另投入的资金( ) 万元每千件装备的市场
若不等式 的解集是{ },则不等式ax+1 的解集为 10 R 10 = 2100 .
15. ax2+bx-1>0 x 1<x<2 >0 . 售价为 万元,从市场调查来看, 年最多能售出 千件
bx-1 300 2023 150 .
, , ( )写出 年利润(万元)关于年产量(千件)的函数;(利润销售总额总
{ x-2a x≤2 Ⅰ 2023 W x = -
已知函数() 且()是()的最小值,则实数的取值范围是 成本)
16. f x = 1 , , f 2 f x a
x+ +a x>2 ( )求当 年产量为多少千件时,该企业所获得的利润最大?最大利润是多少?
x-2 Ⅱ 2023
.
四、解答题(共 分解答应写出文字说明,证明过程或演算步骤)
70 .
(本小题满分 分)
17. 10
(本小题满分 分)
( )计算:(27) - 3 2 2 16; 21. 已知函数() 1 是 2 定义在上的偶函数,且当 时, ()
Ⅰ 8 +πlg1+log 2 3 -log 4 9 ( )现已 f 画 x 出函数 R ()在轴左侧的图象 x , ≤ 请 0 补全 f 函 x 数 = x2+2x.
( )已知 1 1 ,求a3+a-3的值 ( Ⅰ )的图象,并根据图 f 象 x 写出 y 函数()( )的单调递增
Ⅱ a2+a- 2 =3 . f x f x x∈R
a+a-1 区间;
( )写出函数()( )的值域;
(本小题满分 分) Ⅱ f x x∈R
18. 12 ( )求出函数()( )的解析式
若集合 { }, { } Ⅲ f x x∈R .
A= x -1≤x≤6 B= x m+1≤x≤3m-1 .
( )当 时,求 ;
Ⅰ m=2 A∩B
( )若 ,求的取值范围
Ⅱ BA m .
(本小题满分 分)
22. 12
已知函数() 6 ,且不等式() 的解集为{ }
f x = ax+ -3 xf x <4 x 1<x<b .
(本小题满分 分)
x
19. 12 ( )解关于的不等式 ( ) ( );
已知指数函数() ( ,且 )过点( , ) Ⅰ x ax2- ac+b x+bc<0 c∈R
f x = ax a>0 a≠1 -2 9 . ( )已知() ,若对任意的 [, ],总存在 (, ],使
( )求函数()的解析式; Ⅱ g x = mx+7-3m x ∈ 2 3 x ∈ 1 4
Ⅰ f x ( ) 1 2
( )若( ) ( ) ,求实数的取值范围
( ) g x 成立,求实数的取值范围
Ⅱ f 2m-1 -f m+3 <0 m . f x = 2 m .
1 x
1
数学 ·第页(共页) 数学 ·第页(共页)
XG 3 4 XG 4 4
{#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}