下关一中教育集团2023～2024学年高一年级上学期期中考数学-答案(1)_2023年11月_0211月合集_2024届云南省大理下关第一中学高三上学期11月期中考试

下关一中教育集团 2023~2024 学年高一年级上学期期中考 数学参考答案 第Ⅰ卷（选择题，共60分） 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题所给出的四个选项中， 只有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 B A C A D C D A 【解析】 1．集合U {1，2，3，4，5}， A{2，3，5} ， B{2，5} ，所以 B A ，  B{1，3，4} ， U AB{2，3，5}，AB{2，5}，故选B． 2．原命题的否定是：x 1， x ≤1，故选A． 0 0 3．由条件知a≥0，则 1 1 1 1  1 1 1 1 1 ，故选C． a2 a2 a  a2 a2 2  a2 a  a2 a2  a a2 4．由 f(2)211，即“x 2” “ f(x )1” 当x≤0时，由 f(x )1，可 0 0 0 2 得x 11，解得x 2，满足；当x0时，由 f(x )1，可得 1，解得x 2， 0 0 0 x 0 0 满足，所以“ f(x )1” “x 2”，所以“x 2”是“ f(x )1”的充分不 0 0 0 0 必要条件，故选A． 1 1 1 1 5．0a2  3 20 1，blog log 10，clog log 1，∴cab，故选D． 2 3 2 1 4 1 3 3 3 3x 3x 3x 3x 6．设 f(x) ，则 f(x)的定义域为R，且 f(x) f(x)，即 f(x)是奇函数， 3x 3x 3x 3x (3x)2 1 2 2 排除D；又 f(x) 1 ，由3x 0，可得(3x)2 11，∴0 2， (3x)2 1 (3x)2 1 (3x)2 1 2 3x 3x 从2 0，因此1 1，即 f(x)的值域为(1，1)，故选C． (3x)2 1 3x 3x f(x ) f(x ) 7．因为函数 f(x)满足对任意的实数x  x ，都有 1 2 0成立，则函数 f(x)在R上 1 2 x x 1 2 数学XG参考答案·第1页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}a20，  13 为减函数，由题意得  1 1 解得 a≤ ，∴实数 a 的取值范围是 2(a2)≤ 2 ， 8   8 2  13 ，  ，故选D．  8  8．若a2x4≤2x22x(a0且a1)对任意的xR都成立. ①当x≥2时，由a2x4≤2x22x，得到 a2≤2x，因为指数函数y2x在(2，)上单调递增，故要使得a2≤2x对任意x≥2成立， 有 a2≤22 4 ，即得 a(0，1)(1，2] ；②当 x2 时， a2(x2)≤2x(x2)≤2x22x 变形为 1 x 1 x a2(2x)≤2x(2x)，即得a2≤2x   ，因为指数函数 y  在(，2)上单调递减， 2 2 1 x 1 2 1 要使得a2≤   对任意x2成立，即有a2≤    ，即a2≥4，即得a[2，)， 2 2 4 因此，结合题意可知要使得对xR，使得a2x4≤2x22x(a0且a1)恒成立，取①②两 种情况下a取值范围的交集可知a{2}，故选A． 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项 是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分） 题号 9 10 11 12 答案 BD BD AD AC 【解析】 x2 1 9．A． f(x)x1的定义域为R，g(x) 的定义域为{x|x1}，定义域不同，故不是 x1 ( x)2 x x x 相同函数；B． f(x)  1(x0)，g(x)  1(x0)，定义域和对应法 x x ( x)2 x 则相同，故为相同函数；C． f(x)x0(x0)与g(x)1(xR)，定义域不同，故不是相 同函数；D．f(x)|x|，g(x) x2 |x|，函数的定义域、对应关系均相同，是相同函数， 故选BD． 1 10．对于 A，C，由 f(x) f(x)，可知 f(x) ， f(x)x3不是偶函数，故 A，C 错；选项 x B，定义域为R， f(x) f(x)是偶函数，又在(，0)上单调递减，符合题意；选项D， 数学XG参考答案·第2页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}函数定义域为R，当x0时， f(x)x1 f(x)，当x0时， f(x)x1 f(x)， 所以在定义域上有 f(x) f(x)，所以 f(x)是偶函数，且在区间在(，0)上单调递减， 符合题意，故选BD． b a 11．对于 A 选项，因为 a ， b 为正实数，则 ， 为正实数，由基本不等式可得 a b b a b a  ≥2  2，当且仅当ab时，等号成立，A选项正确；对于B选项，∵x2 1≥1， a b a b 1 所 以 ， 0 ≤1 ， B 选 项 错 误 ； 对 于 C 选 项 ， 当 a0 时 ， x2 1 4  4   4 a  (a)  ≤2   (a) 4 ，当且仅当a2时，等号成立，C 选项 a  a   a y x 错误；对于 D 选项，因为 x， yR，xy0，则 ， 均为负数，由基本不等式可得 x y x y  x  y  x  y     ≤2     2，当且仅当xy时，等号成立，D选 y x  y  x  y  x 项正确，故选AD． 12．函数 f(x)x2 2|xa|(aR)，当a0时， f(x)x2 2|x|， f(x)(x)2 2|x| x2 2|x| f(x)为偶函数，故A正确；当a0时，由 f(a)a2，f(a)a2 4|a|，则 f(a) f(a)2a2 4|a|0，函数不可能为奇函数，故B错误； f(x)x2 2|xa| x2 2x2a，x≥a (x1)2 12a，x≥a，   当1a1时，x≥a时，函数单调递 x2 2x2a，xa (x1)2 12a，xa， 增，xa时，函数单调递减，所以函数的最小值为 f(a)a2，故C正确；若1a1时， 函数在(，a)上递减，在(a，)上递增，方程 f(x)m0最多有2个根，若a≤1时， 函数在(，1)上递减，在(1，)上递增，方程 f(x)m0最多有2个根，若a≥1时， 函数在(，1)上递减，在(1，)上递增，方程 f(x)m0最多有 2 个根，所以方程 f(x)m0不可能有三个实数根，D错误，故选AC． 数学XG参考答案·第3页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}第Ⅱ卷（非选择题，共90分） 三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16 5 2  答案 9  ，2 [1，6] 2 3  【解析】 2x1 2p1 5 13．因为 f(x) 且 f(p)4，所以 4，解得 p ． x1 p1 2 1 4 1 4 y 4x y 4x 14．由于x0，y0，且x y1，则    (x y)5  ≥52  9， x y x y x y x y 1 2 1 4 当且仅当x ，y 时取等号．故  的最小值为9． 3 3 x y b  3， a 1 15．因为不等式ax2 bx10的解集是{x|1x2}，所以 且a0，解得a ， 1 2 2， a 1  x1 3 ax1 2 x 3  2 b ，所以 0可转化为 0 1 x10，解得 x2. 2 bx1 3 2 2  3 x1 2 |x2a|，x≤2，  16．因为函数 f(x) 1 且 f(2) 是 f(x)的最小值，所以当 x≤2时，函数 x a，x2   x2 f(x)|x2a| 单 调 递 减 ， 所 以 2a≥2 ， 即 a≥1 ； 当 x2 时 ， 函 数 1 1 1 f(x)x ax2 a2，令tx20，设函数g(t)t 为对勾函数， x2 x2 t 可得当t(0，1)时，g(t)单调递减，当t(1，)时，g(t)单调递增，所以当t 1时，g(t) 取得最小值2，即x3时，f(x)取得最小值a4，所以4a≥ f(2)，即4a≥|22a|， 2 解得 ≤a≤6，综上所述，a的取值范围为[1，6]. 3 数学XG参考答案·第4页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） 2 2 解：（Ⅰ）   27   3 πlg1log 2 log 16    2  3 3 π0 log 2 log 4  8  2 3 4 9 3 2 3 2 3 2 2 2 3 4 4   1log    11 ．………………………………………………（5分） 3 2 3 4 9 9 1 1 （Ⅱ）因为a2 a  2 3，  1 1 2  所以aa1 a2 a 2 27，   所以a2 a2 (aa1)2 247， a3 a3 (aa1)(a2 a2 1) 所以  a2 a2 146．……………………………（10分） aa1 aa1 18．（本小题满分12分） 解：（Ⅰ）当m2时，A{x|1≤x≤6}，B{x|3≤x≤5}， 则AB{x|3≤x≤5}.…………………………………………………………………（6分） （Ⅱ）①若m13m1，即m1时，B，符合题意； m1≤3m1，  7 ②若m1≤3m1，即B时，得1≤m1， 解得1≤m≤ ， 3  3m1≤6， 7 综上可知m≤ .…………………………………………………………………………（12分） 3 19．（本小题满分12分） 1 1 x 解：（Ⅰ）将点(2，9)代入到 f(x)ax得a2 9，解得a ，∴f(x)  . 3 3 ……………………………………………………………………………………………（6分） （Ⅱ）∵f(2m1) f(m3)0， ∴f(2m1) f(m3)， 1 x ∵f(x)  为减函数， 3 ∴2m1m3， 解得m4， ∴实数m的取值范围为(4，)． ……………………………………………………（12分） 数学XG参考答案·第5页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}20．（本小题满分12分） 解：（Ⅰ）由题意知，当x10时，R(10)102 10a2100，所以a200， 当0≤x80时，W 300x(x2 200x)1000x2 100x1000； 301x2 2750x10000 10000 当80≤x≤150时，W 300x 1000x 1750． x x x2 100x1000，0≤x80，  所以W  10000 ……………………………………………（6分） x 1750，80≤x≤150. 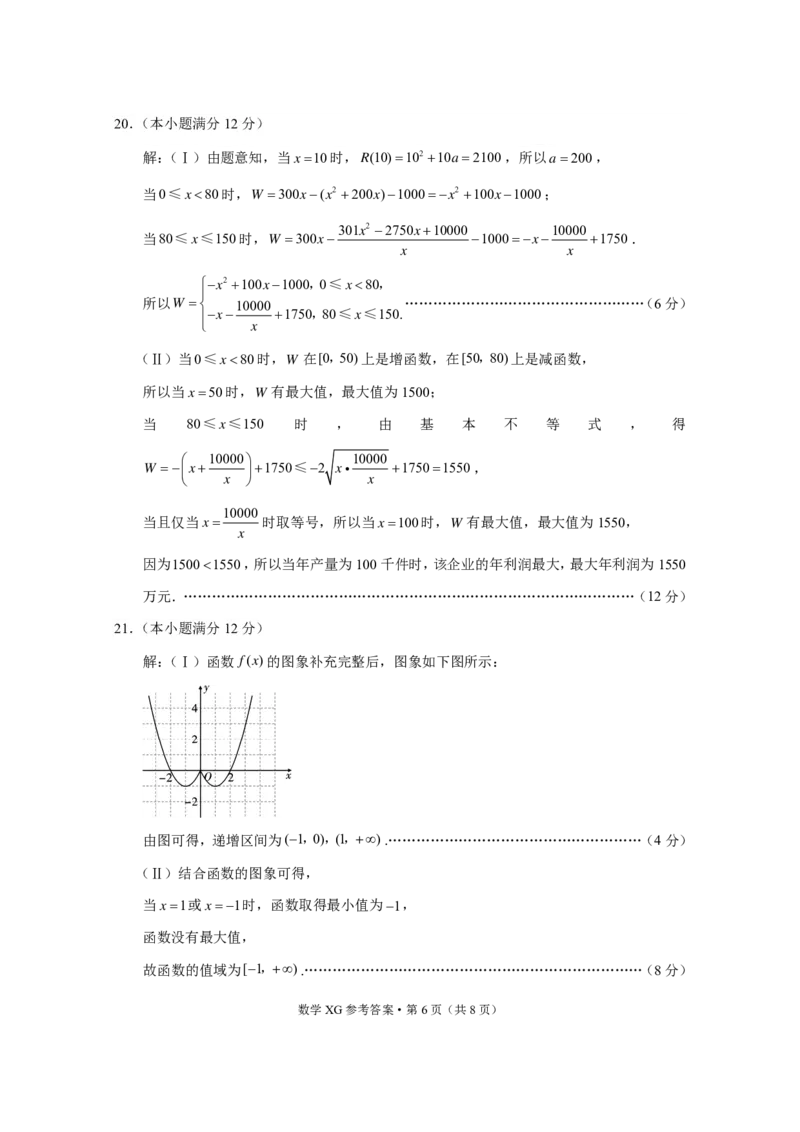 x （Ⅱ）当0≤x80时，W 在[0，50)上是增函数，在[50，80)上是减函数， 所以当x50时，W 有最大值，最大值为1500； 当 80≤x≤150 时 ， 由 基 本 不 等 式 ， 得  10000 10000 W x 1750≤2 x 17501550，  x  x 10000 当且仅当x 时取等号，所以当x100时，W 有最大值，最大值为1550， x 因为15001550，所以当年产量为100千件时，该企业的年利润最大，最大年利润为1550 万元．……………………………………………………………………………………（12分） 21．（本小题满分12分） 解：（Ⅰ）函数 f(x)的图象补充完整后，图象如下图所示： 由图可得，递增区间为(1，0)，(1，).………………………………………………（4分） （Ⅱ）结合函数的图象可得， 当x1或x1时，函数取得最小值为1， 函数没有最大值， 故函数的值域为[1，).………………………………………………………………（8分） 数学XG参考答案·第6页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}（Ⅲ）当x0时，x0， 再根据x≤0时， f(x)x2 2x， 可得 f(x)(x)2 2(x)x2 2x， 再根据函数 f(x)为偶函数， 可得 f(x)x2 2x， x2 2x，x≤0， ∴函数 f(x)的解析式为 f(x) ……………………………………（12分） x2 2x，x0. 22．（本小题满分12分） 6 解：（Ⅰ）因为 f(x)ax 3，所以xf(x)4可化为ax2 63x4，即ax2 3x20， x 因为不等式xf(x)4的解集为{x|1xb}，即1，b是方程ax2 3x20的两根， 将x1代入ax2 3x20，得a320，故a1， 2 再由韦达定理得1b 2，故b2， a 所以ax2 (acb)xbc0可化为x2 (c2)x2c0，即(xc)(x2)0. 当c2时，不等式解得2xc，即其解集为{x|2xc}； 当c2时，不等式为(x2)2 0，显然不等式恒不成立，无解，即x； 当c2时，不等式解得cx2，即其解集为{x|cx2}， 综上：当c2时，不等式解集为{x|2xc}； 当c2时，不等式解集为； 当c2时，不等式解集为{x|cx2}．………………………………………………（6分） g(x ) （Ⅱ）因为对任意的x [2，3]，总存在x (1，4]，使 f(x ) 2 成立，即x f(x )g(x ) 1 2 1 x 1 1 2 1 成立， 所以yxf(x)的值域是g(x)mx73m的值域的子集， 由（Ⅰ）得xf(x)x2 3x6， 3 所以yxf(x)开口向上，对称轴为x ，故yxf(x)在[2，3]上单调递增， 2 当x2时，yxf(x)22 3264；当x3时，yxf(x)32 3366， 数学XG参考答案·第7页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}所以yxf(x)的值域为[4，6]， 当m0时，g(x)在(1，4]上单调递增，故g(1)g(x)≤g(4)，即72mg(x)≤m7，  3 72m4， m ， 3 所以 解得 2 故m ； m7≥6，  m≥1， 2 当m0时，g(x)7，不满足题意； 当m0时，g(x)在(1，4]上单调递减，故g(4)≤g(x)g(1)，即m7≤g(x)72m， m≤3， m7≤4，  所以可得 解得 1 故m≤3. 72m6，  m ，  2 3 3  综上：m 或m≤3，即m(，3]  ，.………………………………（12分） 2 2  数学XG参考答案·第8页（共8页） {#{QQABQY6UggCoQAIAAAgCUwGwCgGQkBACAIoOBBAEsAABwRFABAA=}#}