文档内容
高二数学 3 月考
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
1. 在全球高铁技术竞争中,中国站到了前沿.全国政协委员、中国铁道科学研究院集团有限公司首席研究员赵红卫近日
透露,全球最快 高铁列车 CR450 正在加紧试验,预计将在一年后投入商业运营.小张需要乘坐 G302 次高铁从合肥到
北京,已知此次高铁列车车票还剩下二等座 4 张,一等座 10 张,商务座 5 张,则小张的购票方案种数为( )
A 19 B. 20 C. 90 D. 200
2. 已知等差数列 的前 项和为 ,若 ,则 ( )
A. B. 10 C. 19 D. 38
3. 有 3 名男生和 3 名女生去影院观影,他们买了同一排相连的 6 个座位,若 3 名女生必须相邻,则不同的坐法有( )
A. 24 种 B. 48 种 C. 96 种 D. 144 种
4. 已知 ,则 ( )
A. 364 B. 365 C. 728 D. 730
5. 已知点 是抛物线 : 上任意一点,若点 到抛物线 的准线的距离为 ,到直线 : 的
距离为 ,则 的最小值是( )
A. B. C. D.
6. 函数 的最小值为( )
A B. C. D.
7. 函数 的单调递减区间为( )
A. B.
C. D.
8. 已知函数 的导函数为 ,且 ,则 ( )
A. 1 B. C. D.二、多选题:本题共 3 小题,每小题 6 分,共 18 分,在每小题给出的四个选项中,有多项符合题目要
求.全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分.
9. 已知等差数列 的前 项和为 ,且 ,则( )
A.
B.
C. 当 时, 取最大值
D. 当 时, 最小值为 19
10. 已知直线 与圆 交于点 ,点 中点 ,则( )
A. 的最小值为
B. 的最大值为 4
C. 定值
D. 存在定点 ,使得 定值
11. 已知抛物线 的焦点为 ,从点 发出的光线经过抛物线上的点 (原点除外)反射,则反射光线平
行于 轴.经过点 且垂直于 轴的直线交抛物线 于 两点,经过点 且垂直于 轴的直线交 轴于点 ;抛物
线
在点 处的切线 与 轴分别交于点 ,则( )
A. B.
C. D.
二、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. 已知数列 通项公式为 ,若 是 与 的等比中项,则 ____.
13. 函数 的图象在点 处的切线方程为____.
14. 已知在数列 中, , ,设数列 的前 项和为 ,若不等式 对
恒成立,则 的最小值为____.
四、解答题:本大题共 5 个小题,共 77 分.解答应写出必要的文字说明,证明过程或演算步骤.
15. 已知函数 , .
(1)当 时,求 最小值;(2)若 ,试讨论 的单调性.
16 已知函数 .
(1)求函数 的单调递增区间;
(2)如果函数 的导数为 ,且 在 上的零点从小到大排列后构成数列 ,求 的前 20 项
和.
17. 已知函数 .
(1)讨论函数 的单调性;
(2)若 ,求证:对 且 ,都有 .
18. 已知椭圆 的中心为坐标原点,对称轴为 轴与 轴,且 经过点 , .
(1)求 的标准方程;
(2)若 是 的右焦点,过 作两条互相垂直的直线 , ,直线 与 交于 两点,直线 与 交于 ,
两
点.求四边形 面积的取值范围.
19. 定义 1:若数列 满足① ,② ,则称 为“两点数列”;定义 2:对于给定的数
列
,若数列 满足① ,② ,则称 为 的“生成数列”.已知 为“两点数
列”,
为 的“生成数列”.
(1)若 ,求 的前 项和 ;
(2)设 为常数列, 为等比数列,从充分性和必要性上判断 是 的什么条件;
(3)求 的最大值,并写出使得 取到最大值的 的一个通项公式.ACDBB CBD 9ABD 10ACD 11BCD
12 3 13
14
15 (1)
2 详解】
函数 的定义域为 ,
,
当 时,由 解得 或 ,
由 解得 ;
当 时, 恒成立;
当 时,由 解得 或 ,
由 解得 ;
综上可得,
当 时,函数 在 单调递增, 单调递减, 单调递增;
当 时函数 在 单调递增,;
当 时,函数 单调递增, 单调递减, 单调递增.
16 (1)单调递增区间为 .
(2)
1
,
令 ,可得 ,所以函数 的单调递增区间为 .
2
,则 ,
令 ,可得 ,
因为 在 上的零点从小到大排列后构成数列 ,可知 ,
所以 ,公差 ,
所以 ,
所以 的前 20 项和
17 (1)函数 在 上单调递增,在 上单调递减,在 上单调递增
(2)证明:不妨设 ,要证对 ,都有 ,
只需证 ,即需证 .
构造函数 ,
则需证函数 在 上为增函数,
结合 ,因为 ,
所以函数 在 上为增函数成立,
所以当 时,对 且 ,都有 .
18 (1)
(2)
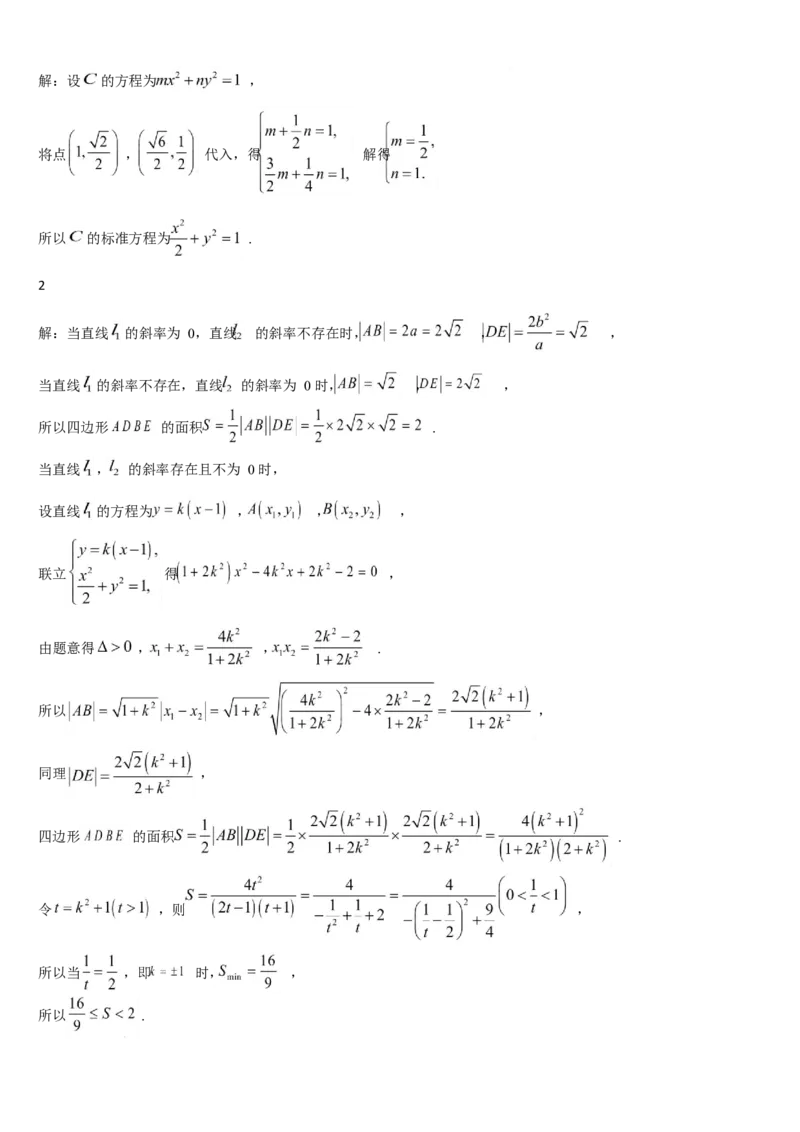
1解:设 的方程为 ,
将点 , 代入,得 解得
所以 的标准方程为 .
2
解:当直线 的斜率为 0,直线 的斜率不存在时, , ,
当直线 的斜率不存在,直线 的斜率为 0 时, , ,
所以四边形 的面积 .
当直线 , 的斜率存在且不为 0 时,
设直线 的方程为 , , ,
联立 得 ,
由题意得 , , .
所以 ,
同理 ,
四边形 的面积 .
令 ,则 ,
所以当 ,即 时, ,
所以 .综上所述,四边形 面积的取值范围 .
19 (1)
(2) 是 充要条件.
(3) 的最大值为 ,