文档内容
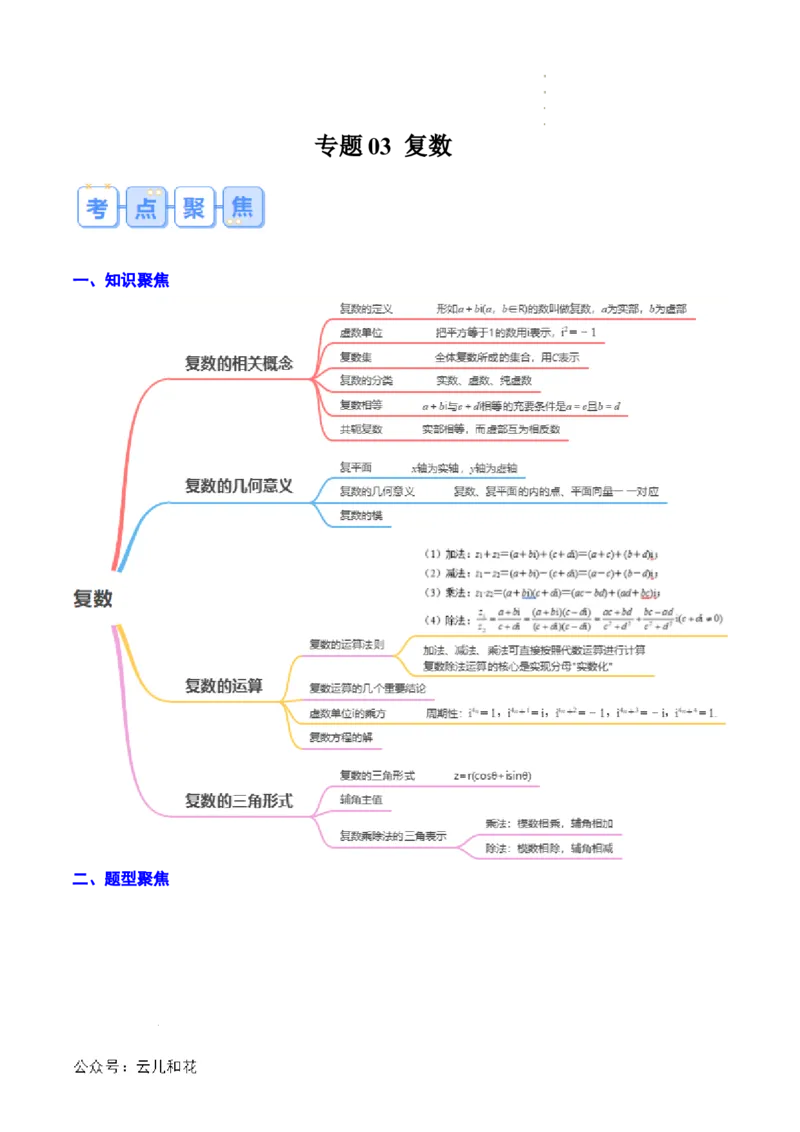
专题 03 复数
一、知识聚焦
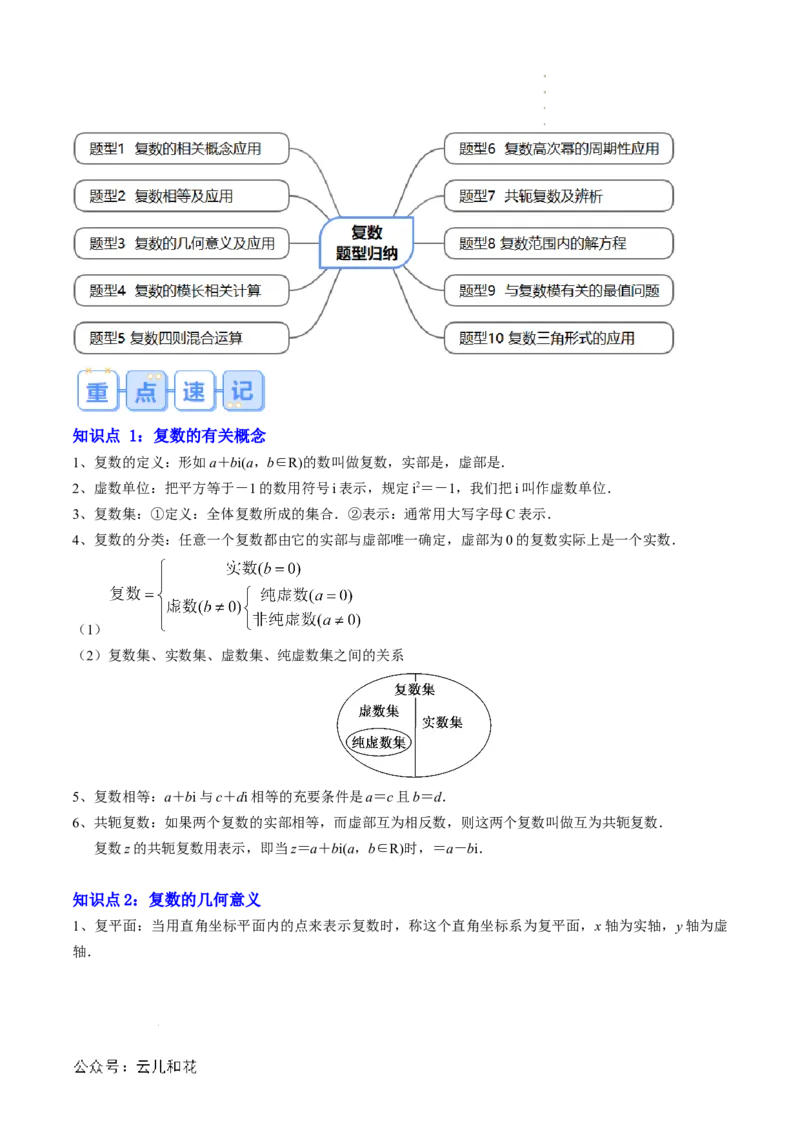
二、题型聚焦
学科网(北京)股份有限公司 学科网(北京)股份有限公司知识点 1:复数的有关概念
1、复数的定义:形如a+bi(a,b∈R)的数叫做复数,实部是,虚部是.
2、虚数单位:把平方等于-1的数用符号i表示,规定i2=-1,我们把i叫作虚数单位.
3、复数集:①定义:全体复数所成的集合.②表示:通常用大写字母C表示.
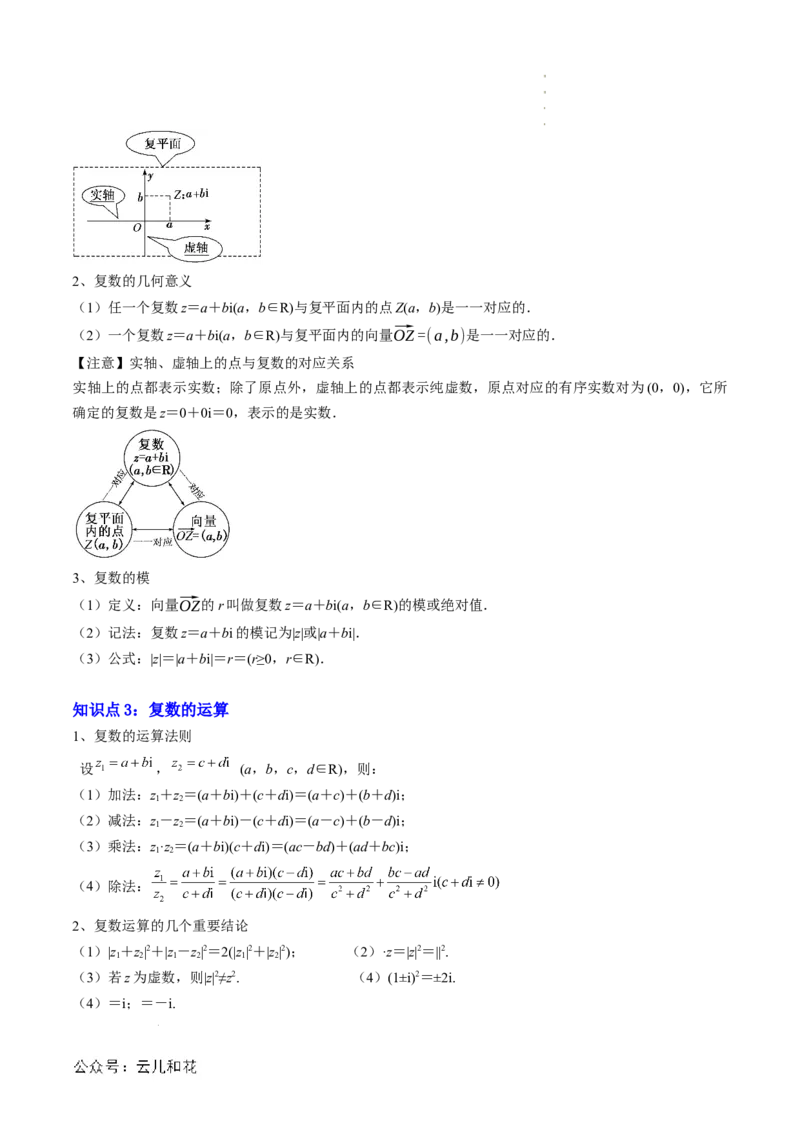
4、复数的分类:任意一个复数都由它的实部与虚部唯一确定,虚部为0的复数实际上是一个实数.
(1)
(2)复数集、实数集、虚数集、纯虚数集之间的关系
5、复数相等:a+bi与c+di相等的充要条件是a=c且b=d.
6、共轭复数:如果两个复数的实部相等,而虚部互为相反数,则这两个复数叫做互为共轭复数.
复数z的共轭复数用表示,即当z=a+bi(a,b∈R)时,=a-bi.
知识点2:复数的几何意义
1、复平面:当用直角坐标平面内的点来表示复数时,称这个直角坐标系为复平面,x轴为实轴,y轴为虚
轴.
学科网(北京)股份有限公司 学科网(北京)股份有限公司2、复数的几何意义
(1)任一个复数z=a+bi(a,b∈R)与复平面内的点Z(a,b)是一一对应的.
(2)一个复数z=a+bi(a,b∈R)与复平面内的向量⃗OZ=(a,b)是一一对应的.
【注意】实轴、虚轴上的点与复数的对应关系
实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,原点对应的有序实数对为(0,0),它所
确定的复数是z=0+0i=0,表示的是实数.
3、复数的模
(1)定义:向量⃗OZ的r叫做复数z=a+bi(a,b∈R)的模或绝对值.
(2)记法:复数z=a+bi的模记为|z|或|a+bi|.
(3)公式:|z|=|a+bi|=r=(r≥0,r∈R).
知识点3:复数的运算
1、复数的运算法则
设 , (a,b,c,d∈R),则:
(1)加法:z+z=(a+bi)+(c+di)=(a+c)+(b+d)i;
1 2
(2)减法:z-z=(a+bi)-(c+di)=(a-c)+(b-d)i;
1 2
(3)乘法:z·z=(a+bi)(c+di)=(ac-bd)+(ad+bc)i;
1 2
(4)除法:
2、复数运算的几个重要结论
(1)|z+z|2+|z-z|2=2(|z|2+|z|2); (2)·z=|z|2=||2.
1 2 1 2 1 2
(3)若z为虚数,则|z|2≠z2. (4)(1±i)2=±2i.
(4)=i;=-i.
学科网(北京)股份有限公司 学科网(北京)股份有限公司3、虚数单位i的乘方
计算复数的乘积要用到虚数的单位i的乘方,in有如下性质:
i1=i,i2=-1,i3=i·i2=-i,i4=i3·i=-i·i=1,
从而对于任何n∈N ,都有i4n+1=i4n·i=(i4)n·i=i,
+
同理可证i4n+2=-1,i4n+3=-i,i4n+4=1.
这就是说,如果n∈N ,那么有i4n+1=i,i4n+2=-1,i4n+3=-i,i4n+4=1.
+
由此可进一步得(1+i)2=2i,(1-i)2=-2i,=-1,=i,=-i.
4、复数方程的解
在复数范围内,实系数一元二次方程ax2+bx+c=0(a≠0)的求解方法:
(1)求根公式法:
−b±√b2−4ac −b±√−(b2−4ac)i
①当∆≥0时,x= ②当∆<0时,x=
2a 2a
(2)利用复数相等的定义求解,设方程的根为x=m+ni(m,n∈R),
将此代入方程ax2+bx+c=0(a≠0),化简后利用复数相等的定义求解.
知识点4:复数的三角形式
1、复数的三角形式:任何一个复数都可以表示成z=r(cosθ+isinθ)的形式,其中r是复数的模,θ是复数
的辅角.
【注意】复数的三角形式必须满足:模非负,角相同,余正弦,加号连.
2、辅角主值
(1)辅角的定义:设复数z=a+bi的对应向量为⃗OZ,以x轴的非负半轴为始边,向量⃗OZ所在的射线(射
线OZ)为终边的角θ,叫做复数z的辅角.
(2)辅角的主值:根据辅角的定义及任意角的概念可知,任何一个不为零的复数辅角有无限多个值,且
这些值相差2π的整数倍.
规定:其中在0≤θ<2π范围内的辅角θ的值为辅角的主值,通常记作argz
【注意】因为复数0对应零向量,而零向量的方向是任意的,所以复数0的辅角是任意的.
3、复数乘、除法的三角表示:已知z =r (cosθ +isinθ ),z =r (cosθ +isinθ ),
1 1 1 1 2 2 2 2
(1)乘法:z z =r r [cos(θ +θ )+isin(θ +θ )],即模数相乘,辅角相加.
1 1 1 2 1 2 1 2
z r (cosθ +isinθ ) r
(2)除法: 1= 1 1 1 = 1[cos(θ −θ )+isin(θ −θ )],即模数相除,辅角相减.
z r (cosθ +isinθ ) r 1 2 1 2
2 2 2 2 2
题型归纳
学科网(北京)股份有限公司 学科网(北京)股份有限公司【题型1 复数的相关概念应用】
满分技法
1、判断复数 的实部、虚部的关键
(1)看形式:看复数的表示是否是 的形式;
(2)看属性:看 , 是否都是实数;
(3)看符号:复数的实部和虚部的符号是易错点.
2、复数的分类:对于复数a+bi,
(1)当且仅当b=0时,它是实数;
(2)当且仅当a=b=0时,它是实数0;
(3)当b≠0时,叫做虚数;
(4)当a=0且b≠0时,叫做纯虚数.
1.(23-24高一下·湖南常德·月考)复数 的虚部是( )
A.5 B. C. D.
【答案】B
【解析】复数 的虚部为 .故选:B.
2.(23-24高一下·甘肃白银·期中)复数 的实部与虚部之和为( )
A. B. C.8 D.6
【答案】B
【解析】因为 ,所以 的实部与虚部之和为 .故选:B.
3.(23-24高一下·四川成都·期中)若纯虚数 ,则 .
【答案】1
【解析】由题意可知, ,得 .
4.(23-24高一下·安徽·月考)复数 ,其中 .
(1)若复数z为实数,求a的值;
(2)若复数z为虚数,求a的取值范围;
(3)若复数z为纯虚数,求a的值
【答案】(1) 或 ;(2) 且 ;(3)
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】(1)由复数z为实数,得 ,解得 或
(2)由复数z为虚数,得 ,解得 且
(3)由复数z为纯虚数,得 ,解得 .
【题型2 复数相等及应用】
满分技法
求解复数相等问题的步骤:(1)等号两侧都写成复数的代数形式;(2)根据两个复数相等的充要条件列
出方程(组);(3)解方程(组).
5.(23-24高一下·浙江金华·期中)设 ,若 ,其中 是虚数单位,则
【答案】7
【解析】因为 ,
所以 ,即 ,所以 ,
6.(23-24高一下·安徽·月考)已知 ,其中 ,i为虚数单位.则实数 ,
.
【答案】1
【解析】由题意 ,得 ,解得 ,
7.(23-24高一下·河南郑州·期中)已知复数 ,
,并且 ,则 .
【答案】
【解析】由题意 ,所以 ,
从而 ,
注意到 的取值范围是 ,
所以 的取值范围是 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司8.(23-24高一下·云南保山·期中)(多选)已知a, , , ,则
( )
A. B. C. D.
【答案】BC
【解析】对于A、B,由 ,解得 ,故A错误,B正确.
对于C, , ,故C正确;
对于D, ,故D错误.故选:BC.
【题型3 复数的几何意义及应用】
满分技法
(1)任一个复数z=a+bi(a,b∈R)与复平面内的点Z(a,b)是一一对应的.
(2)一个复数z=a+bi(a,b∈R)与复平面内的向量⃗OZ=(a,b)是一一对应的.
9.(23-24高一下·四川眉山·月考)设在复平面内,复数 和 对应的点分别为 ,则向量 表
示的复数所对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】由复数的几何意义知, ,故 ,
所以 表示的复数所对应的点 位于第四象限.故选:D
10.(23-24高一下·安徽·月考)复数 在复平面内所对应的点位于( )
A.第―象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【解析】复数 在复平面内所对应的点的坐标为 ,位于第二象限.故选:B.
11.(23-24高一下·山东泰安·期中)当 时,复数 在复平面内对应的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】因为 ,所以 ,
所以复数 在复平面内对应的点位于第四象限.故选:D.
12.(23-24高一下·四川成都·期中)复平面内表示复数 的点位于四象限
时,实数 的取值范围是( )
A. B. C. D.
【答案】B
【解析】由已知复平面内表示复数 的点位于四象限,
则 ,即 ,即 ,故选:B.
【题型4 复数的模长相关计算】
满分技法
计算复数的模时,应先找出复数的实部与虚部,然后再利用复数的模的公式进行计算.两个虚数不能比较大
小,但它们的模可以比较大小.
13.(23-24高一下·福建厦门·月考)复数 ,其中i为虚数单位,则 ( )
A. B.2 C. D.5
【答案】C
【解析】因为 ,则 故选:C
14.(23-24高一下·湖北·期中)(多选)已知复数z满足 ,则( )
A. B. C. D.
【答案】AC
【解析】设复数 ,由 ,得 ,
所以 解得
所以 ,则 .故选:AC
学科网(北京)股份有限公司 学科网(北京)股份有限公司15.(2024·河南商丘·模拟预测)已知复数 和 满足 ,则 ( )
A.1 B. C. D.2
【答案】A
【解析】设
因为 ,所以 ,即 ,①
又 ,所以 ,即 ,②
又 ,所以 ,即 ,③
② ③可得 ,④
把①代入④可得 ,
所以 ,故A正确;故选:A.
16.(23-24高一下·陕西西安·月考)若复数 满足 ,且 在复平面内对应的点位于第四象限,写出一
个符合条件的复数 .
【答案】 (不唯一,符合题意即可)
【解析】设 , ,因为 ,所以 ,
因为 在复平面内对应的点位于第四象限,所以 可以为 .
【题型5 复数四则混合运算】
满分技法
解决复数四则运算问题的思路:
1、复数的加减法:实部与虚部相加减,虚部与虚部相加减分别作为结果的实部与虚部。把i看作字母,类
比多项式加减法中的合并同类项;
2、复数的乘法可以按照多项式的乘法计算,只是在结果中要将 换成 ,并将实部、虚部分别合并. 多
项式展开中的一些重要公式仍适用于复数,常用公式有 ,
, .
2、复数的除法法则在实际操作中不方便适用,一般将除法写成分式形式,采用“分母实数化”的方法,
即将分子、分母同乘分母的共轭复数,使分母成为实数,再计算.
17.(23-24高一下·河南濮阳·月考)设复数 在复平面内对应的点为 ,则 ( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B. C. D.
【答案】C
【解析】因为复数 在复平面内对应的点为 ,所以 ,
所以 .故选:C.
18.(23-24高一下·河南驻马店·月考)已知 为虚数单位,复数 满足 ,则 ( )
A. B. C. D.
【答案】A
【解析】根据题意, ,则 .故选:A
19.(23-24高一下·黑龙江佳木斯·期中)设 , ,则a等于 .
【答案】
【解析】因为 ,
又 , ,所以 ,解得 .
20.(23-24高一下·河南郑州·期中)计算(1) ;(2) ;(3)
【答案】(1)13;(2) (3)
【解析】(1) ;
(2) ;
(3) .
【题型6 复数高次幂的周期性应用】
满分技法
计算复数的乘积要用到虚数的单位i的乘方,in有如下性质:
i1=i,i2=-1,i3=i·i2=-i,i4=i3·i=-i·i=1,
学科网(北京)股份有限公司 学科网(北京)股份有限公司从而对于任何n∈N ,都有i4n+1=i4n·i=(i4)n·i=i,
+
同理可证i4n+2=-1,i4n+3=-i,i4n+4=1.
这就是说,如果n∈N ,那么有i4n+1=i,i4n+2=-1,i4n+3=-i,i4n+4=1.
+
由此可进一步得(1+i)2=2i,(1-i)2=-2i,=-1,=i,=-i.
21.(23-24高一下·江西·月考)已知复数 满足 ,则 ( )
A.1 B. C. D.
【答案】D
【解析】 , .故选:D.
22.(23-24高一下·河南·期中) ( )
A.0 B. C.1 D.
【答案】A
【解析】因为 , , , ,所以具有周期性,周期为 ,
所以 ,所以 .故选:A
23.(22-23高一下·广东广州·期中)已知i是虚数单位,则 .
【答案】
【解析】 ,故 .
24.(23-24高一下·山东滨州·月考) .
【答案】
【解析】因为 ,所以 .
【题型7 共轭复数及辨析】
满分技法
共轭复数问题的求解技巧:
学科网(北京)股份有限公司 学科网(北京)股份有限公司1、若复数 的代数式已知,则根据共轭复数的定义,可以写出 ,再进行复数的四则运算.
2、已知关于 和 的方程,而复数 的代数形式位置,求解 .
解决此类问题的常规思路是:设 ,则 ,代入所给等式,利用复数相等的充要
条件,转化为方程(组)求解.
25.(23-24高一下·河南商丘·月考)设 ,则 的虚部是( )
A.1 B.-1 C. D.
【答案】B
【解析】依题意, ,
则 ,所以 的虚部是 .故选:B
26.(23-24高一下·天津河西·期中)复数 的共轭复数是( )
A. B. C. D.
【答案】C
【解析】因为 ,
所以 ,
所以复数 的共轭复数是 .故选:C
27.(2024·福建莆田·三模)(多选)若z是非零复数,则下列说法正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【答案】BCD
【解析】对于A,由 ,得 ,则A错误.
对于B,因为 ,所以 ,解得 或 (舍去),则B正确.
对于C,设 ( ,且 ),
则 ,所以 ,则C正确.
学科网(北京)股份有限公司 学科网(北京)股份有限公司对于D,由 ,得 .
设 ( ,且 ),则 ,
,从而 ,则D正确.故选:BCD
28.(23-24高一下·江苏南京·月考)已知虚数 满足: 为实数,则 .
【答案】1
【解析】设 ,则 ,
为实数,
于是 ,即 ,故 .
【题型8 复数范围内的解方程】
满分技法
在复数范围内,实系数一元二次方程ax2+bx+c=0(a≠0)的求解方法:
(1)求根公式法:
−b±√b2−4ac
** 错误的表达式 **当∆≥0时,x= ** 错误的表达式 **当∆<0时,
2a
−b±√−(b2−4ac)i
x=
2a
(2)利用复数相等的定义求解,设方程的根为x=m+ni(m,n∈R),
将此代入方程ax2+bx+c=0(a≠0),化简后利用复数相等的定义求解.
29.(23-24高一下·湖南岳阳·期中)在复数范围内,方程 的解集为 .
【答案】
【解析】由 ,得 或 ,即 或 .
30.(23-24高一下·河南安阳·月考)已知p,q为实数, 是关于x的方程 的一个根,则
的值为( )
A.14 B.-14 C.38 D.-38
【答案】C
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】由题意 ,即 ,
,解得 ,所以 .故选:C
31.(23-24高一下·天津河西·期中)已知 是关于 的实系数方程 的两个虚根,则
.
【答案】
【解析】因为 ,即 ,
所以 , ,
则 , ,
所以 .
32.(23-24高一下·吉林·期中)(多选)设方程 在复数范围内的两根分别为 ,则下列关
于 的说法正确的有( )
A. B. C. D.
【答案】ABD
【解析】对A,由实系数一元二次方程求根公式知 ,
则 (与 顺序无关),故A正确;
对B,因为 ,所以 ,故B正确;
对C,由A, ,故C错误;
对D,由韦达定理可得 ,故D正确.故选:ABD
【题型9 与复数模有关的最值问题】
满分技法
1、求复数在复平面内对应点的集合表示的图形时,常用的方法是通过化简得到关于复数模的最简等式或
不等式,然后根据复数的模的几何意义直接判断图形的形状.
学科网(北京)股份有限公司 学科网(北京)股份有限公司2、复数的几何意义是复平面内两点之间的距离公式,
若z=x+ yi,则|z−(a+bi)|表示复平面内点(x,y)与点(a,b)之间的距离,
则|z−(a+bi)|=r表示以(a,b)为圆心,以r为半径的圆上的点.
33.(23-24高一下·河北石家庄·期中)当复数z满足 时,则 的最小值是( )
A.3 B.4 C.5 D.6
【答案】B
【解析】设 ,复数 满足 ,
所以 ,表示 到点 的距离为1,
所以 到原点的距离的最小值为 ,即 的最小值是4.故选:B
34.(23-24高一下·福建·期中)已知复数 满足 ,则 的最小值为 .
【答案】
【解析】根据复数模的几何意义可知, 表示复数 与复数 对应两点间的距离为1,
所以复数 对应的点是以点 为圆心,1为半径的圆,如图,
表示圆上的点到原点的距离,
由图可知, 的最小值为 .
35.(23-24高一下·浙江杭州·期中)复数 满足 , 是虚数单位,则 的最大值为 .
【答案】
【解析】设复数 ,
因为 ,所以 ,即 ,
所以 ,
因为 ,所以 ,
当 时, 最大,即 的最大值为 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司36.(22-23高一下·广东广州·期中)已知 ,且 ,i为虚数单位,则 的最小值是
.
【答案】
【解析】令 ,则 ,
所以,等价于坐标系中点 到定点 的距离恒为1,
即动点 在以 为圆心,半径为1的圆上,如下图:
又 表示动点 到定点 的距离,而 与 的距离为 ,
所以 ,
在 之间且共线,左侧等号成立; 在 之间且共线,右侧等号成立;
所以 的最小值是 .
【题型10 复数三角形式的应用】
满分技法
1、将复数z=a+bi(a,b∈R)化为三角形式z=r(cosθ+isinθ)时,要注意以下两点:
(1)r=√a2+b2,
a b π
(2)cosθ= ,sinθ= ,其中θ终边所在象限与点(a,b)所在象限相同,当a=0,b>0时,arg z=
r r 2
2、每一个不等于零的复数有唯一的模与辅角的主值,并且由它的模与辅角的主值唯一确定。因此,两个
非零复数相等当且仅当它们的模与辅角的主值分别相等。
37.(2023高三·全国·专题练习)复数 的三角形式是( )
A. B.
C. D.
【答案】D
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】依题意,令 ,
则 ,所以 ,
因为 ,所以 ,
所以 的三角形式是 .故选:D.
38.(23-24高一下·全国·专题练习)设复数 的辐角的主值是 ,则 的辐角的主值为
( )
A. B. C. D.
【答案】D
【解析】因为 ,
所以 的辐角的主值为 .故选:D.
39.(23-24高一下·河南安阳·月考)法国数学家棣莫弗发现:
,我们称这个结论为棣莫弗定理,则 ( )
A.1 B. C. D.
【答案】B
【解析】 .故选:B
40.(23-24高一下·全国·专题练习)计算下列各式,并用三角形式表示:
(1) ;
(2) ;
(3) .
学科网(北京)股份有限公司 学科网(北京)股份有限公司【答案】(1) ;(2) ;(3)
【解析】(1)原式
(2)原式
(3)原式 .
过关检测
一、单选题
1.(23-24高一下·河南驻马店·月考)已知复数 ,( , 为虚数单位),且
,则( )
A. B.
C. D.
【答案】D
【解析】由复数 ,( , 为虚数单位),
因为 ,可得 ,则 ,解得 .故选:D.
2.(23-24高一下·浙江·期中)若复数 满足 ,则 的虚部为( )
A. B. C. D.
【答案】B
【解析】因为 ,
所以 ,
所以 的虚部为 .故选:B
3.(23-24高一下·浙江·月考)已知复数 ( 为虚数单位),则 的虚部为( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】 ,所以 .故选:B.
4.(23-24高一下·安徽·月考)若复数z满足 ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 ,
所以 ,
则 .故选:D.
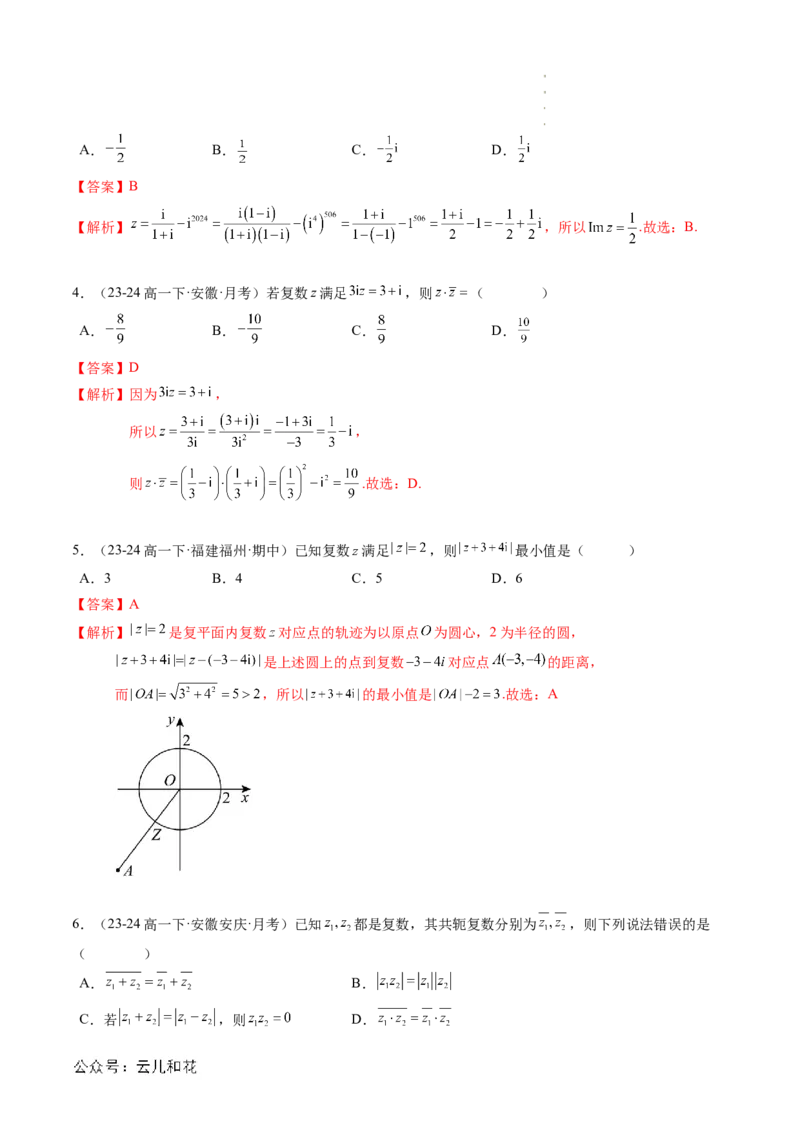
5.(23-24高一下·福建福州·期中)已知复数 满足 ,则 最小值是( )
A.3 B.4 C.5 D.6
【答案】A
【解析】 是复平面内复数 对应点的轨迹为以原点 为圆心,2为半径的圆,
是上述圆上的点到复数 对应点 的距离,
而 ,所以 的最小值是 .故选:A
6.(23-24高一下·安徽安庆·月考)已知 都是复数,其共轭复数分别为 ,则下列说法错误的是
( )
A. B.
C.若 ,则 D.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【答案】C
【解析】对于A,设 ,
则 ,而 ,
故 ,故A正确;
对于B, ,
则 ,
又 ,所以 ,故B正确;
对于C,令 ,则 ,所以 ,
但是 ,故C错误;
对于D, ,又 ,
所以 ,故D正确.故选:C
二、多选题
7.(23-24高一下·河北沧州·期中)已知复数 ,则( )
A.z的虚部为 B.z是纯虚
C.z的模是 D.z在复平面内对应的点位于第四象限
【答案】CD
【解析】对于A.由虚部定义知z的虚部为 .故A错误;
对于B,纯虚数要求实部为0,故B错误;
对于C, ,故C正确;
对于D,z在复平面内对应的点为 ,位于第四象限,故D正确.故选:CD.
8.(23-24高一下·山西忻州·月考)关于复数z,下面是真命题的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【答案】CD
【解析】设 ,则 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司对于选项A:例如 ,则 ,符合题意,但 ,故A错误;
对于选项B:例如 ,则 ,符合题意,但 ,故B错误;
对于选项C:若 ,则 ,
可得 ,解得 ,可知 ,故C正确;
对于选项D:若 ,可知 ,
此时 ,故D正确;故选:CD.
9.(23-24高一下·湖南永州·月考)设 是复数,则下列命题中是真命题的有( )
A.若 ,则 ; B.若 ,则 ;
C.若 ,则 ; D.若 ,则 ;
【答案】BC
【解析】对于A,举例 ,满足前提,由于虚数没有大小,所以选项A是错误的;
对于B,若 ,则 和 互为共轭复数,所以 ,故正确;
对于C,由于只有复数0的模才等于0,所以 ,即 ,所以选项C是正确的;
对于D,由于 ,不妨设 ,
此时 ,显然 ,所以选项D是错误的.故选:BC.
三、填空题
10.(23-24高一下·广东江门·期中)计算: .
【答案】
【解析】 .
11.(23-24高一下·湖南衡阳·期中)若 ( )在复平面内所对应的点在第一象限,则整数
.
【答案】1
学科网(北京)股份有限公司 学科网(北京)股份有限公司【解析】由题意可得 解得 .因为 ,所以 .
12.(23-24高一下·吉林延边·期中)已知复数 满足 ,则复数 在复平面内对应点的集合所构
成的图形面积为
【答案】
【解析】设 ,若 ,则 ,
则点 在以坐标原点为圆心,大圆半径为 ,小圆半径为 的圆环区域内(包括边界),
则复数 在复平面内对应点的集合所构成的图形的面积为 .
四、解答题
13.(23-24高一下·浙江宁波·期中)已知复数 .
(1)若复数 为纯虚数,求 的值;
(2)若 在复平面上对应的点在第三象限,求 的取值范围.
【答案】(1) ;(2)
【解析】(1)由题意得 ,
因为 为纯虚数,
所以 解得
(2)复数
它在复平面上对应的点在第三象限,
所以 ,解得 或 ,
所以实数 的取值范围为 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司14.(22-23高一下·河北邢台·月考)在英语中,实数是Real Quantity,一般取Real的前两个字母“Re”表
示一个复数的实部;虚数是Imaginary Quantity,一般取Imaginary的前两个字母“Im”表示一个复数的虚部.
如: , ; , .已知复数z是方程 的解.
(1)若 ,且 (a, ,i是虚数单位),求 ;
(2)若 ,复数 , ,且 , ,求t的取值范围.
【答案】(1) ;(2)
【解析】(1)因为z是方程 的根,解得 ,
Im( ) , ,
, ,
,解得 ,
;
(2) Im( ) ,复数 , ,且Re( ) ,Im( )
,又 ,
,
Re( ) ,Im( )
,解得 .
所以t的取值范围为 .
15.(23-24高一下·福建泉州·期中)已知复数 ,
(1)求证: ;
(2)化简: ;
(3)若 是方程 的一个根,求 的值.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【答案】(1)证明见解析;(2) .(3)2.
【解析】(1)由 ,得 ,所以 .
(2)由(1)知, ,则 ,
所以 .
(3)依题意, ,即 ,
即 ,
而 ,则 ,解得 ,所以 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司