2025一2026学年度上期高2027届期末考试数学_2024-2025高二（7-7月题库）_2026年1月高二_260128四川省成都市第七中学2025一2026学年度上期高二期末考试

2025—2026 学年度上期高 2027届期末考试 数学试卷 考试时间：120分钟 满分：150分 注意事项： 1．本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分． 2．答题前，考生务必先将自己的姓名、考号填写在答题卡上，并使用2B铅笔填涂． 第I卷（选择题） 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目 要求的. 1．直线xcos30的倾斜角为（ ） A．0 B．90 C．30 D．60 2．抛物线 y 2x2的焦点坐标是（ ） 1  1   1  1 A.  ,0 B.  ,0 C. 0,  D. 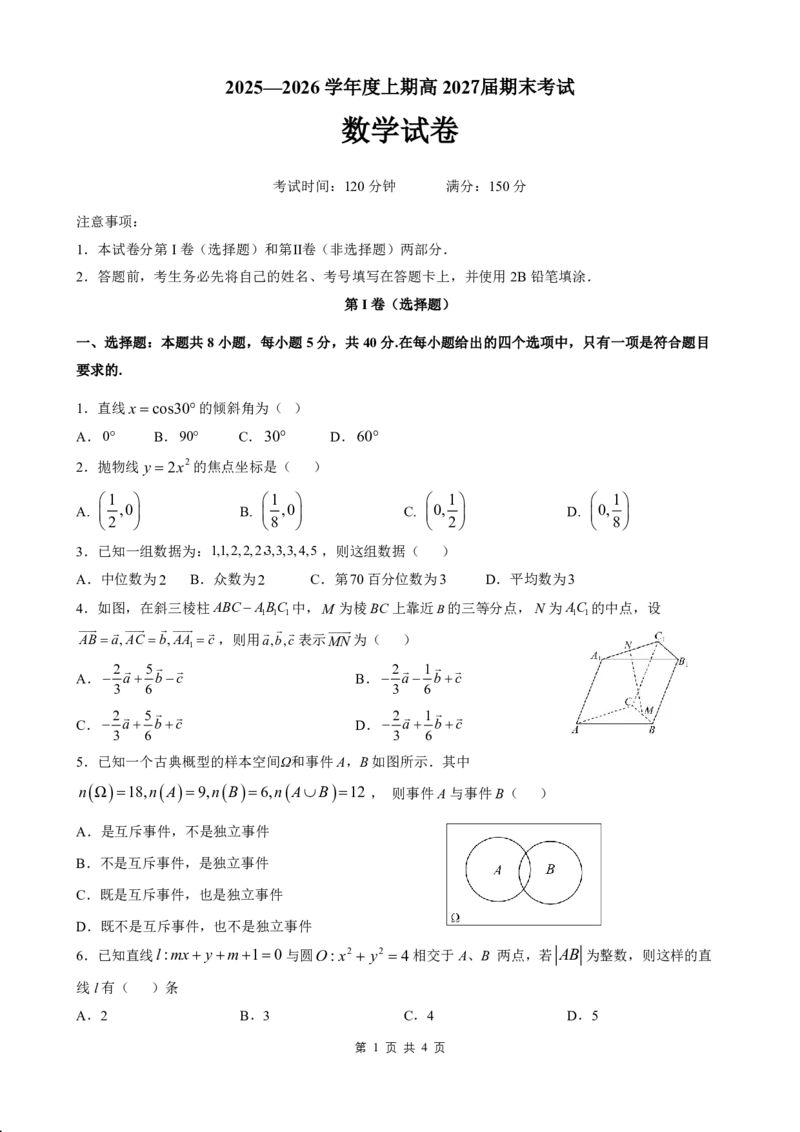0,  2  8   2  8 3．已知一组数据为：1,1,2,2,2，3,3,3,4,5，则这组数据（ ） A．中位数为2 B．众数为2 C．第70百分位数为3 D．平均数为3 4．如图，在斜三棱柱ABCABC 中，M 为棱BC上靠近B的三等分点，N 为AC 的中点，设 1 1 1 1 1           ABa,AC b,AA c，则用a,b,c表示MN为（ ） 1 2  5   2  1   A． a bc B． a bc 3 6 3 6 2  5   2  1   C． a bc D． a bc 3 6 3 6 5．已知一个古典概型的样本空间Ω和事件A，B如图所示．其中 n  Ω 18,n  A 9,n  B 6,n  AB 12 ， 则事件A与事件B（ ） A．是互斥事件，不是独立事件 B．不是互斥事件，是独立事件 C．既是互斥事件，也是独立事件 D．既不是互斥事件，也不是独立事件 6．已知直线l:mx ym10与圆O:x2  y2 4相交于A、B 两点，若 AB 为整数，则这样的直 线l有（ ）条 A．2 B．3 C．4 D．5 第 1 页 共 4 页 {#{QQABBQYg5gA4wJSACJ4KEUFaCgiYkJGjJGgsxQCaKARKgBNABAA=}#}{#{QQABBQYg5gA4wJSACJ4KEUFaCgiYkJGjJGgsxQCaKARKgBNABAA=}#}第II卷（非选择题） 三、填空题：本题共3小题，每小题5分，共15分. x2 y2 12．已知双曲线方程为： - =1，则该双曲线的渐近线方程为 ． 4 9 x2 y2 13．已知点F ，F 为椭圆  1(a b 0)的左、右焦点，点P为该椭圆上一点，且满足 1 2 a2 b2 2 FPF  ，若△PFF 的外接圆面积是其内切圆面积的4倍，则该椭圆的离心率为 ． 1 2 3 1 2 2 14．三棱锥ABCD满足BCAC BDAD  8，二面角CABD的大小为 ，CD AB， 3 AB4，CD 3 3，则三棱锥ABCD外接球的表面积为 ． 四、解答题：本题共5小题，共77分，解答应写出文字说明，证明过程或演算步骤. 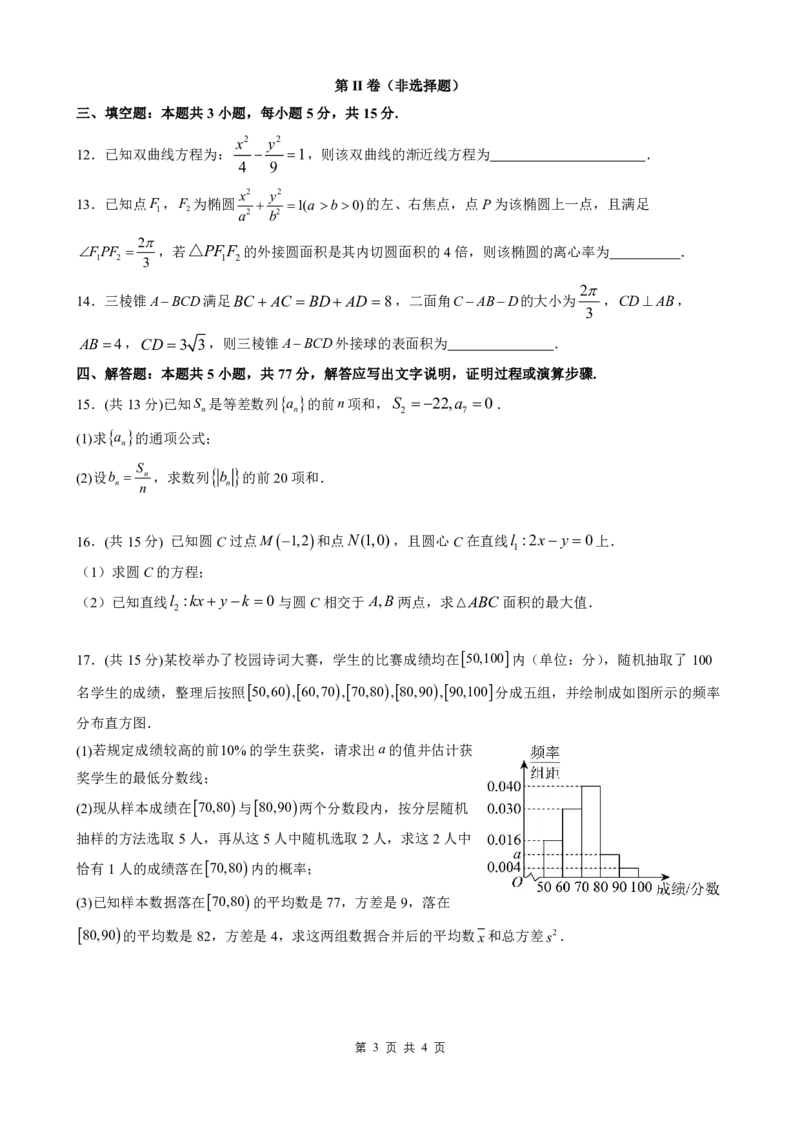15．(共13分)已知S 是等差数列a 的前n项和，S 22,a 0． n n 2 7 (1)求a 的通项公式； n S   (2)设b  n ，求数列 b 的前20项和． n n n 16．(共15分) 已知圆C过点M1,2和点N(1,0)，且圆心C在直线l :2x y 0上． 1 （1）求圆C的方程； （2）已知直线l :kx yk 0与圆C相交于A,B两点，求ABC 面积的最大值． 2 17．(共15分)某校举办了校园诗词大赛，学生的比赛成绩均在50,100内（单位：分），随机抽取了100 名学生的成绩，整理后按照 50,60,  60,70,  70,80,  80,90,  90,100 分成五组，并绘制成如图所示的频率 分布直方图． (1)若规定成绩较高的前10%的学生获奖，请求出a的值并估计获 奖学生的最低分数线； (2)现从样本成绩在 70,80与 80,90两个分数段内，按分层随机 抽样的方法选取5人，再从这5人中随机选取2人，求这2人中 恰有1人的成绩落在 70,80内的概率； (3)已知样本数据落在 70,80的平均数是77，方差是9，落在  80,90的平均数是82，方差是4，求这两组数据合并后的平均数x和总方差s2． 第 3 页 共 4 页 {#{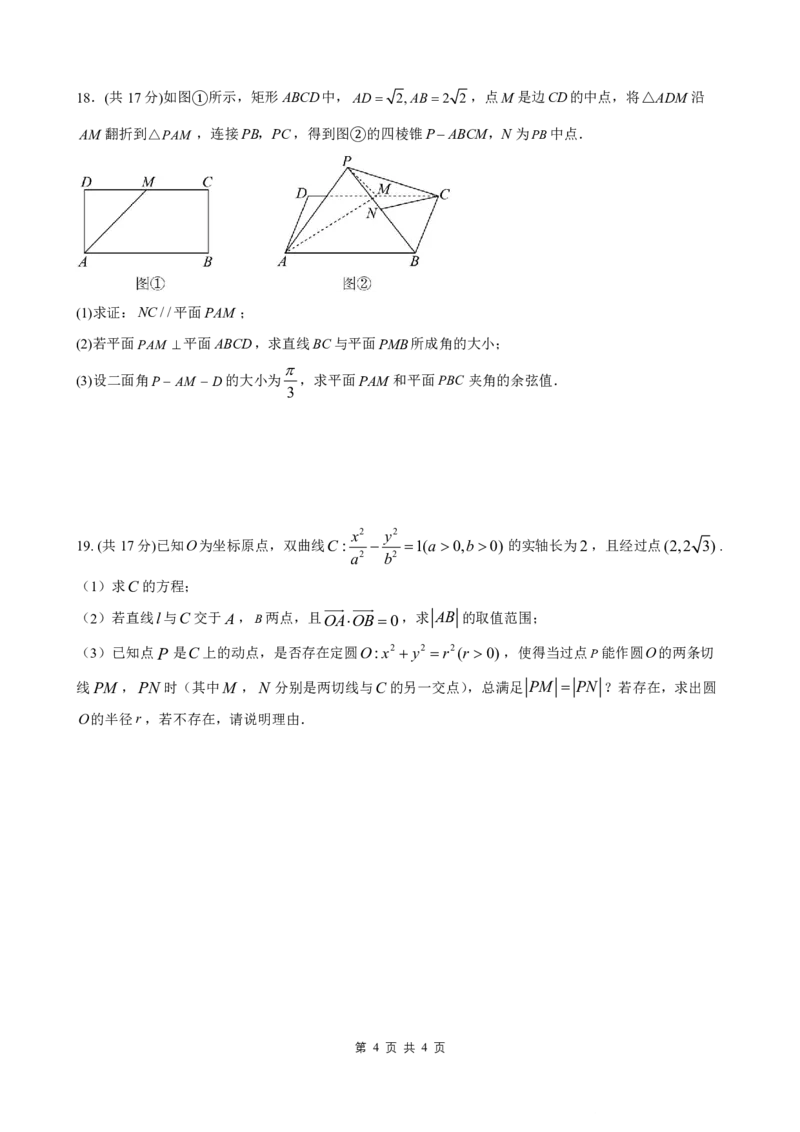QQABBQYg5gA4wJSACJ4KEUFaCgiYkJGjJGgsxQCaKARKgBNABAA=}#}18．(共17分)如图 所示，矩形ABCD中，AD 2,AB2 2，点M 是边CD的中点，将△ADM 沿 AM 翻折到△PAM ①，连接PB，PC，得到图 的四棱锥PABCM，N为PB中点． ② (1)求证：NC//平面PAM ； (2)若平面PAM 平面ABCD，求直线BC与平面PMB所成角的大小；  (3)设二面角P AM D的大小为 ，求平面PAM 和平面PBC 夹角的余弦值． 3 x2 y2 19.(共17分)已知O为坐标原点，双曲线C:  1(a 0,b0) 的实轴长为2，且经过点(2,2 3). a2 b2 （1）求C的方程；   （2）若直线l与C交于A，B两点，且OAOB0，求 AB 的取值范围； （3）已知点P 是C上的动点，是否存在定圆O:x2  y2 r2(r  0)，使得当过点P能作圆O的两条切 线PM ，PN 时（其中M ，N 分别是两切线与C的另一交点），总满足 PM  PN ？若存在，求出圆 O的半径r，若不存在，请说明理由． 第 4 页 共 4 页 {#{QQABBQYg5gA4wJSACJ4KEUFaCgiYkJGjJGgsxQCaKARKgBNABAA=}#}