文档内容
数学新题型研究
湖北省黄冈中学目 录
有什么新题型
新题型的特点
新题型的备考策略有什么新题型
01
一、新定义
二、新背景
三、新方法有什么新题型
01
一、新定义
(2024年北京卷)有什么新题型
01
一、新定义有什么新题型
01
一、新定义
( 年北京高考题)
2022有什么新题型
01
一、新背景
(2024年新课标Ⅰ卷)有什么新题型
01
一、新背景
(2024年新课标Ⅰ卷)有什么新题型
01
一、新方法
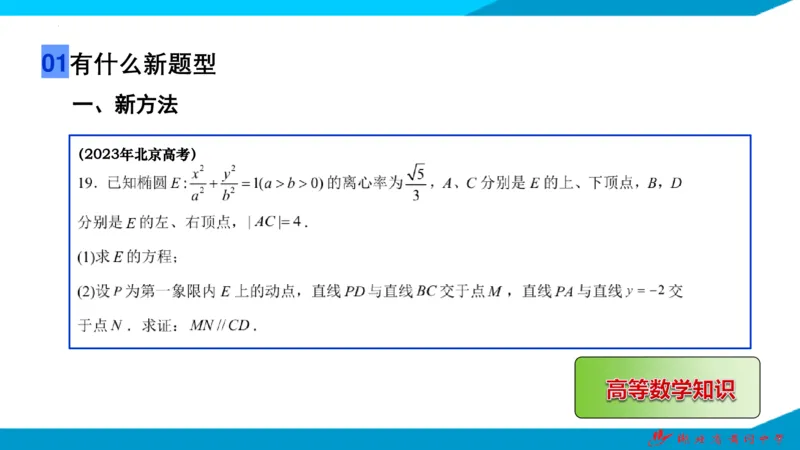
(2023年北京高考)有什么新题型
01
一、新方法新题型有何特点
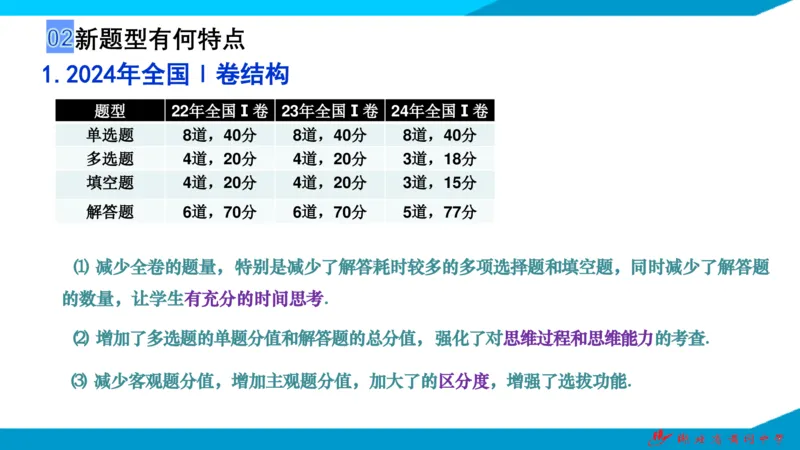
1.2024年全国Ⅰ卷结构
题型
22
年全国Ⅰ卷
23
年全国Ⅰ卷
24
年全国Ⅰ卷
单选题 道, 分 道, 分 道, 分
8 40 8 40 8 40
多选题 道, 分 道, 分 道, 分
4 20 4 20 3 18
填空题 道, 分 道, 分 道, 分
4 20 4 20 3 15
解答题 道, 分 道, 分 道, 分
6 70 6 70 5 77
(1)减少全卷的题量,特别是减少了解答耗时较多的多项选择题和填空题,同时减少了解答题
的数量,让学生有充分的时间思考.
(2)增加了多选题的单题分值和解答题的总分值,强化了对思维过程和思维能力的考查.
(3)减少客观题分值,增加主观题分值,加大了的区分度,增强了选拔功能.新题型有何特点
(1)呈现方式的多样性:图象、表格、文本、符号等;
(2)阅读量大,信息多,翻译成数学符号语言较难;
(3)题目简短,寻找切入口难;
(4)以竞赛为背景,即时学习、应用要求高;
(5)思维与计算并重
.新题型有何特点--呈现方式的多样性
(2024年新课标Ⅰ卷)新题型有何特点--阅读量大,信息多。新题型有何特点--题目简短,寻找切入口难;
( 年北京高考题)
2022新题型有何特点--以竞赛为背景。
(2024年新课标Ⅰ卷)新题型有何特点--思维与计算并重
.新题型的备考策略
一.强化阅读理解 突破审题瓶颈 提升数学素养
“数学阅读理解能力”是指学生看数学材料并领会其内容的能力,对
数学材料的阅读过程是一个完整的心理过程,包括对数学语言(文字、
数学符号、公式、图表等)的认读和感知,对新概念的同化和顺应,对
材料的理解和记忆等各种心理活动
.
阅读包括获取信息、加工信息、整理信息,即审题理解及初步的思考新题型的备考策略
一.强化阅读理解 突破审题瓶颈 提升数学素养
这题需要学生通过阅读,将问题转化为随机变量问题,利用期望的可加性得到等量
关系,从而避免繁琐的列举。新题型的备考策略
一.强化阅读理解 突破审题瓶颈 提升数学素养
(2024年新课标Ⅰ卷)
考察学生的阅读理解能力,如果理解定义的本质,考生是可以顺利完成的。新题型的备考策略
一.强化阅读理解 突破审题瓶颈 提升数学素养
举措:
、高中数学教材共涉及 余篇阅读材料,内容广泛,为数学阅读活动提供了有
1 40
力支持,可以让学生阅读各类的材料,提升数学阅读能力。
、引导学生熟悉数学符号和图形语言,掌握数学分析方法并学会做数学阅读笔记,
2
培养学生良好的阅读习惯。新题型的备考策略
二. 提高复习效率,避免复习盲点
为了避免复习盲点,制定《高考数学考点
细目表》,对每一个模块、章节的考点,印发
给学生,一方面可以让复习与测试更有针对性,
另一方面也为学生提供参照,结合每次测试,
梳理考查的重点与热点问题,了解自身的弱点
和易错点,从而能更好的应对新高考。新题型备考的策略
三.研究有简单竞赛背景的试题
有竞赛背景的
2024
年全国Ⅰ卷第
19
题,与
2024
年北京海淀二模定义相似
.
高考题:把从 开始的有限个正整
1
数平均分成若干个等差数列
模拟题:把所有的正整数分成
个等差数列
n新题型的备考策略
三.研究有简单竞赛背景的试题
与 年北京高考题架构相似。
2022
( 年北京高考题)
2022
基础定义 特殊情况 普适性质,引导考生从特殊到一般的路径研究新定义。
→ →新题型的备考策略
1.梳理过往高考和联赛中有可能的关联试题,并研究通性通法
x2 y2
(2022 年)已知点 A(2,1) C: − =1(a >1) l 交 C 于 P , Q 两
a2 a2 −1
, 的
AP AQ
的斜
l
若 tan∠PAQ = 2 2 ∆PAQ
1
(2011年全国高中数学联合竞赛试卷一试)作斜率为 的 l与椭
3
x2 y2
C: + =1 A , B 两 P(3 2, 2) l的左
36 4
∆PAB
∠APB =60° ∆PAB新题型的备考策略
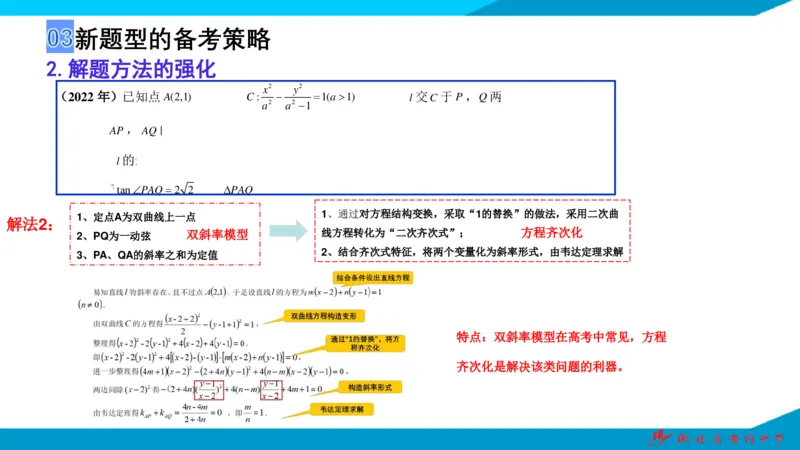
2.解题方法的强化
x2 y2
(2022 年)已知点 A(2,1) C: − =1(a >1) l 交 C 于 P , Q 两
a2 a2 −1
, 的
AP AQ
的斜
l
若 tan∠PAQ = 2 2 ∆PAQ
联立方程,由韦达定理求 ,
直线 与双曲线 相交,直线 消掉 , 得到关于斜
解法 :
1
,由直线斜率的坐标构造关于
,
𝒍𝒍
的斜率
𝐶𝐶
之和为0 𝑥𝑥1 +𝑥𝑥2
率 的𝑥𝑥1 式子𝑥𝑥2
, 等式
𝑥𝑥1 � 𝑥𝑥2
𝑨𝑨𝑨𝑨 𝑨𝑨𝑨𝑨
𝒌𝒌
𝑥𝑥1 +𝑥𝑥𝟐𝟐 𝑥𝑥1 � 𝑥𝑥2
特点:解法常规,易想,但计算量大新题型的备考策略
2.解题方法的强化
x2 y2
(2022 年)已知点 A(2,1) C: − =1(a >1) l 交 C 于 P , Q 两
a2 a2 −1
, 的
AP AQ
的斜
l
若 tan∠PAQ = 2 2 ∆PAQ
解法 :
1、定点A为双曲线上一点
1、通过对方程结构变换,采取“1的替换”的做法,采用二次曲
2
2、PQ为一动弦 双斜率模型 线方程转化为“二次齐次式”; 方程齐次化
3、PA、QA的斜率之和为定值
2、结合齐次式特征,将两个变量化为斜率形式,由韦达定理求解
特点:双斜率模型在高考中常见,方程
齐次化是解决该类问题的利器。新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
解 ( )根据 可分数列的定义,只需要剩余的 项为连续自然数即可,可知
: 1 4
𝒊𝒊,𝒋𝒋 − 𝑖𝑖,𝑗𝑗 = 𝟏𝟏,𝟐𝟐 , 𝟓𝟓,𝟔𝟔 ,(𝟏𝟏,𝟔𝟔)新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
根据定义,直接通过枚举法是比较困难的,即使通过枚举法试出来,将降低第二问本
身的效率,更影响第三问的作答。新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
我们就可以由“一般 特殊”思维来研究对象
→
特殊化
条件“ ” 研究 的情形,再推广到一般情形
特殊化
𝑚𝑚 ≥ 3 𝑚𝑚 = 𝟑𝟑
条件“公差不为0的等差数列 …, ” 数列1,2, …, +2
𝟏𝟏 𝟐𝟐 𝟒𝟒𝟒𝟒+𝟐𝟐
𝒂𝒂 , 𝒂𝒂 , 𝒂𝒂 𝟒𝟒𝟒𝟒新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
挖掘新定义中的隐性关联
性质 :如果数列 是 可分,那么 也是 可分
1 , ,…, , ,… , .
性质 2 :如果数列 𝒂𝒂𝟏𝟏, 𝑎𝑎𝟐𝟐,… ,𝑎𝑎𝟏𝟏𝟒𝟒 ( 是 𝒊𝒊,𝒋𝒋) 可分,数 𝑎𝑎 列1 𝑎𝑎,22,…, 𝑎𝑎𝟒𝟒𝑚𝑚++2𝟐𝟐也是 (𝑖𝑖,𝑗𝑗) 可分 .
性质 3 :如果数列 𝒂𝒂𝟏𝟏, 𝑎𝑎𝟐𝟐,… ,𝑎𝑎𝟒𝟒𝟒𝟒+𝟐𝟐是 (𝒊𝒊,𝒋𝒋) 可分,则等差 𝟏𝟏 数列 𝟒𝟒𝑚𝑚 , (𝑖𝑖,,𝑗𝑗…) , , 也是可分数列 .
性质 4 :如果数列 𝒂𝒂�𝟏𝟏�𝑎𝑎𝟐𝟐, ,…𝑎𝑎𝟒𝟒 𝟒𝟒,+𝟐𝟐 (𝒊𝒊 是 ,𝒋𝒋) 可分,删去 , 𝑎𝑎4后𝑚𝑚+余2 下 𝑎𝑎4𝑚𝑚+𝟏𝟏个奇数 𝑎𝑎2, 𝑎𝑎𝟏𝟏 个偶数 .
𝟏𝟏 𝑎𝑎𝟐𝟐 𝑎𝑎𝟒𝟒𝟒𝟒+𝟐𝟐 (𝒊𝒊,𝒋𝒋) 𝒂𝒂𝒊𝒊 𝑎𝑎𝒋𝒋 𝟐𝟐𝟒𝟒 2𝑚𝑚新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
解:当 时,要证数列 是( ) 可分数列
, ,… , 2,13 — 经过对数列新定义的探索,是可以
𝟒𝟒 ≥ 𝟑𝟑 只需要证明𝑎𝑎1 𝑎𝑎2 𝑎𝑎4𝑚𝑚+2 是( ) 可分数列
, ,… , , 2,13 —
提高答题效率的,体现了高考命题“突
只需证数列𝑎𝑎1 𝑎𝑎2 𝑎𝑎𝟏𝟏𝟑𝟑 是𝑎𝑎( 1𝟒𝟒 ) 可分数列
1,2,…,13,14 2,13 —
出思维品质的考察”
所以依定义,数列 是( ) 可分数列
1,2,…,13,14 2,13 —新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)
由“特殊 一般”思维,挖掘新定义中的隐性关联
→
性质 :如果数列 是 可分,则也是( , )可分,
5 , ,… , + +
(其中, ,𝒂𝒂𝟏𝟏 𝑎𝑎𝟐𝟐 𝑎𝑎𝟒𝟒𝟒𝟒+𝟐𝟐 ) (𝒊𝒊,𝑗𝑗) 𝟒𝟒𝒌𝒌 𝑖𝑖 𝟒𝟒𝒌𝒌 𝑗𝑗
+ +2
𝒌𝒌 ∈ 𝑍𝑍 4𝑘𝑘 𝑗𝑗 ≤ 𝟒𝟒𝟒𝟒新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)新题型的备考策略
四.研究数列新定义问题的解题路径
(2024年新课标Ⅰ卷)新题型的备考策略
五.研究数列新定义问题的解题路径
题目价值与教学启示
、在解题过程中,引导学生用“特殊到一般” ,“归纳”,“命题构造
1
等手段获取新知识”
、在数学新定义的教学实践中,允许学生犯错,引导学生在错误中不断纠错,
2
寻求思维的正向或反向创新突破。新题型的备考策略
六.有针对性地命题和训练:
专题练以时间量命题,针对当下复习的重、难点及学生的痛点,并有
原题和高仿题再现 同时控制题量,给学生充足的时间思考
. .新题型的备考策略
七.新高考第19题
可能的方向
1.
(1) 导数相关的综合性压轴题:
( 年黄冈市 月联考)
2024 9新题型的备考策略
七.新高考第19题
可能的方向
1.
(2)数列相关的综合性压轴题:
(
2024
年新课标全国Ⅱ卷)新题型的备考策略
七.新高考第19题
可能的方向
1.
(2)数列相关的综合性压轴题:
( 年北京高考题)
2022新题型的备考策略
七.新高考第19题
应对措施
2.
分类整合第 题新定义压轴题,并将各类题型适时的在考试和训练
(2) 19
中加以练习:新题型的备考策略
七.新高考第19题
可能的方向
1.
(3)高等数学知识为背景的题型:
(2023年北京高考)新题型的备考策略
七.新高考第19题
应对措施
2.
(1)分层分类进行相关训练
:
清北的关键生:竞赛教练和特优班老师做一些知识的拓展与培训,再辅以适当的训练;
(1)
实验班老师:考试与训练中进行适当难度新题型训练:
(2)
平行班老师:适当引入加强阅读理解能力训练的一些题目
(3) .新题型的备考策略
八.新高考第19题
应对措施
2.
梳理教材中可能作为试题背景的内容:
(3)