文档内容
山东师范大学附属中学2024-2025学年高二下学期3月阶段检
测检测数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数 ,则 ( )
A.0 B.1 C. D.
2.设曲线 在点 处的切线方程为 ,则 ( )
A.1 B. C. D.
3.一木块沿某一斜面自由下滑,测得下滑的水平距离 与时间 之间的函数关系式
为 ,则 时,此木块在水平方向的瞬时速度为( )
A. B. C. D.
4.已知函数 的部分图象如图所示, 为 的导函数,则( )
A. B.
C. D.
5.当 是函数 的极值点,则 的值为
A.-2 B.3 C.-2或3 D.-3或2
6.已知函数 在区间 单调递增,则 的最大值为( )A.1 B. C. D.
7.设 , , ,则 , , 大小关系是
A. B. C. D.
8.若函数 和 的图象上恰好有两对关于x轴对称的点,则函数 和 为
“对偶函数”.已知 , 是“对偶函数”,则实数a的取值范
围为( )
A. B. C. D.
二、多选题
9.函数 的导函数的图像如图所示,以下命题正确的是( )
A.函数 在 处取得最小值 B. 在区间 上单调递增
C. 是函数 的极小值点 D. 在 处切线的斜率大于零
10.设函数 ,则( )
A. 是 的极大值点
B.当 时,
C.当 时,D.曲线 有且只有一个对称中心,且该对称中心坐标为
11.已知函数 ,对定义域内任意 ,都有 ,则正实
数 的取值可能是( )
A. B. C.1 D.
三、填空题
12.已知直线 与曲线 在点 处的切线垂直,则直线 的斜率为
.
13.若函数 ,则使得 成立的 的取值范围是 .
14.已知函数 ,函数 ,若函数 恰有
三个零点,则 的取值范围是 .
四、解答题
15.已知函数
(1)求曲线 在点 处的切线方程;
(2)求函数 的单调区间.
16.已知函数 在 处的切线方程为 .
(1)求a的值;
(2)证明: 时, .
17.将一个边长为1米的正六边形铁皮的六个角截去六个全等的四边形,再把它沿虚线折起(如图),做成一个无盖的正六棱柱铁皮盒.
(1)试把这个正六棱柱铁皮盒的容积 表示为盒底边长 的函数;
(2) 多大时,盒子的容积 最大?并求出最大值.
18.已知函数 ,其中 .
(1)讨论 的单调性;
(2)证明: 在 上均恰有一个零点.
19.已知
(1)设 ,求 的极值.
(2)若 在 上恒成立,求 的取值范围.
(3)若存在常数 ,使得对任意 , 恒成立,则称 在 上有上界 ,函
数 称为有上界函数.如 是在 上没有上界的函数, 是在 上没有
上界的函数; 都是在 上有上界的函数.若 ,
则 是否在 上有上界?若有,求出上界;若没有,给出证明.山东师范大学附属中学2024-2025学年高二下学期3月阶段检测检测
数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A D B B A A ABD ACD
题号 11
答案 ACD
1.A
【详解】由题, ,故 .
故选:A.
2.C
【详解】切线 的斜率为 ,
由 ,
故选:C
3.A
【详解】因为 ,所以 时,此木块在水平方向的瞬时速度为
.
故选:A
4.D
【详解】由导数的几何意义可知, 表示曲线 在 处的切线斜率,
表示曲线 在 处的切线斜率,
表示 , 两点连线的斜率,
由图可知,当 从0变化到1时, 切线斜率越来越大,
所以 ,对比选项可知,D正确.
故选:D.
5.B
【详解】由 ,得 ,
∵x=1是函数f(x)的极值点,
∴ (1)=6﹣ +a=0,解得 或 2,
当 2时, 恒成立,即 单增,无极值点,舍去;
当 3时, 时,x=1或x= 9,
满足x=1为函数f(x)的极值点,
∴ .
故选B.
6.B
【详解】因为函数 在区间 单调递增,所以 在区间
上恒成立,即 ,
令 , ,则 ,所以 在 上单调递增,则
,故 ,即 的最大值为 ,
故选:B
7.A
【详解】考查函数 ,则 , 在 上单调递增,
, (3) ,即 ,
,
故选: .
8.A
【详解】因为 , 是“对偶函数”,
所以函数 与 的图象上恰好有两对关于x轴对称的点,所以 ,即 有两个不相等的实数解,
则 有两个不相等的实数解.
令 ,则 ,
所以当 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 在 处取得极小值,且 , .
又 ,所以 ,a的取值范围为 ,
故选:A.
9.ABD
【详解】由图可知,
当 时, ,当 时, ,∴函数 在 处取得最小值,
A选项正确;
当 时, ,∴ 在区间 上单调递增,B选项正确;
当 时, ,当 时, ,∴ 在 处没有极值,C选项错
误;
当 时, ,∴ 在 处切线的斜率大于零,C选项正确.
故选:ABD.
10.ACD
【详解】函数 的定义域为R,求导得 ,
当 或 时, ;当 时, ,
函数 在 上单调递增,在 上单调递减,对于A, 是 的极大值点,A正确;
对于B, 在 上单调递减, ,则 ,B错误;
对于C,当 时, , , ,C正
确;
对于D,令 , ,函数 是奇函数,
函数 的图象关于原点对称,则函数 的图象关于点 对称,
若函数 的图象还有一个对称中心 ,则
,而 不为常数,
因此点 不是函数 图象的对称中心,即函数 的图象有且只有一个对称中
心,
则曲线 有且只有一个对称中心,且该对称中心坐标为 ,D正确.
故选:ACD
11.ACD
【详解】因为 ,所以 ,
所以 可化为 ,
即 ;令 ,
则有对于定义域内任意 ,都有 ,
所以 在 上单调递减,所以在 上, ;
因为 ,所以 ,即 ,
因为 ,所以 ,即 ;令 , ,当 时,解得 ,
所以当 时, , 单调递减,
当 时, , 单调递增;
可化为 , ,因为 所以 ;
由 ,可知当 时, ,当 时, ,
根据 在 上的单调性以及 的正负情况,
有:若 ,则 在 上恒成立,所以 ,
即 在 上恒成立;令 ,则 ,
,解得 ,所以当 时, , 单调递增,
当 时, , 单调递增减,
所以 时, 取得最大值, ,所以 ;
因为 , , 均满足题意, 不合题意,所以ACD正确,B错误.
故选:ACD.
12. /
【详解】由题设 ,则 ,
所以与曲线 在点 处的切线垂直的直线 斜率为 .
故答案为:
13.
【详解】由 可得:函数定义域为 , .因为 ,当且仅当 时等号成立,
所以 ,
则函数 为 上的增函数.
所以 等价于 ,解得: .
故答案为: .
14.
【详解】解:当 时, ,所以 ,
当 时, ,函数 在 上单调递减,
当 时, ,函数 在 上单调递增,
且 , , ,
当 时, ,当 时, ,
当 时,与一次函数 相比,函数 增长更快,
从而 ,
当 时, ,所以 ,
当 时, ,函数 在 上单调递增,
当 时, ,函数 在 上单调递减,
且 , ,
当 时, ,当 时, ,当 时,与对数函数 相比,一次函数 增长更快,
从而
当 ,且 时, ,
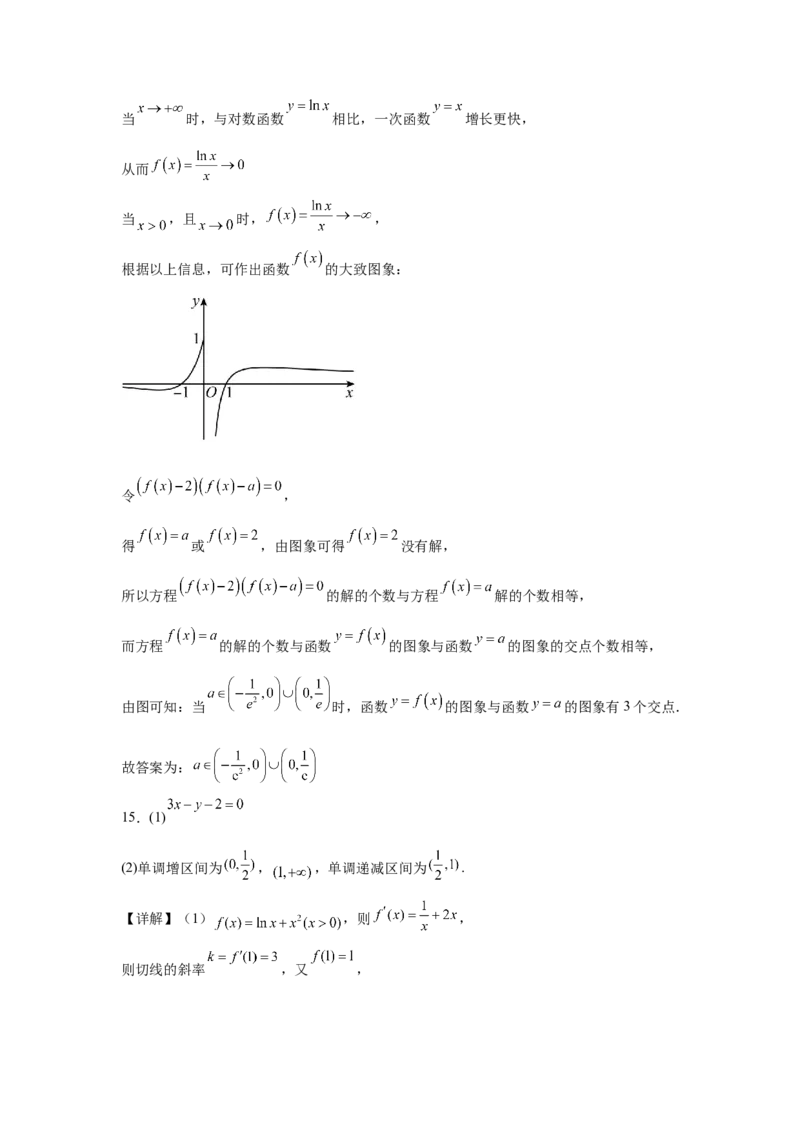
根据以上信息,可作出函数 的大致图象:
令 ,
得 或 ,由图象可得 没有解,
所以方程 的解的个数与方程 解的个数相等,
而方程 的解的个数与函数 的图象与函数 的图象的交点个数相等,
由图可知:当 时,函数 的图象与函数 的图象有3个交点.
故答案为:
15.(1)
(2)单调增区间为 , ,单调递减区间为 .
【详解】(1) ,则 ,
则切线的斜率 ,又 ,所以曲线 在点 处的切线方程为 .
(2) ,
则 ,
由 ,可得 或 ;由 ,可得 ,
所以函数 的单调增区间为 , ,单调递减区间为 .
16.(1)1
(2)证明见解析
【详解】(1)已知函数 ,对其求导可得 .
因为函数 在 处的切线方程为 ,将 代入 可得:
.
由于切线方程为 ,其斜率为 ,所以 ,解得 .
(2)当 时, .
要证明 时, ,即证明 ,移项可得 .
设 , ,对 求导得 .
因为 的值域是 ,所以对于 ,有 ,即 .
这说明 在 上单调递减.
那么 ,将 代入 可得 .
所以 ,即 时, .17.(1)
(2)当 米时,盒子的容积 最大为 立方米
【详解】(1)如图, ,
则盒子的高 ,
所以盒子的底面积 ,
所以盒子的容积 ,
(2)由(1)可得 ,
所以 ,
令 ,解得 (舍去),
所以当 时 ,则 单调递增,
当 时 ,则 单调递减,
所以当 时 取得极大值,即最大值,
所以当 米时,盒子的容积 最大为 立方米.
18.(1)答案见解析
(2)证明见解析【详解】(1)首先求函数 的定义域和导数.
函数 的定义域为 .
对 求导可得 , , .
然后令 ,即 ,则 ,解得 或 .
接着分情况讨论:
当 时, ,当且仅当 时取等号.所以 在 上单调递增.
当 时, .
在区间 和 上, ,所以 在 , 上单调递增;
在区间 上, ,所以 在 上单调递减.
当 时, .
在区间 和 上, ,所以 在 , 上单调递增;
在区间 上, ,所以 在 上单调递减.
综上所得,
当 时, 在 上单调递增;
当 时, 在 , 上单调递增,在 上单调递减;
当 时, 在 , 上单调递增,在 上单调递减.
(2)当 时, ;当 时, ,且 ,由
(1)可知,
当 时, 在 取得极大值, 在 上恰有一个零点.当 时, 在 上单调递增. 在 上恰有一个零点.
当 时, 在 取得极大值,且 ,
所以 在 上恰有一个零点.
综上所得, , 在 上均恰有一个零点.
19.(1)极小值 ,没有极大值
(2)
(3)没有,证明见解析
【详解】(1) ,
令 ,解得 .
所以在 上 单调递减;
在 上, 单调递增;
所以函数 有极小值 ,没有极大值.
(2)依题意, 在 上恒成立,
设 , ,
当 时, 单调递增, ,不符合题意.
当 时, ,
令 ,解得 ,即 使 ,在 上, 单调递增;
在 上, 单调递减,不符合题意;
当 时, 单调递减, ,符合题意;
综上: .
(3)没有上界,理由如下:
由(2)可知, 在 上恒成立,
令 ,则 ,
所以 ,
将上述式子相加得