福建名校联盟优质校数学试题_2024年2月_01每日更新_19号_2024届名校联盟全国优质校高三大联考_2024届名校联盟全国优质校高三大联考数学

保密★启用前 试卷类型：A 准考证号______ 姓名______ （在此卷上答题无效） 名校联盟全国优质校 2024 届高三大联考 数学试题 2024.2 本试卷共 4页，考试时间 120分钟，总分 150分。 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改 动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本 试卷上无效。 3．考试结束后，将答题卡交回。 一、选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一项 是符合题目要求的． 1．已知集合A= { x 2x2 −5x+2<0 } ,B = { x x >1 } ，则AB =（ ）  1 1  1  A．0,  B． ,1 C． ,2 D．( 1,2 )  2 2  2  1−i 2．已知i为虚数单位， =（ ） 1−2i 5 10 5 2 A． B． C． D． 5 5 2 5       3．已知a,b是两个单位向量，若 a−b = 3，则a与b 的夹角为（ ） π π 2π 5π A． B． C． D． 6 3 3 6 x2 y2 4．设直线x−3y+m =0 ( m ≠0 )与双曲线 − =1(a >b>0)分别交于A、B两点，若线段AB的中 a2 b2 4 点横坐标是 m，则该双曲线的离心率是（ ） 5 学科网（北京）股份有限公司5 7 A． B． C．2 D． 2 2 2 (x−µ)2 − 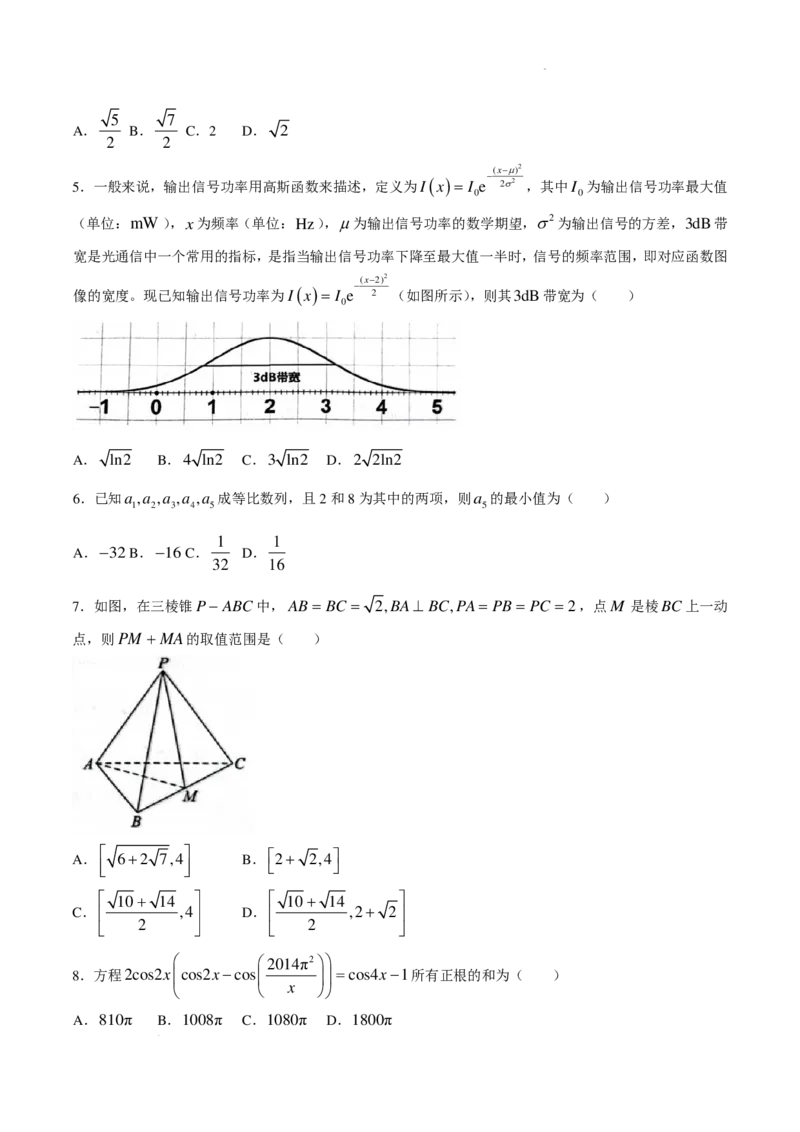5．一般来说，输出信号功率用高斯函数来描述，定义为I ( x )= I e 2σ2 ，其中I 为输出信号功率最大值 0 0 （单位：mW），x为频率（单位：Hz），µ为输出信号功率的数学期望，σ2为输出信号的方差，3dB带 宽是光通信中一个常用的指标，是指当输出信号功率下降至最大值一半时，信号的频率范围，即对应函数图 (x−2)2 − 像的宽度。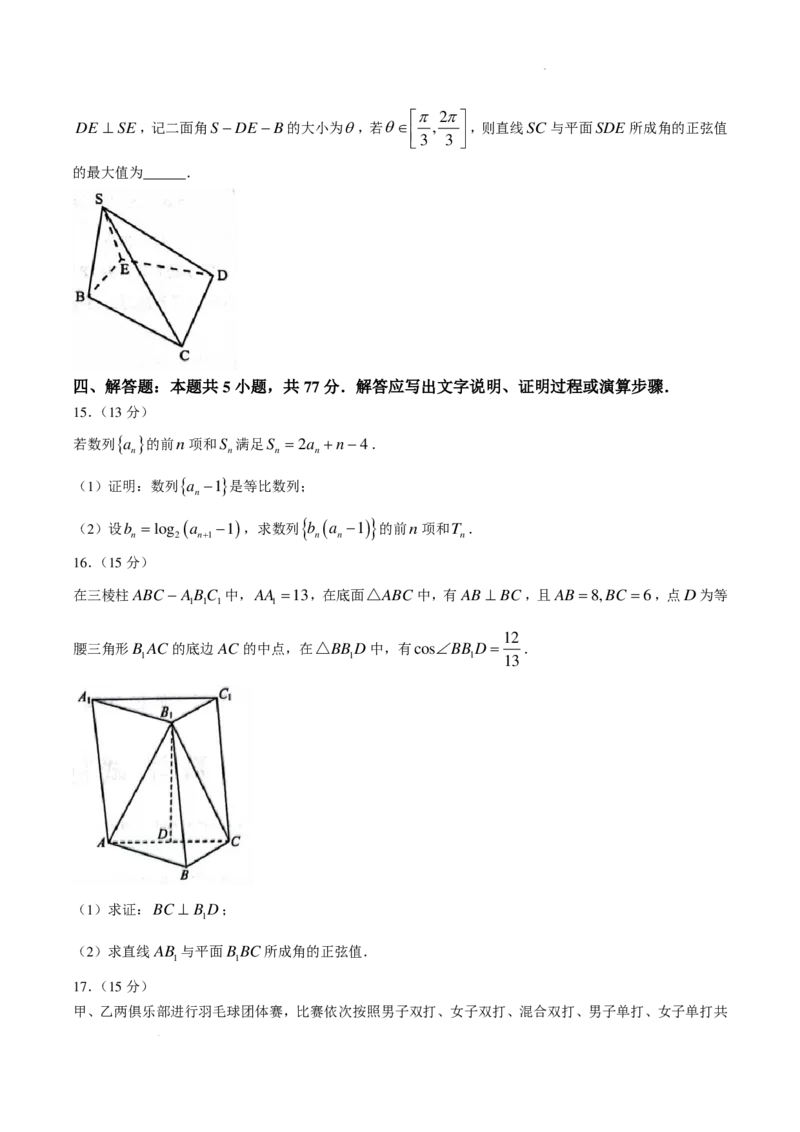现已知输出信号功率为I ( x )= I e 2 （如图所示），则其3dB带宽为（ ） 0 A． ln2 B．4 ln2 C．3 ln2 D．2 2ln2 6．已知a ,a ,a ,a ,a 成等比数列，且2和8为其中的两项，则a 的最小值为（ ） 1 2 3 4 5 5 1 1 A．−32 B．−16 C． D． 32 16 7．如图，在三棱锥P− ABC中，AB = BC = 2,BA⊥ BC,PA= PB = PC =2，点M 是棱BC上一动 点，则PM +MA的取值范围是（ ） A．  6+2 7,4  B．2+ 2,4      10 + 14   10 + 14  C． ,4 D． ,2+ 2 2 2      2014π2  8．方程2cos2xcos2x−cos =cos4x−1所有正根的和为（ ）   x  A．810π B．1008π C．1080π D．1800π 学科网（北京）股份有限公司二、多项选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，有多项符 合题目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分． 9．下列命题正确的是（ ） A．若A、B两组成对数据的样本相关系数分别为r =0.97,r = −0.99，则A组数据比B组数据的相关性 A B 较强 B．若样本数据x ,x ,⋅⋅⋅,x 的方差为2，则数据2x −1,2x −1,⋅⋅⋅,2x −1的方差为8 1 2 6 1 2 6 C．已知互不相同的30个样本数据，若去掉其中最大和最小的数据，剩下28个数据的22%分位数不等于原 样本数据的22%分位数 D．某人解答5个问题，答对题数为X ，若X ∼ B ( 5,0.6 )，则E ( X )=3 lnx 10．对于函数 f ( x )= ，下列说法正确的是（ ） x 1 A． f ( x )在x =e处取得极大值 e B． f ( x )有两个不同的零点 C． f ( 4 )< f (π)< f ( 3 ) D．π4 <4π 11．已知M 是圆O :x2 + y2 −2nx−2ny+n2 =0 ( n∈N* ) 上任意一点，过点P (−1,n )向圆O 引斜率为 n n n n k ( k >0 )的切线l ，切点为Q ( x ,y )，点A ( 3n,n )，则下列说法正确的是（ ） n n n n n n n n 2n+1 A．n =1时，k = 3 B．y = +n 1 n n+1 1−x  x  1 3 C． n < 2sin n  D． M A + M P 的最小值是 n+1 1+ x  y −n 2 n n n n 2 n n 三、填空题：本题共 3小题，每小题 5分，共 15分． S S 12．设S 是数列{ a }的前n项和， n+1 − n =1,a =5，则a =______． n n n+1 n 3 2024  π 13．设函数 f ( x )=sin ωx+ (ω>0)在区间( 0,π)上恰有两个零点，则ω的取值范围是______．  3 14．如图，在△SBE 中，SE = BE =1，在直角梯形BEDC中，BE ⊥ DE,CD∥BE,CD =2,DE = 3， 学科网（北京）股份有限公司π 2π DE ⊥ SE，记二面角S −DE −B的大小为θ，若θ∈ , ，则直线SC 与平面SDE所成角的正弦值   3 3  的最大值为______． 四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤． 15．（13分） 若数列{ a }的前n项和S 满足S =2a +n−4． n n n n （1）证明：数列{ a −1 }是等比数列； n （2）设b =log ( a −1 )，求数列 { b ( a −1 )} 的前n项和T ． n 2 n+1 n n n 16．（15分） 在三棱柱ABC− ABC 中，AA =13，在底面△ABC 中，有AB ⊥ BC，且AB =8,BC =6，点D为等 1 1 1 1 12 腰三角形B AC的底边AC的中点，在△BBD中，有cos∠BBD = ． 1 1 1 13 （1）求证：BC ⊥ BD； 1 （2）求直线AB 与平面BBC所成角的正弦值． 1 1 17．（15分） 甲、乙两俱乐部进行羽毛球团体赛，比赛依次按照男子双打、女子双打、混合双打、男子单打、女子单打共 学科网（北京）股份有限公司五个项目进行，规定每个项目均采取三局两胜制，且在上述五项中率先赢下三项的俱乐部获胜（后续项目不 再进行比赛）．已知在男双项目、女双项目、男单项目这三项的每局中，甲俱乐部获胜的概率均为0.7；在混 双项目、女单项目这两项的每局中，乙俱乐部获胜的概率均为0.8，假设每局比赛之间互不影响．（注：比赛 没有平局，且所有结果均保留一位小数．） （1）求甲俱乐部在男子双打项目中获胜的概率； （2）记比赛结束时所完成的比赛项目数量为随机变量X，求X的分布列和数学期望． 18．（17分） x2 y2 1 已知椭圆E的方程为 + =1(a >b>0),A为E的左顶点，B为E的上顶点，E的离心率为 ,△ABO a2 b2 2 的面积为 3． （1）求E的方程； （2）过点P (−2,1 )的直线交E于M、N 两点，点M 且垂直于x轴的直线交直线AN 于点H ，证明：线 段MN 的中点在定直线上． 19．（17分） a 已知函数 f ( x )=lnx− ． x （1）当a = −1时，求 f ( x )的极值； （2）若存在实数0< x < 1 ，满足 f ( x )= f   x 0 2  ，求 f ( a2 ) 的取值范围． 0 2 0 1−x  0 学科网（北京）股份有限公司