宝鸡中学2023级高二第一学期阶段考试（一）试题-数学_2024-2025高二（7-7月题库）_2024年10月试卷_1024陕西省宝鸡中学2024-2025学年高二上学期10月月考

宝鸡中学 2023 级高二第一学期阶段考试(一)试题 数 学 本试卷共四大题，19小题；考试时长 120分钟，卷面满分 150分。 注意事项： 1.答卷前，考生务必将自己的姓名、班级、考场/座位号填写在答题卡上，将条形码准确粘贴 在条形码粘贴处。 2.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需 改动，用橡皮擦干净后，再选涂其它答案标号。涂写在本试卷上无效。 3.作答非选择题时，将答案书写在答题卡上，书写在本试卷上无效。 4.考试结束后，将答题卡交回。 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题 目要求的。 1．设m，n是不同的直线，，是不同的平面，下列说法正确的是( ) A．若m//，m//，则// B．若m//，n，mn，则 C．若m，m，则 D．若m//，n，m//n，则// 2.已知三角形 的三个顶点分别为 ， ， ，则 边上的中线所在直线的方程 为( ) (1,0) (2,−3) (3,3) A. B. C. − =0 D. + −6=0 3.过3 点− −6作=直0 线 ，与两坐3 标+轴 相−交12所=得0三角形面积为 ，则直线 有( ) A.1条 (1,1) B.2条 C.3条 1 D. 4条 4.已知圆C：(x－a)2＋(y－b)2＝1过点A(1，0)，则圆C的圆心的轨迹是( ) A.点 B.直线 C.线段 D.圆 5.若a2＋b2＝2c2(c≠0)，则直线ax＋by＋c＝0被圆x2＋y2＝1所截得的弦长为( ) 1 2 A. B.1 C. D. 2 2 2 6.在长方体ABCD－A B C D ，AB＝1，BC＝2，AA ＝3，则点B到直线A C的距离为( ) 1 1 1 1 1 1 数学试题 （第 1 页，共 4 页） {#{QQABLQQEogioQJJAAQgCAwVYCAMQkBCAASgGBBAAMAIAiBFABCA=}#}2 2 35 35 A. B. C. D.1 7 7 7 x2 y2 7.P是椭圆 ＋ ＝1上一点，F ，F 分别是椭圆的左、右焦点，若|PF |·|PF |＝12，则∠F PF 的 1 2 1 2 1 2 16 9 大小为( ) A.30° B.60° C.120° D.150° 8.设两圆C ，C 都和两坐标轴相切，且都过点(4，1)，则两圆心的距离|C C |等于( ) 1 2 1 2 A.4 B.4 2 C.8 D.8 2 二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对 的得6分，部分选对的得部分分，有选错的得0分。 9.下列说法中正确的是( ) A. 1是直线 与直线 0平行的充分不必要条件 B. =1是直线 − =11与直线 − −1=0垂直的充分不必要条件 2 C. 经 过=点 ， 且−在 两=坐标轴上 的+截 距 相−反1的=直线方程是 0 D. 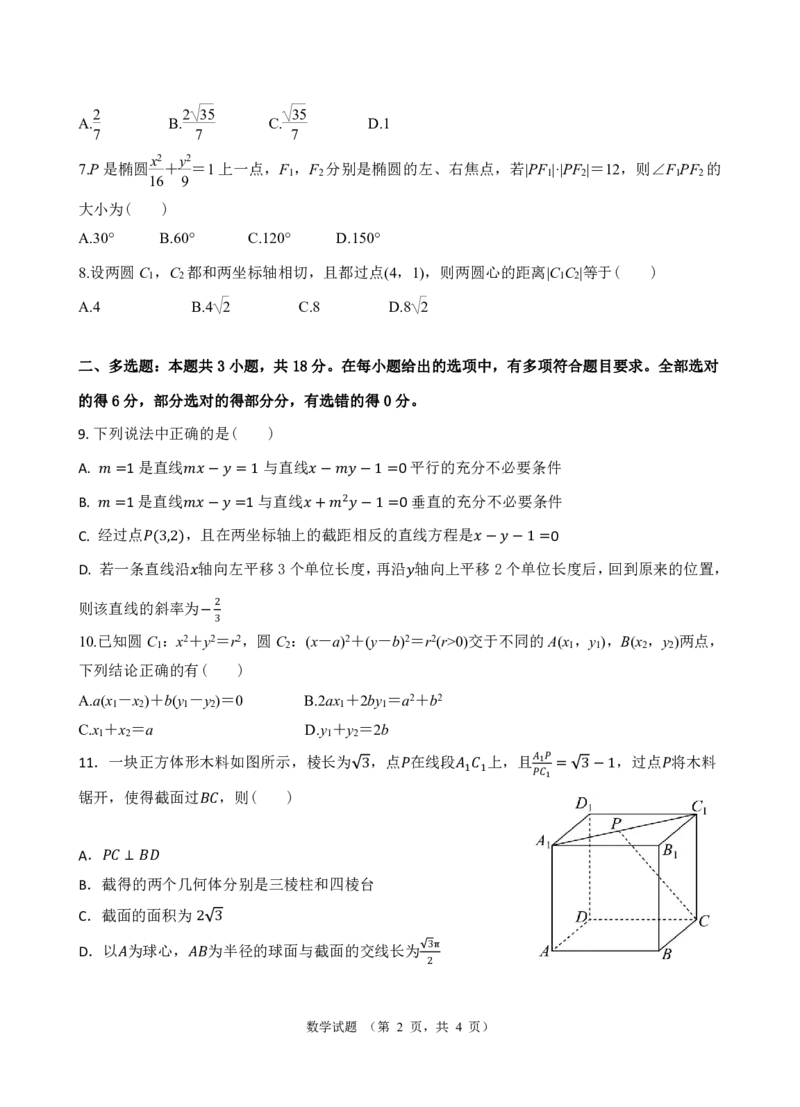若一条 直(3线,2沿) 轴向左平移3个单位长度，再沿 轴向上平 移−2 个−单1位=长度后，回到原来的位置， 则该直线的斜率为 2 10.已知圆C 1 ：x2＋−y23＝r2，圆C 2 ：(x－a)2＋(y－b)2＝r2(r>0)交于不同的A(x 1 ，y 1 )，B(x 2 ，y 2 )两点， 下列结论正确的有( ) A.a(x －x )＋b(y －y )＝0 B.2ax ＋2by ＝a2＋b2 1 2 1 2 1 1 C.x ＋x ＝a D.y ＋y ＝2b 1 2 1 2 11．一块正方体形木料如图所示，棱长为 ，点 在线段 上，且 ，过点 将木料 1 锯开，使得截面过 ，则( ) 3 1 1 1 = 3−1 A． B．截 得 ⊥ 的 两 个几何体分别是三棱柱和四棱台 C．截面的面积为 D．以 为球心， 2为3半径的球面与截面的交线长为 3π 2 数学试题 （第 2 页，共 4 页） {#{QQABLQQEogioQJJAAQgCAwVYCAMQkBCAASgGBBAAMAIAiBFABCA=}#}三、填空题：本题共3小题，每小题5分，共15分。 → → → 12.已知A(1，0，0)，B(0，－1，1)，O(0，0，0)，OA＋λOB与OB的夹角为120°，则λ=_________. 13.如图所示，椭圆的中心在原点，焦点F ，F 在x轴上，A，B是椭圆的顶点，P是椭圆上一点， 1 2 且PF ⊥x轴，PF ∥AB，则此椭圆的离心率是_________. 1 2 14.已知直线 与曲线 有两个交点，则 的取值范围为 ． 2 : − +2 =0 : =2− 4− 四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。 15. (13分)设 两点的坐标分别为 , .直线 相交于点 ,且它们的斜率之 积是 . , (− 5,0) ( 5,0) , 1 −5 (1)求点 的轨迹方程. (2)若 （0,1），在M的轨迹上任取一点 异于点 ，求线段 长的最大值． ( ) 16. (15分)已知 分别为 三个内角 的对边,且 . (1)求 ; , , △ , , + − − = (2)若 ,则 的面积为 ,求 . =2 △ 3 , 17. (15分)从两名男生(记为 和 )、两名女生(记为 和 )中任意抽取两人. 1 2 1 2 (1)分别写出有放回简单随机抽样、不放回简单随机抽样和按性别等比例分层抽样的样本空间. (2)在三种抽样方式下,分别计算抽到的两人都是男生的概率. 数学试题 （第 3 页，共 4 页） {#{QQABLQQEogioQJJAAQgCAwVYCAMQkBCAASgGBBAAMAIAiBFABCA=}#}18．(17分)如图，在四棱锥PABCD中，底面ABCD为直角梯形，AD∥BC,CD AD， ADCD2BC2，平面PAD 平面ABCD,PAPD,PAPD ． (1)求证：CDPA； (2)求平面APB与平面PBC夹角的余弦值； PM (3)在棱PB上是否存在点M ，使得DM 平面PAB？若存在，求 的值；若不存在，说明理由． PB 19. (17分)已知点Q为圆M: 4上的动点,点N（6,0），延长NQ至点S使得Q为 2 2 NS的中点． ( −2) + = 求点S的轨迹方程． (1)过圆 外点 向圆 引两条切线，且切点分别为 ， 两点，求： 最小值. (2)若直 线 3 与圆 交于 ，E两点，且直 线 ， 的斜 率 分· 别 为 ， ，则 是 (否3)为定值 若: 是=， 求 +出该定值 若不是 ，请说明理由． 1 2 1+ 2 ? ; 数学试题 （第 4 页，共 4 页） {#{QQABLQQEogioQJJAAQgCAwVYCAMQkBCAASgGBBAAMAIAiBFABCA=}#}