福建4月质检数学答案_2024年4月_01按日期_10号_2024届福建省九市联考高三4月_2024届福建省部分地市高三下学期4月诊断检测（三模）数学

绝密★启用前 试卷类型：A 2023-2024 学年福州市高三年级第三质量检测评分参考 数 学 2024.4 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的． 题号 1 2 3 4 5 6 7 8 答案 C D A B B C A D 1．已知复数z满足(z1)i1i（i是虚数单位），则z  A．1 B．1 C．i D．i 解析：∵zii1i，∴zi1，即zi，故选C. 5 2．已知角的顶点在坐标原点，始边与x轴非负半轴重合，cos ，P(m,2)为其终边 5 上一点，则m A．4 B．4 C．1 D．1 5 2 解析：∵cos ，∴tan 2，∴m1，故选D. 5 m x2 3 3．函数 f(x) 的图象大致为 x2 1 解析：结合该函数为偶函数，及 f 03可判断应选A.       4．在菱形ABCD中，若|ABAD||AB|，且AD在AB上的投影向量为AB，则 A．  1 B．1 C．  2 D． 2 2 2 2 2    解析：由已知 ABAD  AB 知该菱形中AB ADBD， 1 ∴由D向AB作垂线，垂足即为AB中点，∴ ，故选B . 2 1 5．已知 alog 2，blog a，c( )b，则 5 2 2 数学参考答案及评分标准 第 1 页 共 12 页A. cba B. cab C. abc D. bca 1 解析：∵alog 2log 51，∴blog a0，c( )b 1，∴cab，故选B. 5 5 2 2 6．棱长为1的正方体ABCDABCD 中，点P为BD 上的动点，O为底面ABCD的中心， 1 1 1 1 1 则OP的最小值为 3 6 6 3 A. B. C. D. 3 3 6 2 解析：在正方体中，易知AC BD，AC DD ，且BDDD D ，∴AC 平面BDD ， 1 1 1 易知当OP平面BDD ，且OPBD 时，OP的长度最小， 1 1 6 在RT△BDD 中,不难求得OP ，故选C. 1 6 7．若直线 y axb与曲线 yex相切，则 ab的取值范围为 A．(,e] B．[2,e] C．[e,) D．[2,) 解析：设切点为(x ,ex0)，则aex0, 0 ∴切线方程为yex0(xx )ex0 ，则b(1x )ex0 ，∴ab(2x )ex0 ， 0 0 0 设 f(x)(2x )ex0 ，则 f(x)(1x )ex0 ， 0 0 易知函数 f(x) f(1)e，又 f(2)02，故可判断选A. （由图象知当且仅当切线与曲线相切于1,e时，aba1be1 e最大，亦可知选A.） π 8．已知函数 f(x)2sinx( 3sinxcosx) (0)在(0, )上单调递增，且对任意的实 3 数a， f(x)在(a,aπ)上不单调，则的取值范围为 5 5 1 5 1 5 A．(1, ] B．(1, ] C．( , ] D．( , ] 2 4 2 2 2 4 π 解析：∵ f(x)2sinx( 3sinxcosx)2sin(2x ) 3 ， 3 π π π π 5 ∵ f(x)在(0, )上单调递增，∴2   ，∴ ， 3 3 3 2 4 ∵对任意的实数a， f(x)在区间(a,aπ)上不单调，∴ f(x)的周期T 2π， 2π 1 1 5 ∴T  2π，∴ ，∴  ，故选D． 2 2 2 4 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中,有多 项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 数学参考答案及评分标准 第 2 页 共 12 页题号 9 10 11 答案 ABD ACD BC x2 y2 9．双曲线C:  1 (a0)的左、右焦点分别为F，F ，且C 的两条渐近线的夹角 a2 3a2 1 2 为，若|FF |2e（e为C 的离心率），则 1 2 π A．a1 B． C．e 2 D．C 的一条渐近线的斜率为 3 3 解析：易知该双曲线实半轴为a，虚半轴为 3a，半焦距为2a， 2a ∴离心率e 2，∴焦距4a4，即a1，∴选项A正确，选项C错误； a 3a π 2π 易知C 的两条渐近线的斜率为k   3，∴这两条渐近线的倾斜角分别为 和 ， a 3 3 π ∴C 的两条渐近线的夹角为 ，∴选项B，D正确； 3 综上所述，应选ABD. 10. 定义在R上的函数 f(x)的值域为(,0)，且 f(2x) f(x y)f(x y)0，则 A． f(0)1 B． f(4)[f(1)]2 0 C． f(x)f(x)1 D． f(x) f(x)2 解析：令x y0，则 f 0 f 200， ∵函数 f(x)的值域为(,0)，∴ f(0)1，选项A正确； 令x1，y0，则 f(2)[f(1)]2， 令x2，y0，则 f(4)[f(2)]2 [f(1)]4 ，∴选项B错误； 令x0，则 f(0) f(y)f(y)0， ∴ f(y)f(y)f(0)1，即 f(x)f(x)1，∴选项C正确； ∵f(x)0，f(x)0，∴[f(x) f(x)]2 f(x)f(x) 2 ∴ f(x) f(x)2，故选项D正确； 综上所述，应选ACD. 1, 第n次投出正面, 11. 投掷一枚质地均匀的硬币三次，设随机变量X  (n1,2,3) ．记A n 1, 第n次投出反面, 表示事件“X X 0”，B表示事件“X 1”， C 表示事件“X X X 1”，则 1 2 2 1 2 3 数学参考答案及评分标准 第 3 页 共 12 页A．B和C互为对立事件 B．事件A和C不互斥 C．事件A和B相互独立 D．事件B和C相互独立 解析：考查选项A，事件B和C均会出现“反，正，反”的情况，故选项A错误； 考查选项B，事件A和C均会出现“反，正，反”的情况，故选项B正确； 1 1 1 考查选项C，易知P(A)C1( )2  ，P(B) ， 2 2 2 2 1 事件AB为前两次投出的硬币结果为“反，正”，则P(AB) ， 4 1 ∴P(AB)P(A)P(B) ，故选项C正确； 4 1 1 1 考查选项D，由选项AC可知P(BC)( )3  ，P(B) ， 2 8 2 1 3 在事件C中三次投出的硬币有一次正面，两次反面，则P(C)C2( )3  ， 3 2 8 ∴P(BC) P(B)P(C)，故选项D错误； 综上所述，应选BC． 三、填空题：本题共3小题，每小题5分，共15分． 2m 12.160； 13.2； 14. ；1或2． m2 2 12. (x )6的展开式中常数项为 ． x 2 解析：易知该二项展开式通项为Crx6r( )r ，∴当r 3时，得到常数项为160，故应填160． 6 x 3 13．某圆锥的体积为 π，其侧面展开图为半圆，则该圆锥的母线长为 ． 3 解析：设该圆锥的母线长为l，底面圆半径为r ，根据侧面展开图为半圆得2πr πl， 1 3 即l 2r，又根据圆锥体积得 πr2 l2 r2  π，解得r 1，l 2，故应填2． 3 3 14. 设T 为数列{a }的前n项积，若T a m，其中常数m0．则a  （结 n n n n 2 1 果用m表示）；若数列{ }为等差数列，则m ． T n m m 2m 2m 解析：易知T a  ，∴maa a a ( 1)，解得a  ，故应填 ； 1 1 2 1 2 2 2 2 2 m2 m2 1 1 1 1 1 1 1a       n1 （方法一）T T ma ma m ma m2 ma (n2)， n n1 n n1 m n1 n1 ma 1 n1 数学参考答案及评分标准 第 4 页 共 12 页1 1a 若数列{ }为等差数列，则 n1 为常数d ， T m2 ma n n1 ①若d 0，则a 1(n2)恒成立，即a 1(n1)恒成立，∴m2； n1 n 1dm2, m1, ②若d 0，则1a dm2 dma ，∴ 解得 n1 n1 1dm, d 1, 1 综上所述，若数列{ }为等差数列，则m1，或m2，故应填1或2． T n 1 1 1 1 2 1 2 （方法二）∵{ }为等差数列，∴  d (n2)，易知  ，且  (n1)d， T T T T m T m n n n1 1 n T m 1 当n2时，∵T a m，∴T  n m，∴ 1 ， n n n T T T n1 n n1 1 2 2 ∴由  (n1)d ，可得2m(n1)d 1 (n2)d ， T m m n 2 ∴(m1)dn1 (m2)d 对于任意n恒成立， m m1, d 0,   m1, d 0, ∴ 2 或 2 解得 或  1 (m2)d 0,  1 (m2)d 0, d 1, m2,  m  m 1 综上所述，若数列{ }为等差数列，则m1，或m2，故应填1或2． T n 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15．（13分） 2π △ABC中，角A，B，C的对边分别是a，b，c，且asinCcsinB，C . 3 （1）求B的大小； 3 3 （2）若△ABC的面积为 ，求BC边上中线的长. 4 解：（1）∵asinC csinB，∴由正弦定理，得sinAsinC sinCsinB， …………2分 ∵0C π，∴sinC 0，∴sinAsinB， ………………………………………3分 ∵0 Aπ，0Bπ，∴AB， ……………………………………………………5分 2π π ∵ABC π，且C  ，∴B . ……………………………………………6分 3 6 数学参考答案及评分标准 第 5 页 共 12 页3 3 1 （2）依题意  absinC，………………………………………………………………7分 4 2 ∵AB，∴ab， ………………………………………………………………8分 3 3 1 2π 3a2 ∴  a2sin  ，解得a 3， …………………………………………10分 4 2 3 4 3 设边BC的中点为D，∴CD ,AC  3， 2 ∴在△ACD中，由余弦定理知AD2  AC2 CD2 2ACCDcosC 3 3 2π 21 3 2 3 cos  ， ………………………………………………………12分 4 2 3 4 21 ∴BC边上中线的长为 . 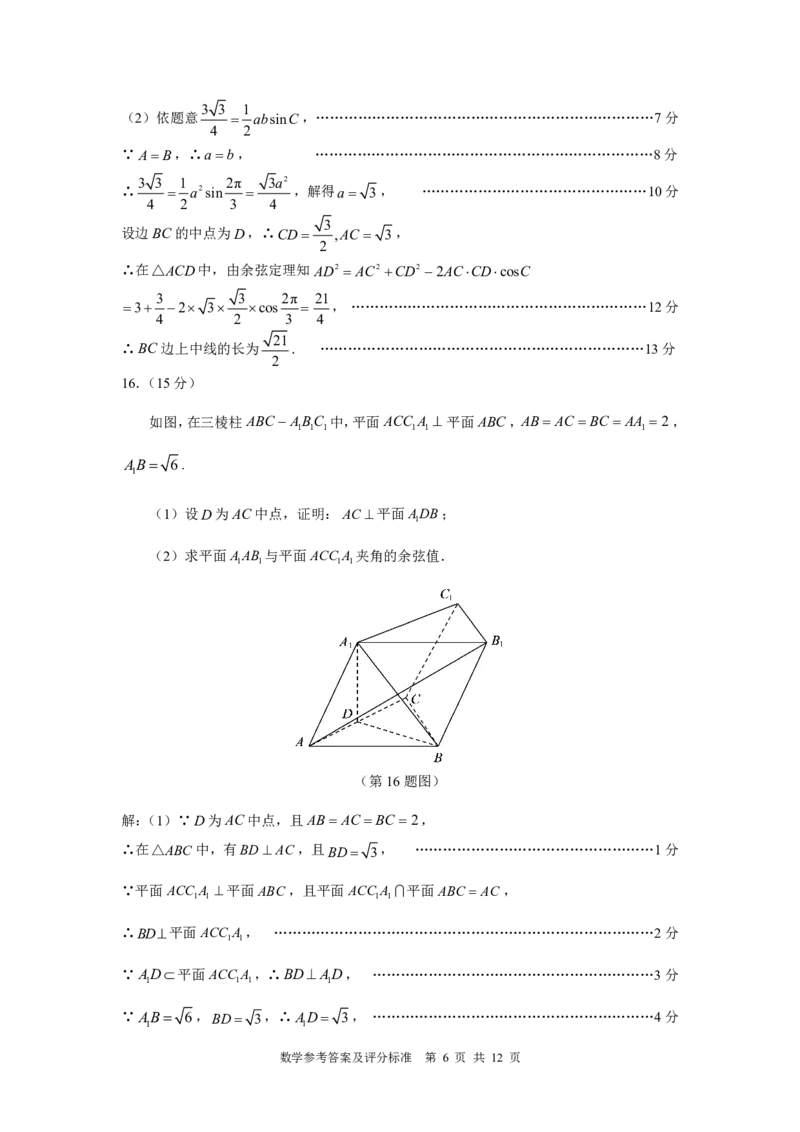……………………………………………………………13分 2 16．（15分） 如图，在三棱柱ABC ABC 中，平面ACC A 平面ABC，AB AC BC  AA  2， 1 1 1 1 1 1 AB 6. 1 （1）设D为AC中点，证明：AC 平面ADB； 1 （2）求平面AAB 与平面ACC A 夹角的余弦值． 1 1 1 1 （第16题图） 解：（1）∵D为AC中点，且AB AC BC 2， ∴在△ABC中，有BD AC，且 BD 3 ， ……………………………………………1分 ∵平面ACC A 平面ABC，且平面ACC A 平面ABC  AC ， 1 1 1 1 ∴BD平面ACC A ， ………………………………………………………………………2分 1 1 ∵AD平面ACC A ，∴BDAD， ……………………………………………………3分 1 1 1 1 ∵AB 6， BD 3 ，∴AD 3， ……………………………………………………4分 1 1 数学参考答案及评分标准 第 6 页 共 12 页∵AD1，AA 2，AD 3， 1 1 ∴由勾股定理，有AC AD， ……………………………………………………………6分 1 ∵AC BD，ADBDD， 1 ∴AC平面ADB， …………………………………………………………………………7分 1 （2）如图所示，以D为原点，DA，DB，DA 所在直线分别为x轴，y轴，z轴建立空间 1 直角坐标系Dxyz， 可得A(1,0,0)，A(0,0, 3)，B(0, 3,0)， ………………………………………………9分 1   ∴AA (1,0, 3)，AB(1, 3,0)， …………………………………………………10分 1 设平面AAB 的法向量为n(x,y,z)， 1 1   nAA 0,  x 3z0, 则由  1 得 nAB0, x 3y0, 令x 3，则 y1，z1，∴n( 3,1,1)， …………………………………………12分 由（1）可知，BD平面ACC A ， 1 1  ∴平面ACC A 的一个法向量为BD(0, 3,0)，…………………………………………13分 1 1 记平面AAB 与平面ACC A 的夹角为， 1 1 1 1  nBD 3 5 ∴cos| |  ， |n||BD| 5 3 5 5 ∴平面AAB 与平面ACC A 夹角的余弦值为 ． ………………………………………15分 1 1 1 1 5 数学参考答案及评分标准 第 7 页 共 12 页17．（15分） 从一副扑克牌中挑出4张Q和4张K，将其中2张Q和2张K装在一个不透明的袋中， 剩余的2张Q和2张K放在外面．现从袋中随机抽出一张扑克牌，若抽出Q，则把它放回袋 中；若抽出K，则该扑克牌不再放回，并将袋外的一张Q放入袋中.如此操作若干次，直到 将袋中的K全部置换为Q. （1）在操作2次后，袋中K的张数记为随机变量X ，求X 的分布列及数学期望； （2）记事件“在操作n1(nN)次后，恰好将袋中的K全部置换为Q．”为A ，记 n P  P(A ). n n （i）在第1次取到Q的条件下，求总共4次操作恰好完成置换的概率； （ii）试探究P 与P 的递推关系，并说明理由. n1 n 解：（1）由题意X 的取值可能为0，1，2， ……………………………………………1分 当X 0时，即第一次取出K，第二次也取出K， 2 1 1 ∴P(X 0)   ， …………………………………………………………2分 22 31 8 当X 1时，即第一次取出Q，第二次取出K，或第一次取出K，第二次取出Q， 2 2 2 3 1 3 5 ∴P(X 1)       ， ……………………………3分 22 22 22 31 4 8 8 当X 2时，即第一次取出Q，第二次也取出Q， 2 2 1 ∴P(X 2)   ， …………………………………………………………4分 22 22 4 ∴X 的概率分布列为 X 0 1 2 1 5 1 P 8 8 4 …………………………………………………………………5分 1 5 1 9 ∴X 的数学期望E(X)0 1 2  ． ……………………………………6分 8 8 4 8 1 （2）（i）记事件“第1次取到Q”为B，事件“总共4次操作恰好完成置换”为C，则P(B) ， 2 ………………………………………………………………………………7分 依题意，若第1次取出Q，则剩余的3次操作，须将袋中K全部置换为Q， ①若第2次亦取出Q，则第3次和第4次均须取出K， 数学参考答案及评分标准 第 8 页 共 12 页1 2 2 1 1 其概率为     ； ………………………………………………………8分 2 2+2 2+2 3+1 32 ①若第2次取出K，则第3次须取出Q，第4次须取出K， 1 2 3 1 3 其概率为     ； ………………………………………………………9分 2 2+2 3+1 3+1 64 1 3  P(CB) 32 64 5 ∴P(C|B)   ，即在第1次取到Q的条件下，总共4次操作恰好完成置 P(B) 1 32 2 5 换的概率为 ． …………………………………………………………………………10分 32 （ii）（方法一）由题可知若事件A 发生，即操作n2次后，恰好将袋中的K全部置换为Q， n1 ①当第1次取出Q，则剩余的n1次操作，须将袋中K全部置换为Q， 2 1 概率为 P  P ； ……………………………………………………………………12分 2+2 n 2 n ②当第1次取出K，则从第2次起，直到第n1次均须取出Q，且第n2次取出K， 2 3 1 1 3 概率为 ( )n  ( )n； ………………………………………………………14分 2+2 3+1 3+1 8 4 1 1 3 ∴P  P + ( )n． …………………………………………………………………15分 n1 2 n 8 4 （方法二）由题可知若事件A 发生，即操作n2次后，恰好将袋中的K全部置换为Q， n1 则一定有第n2次（最后一次）取出K， ①当第n1次（倒数第二次）取出Q，则须在之前的n次操作中的某一次取出K， 3 3 概率为 P  P ； ……………………………………………………………………12分 3+1 n 4 n ②当第n1次（倒数第二次）取出K，则从第1次起，直到第n次均须取出Q， 2 2 1 1 1 1 概率为( )n   ( )n ( )n3； …………………………………………14分 2+2 2+2 3+1 8 2 2 3 1 ∴P  P +( )n3． ……………………………………………………………………15分 n1 4 n 2 18．（17分） 在直角坐标系xOy中，已知抛物线C:y2 2px(p0)的焦点为F ，过F 的直线l与C交 于M ，N 两点，且当l的斜率为1时，|MN |8． （1）求C 的方程； （2）设l与C 的准线交于点P，直线PO与C交于点Q（异于原点）．记线段MN 的中 数学参考答案及评分标准 第 9 页 共 12 页点为R，若|QR|3，求△MNQ面积的取值范围． p 解：(1) 不妨设l的方程为xmy ，M(x ,y )，N(x ,y )， 2 1 1 2 2 联立l与C 的方程，得y2 2mpy p2 0， …………………………………………1分 ∴y  y 2mp，y y p2， …………………………………………………………2分 1 2 1 2 则|MN|x x  pm(y  y )2p2p(m21) ， …………………………………3分 1 2 1 2 ∴由题可知当m1时，|MN|8，∴ p2， …………………………………………4分 ∴C 的方程为 y2 4x． ……………………………………………………………………5分 y  y (2) 由(1)知y  1 2 2m， R 2 将R的纵坐标2m代入xmy1，得R(2m2 1,2m)， ……………………………6分 2 易知C 的准线方程为x1，又l与C 的准线交于点P，∴P(1, )， ……………7分 m m 则直线OP的方程为x y， ………………………………………………………………8分 2 联立OP与C 的方程，得y2 2my ，∴Q(m2,2m)， ……………………………………9分 ∴Q，R的纵坐标相等，∴直线QR∥x轴， ……………………………………………11分 ∴|QR||2m2 1m2|m2 1， …………………………………………………………12分 ∴S △MNQ S △QRM S △QRN  1 2 |QR|| y 1  y 2 | 2(m2 1) m2 12|QR| 3 2 ， …………14分 ∵点Q（异于原点），∴m0， …………………………………………………………15分 ∵|QR|3，∴1|QR|3， 3 ∴ 22|QR|26 3 ，即S △MNQ (2,6 3]． …………………………………………17分 19．（17分） 若实数集A，B对aA，bB ，均有(1a)b 1ab，则称 A B 具有Bernoulli 型关系. （1）判断集合M {x|x1}，N {1,2}是否具有Bernoulli型关系，并说明理由； （2）设集合S {x|x1}，T {x|xt}，若S T 具有Bernoulli型关系，求非负 实数t的取值范围； 数学参考答案及评分标准 第 10 页 共 12 页1 （3）当nN*时，证明： n ( k )  k n 5 ． k1 1k2 8 解：（1）依题意，M N 是否具有Bernoulli型关系，等价于判定以下两个不等式对于x1 是否均成立：①(1 x)1 1 x，②(1 x)2 12x， …………………………………2分 ∵x1，(1x)1 1x，(1x)2 12xx2 12x ∴M N 具有Bernoulli型关系． ………………………………………………………4分 （2）（方法一）令 f(x)(1 x)b bx1，xS ，b(0,)， 则 f(x)b[(1 x)b11]， …………………………………………………………………5分 ①当b 1时，显然有(1a)b 1ab，∴(1 x)b 1 xb成立； ………………………6分 ②当b 1时， 若1 x0，则(1x)b1 (1x)0 1，即 f(x)0，∴ f(x)在区间(1,0)上单调递减， 若x0，则(10)b110，即 f(0)0， 若x0，则(1x)b1 (1x)0 1，即 f(x)0，∴ f(x)在区间(0,)上单调递增， ∴ f(x)的最小值为 f(0)0，∴ f(x) f(0)0， ∴(1x)b (bx1)0， ∴(1 x)b 1 xb成立； ………………………………………………………………8分 ③当0b1时， 若1 x0，则(1 x)b1 (1 x)0 1，即 f(x)0，∴ f(x)在区间(1,0)上单调递增， 若x0，则(10)b110，即 f(0)0， 若x0，则(1 x)b1 (1 x)0 1，即 f(x)0，∴ f(x)在区间(0,)上单调递减， ∴ f(x)的最大值为 f(0)0，∴ f(x) f(0)0， ∴(1x)b (bx1)0，即(1 x)b bx1， ∴当xS，且0b1时，(1 x)b 1 xb不能恒成立， …………………………10分 综上所述，可知若S T 具有Bernoulli型关系，则T {x|x1}， ∴非负实数t的取值范围为[1,)． ……………………………………………………11分 （方法二）当b 1，或0b1时，与方法一相同； …………………………………8分 数学参考答案及评分标准 第 11 页 共 12 页当b 1时， 若ab10，∵(1a)b 01ab，∴(1a)b 1ab， 1 若ab10，则ab1，又b 1，∴0 1， b 1 1 ∴由方法一的结论，可知(1ab)b 1ab 1a， b 1 即 (1ab)b 1a ， …………………………………………………………………………9分 ∵1ab0，且a(1,)， 1 ∴ [(1ab)b]b (1a)b ，即1ab(1a)b，即(1a)b 1ab；………………………10分 ∴若集合S {x|x1}，T {x|xt}具有Bernoulli型关系，则T {x|x1}， ∴非负实数t的取值范围为为[1,)． …………………………………………………11分 k  1 k2 1 1 1 1 （3）∵( ) k ( )2k (1 )2k ， …………………………………………12分 1k2 k2 k2 1 1 显然  1，且0 1， k2 2k 1 1 1 1 1 由（2）中的结论：当0b1时，(1 x)b 1 xb，可知(1 )2k 1+  1 ， k2 k2 2k 2k3 ………………………………………………………………………………………13分 1 2 k 1(k 1) 1 1 1 当k  2时，    [  ]， 2k3 4(k3 k) 4(k 1)k(k 1) 4 (k 1)k k(k 1) 1 1 1 1 1 ∴(1 )2k 1 [  ]，k  2，………………………………………15分 k2 4 (k 1)k k(k 1) 1 当n1时， n ( k )  k  n 5 显然成立； …………………………………………16分 k1 1 k2 8 1 1 当n 2时， n ( k )  k  2   n ( k )  k  3   n [1 1  1 ] k1 1 k2 k2 1 k2 2 k2 4(k 1)k 4k(k 1) 1 1 n 1 1 1 1 1 1 5 1 5 n  [  ]n  [  ]n  n ， 2 4 (k1)k k(k1) 2 4 2 n(n1) 8 4n(n1) 8 k2 1 综上所述，当nN*时， n ( k )  k  n 5 . ……………………………………17分 k1 1 k2 8 数学参考答案及评分标准 第 12 页 共 12 页