2025届江苏省如皋中学高三上学期期初考试-数学_2024-2025高三（6-6月题库）_2024年09月试卷_09212025江苏省如皋中学高三上学期期初考试_2025届江苏省如皋中学高三上学期期初考试PDF

江苏省如皋中学 2024—2025 学年度高三年级测试 数学试卷 一、选择题:本大题共8小题，每小题5分，共40分，在每个小题给出的选项中，只有一 项是符合题目要求的. 1.已知集合U R，集合Ax 3x1 ，Bx 0x2 ，则图中阴影部分表示的集 合为（ ） A．3,0 B．1,0 C．(0,1) D．(2,3) 2. 已知圆锥的底面半径为 2，其侧面展开图为一个半圆，则该圆锥的体积为（ ） 6 2 6 4 6 8 6 A. π B. π C. π D. π 3 3 3 3 3. 顶点在原点，对称轴是y轴，并且顶点与焦点的距离为3的抛物线的标准方程为（ ） A．x2 3y B．y2 6x C．x2 12y D．y2 12x 4. 方程log xlog xlog x的实数解有（ ） 3 6 9 A. 0个 B. 1个 C. 2个 D. 3个 x2 y2 5. 已知直线x4y90与椭圆  10b4相交于A,B两点，椭圆的两个焦点是 16 b2 F ，F ，线段AB的中点为C1,2，则△CFF 的面积为（ ） 1 2 1 2 A．2 2 B．4 2 C．2 3 D．4 3 6. 已知圆C的方程为x2 (y2)2 a，则“a2”是“函数y  x 的图象与圆C有四个公 共点”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 x2 y2 7. 已知双曲线C：  1a0,b0的左、右焦点分别为F ，F ，点M 是双曲线C a2 b2 1 2 右支上一点，直线FM 交双曲线C的左支于N 点．若 FN 2， FM 3， MN 4， 1 1 2 且△MFF 的外接圆交双曲线C的一条渐近线于点Px ,y ，则 y 的值为（ ） 1 2 0 0 03 2 3 5 A． 3 B． C． D．3 2 2 x2 y2 8. 已知F ,F 分别是椭圆  1(a b0)的左右焦点，过F 作直线交椭圆于A、B 1, 2 a2 b2 2 两点，已知AF BF ，ABF 30，则椭圆的离心率为 （ ） 1 1 1 6 2 6 3 A． B． C． 6 2 D． 6 3 2 2 二、多选题:本大题共3小题，每小题6分，共18分，全部选对的得6分，部分选对的得 部分，有选错的得0分. 9. 已知曲线C：mx2ny2 1，下列结论中正确的有（ ） A．若mn0，则C是椭圆，其焦点在x轴上 B．若mn0，则C是圆，其半径为 n m C．若mn0，则C是双曲线，其渐近线方程为y  x n D．若m0，n0，则C是两条直线 10. 如图，正方体ABCDABCD 的棱长为4， 1 1 1 1 点M 是其侧面ADDA上的一个动点（含边界）， 1 1 点P是线段CC 上的动点，则下列结论正确的是（ ） 1 5π A．存在点P,M ，使得二面角M DCP大小为 6 B．存在点P,M ，使得平面BDM 与平面PBD平行 1 1 C．当P为棱CC 的中点且PM 2 6时，则点M 的轨迹长度为 2π 1 32π D．当M 为AD的中点时，四棱锥M ABCD外接球的表面积为 1 3 11. 已知抛物线C:y2 2pxp0上存在一点E2,t到其焦点的距离为3，点P为直线 x2上一点，过点P作抛物线C的两条切线，切点分别为A,B,O为坐标原点．则 A．抛物线的方程为y2 4x B．直线AB一定过抛物线的焦点 （ ） C．线段AB长的最小值为4 2 D．OP AB三、填空题:本题共3小题,每小题5分,共15分。 12. 过点P(2,3)的等轴双曲线的方程为 . 13. 过点P1,2的直线l与曲线y 4x2 有且仅有两个不同的交点，则l斜率的取值范围 为 ． x3 14. 已知过点(0,a)可作三条直线与曲线 f(x) x21相切，则实数a的取值范围 3 为 ． 四、解答题:本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤. 15. 已知函数 f(x)2ex(x1)． (1)求函数 f(x)的极值； (2)求函数 f(x)在区间[t,t1](t 3)上的最小值g(t)． x2 y2 1 16. 设椭圆  1ab0的左焦点为F ，右顶点为A，离心率为 ．已知A是抛物 a2 b2 2 线y2 2pxp0的焦点，F到抛物线的准线l的距离为 1 ． 2 (1)求椭圆的方程和抛物线的方程; (2)设l上两点P，Q，关于x轴对称，直线AP与椭圆相交于点B（B异于点A），直线BQ 6 与x轴相交于点D．若△APD的面积为 ，求直线AP的方程． 2 17. 如图，直三棱柱ABCABC 的体积为1，ABBC，AB2，BC1． 1 1 1 (1)求证：BC ^ AC； 1 1 (2)求二面角B ACB的余弦值． 1 1x2 y2 18. 设双曲线C的方程为  1(a0,b0)，直线l过抛物线y2 8x的焦点和点 a2 b2 0,b .已知C的焦距为6且一条渐近线与l平行. （1）求双曲线C的方程； （2）已知直线m过双曲线C上的右焦点，若m与C交于点A,B（其中点A在第一象 4 限），与直线x 交于点T ，过T 作平行于OA的直线分别交直线OB,x轴于 3 TP 点P,Q，求 . PQ lnex 19. 已知函数 f x ，其中e为自然对数的底数． ax (1)讨论 f x的单调性； (2)若方程 f x1有两个不同的根x,x ． 1 2 (i)求a的取值范围； (ii)证明：x2x2 2． 1 2江苏省如皋中学 2024—2025 学年度高三年级测试 数学答案 1.【答案】A 【详解】因为Ax 3x1 ，Bx 0x2 ， 所以ABx|0x1，所以ð A A  Bx|3x03,0， 即图中阴影部分表示的集合为3,0 .故选：A 2. 【答案】B 【详解】设圆锥母线长为l，高为h，底面半径为r  2， 则由2π 2 πl，得l 2 2 ，所以h  l2 r2  6 ， 1 1 2 2 6 所以V  πr2h π 2  6  π．故选：B． 3 3 3 3. 【答案】C 【详解】设抛物线方程为x2 2pyp0或x2 2pyp0， p 依题意知 =3，∴p=6.∴抛物线方程为x2 12y.故选：C. 2 4. 【答案】C lnx lnx lnx 【详解】log x =  =log xlog x，所以lnx0或 3 ln3 ln6 ln9 6 9 ln6ln9 lnx 2ln6ln36，所以x1或x36， ln3 所以方程log xlog xlog x的实数解有2个.故选：C. 3 6 9 5. 【答案】B y y 1 【详解】设𝐴(𝑥 1 ,𝑦 1 ),𝐵(𝑥 2 ,𝑦 2 )，由题可知 x 1 x 2  4 ，x 1 x 2 2,y 1 y 2 4， 1 2 x2 y2  1 1 6  b 1 2 1 y y b2x x  1 2b2 则 ，所以 1 2  1 2 ，即  ，解得b2 8， x 2 2  y 2 2 1 x 1 x 2 16y 1 y 2  4 416 16 b2 1 所以c2 a2b2 1688，则c2 2，所以S  2c24 2，故选：B． CF1F2 26. 【答案】B 【详解】由圆C的方程为x2 (y2)2 a可得圆心 0,2 ，半径r  a ， 20 若圆与函数y  x相交，则圆心到直线y  x的距离d   2  a， 2 即a2，若函数y  x 的图象与圆C有四个公共点，则原点在圆的外部， 即02 (02)2 a，解得a4， 综上函数y  x 的图象与圆C有四个公共点则2a4， 所以“a2”是“函数y  x 的图象与圆C有四个公共点”的必要不充分条件，故选：B 7. 【答案】D 【详解】因为点M，N分别在双曲线C的右支和左支上，所以 MF  MF  NF  NF 2a．又 FN 2， FM 3， MN 4，所以2a2433 1 2 2 1 1 2 3 ，解得a ， NF 2a NF 325， 2 2 1 所以 NF 2  MN 2 MF 2，所以NMF 是直角． 2 2 2 45 在Rt△MFF 中， FF 2  FM 2 MF 2，所以2c2 6232，解得c2  ， 1 2 1 2 1 2 4 45 9 所以b2 c2a2   9，即b3．又△MFF 的外接圆交双曲线C的一条渐近线于点 4 4 1 2 x2y2 c2  0 0 x2 a2 𝑃(𝑥 0 ,𝑦 0 )，所以OP c，所以点𝑃(𝑥 0 ,𝑦 0 )的坐标满足x2 y2 ，解得 0 ，  a 0 2  b 0 2 0 y 0 2 b2 x a 所以 0 ，故 y 3.故选：D．  y 0 b 0 8. A 解：试题分析：如图所示，设 AF m，因为 AF  BF,ABF 30，所以 1 1 1 1 AB 2m, AF 2am， 2 BF  3m, BF 2m(2am)3m2a， 1 24a 2a(3 3) 所以 3m3m2a 2a，解得m  ，所以3m2 (168 3)a2， 3 3 3 6am(124 3)a2，在AFF 中，由余弦定理得 1 2 (2c)2 m2 (2am)2 2m(2am)cos600，化为4c2 4a2 6am3m2 0，所以 6 2 4c2 4a2 (124 3)a2 (168 3)a2 0，化简得e2 2 3，所以e ， 2 9. 【答案】CD x2 y2  1 1 1 【详解】对于A，若mn0，则mx2ny2 1可化为 1 1 ，∴mn0，∴  m n m n ，即曲线C表示焦点在x轴上的椭圆，故A不正确； 1 对于B，若mn0，则mx2ny2 1可化为x2y2  ，此时曲线C表示圆心在原点， n n 半径为 的圆，故B不正确； n x2 y2  1 对于C，若mn0，则mx2my2 1可化为 1 1 ，此时曲线C表示双曲线，由 m n m mx2ny2 0可得y  x，故C正确； n 1 n 对于D，若m0，n0，则mx2ny2 1可化为y2  ，y ，此时曲线C表示平行 n n 于x轴的两条直线，故D正确． 故选： CD. 10. 【答案】BC 【详解】对于A，在正方体ABCDABCD 中，可得CD平面ADDA， 1 1 1 1 1 1 因为MD平面ADDA，DD 平面ADDA，所以CDMD,CDDD ， 1 1 1 1 1 1  π 所以二面角M DCP的平面角为MDD ，其中MDD  0, ，所以A错误； 1 1   2   对于B，如图所示，当M为AA 中点，P为CC 中点时， 1 1 在正方体ABCDABCD 中，可得BD //BD， 1 1 1 1 1 1 因为BD 平面BDP，且BD平面BDP，所以BD //平面BDP， 1 1 1 1又因为MB //DP，且MB 平面BDP，且DP平面BDP，所以MB //平面BDP， 1 1 1 因为B 1 D 1 MB 1 B 1 ，且B 1 D 1 ,MB 1 平面MB 1 D 1 ，所以平面BDP//平面MB 1 D 1 ，所以B正 确； 对于C，如图所示，取DD 中点E，连接PE，ME，PM ， 1 在正方体ABCDABCD 中，CD平面ADDA，且CD//PE， 1 1 1 1 1 1 所以PE平面ADDA，因为ME平面ADDA，可得PEME， 1 1 1 1 则ME PM2PE2  (2 6)242 2 2， 则点M 在侧面ADDA内运动轨迹是以E为圆心、半径为2的劣弧， 1 1 分别交AD，AD 于M ,M ，如图所示，则M D  84 2DE， 1 1 2 1 1 1 1 π 结合对称性可知，M ED M ED ， 1 1 2 4 π π 则M EM  ，劣弧M M 的长为 2 2  2π，所以C正确； 1 2 2 1 2 2 对于D，当M 为AD中点时，可得 AMD为等腰直角三角形，且平面ABCD平面 1  ADDA， 1 1 连接AC与BD交于点O，可得OM OAOBOC OD2 2， 所以四棱锥M ABCD外接球的球心即为AC与BD的交点O，  2 所以四棱锥M ABCD外接球的半径为2 2，其外接球的体积为4π 2 2 32π，所以 D错误.故选：BC. 11. 【答案】ACD p p 【详解】由抛物线C:y2 2px，可得焦点坐标F( ,0)，准线方程为x ， 2 2因为抛物线C上存在一点E2,t到其焦点的距离为3， p 由抛物线的定义可得2 3，可得p2， 2 所以抛物线的方程为y2 4x，所以A正确； 设P(2,m)，显然直线PA的斜率存在且不为0，设斜率为k ， 1 可得PA的方程为ymk (x2)， 1 ymk (x2) 联立方程组 1 ，整理得k y24y8k 4m0， y2 4x 1 1 因为PA是抛物线的切线，所以(4)24k 8k 4m0，即2k2km10， 1 1 1 1 4 2 1 1 2 且点A的纵坐标为  ，代入抛物线方程，可得A横坐标为 ，即A( , )， 2k k k2 k2 k 1 1 1 1 1 设直线PB的斜率存在且不为0，设斜率为k ， 2 1 2 同理可得：2k2k m10，且B( , )， 2 2 k2 k 2 2 m 1 所以k ,k 是方程2k2km10的两个不等式的实数根，所以k k  ,kk  ， 1 2 1 2 2 1 2 2 2 2 1   2 k k m 2kk m 2 m 因为k k  2 1 ( ) 1 2 ( ) ( )1， AB OP 1 1 2 k k 2 m 2  1 2  k2 k2 2 2 1 所以OP AB，所以D正确； m 2 由OP AB，且k  ，可得k  ， OP 2 AB m 2 2 1 则直线AB的方程为y  (x )，即mk2y2mk 2k2x2， k m k2 1 1 1 1 1 又由2k2km10，可得km12k2， 1 1 1 1 所以(k 2k3)y2(12k2)2k2x2，即(12k2)y2k (x2)， 1 1 1 1 1 1 所以直线AB一定过定点(2,0)，该点不是抛物线的焦点，所以B不正确. 由直线AB的斜率不为0，设直线AB的方程为xmy2，且A(x,y ),B(x ,y )， 1 1 2 2 xmy2 联立方程组 ，整理得y24my80，所以y y 4m,y y 8， y2 4x 1 2 1 2 则 AB  1m2  y y  1m2  (y y )4y y  (1m2)(16m232) 1 2 1 2 1 23 1 4 m43m22 4 (m2 )2 4 2，当且仅当m0时，等号成立， 2 4 即 AB 的最小值为4 2，所以C正确.故选：ACD. 三、填空题:本题共3小题,每小题5分,共15分。 y2 x2 12. 过点P(2,3)的等轴双曲线的方程为 .  1 5 5 13. 过点P1,2的直线l与曲线y 4x2 有且仅有两个不同的交点，则l斜率的取值范围 为 ．  4  2 【答案】  2, 0,  ．  3  3 【分析】根据题意，将曲线y 4x2 ，变形为x2y2 4，y0，分析可得其为圆的上部 分， 结合直线与圆的位置关系即可． 【详解】由题意可设直线l:ykx12，又曲线y 4x2 可化为x2y2 4，y0， 作出直线l与曲线y 4x2 的图象如图所示： 设图中直线l ，l ，l ，l 的斜率分别为k ，k ，k ，k ， 1 2 3 4 1 2 3 4 20 2 20 则k   ，k 0，k  2， 1 12 3 2 3 12 又直线l 的方程为y2k x1， 4 4 2k 4 圆心0,0到直线l 的距离为 4 2，解得k 0（舍去）或k  ， 4 k21 4 4 3 4  4  2  4  2 要使两图象有两个不同的交点，则k  2, 0,  ．故答案为：  2, 0,   3  3  3  3 x3 14. 已知过点(0,a)可作三条直线与曲线 f(x) x21相切，则实数a的取值范围 3 为 ． 4 【答案】(1, ) 3 【详解】 f(x)x22x，设点(x, f(x ))为曲线y f(x)的切点， 1 1 2 则切线方程为y f(x )(x22x )(xx )，整理得y(x22x )x x3x21， 1 1 1 1 1 1 3 1 12 将点(0,a)代入可得a x3x21． 3 1 1 2 令g(x) x3x21，则g(x)2x22x2x(1x)， 3 当x0时，g(x)0，g(x)单调递减；当0x1时，g(x)0，g(x)单调递增；当 x1时，g(x)0，g(x)单调递减． 4 4 又g(0)1，g(1) ，当1a 时，方程g(x)a有3个不同的实数根， 3 3 4 2 即当1a 时，有3个不同的x满足方程a x3x21， 3 1 3 1 1 x3 即过点(0,a)可作三条直线与曲线 f(x) x21相切． 3 4 故答案为：(1, ). 3 四、解答题:本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤. 15. 已知函数 f(x)2ex(x1)． (1)求函数 f(x)的极值； (2)求函数 f(x)在区间[t,t1](t 3)上的最小值g(t)． 【详解】（1） fx2exx2， 由 fx0，得x2；由 fx0，得x2． f(x)在(2,)上单调递增，在(,2)上单调递减． f(x)的极小值为 f(2)2e2，无极大值． （2）由（1）知 f(x)在(2,)上单调递增，在(,2)上单调递减． t3，t12．  ①当3t2时， f(x)在[t,2)上单调递减，在(2,t1]上单调递增， g(t) f(2)2e2. ②当t2时， f(x)在[t,t1]上单调递增，g(t) f(t)2et(t1)． 2e2,3t2 gt .  2ett1,t2 c 1 p 16. 【详解】（1）依题意设点F (c,0)，因e  ，且 a， a 2 2 1 由对称性知抛物线的准线l方程为xa，则ac 1，解得a1，c ，p2， 2 23 于是b2 a2c2  ． 4 4y2 从而得椭圆的方程为x2 1，抛物线的方程为y2 4x． 3 （2）由于准线l方程为x=1，依题意设P(1,t) t0，则Q(1,t)． t t 因A(1,0)，则k  ，得直线AP方程为y x1①， AP 2 2 将①式代入x2 4y2 1中化简，得  t23  x22t2xt230， 3 t23 t 3t 设Bx ,y ，由韦达定理得x x x  ，则y  x 1 ， 0 0 0 0 A t23 0 2 0 t23 t23 3t  t26 t26 即B , ，则k  ，于是得直线BQ方程为yt  x1， t23 t23 BQ 2t 2t t26 t26  t26 12 令y0，解得x ，即D ,0．则|AD|1  ， t26 t26  t26 t26 6 1 12  2 于是 S   |t|，化简得 t  6 0，即得t 6， 2 APD 2 t26 代入①式化简，得直线AP方程为3x 6y30，或3x 6y30. 1 1 17. 【详解】（1）直三棱柱ABCABC 的体积为：V  ABBCAA  21AA 1 1 1 1 2 1 2 1 ， 则AA 1BC，四边形BCCB 为正方形， 1 1 1 法一：在直棱柱ABCABC 中，BB 面ABC，AB∥AB ， 1 1 1 1 1 1 又AB平面ABC，则ABBB ， 1 因为ABBC，ABBB 1 ，BB 1 BC B，BB 1 ,BC平面BCC 1 B 1 ， 所以AB平面BCCB ，又BC 平面BCCB ， 1 1 1 1 1 所以ABBC ， 1 因为AB∥AB ，所以AB  BC ， 1 1 1 1 1 在正方形BCCB 中，有BC BC， 1 1 1 1 因为BC 1 B 1 C，A 1 B 1  B 1 C，A 1 B 1 B 1 C B 1 ，A 1 B 1 ,B 1 C平面A 1 CB 1 ，所以BC 平面ACB ，又AC平面ACB ， 1 1 1 1 1 1 所以BC ^ AC． 1 1 法二：直棱柱ABCABC ，BB 平面ABC，又ABBC， 1 1 1 1 以B为原点，BC，BA，BB 所在直线为x轴，y轴， z轴，建立空间直角坐标系， 1 则B0,0,0，B 0,0,1，C1,0,0，A(0,2,1)，C (1,0,1)， 1 1 1   BC (1,0,1)，AC (1,2,1)， 1 1   BC AC 110(2)1(1)0，所以BC ^ AC． 1 1 1 1 （2）由（1）得BC ^ AC， 1 1 设B 1 C  BC 1 O，在  A 1 B 1 C中，过O作OH  A 1 C于H，连接BH ， 因为OH  AC，BC ^ AC，OH,BC 平面BHO，且OHBC O， 1 1 1 1 1 所以AC平面BHO，又BH 平面BHO， 1 所以AC BH ， 1 所以BHO为二面角B ACB的平面角， 1 1 CO CA 3 因为Rt△COH∽Rt△CAB ，  1 ，得OH  ， 1 1 OH AB 3 1 1 2 30 又在Rt  BOH 中，BO ，得BH  ， 2 6 3 OH 3 10 cosBHO   ， BH 30 5 6 10 所以二面角B ACB的余弦值为 ． 1 1 5 法二： B0,0,0，B 0,0,1，C1,0,0，A(0,2,1)，C (1,0,1)， 1 1 1    BC (1,0,0)，BA (0,2,1)，设平面BCA的法向量：n (x,y ,z )， 1 1 1 1 1 1   则    n  1   B  C  x 1 0 ，取y 1 1，得n  1 (0,1,2)， n BA 2y z 0 1 1 1 1   BC (1,0,1)，BA (0,2,0)，设面BCA的法向量n (x ,y ,z )， 1 1 1 1 1 2 2 2 2   则    n  2   B  1  C  x 2 z 2 0 ，取x 2 1，得n  2 (1,0,1)， n BA 2y 0 2 1 1 2 设二面角B ACB的大小为，则： 1 1     |n n | |2| 10 |cos||cosn 1 ,n 2 | |n  1 ||n  2  |  5 2  5 ， 1 2 10 因为为锐角，所以二面角B ACB余弦值为 ． 1 1 5 b 18.解：因为拋物线y2 8x的焦点为 2,0 ，所以直线l的斜率k  ， l 2 b b 因为双曲线C的一条渐近线与l平行，所以  ，即a2.又因为双曲线C的焦距为 a 2 2c 6，即c3， x2 y2 所以b2 c2 a2 5，所以双曲线C的方程为  1. 4 5 【小问2详解】 双曲线C的右焦点为 3,0 ， 由题意知直线m的斜率存在且不为0， 设直线m的方程为xmy3m0,Ax ,y ,Bx ,y  ， 1 1 2 2 x2 y2   1 联立 4 5 ，消去x得  5m2 4  y2 30my250,5m2 40，  xmy3 30m 25 且Δ400  1m2 0，所以y  y  ,y y  ， 1 2 5m2 4 1 2 5m2 4 4 5 4 5  将x 代入xmy3得y  ，所以T  , . 3 T 3m 3 3m y  4 5 y 直线PQ方程为y  1  x   ，与直线OB: y  2 x联立， x  3 3m x 1 2 4my y 5x y 4my y 5my 3y 3my y 5y 可得y  1 2 1 2  1 2 1 2  1 2 2 ， P 3mx y x y  3mmy 3y my 3y  3my  y  2 1 1 2  2 1 1 2 1 25 5 5  y  y 5y  y  y  因为y y  y  y ，所以 2 1 2 2 2 1 2 5 . 1 2 6m 1 2 y P  3my  y   3my  y   6m 1 2 1 2 y  y TP 因为y 0，所以y  T Q ，所以P为TQ的中点，即 1. Q P 2 PQ lnex 19. 已知函数 f x ，其中e为自然对数的底数． ax (1)讨论 f x的单调性； (2)若方程 f x1有两个不同的根x,x ． 1 2 (i)求a的取值范围； (ii)证明：x2x2 2． 1 2 lnex 1lnx lnx 【详解】（1）由题意得 f x  ，x0,，则 fx ， ax ax ax2 由 fx0，解得x1．显然a0， 若a0，则当0x1时， fx0, f x单调递增，当x1时， fx0, f x单调递 减； 若a0，则当0x1时， fx0, f x单调递减，当x1时， fx0, f x单调递 增． 综上，当a0时， f x在区间0,1内单调递增，在区间1,内单调递减； 当a<0时， f x在区间0,1内单调递减，在区间1,内单调递增． lnex 1lnx （2）（i）由 1，得 a， ax x 1lnx 设gx ，由(1)得gx在区间0,1内单调递增，在区间1,内单调递减， x 1 又g 0,g11，当x1时，gx0，且当x时，gx0， e 1lnx lnex 所以当0a1时，方程 a有两个不同的根，即方程 1有两个不同的根，故 x ax a的取值范围是0,1． lnx 1 lnx 1 （ii）不妨设x x ，则0x 1x ，且 1  2 ． 1 2 1 2 x x 1 2解法一： 当x 2,时，x2x2 x2 42，即x2x2 2； 2 1 2 2 1 2 当x 1,2时，2x 0,1． 2 2 lnx 1 ln2x 1 设pxgxg2x    ,0x1, x x 2x 2x 则px lnx  ln2x  lnx  ln2x ln  x121  x2 2x2 x2 x2  x2 0, 所以px在区间0,1内单调递增， 则px p10，即gxg2x， 所以g2x gx gx , 1 1 2 又x 0,1,2x 1,x 1,gx在区间1,内单调递减， 1 1 2 所以2x x ，即x x 2， 1 2 1 2 又x  x ，所以x2x2 2xx ， 1 2 1 2 1 2 故2x22x2 x2x22xx x x 2 4，所以x2x2 2，得证． 1 2 1 2 1 2 1 2 1 2 解法二： 1 1lnx 设hxgxg  x1lnx，x0,， x x lnx x21 则hx lnxlnx 0， x2 x2 所以hx在区间0,内单调递增， 又h10，  1   1  所以hx gx g 0，即gx g ． 1 1 x  1 x  1 1  1  又gx gx ，所以gx g ， 2 1 2 x  1 1 又x 1, 1,gx 在区间1,内单调递减． 2 x 11 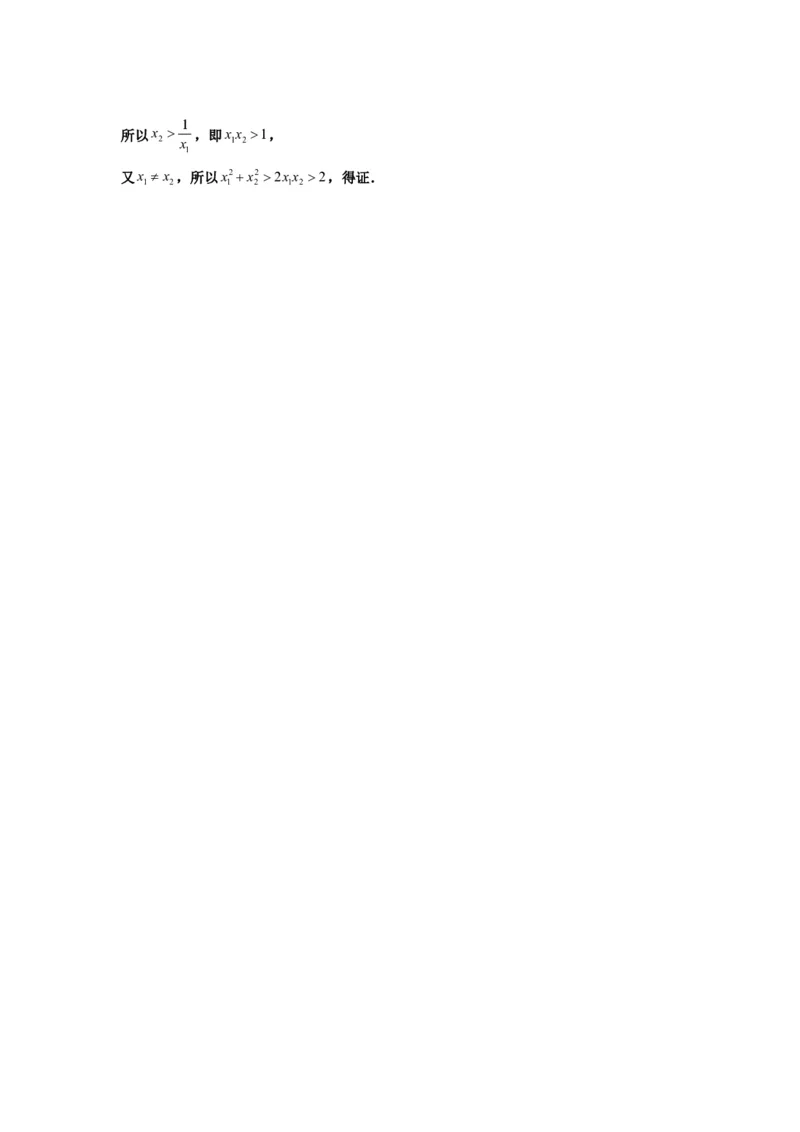所以x  ，即xx 1， 2 x 1 2 1 又x  x ，所以x2x2 2xx 2，得证． 1 2 1 2 1 2