4.物理答案_2024-2025高二（7-7月题库）_2025年04月试卷(1)_0410广东省湛江市第二十一中学2024-2025学年高二下学期4月月考

2024—2025学年第二学期高二物理月考试卷 姓名：__________ 班级：__________ 考号：__________ 一、单选题 1. 下列关于电磁波的叙述中，正确的是( ) A. 电磁波的频率都相同 B. 电磁波在任何介质中的传播速度均为 3×108m/s C. 麦克斯韦证实了电磁波的存在 D. 电磁波具有波的一切特征 【答案】 D 【解析】 不同的电磁波，波长不同，频率不同，故A错误；电磁波只有在真空中传播 时，其速度才为3×108m/s，故B错误；麦克斯韦预言了电磁波的存在，赫兹用 实验证实了电磁波的存在，故C错误；因为电磁波也是一种波，故电磁波具有 波的一切特征，故D正确。故选D。 2. 如图所示，三只完全相同的灯泡a、b、c分别与电阻R、电感L、电容C串联，再将三者关 联，接在220V，50Hz的交变电压两端，三只灯泡亮度相同。若将交变电压改为220V，25Hz， 则( ) A. 三只灯泡亮度不变 B. 三只灯泡都将变亮 C. a亮度不变，b变亮，c变暗 D. a亮度不变，b变暗，c变亮 【答案】 C 【解析】 根据电感的特性：通低频、阻高频，当电源的频率变低时，电感对电流的感抗 减小，b灯变亮；根据电容器的特性：通高频、阻低频，当电源的频率变低 时，电容器对电流的容抗增大，c灯变暗。而电阻的亮度与频率无关，a灯亮度 不变。故选C。 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}3. 如图所示为电流天平，它的右臂挂着矩形线圈，匝数为n，线圈的水平边长为L，处于匀强 磁场内，磁感应强度大小为B，方向与线圈平面垂直，当线圈中通过方向如图所示的电流I时， 调节砝码使两臂达到平衡，然后使电流反向，大小不变，这时为使天平两臂再达到新的平 衡，则需（ ） nBIL 2nBIL A. 在天平右盘中增加质量m = 的砝码 B. 在天平右盘中增加质量m = 的砝码 g g nBIL 2nBIL C. 在天平左盘中增加质量m = 的砝码 D. 在天平左盘中增加质量m = 的砝码 g g 【答案】 D 【解析】 开始时底边所受的安培力方向竖直向上，电流反向后，安培力的方向变为竖直 1 向下，相当于右边多了两个安培力的重量，即mg = 2F ，解得F = mg，由 A A 2 2nBIL 于F = nBIL，解得m = ，要重新平衡，需要在天平左盘中增加质量为 A g 2nBIL m = 的砝码，ABC错误，D正确。故选D。 g 4. 图甲为某款“自发电”无线门铃按钮，其“发电”原理如图乙所示，按下门铃按钮过程磁铁靠近 螺线管，松开门铃按钮磁铁远离螺线管回归原位置，P、Q端与门铃（图中未画出）连接构成 回路。下列说法正确的是（ ） A. 按下按钮的过程，螺线管P端电势较高 B. 松开按钮的过程，螺线管Q端电势较高 C. 按下和松开按钮的过程，螺线管产生的感应 D. 按下和松开按钮的过程，螺线管所受磁铁的 电流方向相同 安培力方向相反 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}【答案】 D 【解析】 按下按钮过程中，穿过线圈的磁通量向左增加，根据楞次定律可知，感应电流 的方向从P端经螺线管向Q端，再根据电路中电源内部电流方向是由负极流向 正极，故螺线管Q端电势较高，故A错误；松开按钮过程中，穿过线圈的磁通 量向左减小，根据楞次定律可知，感应电流的方向从Q端经螺线管向P端，同 理，电源内部电流方向是由低电势到高电势，此时螺线管P端电势较高，故B 错误；按下和松开按钮的过程，螺线管中磁通量的变化情况相反，所以产生的 感应电流方向相反，故C错误；按下和松开按钮的过程，螺线管产生的感应电 流方向相反，磁场方向不变，螺线管所受磁铁的安培力方向相反，故D正确。 5. LC振荡电路如图所示，t = 0时刻，线圈中磁场的方向如图所示，且磁场正在减弱。M、N 分别为电容器的上、下极板，a、b为回路中的两个点。已知LC振荡电路的周期为T，下列说 法正确的是( ) T A. 此时回路中的电流由b流向a B. t = 时刻，N板带负电，电容器储存的电场 2 能正在增加 C. 此时两板间的电场强度正在减小 D. 若将N板下移，则该振荡电路激发的电磁波 波长变长 【答案】 B 【解析】 t = 0时刻磁场正在减弱，由右手螺旋定则可知，电流由a流向b，故A错误； T t = 0时刻磁场正在减弱，故电容器正在充电，则t = 时刻，电容器也正在反向 2 充电，故M板带正电，N板带负电，电荷量正在增大，电场能正在增加，故B 正确；t = 0时刻电容器正在充电，电荷量正在增大，则M、N板间的电压正在 增大，两板间的电场强度正在增大，故C错误；若将N板下移，电容器极板间 ε r S 1 距增大，根据C = ，可知电容器的电容减小，由f = ，可知振荡电 4πkd 2π√LC {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}路的频率增大，电磁波频率增大，由c = λf，可知，振荡电路激发的电磁波波 长变短，故D错误。故选B。 6. 如图所示，交流发电机为右侧的电路供电，发电机线圈电阻和输电线电阻均不计，电压表 和电流表均为理想电表，变压器为理想变压器，副线圈两端接有开关S、滑动变阻器R以及两 个定值电阻R 、R 。保持线圈ABCD在磁场中匀速转动，电流表A和电压表V 、V 的示数变化 1 2 1 2 大小分别为ΔI和ΔU 、ΔU ，下列说法正确的是（ ） 1 2 A. 当线圈ABCD位于如图所示的位置时，线圈ABCD产生的感应电动势最大 B. 若发电机线圈的转速变为原来的2倍，原线圈的输入功率变为原来的8倍 C. 当滑动变阻器的滑动触头向下滑动，电压表V 的示数变小 1 D. 闭合开关S，移动滑动变阻器的滑动触头，ΔU 与ΔI比值不变 2 【答案】 D 【解析】 当线圈ABCD位于如图所示的位置时，穿过线圈的磁通量最大，但磁通量的变 化率为零，根据法拉第电磁感应定律可知，线圈ABCD产生的感应电动势为 零，故 A 错误； 由题意知，若发电机线圈的转速n变为原来的2倍，其他条件不变，根据法拉第 电磁感应定律可得E = NBSω = 2πNnBS，可知原线圈产生交流电的感应电动 m 势的最大值E 变为原来的2倍，有效值也增大为原来的2倍，根据理想变压器 m ( ) n 2 2 U 2 n 1 ⋅U 有 1 输入功率等于输出功率，U 为输出端电压，即P = P = = ， 1 入 出 R R 总 总 可得原线圈的输入功率将变为原来的4倍，故B错误； 电压表V 测量的是变压器输出端的电压，输出端的电压取决于输入端电压及变 1 压器原副线圈的匝数比，所以，当滑动变阻器的滑片向下滑动而其他条件不变 时，电压表V 示数保持不变，故C错误；闭合开关，移动滑动变阻器的滑片而 1 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}其他条件不变时，根据闭合电路欧姆定律可得U = U -IR ，可得ΔU 与ΔI比 2 1 1 2 | | ΔU 2 值大小为 = R ，R 不变，所以ΔU 与ΔI比值不变，故D正确；故选D。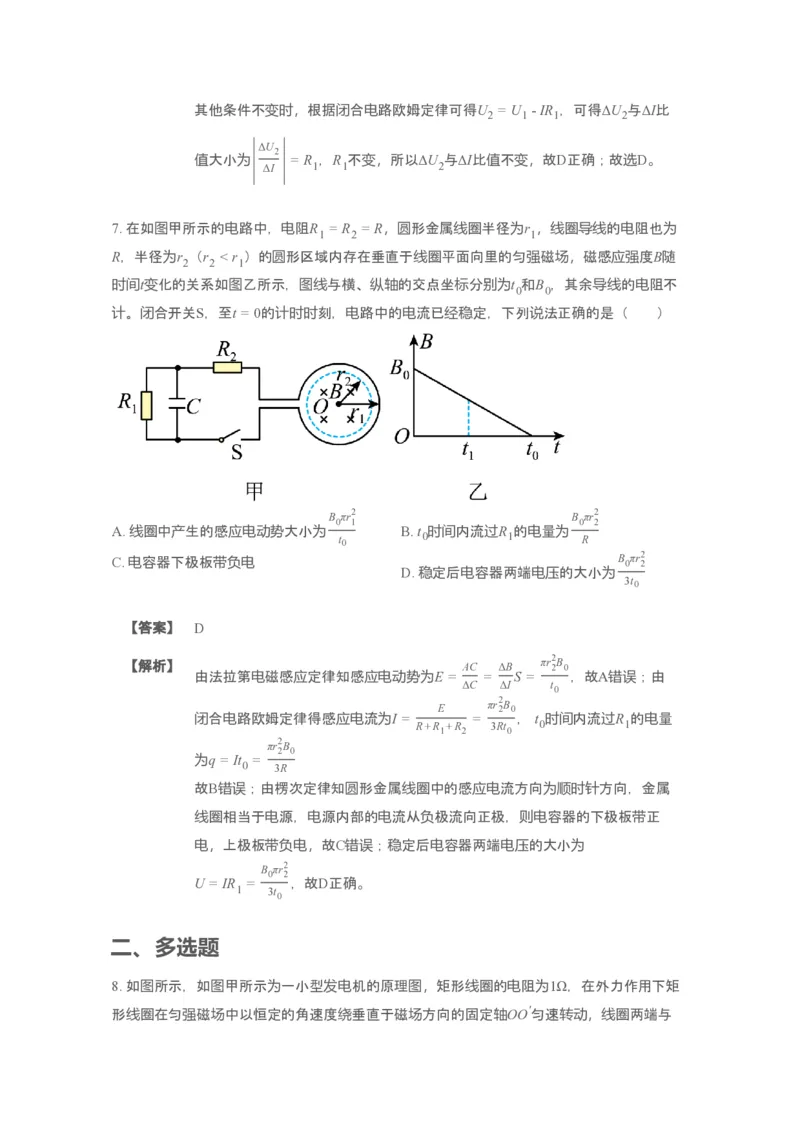 ΔI 1 1 2 7. 在如图甲所示的电路中，电阻R = R = R，圆形金属线圈半径为r ，线圈导线的电阻也为 1 2 1 R，半径为r （r < r ）的圆形区域内存在垂直于线圈平面向里的匀强磁场，磁感应强度B随 2 2 1 时间t变化的关系如图乙所示，图线与横、纵轴的交点坐标分别为t 和B ，其余导线的电阻不 0 0 计。闭合开关S，至t = 0的计时时刻，电路中的电流已经稳定，下列说法正确的是（ ） 2 2 B πr B πr 0 1 0 2 A. 线圈中产生的感应电动势大小为 B. t 时间内流过R 的电量为 t 0 1 R 0 C. 电容器下极板带负电 B 0 πr2 2 D. 稳定后电容器两端电压的大小为 3t 0 【答案】 D 【解析】 AC ΔB πr2 2 B 0 由法拉第电磁感应定律知感应电动势为E = = S = ，故A错误；由 ΔC ΔI t 0 2 E πr 2 B 0 闭合电路欧姆定律得感应电流为I = = ， t 时间内流过R 的电量 R+R +R 3Rt 0 1 1 2 0 2 πr B 2 0 为q = It = 0 3R 故B错误；由楞次定律知圆形金属线圈中的感应电流方向为顺时针方向，金属 线圈相当于电源，电源内部的电流从负极流向正极，则电容器的下极板带正 电，上极板带负电，故C错误；稳定后电容器两端电压的大小为 B πr2 0 2 U = IR = ，故D正确。 1 3t 0 二、多选题 8. 如图所示，如图甲所示为一小型发电机的原理图，矩形线圈的电阻为1Ω，在外力作用下矩 形线圈在匀强磁场中以恒定的角速度绕垂直于磁场方向的固定轴OO'匀速转动，线圈两端与 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}R=10Ω的电阻构成闭合回路。通过电阻R的电流随时间变化的图像如图乙所示。下列说法正确 的是（ ） A. 该发电机线圈转动的角速度为200πrad/s B. 线圈转至图甲位置时，线圈中感应电流最小 C. 该发电机产生交流电的感应电动势峰值为200√2V D. 电阻R消耗的电功率为4000W 【答案】 BD 2π 2π 【解析】 线圈转动的角速度为ω = = rad/s = 100πrad/s，故A错误；线圈转至图甲 T 0.02 位置时，通过线圈的磁通量最大，磁通量变化率最小，产生的感应电动势最 小，感应电流最小，故B正确；感应电动势峰值 ( ) ( ) E = i R+r = 20√2× 10+1 V = 220√2V，故C错误；电阻R消耗的电功 m m ( ) 20√2 2 率P = I 2 R = ×10W = 4000W，故D正确。故选BD。 R 有 √2 9. 如图所示，关于不计重力的粒子在以下四种器件中的运动，说法正确的是（ ） E A. 甲图中从左侧射入的带电粒子，若能沿直线射出， 其速度大小为v = B B. 乙图中等离子体进入上下极板之间后上极板a带正电 C. 丙图中通过励磁线圈的电流越大，电子的运动径迹半径越小 D. 丁图中只要回旋加速器D形盒足够大，粒子就能获得无限大的速度 【答案】 AC 【解析】 甲图中带正电的粒子从左侧射入复合场中时，带电粒子沿直线射出，则粒子受 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}E 力平衡，有qvB = qE，解得v = ，故A正确；乙图中等离子体进入上下极板之 B 间后，受到洛伦兹力作用，由左手定则可知，正粒子向b极板偏转，负粒子向a 极板偏转，因此极板a带负电，极板b带正电，故B错误；丙图中通过励磁线圈 的电流越大，线圈产生的磁场越强，电子的运动由洛伦兹力提供向心力，则有 v2 mv evB = m ，解得r = ；由上式可知，当电子的速度一定时，磁感应强度越 r eB 大，电子的运动径迹半径越小，故C正确；丁图中只要回旋加速器的D形盒足 够大，加速粒子就能获得较大的能量，具有较大的速度，可当能量达到 25MeV~30 MeV后就很难再加速了，原因是按照狭义相对论，粒子的质量随速 度的增大而增大，而质量的变化会导致其回旋周期的变化，从而破坏了与电场 变化周期的同步，因此加速粒子就不能获得无限大的速度，故D错误。 10. 质谱仪是一种测量带电粒子质量和分析同位素的重要工具，它的构造原理如图，离子源A 产生电荷量相同而质量不同的离子束(初速度可视为零)，从狭缝S 进入电场，经电压为U的加 1 速电场加速后，再通过狭缝S 从小孔垂直MN射入圆形匀强磁场，该匀强磁场的磁感应强度为 2 B，方向垂直于纸面向外，半径为R，磁场边界与直线MN相切，E为切点，离子离开磁场最终 到达感光底片MN上，设离子电荷量为q，到达感光底片上的点与E点的距离为x，不计重力， 可以判断( ) A. 离子束带正电 B. x越大，则离子的比荷一定越大 qB2R2 D. 到达x = √3R处的离子在匀强磁场运动时间 C. 到达x = √3R处的离子质量为 6U πBR2 为 3U 【答案】 AC 【解析】 离子进入磁场后向右偏转，对离子受力分析，由左手定则可知，离子束带正 电，A正确；带电离子在加速电场中做匀加速直线运动，设加速后的速度大小 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}为v，根据动能定理有qU = 1 mv2-0，解得v = √2qU ，然后匀速运动到E点 2 m 进入有界磁场中，其运动轨迹如下图所示 v2 粒子从E点先沿虚线圆弧，再沿直线做匀速直线运动到N点，由qvB = m ， r mv 1√2mU q 则r = = ，故x越大则r越大，则比荷 越小，故B错误；如图，到 qB B q m x 达x = √3R处的离子在 △ ENO中tanθ = ，解得θ=60°，设带电粒子运动的轨 R √3 qB2R2 迹圆的半径为r，根据几何关系有r = Rtan30∘ = R，解得m = ，C正 3 6U α α 2πm 确；设到达x = √3R处的离子轨迹圆心角为α，t = T = × ， 由 360∘ 360∘ qB πBR2 几何关系圆弧圆心角α=120°，联立可得t = ，D错误。故选AC。 9U 三、实验题 11. 某物理兴趣小组用可拆变压器探究变压器原、副线圈电压与匝数的关系。 (1)可拆变压器如图1所示。下列说法正确的是_______。 A．实验采用控制变量法进行探究 B．变压器的铁芯是用整块硅钢制成的 C．匝数多的线圈，要用粗一些的导线绕制 (2)关于实验操作，下列说法正确的是_______。 A．实验可以用多节干电池串联起来作为电源 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}B．实验中手不能接触裸露的导线、接线柱 C．用交流电压表测副线圈两端电压时，副线圈应接小灯泡 (3)某次实验中用多用电表的交流电压10V档测线圈两端电压，其示数如图2所示，则电压为 _________V。 U n 1 1 (4)若变压器为理想变压器，由原、副线圈若干组电压比 与匝数比 作出如图3所示的关系图 U n 2 2 像，该图像的斜率为__________。 (5)实际实验中测得的原、副线圈的电压比___________原、副线圈的匝数比。（选填“大 于”、“等于”、“小于”） 【答案】 (1)A (2)B (3)7.4 (4)1 (5)大于 【解析】 （1）探究变压器原、副线圈电压与匝数的关系时，应采用控制变量法进行探 究，A正确；变压器的铁芯是用硅钢片叠装而成，B错误；匝数少的线圈电流 较大，为减小电能损失，应用粗一些的电阻较小的导线绕制，C错误。故选 A。 （2）该实验应使用交流电源，A错误；手接触裸露导线、接线柱，会使人体接 入电路中，导致数据不准确，B正确；若副线圈接小灯泡，测得电压为小灯泡 两端电压，小于副线圈电压，C错误。故选B。 （3）读数为7.4V。 U n U n 1 1 1 1 （4）由于是理想变压器，则 = ，故 - 图像的斜率为1。 U n U n 2 2 2 2 （5）由于实际上变压器的铁芯会损失一部分能量，所以副线圈的电压真实值 会小于理论值，故原线圈与副线圈的电压比大于原线圈与副线圈的匝数比。 12. 如图甲所示是“探究感应电流方向”的实验装置． （1）开关闭合前，滑动变阻器的滑片应放置在_______（选填“a”或“b”）位置． {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}（2）电路连接如图甲所示，下列操作不能产生感应电流的是( ) A．开关闭合瞬间 B．开关闭合后，滑动变阻器滑片不动 C．开关断开瞬间 D．开关闭合后，迅速移动滑动变阻器的滑片 （3）如果在闭合开关时发现灵敏电流计的指针向左偏了一下，那么合上开关后把线圈A迅速 从线圈B中拔出时，电流计指针将_______（选填“向右偏”、“向左偏”或“不偏转”）；如果闭合 开关后，滑动变阻器滑片向b端移动，则电流表指针将_________（选填“向右偏”、“向左 偏”或“不偏转”）． （4）上述实验中，线圈A可等效为一个条形磁铁，将线圈B和灵敏电流计简化如图乙所示．将 磁体从线圈B中拨出，电流从正接线柱流入灵敏电流计．画出图乙线圈B的线圈绕向______． 【答案】 （1）a （2）B （3）向右偏 向左偏 （4） 【解析】 （1）开关闭合前，为保护电路，滑动变阻器的滑片应放置在a位置； （2）根据产生感应电流的条件可知，当电路电流发生变化，则线圈中磁通量 发生变化，从而产生感应电流，所以开关闭合后，滑动变阻器滑片不动时不能 产生感应电流。 （3）在闭合开关时，线圈磁通量变大，灵敏电流计的指针向左偏，合上开关 后把线圈A迅速从线圈B中拔出时，磁通量减小，则灵敏电流计的指针向右偏； 滑动变阻器滑片向b端移动，电流增大，线圈磁通量变大，灵敏电流计的指针 向左偏。 （4）将磁体从线圈B中拨出，磁通量减小，结合楞次定律可知绕线方式如图： 四、计算题 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}13. 如图甲所示为某小型水电站的发电机示意图，已知正方形线圈边长L = 100cm，匝数 N = 100匝，线圈电阻不计；线圈在匀强磁场中绕垂直于磁场的转轴OO'匀速转动，转速 n = 100r/s；已知电动势最大值E = 500√2V。 m （1）求发电机中匀强磁场的磁感应强度大小； （2）从线圈在图甲所示位置开始计时，写出感应电动势随时间变化的函数表达式； （3）如图乙所示，将发电机通过升压变压器T 升压后向远处输电，发电机的输出功率为 1 200kW，输电线的总电阻为4Ω，在用户端用降压变压器T 把电压降为220V，要求在输电线上 2 n n 1 3 损失的功率控制在10kW，则T 、T 的原副线圈匝数比 和 分别为多少？ 1 2 n n 2 4 【答案】 √2 n 1 1 n 3 190 （1）B = T；（2）e = 500√2cos200πt(V)；（3） = ， = 40π n 8 n 11 2 4 【解析】 （1）线圈转动的角速度 ω = 2πn = 200πrad/s 由E = NBSω m √2 得B = T 40π （2）线圈与中性面位置垂直，则感应电动势随时间变化的函数表达式 e = E cosωt = 500√2cos200πt(V) m P √ 损 输电线上的电流 I = = 50A 线 r 线 P T 的输入电流 I = = 400A 1 1 U 1 n 1 I 2 1 则T 原、副线圈匝数比 = = 1 n I 8 2 1 n 2 T 副线圈两端电压 U = = 4000V 1 2 n 1 T 原线圈两端电压 U = U -I r = 3800V 2 3 2 2 线 n 3 U 3 190 则T 原、副线圈匝数比 = = 2 n U 11 4 4 14. 如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里．一带正电的粒子(不计重力)从O点沿 y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t 时间从P点射出． 0 (1)求电场强度的大小和方向； (2)若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经 时间恰从半圆形区域的边界射 出，求粒子运动加速度的大小； (3)在(2)的情况下，若仅撤去电场，带电粒子仍从O点射入，但速度为原来的4倍，求粒子在磁 场中运动的时间． 【答案】 (1) 沿x轴正方向 (2) (3) t 0 【解析】 (1)设带电粒子的质量为m，电荷量为q，初速度为v，电场强度为E.可判断出粒 子受到的洛伦兹力沿x轴负方向，于是可知电场强度方向沿x轴正方向，且有qE ＝qvB① 又R＝vt ② 0 则E＝ .③ (2)仅有电场时，带电粒子在匀强电场中做类平抛运动，在y方向上的位移为y＝ v ④ 由②④式得y＝ ⑤ 设在水平方向的位移为x，因射出位置在半圆形区域边界上，于是x＝ R，又 x＝ a( )2⑥ 得a＝ .⑦ (3)仅有磁场时，入射速度v′＝4v⑧ 带电粒子在匀强磁场中做匀速圆周运动，如图所示，设轨道半径为r，由牛顿 第二定律 有qv′B＝ ⑨ 又qE＝ma⑩ {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}由②③⑦⑧⑨⑩式得r＝ ⑪ 由几何知识得sin α＝ ⑫ 即sin α＝ ，α＝ ⑬ 带电粒子在磁场中的运动周期T＝ ⑭ 由③⑦⑩⑬⑭得带电粒子在磁场中的运动时间t ＝ T＝ t . B 0 15. 如图所示为两条间距为d的固定光滑金属导轨，其中ACA C 部分为半径为R的四分之一圆 1 1 弧轨道，CDC D 部分为足够长水平直轨道，水平轨道位于竖直向上的匀强磁场中，磁感应强 1 1 度大小为B。现将质量为m、电阻为r的金属棒S静置于距CC 足够远的水平轨道上，将与其完 1 全相同的金属棒T由AA 处静止释放，一段时间后，金属棒T运动到水平轨道上。在运动过程 1 中，两棒始终与导轨垂直且保持良好接触，除金属棒电阻之外其他电阻不计，已知重力加速 度为g。求： (1)金属棒T运动至圆弧轨道最底端CC 处时的速度v 和金属棒T对轨道的压力大小； 1 0 (2)金属棒T刚进入水平轨道时，通过金属棒S的电流大小； (3)从金属棒T进入水平轨道到两棒运动稳定的共同速度v； (4)从金属棒T进入水平轨道到两棒运动稳定的过程中金属棒S产生的热量。 【答案】 Bd√2gR √2gR 1 (1)√2gR，3mg (2) (3) (4) mgR 2r 2 4 【解析】 (1)金属棒T由静止释放运动到CC 处的过程中，根据动能定理有mgR = 1 mv 2 1 2 0 求得v = √2gR 0 v 2 0 金属棒T运动到CC 处时，由牛顿第二定律有F -mg = m 1 N R 解得F = 3mg N 根据牛顿第三定律，金属棒T运动至CC 处时对轨道的压力大小为 1 F' = F = 3mg N N (2)金属棒T刚进入水平轨道时，金属棒T产生的电动势为E = Bdv 0 Bdv Bd√2gR 0 通过金属棒S的电流大小I = = 2r 2r {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}(3)两棒组成的系统动量守恒，有mv = 2mv 0 √2gR 联立解得共同速度为v = 2 (4)金属棒T从进入水平轨道到两棒运动稳定的过程中，两棒产生的总热量为 1 1 Q 总 = 2 mv 0 2- 2 ⋅2mv2 1 金属棒S产生的热量为Q = Q S 2 总 1 联立得Q = mgR S 4 {#{QQABIYQAggCAQAIAAQhCAwHSCAMQkAGCCaoOwAAUMAABgBFABAA=}#}