文档内容
专题 1.5 空间向量的应用【十大题型】
【人教A版(2019)】
【题型1 求平面的法向量】......................................................................................................................................2
【题型2 利用空间向量证明线线平行】..................................................................................................................3
【题型3 利用空间向量证明线面平行】..................................................................................................................5
【题型4 利用空间向量证明面面平行】..................................................................................................................7
【题型5 利用空间向量证明线线垂直】..................................................................................................................9
【题型6 利用空间向量证明线面垂直】................................................................................................................10
【题型7 利用空间向量证明面面垂直】................................................................................................................12
【题型8 利用空间向量研究距离问题】................................................................................................................15
【题型9 利用空间向量求空间角】........................................................................................................................17
【题型10 利用空间向量研究存在性问题】.........................................................................................................18
【知识点1 空间中点、直线和平面的向量表示】
1.空间中点、直线和平面的向量表示
(1)空间中点的位置向量:如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以
用向量OP来表示.我们把向量OP称为点P的位置向量.
(2)空间中直线的向量表示式:直线l的方向向量为a ,且过点A.如图,取定空间中的任意一点O,可
以得到点P在直线l上的充要条件是存在实数t,使 OP=OA+ta①,把AB=a代入①式得OP=OA+
tAB②,
①式和②式都称为空间直线的向量表示式.
(3)平面的法向量定义:
直线l⊥α,取直线l的方向向量a ,我们称向量a为平面α的法向量.给定一个点A和一个向量a,那
么过点A,且以向量a为法向量的平面完全确定,可以表示为集合 .
学科网(北京)股份有限公司【注】一个平面的法向量不是唯一的,在应用时,可适当取平面的一个法向量.已知一平面内两条相
交直线的方向向量,可求出该平面的一个法向量.
【题型1 求平面的法向量】
【例1】(2023春·高二课时练习)已知A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的一个单位法向量是
( )
√3 √3 √3
A.(1,1,1) B.( , , )
3 3 3
1 1 1 √3 √3 √3
C.( , , ) D.( , ,− )
3 3 3 3 3 3
【变式1-1】(2023秋·云南昆明·高二昆明一中校考期末)空间直角坐标系O−xyz中,已知点
A(2,0,2),B(2,1,0),C(0,2,0),则平面ABC的一个法向量可以是( )
A.(1,2,1) B.(−1,2,1) C.(2,1,2) D.(2,−1,2)
【变式1-2】(2023·全国·高二专题练习)如图,四棱柱ABCD−A B C D 的底面ABCD是正方形,O
1 1 1 1
为底面中心, 平面 , .平面 的法向量 为( )
A O⊥ ABCD AB=A A =√2 OCB ⃗n=(x,y,z)
1 1 1
A.(0,1,1) B.(1,−1,1) C.(1,0,−1) D.(−1,−1,1)
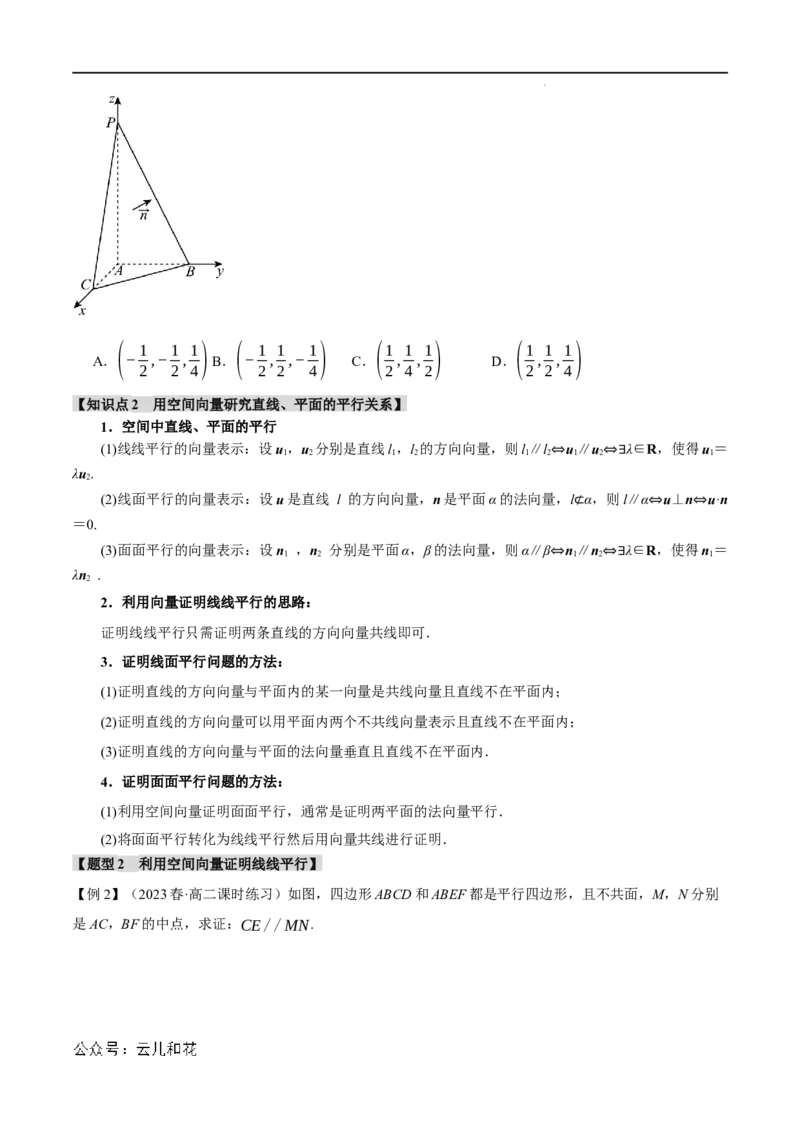
【变式1-3】(2023秋·北京石景山·高二统考期末)如图,在三棱锥P−ABC中,PA⊥平面ABC,
AB⊥AC,AB=AC=1,PA=2,以A为原点建立空间直角坐标系,如图所示,⃗n为平面PBC的一个法向
量,则⃗n的坐标可能是( )
学科网(北京)股份有限公司( 1 1 1) ( 1 1 1) (1 1 1) (1 1 1)
A. − ,− , B. − , ,− C. , , D. , ,
2 2 4 2 2 4 2 4 2 2 2 4
【知识点2 用空间向量研究直线、平面的平行关系】
1.空间中直线、平面的平行
(1)线线平行的向量表示:设u,u 分别是直线l,l 的方向向量,则l∥l u∥u λ∈R,使得u=
1 2 1 2 1 2 1 2 1
λu.
2 ⇔ ⇔∃
(2)线面平行的向量表示:设u是直线 l 的方向向量,n是平面α的法向量,l α,则l∥α u⊥n u·n
=0.
⊄ ⇔ ⇔
(3)面面平行的向量表示:设n ,n 分别是平面α,β的法向量,则α∥β n∥n λ∈R,使得n =
1 2 1 2 1
λn .
2 ⇔ ⇔∃
2.利用向量证明线线平行的思路:
证明线线平行只需证明两条直线的方向向量共线即可.
3.证明线面平行问题的方法:
(1)证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内;
(2)证明直线的方向向量可以用平面内两个不共线向量表示且直线不在平面内;
(3)证明直线的方向向量与平面的法向量垂直且直线不在平面内.
4.证明面面平行问题的方法:
(1)利用空间向量证明面面平行,通常是证明两平面的法向量平行.
(2)将面面平行转化为线线平行然后用向量共线进行证明.
【题型2 利用空间向量证明线线平行】
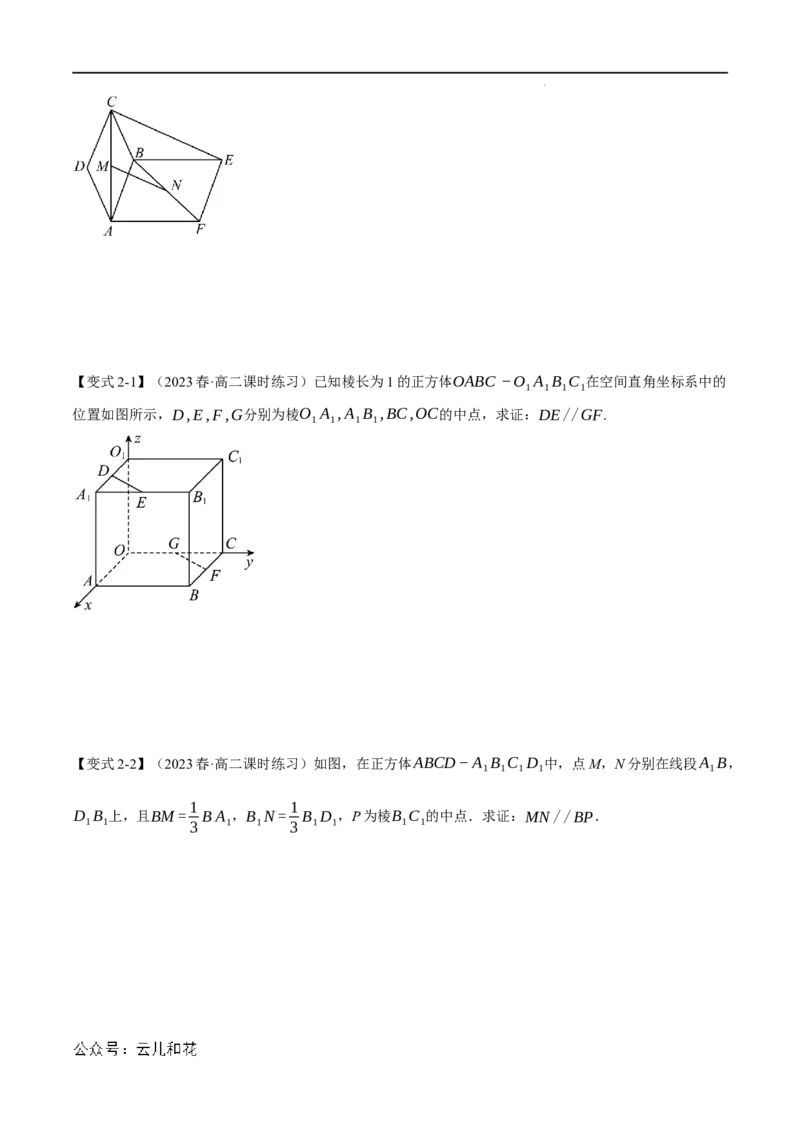
【例2】(2023春·高二课时练习)如图,四边形ABCD和ABEF都是平行四边形,且不共面,M,N分别
是AC,BF的中点,求证:CE//MN.
学科网(北京)股份有限公司【变式2-1】(2023春·高二课时练习)已知棱长为1的正方体OABC−O A B C 在空间直角坐标系中的
1 1 1 1
位置如图所示,D,E,F,G分别为棱O A ,A B ,BC,OC的中点,求证:DE//GF.
1 1 1 1
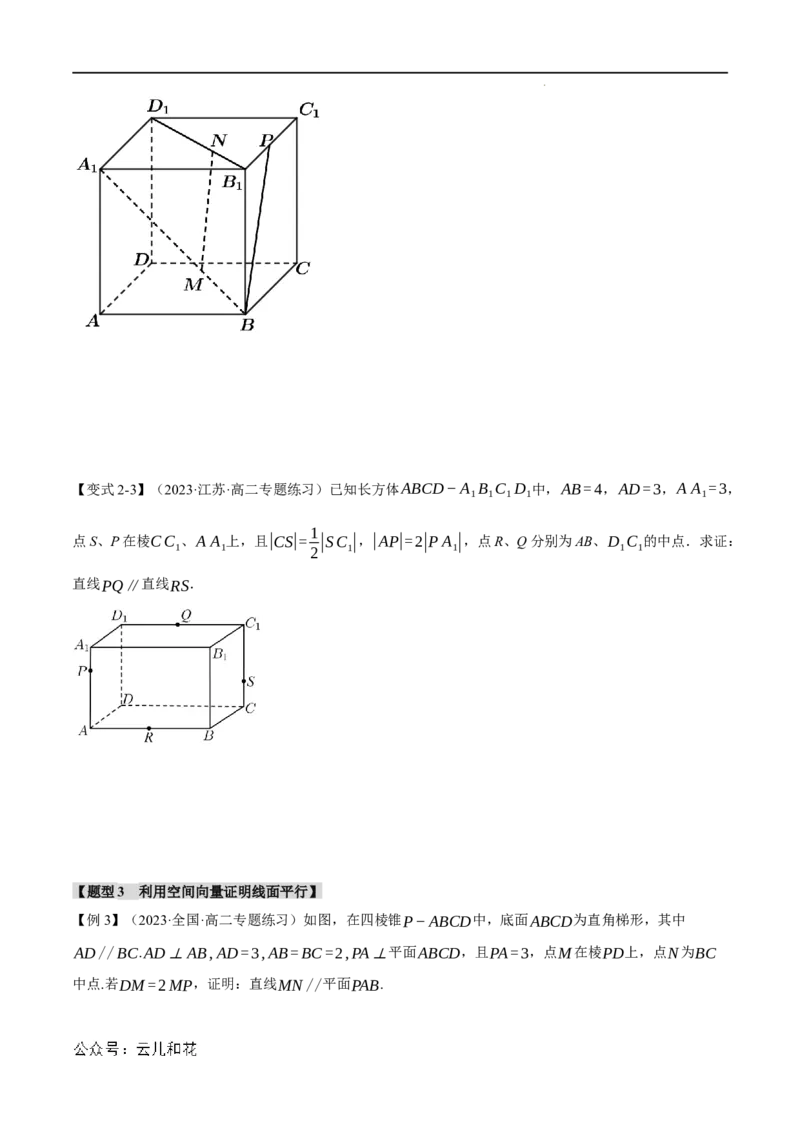
【变式2-2】(2023春·高二课时练习)如图,在正方体ABCD−A B C D 中,点M,N分别在线段A B,
1 1 1 1 1
1 1
D B 上,且BM= BA ,B N= B D ,P为棱B C 的中点.求证:MN//BP.
1 1 3 1 1 3 1 1 1 1
学科网(北京)股份有限公司【变式2-3】(2023·江苏·高二专题练习)已知长方体ABCD−A B C D 中,AB=4,AD=3,A A =3,
1 1 1 1 1
1
点S、P在棱CC 、A A 上,且|CS|= |SC |,|AP|=2|PA |,点R、Q分别为AB、D C 的中点.求证:
1 1 2 1 1 1 1
直线PQ∥直线RS.
【题型3 利用空间向量证明线面平行】
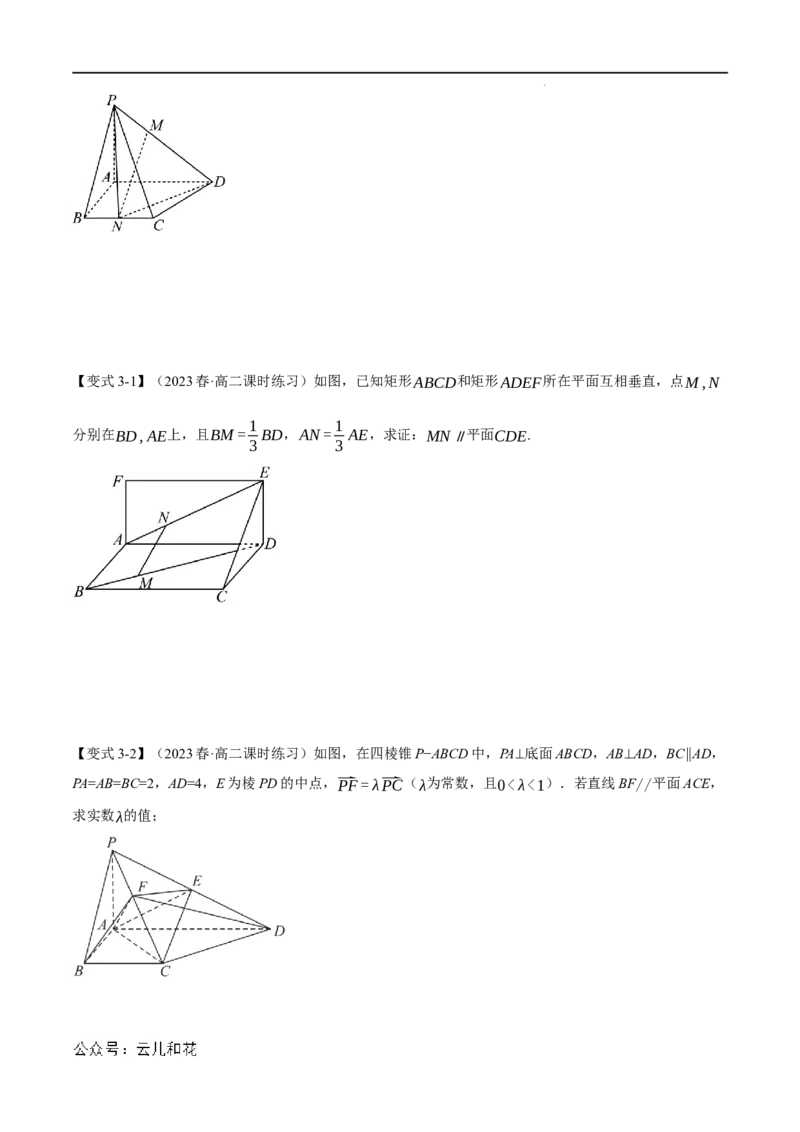
【例3】(2023·全国·高二专题练习)如图,在四棱锥P−ABCD中,底面ABCD为直角梯形,其中
AD//BC.AD⊥AB,AD=3,AB=BC=2,PA⊥平面ABCD,且PA=3,点M在棱PD上,点N为BC
中点.若DM=2MP,证明:直线MN//平面PAB.
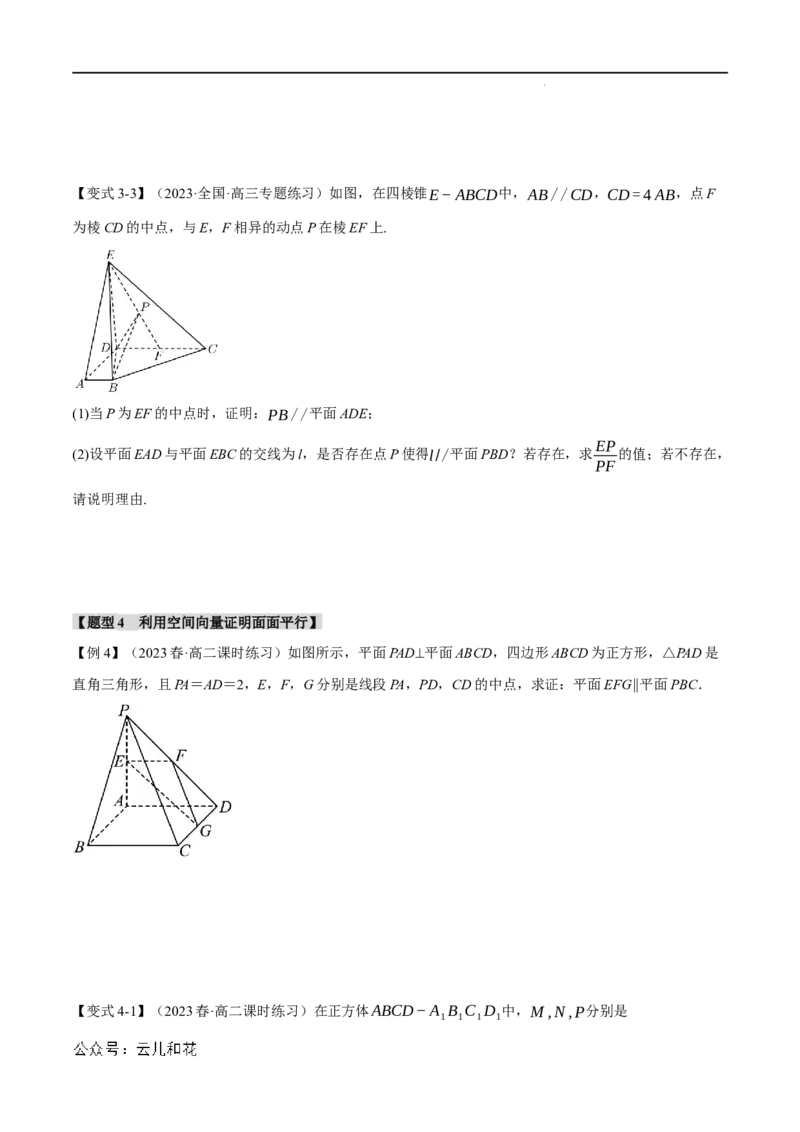
学科网(北京)股份有限公司【变式3-1】(2023春·高二课时练习)如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N
1 1
分别在BD,AE上,且BM= BD,AN= AE,求证:MN∥平面CDE.
3 3
【变式3-2】(2023春·高二课时练习)如图,在四棱锥P−ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,
PA=AB=BC=2,AD=4,E为棱PD的中点,⃑PF=λ⃑PC(λ为常数,且0<λ<1).若直线BF//平面ACE,
求实数λ的值;
学科网(北京)股份有限公司【变式3-3】(2023·全国·高三专题练习)如图,在四棱锥E−ABCD中,AB//CD,CD=4AB,点F
为棱CD的中点,与E,F相异的动点P在棱EF上.
(1)当P为EF的中点时,证明:PB//平面ADE;
EP
(2)设平面EAD与平面EBC的交线为l,是否存在点P使得l//平面PBD?若存在,求 的值;若不存在,
PF
请说明理由.
【题型4 利用空间向量证明面面平行】
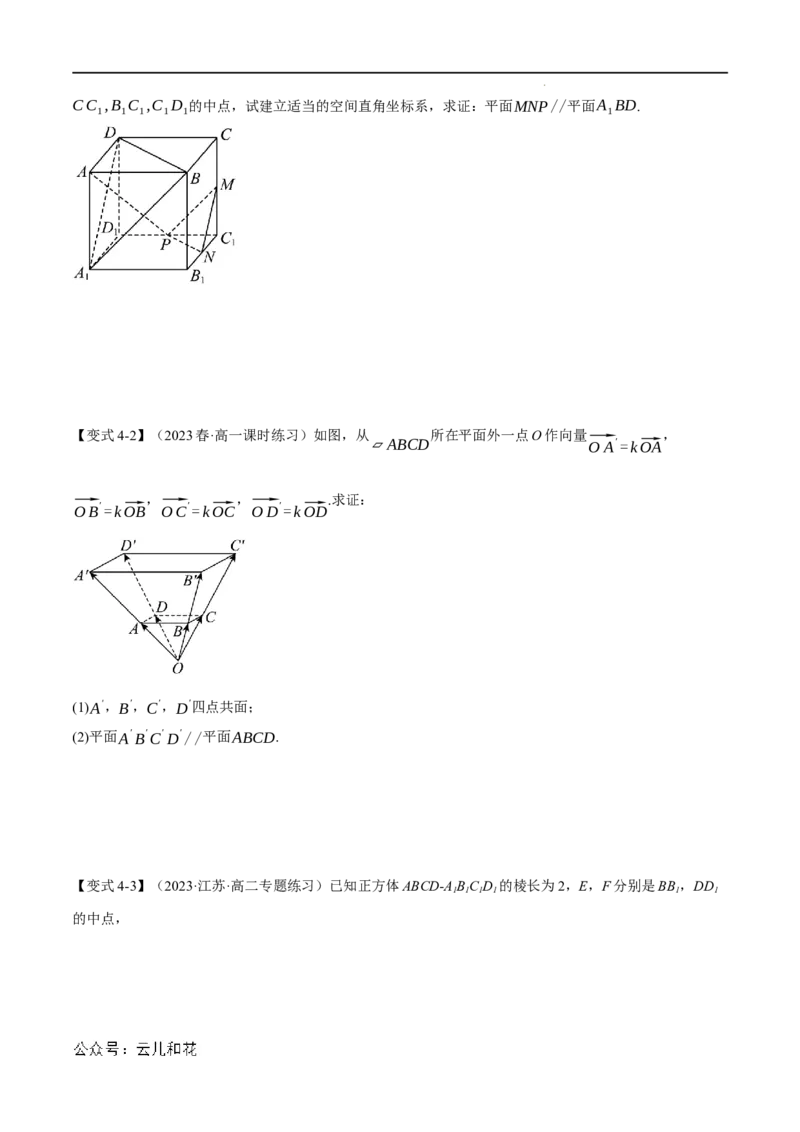
【例4】(2023春·高二课时练习)如图所示,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是
直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,求证:平面EFG∥平面PBC.
【变式4-1】(2023春·高二课时练习)在正方体ABCD−A B C D 中,M,N,P分别是
1 1 1 1
学科网(北京)股份有限公司CC ,B C ,C D 的中点,试建立适当的空间直角坐标系,求证:平面MNP//平面A BD.
1 1 1 1 1 1
【变式4-2】(2023春·高一课时练习)如图,从 所在平面外一点O作向量 ,
▱ABCD ⃗ OA′=k⃗OA
, , .求证:
⃗ OB′=k⃗OB ⃗ OC′=k⃗OC ⃗ OD′=k⃗OD
(1)A′,B′,C′,D′四点共面;
(2)平面A′B′C′D′//平面ABCD.
【变式4-3】(2023·江苏·高二专题练习)已知正方体ABCD-ABC D 的棱长为2,E,F分别是BB,DD
1 1 1 1 1 1
的中点,
学科网(北京)股份有限公司求证:(1)FC ∥平面ADE;
1
(2)平面ADE∥平面BC F.
1 1
【知识点3 用空间向量研究直线、平面的垂直关系】
1.空间中直线、平面的垂直
(1)线线垂直的向量表示:设 u,u 分别是直线 l , l 的方向向量,则l⊥l u⊥u u·u=0.
1 2 1 2 1 2 1 2 1 2
(2)线面垂直的向量表示:设 u 是直线 l 的方向向量,n 是平面 α 的法向量, l α,则
⇔ ⇔
l⊥α u∥n λ∈R,使得u=λn.
⊄
(3)面面垂直的向量表示:设n,n 分别是平面α,β的法向量,则α⊥β n⊥n n·n=0.
⇔ ⇔∃ 1 2 1 2 1 2
2.证明两直线垂直的基本步骤:
⇔ ⇔
建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.
3.用坐标法证明线面垂直的方法及步骤:
(1)利用线线垂直:①将直线的方向向量用坐标表示;②找出平面内两条相交直线,并用坐标表示它们
的方向向量;③判断直线的方向向量与平面内两条直线的方向向量垂直.
(2)利用平面的法向量:①将直线的方向向量用坐标表示;②求出平面的法向量;③判断直线的方向向
量与平面的法向量平行.
4.证明面面垂直的两种方法:
(1)常规法:利用面面垂直的判定定理转化为线面垂直、线线垂直去证明.
(2)法向量法:证明两个平面的法向量互相垂直.
【题型5 利用空间向量证明线线垂直】
【例5】(2023春·高二课时练习)在棱长为1的正方体ABCD−A′B′C′D′中,E,F分别是D′D,DB中
1
点,G在棱CD上,CG= CD,H为C′G的中点,求证:EF⊥B′C;
4
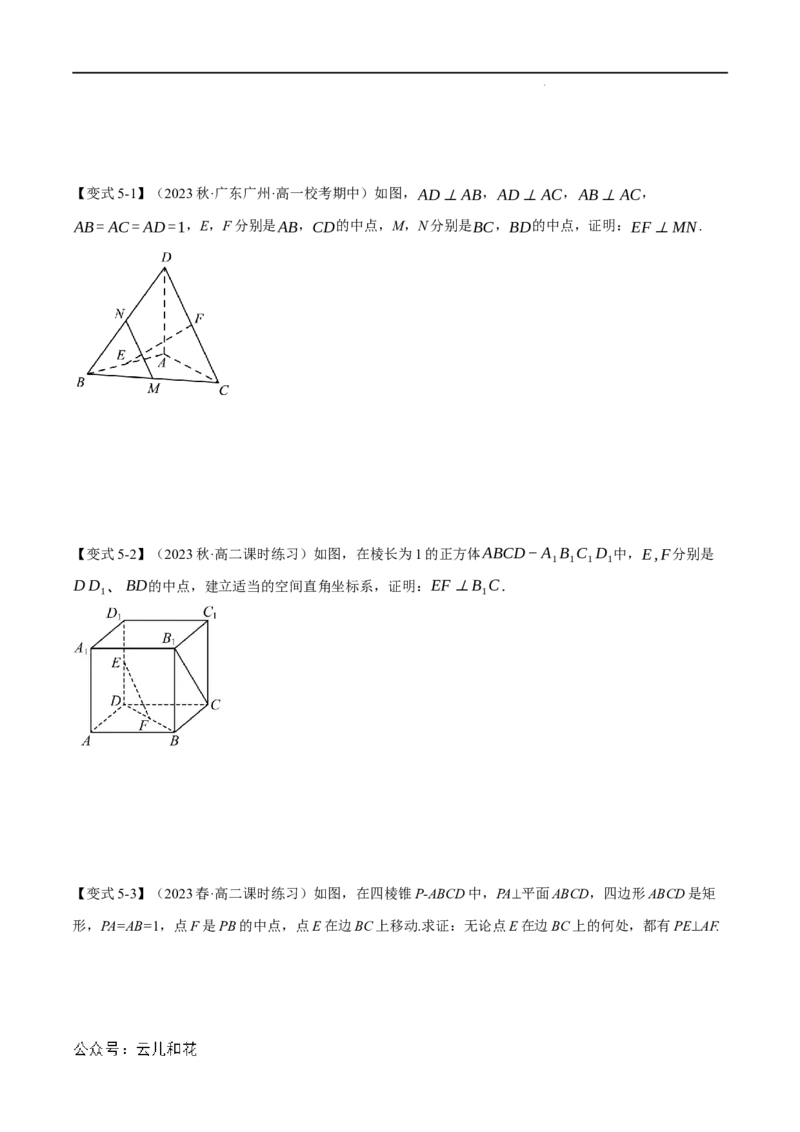
学科网(北京)股份有限公司【变式5-1】(2023秋·广东广州·高一校考期中)如图,AD⊥AB,AD⊥AC,AB⊥AC,
AB=AC=AD=1,E,F分别是AB,CD的中点,M,N分别是BC,BD的中点,证明:EF⊥MN.
【变式5-2】(2023秋·高二课时练习)如图,在棱长为1的正方体ABCD−A B C D 中,E,F分别是
1 1 1 1
DD 、BD的中点,建立适当的空间直角坐标系,证明:EF⊥B C.
1 1
【变式5-3】(2023春·高二课时练习)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩
形,PA=AB=1,点F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.
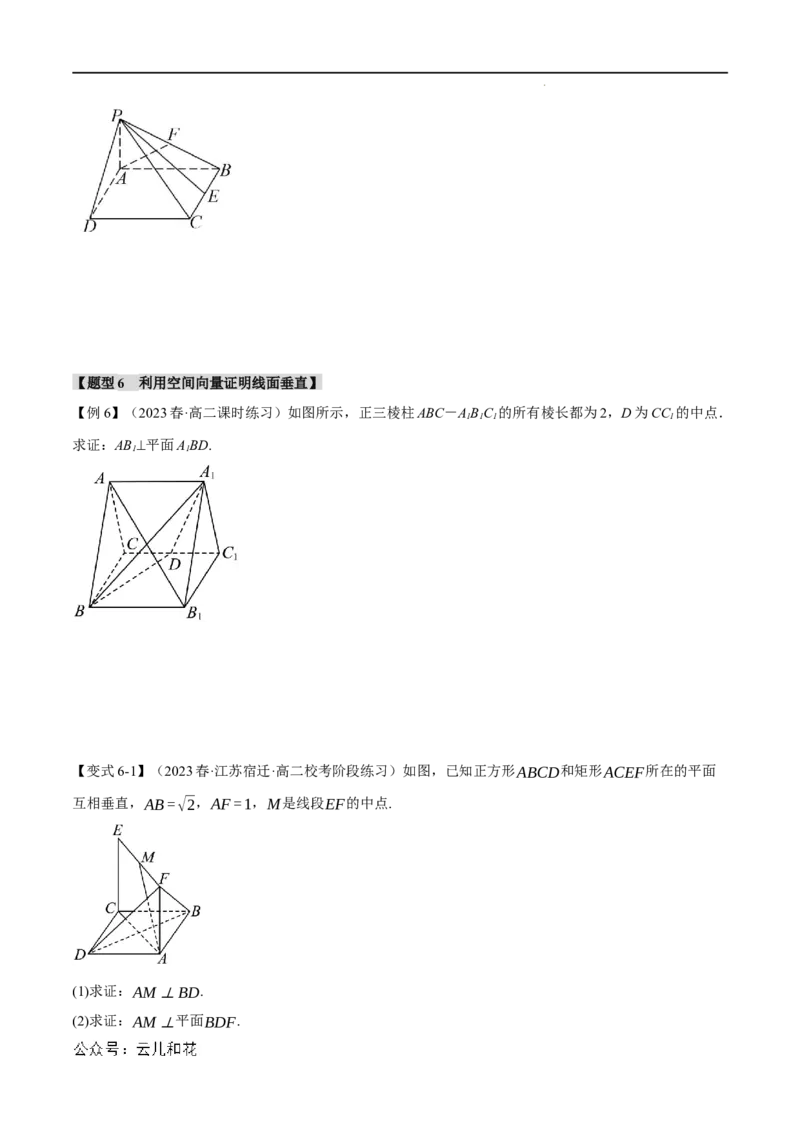
学科网(北京)股份有限公司【题型6 利用空间向量证明线面垂直】
【例6】(2023春·高二课时练习)如图所示,正三棱柱ABC-ABC 的所有棱长都为2,D为CC 的中点.
1 1 1 1
求证:AB⊥平面ABD.
1 1
【变式6-1】(2023春·江苏宿迁·高二校考阶段练习)如图,已知正方形ABCD和矩形ACEF所在的平面
互相垂直,AB=√2,AF=1,M是线段EF的中点.
(1)求证:AM⊥BD.
(2)求证:AM⊥平面BDF.
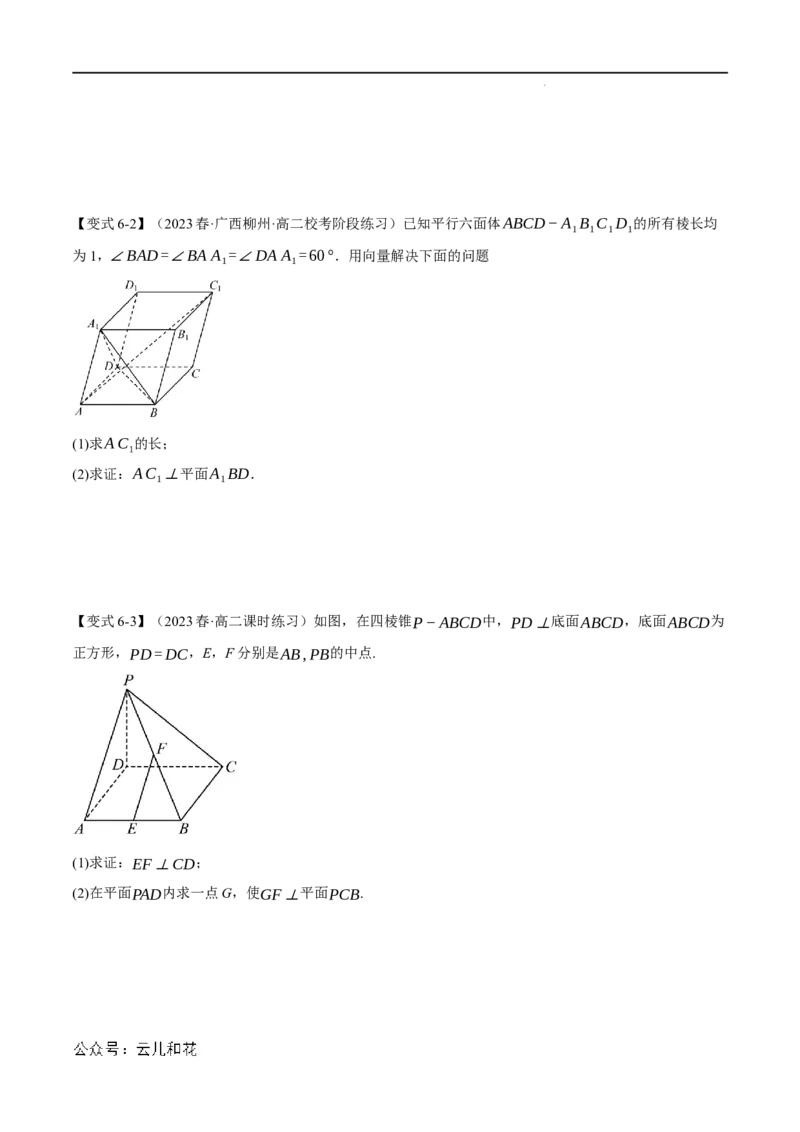
学科网(北京)股份有限公司【变式6-2】(2023春·广西柳州·高二校考阶段练习)已知平行六面体ABCD−A B C D 的所有棱长均
1 1 1 1
为1,∠BAD=∠BA A =∠DA A =60°.用向量解决下面的问题
1 1
(1)求AC 的长;
1
(2)求证:AC ⊥平面A BD.
1 1
【变式6-3】(2023春·高二课时练习)如图,在四棱锥P−ABCD中,PD⊥底面ABCD,底面ABCD为
正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB.
学科网(北京)股份有限公司【题型7 利用空间向量证明面面垂直】
【例7】(2023春·高二课时练习)如图所示, ABC是一个正三角形,EC⊥平面ABC,BD∥CE,且CE=
CA=2BD,M是EA的中点.求证:平面DEA⊥△平面ECA.
【变式7-1】(2023·全国·高三专题练习)如图,在五面体ABCDEF中,FA⊥平面ABCD,
AD∥BC∥FE,AB⊥AD,若AD=2,AF=AB= BC=FE=1.
(1)求五面体ABCDEF的体积;
(2)若M为EC的中点,求证:平面CDE⊥平面AMD.
【变式7-2】(2023秋·新疆昌吉·高二校考期末)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,
AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
学科网(北京)股份有限公司(1)BE∥平面PAD;
(2)平面PCD⊥平面PAD.
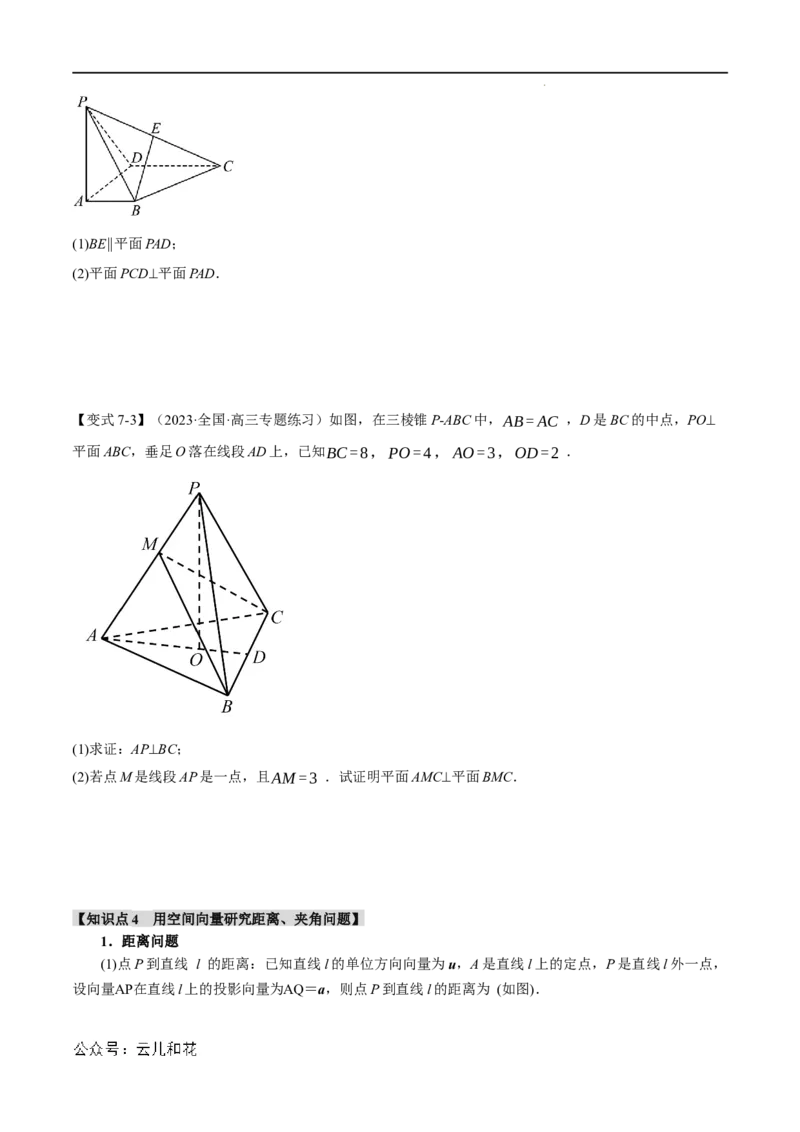
【变式7-3】(2023·全国·高三专题练习)如图,在三棱锥P-ABC中,AB=AC ,D是BC的中点,PO⊥
平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2 .
(1)求证:AP⊥BC;
(2)若点M是线段AP是一点,且AM=3 .试证明平面AMC⊥平面BMC.
【知识点4 用空间向量研究距离、夹角问题】
1.距离问题
(1)点P到直线 l 的距离:已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点,
设向量AP在直线l上的投影向量为AQ=a,则点P到直线l的距离为 (如图).
学科网(北京)股份有限公司(2)点P到平面α的距离:设平面α的法向量为n,A是平面α内的定点,P是平面α外一点,则点P到
平面α的距离为(如图).
2.夹角问题
(1)两个平面的夹角:平面α与平面β的夹角:平面α与平面β相交,形成四个二面角,我们把这四个
二面角中不大于90° 的二面角称为平面α与平面β的夹角.
(2)空间角的向量法解法
角的分类 向量求法 范围
两条异面直 设两异面直线 l,l 所成的角为θ,其方向向
1 2
线所成的角 量分别为u,v,则cos θ=|cos〈u,v〉|=
设直线AB与平面α所成的角为θ,直线AB的
直线与平面
方向向量为u,平面α的法向量为n,则sin θ
所成的角
=|cos 〈u,n〉|=
设平面α与平面β的夹角为θ,平面α,β的法
两个平面的
向量分别为n,n,则cos θ=|cos 〈n,n〉|
1 2 1 2
夹角
=
【题型8 利用空间向量研究距离问题】
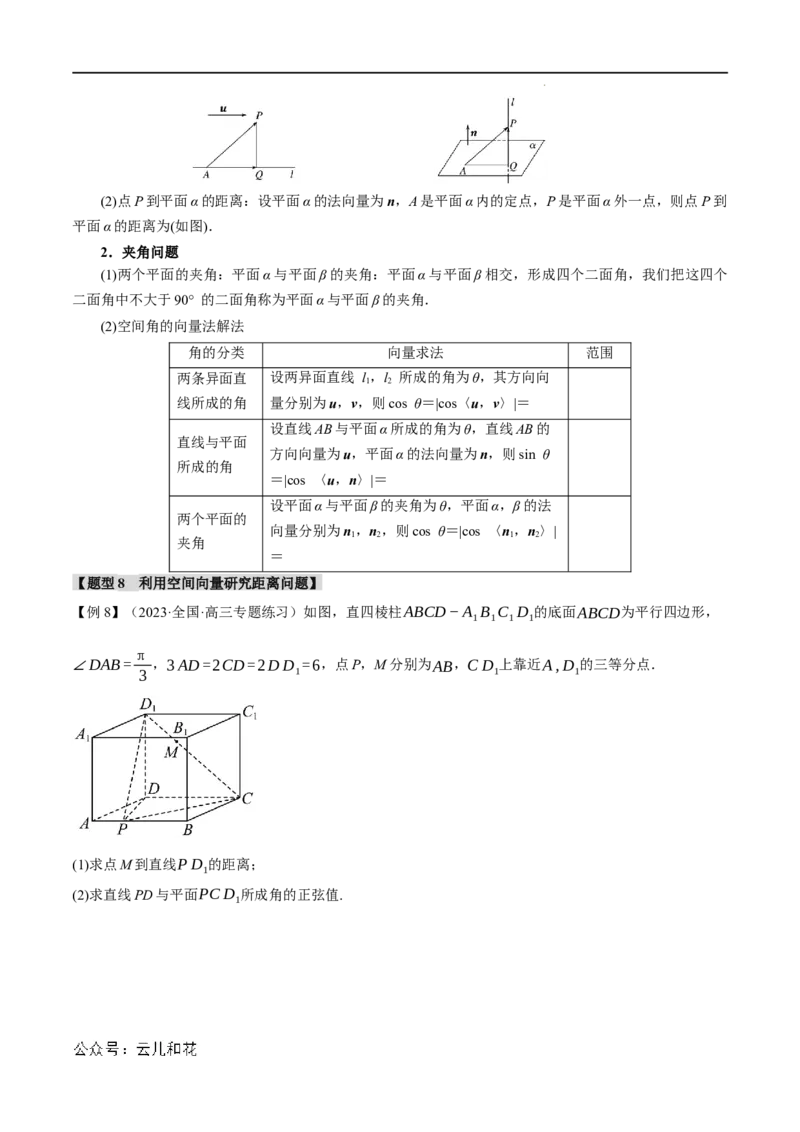
【例8】(2023·全国·高三专题练习)如图,直四棱柱ABCD−A B C D 的底面ABCD为平行四边形,
1 1 1 1
π
∠DAB= ,3AD=2CD=2DD =6,点P,M分别为AB,CD 上靠近A,D 的三等分点.
3 1 1 1
(1)求点M到直线PD 的距离;
1
(2)求直线PD与平面PCD 所成角的正弦值.
1
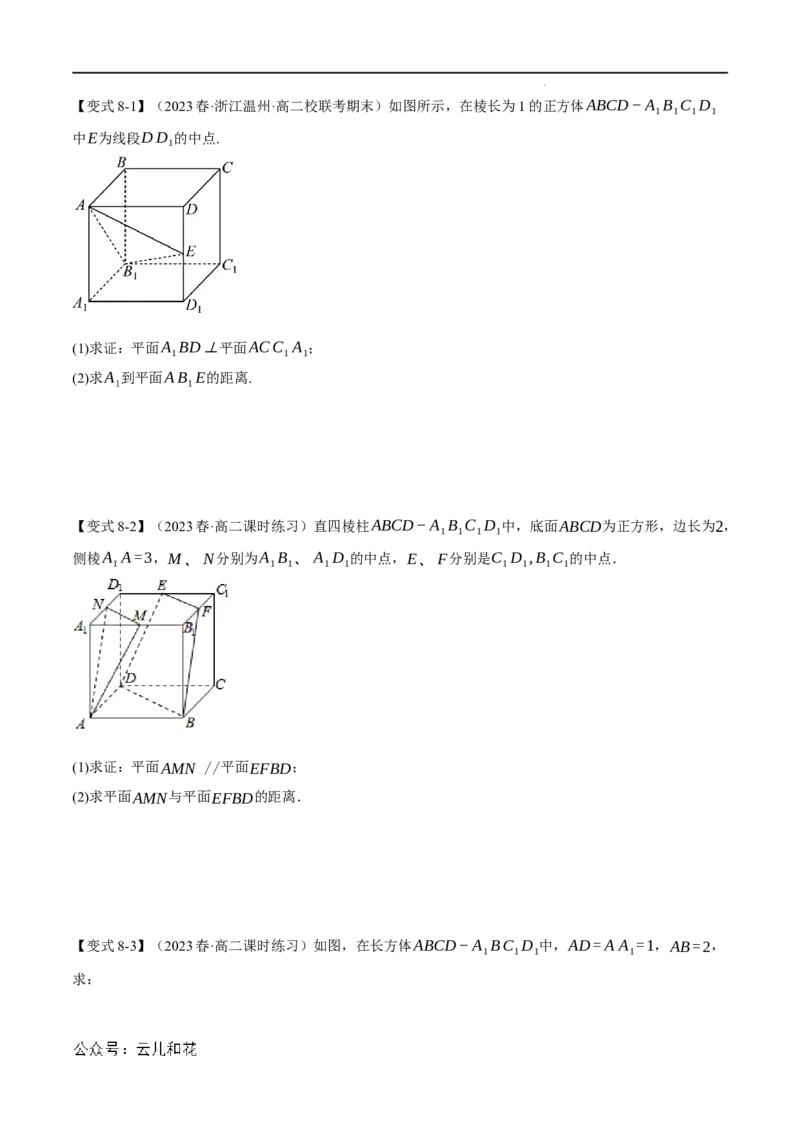
学科网(北京)股份有限公司【变式8-1】(2023春·浙江温州·高二校联考期末)如图所示,在棱长为1的正方体ABCD−A B C D
1 1 1 1
中E为线段DD 的中点.
1
(1)求证:平面A BD⊥平面ACC A ;
1 1 1
(2)求A 到平面AB E的距离.
1 1
【变式8-2】(2023春·高二课时练习)直四棱柱ABCD−A B C D 中,底面ABCD为正方形,边长为2,
1 1 1 1
侧棱A A=3,M、N分别为A B 、A D 的中点,E、F分别是C D ,B C 的中点.
1 1 1 1 1 1 1 1 1
(1)求证:平面AMN //平面EFBD;
(2)求平面AMN与平面EFBD的距离.
【变式8-3】(2023春·高二课时练习)如图,在长方体ABCD−A BC D 中,AD=A A =1,AB=2,
1 1 1 1
求:
学科网(北京)股份有限公司(1)点A 到直线BD的距离;
1
(2)点A 到平面BDC 的距离;
1 1
(3)异面直线BD,CD 之间的距离.
1
【题型9 利用空间向量求空间角】
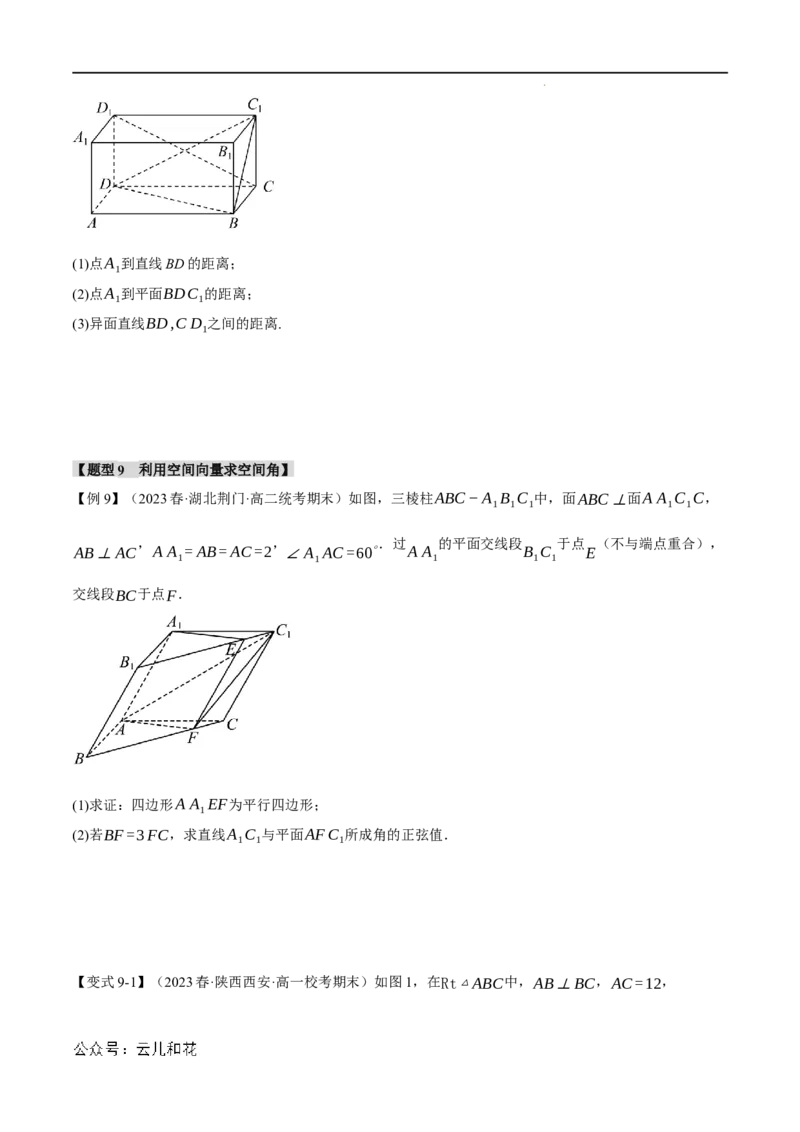
【例9】(2023春·湖北荆门·高二统考期末)如图,三棱柱ABC−A B C 中,面ABC⊥面A A C C,
1 1 1 1 1
, , .过 的平面交线段 于点 (不与端点重合),
AB⊥AC A A =AB=AC=2 ∠A AC=60∘ A A B C E
1 1 1 1 1
交线段BC于点F.
(1)求证:四边形A A EF为平行四边形;
1
(2)若BF=3FC,求直线A C 与平面AFC 所成角的正弦值.
1 1 1
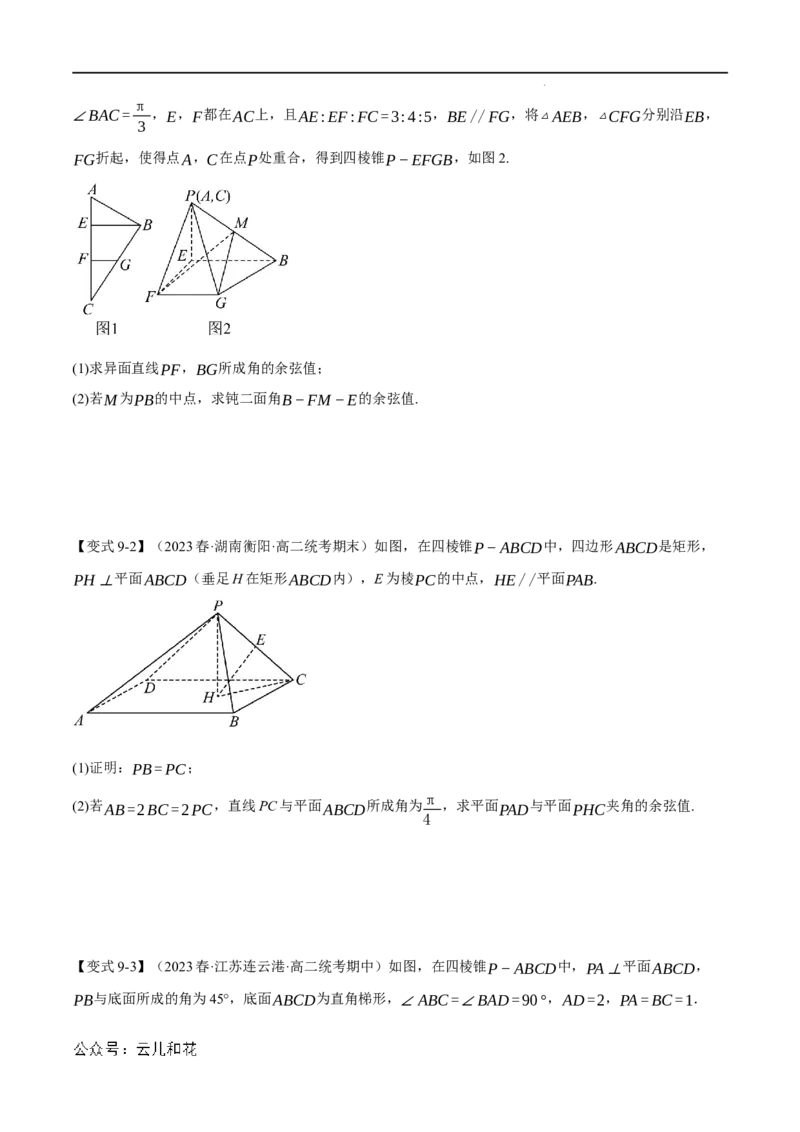
【变式9-1】(2023春·陕西西安·高一校考期末)如图1,在Rt△ABC中,AB⊥BC,AC=12,
学科网(北京)股份有限公司π
∠BAC= ,E,F都在AC上,且AE:EF:FC=3:4:5,BE//FG,将△AEB,△CFG分别沿EB,
3
FG折起,使得点A,C在点P处重合,得到四棱锥P−EFGB,如图2.
(1)求异面直线PF,BG所成角的余弦值;
(2)若M为PB的中点,求钝二面角B−FM−E的余弦值.
【变式9-2】(2023春·湖南衡阳·高二统考期末)如图,在四棱锥P−ABCD中,四边形ABCD是矩形,
PH⊥平面ABCD(垂足H在矩形ABCD内),E为棱PC的中点,HE//平面PAB.
(1)证明:PB=PC;
π
(2)若AB=2BC=2PC,直线PC与平面ABCD所成角为 ,求平面PAD与平面PHC夹角的余弦值.
4
【变式9-3】(2023春·江苏连云港·高二统考期中)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,
PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2,PA=BC=1.
学科网(北京)股份有限公司(1)求直线PC与平面PBD所成角的正弦值;
(2)求平面PAB与平面PCD所成的锐二面角的余弦值.
【题型10 利用空间向量研究存在性问题】
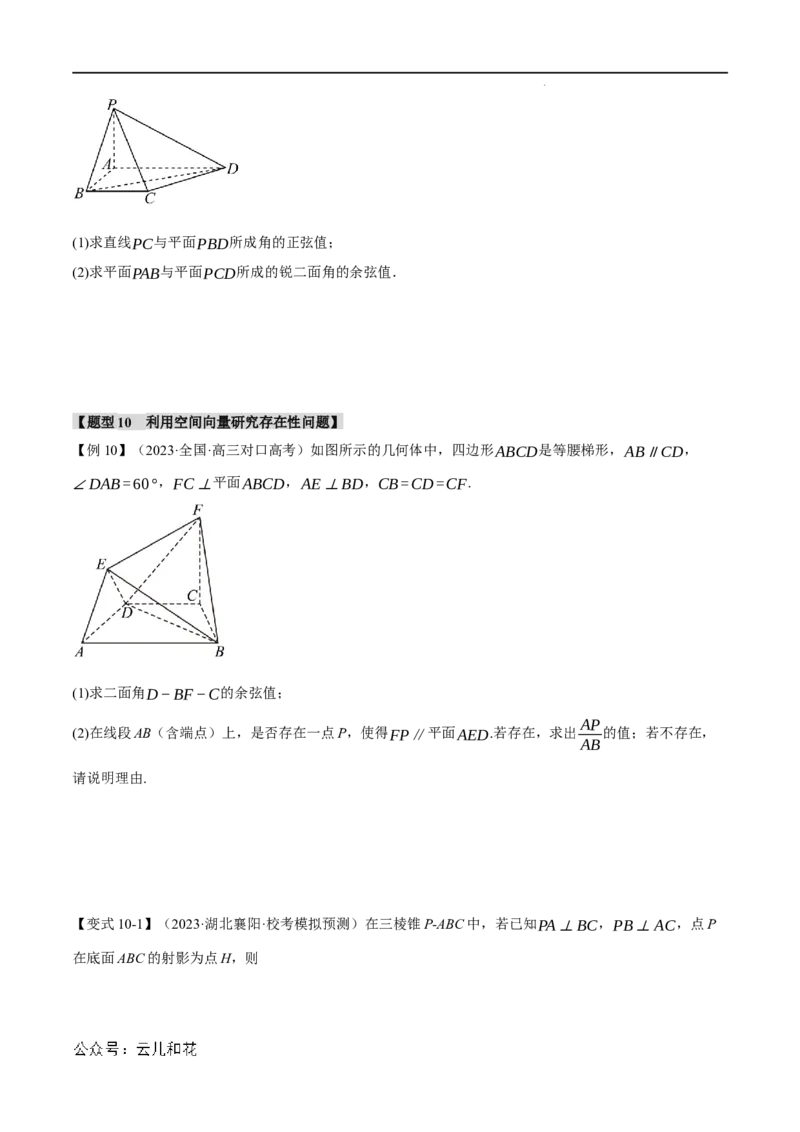
【例10】(2023·全国·高三对口高考)如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,
∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求二面角D−BF−C的余弦值;
AP
(2)在线段AB(含端点)上,是否存在一点P,使得FP∥平面AED.若存在,求出 的值;若不存在,
AB
请说明理由.
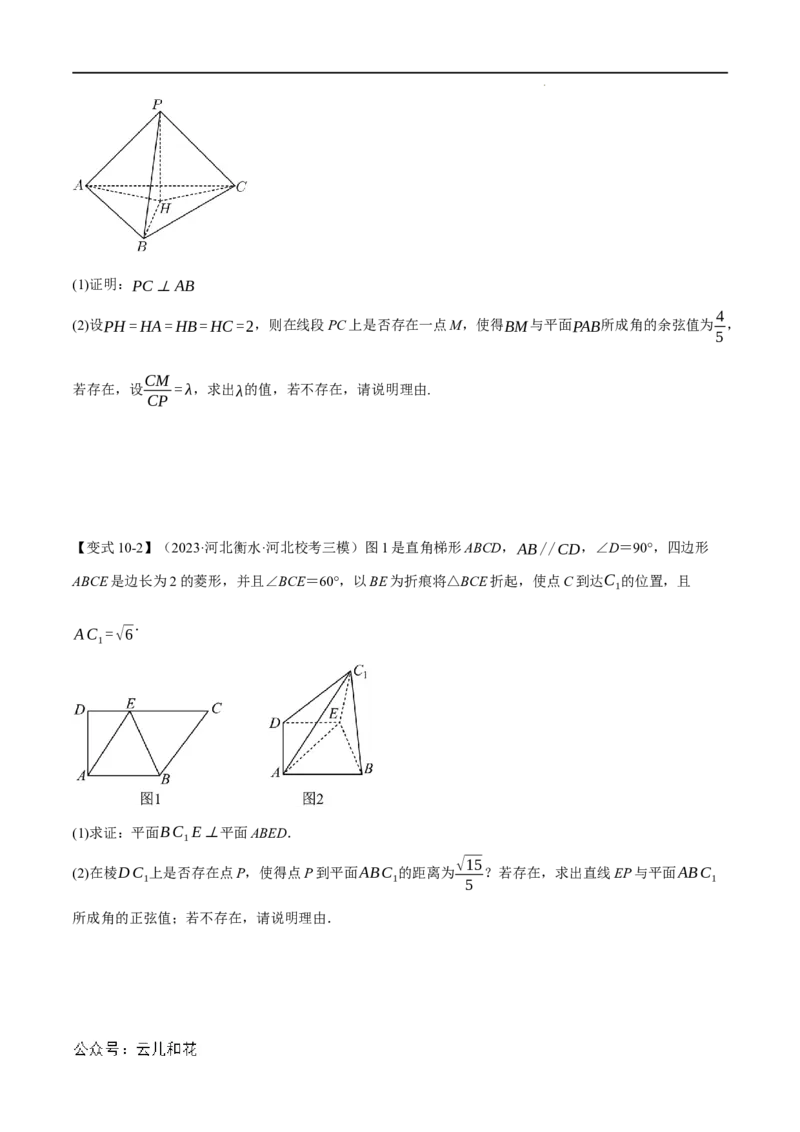
【变式10-1】(2023·湖北襄阳·校考模拟预测)在三棱锥P-ABC中,若已知PA⊥BC,PB⊥AC,点P
在底面ABC的射影为点H,则
学科网(北京)股份有限公司(1)证明:PC⊥AB
4
(2)设PH=HA=HB=HC=2,则在线段PC上是否存在一点M,使得BM与平面PAB所成角的余弦值为 ,
5
CM
若存在,设 =λ,求出λ的值,若不存在,请说明理由.
CP
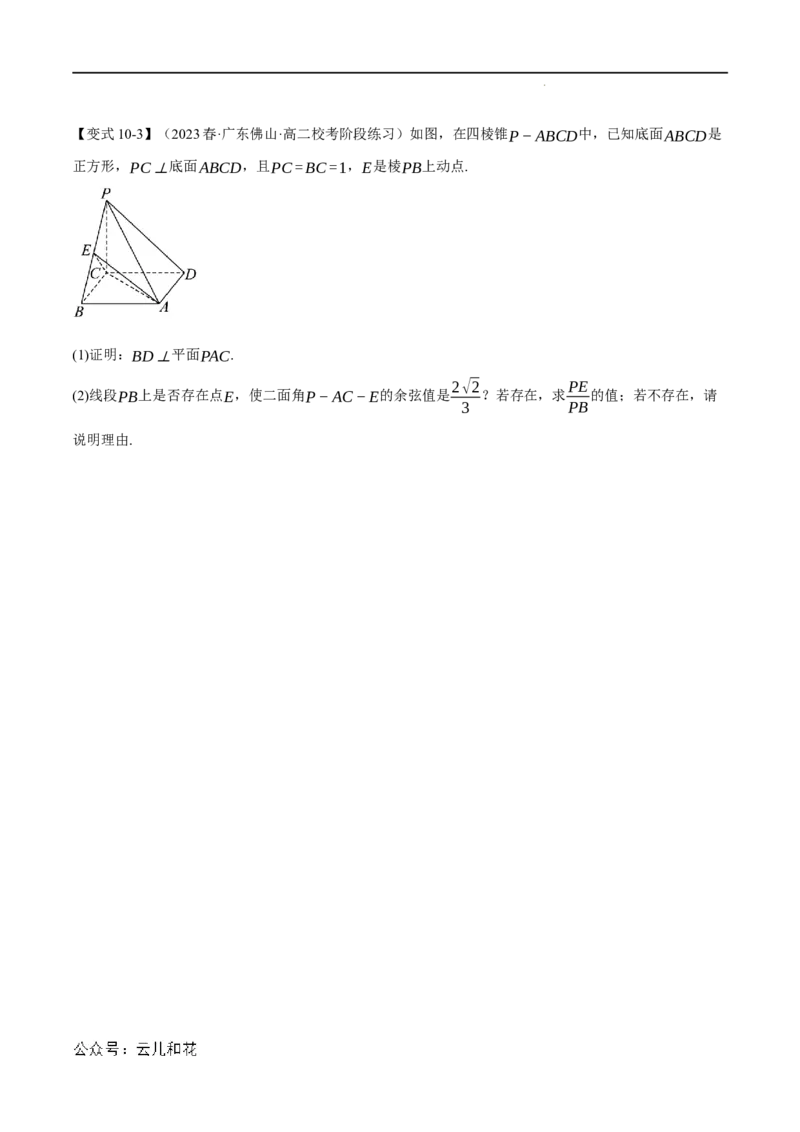
【变式10-2】(2023·河北衡水·河北校考三模)图1是直角梯形ABCD,AB//CD,∠D=90°,四边形
ABCE是边长为2的菱形,并且∠BCE=60°,以BE为折痕将△BCE折起,使点C到达C 的位置,且
1
.
AC =√6
1
(1)求证:平面BC E⊥平面ABED.
1
√15
(2)在棱DC 上是否存在点P,使得点P到平面ABC 的距离为 ?若存在,求出直线EP与平面ABC
1 1 5 1
所成角的正弦值;若不存在,请说明理由.
学科网(北京)股份有限公司【变式10-3】(2023春·广东佛山·高二校考阶段练习)如图,在四棱锥P−ABCD中,已知底面ABCD是
正方形,PC⊥底面ABCD,且PC=BC=1,E是棱PB上动点.
(1)证明:BD⊥平面PAC.
2√2 PE
(2)线段PB上是否存在点E,使二面角P−AC−E的余弦值是 ?若存在,求 的值;若不存在,请
3 PB
说明理由.
学科网(北京)股份有限公司