北京市海淀区2023-2024学年高二下学期期末考试数学试卷_2024-2025高二（7-7月题库）_2024年07月试卷_0721北京市海淀区2023-2024学年高二下学期7月期末

北京市海淀区 2023-2024 学年高二下学期期末考试 数学试卷 本试卷共6页，共两部分。19道题，共100分。考试时长90分钟。试题答案一律填涂或书写在答题 卡上，在试卷上作答无效。考试结束后，请将答题卡交回。 第一部分（选择题共40分） 一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。 1. (x1)5的展开式中，所有二项式的系数和为 A.0 B.25 C. 1D.26 sinx 2.已知函数 f(x) ,则 f(0)的值为 cosx A.0 B.1 C.1 D. 3.若等比数列a 的前n项和S 2n 1，则公比q n n 1 1 A. B. C.2 D.2 2 2 4.下列函数中，在区间1,0上的平均变化率最大的时 x 1 A.yx2 B.yx3 C.y  D. y2x 2 5.将分别写有2,0,2,4的四章卡片，按一定次序排成一行组成一个四位数（首位不为0），则组成的不同四 位数的个数为 A.9 B.12 C.18 D. 24 6.小明投篮3次，每次投中的概率为0.8，且每次投篮互不影响，若投中一次的2分，没投中得0分，总得 分为X ，则 A.EX2.4 B. EX4.8 C. DX0.48 D. DX0.96 7.已知一批产品中，A项指标合格的比例为80%，B项指标合格的比例为90%，A、B两项指标都合格的 比例为60%，从这批产品中随机抽取一个产品，若A项指标合格，则该产品的B项指标也合格的概率是 3 2 3 5 A. B. C. D. 7 3 4 6 8.已知等差数列a 的前n项和为S ，若a 0、则“S 有最大值”是“公差d 0”的 n n 1 n A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 9.设函数 f xln1xasinx.若 f x f 0在1,1上恒成立，则 A.a0 B.a1 C.0a1 D.a1 第1页/共4页 学科网（北京）股份有限公司10.在经济学中，将产品销量为x件时的总收益称为收益函数，记为Rx，相应地把Rx称为边际收益函 数，它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数Rx1000x (注:经济学 中涉及的函数有时是离散型函数，但仍将其看成连续函数来分析).给出下列三个结论: ①当销量为1000件时，总收益最大; ②若销量为800件时，总收益为T，则当销量增加400件时，总收益仍为T; ③当销量从500件增加到501件时，总收益改变量的近似值为500. 其中正确结论的个数为 A.0 B.1 C.2 D.3 第二部分（非选择题 共60分） 二、填空题共5小题，每小题4分，共20分。 11. (12x)4的展开式中含x2项的系数为_________. 12.某学校组织趣味运动会，一共设置了3个项目（其中只包含1个球类项目），每位教师只能从3个项目 中随机选择 2个参加，设李老师选择的 2个项目中所含球类项目的数量为 X ，则 X 的所有可能取值为 _________，数学期望EX_________. 13.已知数列a 1是公比为2的等比数列，若a 0，则a a a  ________. n 1 1 2 n 14.甲乙两人射击一架进入禁飞区的无人机.已知甲乙两人击中无人机的概率分别为0.5，0.4,且甲乙射击互 不影响，则无人机被击中的概率为_________.若无人机恰好被一人击中，则被击落的概率为0.2；若恰好被 两人击中，则被击落的概率为0.6，那么无人机被击落的概率为_______ 15. 已知数列a 的前n项和为S ，满足a 1,当n2时，S2 a2 .给出下列四个结论:①当0 n n 1 n n 1 时,a  ; 3 4 ②当3时,S 2; 2024 ③当4时,n2,S 2恒成立; n ④当1时，a 从第三项起为递增数列. n 其中所有正确结论的序号为_________. 三、解答题共4小题，共40分。解答应写出文字说明、演算步骤或证明过程。 16.（本小题8分） 已知函数 f xx1ex x2. （Ⅰ）判断 f x在,0上的单调性，并证明； （Ⅱ）求 f x在0,上的零点个数. 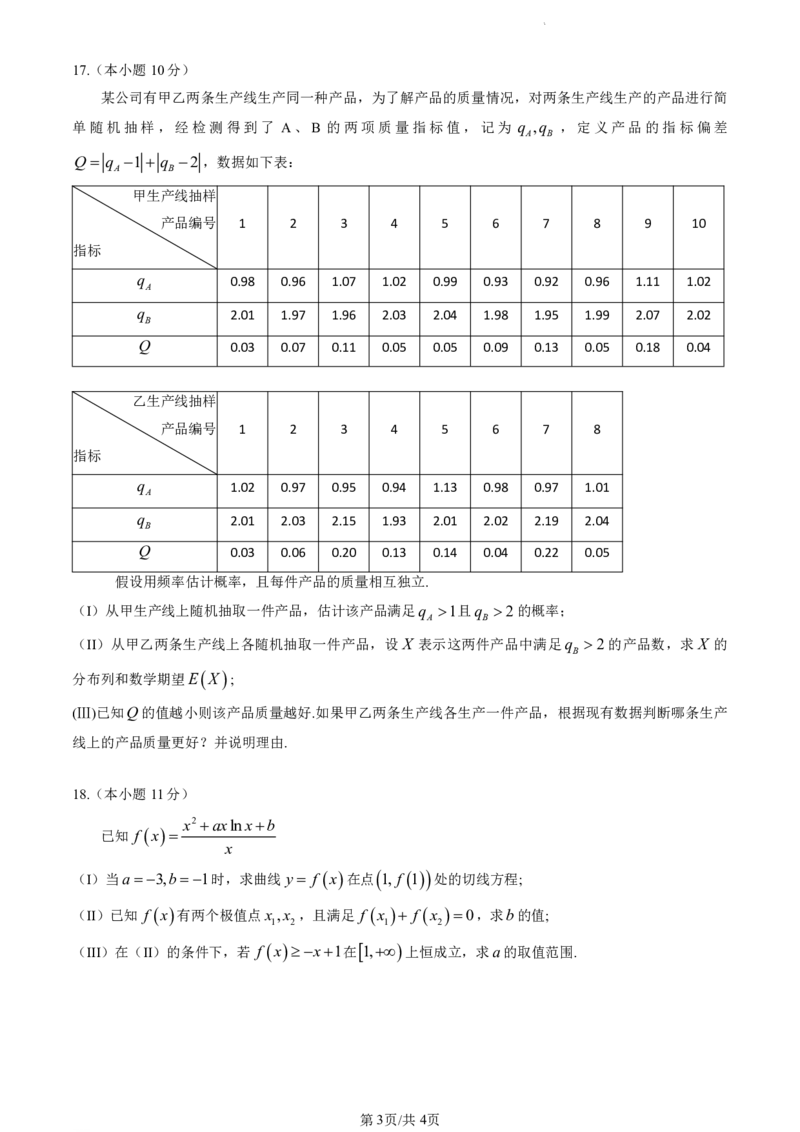第2页/共4页 学科网（北京）股份有限公司17.（本小题10分） 某公司有甲乙两条生产线生产同一种产品，为了解产品的质量情况，对两条生产线生产的产品进行简 单随机抽样，经检测得到了 A、B 的两项质量指标值，记为 q ,q ，定义产品的指标偏差 A B Q q 1 q 2 ，数据如下表： A B 甲生产线抽样 产品编号 1 2 3 4 5 6 7 8 9 10 指标 q 0.98 0.96 1.07 1.02 0.99 0.93 0.92 0.96 1.11 1.02 A q 2.01 1.97 1.96 2.03 2.04 1.98 1.95 1.99 2.07 2.02 B Q 0.03 0.07 0.11 0.05 0.05 0.09 0.13 0.05 0.18 0.04 乙生产线抽样 产品编号 1 2 3 4 5 6 7 8 指标 q 1.02 0.97 0.95 0.94 1.13 0.98 0.97 1.01 A q 2.01 2.03 2.15 1.93 2.01 2.02 2.19 2.04 B Q 0.03 0.06 0.20 0.13 0.14 0.04 0.22 0.05 假设用频率估计概率，且每件产品的质量相互独立. （I）从甲生产线上随机抽取一件产品，估计该产品满足q 1且q 2的概率； A B （II）从甲乙两条生产线上各随机抽取一件产品，设 X 表示这两件产品中满足q 2的产品数，求 X 的 B 分布列和数学期望E  X  ; (Ⅲ)已知Q的值越小则该产品质量越好.如果甲乙两条生产线各生产一件产品，根据现有数据判断哪条生产 线上的产品质量更好？并说明理由. 18.（本小题11分） x2 axlnxb 已知 f  x  x （I）当a 3,b1时，求曲线 y f  x 在点  1, f  1  处的切线方程; （II）已知 f  x 有两个极值点x ,x ，且满足 f  x  f  x 0，求b的值; 1 2 1 2 （III）在（II）的条件下，若 f  x x1在 1,上恒成立，求a的取值范围. 第3页/共4页 学科网（北京）股份有限公司19.（本小题11）   已知数列 A:a ,a ,,a 满足a a a ,集合S  a a 1i j 100 .设S 中有m 个 1 2 100 1 2 100 i j 元素，从小到大排列依次为b,b ,,b 1 2 m （I）若a n,，请直接写出m,b,b ； n 1 m （II）若a 2n,，求b ； n 20 （III）若b a a  i  j ，求 j的最小值 2025 i j 20.（本小题14分） 设函数 f(x)sinx 3cosx (0).从下列三个条件中选择两个作为已知，使函数 f(x)存在. （Ⅰ）求 f(x)的最小正周期及单调递减区间； π （Ⅱ）若对于任意的x[ ,π]，都有 f(x)c，求实数c的取值范围. 2 π 条件①：函数 f(x)的图象经过点( ,2)； 6 5π π 条件②： f(x)在区间[ , ]上单调递增； 12 12 π 条件③：x 是 f(x)的一条对称轴. 12 注：如果选择的条件不符合要求，第（Ⅰ）问得0分；如果选择多个符合要求的条件分析解答，按 第一个解答计分. 21.（本小题15分） 设 n 为正整数，集合 A (t ,t ,,t ),t (0,1),k 1,2,,n  . 对于集合 A 中的任意元素 n 1 2 n k n (x,x ,,x )和(y ,y ,,y )，定义*(x y ,x y ,,x y )， 1 2 n 1 2 n 1 1 2 2 n n (|x  y |,|x  y |,,|x  y |)，以及|| x x x . 1 1 2 2 n n 1 2 n （Ⅰ）若n5，(1,1,1,0,1)，*(0,1,1,0,1)，||4，求； （Ⅱ）若n9，,,, (k 2)均为A 中的元素，且||3 (1ik)，|* |0 (1i jk)，求 1 2 k n i i j k的最大值； （ Ⅲ ） 若 ,,,, (k 2) 均 为 A (n5) 中 的 元 素 ， 其 中 | |0 ， | |n ， 且 满 足 0 1 2 k n 0 k | |n2 (0ik1)，求k的最小值. i i1 第4页/共4页 学科网（北京）股份有限公司