文档内容
专题 1.6 空间角的向量求法大题专项训练(30 道)
【人教A版(2019)】
姓名:___________班级:___________考号:___________
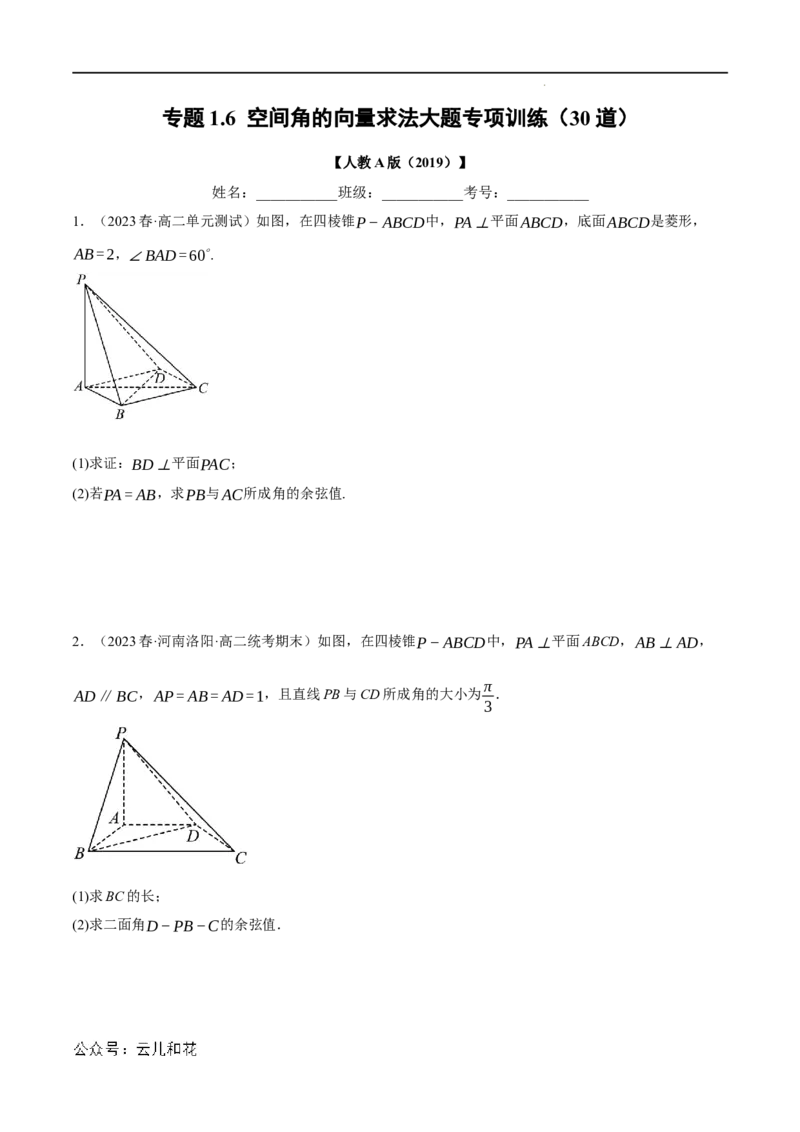
1.(2023春·高二单元测试)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
AB=2,∠BAD=60∘.
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.
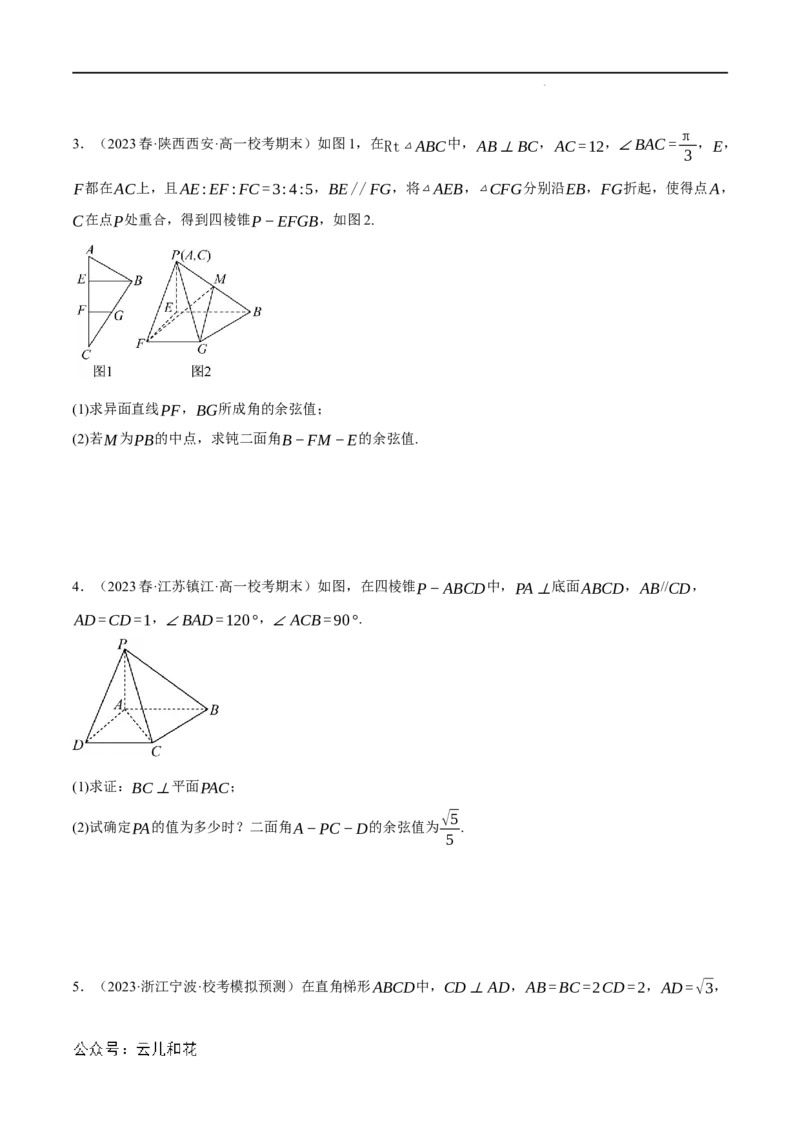
2.(2023春·河南洛阳·高二统考期末)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,AB⊥AD,
π
AD∥BC,AP=AB=AD=1,且直线PB与CD所成角的大小为 .
3
(1)求BC的长;
(2)求二面角D−PB−C的余弦值.
学科网(北京)股份有限公司π
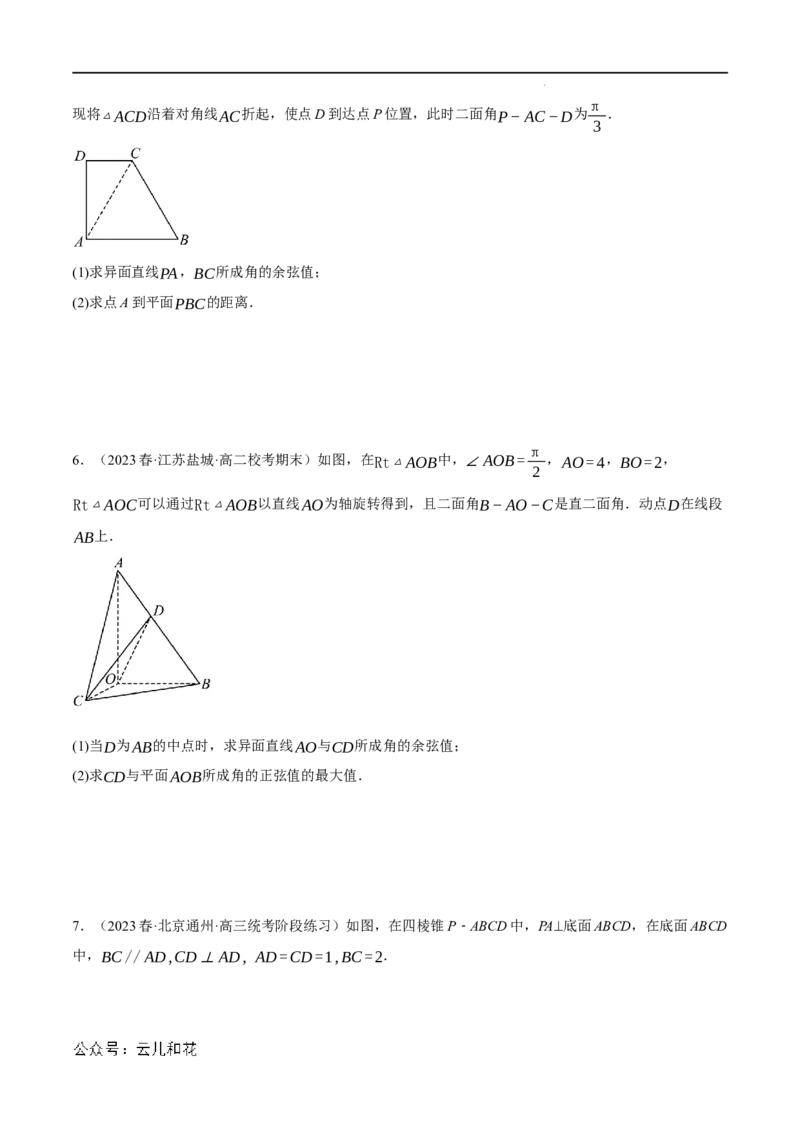
3.(2023春·陕西西安·高一校考期末)如图1,在Rt△ABC中,AB⊥BC,AC=12,∠BAC= ,E,
3
F都在AC上,且AE:EF:FC=3:4:5,BE//FG,将△AEB,△CFG分别沿EB,FG折起,使得点A,
C在点P处重合,得到四棱锥P−EFGB,如图2.
(1)求异面直线PF,BG所成角的余弦值;
(2)若M为PB的中点,求钝二面角B−FM−E的余弦值.
4.(2023春·江苏镇江·高一校考期末)如图,在四棱锥P−ABCD中,PA⊥底面ABCD,AB//CD,
AD=CD=1,∠BAD=120°,∠ACB=90°.
(1)求证:BC⊥平面PAC;
√5
(2)试确定PA的值为多少时?二面角A−PC−D的余弦值为 .
5
5.(2023·浙江宁波·校考模拟预测)在直角梯形ABCD中,CD⊥AD,AB=BC=2CD=2,AD=√3,
学科网(北京)股份有限公司π
现将△ACD沿着对角线AC折起,使点D到达点P位置,此时二面角P−AC−D为 .
3
(1)求异面直线PA,BC所成角的余弦值;
(2)求点A到平面PBC的距离.
π
6.(2023春·江苏盐城·高二校考期末)如图,在Rt△AOB中,∠AOB= ,AO=4,BO=2,
2
Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B−AO−C是直二面角.动点D在线段
AB上.
(1)当D为AB的中点时,求异面直线AO与CD所成角的余弦值;
(2)求CD与平面AOB所成角的正弦值的最大值.
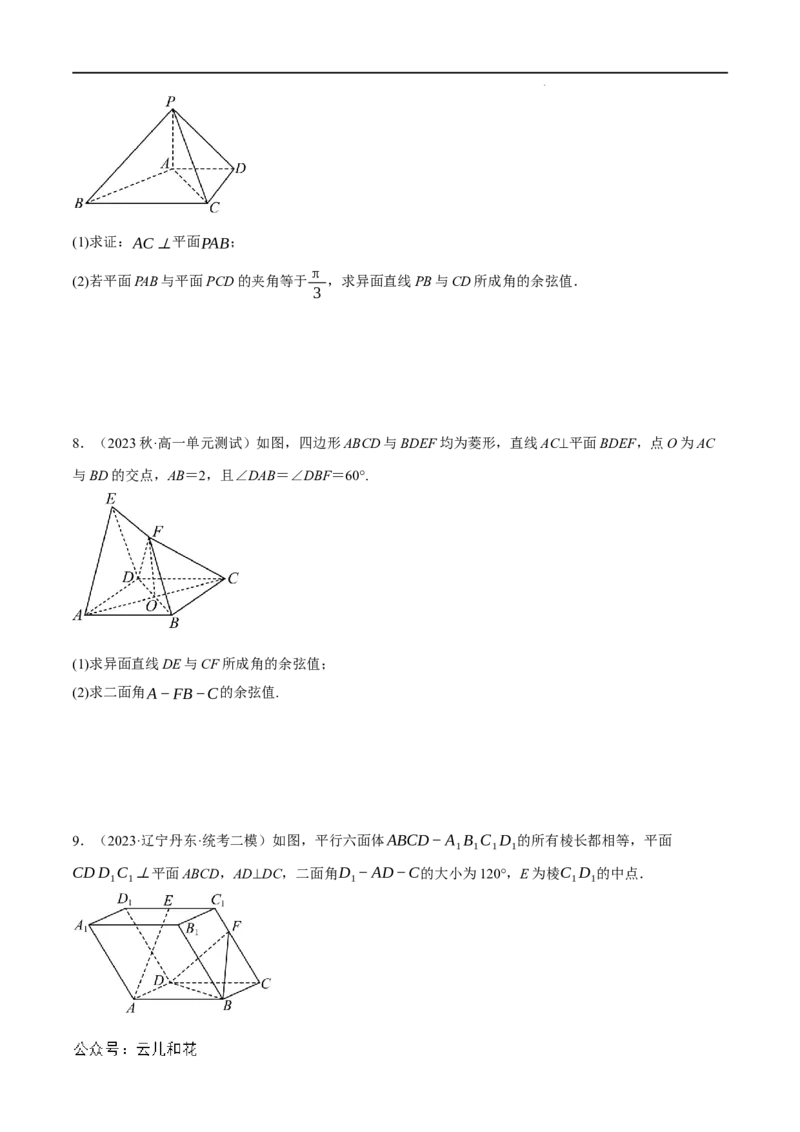
7.(2023春·北京通州·高三统考阶段练习)如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,在底面ABCD
中,BC//AD,CD⊥AD, AD=CD=1,BC=2.
学科网(北京)股份有限公司(1)求证:AC⊥平面PAB;
π
(2)若平面PAB与平面PCD的夹角等于 ,求异面直线PB与CD所成角的余弦值.
3
8.(2023秋·高一单元测试)如图,四边形ABCD与BDEF均为菱形,直线AC⊥平面BDEF,点O为AC
与BD的交点,AB=2,且∠DAB=∠DBF=60°.
(1)求异面直线DE与CF所成角的余弦值;
(2)求二面角A−FB−C的余弦值.
9.(2023·辽宁丹东·统考二模)如图,平行六面体ABCD−A B C D 的所有棱长都相等,平面
1 1 1 1
CDD C ⊥平面ABCD,AD⊥DC,二面角D −AD−C的大小为120°,E为棱C D 的中点.
1 1 1 1 1
学科网(北京)股份有限公司(1)证明:CD⊥AE;
(2)点F在棱CC 上,AE//平面BDF,求直线AE与DF所成角的余弦值.
1
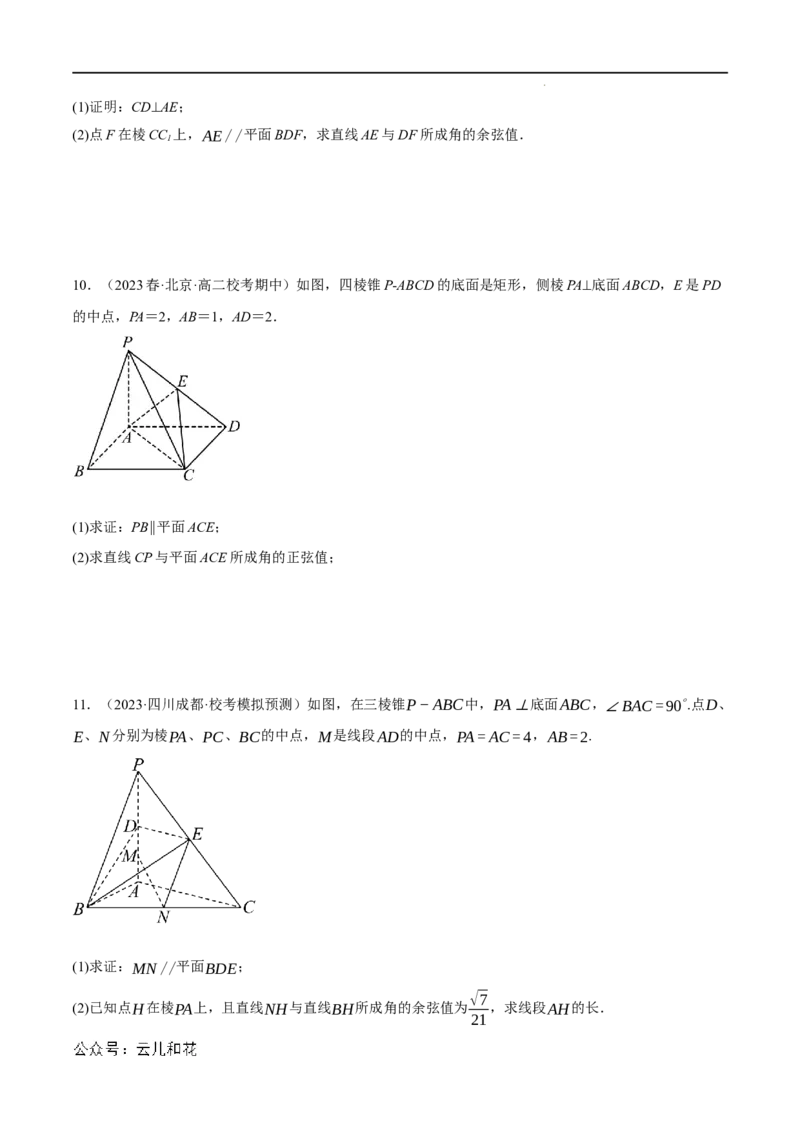
10.(2023春·北京·高二校考期中)如图,四棱锥P-ABCD的底面是矩形,侧棱PA⊥底面ABCD,E是PD
的中点,PA=2,AB=1,AD=2.
(1)求证:PB∥平面ACE;
(2)求直线CP与平面ACE所成角的正弦值;
11.(2023·四川成都·校考模拟预测)如图,在三棱锥P−ABC中,PA⊥底面ABC,∠BAC=90∘.点D、
E、N分别为棱PA、PC、BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(1)求证:MN//平面BDE;
√7
(2)已知点H在棱PA上,且直线NH与直线BH所成角的余弦值为 ,求线段AH的长.
21
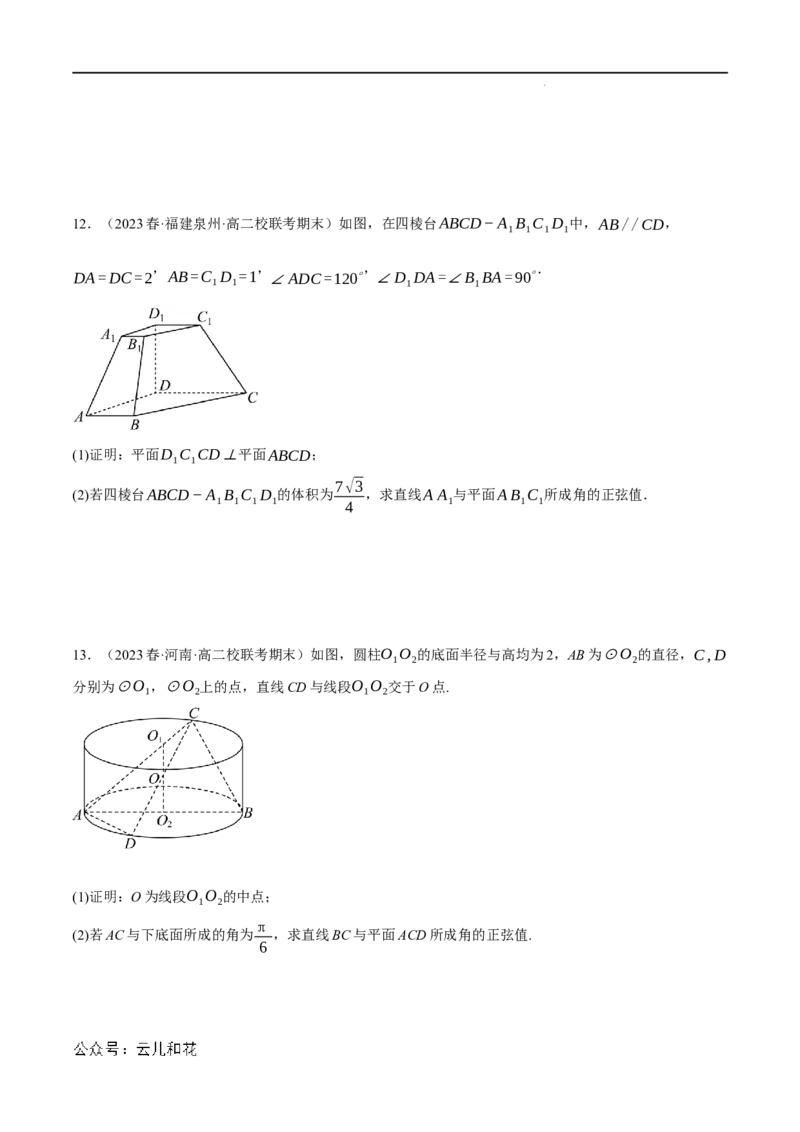
学科网(北京)股份有限公司12.(2023春·福建泉州·高二校联考期末)如图,在四棱台ABCD−A B C D 中,AB//CD,
1 1 1 1
, , , .
DA=DC=2 AB=C D =1 ∠ADC=120∘ ∠D DA=∠B BA=90∘
1 1 1 1
(1)证明:平面D C CD⊥平面ABCD;
1 1
7√3
(2)若四棱台ABCD−A B C D 的体积为 ,求直线A A 与平面AB C 所成角的正弦值.
1 1 1 1 4 1 1 1
13.(2023春·河南·高二校联考期末)如图,圆柱O O 的底面半径与高均为2,AB为⊙O 的直径,C,D
1 2 2
分别为⊙O ,⊙O 上的点,直线CD与线段O O 交于O点.
1 2 1 2
(1)证明:O为线段O O 的中点;
1 2
π
(2)若AC与下底面所成的角为 ,求直线BC与平面ACD所成角的正弦值.
6
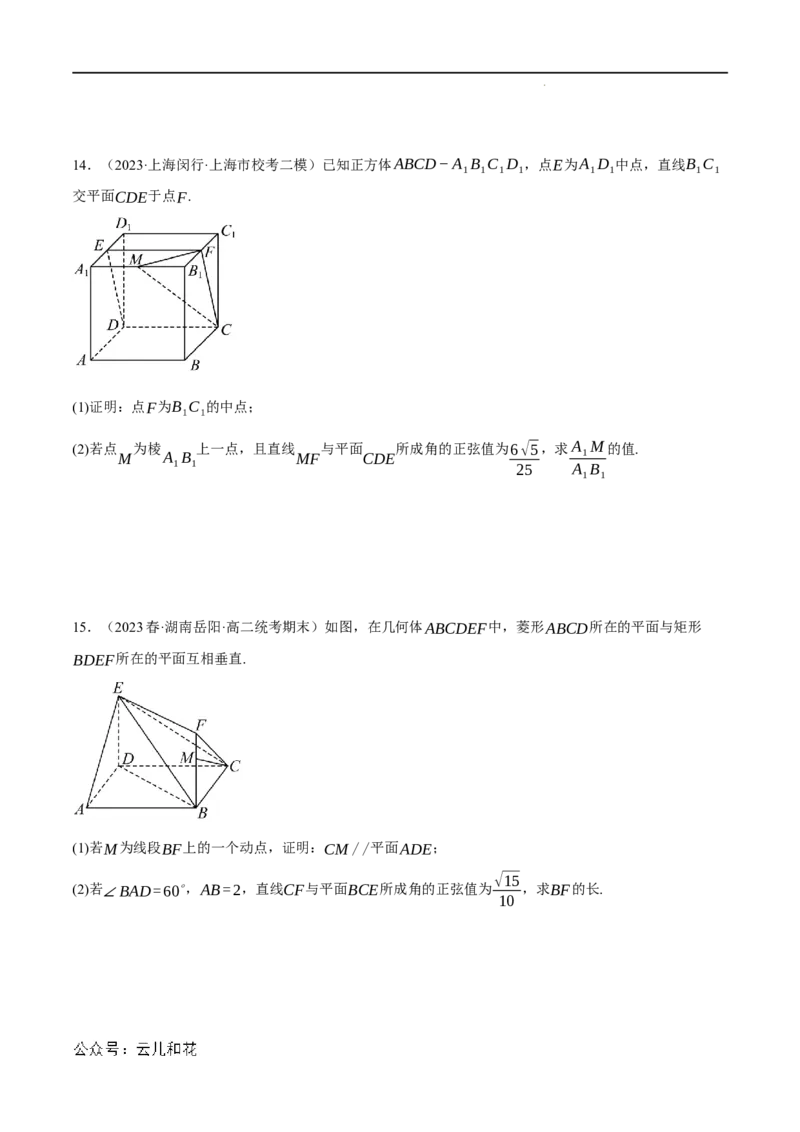
学科网(北京)股份有限公司14.(2023·上海闵行·上海市校考二模)已知正方体ABCD−A B C D ,点E为A D 中点,直线B C
1 1 1 1 1 1 1 1
交平面CDE于点F.
(1)证明:点F为B C 的中点;
1 1
(2)若点 为棱 上一点,且直线 与平面 所成角的正弦值为6√5,求A M的值.
M A B MF CDE 1
1 1 25 A B
1 1
15.(2023春·湖南岳阳·高二统考期末)如图,在几何体ABCDEF中,菱形ABCD所在的平面与矩形
BDEF所在的平面互相垂直.
(1)若M为线段BF上的一个动点,证明:CM//平面ADE;
√15
(2)若∠BAD=60∘,AB=2,直线CF与平面BCE所成角的正弦值为 ,求BF的长.
10
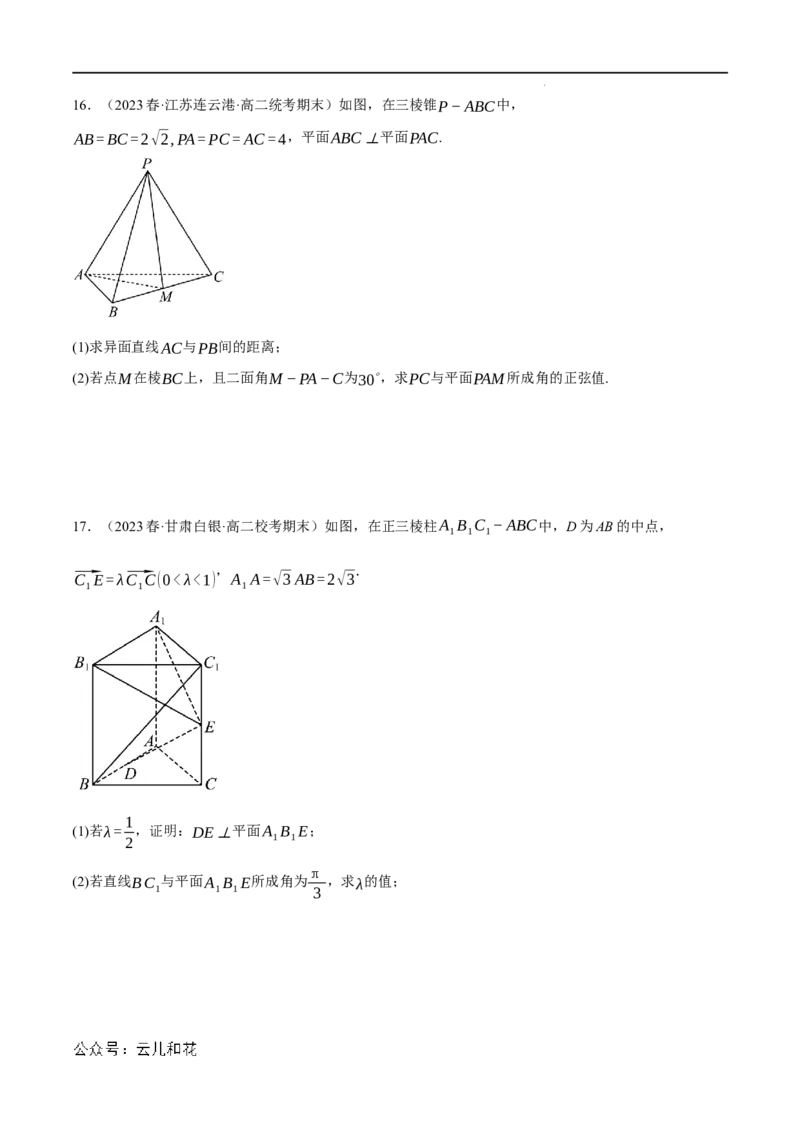
学科网(北京)股份有限公司16.(2023春·江苏连云港·高二统考期末)如图,在三棱锥P−ABC中,
AB=BC=2√2,PA=PC=AC=4,平面ABC⊥平面PAC.
(1)求异面直线AC与PB间的距离;
(2)若点M在棱BC上,且二面角M−PA−C为30∘,求PC与平面PAM所成角的正弦值.
17.(2023春·甘肃白银·高二校考期末)如图,在正三棱柱A B C −ABC中,D为AB的中点,
1 1 1
, .
⃗C E=λ⃗C C(0<λ<1) A A=√3AB=2√3
1 1 1
1
(1)若λ= ,证明:DE⊥平面A B E;
2 1 1
π
(2)若直线BC 与平面A B E所成角为 ,求λ的值;
1 1 1 3
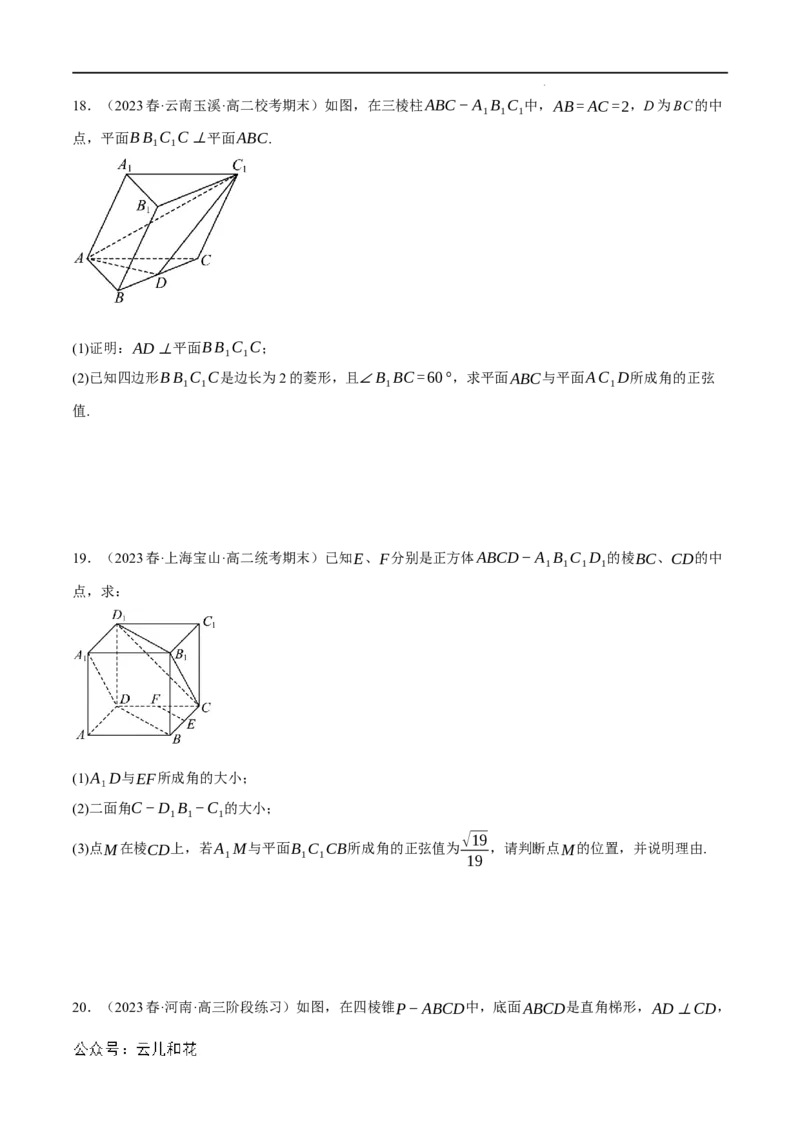
学科网(北京)股份有限公司18.(2023春·云南玉溪·高二校考期末)如图,在三棱柱ABC−A B C 中,AB=AC=2,D为BC的中
1 1 1
点,平面BB C C⊥平面ABC.
1 1
(1)证明:AD⊥平面BB C C;
1 1
(2)已知四边形BB C C是边长为2的菱形,且∠B BC=60°,求平面ABC与平面AC D所成角的正弦
1 1 1 1
值.
19.(2023春·上海宝山·高二统考期末)已知E、F分别是正方体ABCD−A B C D 的棱BC、CD的中
1 1 1 1
点,求:
(1)A D与EF所成角的大小;
1
(2)二面角C−D B −C 的大小;
1 1 1
√19
(3)点M在棱CD上,若A M与平面B C CB所成角的正弦值为 ,请判断点M的位置,并说明理由.
1 1 1 19
20.(2023春·河南·高三阶段练习)如图,在四棱锥P−ABCD中,底面ABCD是直角梯形,AD⊥CD,
学科网(北京)股份有限公司1
AB//CD,AB=2,AD=CD=1,PC⊥底面ABCD,E是AC的中点,⃗PF= ⃗PD.
3
(1)证明:平面PBC⊥平面ACF.
√10
(2)若直线PE与平面PAB所成角的正弦值为 ,且PC>CD,求平面ACF与平面PAB夹角的余弦值.
15
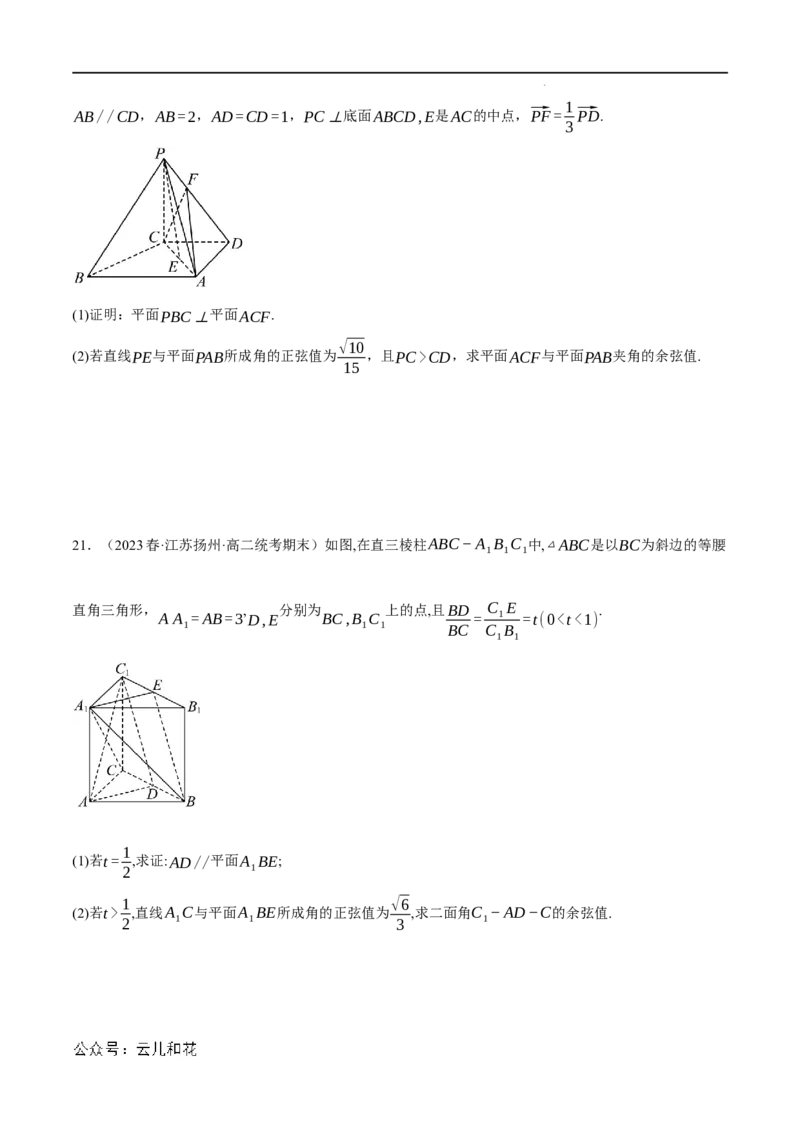
21.(2023春·江苏扬州·高二统考期末)如图,在直三棱柱ABC−A B C 中,△ABC是以BC为斜边的等腰
1 1 1
直角三角形, , 分别为 上的点,且BD C E .
A A =AB=3 D,E BC,B C = 1 =t(0 ,直线A C与平面A BE所成角的正弦值为 ,求二面角C −AD−C的余弦值.
2 1 1 3 1
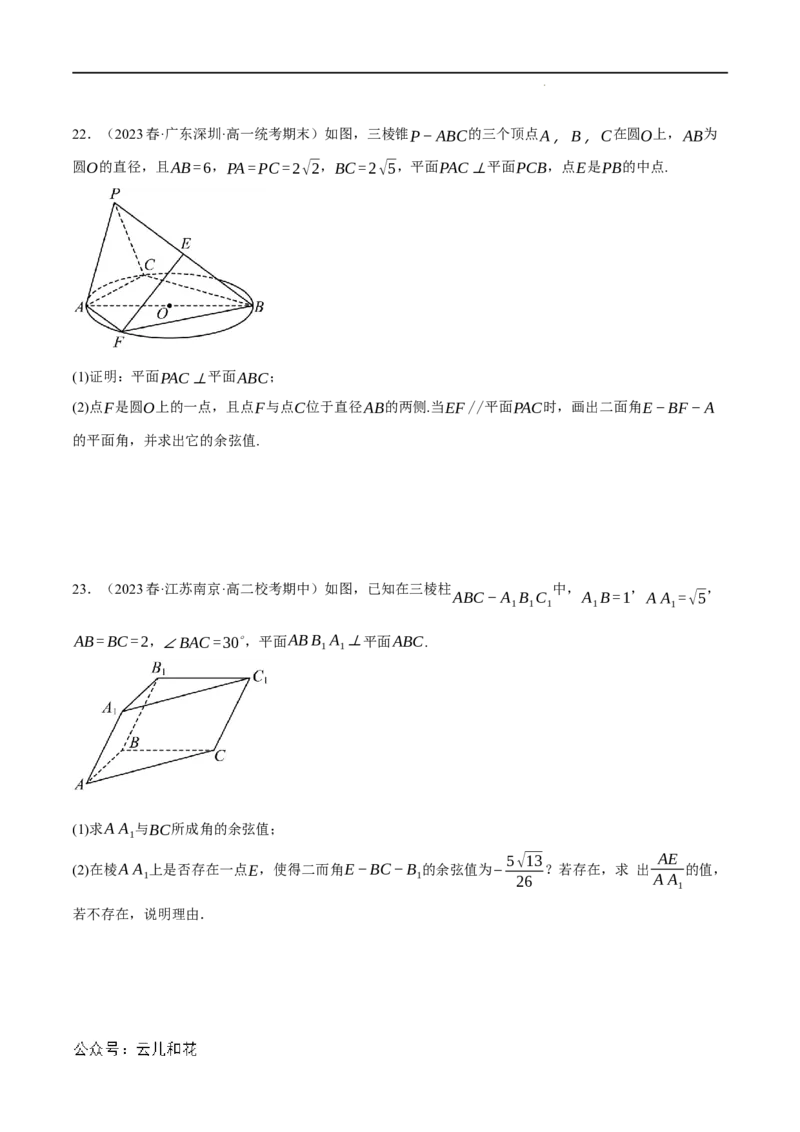
学科网(北京)股份有限公司22.(2023春·广东深圳·高一统考期末)如图,三棱锥P−ABC的三个顶点A,B,C在圆O上,AB为
圆O的直径,且AB=6,PA=PC=2√2,BC=2√5,平面PAC⊥平面PCB,点E是PB的中点.
(1)证明:平面PAC⊥平面ABC;
(2)点F是圆O上的一点,且点F与点C位于直径AB的两侧.当EF//平面PAC时,画出二面角E−BF−A
的平面角,并求出它的余弦值.
23.(2023春·江苏南京·高二校考期中)如图,已知在三棱柱 中, , ,
ABC−A B C A B=1 A A =√5
1 1 1 1 1
AB=BC=2,∠BAC=30∘,平面ABB A ⊥平面ABC.
1 1
(1)求A A 与BC所成角的余弦值;
1
5√13 AE
(2)在棱A A 上是否存在一点E,使得二而角E−BC−B 的余弦值为− ?若存在,求 出 的值,
1 1 26 A A
1
若不存在,说明理由.
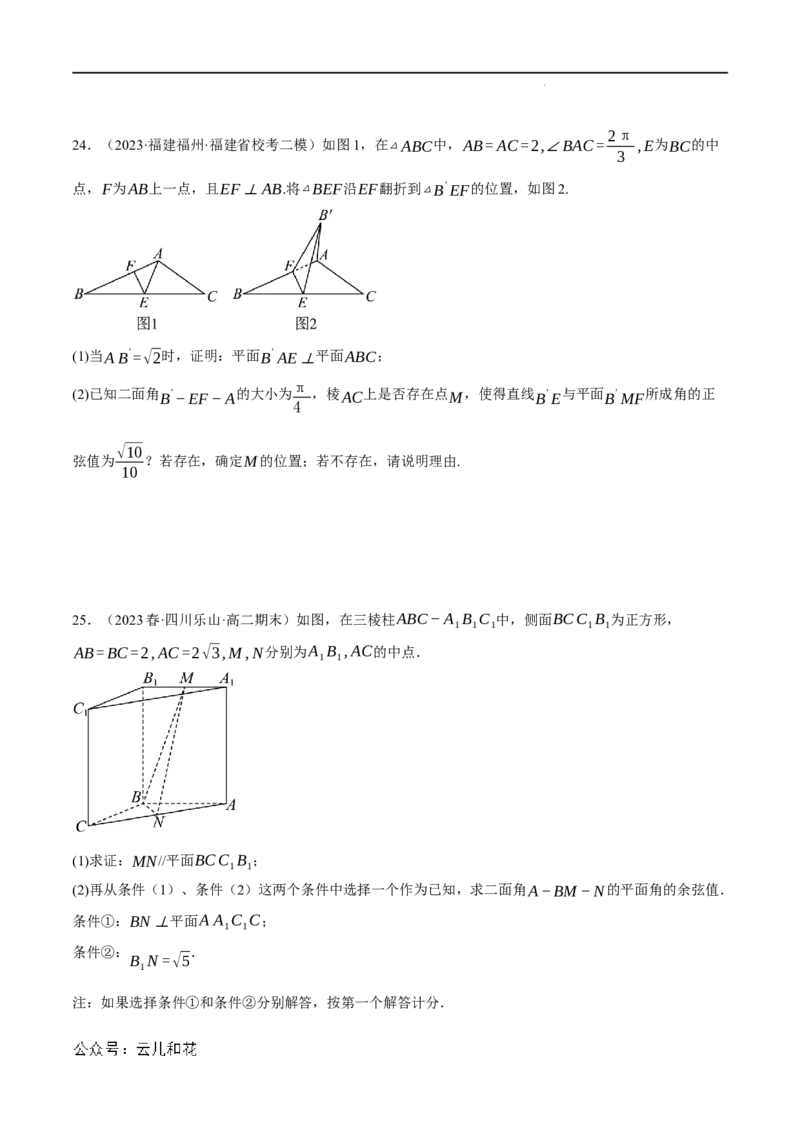
学科网(北京)股份有限公司2π
24.(2023·福建福州·福建省校考二模)如图1,在△ABC中,AB=AC=2,∠BAC= ,E为BC的中
3
点,F为AB上一点,且EF⊥AB.将△BEF沿EF翻折到△B′EF的位置,如图2.
(1)当AB′=√2时,证明:平面B′ AE⊥平面ABC;
π
(2)已知二面角 B′−EF−A 的大小为 ,棱AC上是否存在点M,使得直线 B′E 与平面 B′MF 所成角的正
4
√10
弦值为 ?若存在,确定M的位置;若不存在,请说明理由.
10
25.(2023春·四川乐山·高二期末)如图,在三棱柱ABC−A B C 中,侧面BCC B 为正方形,
1 1 1 1 1
AB=BC=2,AC=2√3,M,N分别为A B ,AC的中点.
1 1
(1)求证:MN//平面BCC B ;
1 1
(2)再从条件(1)、条件(2)这两个条件中选择一个作为已知,求二面角A−BM−N的平面角的余弦值.
条件①:BN⊥平面A A C C;
1 1
条件②: .
B N=√5
1
注:如果选择条件①和条件②分别解答,按第一个解答计分.
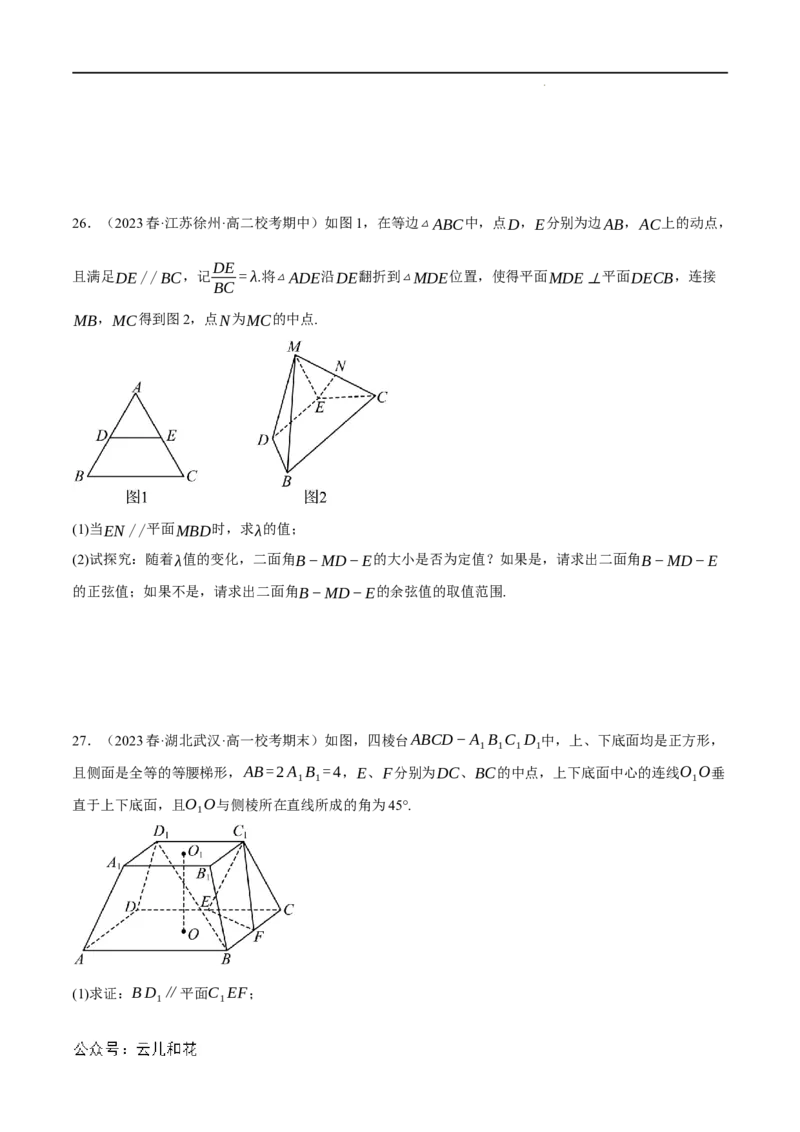
学科网(北京)股份有限公司26.(2023春·江苏徐州·高二校考期中)如图1,在等边△ABC中,点D,E分别为边AB,AC上的动点,
DE
且满足DE//BC,记 =λ.将△ADE沿DE翻折到△MDE位置,使得平面MDE⊥平面DECB,连接
BC
MB,MC得到图2,点N为MC的中点.
(1)当EN//平面MBD时,求λ的值;
(2)试探究:随着λ值的变化,二面角B−MD−E的大小是否为定值?如果是,请求出二面角B−MD−E
的正弦值;如果不是,请求出二面角B−MD−E的余弦值的取值范围.
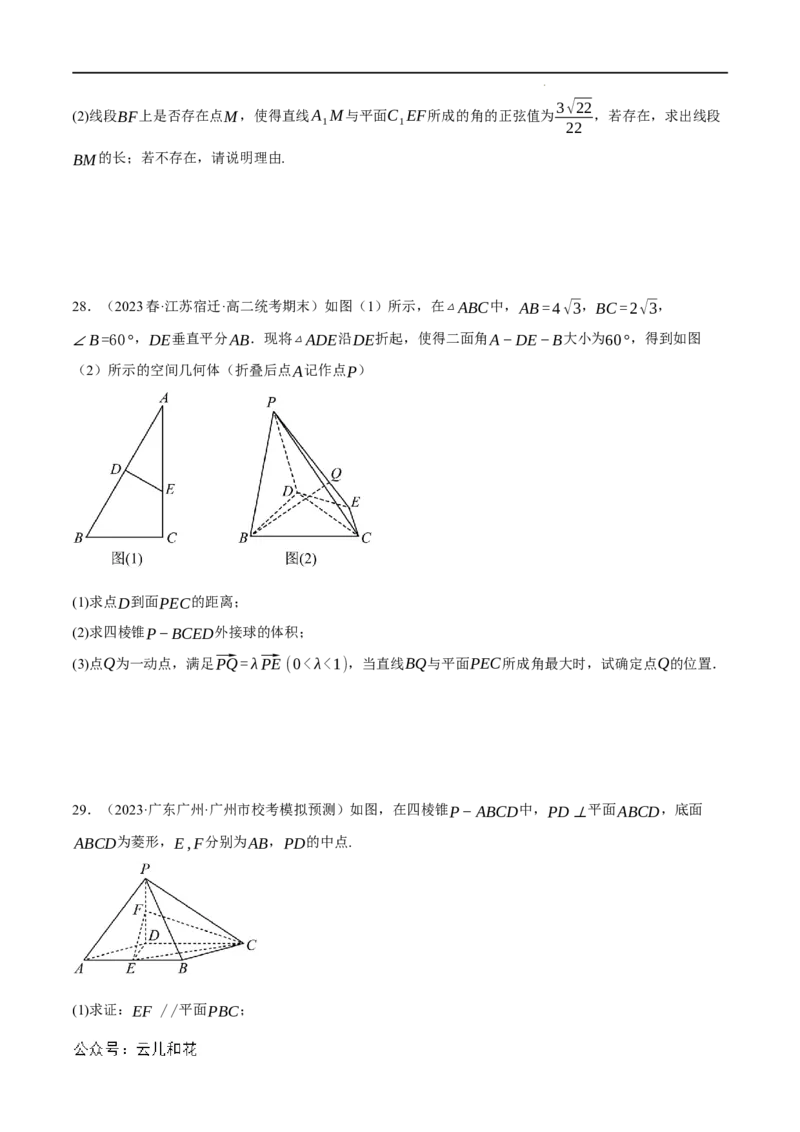
27.(2023春·湖北武汉·高一校考期末)如图,四棱台ABCD−A B C D 中,上、下底面均是正方形,
1 1 1 1
且侧面是全等的等腰梯形,AB=2A B =4,E、F分别为DC、BC的中点,上下底面中心的连线O O垂
1 1 1
直于上下底面,且O O与侧棱所在直线所成的角为45°.
1
(1)求证:BD ∥平面C EF;
1 1
学科网(北京)股份有限公司3√22
(2)线段BF上是否存在点M,使得直线A M与平面C EF所成的角的正弦值为 ,若存在,求出线段
1 1 22
BM的长;若不存在,请说明理由.
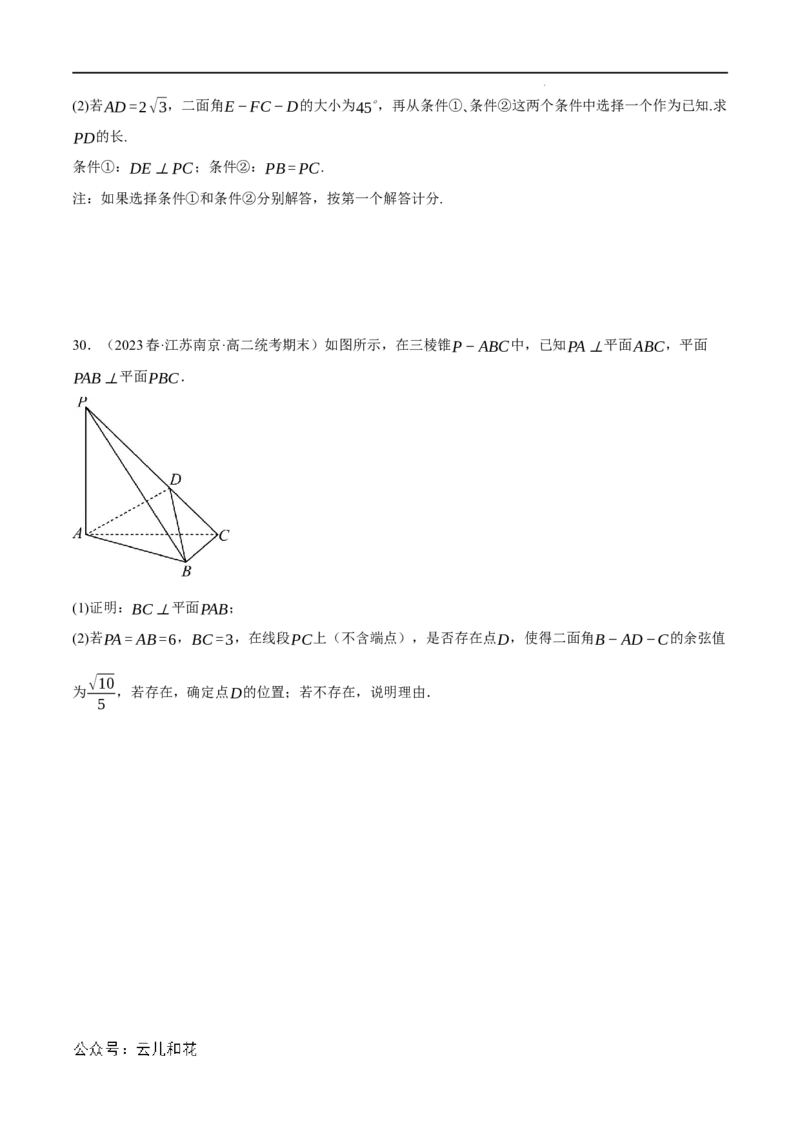
28.(2023春·江苏宿迁·高二统考期末)如图(1)所示,在△ABC中,AB=4√3,BC=2√3,
∠B=60°,DE垂直平分AB.现将△ADE沿DE折起,使得二面角A−DE−B大小为60°,得到如图
(2)所示的空间几何体(折叠后点A记作点P)
(1)求点D到面PEC的距离;
(2)求四棱锥P−BCED外接球的体积;
(3)点Q为一动点,满足⃗PQ=λ⃗PE (0<λ<1),当直线BQ与平面PEC所成角最大时,试确定点Q的位置.
29.(2023·广东广州·广州市校考模拟预测)如图,在四棱锥P−ABCD中,PD⊥平面ABCD,底面
ABCD为菱形,E,F分别为AB,PD的中点.
(1)求证:EF //平面PBC;
学科网(北京)股份有限公司(2)若AD=2√3,二面角E−FC−D的大小为45∘,再从条件①、条件②这两个条件中选择一个作为已知.求
PD的长.
条件①:DE⊥PC;条件②:PB=PC.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
30.(2023春·江苏南京·高二统考期末)如图所示,在三棱锥P−ABC中,已知PA⊥平面ABC,平面
PAB⊥平面PBC.
(1)证明:BC⊥平面PAB;
(2)若PA=AB=6,BC=3,在线段PC上(不含端点),是否存在点D,使得二面角B−AD−C的余弦值
√10
为 ,若存在,确定点D的位置;若不存在,说明理由.
5
学科网(北京)股份有限公司