2025届浙江省新阵地教育联盟高三下学期第二次联考数学试卷及答案_2024-2025高三（6-6月题库）_2025年02月试卷_02162025届浙江省新阵地教育联盟高三下学期第二次联考（全科）

{#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}{#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}{#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}{#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}浙江省新阵地教育联盟 2025 届第一次联考 数学参考答案 一、单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项 符合题目要求. 1．【答案】A 【解析】 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 1 页 共 9 页 B = [ − 1 , 2 ] ， A B = { − 1 , 0 ,1 , 2 } 2．【答案】B 【解析】 z 对应的点在第四象限， z = 1 + 2 i ， z 的虚部是−2， z = 5 3．【答案】D 【解析】 s in = 2 3  c o s =  1 2  ta n =  3    ， ta n = 3  s in =  2 3   ， 4．【答案】B 【解析】 S 5 = 5 a 1 + 1 0 d = a 2 + a 5 + a 7 = 3 a 1 + 1 1 d  2 a 1 = d ， d 3d d 9 ∴a = ，a = ，∴a = +(m−1)d = d m=5. 1 2 2 2 m 2 2 5．【答案】D 【解析】法一：运用公式计算得出结果. 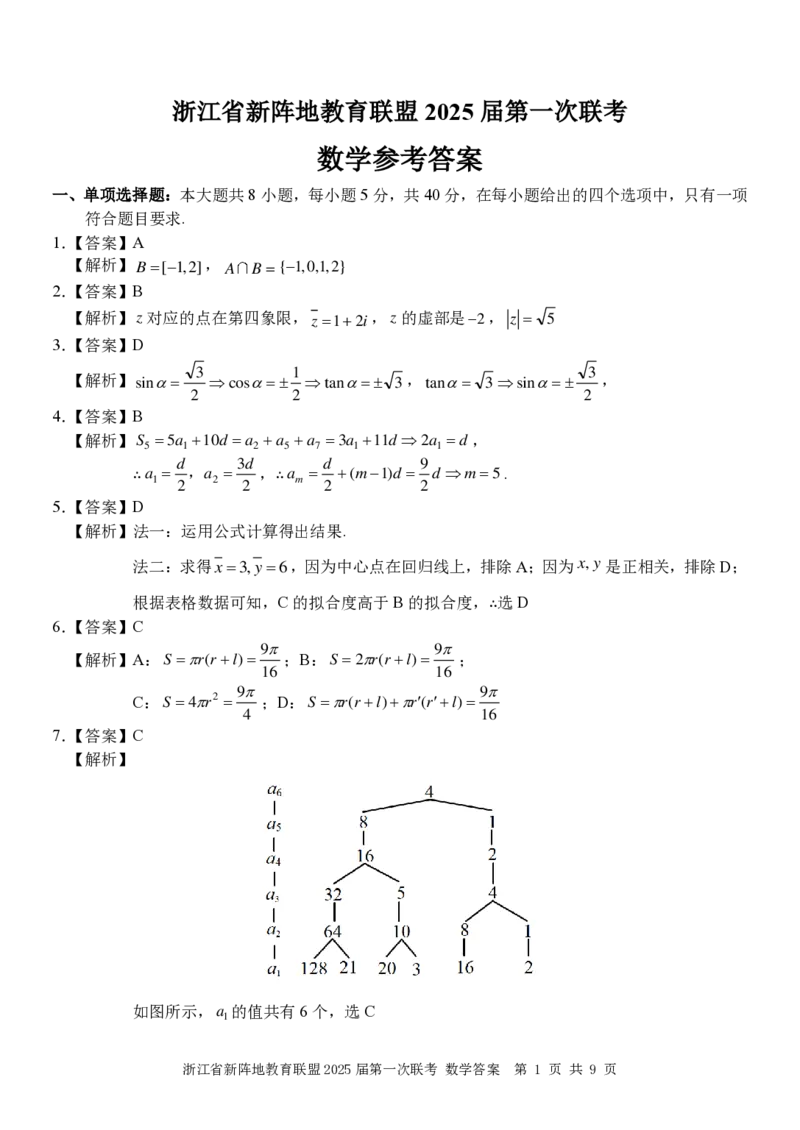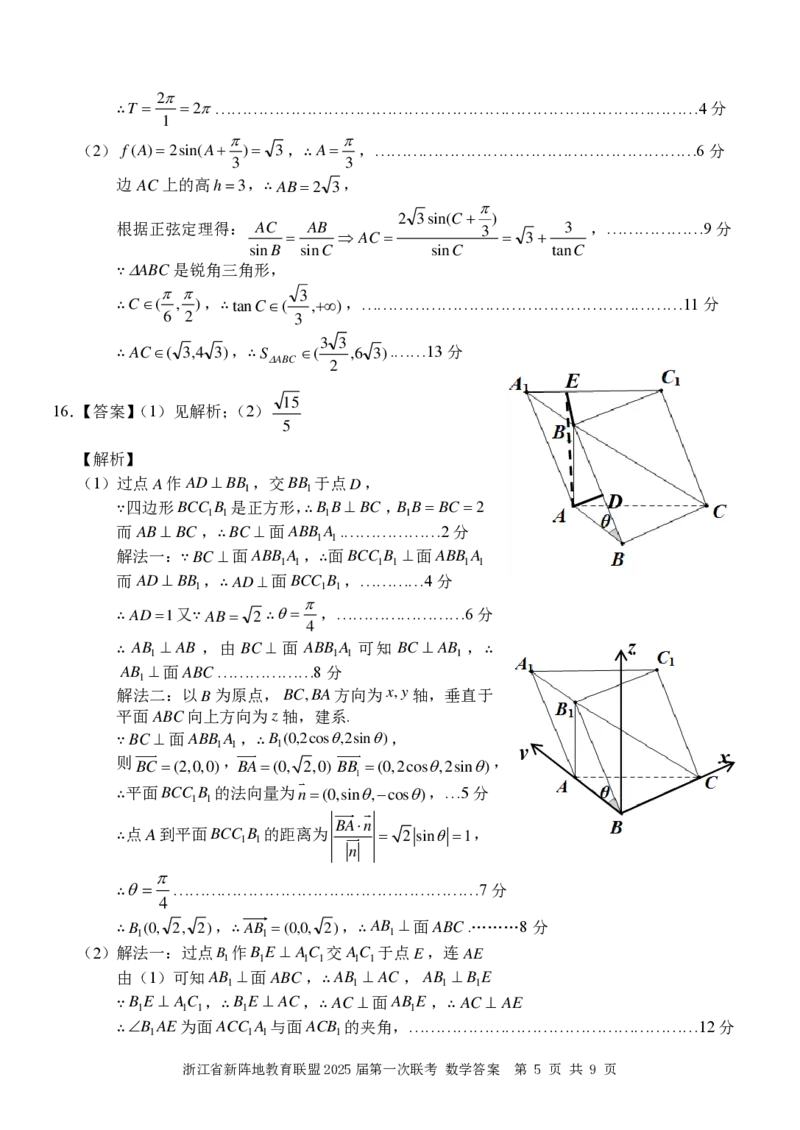法二：求得x=3,y=6，因为中心点在回归线上，排除A；因为 x , y 是正相关，排除D； 根据表格数据可知，C的拟合度高于B的拟合度，∴选D 6．【答案】C 【解析】A： ( ) 9 1 6   S = r r + l = ；B： 2 ( ) 9 1 6   S = r r + l = ； C： 4 2 9 4   S = r = ；D： ( ) ( ) 9 1 6    S = r r + l + r  r  + l = 7．【答案】C 【解析】 如图所示，a 的值共有6个，选C 1 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}8．【答案】A 【解析】画出 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 2 页 共 9 页 y = ln x ， y = x 3 ，y=−x−m的图象：（为使图象清晰，解析里比例有所调整） 二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对得 6分，部分选对得部分分，有选错得得0分. 9．【答案】AD 【解析】A：5男7女， C 15 C 17 = 3 5 种，正确； B：80.7=5.6，第6个数是9.4，错误； n(AB) 4 C：记“选到女生”为事件A，“来自甲班”为事件B，则P(BA)= = ，错误. n(A) 7 2 6 D：X 服从超几何分布，E(X)=3 = ，正确。也可以通过分布列求解. 5 5 X 0 1 2 1 P 10 1 6 0 1 3 0 10．【答案】ABD 【解析】A：∵AO⊥BD，CO⊥BD，∴  A O C = 6 0  ，而 A O = 1 ， C O = 2 ，∴ h = 2 3 ， ∴ V A − B C D = 1 3  2 3  1 2  3  2 = 2 3 是定值，正确. B：由A可知， B D ⊥ 面AOC，∴ B D ⊥ A C ，而AO⊥ AC ，∴ A C ⊥ 面 A B D ，∴正确. C：由 B 可知，当a=1时，易得： S 表 = 9 + 6 2 + 1 5 ，考虑对称性， a = 2 的表面积也 是该值，∴错误. 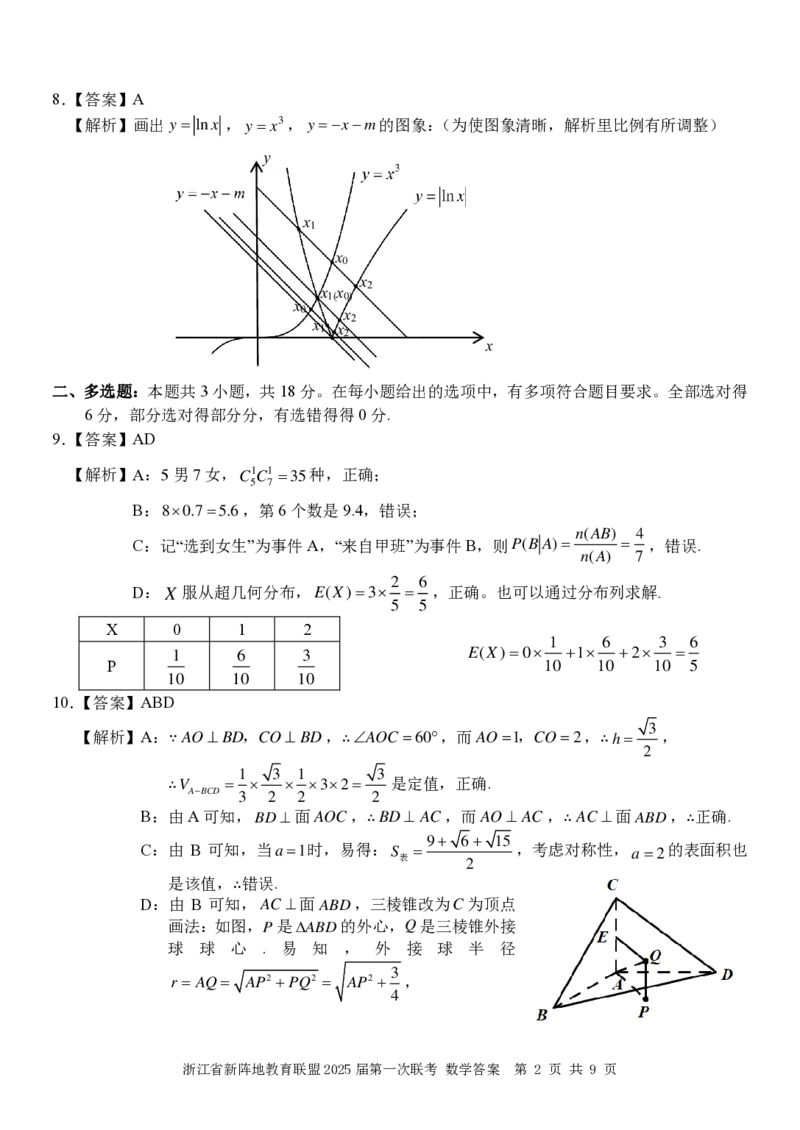D：由 B 可知， A C ⊥ 面 A B D ，三棱锥改为C为顶点 画法：如图，P是  A B D y x 1 x 0 x 2 x x 1( 0) x 0 x 2 x 1 x 2 x 的外心，Q是三棱锥外接 球 球 心 . 易 知 ， 外 接 球 半 径 3 r= AQ= AP2 +PQ2 = AP2 + ， 4 E ( X ) = 0  1 1 0 + 1  1 6 0 + 2  1 3 0 = 6 5 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}BD 3 3 2AP=  AP=  ， sinBAD 2sinBAD 2 ∴ r 3 ，即当ABD是直角三角形时，外接球半径最小值 为 3. 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 3 页 共 9 页 a ( 3 − a ) = 1 有解，∴ABD能取到直角三角形，∴D正确. 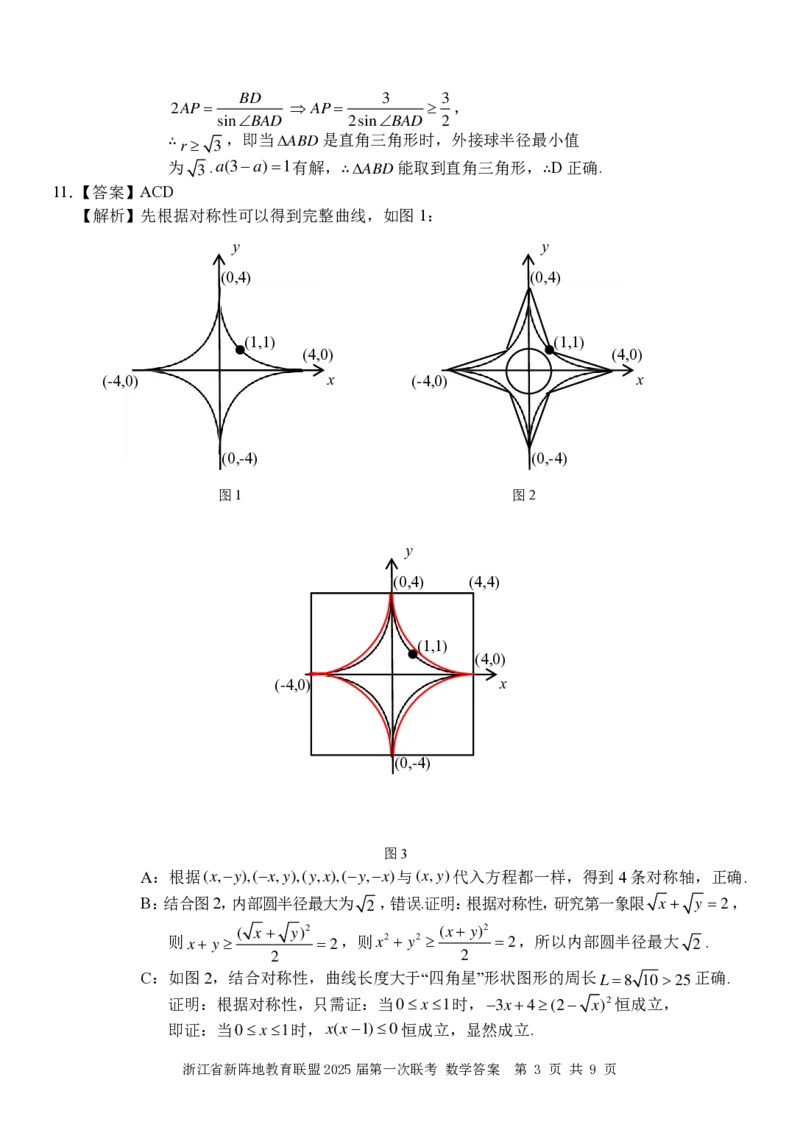11．【答案】ACD 【解析】先根据对称性可以得到完整曲线，如图1： 图1 图2 图3 A：根据(x,−y),(−x,y),(y,x),(−y,−x)与(x,y)代入方程都一样，得到4条对称轴，正确. B：结合图2，内部圆半径最大为 2 ，错误.证明：根据对称性，研究第一象限 x + y =2， ( x + y)2 (x+ y)2 则x+ y =2，则x2 + y2  =2，所以内部圆半径最大 2 2 2 y y (0,4) (0,4) (1,1) (1,1) (4,0) (4,0) (-4,0) x (-4,0) x (0,-4) (0,-4) y (0,4) (4,4) (1,1) (4,0) (-4,0) x (0,-4) . C：如图2，结合对称性，曲线长度大于“四角星”形状图形的周长L=8 10 25正确. 证明：根据对称性，只需证：当0x1时，−3x+4(2− x)2恒成立， 即证：当0x1时，x(x−1)0恒成立，显然成立. {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}D：如图 3，以(4,4)为圆心，4 为半径作圆弧，(1,1)到(4,4)距离为3 2 4，所以第一 象限内圆弧在曲线上方，面积S 4(S −S )=64−1614正确. 正方形 扇形 证明：根据对称性，研究第一象限，只需证： x + y =2时， 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 4 页 共 9 页 ( x − 4 ) 2 + ( y − 4 ) 2  1 6 . x + y = 2  x + y = 4 − 2 x y ， ( x − 4 ) 2 + ( y − 4 ) 2 = x 2 + y 2 − 8 ( x + y ) + 3 2 = ( x + y − 4 ) 2 − 2 x y + 1 6 = 2 x y + 1 6  1 6 三、填空题：本题共3小题，共15分. 12．【答案】例： ( 2 2 , 2 2 ) 【解析】设 a = ( x , y ) ，则 a  b b = 2 x 2 + 2 2 y = 1  x + y = 2 ，满足方程的点均可. 13．【答案】 2 − 1 【解析】运用圆锥曲线通径知识， D O F F = 2 b ac = p p 2 = 2  2 a c = b 2 = a 2 − c 2  e 2 + 2 e − 1 = 0  e = 2 − 1 14．【答案】2 【解析】解法一：设切线方程为 y = k x + b ，则 k x + b = 2 x − s in x  s in x = ( 2 − k ) x − b ， ∴ y = s in x 上两个点处的切线均为 y = ( 2 − k ) x − b ，且之间无公共点，结合正弦函数图象 特征可知， y = ( 2 − k ) x − b 只能是直线 y =  1 ，∴ k = 2 解法二：设切点为 ( x 0 ,2 x 0 − s in x 0 ) ， f ( x 0 ) = 2 − c o s x 0 ，切线方程为： y = ( 2 − c o s x 0 ) ( x − x 0 ) + 2 x 0 − s in x 0 = ( 2 − c o s x 0 ) x + x 0 c o s x 0 − s in x 0 ， 用 x ，1 x 2 表示两个切点横坐标，则有 2 − c o s x 1 = 2 − c o s x 2 ， ①若  x 2 = x 1 + 2 k ，则 x 1 c o s x 1 − s in x 1 = x 2 c o s x 2 − s in x 2 = ( x 1 + 2 k ) c o s x 1 − s in x 1  ， ∴ 2 k  c o s x 1 = 0    ，∴x =2k+ 或x =2k− ，代入可得：斜率为2； 1 2 1 2 当 k =  1 时，满足 f(x)与 l 在 A , B 之间无公共点. ②若  x 2 = − x 1 + 2 k ，则x cosx −sinx =x cosx −sinx =(−x +2k)cosx +sinx ， 1 1 1 2 2 2 1 1 1 即 x 1 c o s x 1 − s in x 1 = k  c o s x 1  ③ y=(2−cosx )x+x cosx −sinx  1 1 1 1xcosx −sinx=x cosx −sinx y=2x−sinx 1 1 1 1 结合③式可知， ( ,2 )   k k 是 f ( x ) 与 l y B D A O F x 的公共点，且在A,B之间，该情况无解. 四、解答题：本题共5小题，共77分。解答题应写出文字说明，证明过程或演算步骤。 3 3 15．【答案】（1）2；（2）S ( ,6 3).（作图法答案正确也给满分） ABC 2 【解析】  （1） f(x)=sinx+ 3cosx=2sin(x+ )…………………………………………………………2分 3 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}2 ∴T = =2………………………………………………………………………………4分 1   （2） f(A)=2sin(A+ )= 3，∴A= ，……………………………………………………6分 3 3 边AC上的高h=3，∴ E D z y x 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 5 页 共 9 页 A B = 2 3 ，  2 3sin(C+ ) 根据正弦定理得： AC AB 3 3 ，………………9分 =  AC= = 3+ sinB sinC sinC tanC ∵ A B C  是锐角三角形， ∴ ( 6 , 2 )   C  ，∴ ta n C  ( 3 3 ,+  ) ，……………………………………………………11分 ∴ A C  ( 3 ,4 3 ) ，∴ S A B C  ( 3 2 3 ,6 3 ) .……13分  16．【答案】（1）见解析；（2） 1 5 5 【解析】 （1）过点 A 作AD⊥BB ，交 1 B B 1 于点 D ， ∵四边形 B C C 1 B 1 是正方形，∴ B 1 B ⊥ B C ， B 1 B = B C = 2 而AB⊥BC，∴BC⊥面 A B B 1 A 1 .………………2分 解法一：∵BC⊥面ABB A ，∴面 1 1 B C C 1 B 1 ⊥ 面 A B B 1 A 1 而 A D ⊥ B B 1 ，∴ A D ⊥ 面BCC B ，…………4分 1 1 ∴ A D = 1 又∵ A B = 2 ∴ 4   = ，……………………6分 ∴ A B 1 ⊥ A B ，由 BC⊥ 面 A B B 1 A 1 可知 B C ⊥ A B 1 ，∴ A B 1 ⊥ 面 A B C ………………8分 解法二：以 B 为原点， B C , B A 方向为 x , y 轴，垂直于 平面ABC向上方向为 z 轴，建系. ∵ B C ⊥ 面ABB A ，∴ 1 1 1 ( 0 ,2 c o s ,2 s in )   B ， 则 B C = ( 2 , 0 , 0 ) ，BA=(0, 2,0) B B 1 ( 0 , 2 c o s , 2 s in )   = ， ∴平面BCC B 的法向量为n=(0,sin,−cos)，…5分 1 1 ∴点 A 到平面 B C C 1 B 1 BAn 的距离为 = 2 sin=1， n ∴ 4   = …………………………………………………7分 ∴B (0, 2, 2)，∴AB =(0,0, 2)，∴ 1 1 A B 1 ⊥ 面ABC.………8分 （2）解法一：过点B 作B E⊥ AC 交AC 于点E，连AE 1 1 1 1 1 1 由（1）可知AB ⊥面ABC，∴AB ⊥ AC ，AB ⊥B E 1 1 1 1 ∵B E⊥ AC ，∴B E⊥ AC，∴AC⊥面AB E ，∴AC⊥ AE 1 1 1 1 1 ∴B AE为面ACC A 与面ACB 的夹角，………………………………………………12分 1 1 1 1 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}在 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 6 页 共 9 页 R t A B 1 E  中，AB = 2 ， 1 B 1 E = 2 3 3 ， A E = 3 3 0 ， ∴ c o s  B 1 A E = 1 5 5 …………………………………………………………………………15分 解法二： A B 1 = ( 0 ,0 , 2 ) ， A C = ( 2 ,− 2 ,0 ) ，AA =(0, 2, 2)…………………………9分 1 平面 A C B 1 的法向量 m 1 = (1 , 2 ,0 ) ，………………………………………………………11分 平面 A C C 1 A 1 的法向量m =(1, 2,− 2)，………………………………………………13分 2 ∴ c o s  m 1 , m 2  = 3 3 5 = 1 5 5 .…………………………………………………………15分 17．【答案】（1）增区间： ( −  , 0 ) ， ( 3 2 , +  ) ，减区间： ( 0 ,1 ) ， ( 1 , 3 2 ) ；（2） ( 0 , 1 5 ) 【解析】 （1） f ( x ) 的定义域为 ( −  ,1 )  (1 ,+  ) （答案没考虑定义域扣2分） f ( x ) = e x 2 x x − − 1 1 − e x ( x 1 − 1 ) 2 = e x x ( 2 ( x x − − 1 ) 3 2 ) ………………………………………………2分 ∴ f ( x ) 在 ( −  , 0 ) ， ( 3 2 , +  ) 上单调递增，在 ( 0 ,1 ) ， ( 1 , 3 2 ) 上单调递减.……………6分 （2） f ( x ) = e x a x x − − 1 1 + e x ( 1 x − − a 1 ) 2 = e x a x 2 − ( a ( x + − 1 ) x 2 1 ) + 2 − a .…………………………………9分 设 g ( x ) = a x 2 − ( a + 1 ) x + 2 − a ( a  0 ) 解法一：注意到 g ( 2 ) = a  0 ……………………………………………………………11分 ∴只需满足  a 2 + a= 1 (  a + 2 1 ) 2 + 4 a ( a − 2 )  0 …………………………………………………13分    a 0   1 3 a  1 5  0  a  1 5 …………………………………………………………………15分 a+1 1 解法二：①若 2，即a 时， 2a 3 g ( 2 )  0  a  0 ，∴  ……………………12分 ②若 a 2 + a 1  2 ，即 a  1 3 时， = ( a + 1 ) 2 + 4 a ( a − 2 ) = 5 a 2 − 6 a + 1  0  ，∴ 0  a  1 5 …15分 解法三： a x 2 − ( a + 1 ) x + 2 − a = 0 在(2,+)上有穿根. a ( x 2 − x − 1 ) = x − 2 在 ( 2 ,+  ) 上有穿根. 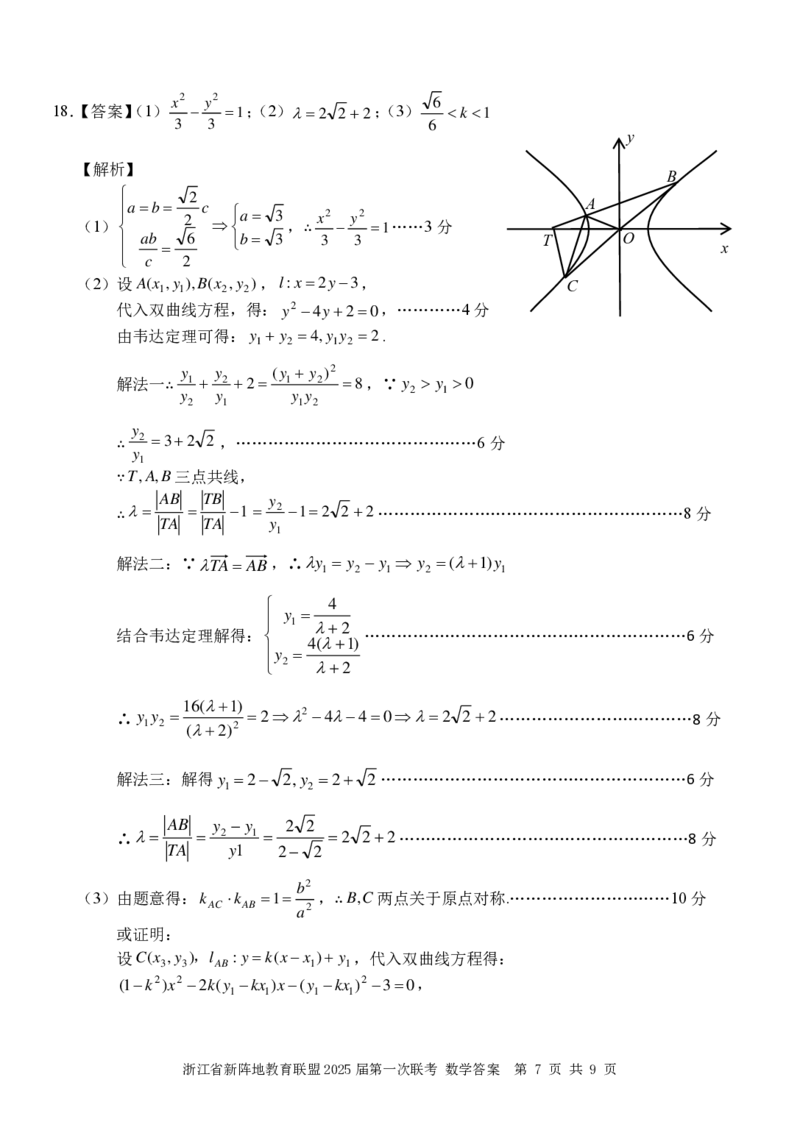1 a = x 2 − x − x 2 − 1 = t 2 + 3 t t + 1 ( t  ( 0 ,+  ) ) ……………………………13分 1 1 结合双勾函数图象可得 (5,+).∴a(0, )…………………15分 a 5 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}x2 y2 18．【答案】（1） − =1；（2） 3 3 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 7 页 共 9 页 = 2 2 + 2 6  ；（3） k 1 6 【解析】 （1）  a = b a b c = = 2 26 2 c   a b = = 3 3 x2 y2 ，∴ − =1……3分 3 3 （2）设A(x ,y ),B(x ,y )，l:x=2y−3， 1 1 2 2 代入双曲线方程，得： y 2 − 4 y + 2 = 0 ，…………4分 由韦达定理可得： y 1 + y 2 = 4 , y 1 y 2 = 2 . 解法一∴ y y 1 2 + y y 2 1 + 2 = ( y 1 + y 1 y 2 y 2 ) 2 = 8 ，∵ y 2  y 1  0 ∴ y y 2 1 = 3 + 2 2 ，………………………………………6分 ∵ T , A , B 三点共线， ∴ = A T B A = T T B A − 1 y  = 2 −1=2 2+2…………………………………………………8分 y 1 解法二：∵ T A = A B  ，∴ y 1 = y 2 − y 1  y 2 = ( + 1 ) y 1    4 y =  1 +2 结合韦达定理解得： ……………………………………………………6分 4(+1) y =  2 +2 ∴ 1 2 = 1 ( 6 ( + + 2 1 ) 2 ) = 2  2 − 4 − 4 = 0  = 2 2 + 2      y y ………………………………8分 解法三：解得 y 1 = 2 − 2 , y 2 = 2 + 2 …………………………………………………6分 AB y − y 2 2 ∴= = 2 1 = =2 2+2………………………………………………8分 TA y1 2− 2 （3）由题意得： k A C  k A B = 1 = b a 2 2 y B A T O x C ，∴B,C两点关于原点对称.…………………………10分 或证明： 设C(x ,y )，l :y=k(x−x )+ y ，代入双曲线方程得： 3 3 AB 1 1 (1−k2)x2 −2k(y −kx )x−(y −kx )2 −3=0， 1 1 1 1 {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}∴ 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 8 页 共 9 页 x 2 = 2 k ( 1 y 1 − − k k 2 x 1 ) − x 1 ， 同理可得： x 3 = 2 k ( y 1 1 − − 1 k1 2 k x 1 ) − x 1 = 2 ( k k y 12 − − x 1 1 ) − x 1 ∴ x 2 + x 3 = 2 x 1 1 (1 − − k k 2 2 ) − 2 x 1 = 0 ， ∴ B , C 两点关于原点对称 ∴ S S   O T A A B C  2  S S   A T B A C C  4  S S   T T B A C C  5  T T B A  5  y y 2 1  5 …………………………12分 解法一：设 l : x = ty − 3 ( t  1 )  x=ty−3 ， (t2 −1)y2 −6ty+6=0， x2 − y2 =3 由韦达定理得： y 1 + y 2 = t 6 2 t − 1 , y 1 y 2 = t 2 6 − 1 ， ∴ y y 1 2 + y y 2 1 + 2 = ( y 1 + y 1 y 2 y 2 ) 2 = t 6 2 2 t − 1  3 6 5 ，……………………………………………15分 解得： 1  t 2  6 ，所以 6 6  k  1 .……………………………………………………17分 解法二：设 l : y = k ( x + 3 ) ( 0  k  1 ) ，  x x = 2 − 1 k y y 2 − = 3 3  (1 − k 2 ) y 2 − 6 k y + 6 k 2 = 0 ， 6k 6k2 由韦达定理得：y + y = ,y y = 1 2 1−k2 1 2 1−k2 y y 1 2 + y y 2 1 + 2 = ( y 1 + y 1 y 2 y 2 ) 2 = 1 − 6 k 2  3 6 5 ………………………………………………15分 解得： 6 6  k  1 ………………………………………………………………………17分 19．【答案】见解析 【解析】 （1） …………4分 {#{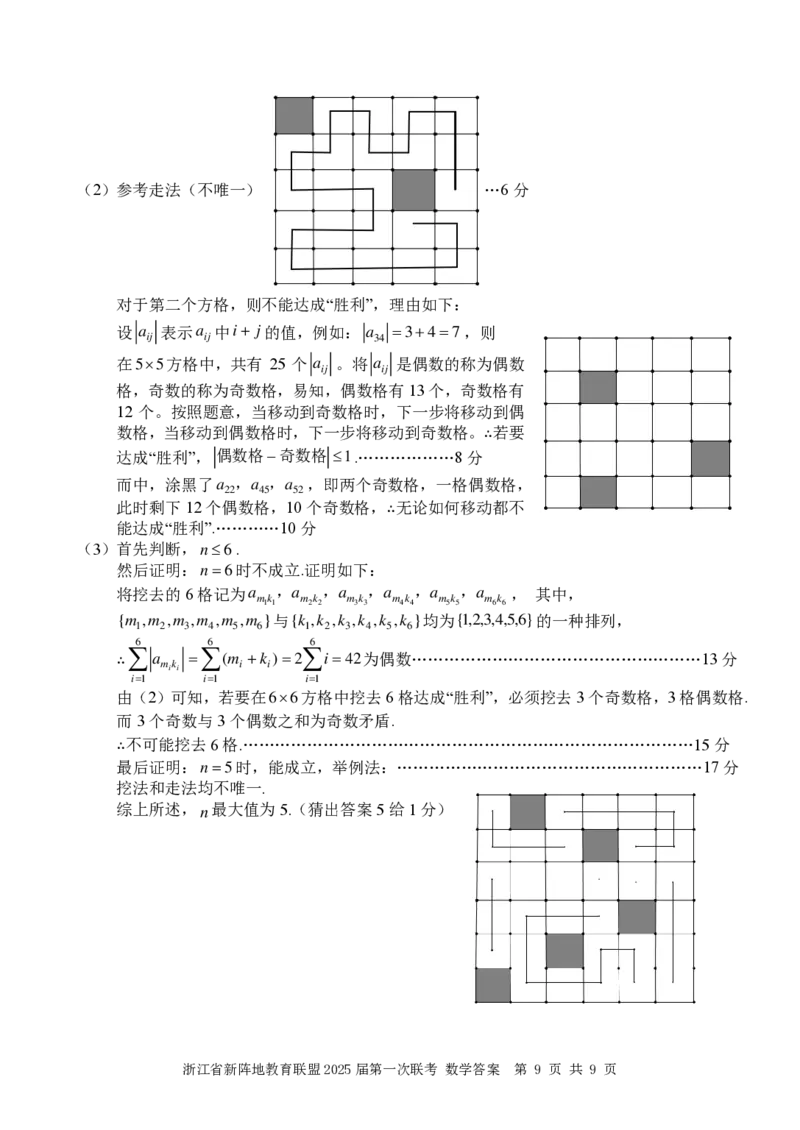QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}（2）参考走法（不唯一） …6分 对于第二个方格，则不能达成“胜利”，理由如下： 设 浙江省新阵地教育联盟2025届第一次联考 数学答案 第 9 页 共 9 页 a ij 表示 a ij 中 i + j 的值，例如： a 3 4 = 3 + 4 = 7 ，则 在 5  5 方格中，共有 25 个 a ij 。将 a ij 是偶数的称为偶数 格，奇数的称为奇数格，易知，偶数格有13个，奇数格有 12 个。按照题意，当移动到奇数格时，下一步将移动到偶 数格，当移动到偶数格时，下一步将移动到奇数格。∴若要 达成“胜利”， 偶数格−奇数格 1.………………8分 而中，涂黑了a ，a ，a ，即两个奇数格，一格偶数格， 22 45 52 此时剩下12个偶数格，10个奇数格，∴无论如何移动都不 能达成“胜利”.…………10分 （3）首先判断，n6. 然后证明： n = 6 时不成立.证明如下： 将挖去的6格记为 a m ， k1 1 a m k2 ，2 a m k3 ，3 a m k4 ，4 a m k5 ，5 a m k6 6 ， 其中， {m ,m ,m ,m ,m ,m }与 1 2 3 4 5 6 { k 1 , k 2 , k 3 , k 4 , k 5 , k 6 } 均为 { 1 ,2 ,3 ,4 ,5 ,6 } 的一种排列， ∴ 6 i= 1 a m ki i = 6 i= 1 ( m i + k i ) = 2 6 i= 1 i = 4 2 为偶数………………………………………………13分 由（2）可知，若要在 6  6 方格中挖去6格达成“胜利”，必须挖去3个奇数格，3格偶数格. 而3个奇数与3个偶数之和为奇数矛盾. ∴不可能挖去6格.…………………………………………………………………………15分 最后证明： n = 5 时，能成立，举例法：…………………………………………………17分 挖法和走法均不唯一. 综上所述，n最大值为5.（猜出答案5给1分） {#{QQABYQKAggigABBAAQgCEQFCCAGQkBGACSoOxBAcoAABAANABAA=}#}