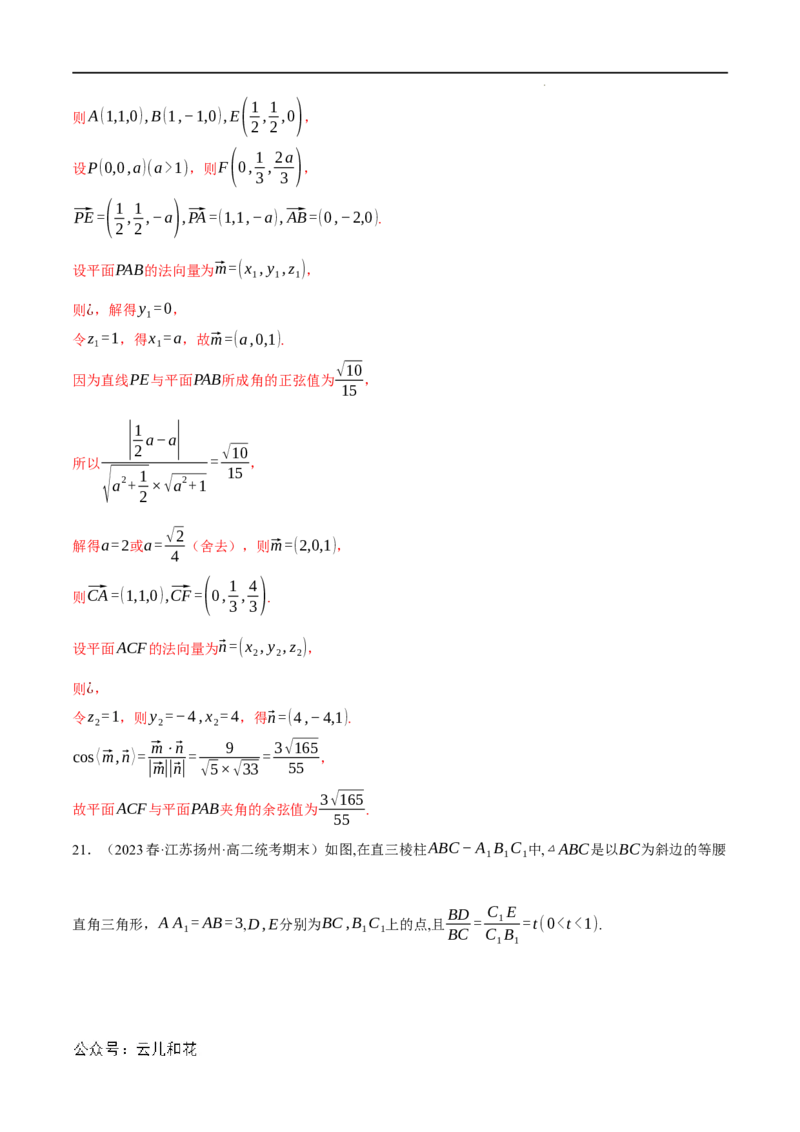文档内容
专题 1.6 空间角的向量求法大题专项训练(30 道)
【人教A版(2019)】
姓名:___________班级:___________考号:___________
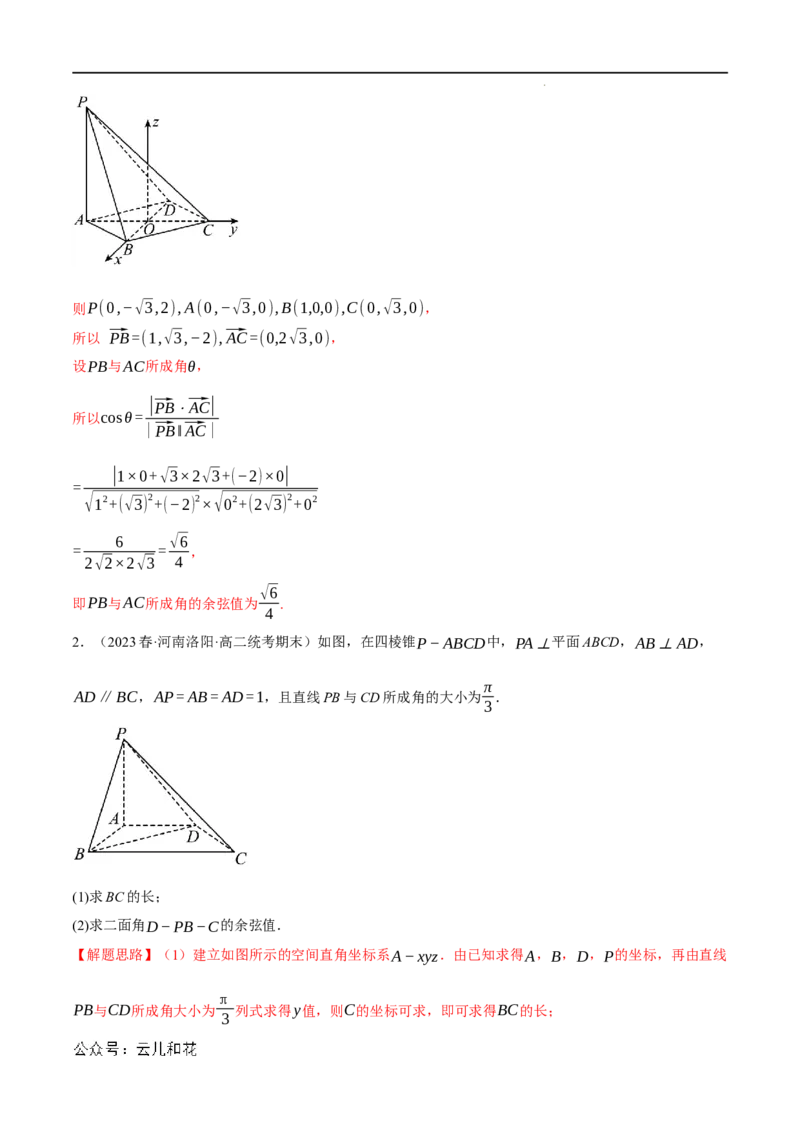
1.(2023春·高二单元测试)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
AB=2,∠BAD=60∘.
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.
【解题思路】(1)利用线面垂直的判定定理证明即可;
(2)通过已知条件建立空间直角坐标系,利用空间向量法求两直线所成角的余弦值即可.
【解答过程】(1)证明:因为底面ABCD是菱形,
所以BD⊥AC,
又PA⊥平面ABCD,BD⊂平面ABCD
所以PA⊥BD,
又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,
所以BD⊥平面PAC.
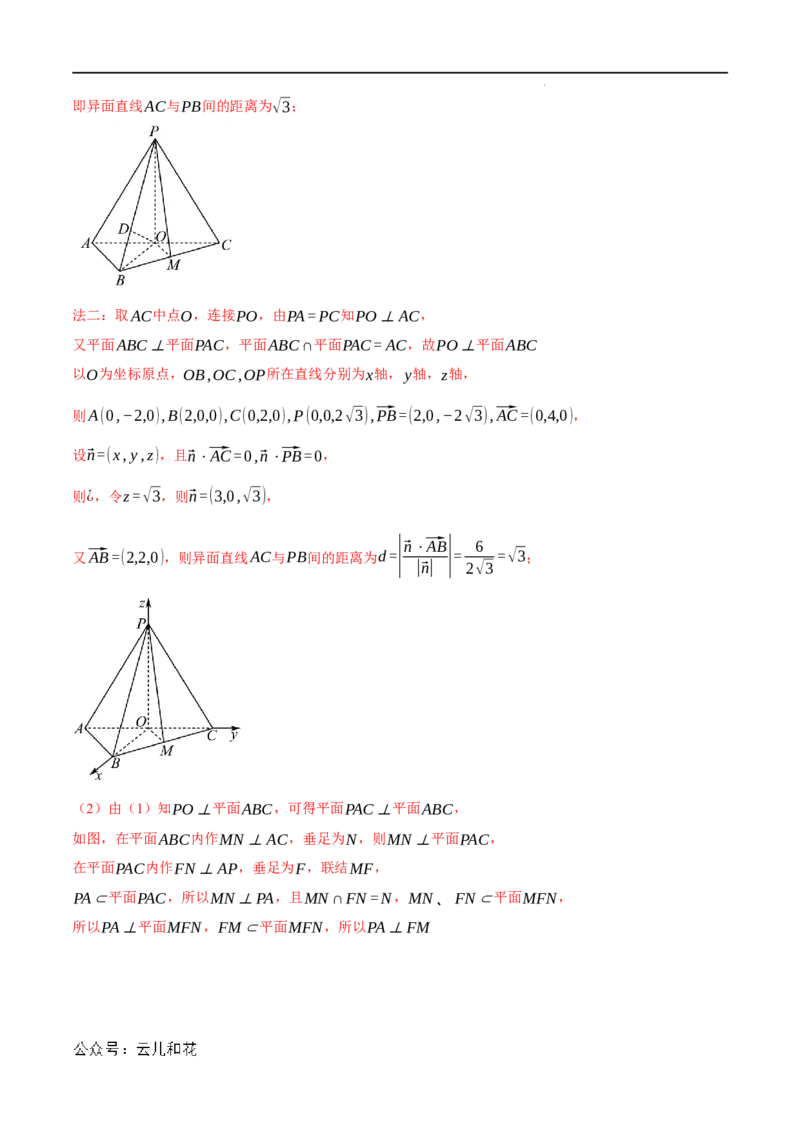
(2)设AC∩BD=O
因为∠BAD=60°,PA=AB=2,
所以BO=1,AO=CO=√3
以O为坐标原点,射线OB,OC分别为x轴,y轴的正半轴
建立空间直角坐标系O−xyz,
如图:
学科网(北京)股份有限公司则P(0,−√3,2),A(0,−√3,0),B(1,0,0),C(0,√3,0),
所以 ⃗PB=(1,√3,−2),⃗AC=(0,2√3,0),
设PB与AC所成角θ,
|⃗PB⋅⃗AC|
所以cosθ=
|⃗PB‖⃗AC|
|1×0+√3×2√3+(−2)×0|
=
√12+(√3) 2+(−2) 2×√02+(2√3) 2+02
6 √6
= = ,
2√2×2√3 4
√6
即PB与AC所成角的余弦值为 .
4
2.(2023春·河南洛阳·高二统考期末)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,AB⊥AD,
π
AD∥BC,AP=AB=AD=1,且直线PB与CD所成角的大小为 .
3
(1)求BC的长;
(2)求二面角D−PB−C的余弦值.
【解题思路】(1)建立如图所示的空间直角坐标系A−xyz.由已知求得A,B,D,P的坐标,再由直线
π
PB与CD所成角大小为 列式求得y值,则C的坐标可求,即可求得BC的长;
3
学科网(北京)股份有限公司(2)分别求出平面PBD与平面PBC的一个法向量,由两法向量所成角的余弦值可得二面角的余弦值.
【解答过程】(1)由于PA⊥平面ABCD,AB⊥AD,所以AB,AD,AP两两垂直,故分别以AB,AD,
AP所在直线为x,y,z轴建立如图所示的空间直角坐标系A−xyz.
∵AP=AB=AD=1,∴A(0,0,0),B(1,0,0),D(0,1,0),P(0,0,1).
设C(1,y,0),则⃗PB=(1,0,−1),⃗CD=(−1,1−y,0).
π
∵直线PB与CD所成角大小为 ,
3
|⃗PB⋅⃗CD| 1
∴|cos<⃗PB,⃗CD>|= = ,
|⃗PB||⃗CD| 2
1 1
即 = ,解得y=2或y=0(舍),
√2×√1+(1−y) 2 2
∴C(1,2,0),则BC的长为2;
(2)设平面PBD的一个法向量为⃗m=(x,y,z).
∵ ⃗PB=(1,0,−1),⃗PD=(0,1,−1),⃗BC=(0,2,0),
∴ ¿,令x=1,则y=1,z=1,⃗m=(1,1,1).
∵平面PBC的一个法向量为⃗n=(a,b,c),
∴ ¿,令a=1,则b=0,c=1,⃗n=(1,0,1),
⃗m⋅⃗n 2 √6
∴cos<⃗m,⃗n>= = = ,
|⃗m||⃗n| √2×√3 3
由几何体的特征可知二面角D−PB−C的平面角为锐角,
√6
∴二面角D−PB−C的余弦值为 .
3
π
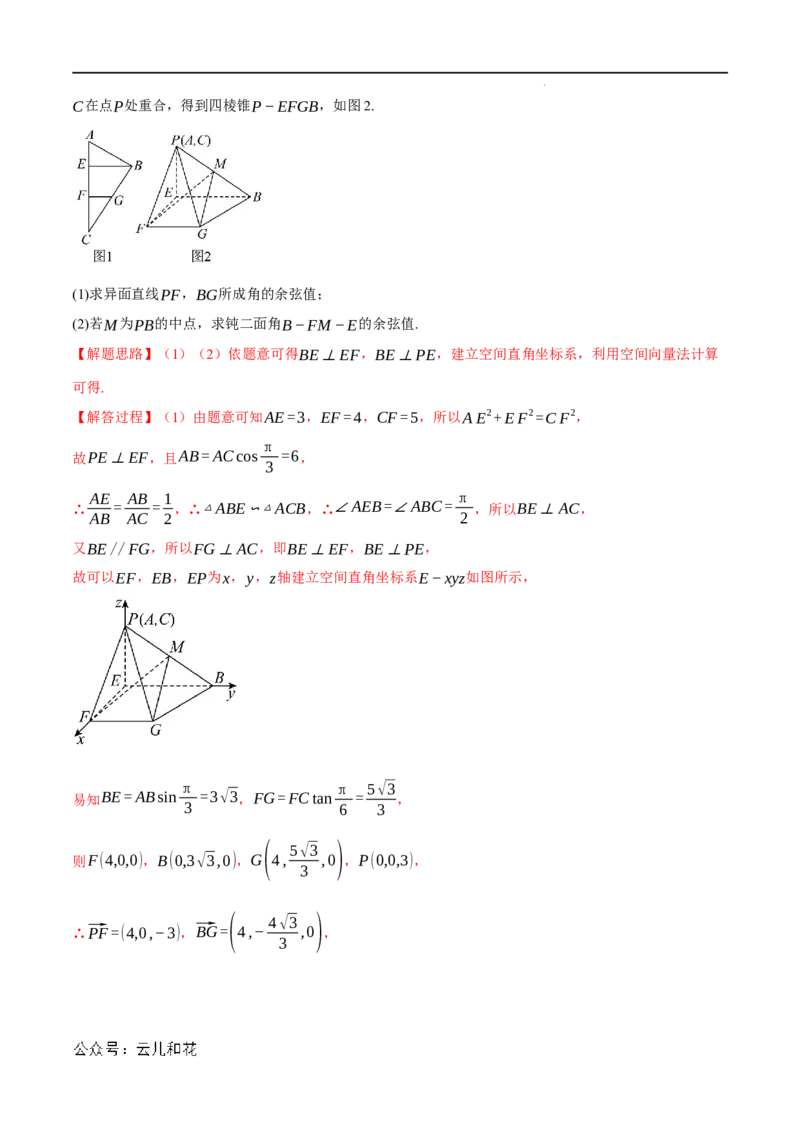
3.(2023春·陕西西安·高一校考期末)如图1,在Rt△ABC中,AB⊥BC,AC=12,∠BAC= ,E,
3
F都在AC上,且AE:EF:FC=3:4:5,BE//FG,将△AEB,△CFG分别沿EB,FG折起,使得点A,
学科网(北京)股份有限公司C在点P处重合,得到四棱锥P−EFGB,如图2.
(1)求异面直线PF,BG所成角的余弦值;
(2)若M为PB的中点,求钝二面角B−FM−E的余弦值.
【解题思路】(1)(2)依题意可得BE⊥EF,BE⊥PE,建立空间直角坐标系,利用空间向量法计算
可得.
【解答过程】(1)由题意可知AE=3,EF=4,CF=5,所以AE2+EF2=CF2,
π
故PE⊥EF,且AB=ACcos =6,
3
AE AB 1 π
∴ = = ,∴△ABE∽△ACB,∴∠AEB=∠ABC= ,所以BE⊥AC,
AB AC 2 2
又BE//FG,所以FG⊥AC,即BE⊥EF,BE⊥PE,
故可以EF,EB,EP为x,y,z轴建立空间直角坐标系E−xyz如图所示,
π π 5√3
易知BE=ABsin =3√3,FG=FCtan = ,
3 6 3
( 5√3 )
则F(4,0,0),B(0,3√3,0),G 4, ,0 ,P(0,0,3),
3
( 4√3 )
∴⃗PF=(4,0,−3),⃗BG= 4,− ,0 ,
3
学科网(北京)股份有限公司⃗PF⋅⃗BG 16 2√3
cos⟨⃗PF,⃗BG⟩= = =
∴ |⃗PF∣| ⋅|⃗BG|
5×
8 5 ,
√3
2√3
故异面直线PF,BG所成角的余弦值为 ;
5
( 3√3 3)
(2)由(1)可知M 0, , ,
2 2
( 3√3 3)
∴⃗MF= 4,− ,− ,⃗BF=(4,−3√3,0),⃗EF=(4,0,0),
2 2
设平面BFM法向量为⃗m=(x ,y ,z ),
1 1 1
由¿,则¿,令y =4得⃗m=(3√3,4,4√3),
1
设平面EFM法向量为⃗n=(x ,y ,z ),
2 2 2
由¿,则¿,令y =1得⃗n=(0,1,−√3),
2
⃗m⋅⃗n 4−12 4√91
所以cos⟨⃗m,⃗n⟩= = =− ,
|⃗m|⋅|⃗n| √91×2 91
4√91
所以钝二面角B−FM−E的余弦值为− .
91
4.(2023春·江苏镇江·高一校考期末)如图,在四棱锥P−ABCD中,PA⊥底面ABCD,AB//CD,
AD=CD=1,∠BAD=120°,∠ACB=90°.
(1)求证:BC⊥平面PAC;
√5
(2)试确定PA的值为多少时?二面角A−PC−D的余弦值为 .
5
【解题思路】(1)根据线面垂直的性质定理和判定定理分析证明;
(2)建系,利用空间向量处理二面角问题.
【解答过程】(1)因为PA⊥底面ABCD,BC⊂底面ABCD,则PA⊥BC,
学科网(北京)股份有限公司且AC⊥BC,PA∩AC=A,PA,AC⊂平面PAC,
所以BC⊥平面PAC.
(2)由题意可知:∠CAD=∠ACD=∠CAB=60°,即△ACD为等边三角形,
取CD的中点E,连接AE,则AE⊥CD,
又因为AB//CD,则AE⊥AB,
如图,以A为坐标原点,AE,AB,AP分别为x,y,z轴建立空间直角坐标系,
(√3 1 ) (√3 1 )
设PA=m>0,则B(0,2,0)C , ,0 ,D ,− ,0 ,P(0,0,m),
2 2 2 2
(√3 1 ) (√3 3 )
可得⃗DC=(0,1,0),⃗PC= , ,−m ,⃗BC= ,− ,0 ,
2 2 2 2
(√3 3 )
由(1)可知:平面PAC的法向量⃗BC= ,− ,0 ,
2 2
设平面PCD的法向量⃗n=(x,y,z),则¿,
令x=2m,则y=0,z=√3,可得⃗n=(2m,0,√3),
|⃗n⋅⃗BC| √3m √5
由题意可得: |cos⟨⃗n,⃗BC⟩|= = = ,解得m=√3,
|⃗n|⋅|⃗BC| √4m2+3×√3 5
√5
所以当PA=√3时,二面角A−PC−D的余弦值为 .
5
5.(2023·浙江宁波·校考模拟预测)在直角梯形ABCD中,CD⊥AD,AB=BC=2CD=2,AD=√3,
π
现将△ACD沿着对角线AC折起,使点D到达点P位置,此时二面角P−AC−D为 .
3
学科网(北京)股份有限公司(1)求异面直线PA,BC所成角的余弦值;
(2)求点A到平面PBC的距离.
【解题思路】(1)作出辅助线,建立空间直角坐标系,写出点的坐标,得到异面直线的夹角;
(2)利用点到平面距离的向量公式进行求解.
【解答过程】(1)过点D做DO⊥AC交AC于O,连接OP,
以O点为原点,以OA为x轴,在平面ABCD内,过点O垂直于AC的线为y轴,
过点O垂直于平面ABCD的直线为z轴,建立空间直角坐标系,如图所示.
因为DO⊥AC,所以PO⊥AC,
π
所以∠DOP为二面角P−AC−D的平面角.所以∠DOP=
,
3
√3 ( √3 3)
又因为OD=OP= ,所以点P 0,− , ,
2 4 4
( 1 ) (3 ) (1 )
又因为C − ,0,0 ,A ,0,0 ,由等边三角形△ABC可得B ,√3,0 ,
2 2 2
( 3 √3 3)
所以⃗AP= − ,− , ,⃗BC=(−1,−√3,0),
2 4 4
3 3
+
⃗AP⋅⃗BC 2 4 3√3
所以cos⟨⃗AP,⃗BC⟩= = =
,
|⃗AP||⃗BC| √9 3 9 8
+ + ⋅2
4 16 16
3√3
所以AP与BC夹角的余弦值为 .
8
学科网(北京)股份有限公司( 1 √3 3)
(2)⃗PC= − , ,− ,⃗BC=(−1,−√3,0),
2 4 4
设⃗n=(x,y,z)为平面PBC的一个法向量,
则¿,
令x=√3,则y=−1,z=−√3,
故⃗n=(√3,−1,−√3),
|⃗AP⋅⃗n| 2√3 2√21
所以点A到平面PBC的距离为d= = = .
|⃗n| √7 7
π
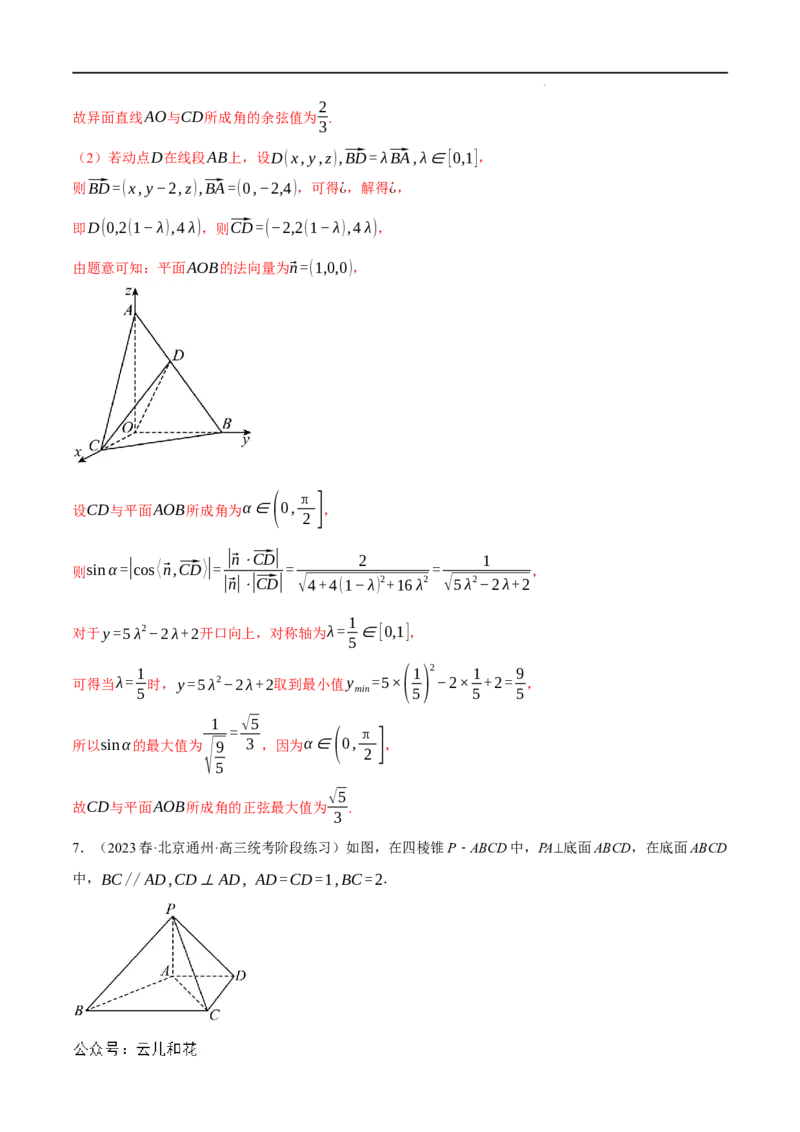
6.(2023春·江苏盐城·高二校考期末)如图,在Rt△AOB中,∠AOB= ,AO=4,BO=2,
2
Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B−AO−C是直二面角.动点D在线段
AB上.
(1)当D为AB的中点时,求异面直线AO与CD所成角的余弦值;
(2)求CD与平面AOB所成角的正弦值的最大值.
【解题思路】(1)建系,利用空间向量求异面直线夹角;
(2)设⃗BD=λ⃗BA可得D(0,2(1−λ),4λ),利用空间向量求线面夹角结合二次函数分析运算.
【解答过程】(1)由题意可得:AO⊥OB,AO⊥OC,平面AOB⊥平面AOC,
平面AOB∩平面AOC=AO,OB⊂平面AOB,所以OB⊥平面AOC,
如图,以O为坐标原点建立空间直角坐标系,则O(0,0,0),A(0,0,4),C(2,0,0),B(0,2,0),
若D为AB的中点,则D(0,1,2),可得⃗OA=(0,0,4),⃗CD=(−2,1,2),
设异面直线AO与CD所成角θ∈ ( 0,
π]
,则cosθ=|cos⟨⃗OA,⃗CD⟩|=
|⃗OA⋅⃗CD|
=
8
=
2
.
2 |⃗OA|⋅|⃗CD| 4×3 3
学科网(北京)股份有限公司2
故异面直线AO与CD所成角的余弦值为 .
3
(2)若动点D在线段AB上,设D(x,y,z),⃗BD=λ⃗BA,λ∈[0,1],
则⃗BD=(x,y−2,z),⃗BA=(0,−2,4),可得¿,解得¿,
即D(0,2(1−λ),4λ),则⃗CD=(−2,2(1−λ),4λ),
由题意可知:平面AOB的法向量为⃗n=(1,0,0),
(
π]
设CD与平面AOB所成角为α∈ 0, ,
2
|⃗n⋅⃗CD| 2 1
则sinα=|cos⟨⃗n,⃗CD⟩|= = = ,
|⃗n|⋅|⃗CD| √4+4(1−λ) 2+16λ2 √5λ2−2λ+2
1
对于y=5λ2−2λ+2开口向上,对称轴为λ= ∈[0,1],
5
1 (1) 2 1 9
可得当λ= 时,y=5λ2−2λ+2取到最小值y =5× −2× +2= ,
5 min 5 5 5
1 √5
=
(
π]
所以sinα的最大值为√9 3 ,因为α∈ 0, ,
2
5
√5
故CD与平面AOB所成角的正弦最大值为 .
3
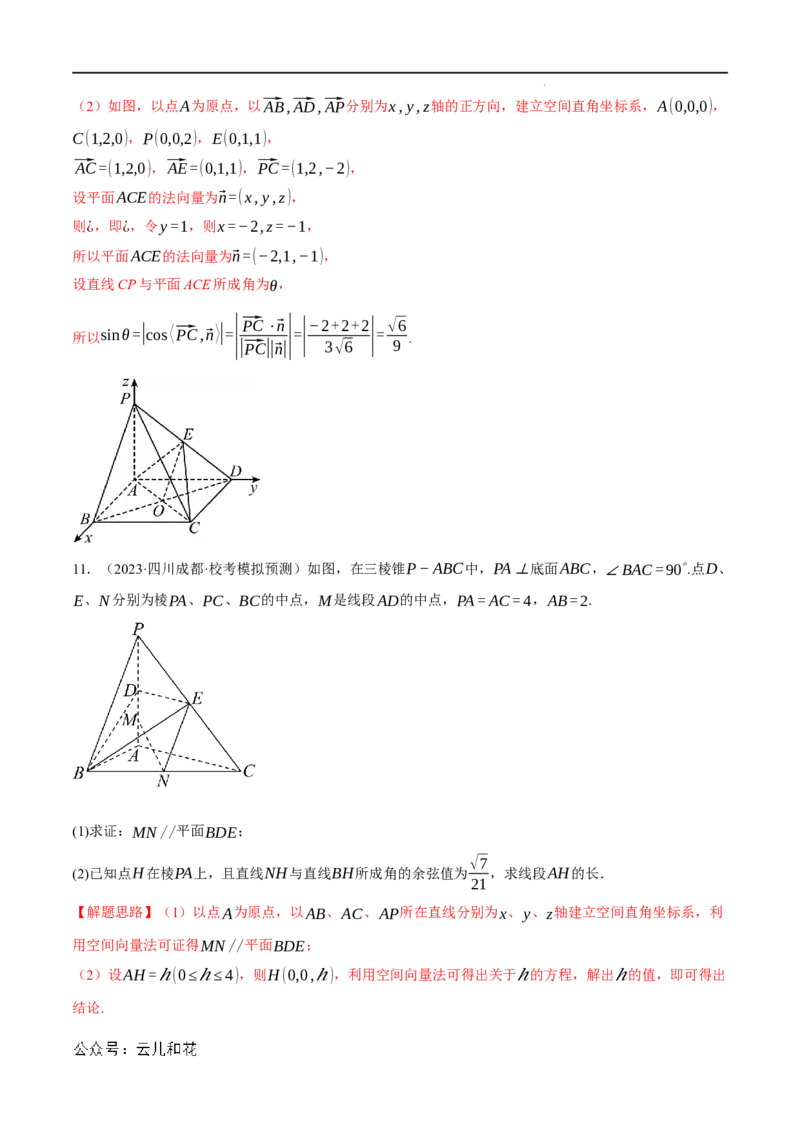
7.(2023春·北京通州·高三统考阶段练习)如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,在底面ABCD
中,BC//AD,CD⊥AD, AD=CD=1,BC=2.
学科网(北京)股份有限公司(1)求证:AC⊥平面PAB;
π
(2)若平面PAB与平面PCD的夹角等于 ,求异面直线PB与CD所成角的余弦值.
3
【解题思路】(1)根据几何关系证明AB⊥AC,根据PA⊥底面ABCD得PA⊥AC,进而证明结论;
(2)根据题意,AE,AD,PA两两互相垂直,进而建立空间直角坐标系,设PA=a(a>0),再根据坐标法
求解异面直线所成角的余弦值即可.
【解答过程】(1)设BC中点为E,连接AE,
易知ADCE为正方形,且AC=√2,AE=1,AB=√2
所以BC2=AB2+AC2,所以AB⊥AC
因为PA⊥底面ABCD,AC⊂底面ABCD,所以PA⊥AC
又PA⊂面PAB,AB⊂面PAB,PA∩AB=A
所以AC⊥平面PAB
(2)因为PA⊥底面ABCD,在正方形ADCE中AE⊥AD,所以AE,AD,PA两两互相垂直.
如图建立空间直角坐标系A−xyz
设PA=a(a>0)
则C(1,1,0),D(0,1,0),B(1,−1,0),P(0,0,a),所以⃗PD=(0,1,−a),⃗DC=(1,0,0),
设平面PCD的法向量为⃗n=(x,y,z),则
¿即¿,取z=1,则⃗n=(0,a,1)
由(1)知,平面PAB的法向量为⃗AC=(1,1,0)
π
因为平面PAB与平面PCD的夹角为 ,
3
π |⃗AC⋅⃗n| |(1,1,0)⋅(0,a,1)| |a| 1
所以 cos =|cos⟨⃗AC,⃗n⟩|= = = = ,解得a=1,
3 |⃗AC||⃗n| √2⋅√02+12+(−a) 2 √2⋅√1+a2 2
⃗PB=(1,−1,−1),⃗DC=(1,0,0)
|⃗PB⋅⃗DC| |(1,−1,−1)⋅(1,0,0)| √3
设异面直线PB与CD所成角为θ,则cosθ= = = ,
|⃗PB|⋅|⃗DC| √3×1 3
学科网(北京)股份有限公司8.(2023秋·高一单元测试)如图,四边形ABCD与BDEF均为菱形,直线AC⊥平面BDEF,点O为AC
与BD的交点,AB=2,且∠DAB=∠DBF=60°.
(1)求异面直线DE与CF所成角的余弦值;
(2)求二面角A−FB−C的余弦值.
【解题思路】(1)建立空间直角坐标系O﹣xyz,求出⃗DE=(0,−1,√3),⃗CF=(√3,0,√3),利用空间向
量的数量积求解异面直线所成角的余弦函数值即可;
(2)求出平面ABF的法向量,平面CBF的法向量,利用空间向量的数量积求解二面角A−FB−C的余弦
值即可.
【解答过程】(1)∵AC⊥平面BDEF,FO,BD⊂平面BDEF,∴AC⊥FO,AC⊥BD,
∵四边形BDEF为菱形,且∠DBF=60°,∴△DBF为等边三角形,
∵O为BD的中点,∴FO⊥BD,所以OA,OB,OF两两垂直.
以O为坐标原点,OA、OB、OF所在直线分别为x、y、z轴建立空间直角坐标系O﹣xyz,如图所示.
∵AB=2,四边形ABCD为菱形,∠BAD=60°,
学科网(北京)股份有限公司∴BD=2,OA=√AB2−OB2=√3,
∵△DBF为等边三角形,∴OF=√3,
则A(√3,0,0),B(0,1,0),D(0,−1,0),E(0,−2,√3),F(0,0,√3),C(−√3,0,0),
∴⃗DE=(0,−1,√3),⃗CF=(√3,0,√3),
⃗DE⋅⃗CF √6
设异面直线所成角为θ,则
cosθ=|cos⟨⃗DE,⃗CF⟩|= =
,
|⃗DE|⋅|⃗CF| 4
√6
故cosθ= .
4
(2)由(1)知⃗AB=(−√3,1,0),⃗BF=(0,−1,√3),⃗CB=(√3,1,0),
设平面ABF的法向量为⃗m=(x ,y ,z ),
1 1 1
则¿,令y =√3,则x =1,z =1,得⃗m=(1,√3,1).
1 1 1
设平面CBF的法向量为⃗n=(x ,y ,z ),则¿,
2 2 2
令y =√3,则x =−1,z =1,得⃗n=(−1,√3,1).
2 2 2
⃗m⋅⃗n 3
∴cos⟨⃗m,⃗n⟩= =
,
|⃗m|⋅|⃗n| 5
又二面角A−FB−C为钝角,
3
∴二面角A−FB−C的余弦值为− .
5
9.(2023·辽宁丹东·统考二模)如图,平行六面体ABCD−A B C D 的所有棱长都相等,平面
1 1 1 1
CDD C ⊥平面ABCD,AD⊥DC,二面角D −AD−C的大小为120°,E为棱C D 的中点.
1 1 1 1 1
(1)证明:CD⊥AE;
学科网(北京)股份有限公司(2)点F在棱CC 上,AE//平面BDF,求直线AE与DF所成角的余弦值.
1
【解题思路】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D DC=120∘,进
1
而根据中点得线线垂直即可求,
(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间
直角坐标系,利用向量的夹角即可求解.
【解答过程】(1)(1)因为平面CDD C ⊥平面ABCD,且两平面交线为DC,AD⊥DC,AD⊂平面
1 1
ABCD,
所以AD⊥平面CDD C ,所以AD⊥D D,AD⊥DC,∠D DC是二面角D −AD−C的平面角,故
1 1 1 1 1
∠D DC=120∘ .
1
连接DE,E为棱C D 的中点,则DE⊥C D ,C D //CD,从而DE⊥CD.
1 1 1 1 1 1
又AD⊥CD,DE∩AD=D,DE,AD⊂平面AED,所以CD⊥平面AED,ED⊂平面AED,因此
CD⊥AE.
(2)解法1:设AB=2,则DE= √ D D2− (1 D C ) 2 =√3,所以CE=AE=√AD2+DE2=√7.
1 2 1 1
连AC交BD于点O,连接CE交DF于点G,连OG.因为AE//平面BDF,AE⊂平面AEC,平面AEC∩平
面BDF=OG
所以AE∥OG,因为O为AC中点,
1 √7
所以G为CE中点,故OG= AE= .且直线OG与DF所成角等于直线AE与DF所成角.
2 2
1 √7
在Rt△EDC中,DG= CE= ,因为OD=√2,
2 2
2 2
(√7)
+
(√7)
−(√2) 2
2 2 3
所以cos∠OGD= = .
√7 √7 7
2× ×
2 2
学科网(北京)股份有限公司3
因此直线AE与DF所成角的余弦值为 .
7
解法2;设AB=2,则DE= √ D D2− (1 D C ) 2 =√3,所以CE=AE=√AD2+DE2=√7.
1 2 1 1
取DC中点为G,连接EG交DF于点H,则EG=DD =2.
1
连接AG交BD于点I,连HI,因为AE//平面BDF,AE⊂平面AGE,平面AGE∩平面BDF=IH,所以
AE∥IH.
HI与DH所成角等于直线AE与DF所成角.
1 1 2√2 1 1 √7
正方形ABCD中,GI= AG,DI= DB= ,所以GH= EG,故HI= AE= .
3 3 3 3 3 3
1 2
在△DHG中,GH= EG= ,GD=1,∠EGD=60°,
3 3
2 2 2
(√7) (√7) (2√2)
+ −
√ 4 2 √7 3 3 3 3
由余弦定理DH= 1+ −1× = .在△DHI中,cos∠DHI= = .
9 3 3 √7 √7 7
2× ×
3 3
3
因此直线AE与DF所成角的余弦值为 .
7
解法3:由(1)知DE⊥平面ABCD,以D为坐标原点,⃗DA为x轴正方向,|⃗DA|为2个单位长,建立如图
所示的空间直角坐标系D−xyz.
学科网(北京)股份有限公司由(1)知DE=√3,得A(2,0,0),B(2,2,0),C(0,2,0), E(0,0,√3),C (0,1,√3).
1
则⃗CC =(0,−1,√3),⃗DC=(0,2,0),⃗AE=(−2,0,√3),⃗DB=(2,2,0).
1
由⃗CF=t⃗CC (0≤t≤1),得⃗DF=⃗DC+⃗CF=(0,2−t,√3t).
1
因为AE//平面BDF,所以存在唯一的λ,μ∈R,
使得⃗AE=λ⃗DB+μ⃗DF=λ(2,2,0)+μ(0,2−t,√3t)=(2λ,2λ+2μ−tμ,√3μt),
2
故2λ=−2,2λ+2μ−tμ=0,√3μt=√3,解得t= ,
3
( 4 2 )
从而⃗DF= 0, , √3 .
3 3
| ⃗AE⋅⃗DF | 3
所以直线AE与DF所成角的余弦值为|cos⟨⃗AE,⃗DF⟩|= = .
|⃗AE||⃗DF| 7
10.(2023春·北京·高二校考期中)如图,四棱锥P-ABCD的底面是矩形,侧棱PA⊥底面ABCD,E是PD
的中点,PA=2,AB=1,AD=2.
(1)求证:PB∥平面ACE;
(2)求直线CP与平面ACE所成角的正弦值;
【解题思路】(1)根据线面平行的判断,转化为证明线线平行,即可证明;
(2)以点A为原点,建立空间直角坐标系,求平面ACE的法向量,利用线面角的向量公式,即可求线面
角的正弦值.
【解答过程】(1)连结BD,交AC于点O,连结OE,
因为点O,E分别是BD,PD的中点,
所以PB//OE,PB⊄平面ACE,OE⊂平面ACE,
所以PB//平面ACE;
学科网(北京)股份有限公司(2)如图,以点A为原点,以⃗AB,⃗AD,⃗AP分别为x,y,z轴的正方向,建立空间直角坐标系,A(0,0,0),
C(1,2,0),P(0,0,2),E(0,1,1),
⃗AC=(1,2,0),⃗AE=(0,1,1),⃗PC=(1,2,−2),
设平面ACE的法向量为⃗n=(x,y,z),
则¿,即¿,令y=1,则x=−2,z=−1,
所以平面ACE的法向量为⃗n=(−2,1,−1),
设直线CP与平面ACE所成角为θ,
|⃗PC⋅⃗n| |−2+2+2| √6
所以sinθ=|cos⟨⃗PC,⃗n⟩|= = =
.
|⃗PC||⃗n| 3√6 9
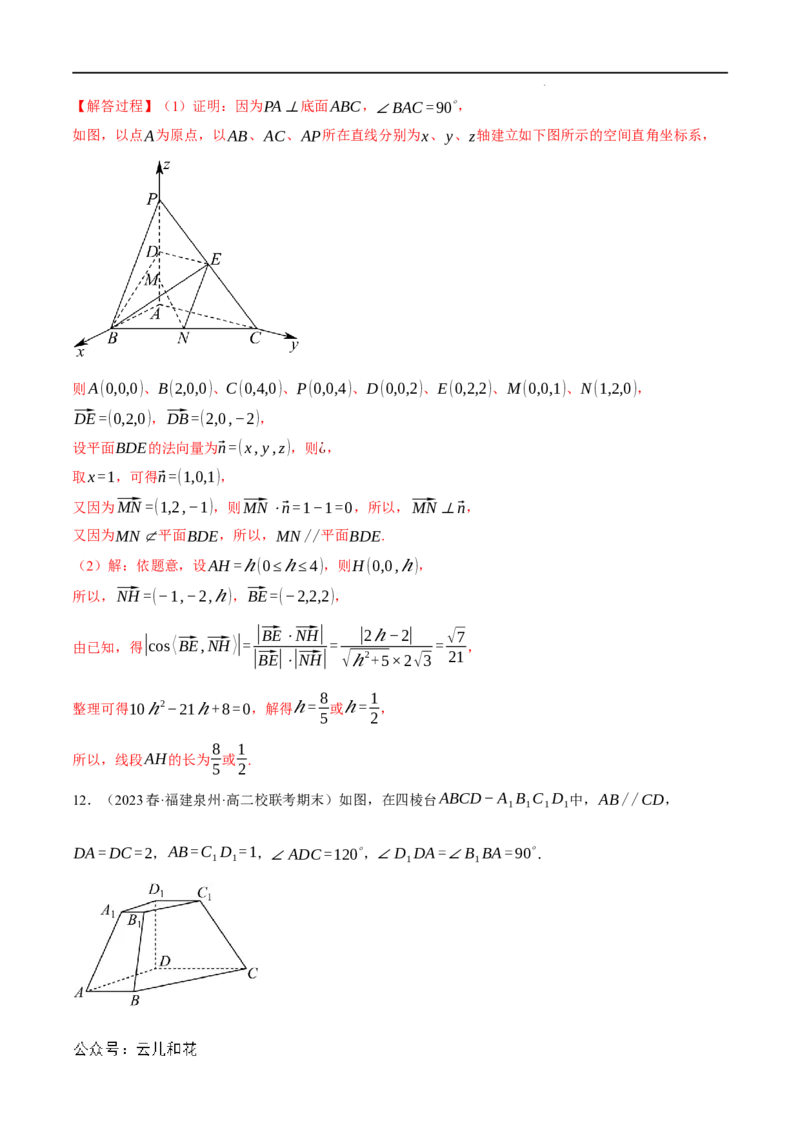
11.(2023·四川成都·校考模拟预测)如图,在三棱锥P−ABC中,PA⊥底面ABC,∠BAC=90∘.点D、
E、N分别为棱PA、PC、BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(1)求证:MN//平面BDE;
√7
(2)已知点H在棱PA上,且直线NH与直线BH所成角的余弦值为 ,求线段AH的长.
21
【解题思路】(1)以点A为原点,以AB、AC、AP所在直线分别为x、y、z轴建立空间直角坐标系,利
用空间向量法可证得MN//平面BDE;
(2)设AH= ℎ(0≤ℎ≤4),则H(0,0,ℎ),利用空间向量法可得出关于ℎ的方程,解出ℎ的值,即可得出
结论.
学科网(北京)股份有限公司【解答过程】(1)证明:因为PA⊥底面ABC,∠BAC=90∘,
如图,以点A为原点,以AB、AC、AP所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系,
则A(0,0,0)、B(2,0,0)、C(0,4,0)、P(0,0,4)、D(0,0,2)、E(0,2,2)、M(0,0,1)、N(1,2,0),
⃗DE=(0,2,0),⃗DB=(2,0,−2),
设平面BDE的法向量为⃗n=(x,y,z),则¿,
取x=1,可得⃗n=(1,0,1),
又因为⃗MN=(1,2,−1),则⃗MN⋅⃗n=1−1=0,所以,⃗MN⊥⃗n,
又因为MN⊄平面BDE,所以,MN//平面BDE.
(2)解:依题意,设AH= ℎ(0≤ℎ≤4),则H(0,0,ℎ),
所以,⃗NH=(−1,−2,ℎ),⃗BE=(−2,2,2),
由已知,得 |cos⟨⃗BE,⃗NH⟩|=
|⃗BE⋅⃗NH|
=
|2ℎ−2|
=
√7
,
|⃗BE|⋅|⃗NH| √
ℎ
2+5×2√3 21
8 1
整理可得10ℎ 2−21ℎ +8=0,解得ℎ = 或ℎ = ,
5 2
8 1
所以,线段AH的长为 或 .
5 2
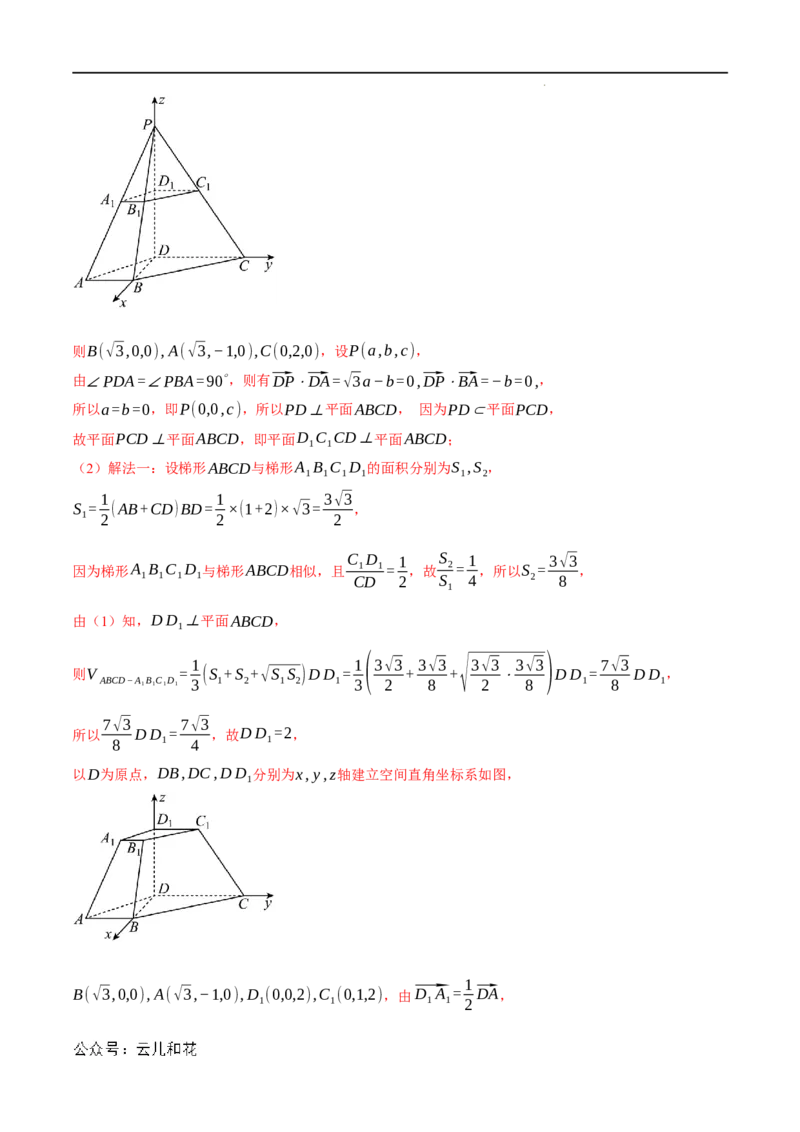
12.(2023春·福建泉州·高二校联考期末)如图,在四棱台ABCD−A B C D 中,AB//CD,
1 1 1 1
DA=DC=2,AB=C D =1,∠ADC=120∘,∠D DA=∠B BA=90∘.
1 1 1 1
学科网(北京)股份有限公司(1)证明:平面D C CD⊥平面ABCD;
1 1
7√3
(2)若四棱台ABCD−A B C D 的体积为 ,求直线A A 与平面AB C 所成角的正弦值.
1 1 1 1 4 1 1 1
【解题思路】(1)解法一:证明AB⊥BD,AB⊥BB 从而得到AB⊥DD ,结合AD⊥DD 面面垂
1 1 1
直的判定即可证明;解法二:建立合适的空间直角坐标系,利用空间向量法证明即可;
(2)解法一:利用锥体体积公式求出DD =2,建立合适的空间直角坐标系,利用线面角的空间向量求法
1
即可;解法二:利用锥体体积比从而得到PD=4,再建立空间直角坐标系,利用线面角的空间向量求法即
可.
【解答过程】(1)解法一:∵AB//CD,∵∠ADC=120∘,∴∠DAB=60∘,
在△ABD中,AB=1,AD=2,∠DAB=60∘,
由余弦定理得BD=√12+22−2×1×2cos60∘=√3,
故AB2+BD2=AD2,则AB⊥BD,
因为棱台ABCD−A B C D ,故BB ,DD 交于一点,即BB ,DD 共面,
1 1 1 1 1 1 1 1
又∠B BA=90° ,即AB⊥BB ,BB ∩BD=B,BB ,BD⊂平面BB D D,所以AB⊥平面
1 1 1 1 1 1
BB D D,
1 1
因为DD ⊂面BB D D,所以AB⊥DD ,又∠D DA=90∘,即AD⊥DD ,AB∩AD=A,
1 1 1 1 1 1
AB,AD⊂平面ABCD,所以DD ⊥平面ABCD,又因为DD ⊂平面D C CD,
1 1 1 1
所以平面D C CD⊥平面ABCD;
1 1
解法二:由棱台的定义,把四棱台ABCD−A B C D 的侧棱延长交于点P,
1 1 1 1
得到四棱锥P−ABCD,则∠PDA=∠PBA=90°,
同解法一,可得AB⊥BD,
以D为原点,DB,DC分别为x,y轴建立空间直角坐标系如图,
学科网(北京)股份有限公司则B(√3,0,0),A(√3,−1,0),C(0,2,0),设P(a,b,c),
由∠PDA=∠PBA=90∘,则有⃗DP⋅⃗DA=√3a−b=0,⃗DP⋅⃗BA=−b=0,,
所以a=b=0,即P(0,0,c),所以PD⊥平面ABCD, 因为PD⊂平面PCD,
故平面PCD⊥平面ABCD,即平面D C CD⊥平面ABCD;
1 1
(2)解法一:设梯形ABCD与梯形A B C D 的面积分别为S ,S ,
1 1 1 1 1 2
1 1 3√3
S = (AB+CD)BD= ×(1+2)×√3= ,
1 2 2 2
C D 1 S 1 3√3
因为梯形A B C D 与梯形ABCD相似,且 1 1= ,故 2= ,所以S = ,
1 1 1 1 CD 2 S 4 2 8
1
由(1)知,DD ⊥平面ABCD,
1
1 1(3√3 3√3 √3√3 3√3) 7√3
则V = (S +S +√S S )DD = + + ⋅ DD = DD ,
ABCD−A 1 B 1 C 1 D 1 3 1 2 1 2 1 3 2 8 2 8 1 8 1
7√3 7√3
所以 DD = ,故DD =2,
8 1 4 1
以D为原点,DB,DC,DD 分别为x,y,z轴建立空间直角坐标系如图,
1
1
B(√3,0,0),A(√3,−1,0),D (0,0,2),C (0,1,2),由⃗D A = ⃗DA,
1 1 1 1 2
学科网(北京)股份有限公司√3 1 1 √3
得A ( ,− ,2),由⃗A B = ⃗AB,得B ( ,0,2),
1 2 2 1 1 2 1 2
( √3 1 ) ( √3 ) ( √3 )
所以⃗A A = − , ,2 ,⃗AB = − ,1,2 ,⃗B C = − ,1,0 ,
1 2 2 1 2 1 1 2
设平面AB C 的法向量为⃗n=(x,y,z),
1 1
√3 √3
则⃗n⋅⃗AB =− x+ y+2z=0,⃗n⋅⃗B C =− x+ y=0,取⃗n=(2,√3,0),
1 2 1 1 2
设直线A A 与平面AB C 所成的角为θ,则
1 1 1
| √3 |
−√3+ +0
sinθ=|cos<⃗A A ,⃗n>|=
|⃗A A
1
⋅⃗n|
=
2
=
√105.
1 |⃗A A |⋅|⃗n| √5⋅√7 70
1
解法二:可知四棱锥P−A B C D 与四棱锥P−ABCD,
1 1 1 1
C D 1 V 1 7 7√3
相似比为 1 1= ,故体积比为 P−A 1 B 1 C 1 D 1= ,故V = V = ,
CD 2 V 8 ABCD−A 1 B 1 C 1 D 1 8 P−ABCD 4
P−ABCD
1 1 3√3
所以V =2√3,又S = (AB+CD)BD= ×(1+2)×√3= ,
P−ABCD ABCD 2 2 2
1 3√3
所以 × ×PD=2√3,故PD=4,所以P(0,0,4),
3 2
√3 √3 1
故B ( ,0,2),A ( ,− ,2),C (0,1,2),
1 2 1 2 2 1
下同解法一.
13.(2023春·河南·高二校联考期末)如图,圆柱O O 的底面半径与高均为2,AB为⊙O 的直径,C,D
1 2 2
分别为⊙O ,⊙O 上的点,直线CD与线段O O 交于O点.
1 2 1 2
(1)证明:O为线段O O 的中点;
1 2
π
(2)若AC与下底面所成的角为 ,求直线BC与平面ACD所成角的正弦值.
6
学科网(北京)股份有限公司【解题思路】(1)利用面面平行的性质,可证明O DO C是平行四边形,即可证明;
1 2
(2)首先作辅助线,延长DO 交⊙O 于点E,并连结EA,EB,EC,利用垂直关系,可证明
2 2
EA,EB,EC两两互相垂直,则以点E为原点,建立空间直角坐标系,利用向量公式,求线面角的正弦值.
【解答过程】(1)连接O C,O C,O D,O D,如图所示.
1 2 1 2
因为C,O ,D,O 四点共面,且圆柱O O 的上、下底面平行,所以O C∥O D.
1 2 1 2 1 2
因为O C=O D,所以四边形CO DO 为平行四边形,
1 2 1 2
所以O O=OO ,即O为O O 的中点.
1 2 1 2
(2)延长DO 交⊙O 于点E,连接CE,AE,BE.
2 2
因为E在⊙O 上,AB为⊙O 的直径,
2 2
所以AE⊥BE,O C=O E,O C∥O E,
1 2 1 2
所以四边形CO O E为平行四边形,
1 2
所以O O ∥CE,所以CE⊥平面ABE.
1 2
π
所以∠CAE为直线AC与下底面所成的角,所以∠CAE=
.
6
因为CE=2,所以AE=2√3,BE=2.
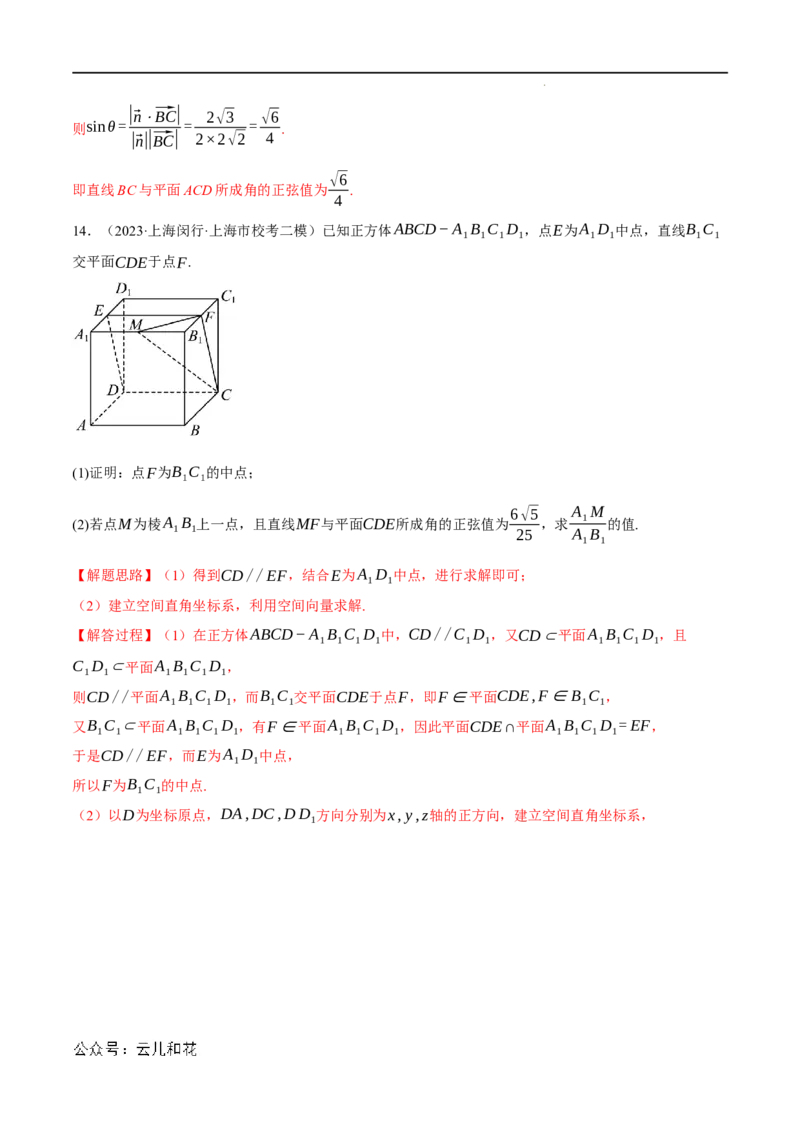
如图所示,以E为坐标原点,⃗EA,⃗EB,⃗EC的方向分别为x轴、y轴,z轴的正方向,建立空间直角坐标
系E−xyz.
则A(2√3,0,0),B(0,2,0),C(0,0,2),D(2√3,2,0).
所以⃗AD=(0,2,0),⃗CD=(2√3,2,−2),⃗BC=(0,−2,2).
设平面ACD的法向量为⃗n=(x,y,z).
则¿不妨取x=1,则⃗n=(1,0,√3).
设直线BC与平面ACD所成的角为θ,
学科网(北京)股份有限公司|⃗n⋅⃗BC| 2√3 √6
则sinθ= = =
.
|⃗n||⃗BC| 2×2√2 4
√6
即直线BC与平面ACD所成角的正弦值为 .
4
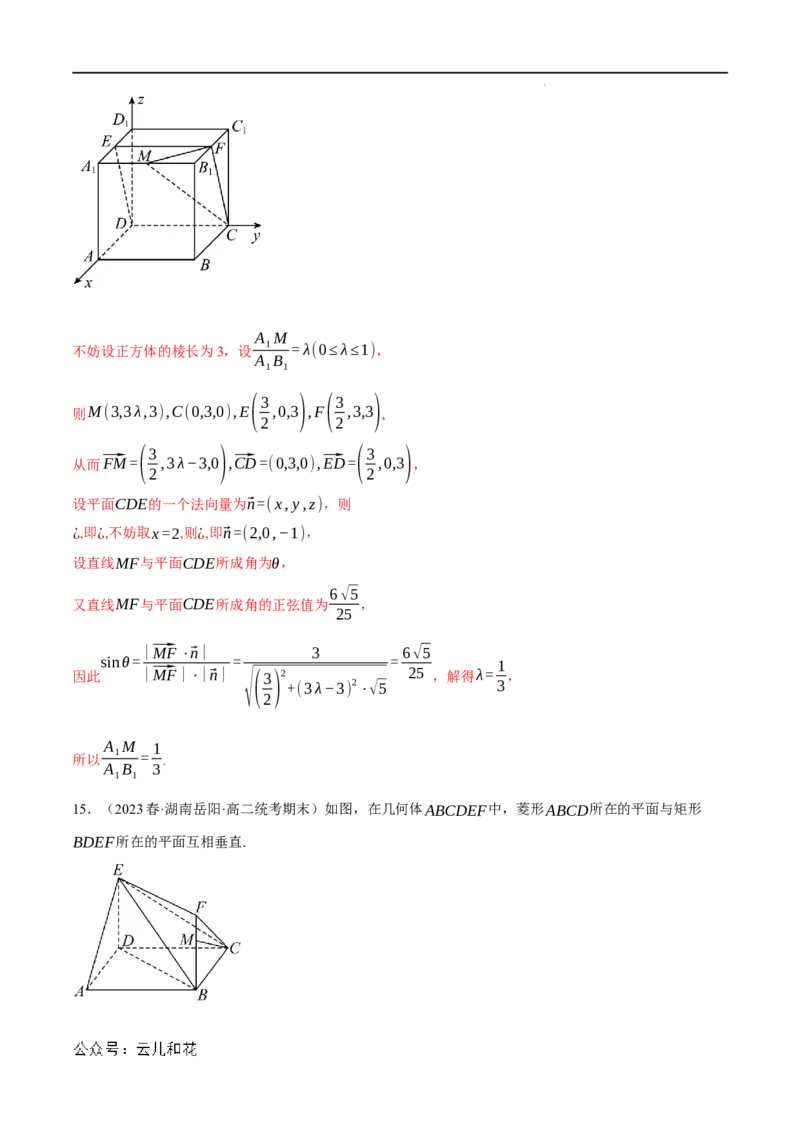
14.(2023·上海闵行·上海市校考二模)已知正方体ABCD−A B C D ,点E为A D 中点,直线B C
1 1 1 1 1 1 1 1
交平面CDE于点F.
(1)证明:点F为B C 的中点;
1 1
6√5 A M
(2)若点M为棱A B 上一点,且直线MF与平面CDE所成角的正弦值为 ,求 1 的值.
1 1 25 A B
1 1
【解题思路】(1)得到CD//EF,结合E为A D 中点,进行求解即可;
1 1
(2)建立空间直角坐标系,利用空间向量求解.
【解答过程】(1)在正方体ABCD−A B C D 中,CD//C D ,又CD⊂平面A B C D ,且
1 1 1 1 1 1 1 1 1 1
C D ⊂平面A B C D ,
1 1 1 1 1 1
则CD//平面A B C D ,而B C 交平面CDE于点F,即F∈平面CDE,F∈B C ,
1 1 1 1 1 1 1 1
又B C ⊂平面A B C D ,有F∈平面A B C D ,因此平面CDE∩平面A B C D =EF,
1 1 1 1 1 1 1 1 1 1 1 1 1 1
于是CD//EF,而E为A D 中点,
1 1
所以F为B C 的中点.
1 1
(2)以D为坐标原点,DA,DC,DD 方向分别为x,y,z轴的正方向,建立空间直角坐标系,
1
学科网(北京)股份有限公司A M
不妨设正方体的棱长为3,设 1 =λ(0≤λ≤1),
A B
1 1
(3 ) (3 )
则M(3,3λ,3),C(0,3,0),E ,0,3 ,F ,3,3 ,
2 2
从而⃗FM= (3 ,3λ−3,0 ) ,⃗CD=(0,3,0),⃗ED= (3 ,0,3 ) ,
2 2
设平面CDE的一个法向量为⃗n=(x,y,z),则
¿,即¿,不妨取x=2,则¿,即⃗n=(2,0,−1),
设直线MF与平面CDE所成角为θ,
6√5
又直线MF与平面CDE所成角的正弦值为 ,
25
|⃗MF⋅⃗n| 3 6√5
sinθ= = =
1
因此 |⃗MF|⋅|⃗n| √ (3) 2
+(3λ−3) 2 ⋅√5
25 ,解得λ=
3
,
2
A M 1
所以 1 = .
A B 3
1 1
15.(2023春·湖南岳阳·高二统考期末)如图,在几何体ABCDEF中,菱形ABCD所在的平面与矩形
BDEF所在的平面互相垂直.
学科网(北京)股份有限公司(1)若M为线段BF上的一个动点,证明:CM//平面ADE;
√15
(2)若∠BAD=60∘,AB=2,直线CF与平面BCE所成角的正弦值为 ,求BF的长.
10
【解题思路】(1)利用面面平行的性质定理证明;
(2)建立空间直角坐标系,利用线面角的向量公式求解.
【解答过程】(1)由题知,四边形BDEF为矩形,所以BF//DE,
又因为BF⊄̸)平面ADE,DE⊂平面ADE,所以BF//平面ADE,
同理可证BC//平面ADE,又因为BC∩BF=B,BC、BF⊂平面BCF,
所以平面BCF//平面ADE,又因为CM⊂平面BCF,所以CM//平面ADE.
(2)因为平面ABCD⊥平面BDEF,
且平面ABCD∩平面BDEF=BD,DE⊥DB,
DE⊂平面BDEF,所以DE⊥平面ABCD.
又因为底面ABCD为菱形,且∠BAD=60∘,AB=2,
所以△ABD为等边三角形,且AB=BD=2,设BF=a,
取AB的中点为G,连接DG,以D为坐标原点,分别以⃗DG,⃗DC,⃗DE的方向为x轴、y轴、z轴正方向,建
立如图所示的空间直角坐标系D−xyz,
则B(√3,1,0),C(0,2,0),E(0,0,a),F(√3,1,a),
→ → →
则CF=(√3,−1,a),BC=(−√3,1,0),CE=(0,−2,a) ,
→
设平面BCE的法向量为n=(x,y,z) ,¿,则¿,
2√3 → ( 2√3)
取x=1,则y=√3,z= ,即n= 1,√3, ,
a a
设直线CF与平面BCE所成角为θ,则
学科网(北京)股份有限公司| 2√3|
√3−√3+a⋅
|⃗CF⋅⃗n| a √15
sinθ=|cos<⃗CF,⃗n>|= = = ,
|⃗CF|⋅|⃗n| √ 12 10
√4+a2 ⋅ 4+
a2
化简可得a4−13a2+12=0,解得a=2√3或a=1,
故BF的长可为2√3或1.
16.(2023春·江苏连云港·高二统考期末)如图,在三棱锥P−ABC中,
AB=BC=2√2,PA=PC=AC=4,平面ABC⊥平面PAC.
(1)求异面直线AC与PB间的距离;
(2)若点M在棱BC上,且二面角M−PA−C为30∘,求PC与平面PAM所成角的正弦值.
【解题思路】(1)法一:根据等腰三角形性质得PO垂直AC,BO⊥AC,根据线面垂直的判定定理得
AC⊥面PBO,在面PBO中,作OD⊥PB,知OD为异面直线AC与PB间的距离可得答案;法二:以O
为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,设⃗n=(x,y,z),且
⃗n⋅⃗AC=0,⃗n⋅⃗PB=0可得⃗n,由异面直线AC与PB间的距离向量求法可得答案;
(2)方法一:在平面ABC内作MN⊥AC,则MN⊥平面PAC,在平面PAC内作NF⊥AP,则
MF⊥AP,得∠MFN为二面角M−PA−C的平面角,法一:设点C到平面PAM的距离为
ℎ
,利用
V
M−APC
=V
C−APM
得ℎ可得答案;法二:以O为坐标原点,OB、OC、OP所在直线分别为x轴,y轴,z轴,
建空间直角坐标系,求出平面PAM的法向量,由线面角的向量求法可得答案.
【解答过程】(1)法一:取AC中点O,连接PO,由PA=PC知PO⊥AC,
又平面ABC⊥平面PAC,平面ABC∩平面PAC=AC,故PO⊥平面ABC,
连接BO,则∠POB=90∘,
又因为AB=BC,O为AC中点,故BO⊥AC,
BO,PO⊂面PBO,BO∩PO=O,故AC⊥面PBO,
在面PBO中,作OD⊥PB,则由OD⊥AC知OD为异面直线AC与PB间的距离,
由PO=2√3,OB=2,PB=4,PO×OB=PB×OD知OD=√3,
学科网(北京)股份有限公司即异面直线AC与PB间的距离为√3;
法二:取AC中点O,连接PO,由PA=PC知PO⊥AC,
又平面ABC⊥平面PAC,平面ABC∩平面PAC=AC,故PO⊥平面ABC
以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴,
则A(0,−2,0),B(2,0,0),C(0,2,0),P(0,0,2√3),⃗PB=(2,0,−2√3),⃗AC=(0,4,0),
设⃗n=(x,y,z),且⃗n⋅⃗AC=0,⃗n⋅⃗PB=0,
则¿,令z=√3,则⃗n=(3,0,√3),
|⃗n⋅⃗AB| 6
又⃗AB=(2,2,0),则异面直线AC与PB间的距离为d= = =√3;
|⃗n| 2√3
(2)由(1)知PO⊥平面ABC,可得平面PAC⊥平面ABC,
如图,在平面ABC内作MN⊥AC,垂足为N,则MN⊥平面PAC,
在平面PAC内作FN⊥AP,垂足为F,联结MF,
PA⊂平面PAC,所以MN⊥PA,且MN∩FN=N,MN、FN⊂平面MFN,
所以PA⊥平面MFN,FM⊂平面MFN,所以PA⊥FM
学科网(北京)股份有限公司故∠MFN为二面角M−PA−C的平面角,即∠MFN=30∘,
√3
设MN=a,则NC=a,AN=4−a,在Rt△AFN中,FN= (4−a),
2
4
在Rt△MFN中,由∠MFN=30∘知FN=√3MN,得a= ,
3
1 1
法一:设点C到平面PAM的距离为ℎ,由V
M−APC
=V
C−APM
,得
3
S
△APC
MN=
3
S
△APM
ℎ,即
1 1 1 1
× ×AC×MN×PO= × ×PA×MF×ℎ,
3 2 3 2
又AC=PA=4,MF=2MN,PO=2√3,
√3
解得ℎ =√3,则PC与平面PAM所成角的正弦值为 ;
4
法二:以O为坐标原点,OB、OC、OP所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系如图,
(4 2 )
则A(0,−2,0),B(2,0,0),C(0,2,0),P(0,0,2√3),M , ,0 ,
3 3
⃗PC=(0,2,−2√3),⃗AP=(0,2,2√3),⃗AM= (4 , 8 ,0 ) ,
3 3
设平面PAM的法向量为⃗n=(x,y,z),则由⃗n⋅⃗AP=0,⃗n⋅⃗AM=0,
知¿,令z=√3,则⃗n=(6,−3,√3),
⃗n⋅⃗PC √3
则⃗PC与⃗n所成角的余弦值为 cosθ= =− ,
|⃗n||⃗PC| 4
√3
则PC与平面PAM所成角的正弦值sinα=|cosθ|= .
4
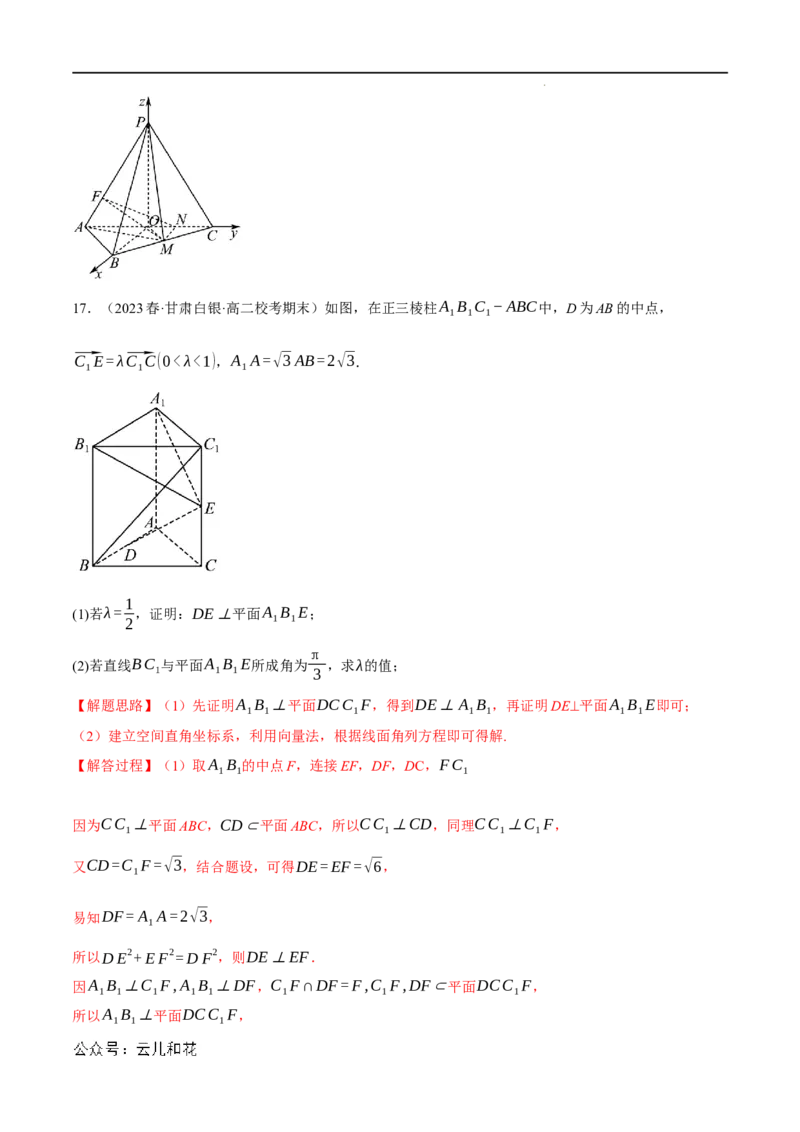
学科网(北京)股份有限公司17.(2023春·甘肃白银·高二校考期末)如图,在正三棱柱A B C −ABC中,D为AB的中点,
1 1 1
⃗C E=λ⃗C C(0<λ<1),A A=√3AB=2√3.
1 1 1
1
(1)若λ= ,证明:DE⊥平面A B E;
2 1 1
π
(2)若直线BC 与平面A B E所成角为 ,求λ的值;
1 1 1 3
【解题思路】(1)先证明A B ⊥平面DCC F,得到DE⊥A B ,再证明DE⊥平面A B E即可;
1 1 1 1 1 1 1
(2)建立空间直角坐标系,利用向量法,根据线面角列方程即可得解.
【解答过程】(1)取A B 的中点F,连接EF,DF,DC,FC
1 1 1
因为CC ⊥平面ABC,CD⊂平面ABC,所以CC ⊥CD,同理CC ⊥C F,
1 1 1 1
又CD=C F=√3,结合题设,可得DE=EF=√6,
1
易知DF=A A=2√3,
1
所以DE2+EF2=DF2,则DE⊥EF.
因A B ⊥C F,A B ⊥DF,C F∩DF=F,C F,DF⊂平面DCC F,
1 1 1 1 1 1 1 1
所以A B ⊥平面DCC F,
1 1 1
学科网(北京)股份有限公司又DE⊂平面DCC F,所以DE⊥A B ,
1 1 1
因为A B ∩EF=F,A B ,EF⊂平面A B E,
1 1 1 1 1 1
所以DE⊥平面A B E.
1 1
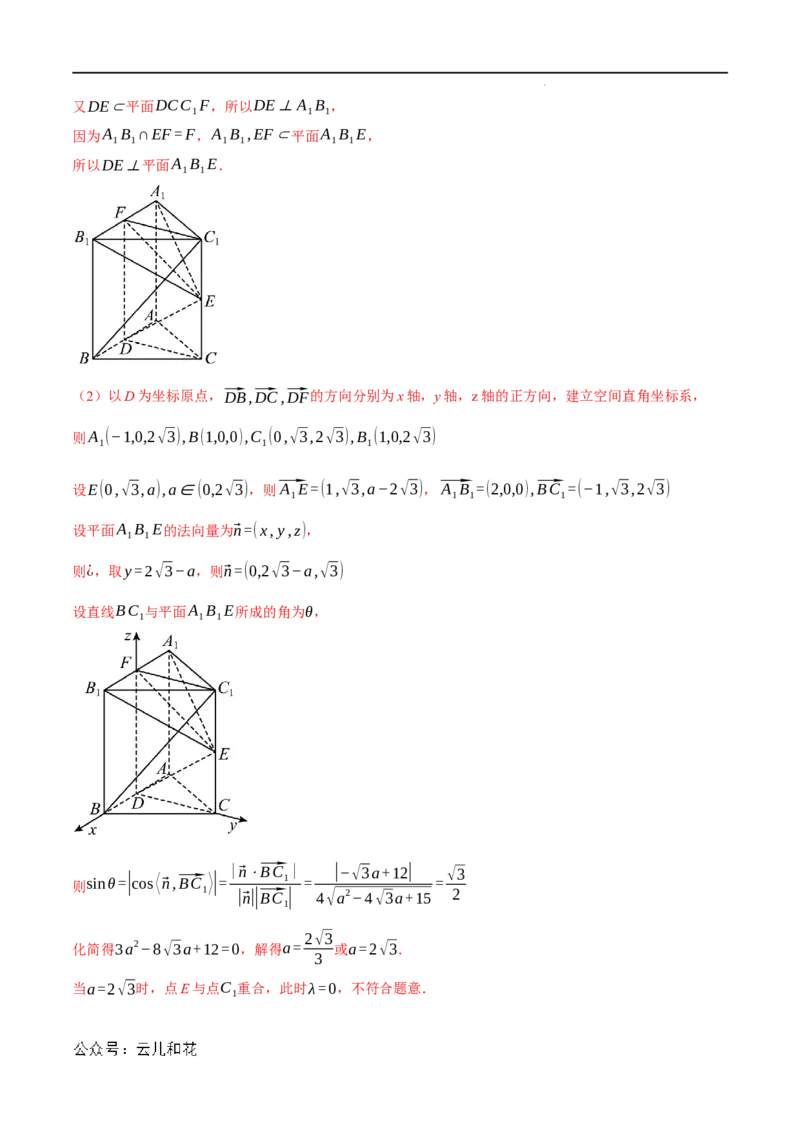
(2)以D为坐标原点,⃗DB,⃗DC,⃗DF的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系,
则A (−1,0,2√3),B(1,0,0),C (0,√3,2√3),B (1,0,2√3)
1 1 1
设E(0,√3,a),a∈(0,2√3),则⃗A E=(1,√3,a−2√3),⃗A B =(2,0,0),⃗BC =(−1,√3,2√3)
1 1 1 1
设平面A B E的法向量为⃗n=(x,y,z),
1 1
则¿,取y=2√3−a,则⃗n=(0,2√3−a,√3)
设直线BC 与平面A B E所成的角为θ,
1 1 1
|⃗n⋅⃗BC | |−√3a+12| √3
则sinθ=|cos⟨⃗n,⃗BC ⟩|= 1 = =
1 |⃗n||⃗BC | 4√a2−4√3a+15 2
1
2√3
化简得3a2−8√3a+12=0,解得a= 或a=2√3.
3
当a=2√3时,点E与点C 重合,此时λ=0,不符合题意.
1
学科网(北京)股份有限公司|⃗C E|
2 2
所以λ= 1 = ,即λ的值为 .
|⃗C C| 3 3
1
18.(2023春·云南玉溪·高二校考期末)如图,在三棱柱ABC−A B C 中,AB=AC=2,D为BC的中
1 1 1
点,平面BB C C⊥平面ABC.
1 1
(1)证明:AD⊥平面BB C C;
1 1
(2)已知四边形BB C C是边长为2的菱形,且∠B BC=60°,求平面ABC与平面AC D所成角的正弦
1 1 1 1
值.
【解题思路】(1)利用等腰三角形性质,面面垂直的性质推理作答.
(2)以点D为原点,建立空间直角坐标系,利用空间向量求解作答.
【解答过程】(1)在三棱柱ABC−A B C 中,由AB=AC=2,D是BC的中点,得AD⊥BC,
1 1 1
而平面BB C C⊥平面ABC,且平面BB C C∩平面ABC=BC,AD⊂平面ABC,
1 1 1 1
所以AD⊥平面BB C C.
1 1
(2)因为四边形BB C C为菱形,∠B BC=60°,则△B BC为正三角形,连接B D,有B D⊥BC,
1 1 1 1 1 1
而平面BB C C⊥平面ABC,平面BB C C∩平面ABC=BC,因此B D⊥平面ABC,DC,DA,DB
1 1 1 1 1 1
两两垂直,
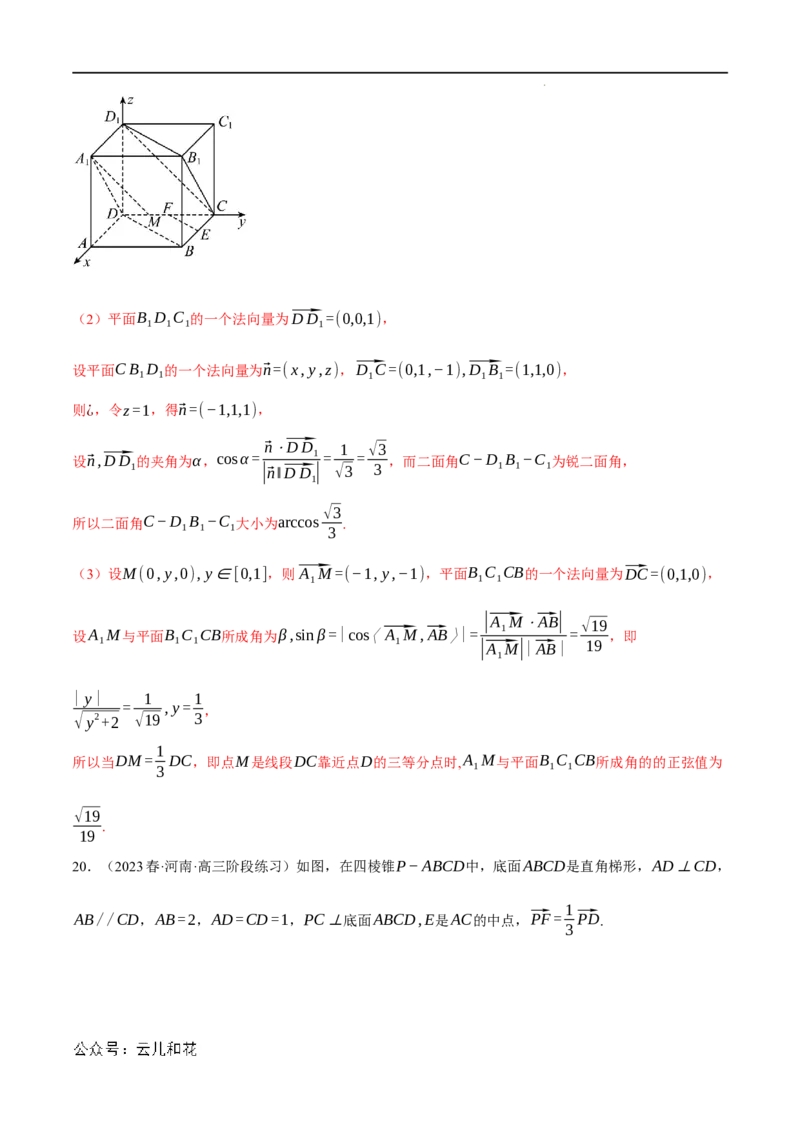
以D为坐标原点,DC,DA,DB 分别为x轴,y轴,z轴,建立空间直角坐标系,
1
则D(0,0,0),C(1,0,0),A(0,√3,0),C (2,0,√3),⃗DC =(2,0,√3),⃗DA=(0,√3,0),
1 1
学科网(北京)股份有限公司设平面AC D的法向量⃗n=(x ,y ,z ),则¿,令x =√3,得⃗n=(√3,0,−2),
1 1 1 1 1
显然平面ABC的法向量⃗m=(0,0,1),设平面ABC与平面AC D所成角为θ,
1
|⃗m⋅⃗n| 2 √21
则cosθ=|cos〈⃗m,⃗n〉|= = ,sinθ=√1−cos2θ= ,
|⃗m||⃗n| √7 7
√21
所以平面ABC与平面AC D所成角的正弦值为 .
1 7
19.(2023春·上海宝山·高二统考期末)已知E、F分别是正方体ABCD−A B C D 的棱BC、CD的中
1 1 1 1
点,求:
(1)A D与EF所成角的大小;
1
(2)二面角C−D B −C 的大小;
1 1 1
√19
(3)点M在棱CD上,若A M与平面B C CB所成角的正弦值为 ,请判断点M的位置,并说明理由.
1 1 1 19
【解题思路】(1)(2)建立空间直角坐标系,利用空间向量求出异面直线的夹角、二面角大小作答.
(3)利用(1)中坐标系,设出点M的坐标,利用线面角的正弦值求解作答.
【解答过程】(1)在正方体ABCD−A B C D 中,令AB=1,
1 1 1 1
以点D为原点,以⃗DA,⃗DC,⃗DD 的方向分别为x,y,z轴正方向,建立空间直角坐标系D−xyz,如图,
1
则D(0,0,0),A (1,0,1),E( 1 ,1,0),F(0, 1 ,0), ⃗A D=(−1,0,−1),⃗EF= ( − 1 ,− 1 ,0 ) ,
1 2 2 1 2 2
1
|⃗A D⋅⃗EF|
2 1
设A D与EF所成角为θ,cosθ=|cos〈⃗A D,⃗EF〉|= 1 = = ,
1 1 |⃗A D||⃗EF| √2 2
1 √2×
2
π
所以A D与EF所成角的大小是 .
1 3
学科网(北京)股份有限公司(2)平面B D C 的一个法向量为⃗DD =(0,0,1),
1 1 1 1
设平面CB D 的一个法向量为⃗n=(x,y,z),⃗D C=(0,1,−1),⃗D B =(1,1,0),
1 1 1 1 1
则¿,令z=1,得⃗n=(−1,1,1),
⃗n⋅⃗DD 1 √3
设⃗n,⃗DD 的夹角为α,cosα= 1 = = ,而二面角C−D B −C 为锐二面角,
1 |⃗n‖⃗DD | √3 3 1 1 1
1
√3
所以二面角C−D B −C 大小为arccos .
1 1 1 3
(3)设M(0,y,0),y∈[0,1],则⃗A M=(−1,y,−1),平面B C CB的一个法向量为⃗DC=(0,1,0),
1 1 1
|⃗A M⋅⃗AB|
√19
设A M与平面B C CB所成角为β,sinβ=|cos〈⃗A M,⃗AB〉|= 1 = ,即
1 1 1 1 |⃗A M||⃗AB| 19
1
|y| 1 1
= ,y=
,
√y2+2 √19 3
1
所以当DM= DC,即点M是线段DC靠近点D的三等分点时,A M与平面B C CB所成角的的正弦值为
3 1 1 1
√19
.
19
20.(2023春·河南·高三阶段练习)如图,在四棱锥P−ABCD中,底面ABCD是直角梯形,AD⊥CD,
1
AB//CD,AB=2,AD=CD=1,PC⊥底面ABCD,E是AC的中点,⃗PF= ⃗PD.
3
学科网(北京)股份有限公司(1)证明:平面PBC⊥平面ACF.
√10
(2)若直线PE与平面PAB所成角的正弦值为 ,且PC>CD,求平面ACF与平面PAB夹角的余弦值.
15
【解题思路】(1)由余弦定理求出BC2=2,由勾股定理逆定理得到线线垂直,进而得到线面垂直,证明
出面面垂直;
(2)建立空间直角坐标系,设出点的坐标P(0,0,a),利用线面角的大小列出方程,求出a,从而利用空间
向量求出面面角的余弦值
【解答过程】(1)因为PC⊥底面ABCD,AC⊂平面ABCD,所以PC⊥AC.
因为AD=CD=1,AD⊥CD,所以AC=√AD2+CD2=√2,∠CAD=45°.
又AB//CD,AB=2,
所以∠BAC=45°,BC2=AB2+AC2−2AB⋅ACcos∠BAC=2,
则BC2+AC2=AB2,故AC⊥BC.
因为PC∩BC=C,PC,BC⊂平面PBC,所以AC⊥平面PBC.
又AC⊂平面ACF,所以平面PBC⊥平面ACF.
(2)取AB中点N,连接CN,
因为底面ABCD是直角梯形,AD⊥CD,AB//CD,AB=2,AD=CD=1,
所以CN⊥AB,
因为PC⊥底面ABCD,CD,CN⊂平面ABCD,所以PC⊥CN,PC⊥CD,
以C为坐标原点,CN,CD,CP所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
学科网(北京)股份有限公司(1 1 )
则A(1,1,0),B(1,−1,0),E , ,0 ,
2 2
( 1 2a)
设P(0,0,a)(a>1),则F 0, , ,
3 3
⃗PE= (1 , 1 ,−a ) ,⃗PA=(1,1,−a),⃗AB=(0,−2,0).
2 2
设平面PAB的法向量为⃗m=(x ,y ,z ),
1 1 1
则¿,解得y =0,
1
令z =1,得x =a,故⃗m=(a,0,1).
1 1
√10
因为直线PE与平面PAB所成角的正弦值为 ,
15
|1 |
a−a
2 √10
所以 = ,
√ 1 15
a2+ ×√a2+1
2
√2
解得a=2或a= (舍去),则⃗m=(2,0,1),
4
则⃗CA=(1,1,0),⃗CF= ( 0, 1 , 4) .
3 3
设平面ACF的法向量为⃗n=(x ,y ,z ),
2 2 2
则¿,
令z =1,则y =−4,x =4,得⃗n=(4,−4,1).
2 2 2
⃗m⋅⃗n 9 3√165
cos⟨⃗m,⃗n⟩= = = ,
|⃗m||⃗n| √5×√33 55
3√165
故平面ACF与平面PAB夹角的余弦值为 .
55
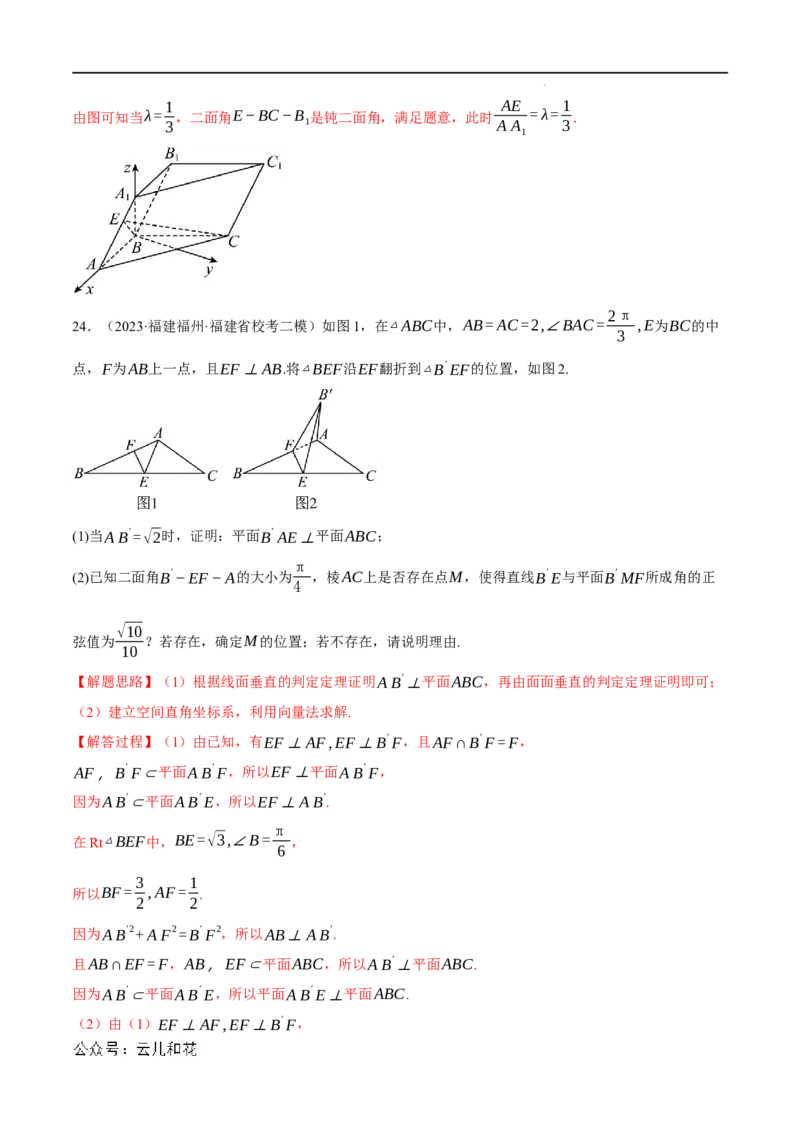
21.(2023春·江苏扬州·高二统考期末)如图,在直三棱柱ABC−A B C 中,△ABC是以BC为斜边的等腰
1 1 1
BD C E
直角三角形,A A =AB=3,D,E分别为BC,B C 上的点,且 = 1 =t(0 ,直线A C与平面A BE所成角的正弦值为 ,求二面角C −AD−C的余弦值.
2 1 1 3 1
1
【解题思路】(1)当t= 时可得点D,E分别为BC,B C 的中点,根据已知条件证明四边形BB ED为平
2 1 1 1
行四边形,再依据线面平行的判定定理即可证明.
(2)以{⃗AB,⃗AC,⃗A A }为正交基底空间直角坐标系A−xyz,写出各个点的坐标,根据直线A C与平面
1 1
√6
A BE所成角的正弦值为 求出t值,再分别求出平面AC D和平面ADC的法向量,根据公式求解即可.
1 3 1
【解答过程】(1)
1 BD C E 1
当t= 时, = 1 = ,即点D,E分别为BC,B C 的中点,
2 BC C B 2 1 1
1 1
在直三棱柱ABC−A B C 中,B C ∥BC,B C =BC,所以B E∥BD,B E=BD,
1 1 1 1 1 1 1 1 1
所以四边形BB ED为平行四边形,所以BB ∥ DE,BB = DE,
1 1 1
又A A ∥BB ,A A =BB ,所以A A ∥DE,A A =DE,
1 1 1 1 1 1
所以四边形A A ED为平行四边形,则AD∥A E,
1 1
又因为AD⊄平面A EB,A E⊂平面A EB,
1 1 1
所以AD ∥平面A EB.
1
(2)A A ⊥平面ABC,又∠BAC=90∘,以{⃗AB,⃗AC,⃗A A }为正交基底建立如图所示的空间直角坐标系
1 1
A−xyz,
学科网(北京)股份有限公司则点A(0,0,0),C (0,3,3),A (0,0,3),B(3,0,0),C(0,3,0),
1 1
BD C E
由 = 1 =t(0 ,所以t= .
2 6 2 6
而⃗AC =(0,3,3),⃗AB=(3,0,0),⃗BC=(−3,3,0),⃗BD=t⃗BC=(−3t,3t,0),
1
所以⃗AD=⃗AB+⃗BD=(3−3t,3t,0)= (1 , 5 ,0 ) ,
2 2
设平面AC D的一个法向量为⃗n =(x,y,z),则¿,即¿,
1 1
取y=−1,则⃗n =(5,−1,1),
1
1 √3
又平面ADC的一个法向量为⃗n =(0,0,1),得 cos⟨⃗n ,⃗n ⟩= = ,
2 1 2 1⋅ √52+(−1) 2+12 9
√3
观察得二面角C −AD−C为锐角,所以二面角C −AD−C的余弦值为 .
1 1 9
22.(2023春·广东深圳·高一统考期末)如图,三棱锥P−ABC的三个顶点A,B,C在圆O上,AB为
圆O的直径,且AB=6,PA=PC=2√2,BC=2√5,平面PAC⊥平面PCB,点E是PB的中点.
学科网(北京)股份有限公司(1)证明:平面PAC⊥平面ABC;
(2)点F是圆O上的一点,且点F与点C位于直径AB的两侧.当EF//平面PAC时,画出二面角E−BF−A
的平面角,并求出它的余弦值.
【解题思路】(1)要证明平面PAC⊥平面ABC,只需证明BC⊥平面PAC即可;
(2)建立空间坐标系,运用空间向量求解.
【解答过程】(1)因为点C在圆O上,∴AC=√AB2−BC2=4,又PA2+PC2=AC2,所以△PAC是
等腰直角三角形,
即AP⊥PC,由条件:平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,∴AP⊥ 平面PBC,BC⊂
平面PBC,∴BC⊥PA,
又BC⊥AC,PA⊂平面PAC,AC⊂平面PAC,PA∩AC=A,∴BC⊥平面PAC,
又BC⊂平面ABC,∴平面PAC⊥平面ABC;
(2)取AC的中点M,连接PM,则PM⊥AC,由(1)可知平面PAC⊥平面ABC,平面PAC∩平面
ABC=AC,∴PM⊥平面ABC,
连接OM,OE,OF,则OM是△ABC中BC边的中位线,∴OM⊥AC,OM⊂平面ABC,∴PM⊥OM
,
即PM,AC,OM两两垂直,以M为原点,AC,OM,PM分别为x,y,z轴建立空间直角坐标系如下图:
由于O,E分别是AB,PB的中点,连接BM,取BM的中点N,连接EN,则有
学科网(北京)股份有限公司EN//PM,∵PM⊥平面ABC,∴EN⊥平面ABC,BF⊂平面ABC,∴BF⊥EN,
过N点作FB的垂线,得垂足S,
BF⊥NS,EN∩NS=N,∴BF⊥平面ENS,ES⊂平面ENS,∴ES⊥BF,
∴∠ESN就是二面角E−BF−A的平面角;
∴OE//PA,OE⊄平面PAC,PA⊂平面PAC,∴OE//平面PAC,
OE∩FE=E,∴平面EFO//平面PAC,OF⊂平面EFO,∴FO//平面PAC,AC,FO⊂平面ABC,
∴AC//FO,
1
其中|OF|= |AB|,∴A(2,0,0),B(−2,2√5,0),P(0,0,2),E(−1,√5,1),F(3,√5,0),
2
⃗FE=(−4,0,1),⃗FB=(−5,√5,0),设平面EFB的一个法向量为⃗m=(x,y,z),
则¿,¿,令x=1,得y=√5,z=4,∴⃗m=(1,√5,4),
显然平面ABC的一个法向量⃗n=(0,0,1),
⃗m·⃗n 2√22
设平面ABC与平面EFB的二面角为α,则cosα= = ,
|⃗m|·|⃗n| 11
2√22
综上,二面角E−BF−A的余弦值为 .
11
23.(2023春·江苏南京·高二校考期中)如图,已知在三棱柱ABC−A B C 中,A B=1,A A =√5,
1 1 1 1 1
AB=BC=2,∠BAC=30∘,平面ABB A ⊥平面ABC.
1 1
(1)求A A 与BC所成角的余弦值;
1
5√13 AE
(2)在棱A A 上是否存在一点E,使得二而角E−BC−B 的余弦值为− ?若存在,求 出 的值,
1 1 26 A A
1
若不存在,说明理由.
【解题思路】(1)建立如图所示的空间直角坐标系,由空间向量法求异面直线所成的角;
(2)假设存在点E满足题意,设⃗AE=λ⃗A A ((0≤λ≤1),由空间向量法求二面角得λ值,从而得出结论.
1
学科网(北京)股份有限公司【解答过程】(1)因为A B=1,A A =√5,AB=BC=2,∠BAC=30∘,
1 1
所以A A2=AB2+A B2 ,所以A B⊥AB,∠ABC=120°,∠ACB=30°,
1 1 1
以BA为x轴,平面ABC内,过B与AB垂直的直线为y轴,BA 为z轴,建立如图所示的空间直角坐标系,
1
则A(2,0,0),B(0,0,0),C(−1,−√3,0),A (0,0,1),
1
⃗A A =(−2,0,1),⃗BC=(−1,−√3,0),
1
⃗A A ⋅⃗BC 2 √5
cos⟨⃗A A ,⃗BC⟩= 1 = = ,
1 |⃗A A ||⃗BC| √5×2 5
1
√5
所以A A 与BC所成角的余弦值是 ;
1 5
(2)假设存在点E满足题意,设⃗AE=λ⃗A A ((0≤λ≤1),则⃗AE=(−2λ,0,λ),
1
⃗BE=⃗AE+⃗BA=(2−2λ,0,λ),⃗BB =⃗A A =(−2,0,1),
1 1
设平面EBC的一个法向量是⃗m=(x ,y ,z ),则
1 1 1
2√3(λ−1)
¿,取y =−1,则x =√3,z = ,
1 1 1 λ
2√3(λ−1)
⃗m=(√3,−1, ),
λ
设平面BCC B 的一个法向量是⃗n=(x ,y ,z ),则
1 1 2 2 2
¿,取y =1,则x =−√3,z =−2√3,即⃗n=(−√3,1,−2√3),
2 2 2
| 12(λ−1|
−3−1−
|⃗m⋅⃗n| λ 5√13 1 7
|cos⟨⃗m,⃗n⟩|= = = ,解得λ= 或λ= (舍去),
|⃗m||⃗n| √ 12(λ−1) 2 26 3 6
1+3+ ×√3+1+12
λ2
学科网(北京)股份有限公司1 AE 1
由图可知当λ= ,二面角E−BC−B 是钝二面角,满足题意,此时 =λ= .
3 1 A A 3
1
2π
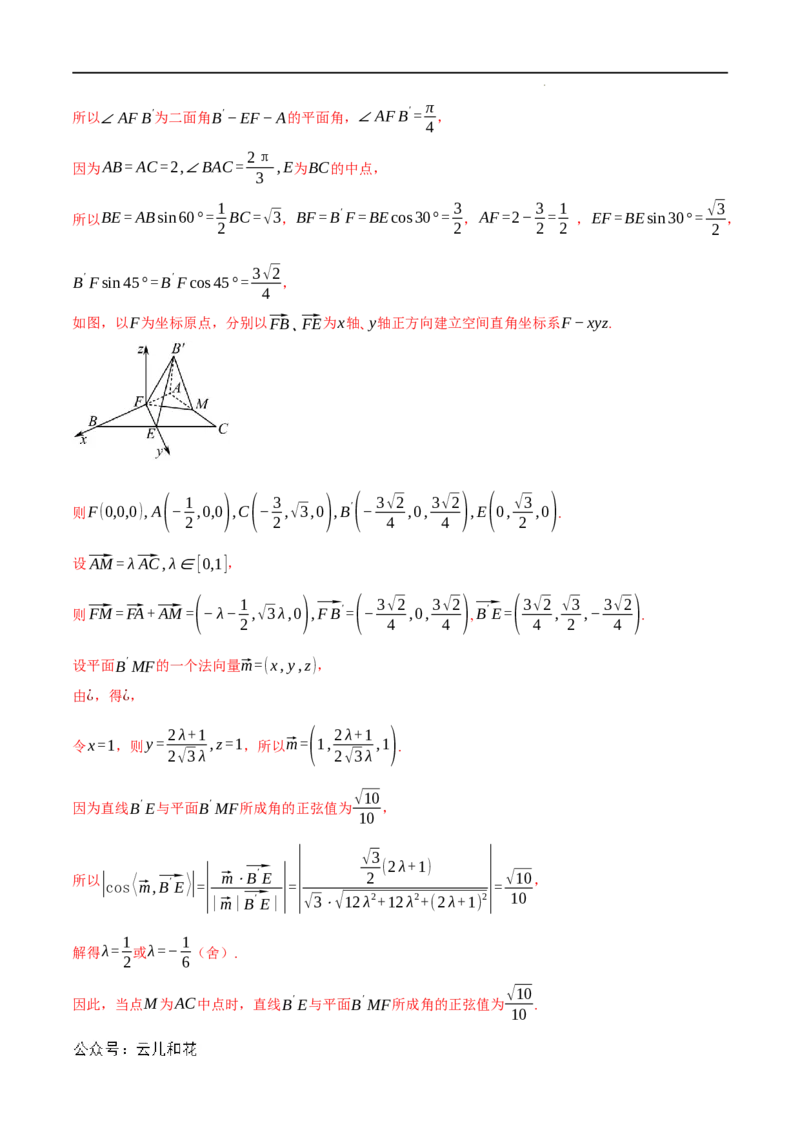
24.(2023·福建福州·福建省校考二模)如图1,在△ABC中,AB=AC=2,∠BAC= ,E为BC的中
3
点,F为AB上一点,且EF⊥AB.将△BEF沿EF翻折到△B′EF的位置,如图2.
(1)当AB′=√2时,证明:平面B′ AE⊥平面ABC;
π
(2)已知二面角B′−EF−A的大小为 ,棱AC上是否存在点M,使得直线B′E与平面B′MF所成角的正
4
√10
弦值为 ?若存在,确定M的位置;若不存在,请说明理由.
10
【解题思路】(1)根据线面垂直的判定定理证明AB′⊥平面ABC,再由面面垂直的判定定理证明即可;
(2)建立空间直角坐标系,利用向量法求解.
【解答过程】(1)由已知,有EF⊥AF,EF⊥B′F,且AF∩B′F=F,
AF,B′F⊂平面AB′F,所以EF⊥平面AB′F,
因为AB′ ⊂平面AB′E,所以EF⊥AB′.
π
在Rt△BEF中,BE=√3,∠B= ,
6
3 1
所以BF= ,AF=
.
2 2
因为AB′2+AF2=B′F2,所以AB⊥AB′.
且AB∩EF=F,AB,EF⊂平面ABC,所以AB′⊥平面ABC.
因为AB′ ⊂平面AB′E,所以平面AB′E⊥平面ABC.
(2)由(1)EF⊥AF,EF⊥B′F,
学科网(北京)股份有限公司π
所以∠AFB′为二面角B′−EF−A的平面角,∠AFB′=
,
4
2π
因为AB=AC=2,∠BAC= ,E为BC的中点,
3
1 3 3 1 √3
所以BE=ABsin60°= BC=√3,BF=B′F=BEcos30°= ,AF=2− = ,EF=BEsin30°= ,
2 2 2 2 2
3√2
B′Fsin45°=B′Fcos45°=
,
4
如图,以F为坐标原点,分别以⃗FB、⃗FE为x轴、y轴正方向建立空间直角坐标系F−xyz.
则F(0,0,0),A
(
−
1
,0,0
)
,C
(
−
3
,√3,0
) ,B′(
−
3√2
,0,
3√2)
,E
(
0,
√3
,0
)
.
2 2 4 4 2
设⃗AM=λ⃗AC,λ∈[0,1],
则⃗FM=⃗FA+⃗AM= ( −λ− 1 ,√3λ,0 ) , ⃗ FB′= ( − 3√2 ,0, 3√2) , ⃗ B′E= (3√2 , √3 ,− 3√2) .
2 4 4 4 2 4
设平面B′MF的一个法向量⃗m=(x,y,z),
由¿,得¿,
2λ+1
(
2λ+1
)
令x=1,则y= ,z=1,所以⃗m= 1, ,1 .
2√3λ 2√3λ
√10
因为直线B′E与平面B′MF所成角的正弦值为 ,
10
| √3 |
(2λ+1)
所以| cos ⟨ ⃗m, ⃗ B′E ⟩| = | ⃗m⋅ ⃗ B′E | = 2 = √10,
|⃗m|⃗ B′E| √3⋅√12λ2+12λ2+(2λ+1) 2 10
1 1
解得λ= 或λ=− (舍).
2 6
√10
因此,当点M为AC中点时,直线B′E与平面B′MF所成角的正弦值为
.
10
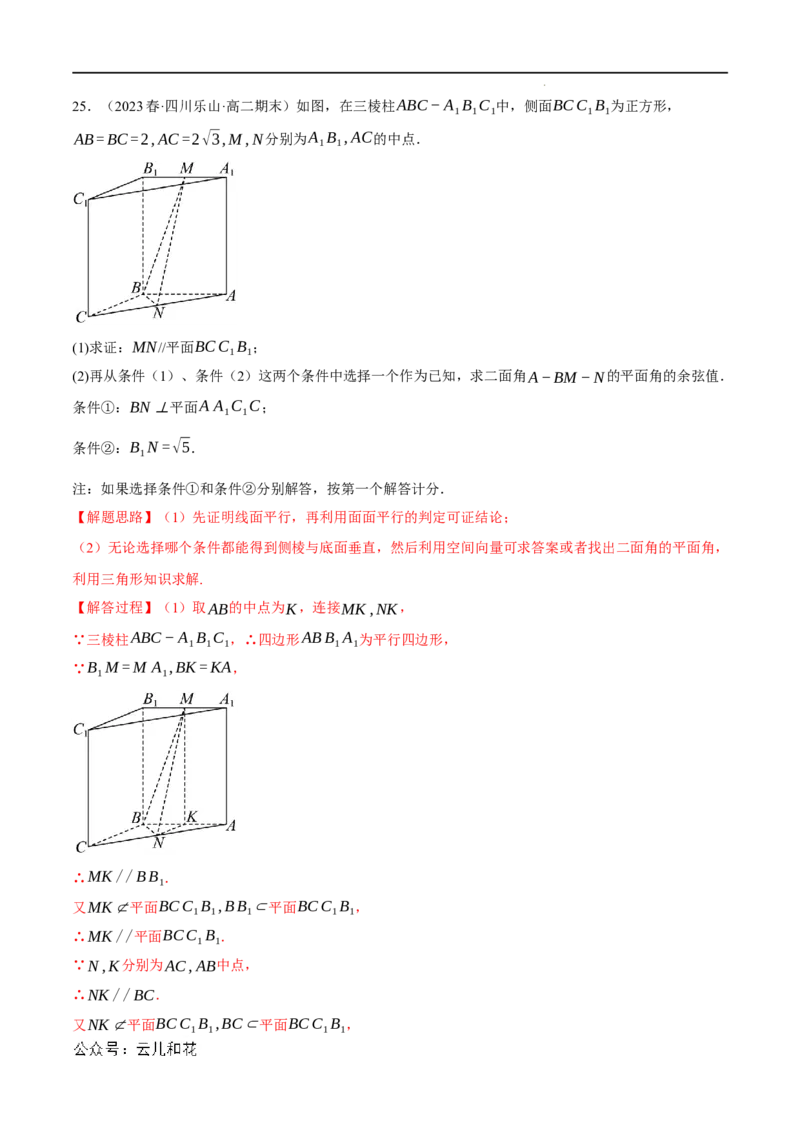
学科网(北京)股份有限公司25.(2023春·四川乐山·高二期末)如图,在三棱柱ABC−A B C 中,侧面BCC B 为正方形,
1 1 1 1 1
AB=BC=2,AC=2√3,M,N分别为A B ,AC的中点.
1 1
(1)求证:MN//平面BCC B ;
1 1
(2)再从条件(1)、条件(2)这两个条件中选择一个作为已知,求二面角A−BM−N的平面角的余弦值.
条件①:BN⊥平面A A C C;
1 1
条件②:B N=√5.
1
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解题思路】(1)先证明线面平行,再利用面面平行的判定可证结论;
(2)无论选择哪个条件都能得到侧棱与底面垂直,然后利用空间向量可求答案或者找出二面角的平面角,
利用三角形知识求解.
【解答过程】(1)取AB的中点为K,连接MK,NK,
∵三棱柱ABC−A B C ,∴四边形ABB A 为平行四边形,
1 1 1 1 1
∵B M=M A ,BK=KA,
1 1
∴MK//BB .
1
又MK⊄平面BCC B ,BB ⊂平面BCC B ,
1 1 1 1 1
∴MK//平面BCC B .
1 1
∵N,K分别为AC,AB中点,
∴NK//BC.
又NK⊄平面BCC B ,BC⊂平面BCC B ,
1 1 1 1
学科网(北京)股份有限公司∴NK//平面BCC B .
1 1
∵NK∩MK=K,NK,MK⊂平面MKN,
∴平面MKN//平面BCC B .
1 1
又MN⊂平面MKN,
∴MN//平面BCC B .
1 1
(2)选条件①
∵BN⊥平面A A C C,∴BN⊥CC .
1 1 1
又∵侧面BCC B 为正方形,∴CC ⊥BC.
1 1 1
∵BC∩BN=B,∴CC ⊥平面ABC.
1
选条件②
∵在△B BN中,BB =2,BN=1,B N=√5,∴BB2+BN2=B N2 .
1 1 1 1 1
∴BB ⊥BN.
1
又∵侧面BCC B 为正方形,∴BB ⊥BC.
1 1 1
∵BC∩BN=B,∴BB ⊥平面ABC.
1
解法一:如图建立空间直角坐标系,
(√3 1 )
A(√3,0,0),B(0,1,0),N(0,0,0),M , ,2 ;
2 2
(√3 1 )
⃗NB=(0,1,0),⃗NM= , ,2 ;
2 2
设平面NBM的法向量为⃗m=(x,y,z),
¿
√3 ( √3)
令x=2得y=0,z=− ,即⃗m= 2,0,− .
2 2
学科网(北京)股份有限公司(√3 1 )
⃗BA=(√3,−1,0),⃗BM= ,− ,2 ,
2 2
设平面ABM的法向量为⃗n=(x ,y ,z ),
1 1 1
¿,
令x =1得y =√3,z =0,即平面ABM的法向量为⃗n=(1,√3,0).
1 1 1
2 2√19
cos⟨⃗m,⃗n⟩= =
∴ √19 19 .
×2
2
2√19
即二面角A−BM−N的平面角的余弦值为 .
19
解法二:过点N作NO⊥AB交AB于点O,
过点O作OD⊥BM交BM于点D,连结DN,
∵BB ⊥平面ABC,∴BB ⊥NO.
1 1
∵BB ⊥NO,NO⊥AB,BB ∩AB=B,∴NO⊥平面ABB A .
1 1 1 1
又BM⊂平面ABB A ,∴NO⊥BM.
1 1
∵OD∩NO=O,∴BM⊥平面NOD.
∴BM⊥ND.∴∠NDO即为所求角.
学科网(北京)股份有限公司√3 1
在直角三角形ANB中,BN=1,AN=√3,AB=2,∴NO= ,OB=√BN2−NO2= ;
2 2
在正方形ABB A 中,BB =2,B M=1,∴BM=√5;
1 1 1 1
√5
在△BOM中,由等面积可得OD= ,
5
√19 √95
∴ND=√OD2+NO2= = ,
2√5 10
OD 2√19
∴cos∠NDO= = .
ND 19
2√19
即二面角A−BM−N的平面角的余弦值为 .
19
26.(2023春·江苏徐州·高二校考期中)如图1,在等边△ABC中,点D,E分别为边AB,AC上的动点,
DE
且满足DE//BC,记 =λ.将△ADE沿DE翻折到△MDE位置,使得平面MDE⊥平面DECB,连接
BC
MB,MC得到图2,点N为MC的中点.
(1)当EN//平面MBD时,求λ的值;
(2)试探究:随着λ值的变化,二面角B−MD−E的大小是否为定值?如果是,请求出二面角B−MD−E
的正弦值;如果不是,请求出二面角B−MD−E的余弦值的取值范围.
【解题思路】(1)建立空间直角坐标系,利用向量的夹角即可求解,
(2)由法向量的夹角即可求解二面角.
学科网(北京)股份有限公司【解答过程】(1)取DE的中点O,连接AO并延长与BC相交,因为AD=AE,DO=OE,所以
AO⊥DE,即MO⊥DE,
又平面MDE⊥平面DECB,平面MDE∩平面DECB=DE,MO⊂平面MDE,
所以MO⊥平面DECB,建立如图空间直角坐标系,不妨设BC=2,则M(0,0,√3λ),D(λ,0,0),
( 1 √3 √3 )
E(−λ,0,0),B(1,√3(1−λ),0),C(−1,√3(1−λ),0),N − , (1−λ), λ ,
2 2 2
( 1 √3 √3 )
所以⃗EN= λ− , (1−λ), λ ,⃗MD=(λ,0,−√3λ),⃗DB=(1−λ,√3(1−λ),0).
2 2 2
设平面BMD的法向量为⃗m=(x,y,z),则¿,
令x=√3,则y=−1,z=1,所以即⃗m=(√3,−1,1)是平面BMD的一个法向量,
( 1) √3 √3 1
因为EN∥平面MBD,所以⃗EN⊥⃗m,⃗EN⋅⃗m=√3 λ− − (1−λ)+ λ=0,解得λ= ;
2 2 2 2
(2)
由(1)知,⃗m=(√3,−1,1)是平面BMD的一个法向量,
同理可求平面EMD的一个法向量为⃗n=(0,1,0),
⃗m⋅⃗n −1 √5
cos⟨⃗m,⃗n⟩= = =− ,即随着λ值的变化,二面角B−MD−E的大小为定值.
|⃗m||⃗n| √5 5
2√5 2√5
且sin⟨⃗m,⃗n⟩=√1−cos2⟨⃗m,⃗n⟩= ,所以二面角B−MD−E的正弦值为 .
5 5
27.(2023春·湖北武汉·高一校考期末)如图,四棱台ABCD−A B C D 中,上、下底面均是正方形,
1 1 1 1
且侧面是全等的等腰梯形,AB=2A B =4,E、F分别为DC、BC的中点,上下底面中心的连线O O垂
1 1 1
直于上下底面,且O O与侧棱所在直线所成的角为45°.
1
学科网(北京)股份有限公司(1)求证:BD ∥平面C EF;
1 1
3√22
(2)线段BF上是否存在点M,使得直线A M与平面C EF所成的角的正弦值为 ,若存在,求出线段
1 1 22
BM的长;若不存在,请说明理由.
【解题思路】(1)作出辅助线,得到四边形CED C 为平行四边形,从而得到MF是△BCD 的中位线,
1 1 1
得到线线平行,证明出线面平行;
(2)法一:作出辅助线,建立空间直角坐标系,写出点到坐标,设出M(m,2,0),0≤m≤2,利用空间向
量线面角的求解公式列出方程,求出答案;
法二:作出辅助线,得到平面C EF//平面BDD B ,得到直线A M与平面C EF所成的角即为A M与
1 1 1 1 1 1
A D A S √44
平面BDD B 所成的角,设BM=x,由三角形相似得到 1 1= 1 ,表达出SM= x,
1 1 BM SM 6
√44 √44
A M=A S+SM= + x,进而表达出BR=1,MR=x−1或1−x,故W M2=(x−1) 2+32,从而
1 1 3 6
列出方程,求出x,得到答案.
【解答过程】(1)连接D C,与C E相交于点M,连接D E,
1 1 1
因为AB=2A B =4,E为DC的中点,
1 1
所以CE=C D 且CE//C D ,故四边形CED C 为平行四边形,
1 1 1 1 1 1
故CM=D M,
1
又因为F为BC的中点,所以MF是△BCD 的中位线,
1
故MF//BD ,
1
因为MF⊂平面C EF,BD ⊄平面C EF,
1 1 1
所以BD ∥平面C EF;
1 1
学科网(北京)股份有限公司(2)法一:存在,线段BM的长为1,理由如下:
取AB的中点Q,连接OQ,以O为坐标原点,分别以OQ,OF,OO 为x,y,z轴,建立空间直角坐标系,
1
连接AO,A O ,过点A 作A W⊥AO于点W,因为AB=2A B =4,
1 1 1 1 1 1
则AO=2√2,A O =WO=√2,AW =2√2−√2=√2,
1 1
因为O O与侧棱所在直线所成的角为45°,所以∠A AW =45°,A W =AW =√2,
1 1 1
所以A (1,−1,√2),C (−1,1,√2),E(−2,0,0),F(0,2,0),
1 1
设M(m,2,0),0≤m≤2,⃗A M=(m−1,3,√2),
1
设平面C EF的法向量为⃗n=(x,y,z),
1
则¿,
令x=1得y=−1,z=0,
则⃗n=(1,−1,0),
设直线A M与平面C EF所成的角的大小为θ,
1 1
|(m−1,3,√2)⋅(1,−1,0)| |m−4| 3√22
则sinθ=|cos⟨⃗A M,⃗n⟩|= = = ,
1 √(m−1) 2+9+2⋅√1+1 √2⋅ √(m−1) 2+11 22
解得m=1或34(舍去),
故M(1,2,0),线段BM的长为2−1=1.
法二:存在,线段BM的长为1,理由如下:
学科网(北京)股份有限公司连接B D ,显然过点O ,连接BD,过点O,
1 1 1
因为E、F分别为DC、BC的中点,所以EF//BD,
因为EF⊄平面BDD B ,BD⊂平面BDD B ,
1 1 1 1
所以EF//平面BDD B ,
1 1
由(1)知:DE=D C 且DE//D C ,故四边形DEC D 为平行四边形,
1 1 1 1 1 1
故C E//D D,
1 1
因为C E⊄平面BDD B ,D D⊂平面BDD B ,
1 1 1 1 1 1
所以C E//平面BDD B ,
1 1 1
因为C E∩EF=E,C E,EF⊂平面C EF,
1 1 1
所以平面C EF//平面BDD B ,
1 1 1
故直线A M与平面C EF所成的角即为A M与平面BDD B 所成的角,
1 1 1 1 1
设A M∩BD =S,连接O S,A O ,
1 1 1 1 1
因为O O垂直于上下底面,上、下底面均是正方形,
1
所以A O ⊥平面BDD B ,故∠A SO 即为A M与平面BDD B 所成的角,
1 1 1 1 1 1 1 1 1
连接AO,过点A 作A W⊥AO于点W,因为AB=2A B =4,
1 1 1 1
则AO=2√2,A O =WO=√2,AW =2√2−√2=√2,
1 1
因为O O与侧棱所在直线所成的角为45°,所以∠A AW =45°,A W =AW =√2,
1 1 1
A O √2 3√22 √44
sin∠A SO = 1 1= = ,解得A S= ,
1 1 A S A S 22 1 3
1 1
因为A D //BF,所以△A D S~ △MBS,设BM=x,
1 1 1 1
√44
A D A S √44
则 1 1= 1 ,即2 3 ,解得SM= x,
BM SM = 6
x SM
√44 √44
故A M=A S+SM= + x,
1 1 3 6
过点W作WR⊥BC于点R,则BR=1,MR=x−1或1−x,
故W M2=(x−1) 2+32,
2
由勾股定理得A W2+W M2=A M2 ,即(√2) 2+(x−1) 2+32= (√44 + √44 x ) ,
1 1 3 6
学科网(北京)股份有限公司解得x=1,
故线段BM的长为2−1=1.
28.(2023春·江苏宿迁·高二统考期末)如图(1)所示,在△ABC中,AB=4√3,BC=2√3,
∠B=60°,DE垂直平分AB.现将△ADE沿DE折起,使得二面角A−DE−B大小为60°,得到如图
(2)所示的空间几何体(折叠后点A记作点P)
(1)求点D到面PEC的距离;
(2)求四棱锥P−BCED外接球的体积;
(3)点Q为一动点,满足⃗PQ=λ⃗PE (0<λ<1),当直线BQ与平面PEC所成角最大时,试确定点Q的位置.
【解题思路】(1)由已知可证得平面PDB⊥平面BCDE,取BD中点O ,连接PO,OC ,则有
OB,OC,OP两两垂直,所以以{⃗OB,⃗OC,⃗OP}为正交基底建立如图所示的空间直角坐标系O−xyz,然后
利用空间向量求解,
(2)连接BE,则四边形BCED的外接圆圆心在BE的中点O ,△PBD外接圆的圆心为PO的三等分点O ,
1 2
过点圆心O ,O 分别作两面垂线,则垂线交点即为球心M,连接BM,求出其长度可得外接球的半径,
1 2
从而可求出外接球的体积,
(3)由⃗PQ=λ⃗PE (0<λ<1),表示出点Q的坐标,然后利用空间向量表示出直线BQ与平面PEC所成角
的正弦值,求出其最大值可得答案.
π π
【解答过程】(1)由AB=4√3,BC=2√3,∠B= ,得AC=6 ,∠C= ,DC=BC
3 2
学科网(北京)股份有限公司因为DE垂直平分AB,
所以DE⊥PD,DE⊥BD,
所以∠PDB为平面PDE与平面BCED的二面角的平面角,
π
所以∠PDB= ,PD=BD,所以△PDB为等边三角形,
3
取BD中点O ,连接PO,OC ,所以PO⊥BD,OC⊥BD,
因为PD∩BD=D,PD,BD⊂平面PDB,
所以DE⊥平面PDB,
因为DE⊂平面BCDE,
所以平面PDB⊥平面BCDE,
因为PO⊥BD,OC⊥BD
所以∠POC为二面角P−BD−C的平面角,
所以PO⊥OC,
以{⃗OB,⃗OC,⃗OP}为正交基底建立如图所示的空间直角坐标系O−xyz,
则B(√3,0,0),C(0,0,3),P(0,0,3),D(−√3,0,0),E(−√3,2,0),
所以⃗PC=(0,3,−3),⃗PE=(−√3,2,−3),
设平面PEC的一个法向量为⃗n=(x,y,z) ,则
√3
¿,令z=1,则⃗n=(− ,1,1)
3
又⃗DP=(√3,0,3),
√3
|− ×√3+3|
|⃗PD·⃗n| 3 2 2√21
所以点D到面PEC的距离d= = = =
;
|⃗n| √ 1 √7 7
1+1+
3 3
(2)连接BE,由BD⊥DE,BC⊥CE,则四边形BCED的外接圆圆心在BE的中点O ,
1
△PBD为正三角形,则△PBD外接圆的圆心为PO的三等分点O ,
2
过点圆心O ,O 分别作两面垂线,则垂线交点即为球心M,
1 2
如图所示,连接BM,则BM即球的半径.
在Rt△ADE中,AD=2√3,∠DAE=30°,∠ADE=90°,
√3
则DE=ADtan30°=2√3× =2,
3
1 1 √3
在Rt△MO B中,MO =OO = PO= × ×2√3=1,
1 1 2 3 3 2
学科网(北京)股份有限公司1 1 1
BO = BE= √BD2+DE2= ×√(2√3) 2+22=2
1 2 2 2
所以由勾股定理得MB=√MO2+BO2=√12+22=√5,
1 1
4 4 20√5
则球的体积V = πR3= π(√5) 3= π ;
3 3 3
(3)设Q(x ,y ,z ),由⃗PQ=λ⃗PE (0<λ<1)得(x ,y ,z −3)=λ(−√3,2,−3),
1 1 1 1 1 1
所以¿,得Q(−√3λ,2λ,3−3λ), ,
所以⃗BQ=(−√3λ−√3,2λ,3−3λ),
[ π ]
设直线BQ与平面PEC所成角为θ(θ∈ 0, ),
2
| ⃗BQ⋅⃗n | 4
sinθ= =
则 |⃗BQ||⃗n| √7
√ (−√3λ−√3) 2+(2λ) 2+(3−3λ) 2
3
2√21 2√21
= =
7√4λ2−3λ+3 √ 3 2 39
7 4(λ− ) +
8 16
3 8√91
所以当λ= 时,sinθ取得最大值 ,
8 91
此时直线BQ与平面PEC所成角最大,
3
即当⃗PQ= ⃗PE时,直线BQ与平面PEC所成角最大.
8
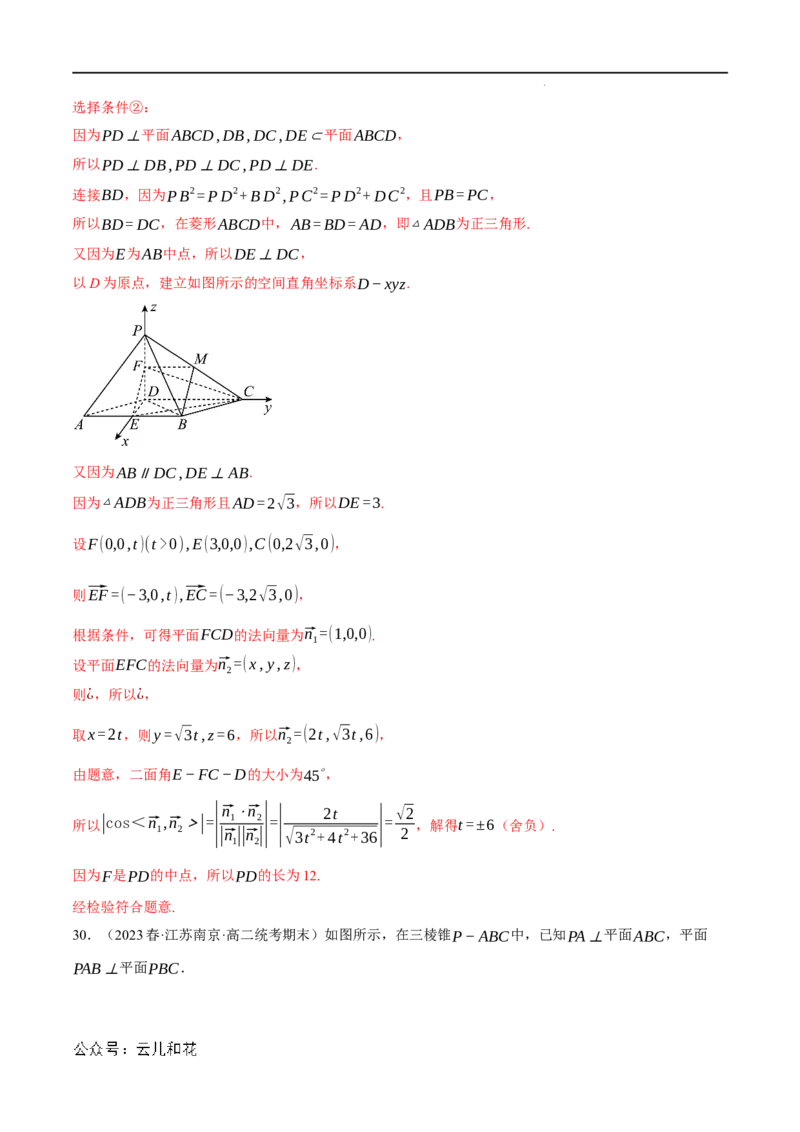
学科网(北京)股份有限公司29.(2023·广东广州·广州市校考模拟预测)如图,在四棱锥P−ABCD中,PD⊥平面ABCD,底面
ABCD为菱形,E,F分别为AB,PD的中点.
(1)求证:EF //平面PBC;
(2)若AD=2√3,二面角E−FC−D的大小为45∘,再从条件①、条件②这两个条件中选择一个作为已知.求
PD的长.
条件①:DE⊥PC;条件②:PB=PC.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解题思路】(1)由线面平行的判定定理证明即可;
(2)由题意可建立以D为坐标原点的空间直角坐标系D−xyz,设F(0,0,t)(t>0),分别求出平面EFC和
平面FCD的法向量,由二面角公式代入解方程即可求出t,进而求出PD的长.
【解答过程】(1)取PC中点M,连接FM,BM.
1
在△PCD中,M,F分别为PC,PD的中点,所以MF//DC,MF= DC.
2
1
在菱形ABCD中,因为AB//DC,BE= DC,
2
所以BE//MF,BE=MF.
学科网(北京)股份有限公司所以四边形BEMF为平行四边形,所以EF//BM.
又因为EF⊄平面PBC,BM⊂平面PBC,
所以EF //平面PBC.
(2)选择条件①:
因为PD⊥平面ABCD,DE,DC⊂平面ABCD,
所以PD⊥DE,PD⊥DC.
又因为DE⊥PC,PD∩PC=P,PD,PC⊂平面PCD,
所以DE⊥平面PCD,又DC⊂平面PCD,
所以DE⊥DC,
以D为原点,建立如图所示的空间直角坐标系D−xyz.
连接BD,因为AB∥DC,所以DE⊥AB,又E为AB中点,所以AD=DB,
所以△ADB为正三角形.因为AD=2√3,所以DE=3.
设F(0,0,t)(t>0),E(3,0,0),C(0,2√3,0),
则⃗EF=(−3,0,t),⃗EC=(−3,2√3,0),
根据条件,可得平面FCD的法向量为⃗n =(1,0,0).
1
设平面EFC的法向量为⃗n =(x,y,z),
2
则¿,所以¿,
取x=2t,则y=√3t,z=6,所以⃗n =(2t,√3t,6),
2
由题意,二面角E−FC−D的大小为45∘,
|⃗n ⋅⃗n | | 2t | √2
所以|cos<⃗n ,⃗n >|= 1 2 = = ,解得t=±6(舍负).
1 2 |⃗n||⃗n | √3t2+4t2+36 2
1 2
因为F是PD的中点,所以PD的长为12.
经检验符合题意.
学科网(北京)股份有限公司选择条件②:
因为PD⊥平面ABCD,DB,DC,DE⊂平面ABCD,
所以PD⊥DB,PD⊥DC,PD⊥DE.
连接BD,因为PB2=PD2+BD2,PC2=PD2+DC2,且PB=PC,
所以BD=DC,在菱形ABCD中,AB=BD=AD,即△ADB为正三角形.
又因为E为AB中点,所以DE⊥DC,
以D为原点,建立如图所示的空间直角坐标系D−xyz.
又因为AB∥DC,DE⊥AB.
因为△ADB为正三角形且AD=2√3,所以DE=3.
设F(0,0,t)(t>0),E(3,0,0),C(0,2√3,0),
则⃗EF=(−3,0,t),⃗EC=(−3,2√3,0),
根据条件,可得平面FCD的法向量为⃗n =(1,0,0).
1
设平面EFC的法向量为⃗n =(x,y,z),
2
则¿,所以¿,
取x=2t,则y=√3t,z=6,所以⃗n =(2t,√3t,6),
2
由题意,二面角E−FC−D的大小为45∘,
|⃗n ⋅⃗n | | 2t | √2
所以|cos<⃗n ,⃗n >|= 1 2 = = ,解得t=±6(舍负).
1 2 |⃗n||⃗n | √3t2+4t2+36 2
1 2
因为F是PD的中点,所以PD的长为12.
经检验符合题意.
30.(2023春·江苏南京·高二统考期末)如图所示,在三棱锥P−ABC中,已知PA⊥平面ABC,平面
PAB⊥平面PBC.
学科网(北京)股份有限公司(1)证明:BC⊥平面PAB;
(2)若PA=AB=6,BC=3,在线段PC上(不含端点),是否存在点D,使得二面角B−AD−C的余弦值
√10
为 ,若存在,确定点D的位置;若不存在,说明理由.
5
【解题思路】(1)过点A作AE⊥PB于点E,由面面垂直性质定理可得AE⊥平面PBC,由此证明
AE⊥BC,再证明PA⊥BC,根据线面垂直判定定理证明结论;
(2)建立空间直角坐标系,求平面ACD,平面ABD的法向量,利用向量夹角公式求法向量夹角,由条件
列方程确定点D的位置;
【解答过程】(1)过点A作AE⊥PB于点E,
因为平面PAB⊥平面PBC,且平面PAB∩平面PBC=PB,AE⊂平面PAB,
所以AE⊥平面PBC,
又BC⊂平面PBC,所以AE⊥BC,
又PA⊥平面ABC,BC⊂平面PBC,
所以PA⊥BC,
又因为AE∩PA=A,AE,PA⊂平面PAB,
所以BC⊥平面PAB.
√10
(2)假设在线段PC上(不含端点),存在点D,使得二面角B−AD−C的余弦值为 ,
5
学科网(北京)股份有限公司以B为原点,分别以⃗BC、⃗BA为x轴,y轴正方向,建立如图所示空间直角坐标系,
则A(0,6,0),B(0,0,0),C(3,0,0),P(0,6,6),
⃗AC=(3,−6,0),⃗AP=(0,0,6),⃗PC=(3,−6,−6),⃗BA=(0,6,0),
设平面ACD的一个法向量为⃗m=(x,y,z),
¿即¿取x=2,y=1,z=0,
所以⃗m=(2,1,0)为平面ACD的一个法向量,
因为D在线段PC上(不含端点),所以可设⃗PD=λ⃗PC=(3λ,−6λ,−6λ),0<λ<1,
所以⃗AD=⃗AP+⃗PD=(3λ,−6λ,6−6λ),
设平面ABD的一个法向量为⃗n=(x,y,z),
¿即¿,
取x=2λ−2,y=0,z=λ,
所以⃗n=(2λ−2,0,λ)为平面ABD的一个法向量,
2×(2λ−2)+1×0+0×λ
cos⟨⃗m,⃗n⟩= ,又0<λ<1,
√5×√(2λ−2) 2+λ2
2×(2λ−2) √10
由已知可得
=−
√5×√(2λ−2) 2+λ2 5
2
解得λ= 或λ=2(舍去),
3
√10
所以,存在点D,使得二面角B−AD−C的余弦值为 ,
5
此时D是PC上靠近C的三等分点.
学科网(北京)股份有限公司