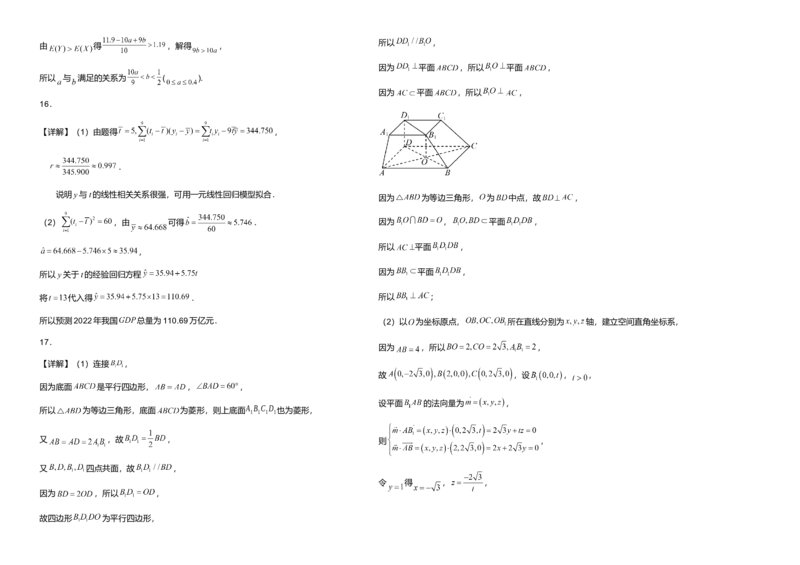文档内容
腾冲市第八中学2024—2025学年下学期高二第一次月考 A. B. C.2 D.
数学试题
6.为促进消费,某商场推出抽奖游戏:甲、乙两袋中装有大小、材质均相同的球,其中甲袋中为4个黑球和6
个白球,乙袋中为3个黑球和5个白球.顾客要从甲袋中随机取出1个球放入乙袋中,充分混合后,再从乙袋中
(考试时间:120分钟:满分:150分)
随机取出1个球,若从乙袋中取出的球是黑球,则获得100元消费券,否则获得50元消费券.则顾客获得100元
消费券的概率为( )
注意事项:
1.本卷为试题卷,考生必须在答题卡上解题作答,答案书写在答题卡相应位
A. B. C. D.
置,在试题卷、草稿纸上作答无效.选择题作答必须用2B铅笔填涂.
7.一个袋中装有大小相同的3个白球和3个黑球,若不放回地依次任取两个球,设事件 为“第一次取出白
2.考试结束后,请将答题卡交给监考教师.
球”,事件 为“第二次取出黑球”,则在 发生的条件下 发生的概率为 ( )
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项
A. B. C. D.
中,只有一项是符合题目要求的.
1.已知由样本数据 组成一个样本,可得到回归直线方程为 8.已知等差数列 满足 ,则 ( )
,且 ,则样本点 的残差为( )
A. B.1 C.0 D.
A.0.3 B.-0.3 C.1.3 D.-1.3 二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
2.某校为了丰富课后服务活动,提高学校办学水平和教育质量,开设近20门选修课供学
生自愿选择.甲、乙2名同学都对其中的合唱、足球、篮球、机器人课程感兴趣,若这2名
9.在调查中发现480名男人中有38名患有色盲,520名女人中有6名患有色盲.下列结论不正确的是( )
同学从这4门课程中各自任选一门课程参加,则不同的选法有( )
A.男人、女人中患色盲的频率分别为0.038,0.006
A.4种 B.6种 C.8种 D.16种
B.男、女患色盲的概率分别为 ,
3.设随机变量 服从两点分布,若 ,则成功概率
( )
C.男人中患色盲的比例比女人中患色盲的比例大,患色盲与性别是有关的
A.0.3 B.0.35 C.0.65 D.0.7 D.不能说明患色盲与性别是否有关
4.甲、乙、丙等6人相约到电影院看电影,恰好买到了六张连号的电影票.若甲、乙两人
10.如图,正方体 的棱长为 ,线段 上有两个动点 ,且 ,则下列结论正确的
必须相邻,则不同的坐法共有( )
是( )
A.120种 B.240种 C.360种 D.720种
A.该正方体的外接球体积为
5. 的内角 的对边分别为 , ,则
B.底面半径为 ,高为 的圆锥体能够被整体放入该正方体C.三棱锥 的体积为定值 表②
口罩等级 100等级 99等级 95等级
D.当 与 重合时,异面直线 与 所成的角为
利润/元
11.已知 为随机事件, ,则下列结论正确的有( )
(1) 表示一个口罩的利润,求 的分布列和数学期望;
A.若 为互斥事件,则 B.若 为互斥事件,则
(2)由于工厂中 工序加工质量层次为高的概率较低,工厂计划通过增加检测环节对 工序进行升级.在升级过
C.若 相互独立,则 D.若 ,则 程中,每个口罩检测成本增加了 ( )元时,相应的 工序加工层次为高的概率在原来的基础上增加了 ;
试问:若工厂升级方案后对一个口罩利润的期望有所提高,则 与 应该满足怎样的关系?
三、填空题:本题共3小题,每小题5分,共15分.
16.如图是我国2010年至2018年 总量 (单位:万亿元)的折线图.
12.在二项式 的展开式中, 系数为有理数的项的个数是 .
13.过三点 的圆的标准方程是 .
14.同时抛掷5枚均匀的硬币160次,设5枚硬币正好出现1枚正面向上,4枚反面向上
的次数为 ,则 的数学期望是 .
四、解答题:本题共5小题,共77分、解答应写出文字说明、证明过程或演算步
骤.
注:年份代码1~9分别对应年份2010~2018.
15.新冠疫情下,为了应对新冠病毒极强的传染性,每个人出门做好口罩防护工作刻不容
缓.某口罩加工厂加工口罩由 三道工序组成,每道工序之间相互独立,且每道工序 (1)由折线图看出,可用一元线性回归模型拟合y与年份代码t的关系,请用相关系数 加以说明( 精确到
0.001);
加工质量分为高和低两种层次级别, 三道工序加工的质量层次决定口罩的过滤等
级; 工序加工质量层次均为高时,口罩过滤等级为100等级(表示最低过滤效率为 (2)建立y关于t的经验回归方程(系数精确到0.01),并据此预测2022年我国 总量.
99.97%); 工序的加工质量层次为高, 工序至少有一个质量层次为低时,口罩过滤
参考数据:
等级为99等级(表示最低过滤效率为99%);其余均为95级(表示最低过滤效率为95%).
表①:表示 三道工序加工质量层次为高的概率;表②:表示加工一个口罩的利润. ,
表①
参考公式:相关系数
工序
经验回归方程 中斜率和截距的最小二乘估计公式分别为
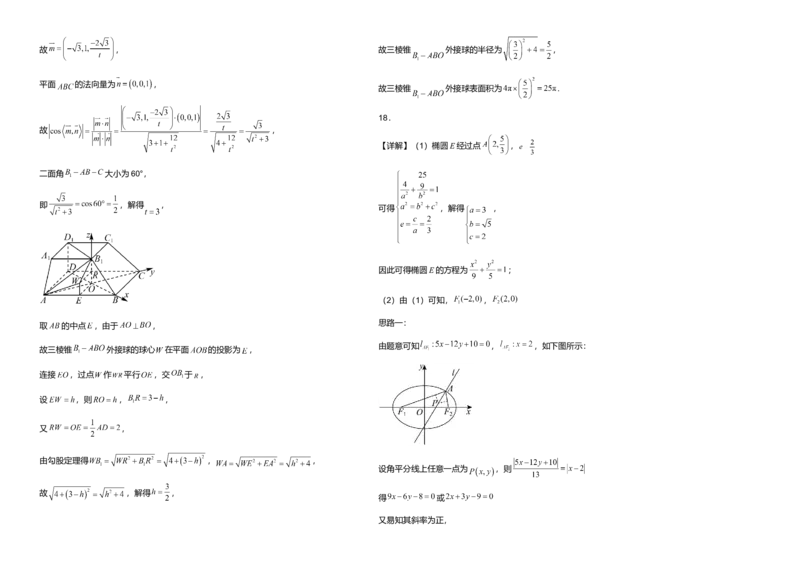
概率17.如图,在四棱台 中, 平面 .底面 是平行四边形, 题号 1 2 3 4 5 6 7 8 9 10
答案 A D C B C B D C ABD BC
, ,连接 、 ,设交点为 ,连接 .
题号 11
答案 BCD
12.6
13.
(1)证明: ; 14.
15.
(2)若 ,且二面角 大小为60°,求三棱锥 外接球的表面积.
【详解】(1) 的可能取值为 , , ,
18.已知椭圆 的左、右焦点分别为 ,离心率为 ,且经过点
; ; ;
所以 的分布列为
(1)求椭圆E的方程;
(2)求 的角平分线所在直线 的方程;
(3)在椭圆E上是否存在关于直线 对称的相异两点?若存在,请找出;若不存在,说明理
由.
19.已知 ,函数 , .
(2)设升级后一件产品的利润为 ,则 的可能取值为 , ,
(1)求曲线 在点 处的切线方程;
;
(2)证明: 存在唯一的极值点;
;
(3)若存在 ,使得 对任意 成立,求实数 的取值范围.
;
所以 ,
参考答案所以 ,
由 得 ,解得 ,
因为 平面 ,所以 平面 ,
所以 与 满足的关系为 ( ).
因为 平面 ,所以 ,
16.
【详解】(1)由题得 ,
.
说明y与t的线性相关关系很强,可用一元线性回归模型拟合.
因为 为等边三角形, 为 中点,故 ⊥ ,
(2) ,由 可得 . 因为 , 平面 ,
所以 ⊥平面 ,
,
所以y关于t的经验回归方程 因为 平面 ,
将 代入得 . 所以 ;
所以预测2022年我国 总量为110.69万亿元. (2)以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,
17.
因为 ,所以 ,
【详解】(1)连接 ,
故 ,设 , ,
因为底面 是平行四边形, , ,
设平面 的法向量为 ,
A B C D
所以 为等边三角形,底面 为菱形,则上底面 1 1 1 1也为菱形,
又 ,故 , 则 ,
又 四点共面,故 ,
令 得 , ,
因为 ,所以 ,
故四边形 为平行四边形,故 , 故三棱锥 外接球的半径为 ,
平面 的法向量为 ,
故三棱锥 外接球表面积为 .
18.
故 ,
【详解】(1)椭圆E经过点 ,
二面角 大小为60°,
即 ,解得 ,
可得 ,解得 ,
因此可得椭圆E的方程为 ;
(2)由(1)可知, ,
思路一:
取 的中点 ,由于 ⊥ ,
由题意可知 , ,如下图所示:
故三棱锥 外接球的球心 在平面 的投影为 ,
连接 ,过点 作 平行 ,交 于 ,
设 ,则 , ,
又 ,
由勾股定理得 , ,
设角平分线上任意一点为 ,则
故 ,解得 ,
得 或
又易知其斜率为正,∴ 的角平分线所在直线为
∴ ,
思路二:椭圆在点 处的切线方程为 ,
因此 ,
根据椭圆的光学性质, 的角平分线所在直线 的斜率为 ,
联立 可得 与点A重合,舍去,
所以 的角平分线所在直线 ,
故不存在满足题设条件的相异的两点.
即
19.
(3)思路一:假设存在关于直线 对称的相异两点 ,
【详解】(1)由题意知, ,
设 ,
所以 ,
又 ,
联立 可得 ,
所以曲线在点 处的切线方程为 ,即 .
∴线段 中点为 在 的角平分线上,
(2)证明:由 , ,
即 ,解得 ;
①当 时, ,则 在 上单调递增,
因此 与点A重合,舍去,故不存在满足题设条件的相异的两点. ②当 时,设 ,则 ,
思路二:假设存在关于直线 对称的相异两点 ,线段 中点
所以 ,故 在 上单调递减,
,
又 , ,
由点差法可得 ,即 ;
所以由零点存在性定理可知,存在唯一 ,使得 ,即 .所以当 时, ,即 ;当 时, ,即 ,
设 , ,则 ,
所以 在 上单调递增,在 上单调递减,
所以 在 上单调递减,
综述: 在 上单调递增,在 上单调递减,存在唯一 ,使得
.
故 ,
故 存在唯一的极值点.
当 时, , ;当 时, , ,
(3)由(2)可知, 在 上单调递增,在 上单调递减,
故 ,
故 在 上单调递减,在 上单调递增,
因为 ,所以 ,
所以 ,所以 .
由题意知, ,
故 的取值范围为 .
即 ,
化简得 , ,
设 , ,
由题存在 ,使得 ,
所以 , .
又