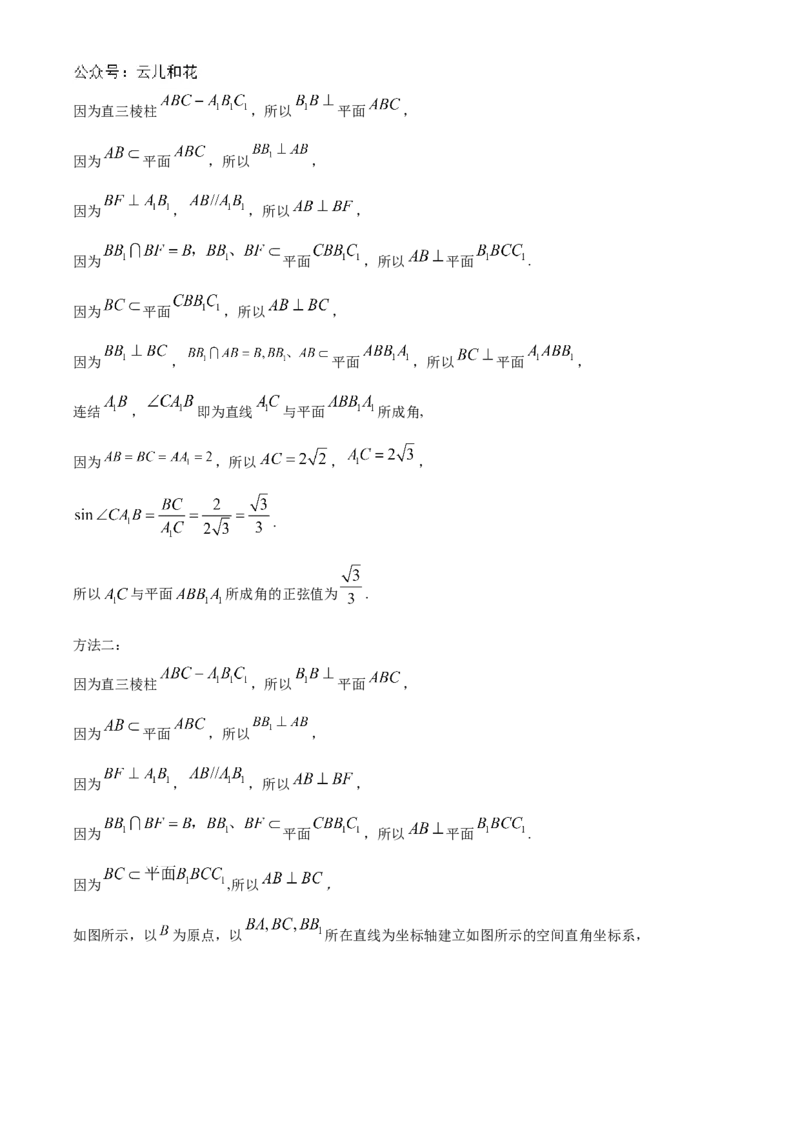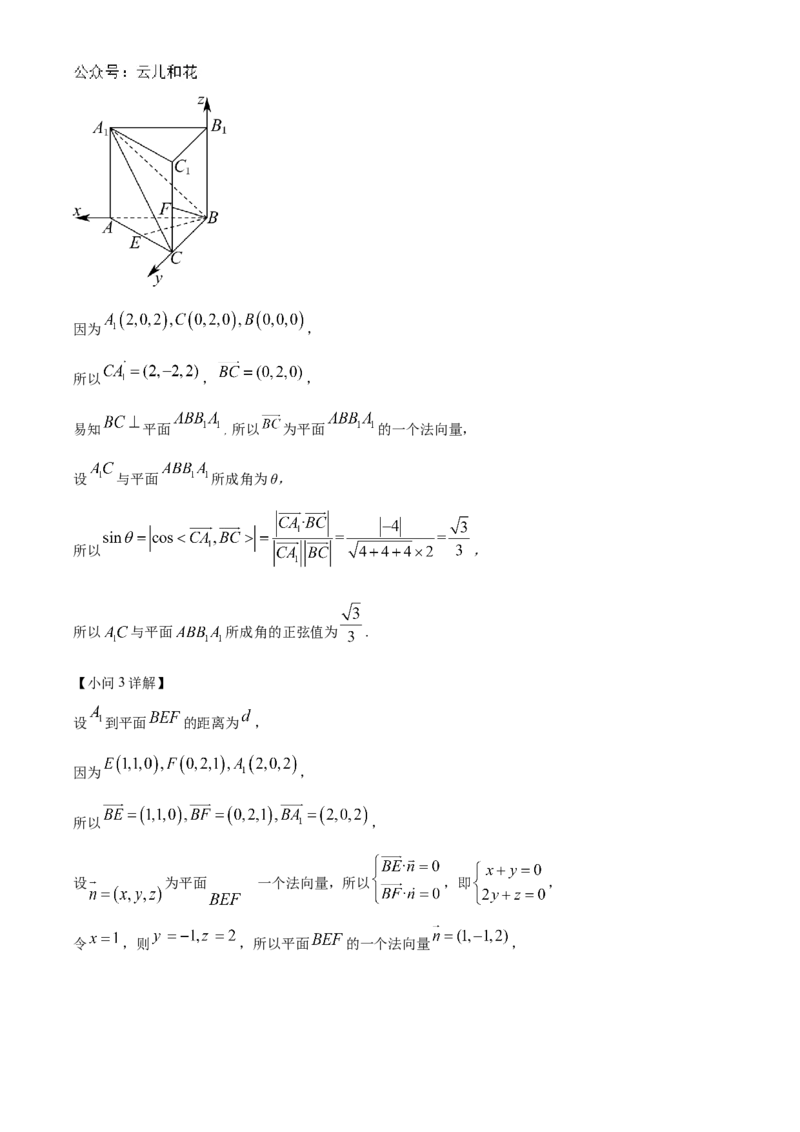文档内容
2024-2025 学年度第一学期高二数学 10 月月考
(2024.10)
班级______姓名______学号______
一、选择题(本大题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符
合题目要求的一项.)
1. 已知点 ,则点 关于 轴的对称点的坐标为( )
A. B. C. D.
【答案】D
【解析】
【分析】关于 轴对称,则 坐标值不变, 坐标变为互为相反数即可.
【详解】解:因为关于 轴对称,则 坐标值不变, 坐标变为互为相反数
所以,点 关于 轴的对称点的坐标为
故选:D.
2. 已知向量 , ,且 ,那么 ( )
A. B. 6 C. 9 D. 18
【答案】A
【解析】
【分析】根据空间向量共线的充要条件求出 的值,然后代入模的计算公式即可求解.
【详解】因为 ,且向量 , ,
所以 ,解得: ,
所以 ,
故选:A.
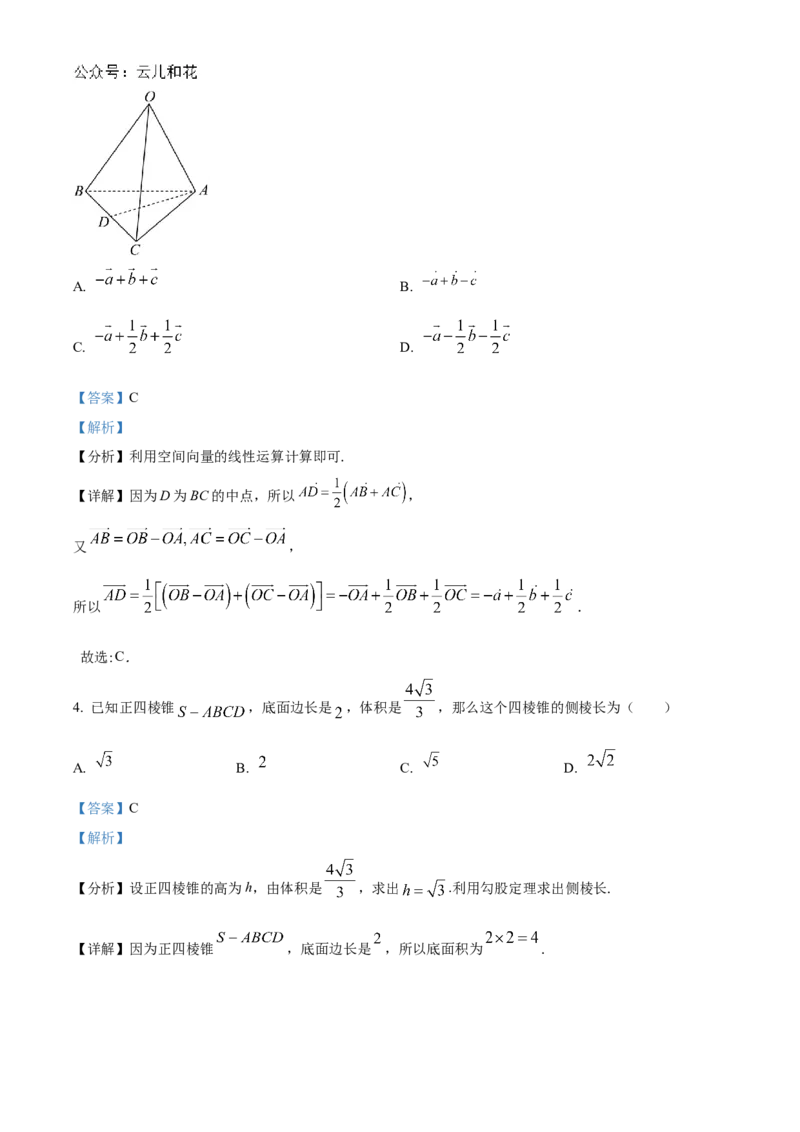
3. 如图,在三棱锥O-ABC中,D是BC的中点,若 , , ,则 等于( )A. B.
C. D.
【答案】C
【解析】
【分析】利用空间向量的线性运算计算即可.
【详解】因为D为BC的中点,所以 ,
又 ,
所以 .
故选:C.
4. 已知正四棱锥 ,底面边长是 ,体积是 ,那么这个四棱锥的侧棱长为( )
A. B. C. D.
【答案】C
【解析】
【分析】设正四棱锥的高为h,由体积是 ,求出 .利用勾股定理求出侧棱长.
【详解】因为正四棱锥 ,底面边长是 ,所以底面积为 .设正四棱锥的高为h,由 ,所以 .
所以侧棱长为 .
即侧棱长为 .
故选:C
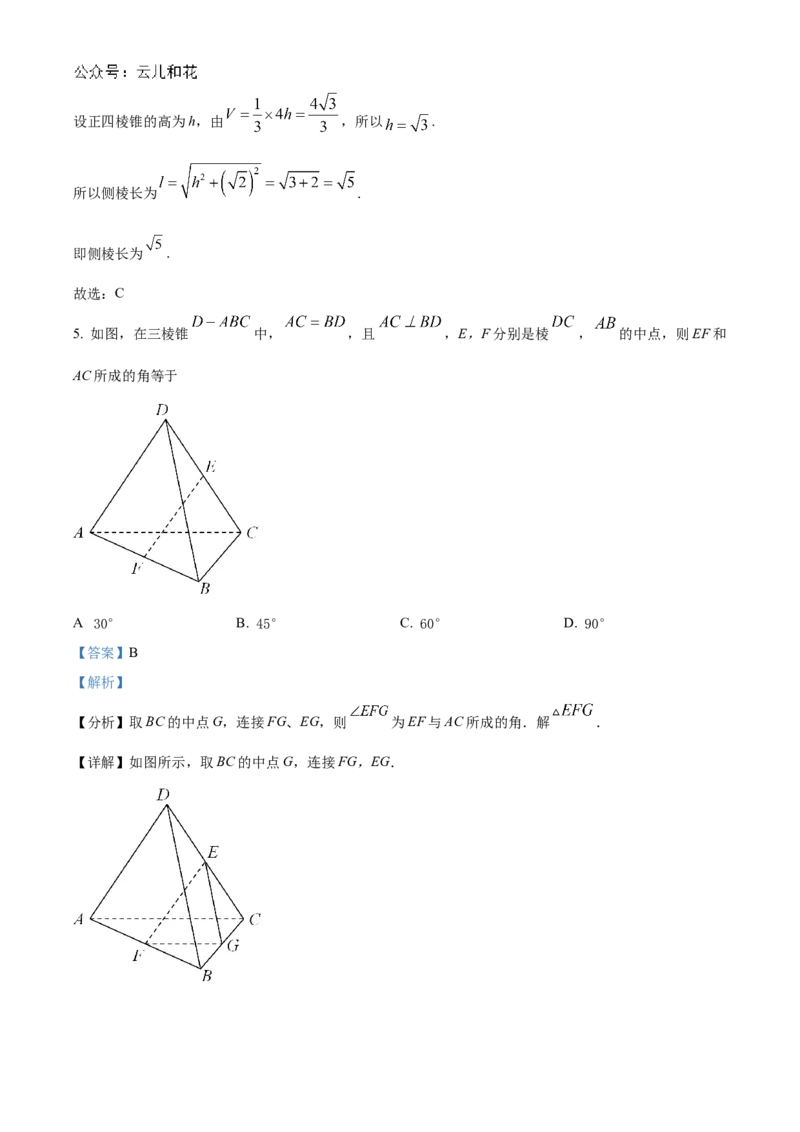
5. 如图,在三棱锥 中, ,且 ,E,F分别是棱 , 的中点,则EF和
AC所成的角等于
.
A 30° B. 45° C. 60° D. 90°
【答案】B
【解析】
【分析】取BC的中点G,连接FG、EG,则 为EF与AC所成的角.解 .
【详解】如图所示,取BC的中点G,连接FG,EG.的
,F分别是CD,AB 中点,
, ,
且 , .
为EF与AC所成的角.
又 , .
又 , , ,
为等腰直角三角形,
,即EF与AC所成的角为45°.
故选:B.
【点睛】本题主要考查异面直线所成的角,找角证角求角,主要是通过平移将空间角转化为平面角,再解
三角形,属于基础题.
6. 已知 是两条不重合的直线, , , 是三个两两不重合的平面,给出下列四个命题:
①若 则 ;
②若 则 ;
③若 则 ;
④若 是异面直线, 则 .其中真命题是( )
A. ①和② B. ①和③ C. ③和④ D. ①和④
【答案】D
【解析】
【分析】由题意逐一考查所给命题的真假即可确定真命题的编号.
【详解】逐一考查所给的命题:
①由线面垂直的性质定理可得若 则α//β,该命题正确;②如图所示的正方体 中,取平面 分别为平面 ,满足
但是不满足α//β,该命题错误;
③如图所示的正方体 中,取平面 分别为平面 ,
直线 分别为 ,满足 但是不满足α//β,该命题错误;
④若 是异面直线, 由面面平行的性质定理易知α//β,该命题正确;
综上可得,真命题是①和④
本题选择D选项.
【点睛】本题考查了空间几何体的线面位置关系判定与证明:
(1)对于异面直线的判定要熟记异面直线的概念:把既不平行也不相交的两条直线称为异面直线;
(2)对于线面位置关系的判定中,熟记线面平行与垂直、面面平行与垂直的定理是关键.
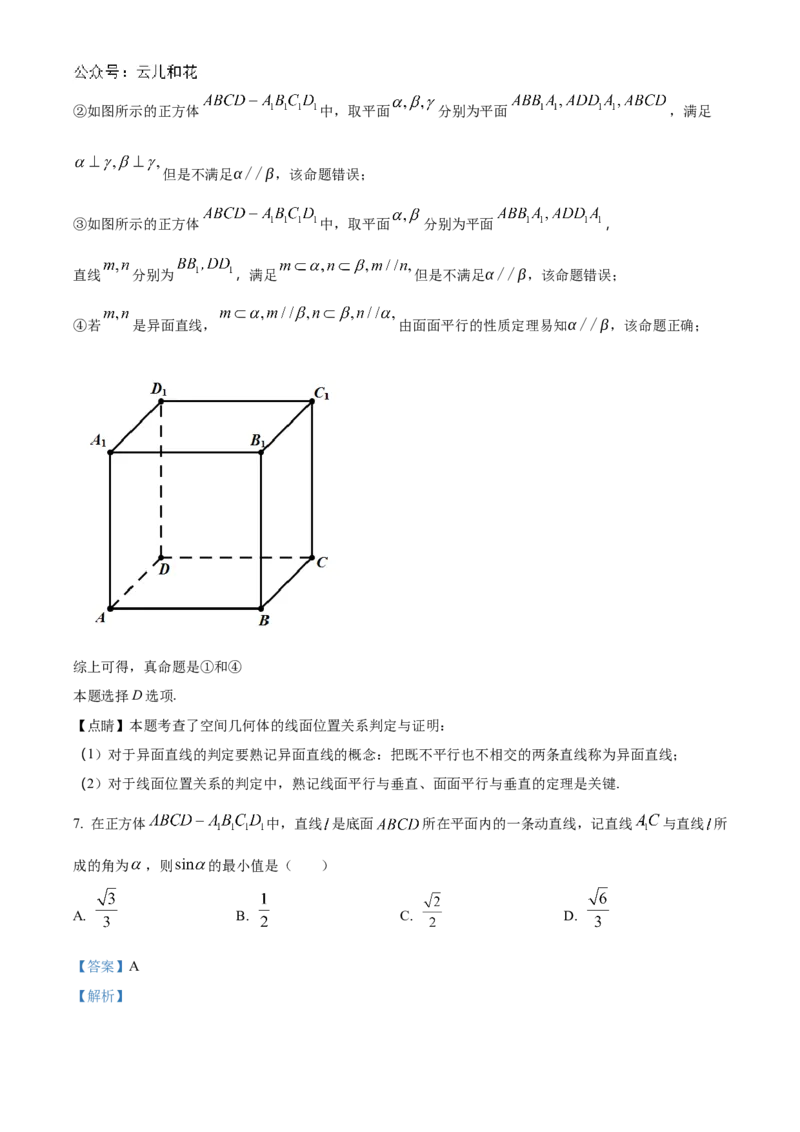
7. 在正方体 中,直线 是底面 所在平面内的一条动直线,记直线 与直线 所
成的角为 ,则 的最小值是( )
A. B. C. D.
【答案】A
【解析】【分析】过 作 的平行线,过 作该平行线的垂线,垂足为 ,则 , ,
根据 可求出结果.
【详解】如图:过 作 的平行线,过 作该平行线的垂线,垂足为 ,
则 ,所以 ,
设正方体的棱长为 ,则 , ,
所以 ,当且仅当 与 重合时,取得等号,
所以 的最小值是 .
故选: .
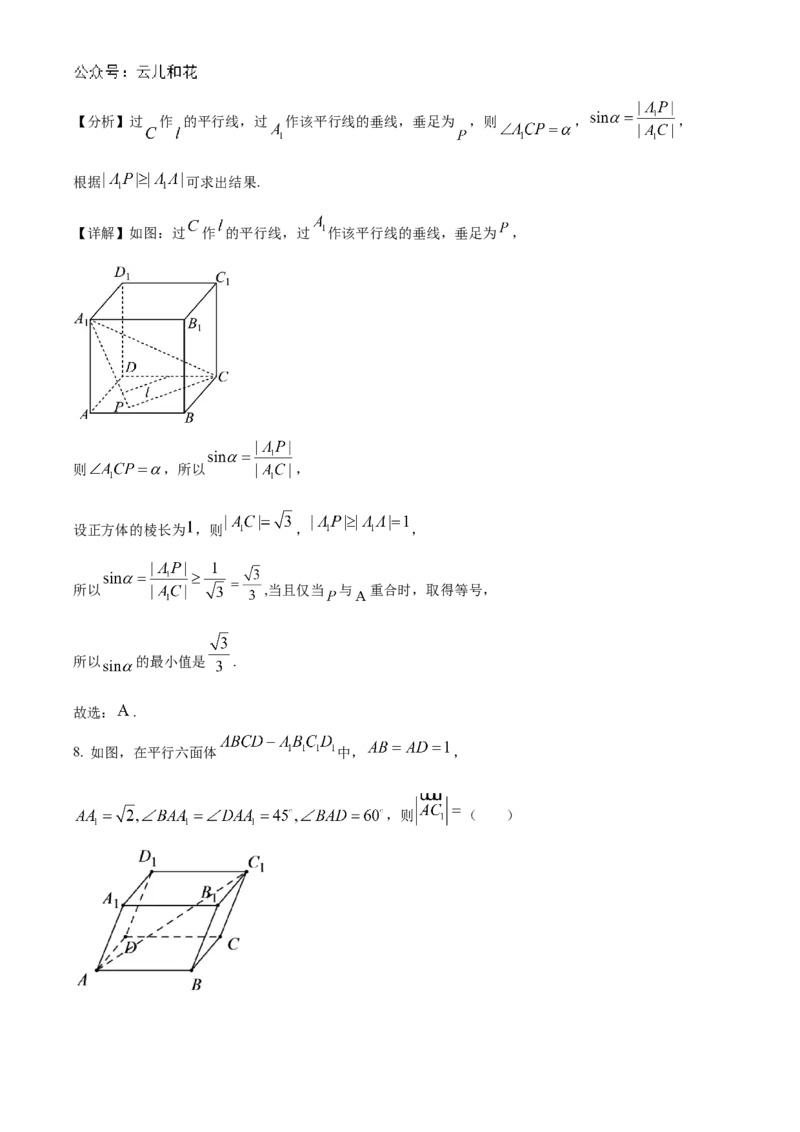
8. 如图,在平行六面体 中, ,
,则 ( )A. 1 B. C. 9 D. 3
【答案】D
【解析】
【分析】根据图形,利用向量的加法法则得到 ,
再利用 求 的模长.
【详解】在平行六面体 中,
有 , ,
由题知, , , , ,
所以 , , 与 的夹角为 ,
与 的夹角为 , 与 的夹角为 ,
所以
.
所以 .
故选:D.
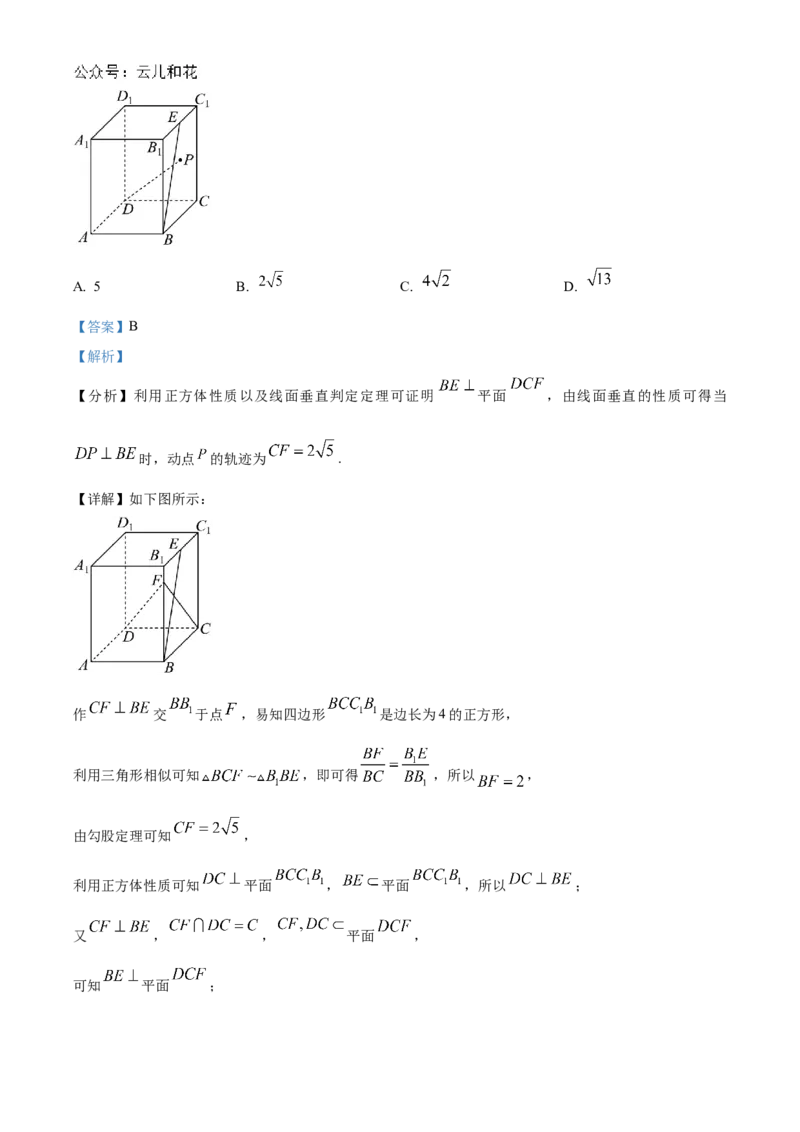
9. 如图,在长方体 中, 为棱 的中点, 为四边形
内(含边界)的一个动点.且 ,则动点 的轨迹长度为( )A. 5 B. C. D.
【答案】B
【解析】
【分析】利用正方体性质以及线面垂直判定定理可证明 平面 ,由线面垂直的性质可得当
时,动点 的轨迹为 .
【详解】如下图所示:
作 交 于点 ,易知四边形 是边长为4的正方形,
利用三角形相似可知 ,即可得 ,所以 ,
由勾股定理可知 ,
利用正方体性质可知 平面 , 平面 ,所以 ;
又 , , 平面 ,
可知 平面 ;由 可知 平面 ,又 为四边形 内(含边界)的一个动点,
所以动点 的轨迹为平面 与四边形 的交线,即为 ,
因此可得动点 的轨迹长度为 .
故选:B
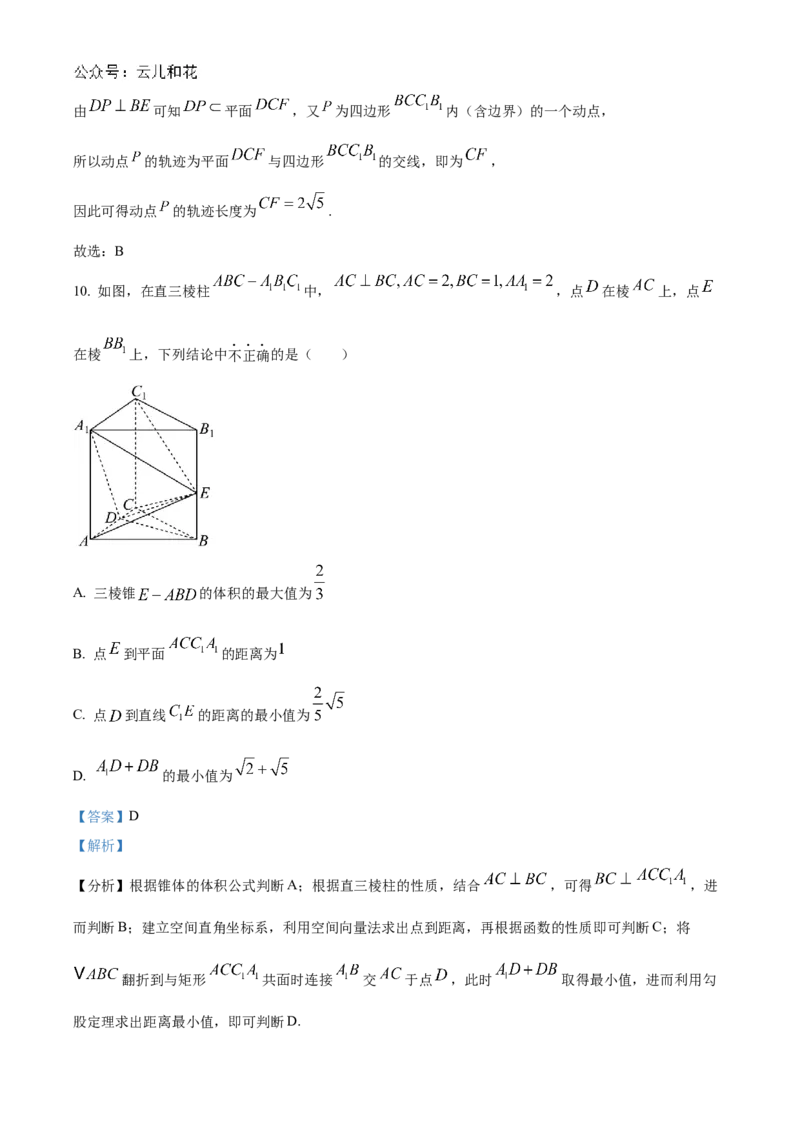
10. 如图,在直三棱柱 中, ,点 在棱 上,点
在棱 上,下列结论中不正确的是( )
A. 三棱锥 的体积的最大值为
B. 点 到平面 的距离为
C. 点 到直线 的距离的最小值为
D. 的最小值为
【答案】D
【解析】
【分析】根据锥体的体积公式判断A;根据直三棱柱的性质,结合 ,可得 ,进
而判断B;建立空间直角坐标系,利用空间向量法求出点到距离,再根据函数的性质即可判断C;将
翻折到与矩形 共面时连接 交 于点 ,此时 取得最小值,进而利用勾
股定理求出距离最小值,即可判断D.【详解】在直三棱柱 中, 平面 ,
对于A:因为点 在棱 上, ,所以 ,
又 , ,点 在棱 上,
所以 , ,
所以 ,
当且仅当 在 点、 在 点时取等号,故①正确;
对于B:在直三棱柱 中, ,
则 ,又点 在棱 上,
所以点 到平面 的距离,即为 ,故B正确;
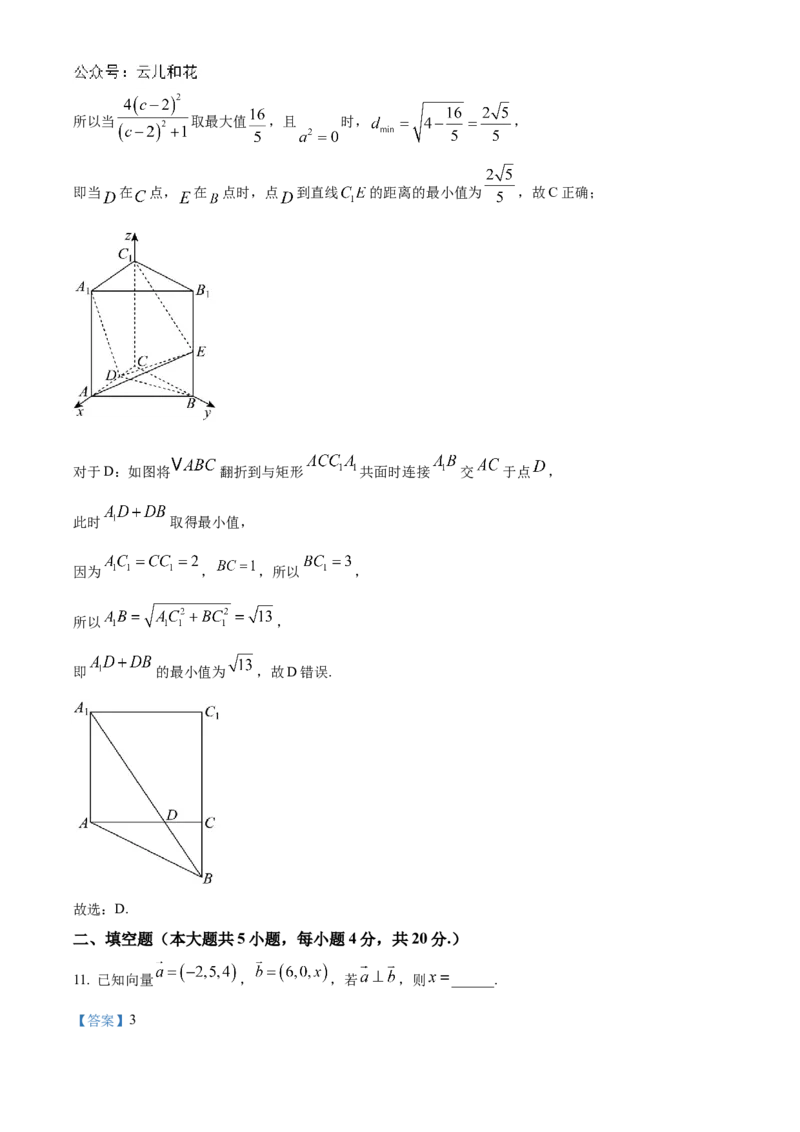
对于C:如图建立空间直角坐标系,设 , , ,
,所以 , ,
所以点 到直线 的距离为
,
当 时, ,
当 时, ,即 ,
则 ,即 ,所以当 取最大值 ,且 时, ,
即当 在 点, 在 点时,点 到直线 的距离的最小值为 ,故C正确;
对于D:如图将 翻折到与矩形 共面时连接 交 于点 ,
此时 取得最小值,
因为 , ,所以 ,
所以 ,
即 的最小值为 ,故D错误.
故选:D.
二、填空题(本大题共5小题,每小题4分,共20分.)
11. 已知向量 , ,若 ,则 ______.
【答案】3【解析】
【分析】根据空间向量数量积的坐标表示计算即可.
【详解】因为 , , ,
所以 ,解得 .
故答案为:3.
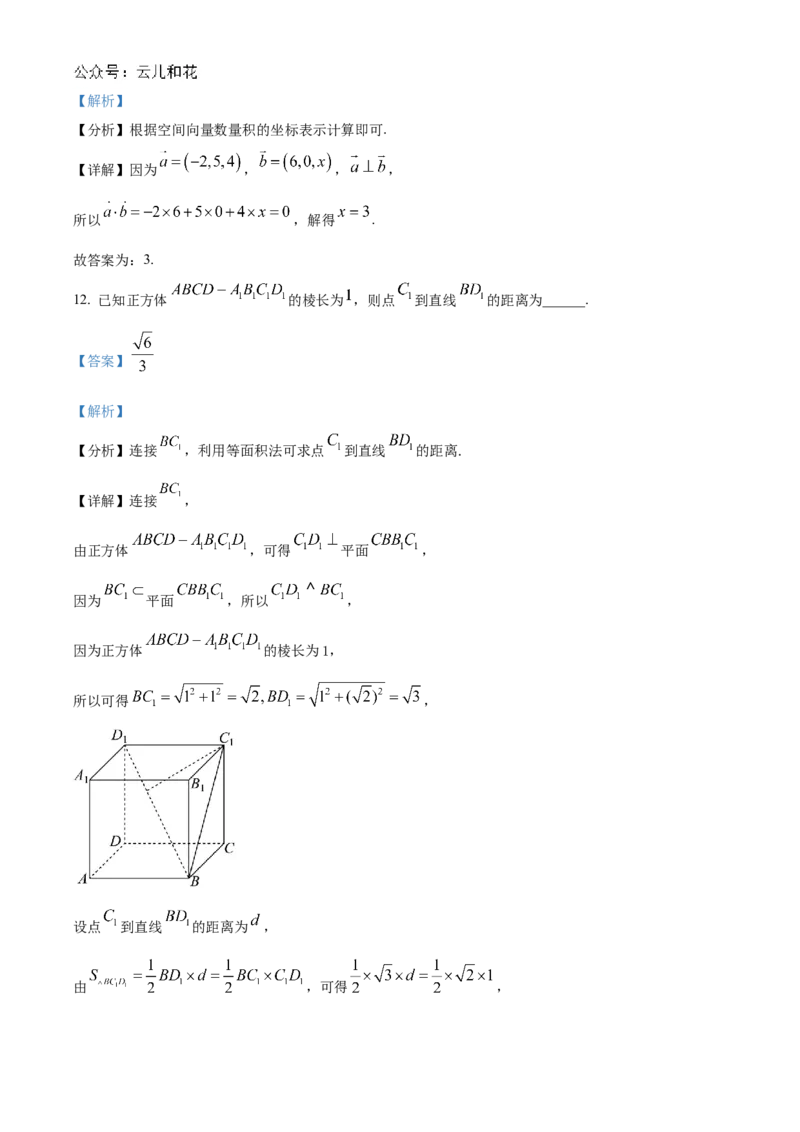
12. 已知正方体 的棱长为 ,则点 到直线 的距离为______.
【答案】
【解析】
【分析】连接 ,利用等面积法可求点 到直线 的距离.
【详解】连接 ,
由正方体 ,可得 平面 ,
因为 平面 ,所以 ,
因为正方体 的棱长为1,
所以可得 ,
设点 到直线 的距离为 ,
由 ,可得 ,解得 ,所以点 到直线 的距离为 .
故答案为: .
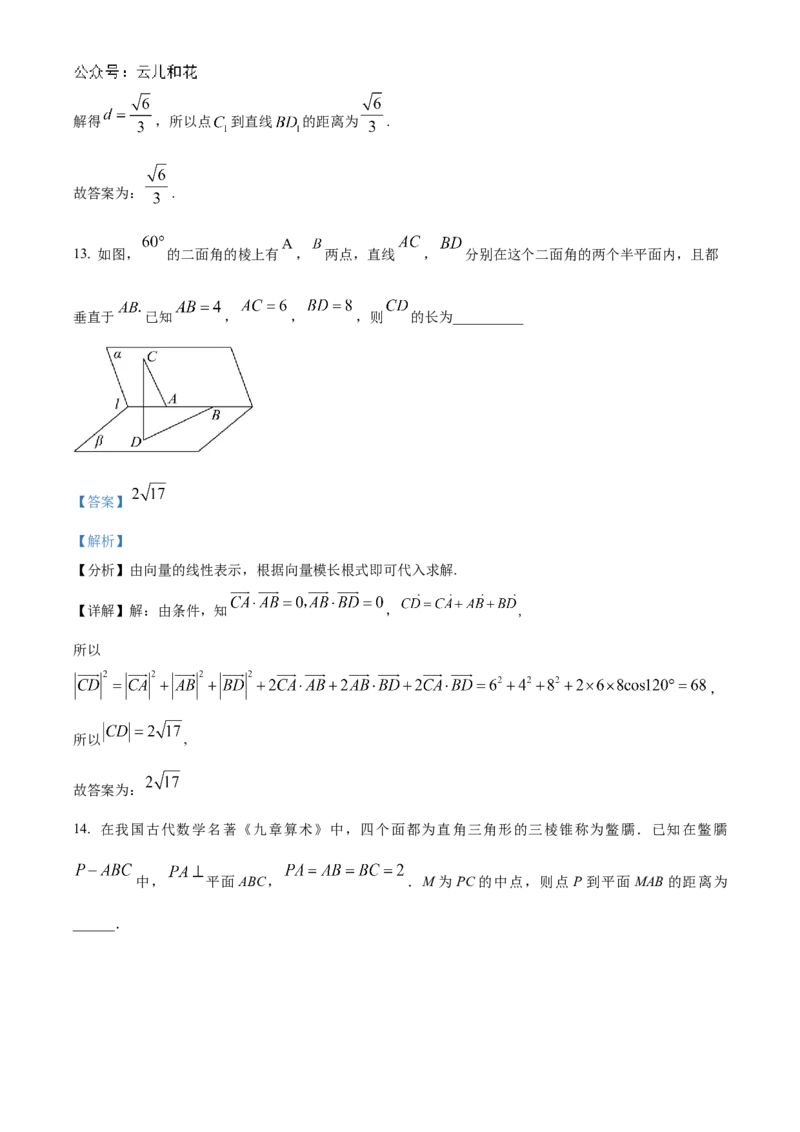
13. 如图, 的二面角的棱上有 , 两点,直线 , 分别在这个二面角的两个半平面内,且都
垂直于 已知 , , ,则 的长为__________
【答案】
【解析】
【分析】由向量的线性表示,根据向量模长根式即可代入求解.
【详解】解:由条件,知 , ,
所以
,
所以 ,
故答案为:
14. 在我国古代数学名著《九章算术》中,四个面都为直角三角形的三棱锥称为鳖臑.已知在鳖臑
中, 平面 ABC, .M为PC 的中点,则点 P到平面 MAB 的距离为
______.【答案】
【解析】
【分析】利用等体积法求得 到平面 的距离.
【详解】因为 平面ABC, 平面ABC,所以 ,
依题意可知 平面 ,
所以 平面 ,
由于 是 的中点,所以 到平面 的距离是 到平面 的距离的一半,
即 到平面 的距离是 .
, ,
所以 ,
由于 ,所以 ,
,
设 到平面 的距离为 ,则 ,
即 .
故答案为:
15. 如图,在正方体 中,点P在线段 上运动,则下列结论正确的是________.①直线 平面
②三棱锥 的体积为定值
③异面直线AP与 所成角的取值范围是
④直线 与平面 所成角的正弦值的最大值为
【答案】①②④
【解析】
【分析】对于①,利用线面垂直的判定定理及线面垂直的性质定理,即可进行判断;对于②,利用线面平
行的判定定理,得出 ∥平面 ,再根据三棱锥的体积的计算方法,即可进行判断;对于③,利用
异面直线所成角的计算方法,即可进行判断;对于④,通过建立空间直角坐标系,利用坐标法求出直线与
平面所成角的正弦值,然后借助二次函数,即可进行判断.
【详解】
对于①,连接 ,
, , , 平面 , 平面 ,
平面 , 平面 ,,同理, ,
, 平面 , 平面 ,
直线 平面 ,故①正确;
对于②, ∥ , 平面 , 平面 , ∥平面 ,
点 在线段 上运动, 点 到平面 的距离为定值,
又 的面积为定值,利用等体积法知三棱锥 的体积为定值,故②正确;
对于③, ∥ , 异面直线 与 所成的角即为 与 所成的角,
当点 位于 点时, 与 所成的角为 ,
当点 位于 的中点时, , ,此时, 与 所成的角为 ,
异面直线 与 所成角的取值范围是 ,故③错误;
对于④,以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,设正方体
的棱长为1, ,
则 , , , , , ,设平面 的法向量 ,则 ,即 ,
令 ,得 ,所以,直线 与平面 所成角的正弦值为:
,
当 时,直线 与平面 所成角的正弦值取得最大值,最大值为 ,故④正确.
故答案为:①②④
三、解答题(本大题共4小题,每小题10分,共40分.解答应写出文字说明、演算步骤或证
明过程.)
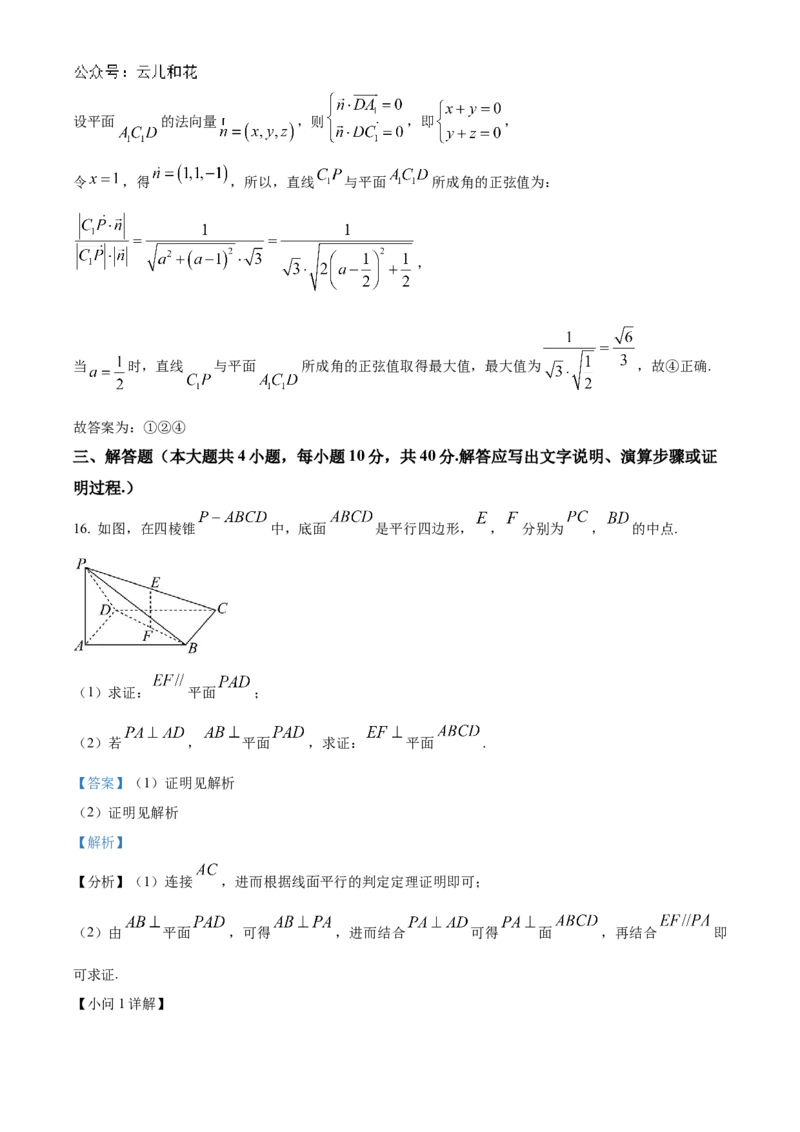
16. 如图,在四棱锥 中,底面 是平行四边形, , 分别为 , 的中点.
(1)求证: 平面 ;
(2)若 , 平面 ,求证: 平面 .
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】(1)连接 ,进而根据线面平行的判定定理证明即可;
(2)由 平面 ,可得 ,进而结合 可得 面 ,再结合 即
可求证.
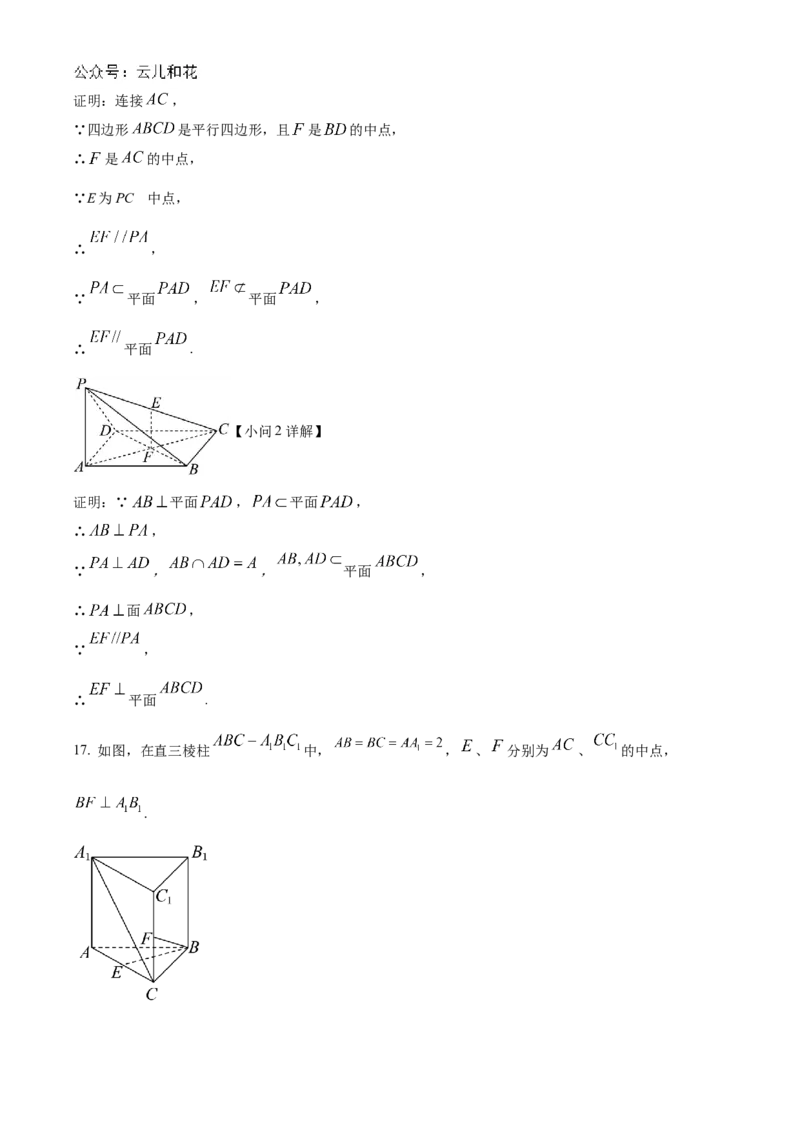
【小问1详解】证明:连接 ,
∵四边形 是平行四边形,且 是 的中点,
∴ 是 的中点,
的
∵E为PC 中点,
∴ ,
∵ 平面 , 平面 ,
∴ 平面 .
【小问2详解】
证明:∵ 平面 , 平面 ,
∴ ,
∵ , , 平面 ,
∴ 面 ,
∵ ,
∴ 平面 .
17. 如图,在直三棱柱 中, , 、 分别为 、 的中点,
.(1)求证: ;
(2)求直线 与平面 所成角的正弦值;
(3)求点 到平面 的距离.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】(1)首先通过线面垂直的判定定理得证 平面 ,从而得证 ;
(2)法一:首先通过线面垂直的判定定理得证 平面 ,从而得到 即为所求角,求出
该角的正弦值即可得到答案.法二:由已知可证 ,建立空间直角坐标系,利用向量的夹角公式可
求 与平面 所成角的正弦值.
(3)利用空间向量法的点到面的距离公式可求解.
【小问1详解】
因为三棱柱 是直三棱柱,所以 平面 ,
因为 平面 ,所以 ,
又因为 , 为 中点,所以 ,
因为 平面 ,所以 平面 ,
因为 平面 ,所以 .
【小问2详解】
方法一:因为直三棱柱 ,所以 平面 ,
因为 平面 ,所以 ,
因为 , ,所以 ,
因为 平面 ,所以 平面 .
因为 平面 ,所以 ,
因为 , 平面 ,所以 平面 ,
连结 , 即为直线 与平面 所成角,
因为 ,所以 , ,
.
所以 与平面 所成角的正弦值为 .
方法二:
因为直三棱柱 ,所以 平面 ,
因为 平面 ,所以 ,
因为 , ,所以 ,
因为 平面 ,所以 平面 .
因为 ,所以 ,
如图所示,以 为原点,以 所在直线为坐标轴建立如图所示的空间直角坐标系,因为 ,
所以 , ,
易知 平面 所以 为平面 的一个法向量,
,
设 与平面 所成角为θ,
所以 ,
所以 与平面 所成角的正弦值为 .
【小问3详解】
设 到平面 的距离为 ,
因为 ,
所以 ,
设 为平面 一个法向量,所以 ,即 ,
的
令 ,则 ,所以平面 的一个法向量 ,所以 ,
因此点 到平面 的距离为 .
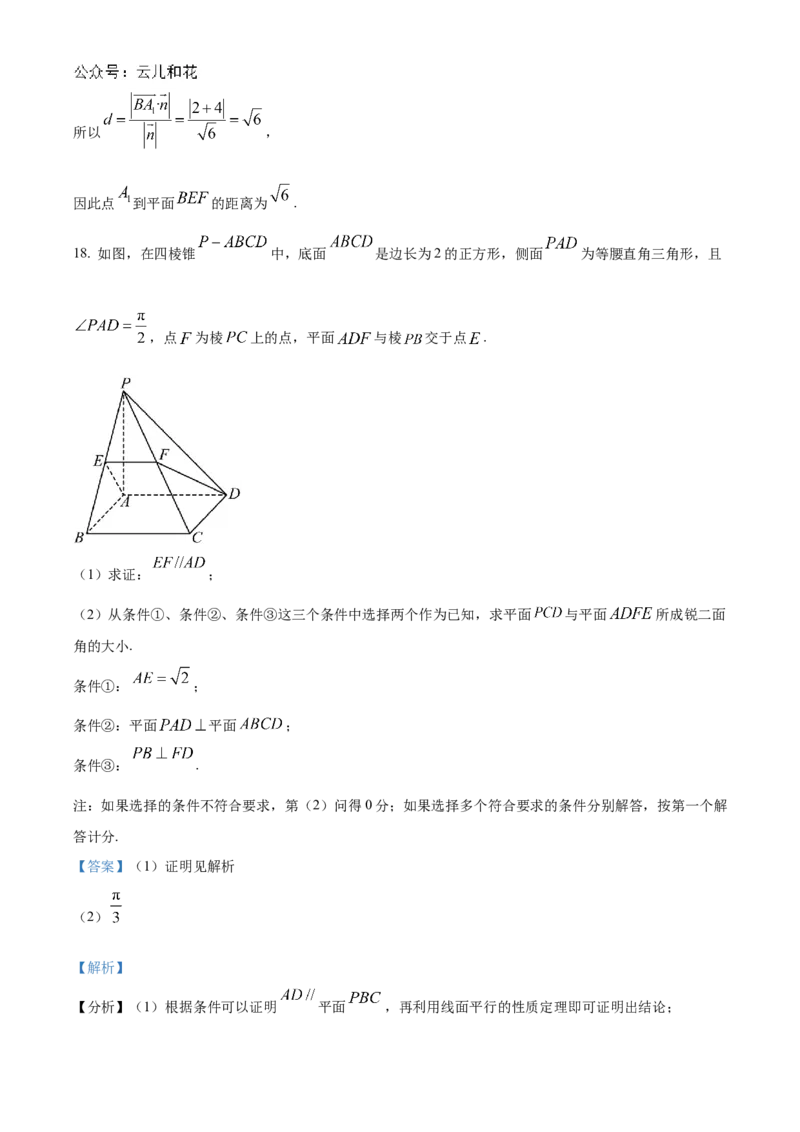
18. 如图,在四棱锥 中,底面 是边长为2的正方形,侧面 为等腰直角三角形,且
,点 为棱 上的点,平面 与棱 交于点 .
(1)求证: ;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面 与平面 所成锐二面
角的大小.
条件①: ;
条件②:平面 平面 ;
条件③: .
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)根据条件可以证明 平面 ,再利用线面平行的性质定理即可证明出结论;(2)选条件①②可以证明出 两两垂直,建立空间直角坐标系 ,求出相应坐标,再求
出两平面的法向量,进而求出结果;选条件①③或②③同样可以证明求解.
【小问1详解】
证明:因为底面 是正方形,所以 ,
平面 , 平面 ,
所以 平面 ,
又因为平面 与 交于点 .
平面 ,平面 平面
所以 .
【小问2详解】
选条件①②
侧面 为等腰直角三角形,且
即 ,
平面 平面 ,
平面 平面 , 平面 ,
则 平面 ,又 为正方形,
所以 .
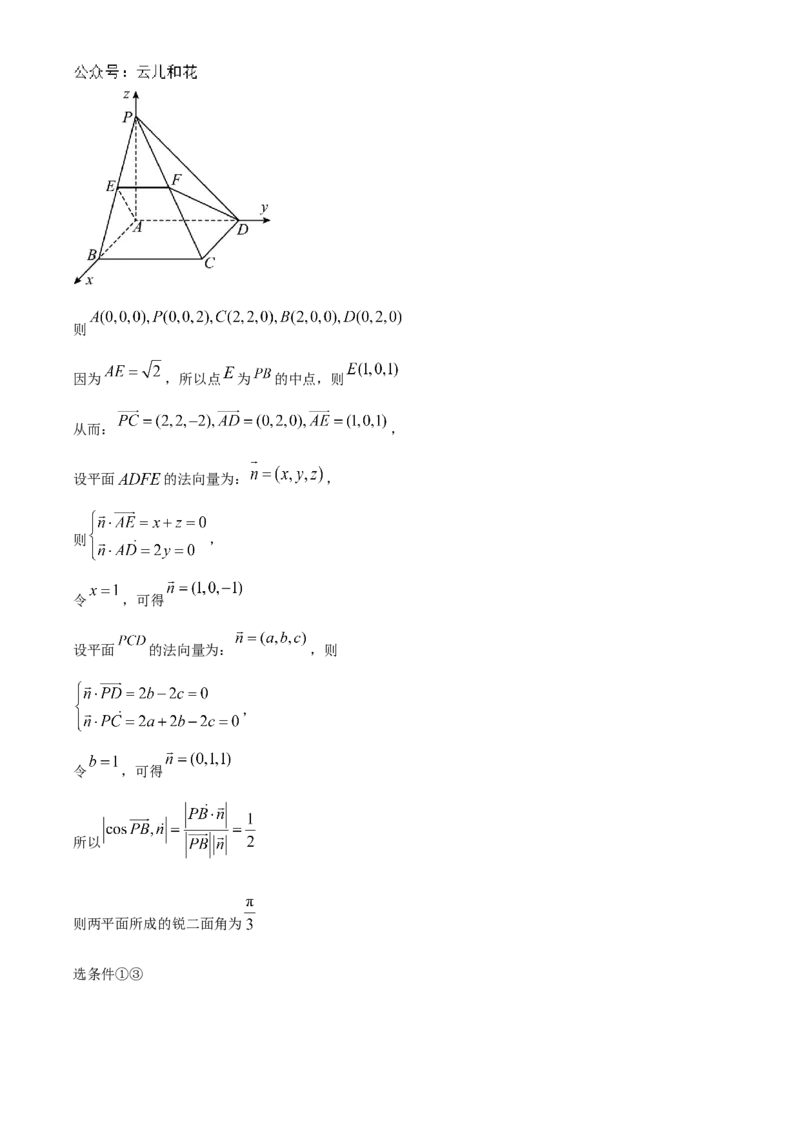
以点 为坐标原点, 分别为 轴, 轴, 轴正方向,建立如图所示空间直角坐标系 ,则
因为 ,所以点 为 的中点,则
从而: ,
设平面 的法向量为: ,
则 ,
令 ,可得
设平面 的法向量为: ,则
,
令 ,可得
所以
则两平面所成的锐二面角为
选条件①③侧面 为等腰直角三角形,且 即
,且两直线在平面内,可得 平面 , 平面 ,则 .
又因为 且两直线在平面内,
则 平面 平面 则
因为 ,所以 为等腰三角形,所以点 为 的中点
又因为 ,所以 为等腰直角三角形,
下面同①②
选条件②③
侧面 为等腰直角三角形,且 ,
即
平面 平面 ,
平面 平面 , 平面 ,
则 平面 为正方形,
所以 .
又因为 且两直线在平面内,则 平面 , 平面
则
因为 ,所以 为等腰三角形,所以点 为 的中点.
下面同①②
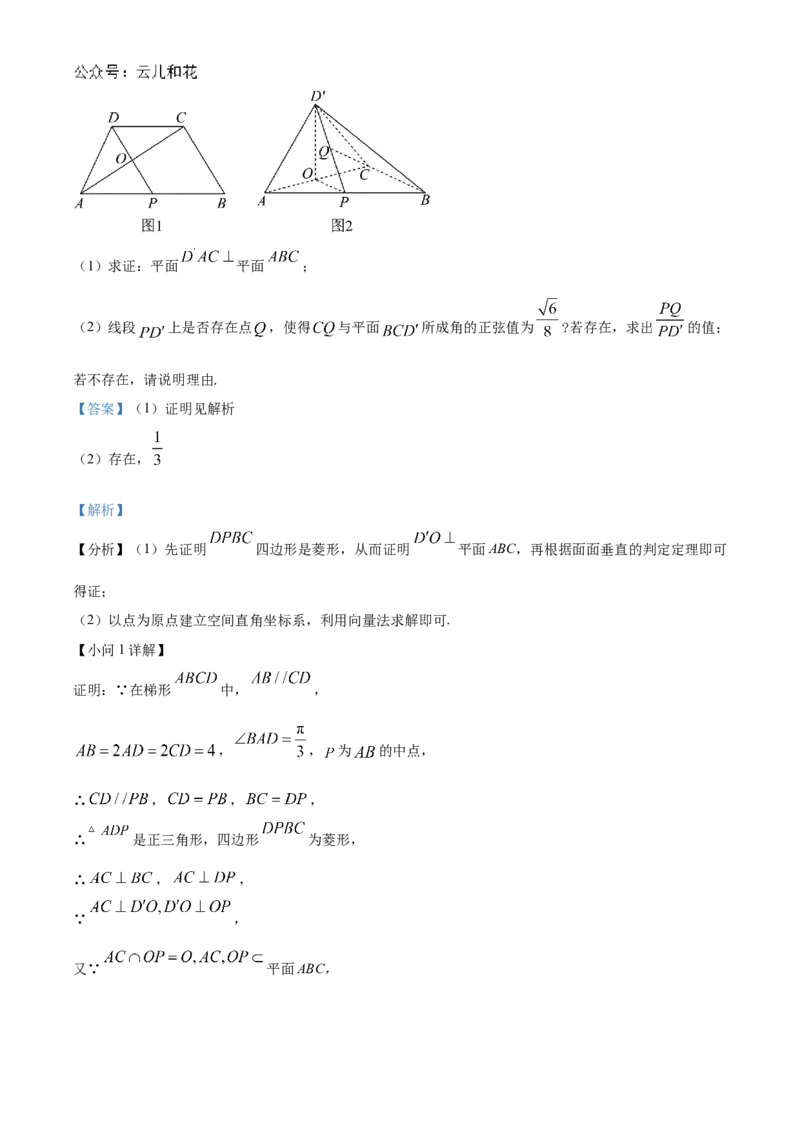
19. 在梯形 中, , , , 为 的中点,线段 与
交于 点(如图1).将△ 沿 折起到△ 位置,使得 (如图2).(1)求证:平面 平面 ;
(2)线段 上是否存在点 ,使得 与平面 所成角的正弦值为 ?若存在,求出 的值;
若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在,
【解析】
【分析】(1)先证明 四边形是菱形,从而证明 平面ABC,再根据面面垂直的判定定理即可
得证;
(2)以点为原点建立空间直角坐标系,利用向量法求解即可.
【小问1详解】
证明:∵在梯形 中, ,
, , 为 的中点,
∴ , , ,
∴ 是正三角形,四边形 为菱形,
∴ , ,
∵ ,
又∵ 平面ABC,∴ 平面ABC,
∵ 平面 ,
∴平面 ⊥平面ABC.
【小问2详解】
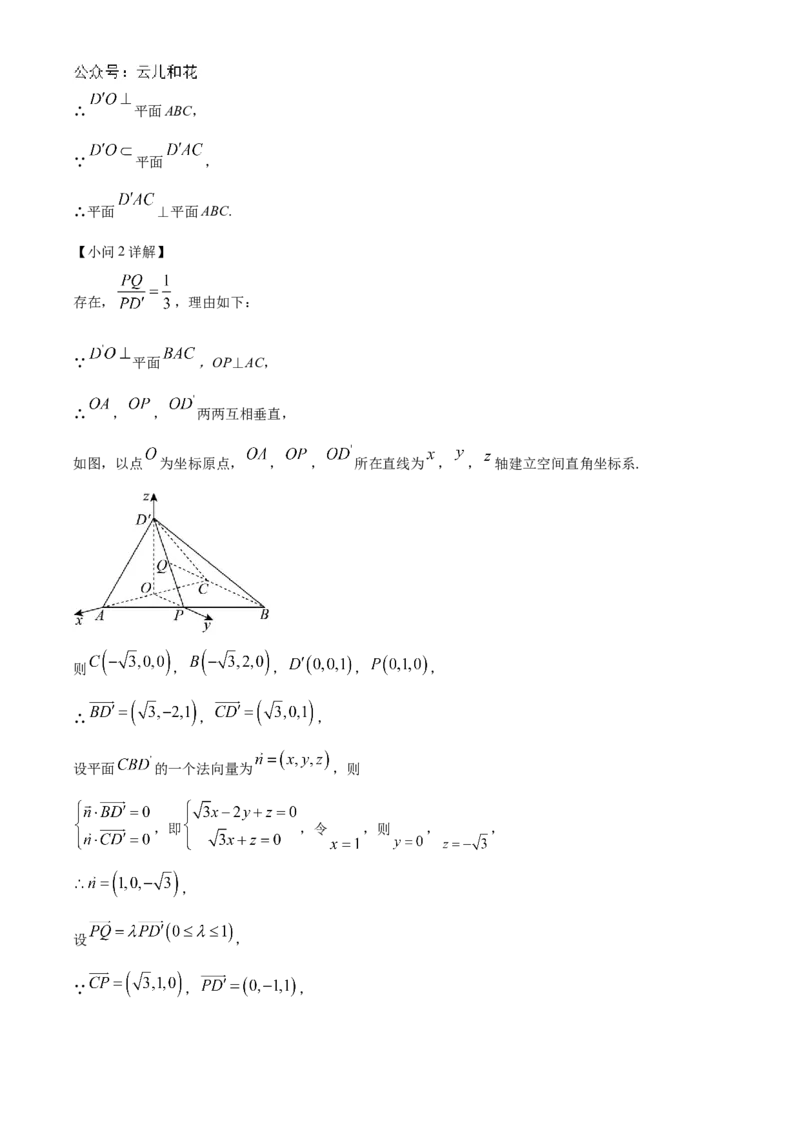
存在, ,理由如下:
∵ 平面 ,OP⊥AC,
∴ , , 两两互相垂直,
如图,以点 为坐标原点, , , 所在直线为 , , 轴建立空间直角坐标系.
则 , , , ,
∴ , ,
设平面 的一个法向量为 ,则
,即 ,令 ,则 , ,
,
设 ,
∵ , ,∴ ,
设 与平面 所成角为 ,则 ,
即 , ,解得 ,
∴线段 上存在点 ,且 ,使得 与平面 所成角的正弦值为 .