文档内容
长春外国语学校2024-2025学年第一学期高二年级期初考试
数学试卷
出题人 :康乐 审题人:郭奇
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 4页。考试结束
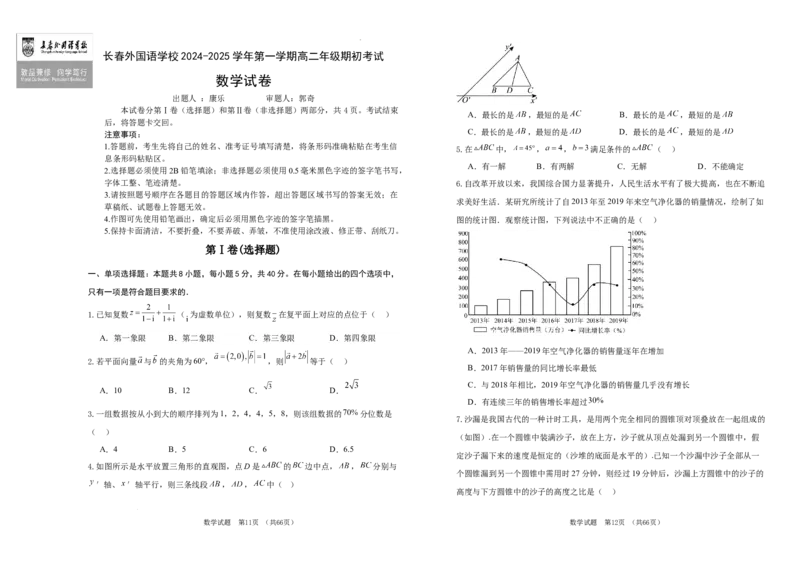
A.最长的是 ,最短的是 B.最长的是 ,最短的是
后,将答题卡交回。
C.最长的是 ,最短的是 D.最长的是 ,最短的是
注意事项:
1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信
5.在 中, , , 满足条件的 ( )
息条形码粘贴区。
A.有一解 B.有两解 C.无解 D.不能确定
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,
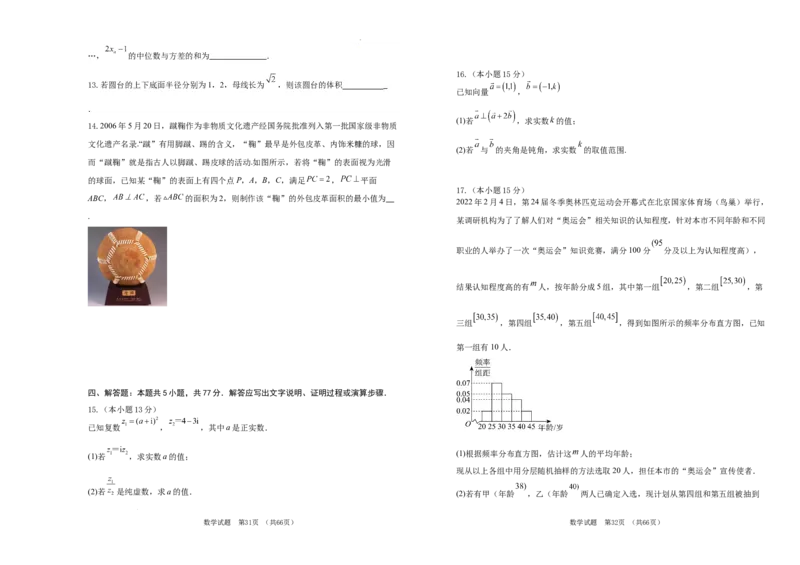
字体工整、笔迹清楚。 6.自改革开放以来,我国综合国力显著提升,人民生活水平有了极大提高,也在不断追
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在
求美好生活.某研究所统计了自2013年至2019年来空气净化器的销量情况,绘制了如
草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。 图的统计图.观察统计图,下列说法中不正确的是( )
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知复数 ( 为虚数单位),则复数 在复平面上对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A.2013年——2019年空气净化器的销售量逐年在增加
2.若平面向量 与 的夹角为60°, ,则 等于( )
B.2017年销售量的同比增长率最低
C.与2018年相比,2019年空气净化器的销售量几乎没有增长
A.10 B.12 C. D.
D.有连续三年的销售增长率超过
3.一组数据按从小到大的顺序排列为1,2,4,4,5,8,则该组数据的 分位数是
7.沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的
( )
(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假
A.4 B.5 C.6 D.6.5
定沙子漏下来的速度是恒定的(沙堆的底面是水平的).已知一个沙漏中沙子全部从一
4.如图所示是水平放置三角形的直观图,点D是 的 边中点, , 分别与
个圆锥漏到另一个圆锥中需用时27分钟,则经过19分钟后,沙漏上方圆锥中的沙子的
′轴、 ′轴平行,则三条线段 , , 中( )
高度与下方圆锥中的沙子的高度之比是( )
数学试题 第11页 (共66页) 数学试题 第12页 (共66页)
学科网(北京)股份有限公司C. D.向量 , 的夹角为
10.下列说法正确的是( )
A.抛掷两枚质地均匀的骰子,至少有一枚骰子的点数是3的概率为
A.2:3 B.2:1 C.1:1 D.3:2
B.甲乙两人独立地解题,已知各人能解出的概率分别是 , ,则题被解出的概率
8.已知正方体 ,点 , , 分别是线段 , 和 上的动点,
是
观察直线 与 , 与 给出下列结论:其中正确的
C.某小组由5名学生组成,其中3名男生,2名女生,现从中任选两名学生参加演
结论是 讲比赛,至少有一名男生与至少有一名女生是互斥事件
D.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
①对于任意给定的点 ,存在点 ,使得 ;
11. 的内角 的对边分别为 ,下列结论正确的是( )
②对于任意给定的点 ,存在点 ,使得 ;
③对于任意给定的点 ,存在点 ,使得 ;
A.若 ,则 的面积为
④对于任意给定的点 ,存在点 ,使得 .
B.若 ,则角
C.若 ,则 为等腰或直角三角形
A.① B.②③ C.①④ D.②④
D.不存在 ,使 成立
二、多项选择题:本题共3题,每小题6分,共18分.在每小题给出的选项中,有多
项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
第Ⅱ卷(非选择题)
9.已知向量 , , 满足 , , ,则下列说法正确
三、填空题:本题共3小题,每小题5分,共15分.
的是( )
12.已知 , , ,…, 的中位数与方差分别为2,1,则 , , ,
A. B.
数学试题 第21页 (共66页) 数学试题 第22页 (共66页)
学科网(北京)股份有限公司…, 的中位数与方差的和为 .
16.(本小题15分)
13.若圆台的上下底面半径分别为1,2,母线长为 ,则该圆台的体积
已知向量 ,
.
(1)若 ,求实数 的值;
14.2006年5月20日,蹴鞠作为非物质文化遗产经国务院批准列入第一批国家级非物质
文化遗产名录.“蹴”有用脚蹴、踢的含义,“鞠”最早是外包皮革、内饰米糠的球,因
(2)若 与 的夹角是钝角,求实数 的取值范围.
而“蹴鞠”就是指古人以脚蹴、踢皮球的活动.如图所示,若将“鞠”的表面视为光滑
的球面,已知某“鞠”的表面上有四个点P,A,B,C,满足 , 平面
17.(本小题15分)
ABC, ,若 的面积为2,则制作该“鞠”的外包皮革面积的最小值为
2022年2月4日,第24届冬季奥林匹克运动会开幕式在北京国家体育场(鸟巢)举行,
.
某调研机构为了了解人们对“奥运会”相关知识的认知程度,针对本市不同年龄和不同
职业的人举办了一次“奥运会”知识竞赛,满分100分 分及以上为认知程度高),
结果认知程度高的有 人,按年龄分成5组,其中第一组 ,第二组 ,第
三组 ,第四组 ,第五组 ,得到如图所示的频率分布直方图,已知
第一组有10人.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题13分)
已知复数 , ,其中a是正实数.
(1)根据频率分布直方图,估计这 人的平均年龄;
(1)若 ,求实数a的值;
现从以上各组中用分层随机抽样的方法选取20人,担任本市的“奥运会”宣传使者.
(2)若 是纯虚数,求a的值. (2)若有甲(年龄 ,乙(年龄 两人已确定入选,现计划从第四组和第五组被抽到
数学试题 第31页 (共66页) 数学试题 第32页 (共66页)
学科网(北京)股份有限公司的使者中,再随机抽取2名作为组长,求甲、乙两人至少有一人被选上的概率;
(3)若第四组宣传使者的年龄的平均数与方差分别为36和 ,第五组宣传使者的年龄的 长春外国语学校2024-2025学年第一学期期初考试高二年级
平均数与方差分别为42和1,据此估计这 人中 岁所有人的年龄的方差.
数学试卷答案
18.(本小题17分)
1. D 2.D 3.B 4.B 5.A 6.C 7.B 8.A
的内角 的对边分别为 ,已知 . 9.AB 10.AD 11.BCD
(1)求 ;
12.7 13. 14.
(2)若 为锐角三角形,且 ,求 面积的取值范围.
15.(1)2 (2)2
【分析】(1)根据复数的定义及复数的运算法则构建关于 的方程组,求解 的值;
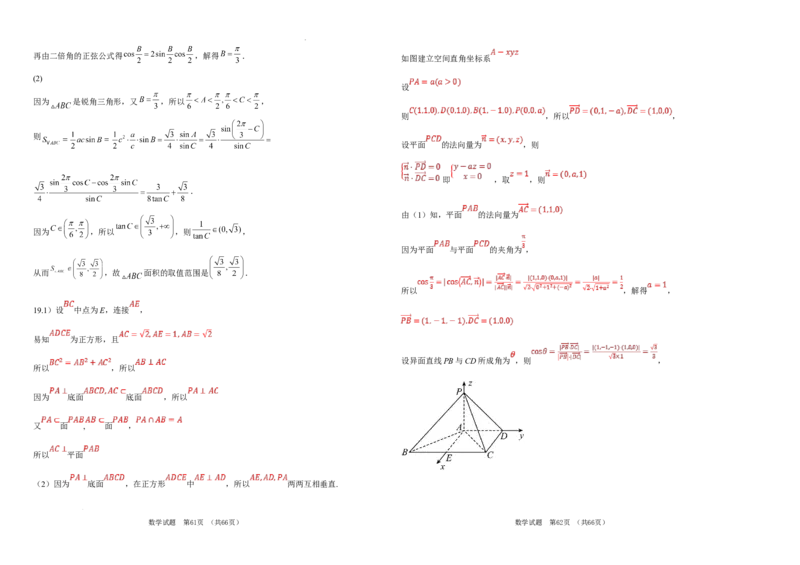
19.(本小题17分)
如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,在底面ABCD中, ,
(2)根据复数的除法运算求解 ,利用复数的定义,构建关于 的方程组,求解 的
, , .
值;
【详解】(1)解:∵ , , ,
∴ ,从而 ,解得 ,
(1)求证: ;
所以实数a的值为2.
(2)依题意得: ,
(2)若平面 与平面 夹角等于 ,求异面直线 与 所成角的余弦值.
因为 是纯虚数,所以: ,解得: 或 ;
又因为a是正实数,所以a=2.
数学试题 第41页 (共66页) 数学试题 第42页 (共66页)
学科网(北京)股份有限公司16.(1) (2) 所以 ;
【详解】(1)因为 , ,所以 , (3)设第四组、第五组的宣传使者的年龄的平均数分别为 , ,方差分别为 , ,
因为 ,所以 ,解得 ; 则 , , , ,
(2)因为 与 的夹角是钝角, , ,所以 设第四组和第五组所有宣传使者的年龄平均数为 ,方差为 ;
则 ,
,解得 ,
又当 ,即 时, ,此时 与 的夹角为 ,故 ,
综上可得 . 因此第四组和第五组所有宣传使者的年龄方差为10,
据此可估计这 人中年龄在 岁的所有人的年龄方差约为10
17.【答案】(1) (2) (3)10
【详解】(1)解:设这 人的平均年龄为 ,
18.(1) ;(2) .
则 (岁 ;
(2)由频率分布直方图可知各组的频率之比为 ,
【详解】(1)
第四组应抽取 人,记为 , , ,甲,第五组抽取
由三角形的内角和定理得 ,
人,记为 ,乙,
此时 就变为 .
对应的样本空间为 , , ,甲), ,乙), , , ,
甲), ,乙), , ,甲) ,乙), ,(甲,乙),(甲, , 由诱导公式得 ,所以 .
(乙, ,共15个样本点.
在 中,由正弦定理知 ,
分设事件 “甲、乙两人至少一人被选上”,
则 ,甲), ,乙), ,甲), ,乙), ,甲), ,乙),(甲,
此时就有 ,即 ,
乙),(甲, ,(乙, ,共有9个样本点,
数学试题 第51页 (共66页) 数学试题 第52页 (共66页)
学科网(北京)股份有限公司再由二倍角的正弦公式得 ,解得 .
如图建立空间直角坐标系
(2)
设
因为 是锐角三角形,又 ,所以 ,
则 ,所以 ,
则
设平面 的法向量为 ,则
即 ,取 ,则
.
由(1)知,平面 的法向量为
因为 ,所以 ,则 ,
因为平面 与平面 的夹角为 ,
从而 ,故 面积的取值范围是 .
所以 ,解得 ,
19.1)设 中点为E,连接 ,
易知 为正方形,且
设异面直线PB与CD所成角为 ,则 ,
所以 ,所以
因为 底面 底面 ,所以
又 面 , 面 ,
所以 平面
(2)因为 底面 ,在正方形 中 ,所以 两两互相垂直.
数学试题 第61页 (共66页) 数学试题 第62页 (共66页)
学科网(北京)股份有限公司