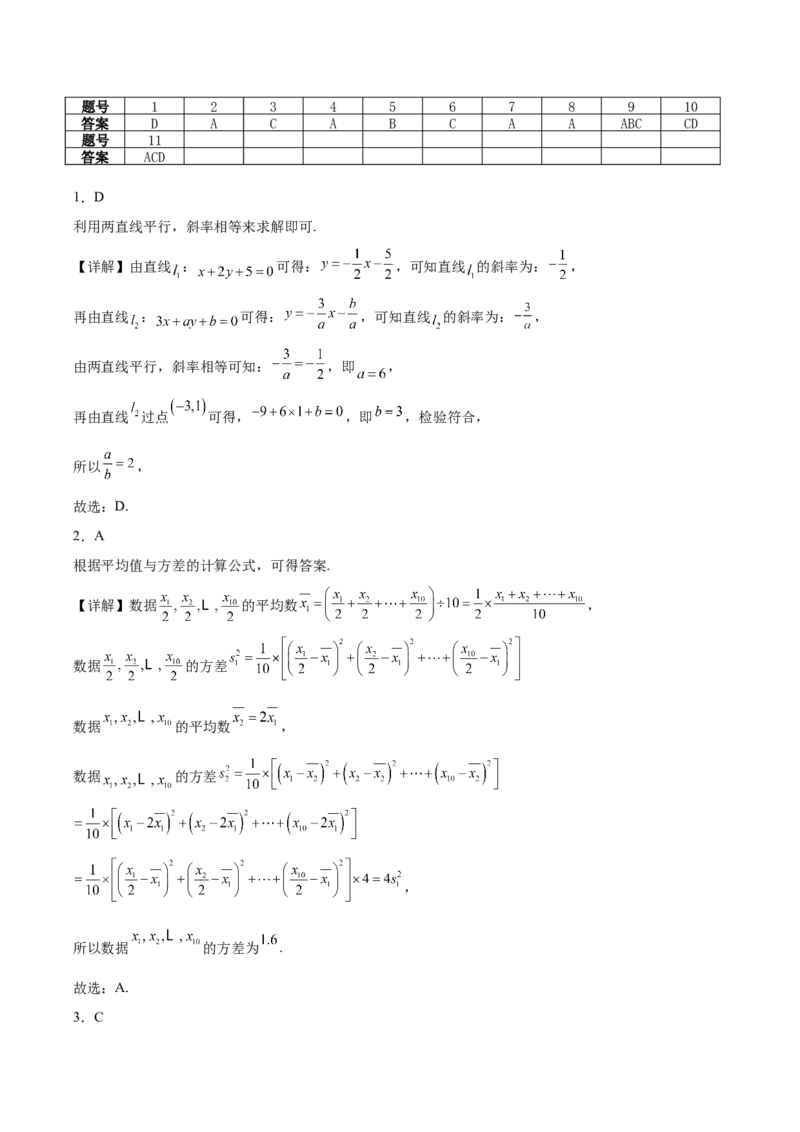文档内容
四平市第一高级中学2024-2025学年高二下学期期初验收考试
数学试题
一、单选题
1.已知直线 : 与 : 平行,且 过点 ,则 ( )
A.-3 B.3 C.-2 D.2
2.若一组数据 的方差为0.4,则另一组数据 的方差为( )
A.1.6 B.0.8 C.0.4 D.0.1
3.在 的展开式中,只有第五项的二项式系数最大,则展开式中 的系数是( )
A. B. C. D.7
4.已知点 是圆 上的动点,点 ,则 的中点 的轨迹方程是( )
A. B.
C. D.
5.当双曲线 的焦距取得最小值时,其渐近线的方程为
A. B. C. D.
6.以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程 ,变量 增加1个单位时, 平均增加5个单位
③线性回归方程 必过
④设具有相关关系的两个变量 的相关系数为 ,那么 越接近于0, 之间的线性相关程度越高;
⑤在一个 列联表中,由计算得 的值,那么 的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )A.0 B.1 C.2 D.3
7.为迎接第 届冬季奥林匹克运动会,某校安排甲、乙、丙、丁、戊共五名学生担任冰球、冰壶和短道
速滑三个项目的志愿者,每个比赛项目至少安排 人,则学生甲被安排到冰球比赛项且做志愿者的概率为
( )
A. B. C. D.
8.已知椭圆 的左顶点和上顶点分别为 , ,左、右焦点分别是 , ,在线段
上有且只有一个点 满足 ,则椭圆的离心率为( )
A. B. C. D.
二、多选题
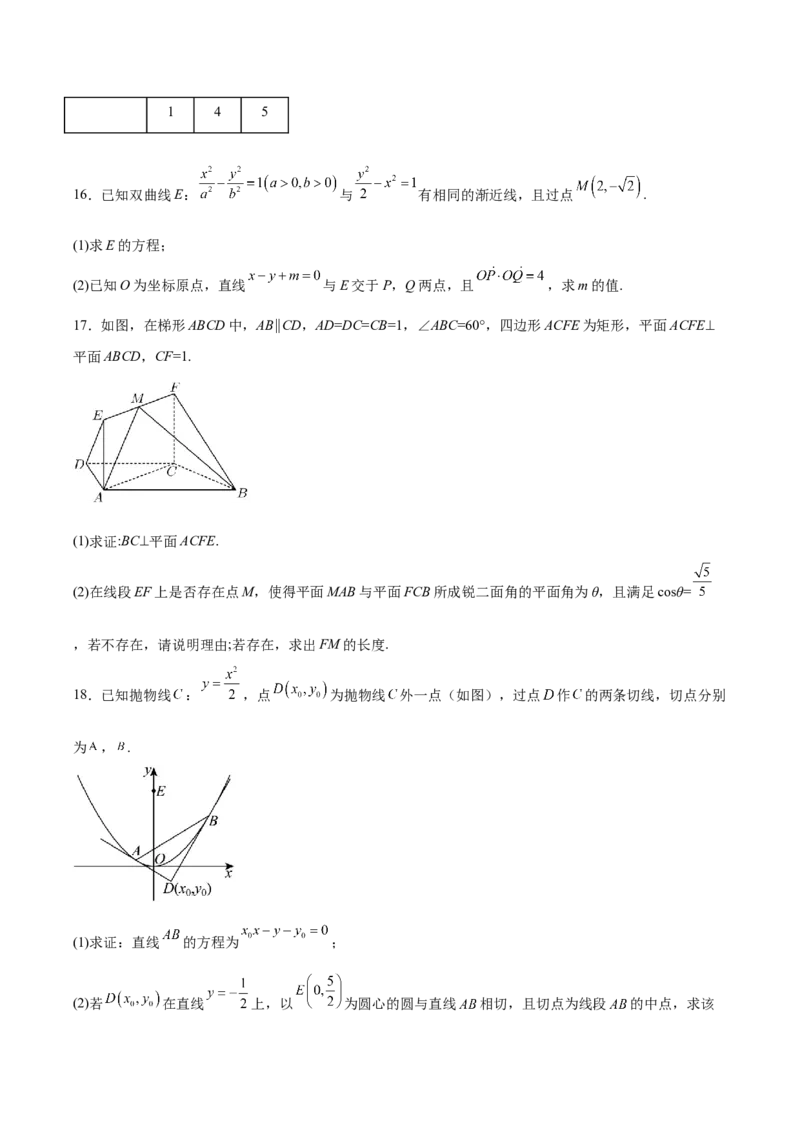
9.2020年,我国全面建成小康社会取得伟大历史性成就,脱贫攻坚战取得了全面胜利.下图是2013—2019
年我国农村减贫人数(按现行农村贫困标准统计)统计图,2019年末我国农村贫困人口仅剩的551万人也在
2020年现行标准下全部脱贫.以下说法中正确的是( )
A.2013—2020年我国农村贫困人口逐年减少
B.2013—2019年我国农村贫困人口平均每年减少了1300万人以上
C.2017年末我国农村贫困人口有3046万人
D.2014年末与2016年末我国农村贫困人口基本持平
10.某单位开展“学习强国”知识答题活动,在5道试题中(有3道选择题和2道填空题),不放回地依
次随机抽取2道题作答,设事件A为“第1次抽到选择题”,事件B为“第2次抽到选择题”,则下列结
论中正确的是( )
A. B.C. D.
11.已知点P是抛物线 上一点,C的准线与x轴交于Q点, 是以点P为圆心且过点
Q的圆,则 与C的交点个数不可能是( )
A.1 B.2 C.3 D.4
三、填空题
12.过点P(3,0)有一条直线l,它夹在两条直线l:2x-y-2=0与l:x+y+3=0之间的线段恰被点P平
1 2
分,则直线l的方程为 .
13.已知函数 有2个不同的零点,则k的取值范围是 .
14.甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.
无论之前投篮情况如何,甲每次投篮的命中率均为0.8,乙每次投篮的命中率均为0.6 . 由抽签确定第1次
投篮的人选,第1次投篮的人是甲、 乙的概率各为0.5 . 则第 次投篮的人是甲的概率是 .
四、解答题
15.手机用户可通过某软件查看自己每天行走的步数,同时也可以和好友进行运动量的比较和点赞.若某人
一天的行走步数超过8000,则评定为“积极型”,否则评定为“懈怠型”.从小王的男性和女性好友中各
随机抽取了50名,统计其一天的步数并给出评定,得到如下数据:
积极 懈怠
型 型
男 20 30
女 10 40
(1)能否有95%的把握认为“评定类型”与“性别”有关?
(2)以样本数据估计总体数据,且以频率估计概率.若从小王的所有男性好友中抽取3人,记其中评定为“积
极型”的人数为 ,求随机变量 的数学期望.
附: ,其中 .
0.05 0.02 0.01
0 5 0
3.84 5.02 6.631 4 5
16.已知双曲线E: 与 有相同的渐近线,且过点 .
(1)求E的方程;
(2)已知O为坐标原点,直线 与E交于P,Q两点,且 ,求m的值.
17.如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥
平面ABCD,CF=1.
(1)求证:BC⊥平面ACFE.
(2)在线段EF上是否存在点M,使得平面MAB与平面FCB所成锐二面角的平面角为θ,且满足cosθ=
,若不存在,请说明理由;若存在,求出FM的长度.
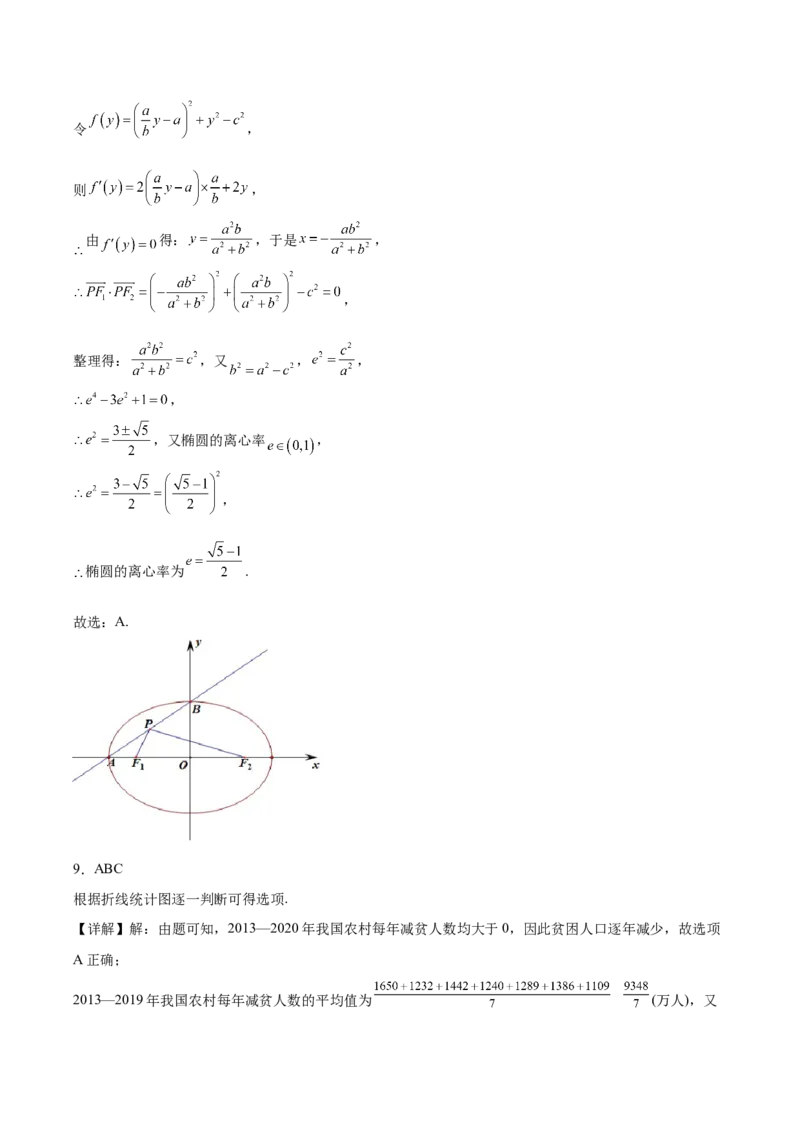
18.已知抛物线 : ,点 为抛物线 外一点(如图),过点 作 的两条切线,切点分别
为 , .
(1)求证:直线 的方程为 ;
(2)若 在直线 上,以 为圆心的圆与直线 相切,且切点为线段 的中点,求该圆的方程.
19.2022年11月4日上午,福建省福州市教育局对2023年初中毕业生体育考试抽考类、抽选考类项目进
行摇号抽签,最终确定排球对墙垫球为抽考项目,立定跳远、50米跑、双手头上前掷实心球三项为抽选考
项目(考生从这三个项目中自选两项考试).此外,体育中考还有必考项目:1000米跑(男)、800米跑
(女)或200米游泳(泳姿不限),考生按性别从2个项目中自选1项考试.若某初三男生参加中考体育测
试的项目为排球对墙垫球、立定跳远、双手头上前掷实心球、1000米跑.为了提高成绩,该男生决定每天
进行多次训练(一次练一项),第一次,在4个项目中等可能地随机选一项开始训练,从第二次起,每次
都是从上一次未训练的3个项目中等可能地随机选1项训练.
(1)若该男生某天进行了3次训练,求第三次训练的是“排球对墙垫球”的概率;
(2)若该男生某天进行了5次训练,4个项目都有训练,且第一次训练的是“1000米跑”,前后训练项目不
同视为不同的训练顺序,设5次训练中选择“1000米跑”的次数为 ,求 的分布列及数学期望.题号 1 2 3 4 5 6 7 8 9 10
答案 D A C A B C A A ABC CD
题号 11
答案 ACD
1.D
利用两直线平行,斜率相等来求解即可.
【详解】由直线 : 可得: ,可知直线 的斜率为: ,
再由直线 : 可得: ,可知直线 的斜率为: ,
由两直线平行,斜率相等可知: ,即 ,
再由直线 过点 可得, ,即 ,检验符合,
所以 ,
故选:D.
2.A
根据平均值与方差的计算公式,可得答案.
【详解】数据 的平均数 ,
数据 的方差
数据 的平均数 ,
数据 的方差
,
所以数据 的方差为 .
故选:A.
3.C由题意利用二项式系数的性质,求得 的值,再利用二项式展开式的通项公式,求得 的系数.
【详解】 在 的展开式中,只有第5项的二项式系数 最大,
它的展开式共计有9项, ,
故二项展开式的通项公式为 ,
令 ,求得 ,可得在 的展开式中 的系数为 ,
故选:C.
4.A
设出线段 中点的坐标,利用中点坐标公式求出 的坐标,根据 在圆上,得到轨迹方程.
【详解】设线段 中点 ,则 .
在圆 上运动,
,即 .
故选:A.
5.B
【详解】由题意可得6−2m>0,即有m<3,
由c2=m2+8+6−2m=(m−1)2+13,
可得当m=1时,焦距2c取得最小值,
双曲线的方程为 ,
即有渐近线方程为 .
故选:B.
6.C
【详解】方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,
故①正确;一个回归方程 ,变量 增加1个单位时, 平均减少5个单位,故②不正确;线性回
归方程 必过样本中心点,故③正确;根据线性回归分析中相关系数的定义:在线性回归分析中,相关系数为r, 越接近于1,相关程度越大,故④不正确;对于观察值 来说, 越大,“x与y有关
系”的可信程度越大,故⑤正确.
故选:C
7.A
【详解】先考虑全部的情况,即将 名学生分为三组,每组的人数分别为 、 、 或 、 、 ,
所有将 名学生担任冰球、冰壶和短道速滑三个项目的志愿者,每个比赛项目至少安排 人,
不同的排法种数为 种;
接下来考虑学生甲被安排到冰球比赛项且做志愿者,则做冰球志愿者的人数可为 或 或 ,
若做冰球志愿者的人数为 且为甲,共有 种;
若做冰球志愿者的人数为 且包含甲,共有 种;
若做冰球志愿者的人数为 且包含甲,共有 种.
因此,所求概率为 .
故选:A.
8.A
【详解】解:依题意,作图如下
, , , ,
直线 的方程为: ,整理得: ,
设直线 上的点 ,则 ,
, ,
,令 ,
则 ,
由 得: ,于是 ,
,
整理得: ,又 , ,
,
,又椭圆的离心率 ,
,
椭圆的离心率为 .
故选:A.
9.ABC
根据折线统计图逐一判断可得选项.
【详解】解:由题可知,2013—2020年我国农村每年减贫人数均大于0,因此贫困人口逐年减少,故选项
A正确;
2013—2019年我国农村每年减贫人数的平均值为 (万人),又,故选项B正确;
2017年末我国农村贫困人口为 (万人),故选项C正确;
由于2013—2019年我国农村贫困人口每一年都大量减少,故选项D错误.
故选:ABC.
10.CD
根据古典概型,对立事件,条件概率的计算公式逐一计算每个选项进行判断.
【详解】由题意可得, ,故A错误,
,故B错误,
, ,
,故C正确,
,故D正确.
故选:CD
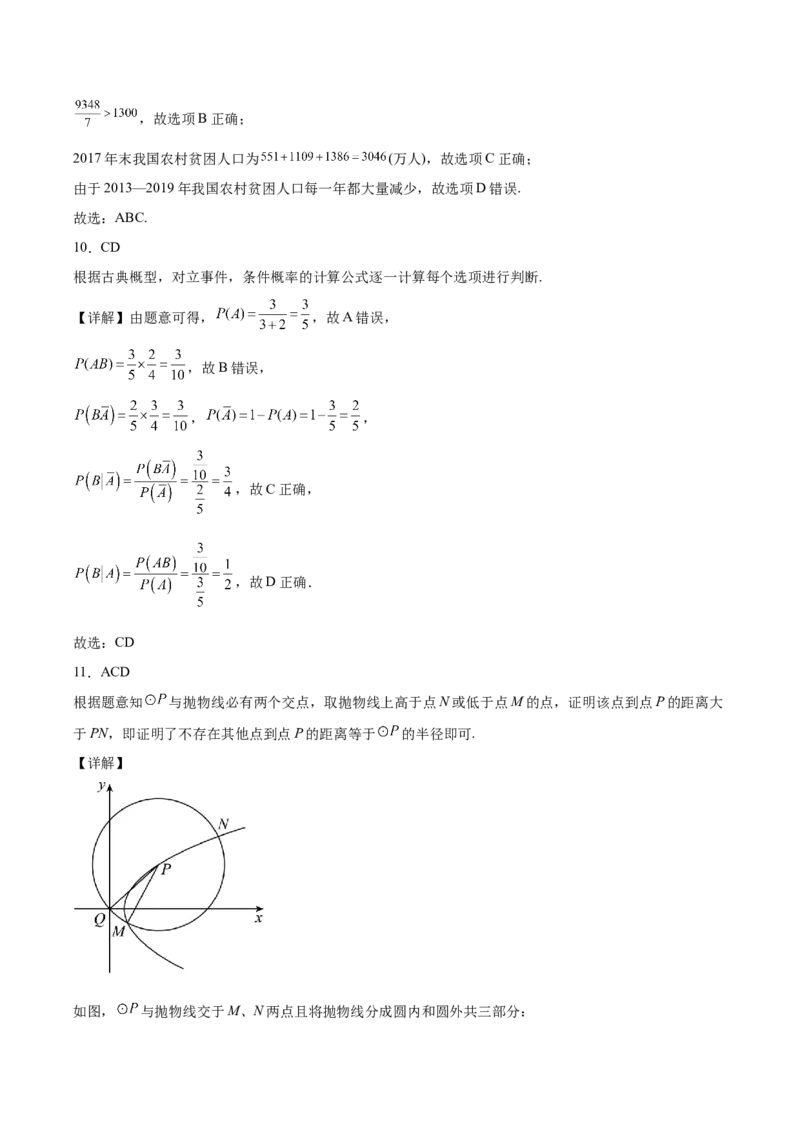
11.ACD
根据题意知 与抛物线必有两个交点,取抛物线上高于点N或低于点M的点,证明该点到点P的距离大
于PN,即证明了不存在其他点到点P的距离等于 的半径即可.
【详解】
如图, 与抛物线交于M、N两点且将抛物线分成圆内和圆外共三部分:显然圆内部分每一点到圆心距离均小于 ,故圆内部分不存在满足条件的点;
设点 坐标为 , , , 为抛物线上高于 点的点且 ,则
有
因为 且 ,
所以 ,即在抛物线上高于N点的部分不存在到P点的距离等于 的点;
同理,圆外部分且在点M下方的抛物线上亦不存在到P点的距离等于 的点;
即 与抛物线的交点只有两个.
故选:ACD
12.8x-y-24=0
【解析】设出 与 两点的坐标,因为 为线段 的中点,利用中点坐标公式即可列出两点坐标的两个关
系式,然后把 的坐标代入直线 ,把 的坐标代入直线 ,又得到两点坐标的两个关系式,把四个关系
式联立即可求出 的坐标,然后由 和 的坐标,利用两点式即可写出直线 的方程.
【详解】设直线 夹在直线 之间的线段是 ( 在 上, 在 上),
的坐标分别是 .
因为 被点 平分,所以
,
于是 .
由于 在 上, 在 上,所以 ,解得 ,即 的坐标是 .
直线 的方程是 ,
即 .
所以直线 的方程是 .
13.
将问题转化为关于 的方程 在区间 内有两个不等的实根,于是画出曲线
与直线 的图象,结合图象求解即可
【详解】因为函数 有2个不同的零点,
所以关于 的方程 在区间 内有两个不等的实根,
即曲线 (圆 的上半部分)与经过定点 的直线 有两个不同的交点,
如图
过 作圆 的切线 ,则点 到切线 的距离 ,解得 (舍去)或 ,
所以 ,得 ,
即k的取值范围是 ,
故答案为:
14.
记“第 次投篮的人是甲”为事件 ,“第 次投篮的人是乙”为事件 ,设 ,利用全概率公式
求得 ,再构造等比数列即可得答案.
【详解】记“第 次投篮的人是甲”为事件 ,“第 次投篮的人是乙”为事件 ,
设 ,则 ,
则 ,
于是 , ,
由 ,得 ,因此数列 是首项为 ,公比为 的等比数列,
则 ,即 ,
所以第 次投篮的人是甲的概率为 .
故答案为:
15.(1)有;
(2) .
【详解】(1) 列联表如下:积极型 懈怠型 合计
男 20 30 50
女 10 40 50
合计 30 70 100
则 的观测值为 ,
所以有95%的把握认为“评定类型”与“性别”有关.
(2)由表格中的数据知,从小王的男性好友中任选一人,评定为“积极型”的概率为 ,
随机变量 的可能值为 , ,
所以随机变量 的数学期望 .
16.(1)
(2) 或
(1)利用待定系数法,结合代入法进行求解即可;
(2)将直线方程与双曲线方程联立,根据一元二次方程根与系数关系,结合平面向量数量积的坐标表示
公式进行求解即可.
【详解】(1)由题意,设E的方程为 ,又E过点 ,
所以 ,解得 ,
所以E的方程为 .
(2)设 , ,由 得 ,因为 ,
所以 , ,
所以
,
所以 ,
解得 或 .
17.(1)证明见解析
(2)存在,
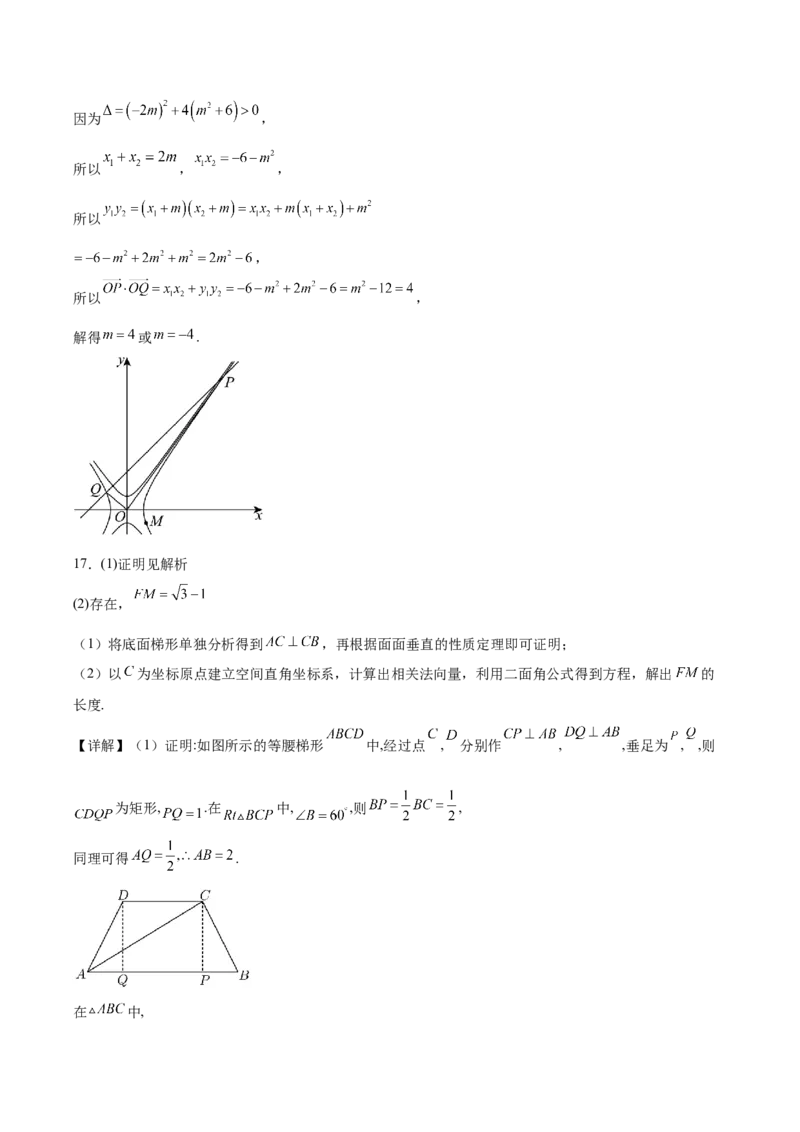
(1)将底面梯形单独分析得到 ,再根据面面垂直的性质定理即可证明;
(2)以 为坐标原点建立空间直角坐标系,计算出相关法向量,利用二面角公式得到方程,解出 的
长度.
【详解】(1)证明:如图所示的等腰梯形 中,经过点 , 分别作 , ,垂足为 , ,则
为矩形, .在 中, ,则 ,
同理可得 .
在 中,,
又 平面 平面 ,平面 平面 平面 , 平面 .
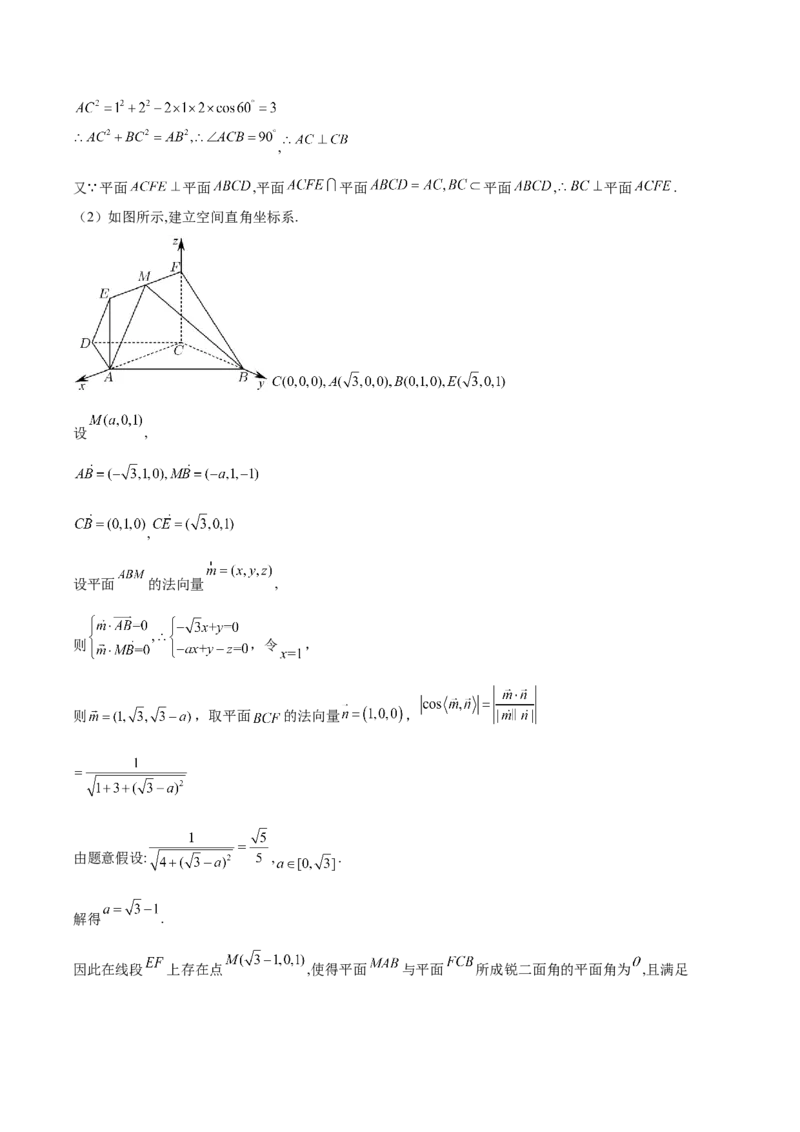
(2)如图所示,建立空间直角坐标系.
设 ,
,
设平面 的法向量 ,
则 ,令 ,
则 ,取平面 的法向量 ,
由题意假设: , .
解得 .
因此在线段 上存在点 ,使得平面 与平面 所成锐二面角的平面角为 ,且满足, .
18.(1)证明见解析
(2) 或
(1)先利用导数几何意义分别求出在 , 两点处的切线方程,再分别代入点 即可发现A,B两
点都在直线 上,进而得到直线 的方程;
(2)由(1)得直线 的方程,与抛物线联立,求出线段 的中点为 ,再根据圆的性质所得
建立方程进行研究即可.
【详解】(1)设 , ,由 得 ,
所以在 处的切线方程为 ,
同理在 处的切线方程为 ,
两条切线都过 ,所以 , ,
显然A,B两点都在直线 上,
所以直线 的方程为 ;
(2)若 在直线 上,则直线 的方程为 ,
即直线 过定点 ,不妨设直线 的方程 ,
由 ,可得 , ,
于是 , ,设 为线段 的中点,则 ,
由于 ,而 , 与向量 平行,
∴ ,解得 或 ,
当 时, ,所求圆的方程为 ;
当 时, ,所求圆的方程为 .
19.(1)
(2)分布列见解析,
(1)设第一次训练的是“排球对墙垫球”的概率为 ,第一次训练的不是“排球对墙垫球”的概率为 ,
则所求概率为 ;
(2)由题可得 的所有可能取值为1,2.
说明后4次训练中除“1000米跑”外的3项中有1项训练了2次,余下的2项都各训练一次,
说明“1000米跑”训练了2次,第三次或第四次或第五次也训练了“1000米跑”,据此可得分布列及期望.
【详解】(1)第一次训练的是“排球对墙垫球”,且第三次训练的是“排球对墙垫球”的概率为
,
第一次训练的不是“排球对墙垫球”,且第三次训练的是“排球对墙垫球”的概率为
,
所以第三次训练的是“排球对墙垫球”的概率为 .
(2)由题意知“1000米跑”最多训练2次,所以 的所有可能取值为1,2.
① 说明后4次训练中除“1000米跑”外的3项中有1项训练了2次,余下的2项都各训练一次,
从除“1000米跑”外的3项中选一项训练2次有 种方法,不妨设训练了2次“排球对墙垫球”,可分为以下两类:
第一类,第二次训练的是“排球对墙垫球”,则第四次或第五次也训练了“排球对墙垫球”,有 种
方法;
第二类,第三次训练的是“排球对墙垫球”,则第五次也训练了“排球对墙垫球”,有 种方法,因此
共有 种方法.
② 说明“1000米跑”训练了2次,第三次或第四次或第五次也训练了“1000米跑”,故有
种方法.
所以 , .
所以 的分布列为:
1 2
所以 .