专题19列举法策略_2024-2025高三（6-6月题库）_2024年08月试卷_0816新高考数学题型全归纳之排列组合（20个专题）

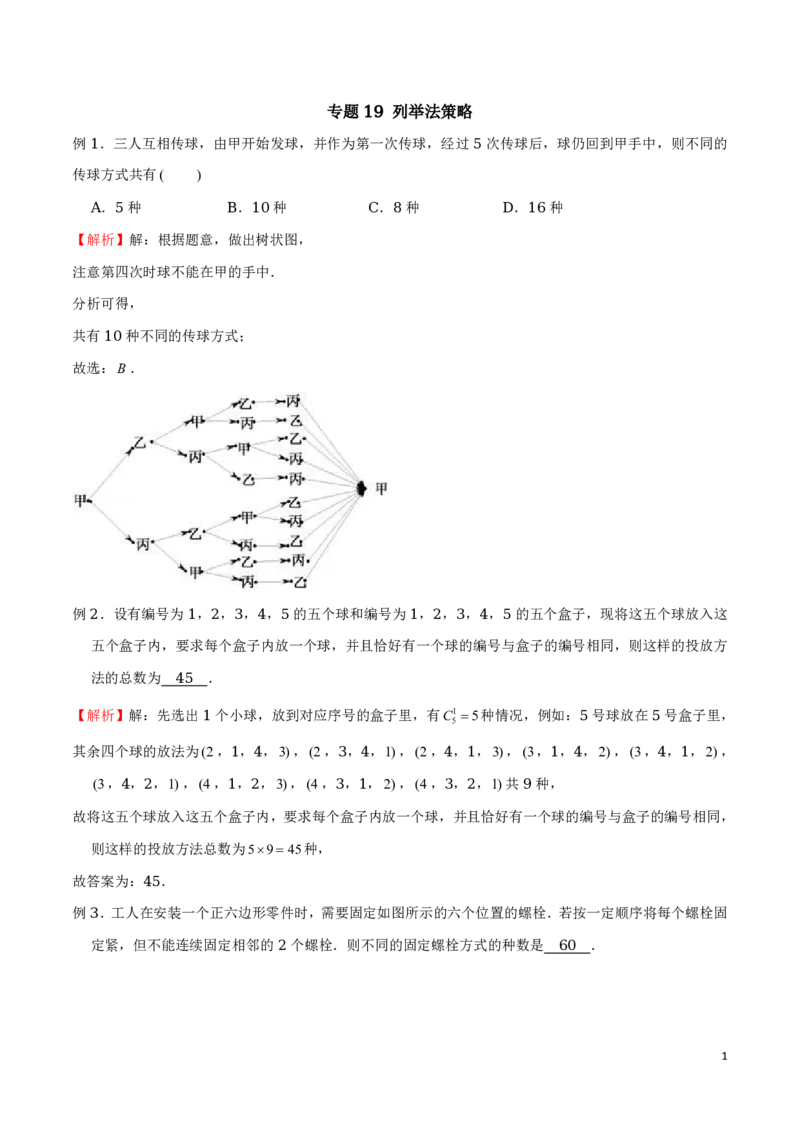
专题 列举法策略 19 例 ．三人互相传球，由甲开始发球，并作为第一次传球，经过 次传球后，球仍回到甲手中，则不同的 1 5 传球方式共有( ) ． 种 ． 种 ． 种 ． 种 A 5 B 10 C 8 D 16 例 ．设有编号为 ， ， ， ， 的五个球和编号为 ， ， ， ， 的五个盒子，现将这五个球放入这 2 1 2 3 4 5 1 2 3 4 5 五个盒子内，要求每个盒子内放一个球，并且恰好有一个球的编号与盒子的编号相同，则这样的投放方 法的总数为 ． 45 例 ．工人在安装一个正六边形零件时，需要固定如图所示的六个位置的螺栓．若按一定顺序将每个螺栓固 3 定紧，但不能连续固定相邻的 个螺栓．则不同的固定螺栓方式的种数是 ． 2 60 例 有红、黄、兰色的球各 只 分别标有 、 、 、 、 五个字母 现从中取 只 要求各字母均有且三 4. 5 , A B C D E , 5 , 色齐备 则共有多少种不同的取法 , 例 ．从， ， ，3， 中选取四元数组(a ，a ，a ，a )，且满足a a 3，a a 4，a a 5， 1 2 3 4 2 1 3 2 4 3 5 1 2 20 则这样的四元数组(a ，a ，a ，a )的个数是( ) 1 2 3 4 ．C4 ．C4 ．C4 ．C4 8 11 14 16 A B C D 例 ．定义 有增有减 数列{a }如下：tN*，满足a a ，且sN*，满足a a ．已知 有增有减 n t t1 S S1 6 “ ” “ ” 数列{a }共 项，若a {x，y，z}(i1， ， ，4)，且x y z，则数列{a }共有( ) n i n 4 2 3 ． 个 ． 个 ． 个 ． 个 A 64 B 57 C 56 D 54 例 ．若一个三位数的各位数字之和为 ，则称这个三位数为 十全十美数 ，如 ， 都是 7 10 “ ” 208 136 十全十美数 ，则这样的 十全十美数 共有( )个 “ ” “ ” ． ． ． ． A 32 B 64 C 54 D 96 例 ．集合I {1， ， ， ，5}．选择I 的两个非空子集A和B，要使B中的最小数大于A中的最大数， 8 2 3 4 则不同的选择方法有 种． 49 1例 ．定义域为集合{1， ， ，，12}上的函数 f(x)满足：① f （ ）1；②| f(x1) f(x)|1(x1， 9 2 3 1 ，，11)；③ f （ ）、 f （ ）、 f(12)成等比数列；这样的不同函数 f(x)的个数为 ． 2 1 6 155 例 ．由海军、空军、陆军各 名士兵组成一个有不同编号的33的小方阵，要求同一军种不在同一行， 10 3 也不在同一列，有 种排法． 2592 例 ．设集合I {1， ， ，4}，选择I 的两个非空子集A和B，使得A中最大的数不大于B中最小的数， 11 2 3 则可组成不同的子集对(A,B) 个． 49 例 ．若集合E\{(p，q，r ，s)|0 ps 4，0 qs 4，0 rs 4且 p，q，r ，sN\}，F \{(t， 12 u，v ，w)|0 tu 4，0 vw 4且t，u，v ，wN\}，用card(X)表示集合X 中的元素个数，则card （ ）card(F)( ) E ． ． ． ． A 200 B 150 C 100 D 50 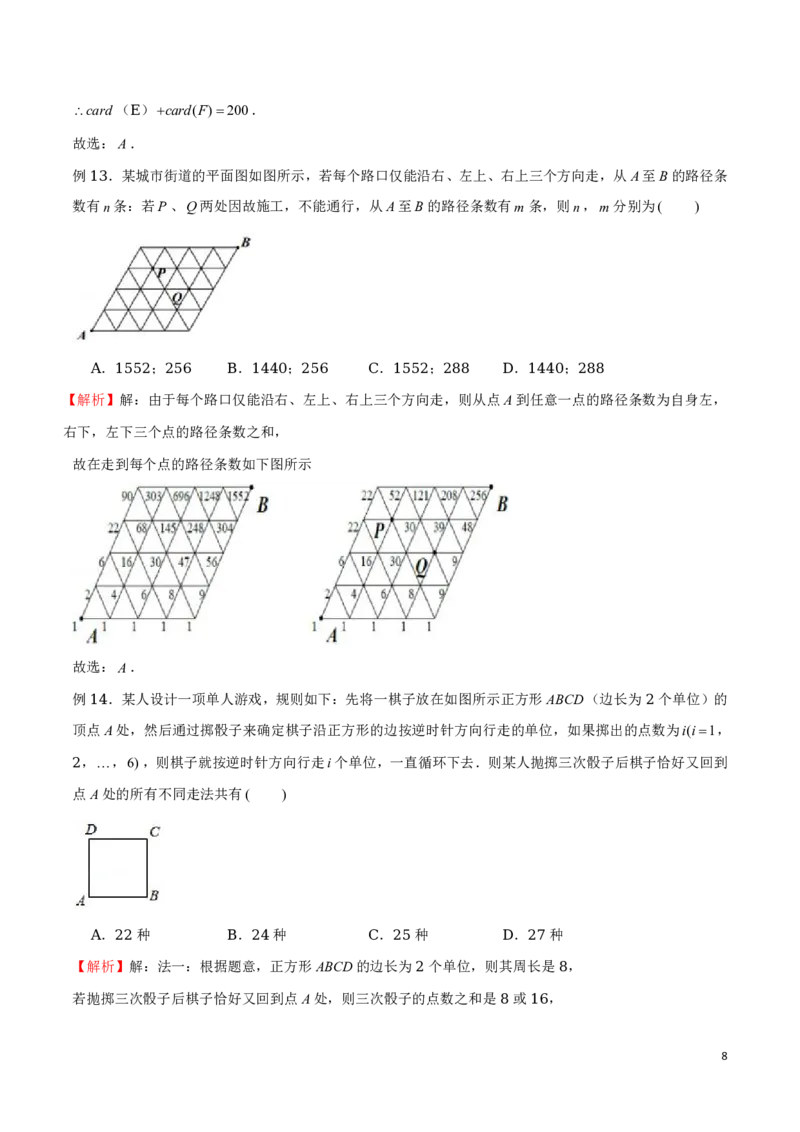例 ．某城市街道的平面图如图所示，若每个路口仅能沿右、左上、右上三个方向走，从A至B的路径条 13 数有n条：若P、Q两处因故施工，不能通行，从A至B的路径条数有m条，则n，m分别为( ) ． ； ． ； ． ； ． ； A 1552 256 B 1440 256 C 1552 288 D 1440 288 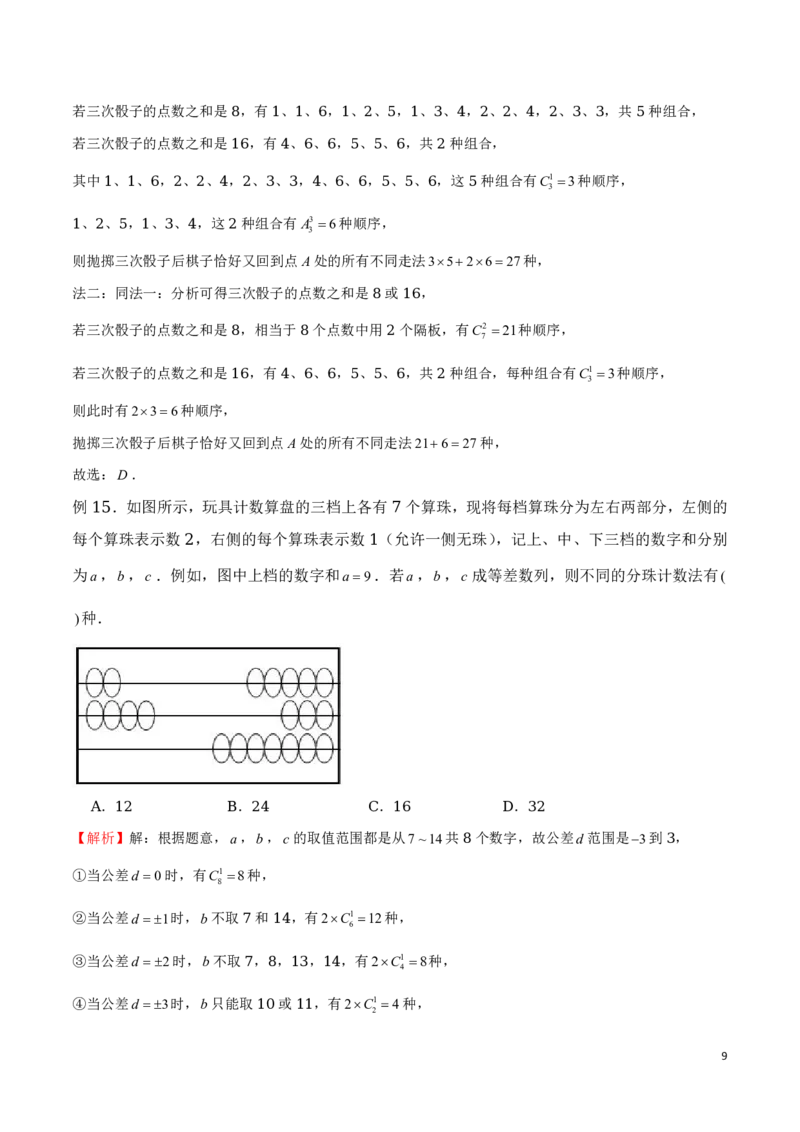例 ．某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形ABCD（边长为 个单位）的 14 2 顶点A处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为i(i1， ，，6)，则棋子就按逆时针方向行走i个单位，一直循环下去．则某人抛掷三次骰子后棋子恰好又回到 2 点A处的所有不同走法共有( ) ． 种 ． 种 ． 种 ． 种 A 22 B 24 C 25 D 27 例 ．如图所示，玩具计数算盘的三档上各有 个算珠，现将每档算珠分为左右两部分，左侧的 15 7 每个算珠表示数 ，右侧的每个算珠表示数 （允许一侧无珠），记上、中、下三档的数字和分别 2 1 为a，b，c．例如，图中上档的数字和a9．若a，b，c 成等差数列，则不同的分珠计数法有( 2)种． ． ． ． ． A 12 B 24 C 16 D 32 例 若一个三位数中任意两相邻数位上两数差的绝对值小于或等于1，则称此三位数为 灵犀数 ，这样 16. “ ” 的三位 灵犀数 共有 个 “ ” 3专题 列举法策略 19 例 ．三人互相传球，由甲开始发球，并作为第一次传球，经过 次传球后，球仍回到甲手中，则不同的 1 5 传球方式共有( ) ． 种 ． 种 ． 种 ． 种 A 5 B 10 C 8 D 16 【解析】解：根据题意，做出树状图， 注意第四次时球不能在甲的手中． 分析可得， 共有 种不同的传球方式； 10 故选：B． 例 ．设有编号为 ， ， ， ， 的五个球和编号为 ， ， ， ， 的五个盒子，现将这五个球放入这 2 1 2 3 4 5 1 2 3 4 5 五个盒子内，要求每个盒子内放一个球，并且恰好有一个球的编号与盒子的编号相同，则这样的投放方 法的总数为 ． 45 【解析】解：先选出 个小球，放到对应序号的盒子里，有C1 5种情况，例如： 号球放在 号盒子里， 5 1 5 5 其余四个球的放法为(2， ， ，3)，(2， ， ，1)，(2， ， ，3)，(3， ， ，2)，(3， ， ，2)， 1 4 3 4 4 1 1 4 4 1 (3， ， ，1)，(4， ， ，3)，(4， ， ，2)，(4， ， ，1)共 种， 4 2 1 2 3 1 3 2 9 故将这五个球放入这五个盒子内，要求每个盒子内放一个球，并且恰好有一个球的编号与盒子的编号相同， 则这样的投放方法总数为5945种， 故答案为： ． 45 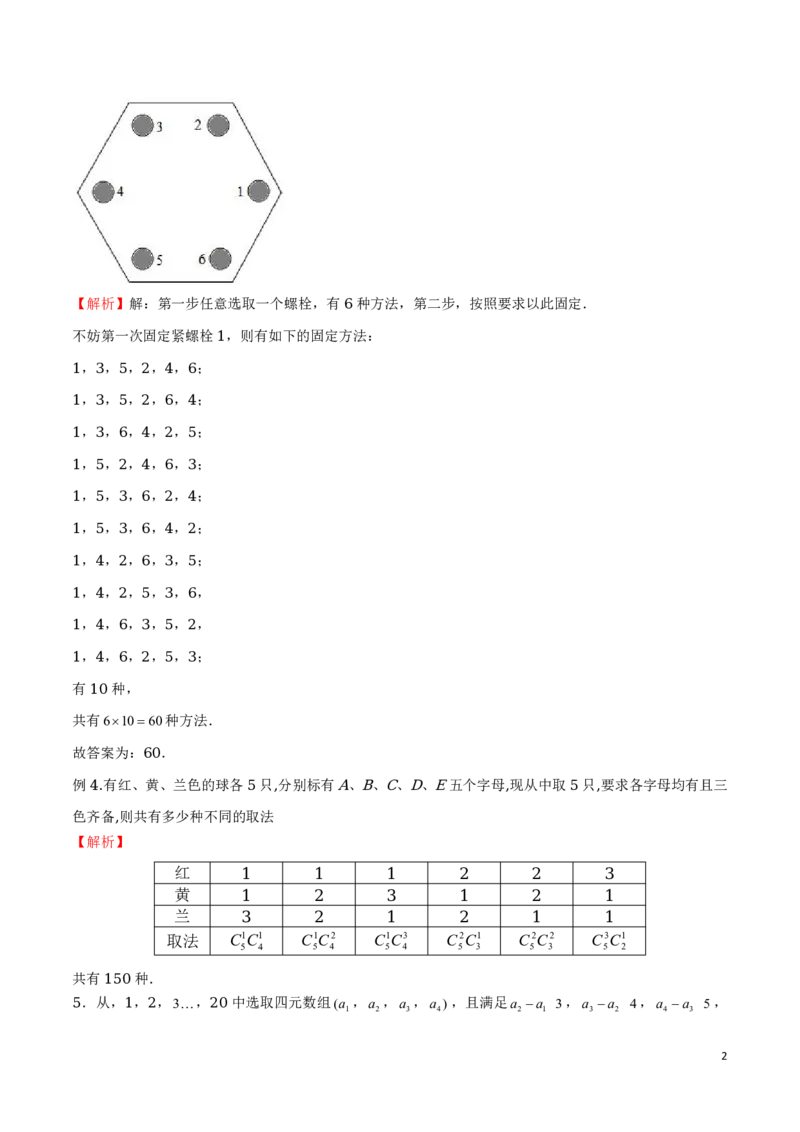例 ．工人在安装一个正六边形零件时，需要固定如图所示的六个位置的螺栓．若按一定顺序将每个螺栓固 3 定紧，但不能连续固定相邻的 个螺栓．则不同的固定螺栓方式的种数是 ． 2 60 1【解析】解：第一步任意选取一个螺栓，有 种方法，第二步，按照要求以此固定． 6 不妨第一次固定紧螺栓 ，则有如下的固定方法： 1 ， ， ， ， ， ； 1 3 5 2 4 6 ， ， ， ， ， ； 1 3 5 2 6 4 ， ， ， ， ， ； 1 3 6 4 2 5 ， ， ， ， ， ； 1 5 2 4 6 3 ， ， ， ， ， ； 1 5 3 6 2 4 ， ， ， ， ， ； 1 5 3 6 4 2 ， ， ， ， ， ； 1 4 2 6 3 5 ， ， ， ， ， ， 1 4 2 5 3 6 ， ， ， ， ， ， 1 4 6 3 5 2 ， ， ， ， ， ； 1 4 6 2 5 3 有 种， 10 共有61060种方法． 故答案为： ． 60 例 有红、黄、兰色的球各 只 分别标有 、 、 、 、 五个字母 现从中取 只 要求各字母均有且三 4. 5 , A B C D E , 5 , 色齐备 则共有多少种不同的取法 【解析】, 红 黄 1 1 1 2 2 3 兰 1 2 3 1 2 1 取法 C3 1C1 C1 2C2 C1 1C3 C2 2C1 C2 1C2 C1 3C1 5 4 5 4 5 4 5 3 5 3 5 2 共有 种 ．从1，50，.，3， 中选取四元数组(a ，a ，a ，a )，且满足a a 3，a a 4，a a 5， 1 2 3 4 2 1 3 2 4 3 5 1 2 20 2则这样的四元数组(a ，a ，a ，a )的个数是( ) 1 2 3 4 ．C4 ．C4 ．C4 ．C4 8 11 14 16 A B C D 【解析】解：将a 连同其右边的 个空位捆绑，a 连同其右边的 个空位捆绑，a 连同其右边的 个空位 1 2 3 2 3 4 捆绑分别看作一个元素，四元数组(a ，a ，a ，a )的个数相当于从 个元素中选取 个，故这样的四 1 2 3 4 11 4 元数组(a ，a ，a ，a )的个数是C4 ． 1 2 3 4 11 故选：B． 例 ．定义 有增有减 数列{a }如下：tN*，满足a a ，且sN*，满足a a ．已知 有增有减 n t t1 S S1 6 “ ” “ ” 数列{a }共 项，若a {x，y，z}(i1， ， ，4)，且x y z，则数列{a }共有( ) n i n 4 2 3 ． 个 ． 个 ． 个 ． 个 A 64 B 57 C 56 D 54 【解析】解：由题意可知 个数值的数列中，只有 个数值，例如：x，x，y，y类型，共有C2412 3 4 2 种． 只有 个数值相同，例如：x，x，y，z类型．共有：C21030种； 3 2 有 个数值相同，例如x，x，x，y类型，共有：C1C1212种． 3 2 3 满足题目的数列类型共有： 种． 54 故选：D． 例 ．若一个三位数的各位数字之和为 ，则称这个三位数为 十全十美数 ，如 ， 都是 7 10 “ ” 208 136 十全十美数 ，则这样的 十全十美数 共有( )个 “ ” “ ” ． ． ． ． A 32 B 64 C 54 D 96 【解析】解：任取一个 十全十美三位数 ， “ ” 包含含有一个 的三位数：44218 0 ， ， ， ， 109 190 901 910 ， ， ， ， 208 280 802 820 ， ， ， ， 307 370 703 730 ， ， ， ， 406 460 604 640 ， ， 505 550 含有相同数字的三位数：4312，分别为： ， ， ， 118 181 811 3， ， ， 226 262 622 ， ， ， 334 343 433 ， ， ， 442 244 424 不含有 ，并且没有相同数字的三位数．4A3 24，分别为： 3 0 ， ， ， ， ， ， 127 172 271 217 721 712 ， ， ， ， ， ， 136 163 316 361 613 631 ， ， ， ， ， ， 145 154 451 415 514 541 ， ， ， ， ， ， 235 253 352 325 523 532 共 个， 54 故选：C． 例 ．集合I {1， ， ， ，5}．选择I 的两个非空子集A和B，要使B中的最小数大于A中的最大数， 8 2 3 4 则不同的选择方法有 种． 49 【解析】解：集合A、B中没有相同的元素，且都不是空集， 从 个元素中选出 个元素，有C2 10种选法，小的给A集合，大的给B集合； 5 5 2 从 个元素中选出 个元素，有C3 10种选法，再分成 一个元素一组、 个元素一组，有两种分法，较 5 5 3 1 2 小元素的一组给A集合， 较大元素的一组的给B集合，共有21020种方法； 从 个元素中选出 个元素，有C4 5种选法，再分成 个元素一组、 三个元素一组； 个元素一组、 5 5 4 1 3 2 2 个元素一组； 个元素一组、 一个元素一组，共三种分法，较小元素的一组给A集合，较大元素的一组的 3 1 给B集合，共有3515种方法； 从 个元素中选出 个元素，有C5 1种选法，再分成 个元素一组、 个元素一组； 个元素一组、 个 5 5 5 1 4 2 3 元素一组； 个元素一组、 个元素一组； 个元素一组、 两个元素一组组，有四种分法，较小元素的一 3 2 4 1 组给A集合，较大元素的一组的给B集合，共有414种方法； 总计为102015449种方法． 故答案为： 49 例 ．定义域为集合{1， ， ，，12}上的函数 f(x)满足：① f （ ）1；②| f(x1) f(x)|1(x1， 9 2 3 1 ，，11)；③ f （ ）、 f （ ）、 f(12)成等比数列；这样的不同函数 f(x)的个数为 ． 2 1 6 155 4【解析】解：经分析， f(x)的取值的最大值为x，最小值为2x，并且成以 为公差的等差数列， 2 故 f （ ）的取值为 ， ， ， ，2，4． 6 6 4 2 0 f(12)的取值为 ， ， ， ， ， ， ，2，4，6，8，10， 12 10 8 6 4 2 0 所以能使 f(x)中的 f （ ）、 f （ ）、 f(12)成等比数列时， f （ ）、 f （ ）、 f(12)的取值只有两种情况： 1 6 1 6 ① f （ ）1、 f （ ）2、 f(12)4；② f （ ）1、 f （ ）2、 f(12)4． 1 6 1 6 | f(x1) f(x)|1(x1， ，，11)， f(x1) f(x)1，或者 f(x1) f(x)1，即得到后项时，把前 2 项加 或者把前项减 ． 1 1 （ ）当 f（ ）1、f（ ）2、f(12)4时；将要构造满足条件的等比数列分为两步，第一步：从 f （ ） 1 1 6 1 变化到 f （ ），第二步：从 f （ ）变化的 f(12)． 6 6 从 f （ ）变化到 f （ ）时有 次变化，函数值从 变化到 ，故应从 次中选择 步加 ，剩余的 1 6 5 1 2 5 3 1 两次减 ．对应的方法数为C3 10种． 5 1 从 f （ ）变化到 f(12)时有 次变化，函数值从 变化到 ，故应从 次变化中选择 次增加 ，剩 6 6 2 4 6 4 1 余两次减少 ，对应的方法数为C4 15种． 6 1 根据分步乘法原理，共有1015150种方法． （ ）当 f （ ）1、 f （ ）2、 f(12)4时，将要构造满足条件的等比数列分为两步，第一步：从 f 2 1 6 （ ）变化到 f （ ），第二步：从 f （ ）变化的 f(12)． 1 6 6 从 f （ ）变化到 f （ ）时有 次变化，函数值从 变化到2，故应从 次中选择 步加 ，剩余 1 6 5 1 5 1 1 的 次减 ．对应的方法数为C1 5 种． 5 4 1 从 f （ ）变化到 f(12)时有 次变化，函数值从2变化到 ，故应从 次变化中选择 次增加 ， 6 6 4 6 6 1 对应的方法数为C6 1种． 6 根据分步乘法原理，共有515种方法． 综上，满足条件的 f(x)共有：1505155种． 故填： ． 155 例 ．由海军、空军、陆军各 名士兵组成一个有不同编号的33的小方阵，要求同一军种不在同一行， 10 3 也不在同一列，有 种排法． 2592 【解析】解：假设海军为a，空军为b，陆军为c，先将a，b，c ，填入33的小方阵， 则有2A3 12种，每个a，b，c 填入 名士兵均有A3 6种， 3 3 3 5故共有126662592， 故答案为： 2592 例 ．设集合I {1， ， ，4}，选择I 的两个非空子集A和B，使得A中最大的数不大于B中最小的数， 11 2 3 则可组成不同的子集对(A,B) 个． 49 【解析】解：根据题意，分 种情况讨论： 4 ①，集合A中最大的元素为 ，此时集合A有 种情况，集合B的数目为{1， ， ，4}的非空子集数目， 1 1 2 3 集合B有24 115种情况， 此时可组成11515个不同的子集对(A,B)， ②，集合A中最大的元素为 ， 2 此时集合A可以为{2}或{1，2}，有 种情况，集合B的数目为{2，，4}的非空子集数目，集合B有23 17 2 3 种情况， 此时可组成2714个不同的子集对(A,B)， ③，集合A中最大的元素为 ， 3 此时集合A可以为{3}或{1，3}或{2，3}或{1， ，3}，有 种情况，集合B的数目为{3，4}的非空子集 2 4 数目，集合B有22 13种情况， 此时可组成4312个不同的子集对(A,B)， ④，集合A中最大的元素为 ， 3 此时集合A的数目为{1， ，3}的子集数目，有23 8种情况，集合B必须为{4}，有 种情况， 2 1 6此时可组成818个不同的子集对(A,B)， 则一共可以组成151412849个不同的子集对(A,B)， 故答案为： ． 49 例 ．若集合E\{(p，q，r ，s)|0 ps 4，0 qs 4，0 rs 4且 p，q，r ，sN\}，F \{(t， 12 u，v ，w)|0 tu 4，0 vw 4且t，u，v ，wN\}，用card(X)表示集合X 中的元素个数，则card （ ）card(F)( ) E ． ． ． ． A 200 B 150 C 100 D 50 【解析】解：（ ）s4时， p，q，r 的取值的排列情况有44464种； 1 s3时， p，q，r 的取值的排列情况有33327种； s2时，有2228种； s1时，有1111种； card（ ）642781100； E （ ）u4时：若w4，t，v的取值的排列情况有4416种； 2 若w3，t，v 的取值的排列情况有4312种； 若w2，有428种； 若w1，有414种； u3时：若w4，t，v的取值的排列情况有3412种； 若w3，t，v 的取值的排列情况有339种； 若w2，有326种； 若w1，有313种； u2时：若w4，t，v 的取值的排列情况有248种； 若w3，有236种； 若w2，有224种； 若w1，有212种； u1时：若w4，t，v 的取值的排列情况有144种； 若w3，有133种； 若w2，有122种； 若w1，有111种； card(F)100； 7card（ ）card(F)200． E 故选：A． 例 ．某城市街道的平面图如图所示，若每个路口仅能沿右、左上、右上三个方向走，从A至B的路径条 13 数有n条：若P、Q两处因故施工，不能通行，从A至B的路径条数有m条，则n，m分别为( ) ． ； ． ； ． ； ． ； A 1552 256 B 1440 256 C 1552 288 D 1440 288 【解析】解：由于每个路口仅能沿右、左上、右上三个方向走，则从点A到任意一点的路径条数为自身左， 右下，左下三个点的路径条数之和， 故在走到每个点的路径条数如下图所示 故选：A． 例 ．某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形ABCD（边长为 个单位）的 14 2 顶点A处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为i(i1， ，，6)，则棋子就按逆时针方向行走i个单位，一直循环下去．则某人抛掷三次骰子后棋子恰好又回到 2 点A处的所有不同走法共有( ) ． 种 ． 种 ． 种 ． 种 A 22 B 24 C 25 D 27 【解析】解：法一：根据题意，正方形ABCD的边长为 个单位，则其周长是 ， 2 8 若抛掷三次骰子后棋子恰好又回到点A处，则三次骰子的点数之和是 或 ， 8 16 8若三次骰子的点数之和是 ，有 、 、 ， 、 、 ， 、 、 ， 、 、 ， 、 、 ，共 种组合， 8 1 1 6 1 2 5 1 3 4 2 2 4 2 3 3 5 若三次骰子的点数之和是 ，有 、 、 ， 、 、 ，共 种组合， 16 4 6 6 5 5 6 2 其中 、 、 ， 、 、 ， 、 、 ， 、 、 ， 、 、 ，这 种组合有C1 3种顺序， 3 1 1 6 2 2 4 2 3 3 4 6 6 5 5 6 5 、 、 ， 、 、 ，这 种组合有A3 6种顺序， 3 1 2 5 1 3 4 2 则抛掷三次骰子后棋子恰好又回到点A处的所有不同走法352627种， 法二：同法一：分析可得三次骰子的点数之和是 或 ， 8 16 若三次骰子的点数之和是 ，相当于 个点数中用 个隔板，有C2 21种顺序， 7 8 8 2 若三次骰子的点数之和是 ，有 、 、 ， 、 、 ，共 种组合，每种组合有C1 3种顺序， 3 16 4 6 6 5 5 6 2 则此时有236种顺序， 抛掷三次骰子后棋子恰好又回到点A处的所有不同走法21627种， 故选：D． 例 ．如图所示，玩具计数算盘的三档上各有 个算珠，现将每档算珠分为左右两部分，左侧的 15 7 每个算珠表示数 ，右侧的每个算珠表示数 （允许一侧无珠），记上、中、下三档的数字和分别 2 1 为 a ，b， c ．例如，图中上档的数字和a9．若 a ，b， c 成等差数列，则不同的分珠计数法有( )种． ． ． ． ． A 12 B 24 C 16 D 32 【解析】解：根据题意，a，b，c的取值范围都是从7~14共 个数字，故公差d范围是3到 ， 8 3 ①当公差d 0时，有C1 8种， 8 ②当公差d 1时，b不取 和 ，有2C1 12种， 6 7 14 ③当公差d 2时，b不取 ， ， ， ，有2C1 8种， 4 7 8 13 14 ④当公差d 3时，b只能取 或 ，有2C1 4种， 2 10 11 9综上共有8128432种， 故选：D． 例 若一个三位数中任意两相邻数位上两数差的绝对值小于或等于1，则称此三位数为 灵犀数 ，这样 16. “ ” 的三位 灵犀数 共有 个 “ ” 【解析】 设灵犀数为abc，若b 0，则a1，c 0,1，此时有2个灵犀数； 若b1，则a 1,2,c 0,1,2，此时有6个灵犀数； 若b 2,3,L ,8，对每个b均有3个a,c可取，此时有63个灵犀数， 若b9，则a,c 8,9则，此时有4个灵犀数，故三位 灵犀数 共有75个 “ ” . 10