专题18圆锥曲线综合（10大考向真题解读）-解析版_2024-2025高三（6-6月题库）_2024年08月试卷_08202025版《真题题源解密-专题分类》数学

专题 18 圆锥曲线综合 命题解读 考向 考查统计 椭圆的标准方程 2024·新高考Ⅰ卷，16（1） 双曲线中的双斜率 2022·新高考Ⅰ卷，21（1） 抛物线的轨迹方程 2023·新高考Ⅰ卷，22（1） 2022·新高考Ⅱ卷，21（1） 1.高考对圆锥曲线综合的考查，重点是 双曲线的标准方程 2023·新高考Ⅱ卷，21（1） 直线与圆锥曲线关系中的求弦长、面积 椭圆中的弦长公式、三角形面积 2024·新高考Ⅰ卷，16（2） 及弦中点、定点、定值、参数取值范围 双曲线与数列的综合知识 2024·新高考Ⅱ卷，19 和最值等问题。 双曲线中的弦长公式、三角形面积 2022·新高考Ⅰ卷，21（2） 抛物线中的弦长公式 2023·新高考Ⅰ卷，22（2） 双曲线中的斜率问题 2022·新高考Ⅱ卷，21（2） 双曲线中的定直线问题 2023·新高考Ⅱ卷，21（2） 命题分析 2024(cid:3)(cid:4)(cid:5)(cid:6)(cid:4)(cid:5)Ⅰ(cid:7)(cid:5)(cid:8)(cid:9)(cid:10)(cid:11)(cid:12)(cid:13)(cid:14)(cid:15)(cid:16)(cid:17)(cid:18)(cid:19)(cid:20)(cid:21)(cid:22)(cid:23)(cid:24)(cid:12)(cid:25)(cid:26)(cid:27)(cid:20)(cid:21)(cid:28)(cid:29)(cid:30)(cid:31)(cid:32)(cid:22)(cid:33)(cid:34)(cid:35)(cid:36)(cid:37) Ⅱ(cid:7)(cid:5)(cid:8)(cid:9)(cid:38)(cid:39)(cid:40)(cid:41)(cid:42)(cid:39)(cid:17)(cid:43)(cid:44)(cid:45)(cid:46)(cid:12)(cid:47)(cid:48)(cid:22)(cid:49)(cid:50)(cid:31)(cid:32)(cid:51)(cid:52)(cid:53)(cid:4)(cid:22)(cid:33)(cid:34)(cid:53)(cid:33)(cid:37)(cid:54)(cid:25)(cid:55)(cid:56)(cid:12)(cid:57)(cid:29)(cid:25)(cid:58)(cid:58)(cid:59)(cid:60)(cid:12)(cid:22) (cid:61)(cid:62)(cid:63)(cid:64)(cid:65)(cid:56)(cid:12)(cid:57)(cid:56)(cid:36)(cid:66)(cid:67)(cid:64)(cid:68)(cid:56)(cid:12)(cid:52)(cid:69)(cid:70)(cid:71)(cid:37)(cid:11)(cid:72)(cid:42)(cid:39)(cid:49)(cid:50)(cid:25)(cid:4)(cid:5)(cid:43)(cid:73)(cid:12)(cid:74)(cid:75)(cid:76)(cid:77)(cid:22)(cid:25)(cid:5)(cid:8)(cid:5)(cid:78)(cid:73)(cid:79)(cid:80) (cid:81)(cid:12)(cid:24)(cid:51)(cid:82)(cid:83)(cid:37)(cid:55)(cid:3)(cid:4)(cid:5)(cid:7)(cid:12)(cid:84)(cid:5)(cid:85)(cid:22)(cid:65)(cid:86)(cid:25)(cid:87)(cid:88)(cid:65)(cid:89)(cid:22)(cid:25)(cid:62)(cid:90)(cid:16)(cid:73)(cid:91)(cid:92)(cid:93)(cid:40)(cid:94)(cid:95)(cid:96)(cid:6)(cid:92)(cid:93)(cid:97)(cid:98)(cid:22)(cid:23)(cid:24)(cid:43) (cid:73)(cid:45)(cid:46)(cid:12)(cid:26)(cid:27)(cid:99)(cid:17)(cid:49)(cid:50)(cid:99)(cid:28)(cid:100)(cid:101)(cid:99)(cid:12)(cid:5)(cid:8)(cid:22)(cid:102)(cid:24)(cid:5)(cid:8)(cid:5)(cid:78)(cid:12)(cid:103)(cid:30)(cid:52)(cid:69)(cid:31)(cid:32)(cid:28)(cid:104)(cid:105)(cid:70)(cid:106)(cid:31)(cid:32)(cid:37)(cid:107)(cid:29)2025(cid:3)(cid:4) (cid:5)(cid:108)(cid:25)(cid:98)(cid:51)(cid:5)(cid:8)(cid:11)(cid:72)(cid:42)(cid:39)(cid:36)(cid:12)(cid:18)(cid:19)(cid:17)(cid:109)(cid:110)(cid:111)(cid:112)(cid:113)(cid:114)(cid:111)(cid:115)(cid:116)(cid:117)(cid:17)(cid:118)(cid:119)(cid:118)(cid:120)(cid:56)(cid:85)(cid:37) 试题精讲 (cid:22)(cid:23)(cid:24)(cid:25)(cid:21) æ 3ö x2 y2 1(cid:26)(cid:27)2024(cid:28)(cid:29)(cid:30)Ⅰ(cid:31)·16(cid:32)(cid:33)(cid:34)A(0,3)(cid:35)Pç3, ÷(cid:36)(cid:37)(cid:38)C: + =1(a>b>0)(cid:39)(cid:40)(cid:41). è 2ø a2 b2 (1)(cid:42)C(cid:43)(cid:44)(cid:45)(cid:46);(2)(cid:47)(cid:48)P(cid:43)(cid:49)(cid:50)l(cid:51)C(cid:52)(cid:53)(cid:22)(cid:41)B(cid:54)(cid:55)VABP(cid:43)(cid:56)(cid:57)(cid:36)9(cid:54)(cid:42)l(cid:43)(cid:58)(cid:59)(cid:26) 1 (cid:60)(cid:25)(cid:61)(cid:62)(1) 2 (2)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)3x-2y-6=0(cid:63)x-2y=0. (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:66)(cid:67)(cid:40)(cid:41)(cid:68)(cid:69)(cid:3)(cid:52)a,b(cid:43)(cid:58)(cid:59)(cid:54)(cid:24)(cid:70)(cid:71)(cid:72)(cid:73) (cid:27)2(cid:32)(cid:58)(cid:74)(cid:22)(cid:10)(cid:75) AP (cid:36)(cid:76)(cid:54)(cid:42)(cid:70)(cid:77)(cid:78)(cid:79)(cid:43)(cid:29)(cid:54)(cid:71)(cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)(cid:54)(cid:81)(cid:82)(cid:83)(cid:84)(cid:85)(cid:50)(cid:80)(cid:44)(cid:7)(cid:86)(cid:68)(cid:69)(cid:84)(cid:87) (cid:88)(cid:43)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54)(cid:89)(cid:90)(cid:37)(cid:38)(cid:58)(cid:59)(cid:68)(cid:69)B(cid:41)(cid:91)(cid:92)(cid:54)(cid:93)(cid:68)(cid:69)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:73)(cid:58)(cid:74)(cid:94)(cid:10)(cid:95)(cid:74)(cid:22)(cid:68)(cid:69)(cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43) (cid:80)(cid:44)(cid:54)(cid:81)(cid:96)Bx ,y (cid:54)(cid:97)(cid:98)(cid:41)(cid:69)(cid:49)(cid:50)(cid:80)(cid:44)(cid:35)(cid:41)(cid:99)(cid:37)(cid:38)(cid:39)(cid:68)(cid:69)(cid:58)(cid:59)(cid:100)(cid:54)(cid:24)(cid:70)(cid:71)(cid:72)(cid:73)(cid:74)(cid:77)(cid:10)(cid:95)(cid:74)(cid:22)(cid:68)(cid:69)(cid:41)B(cid:69) 0 0 (cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)(cid:54)(cid:82)(cid:83)(cid:37)(cid:38)(cid:43)(cid:101)(cid:13)(cid:58)(cid:59)(cid:71)(cid:72)(cid:42)(cid:24)(cid:73)(cid:74)(cid:102)(cid:10)(cid:103)(cid:104)(cid:105)(cid:106)(cid:49)(cid:50)AB(cid:107)(cid:46)(cid:108)(cid:109)(cid:99)(cid:43)(cid:110)(cid:111)(cid:54)(cid:81)(cid:96)(cid:49)(cid:50) y=kx+3(cid:54)(cid:89)(cid:90)(cid:37)(cid:38)(cid:58)(cid:59)(cid:54)(cid:68)(cid:69)(cid:41)B(cid:91)(cid:92)(cid:54)(cid:81)(cid:82)(cid:83)(cid:41)(cid:69)(cid:49)(cid:50)(cid:80)(cid:44)(cid:7)(cid:86)(cid:71)(cid:72)(cid:73)(cid:74)(cid:112)(cid:10)(cid:103)(cid:104)(cid:30)(cid:113)(cid:49)(cid:50)PB(cid:107)(cid:46)(cid:108) 3 (cid:109)(cid:99)(cid:43)(cid:110)(cid:111)(cid:54)(cid:81)(cid:96)PB:y- =k(x-3)(cid:54)(cid:82)(cid:83)(cid:114)(cid:115)(cid:7)(cid:86)(cid:35)(cid:41)(cid:69)(cid:49)(cid:50)(cid:43)(cid:80)(cid:44)(cid:7)(cid:86)(cid:71)(cid:72)(cid:68)(cid:69)(cid:25)(cid:61)(cid:73)(cid:74)(cid:116)(cid:10)(cid:96)(cid:50)(cid:74) 2 1 (cid:117)(cid:74)(cid:112)(cid:22)(cid:118)(cid:54)(cid:82)(cid:83)(cid:119)(cid:84)(cid:120)(cid:121)(cid:122)(cid:123)(cid:29)(cid:121) (cid:124)(cid:125)(cid:56)(cid:57)(cid:71)(cid:72). 2 ì b=3 ïï 9 ìb2 =9 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:68)í (cid:54)(cid:24)(cid:68)í (cid:54) ï 9 + 4 =1 îa2 =12 ïîa2 b2 b2 9 1 (cid:129)(cid:75)e= 1- = 1- = . a2 12 2 3 3- 1 (cid:27)2(cid:32)(cid:74)(cid:22)(cid:10) 2 1(cid:54)(cid:93)(cid:49)(cid:50)AP(cid:43)(cid:58)(cid:59)(cid:36)y =- x+3(cid:54)(cid:71)x+2y-6=0(cid:54) k = =- 2 AP 0-3 2 æ 3ö 2 3 5 x2 y2 AP = 0-32+ç3- ÷ = (cid:54)(cid:127)(cid:27)1(cid:32)(cid:34)C: + =1(cid:54) è 2ø 2 12 9 2´9 12 5 d = = (cid:96)(cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)(cid:36)d(cid:54)(cid:93) 3 5 5 (cid:54) 2 12 5 (cid:93)(cid:130)(cid:49)(cid:50)AP(cid:131)(cid:132)(cid:117)AP(cid:133)(cid:49)(cid:43)(cid:58)(cid:134)(cid:84)(cid:87) (cid:135)(cid:136)(cid:71)(cid:72)(cid:54) 5 (cid:137)(cid:138)(cid:139)(cid:84)(cid:85)(cid:50)(cid:117)(cid:37)(cid:38)(cid:43)(cid:51)(cid:41)(cid:71)(cid:36)(cid:41)B(cid:54) (cid:96)(cid:139)(cid:84)(cid:85)(cid:50)(cid:43)(cid:58)(cid:59)(cid:36)(cid:10)x+2y+C =0(cid:54) C+6 12 5 (cid:93) = (cid:54)(cid:24)(cid:68)C =6(cid:63)C =-18(cid:54) 5 5 ì x2 y2 ìx=-3 ï + =1 ì x=0 ï (cid:140)C =6(cid:138)(cid:54)(cid:89)(cid:90)í 12 9 (cid:54)(cid:24)(cid:68)í (cid:63)í 3(cid:54) ï îy=-3 ïy=- îx+2y+6=0 î 2æ 3ö (cid:71)B0,-3(cid:63)ç-3,- ÷(cid:54) è 2ø 3 3 (cid:140)B0,-3(cid:138)(cid:54)(cid:137)(cid:138)k = (cid:54)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y= x-3(cid:54)(cid:71)3x-2y-6=0(cid:54) l 2 2 æ 3ö 1 1 (cid:140)Bç-3,- ÷(cid:138)(cid:54)(cid:137)(cid:138)k = (cid:54)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y = x(cid:54)(cid:71)x-2y=0(cid:54) è 2ø l 2 2 ì x2 y2 ï + =1 (cid:140)C =-18(cid:138)(cid:54)(cid:89)(cid:90)í 12 9 (cid:68)2y2-27y+117=0(cid:54) ï îx+2y-18=0 D=272-4´2´117=-207<0(cid:54)(cid:137)(cid:138)(cid:139)(cid:49)(cid:50)(cid:117)(cid:37)(cid:38)(cid:141)(cid:51)(cid:41). (cid:142)(cid:39)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)3x-2y-6=0(cid:63)x-2y=0. (cid:74)(cid:94)(cid:10)(cid:95)(cid:74)(cid:22)(cid:68)(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:58)(cid:59)(cid:36)x+2y-6=0(cid:54) 12 5 (cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)d = (cid:54) 5 ì x +2y -6 12 5 ï 0 0 = ìx =-3 (cid:96)Bx ,y (cid:54)(cid:93) ï í 5 5 (cid:54)(cid:24)(cid:68) ï í 0 3(cid:63) ì í x 0 =0 (cid:54) 0 0 ï x 0 2 + y 0 2 =1 ï î y 0 =- 2 îy 0 =-3 ï î 12 9 æ 3ö (cid:71)B0,-3(cid:63)ç-3,- ÷(cid:54)(cid:75)(cid:143)(cid:95)(cid:74)(cid:22). è 2ø (cid:74)(cid:77)(cid:10)(cid:95)(cid:74)(cid:22)(cid:68)(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:58)(cid:59)(cid:36)x+2y-6=0(cid:54) 12 5 (cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)d = (cid:54) 5 (cid:96)B  2 3cosq,3sinq  (cid:54)(cid:144)(cid:145)qÎ0,2p(cid:54)(cid:93)(cid:146) 2 3cosq+6sinq-6 = 12 5 (cid:54) 5 5 ì 3 ï ï cosq=- 2 ìcosq=0 (cid:89)(cid:90)cos2q+sin2q=1(cid:54)(cid:24)(cid:68)í (cid:63)í (cid:54) ï 1 îsinq=-1 sinq=- ïî 2 æ 3ö (cid:71)B0,-3(cid:63)ç-3,- ÷(cid:54)(cid:75)(cid:143)(cid:95)(cid:74)(cid:22)(cid:73) è 2ø (cid:74)(cid:102)(cid:10)(cid:140)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:108)(cid:109)(cid:99)(cid:138)(cid:54)(cid:137)(cid:138)B0,-3(cid:54) 1 3 3 S = ´6´3=9(cid:54)(cid:147)(cid:148)(cid:21)(cid:128)(cid:54)(cid:137)(cid:138)k = (cid:54)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y= x-3(cid:54)(cid:71)3x-2y-6=0(cid:54) VPAB 2 l 2 2 (cid:140)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:138)(cid:54)(cid:96)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:36)y=kx+3(cid:54) ì y=kx+3 (cid:89)(cid:90)(cid:37)(cid:38)(cid:58)(cid:59)(cid:146) ï íx2 y2 (cid:54)(cid:93)  4k2+3  x2+24kx=0(cid:54)(cid:144)(cid:145)k ¹k (cid:54)(cid:71)k ¹- 1 (cid:54) ï + =1 AP 2 î12 9-24k 1 (cid:24)(cid:68)x=0(cid:63)x= (cid:54)k ¹0(cid:54)k ¹- (cid:54) 4k2+3 2 -24k -12k2+9 æ -24k -12k2+9ö (cid:149)x= (cid:54)(cid:93)y= (cid:54)(cid:93)Bç , ÷ 4k2+3 4k2+3 è4k2+3 4k2+3 ø (cid:95)(cid:74)(cid:22)(cid:68)(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:58)(cid:59)(cid:36)x+2y-6=0(cid:54) 12 5 (cid:41)B(cid:69)(cid:49)(cid:50)AP(cid:43)(cid:80)(cid:44)d = (cid:54) 5 -24k -12k2+9 +2´ -6 3 (cid:93) 4k2+3 4k2+3 12 5 (cid:54)(cid:24)(cid:68)k= (cid:54) = 2 5 5 æ 3ö 1 1 (cid:137)(cid:138)Bç-3,- ÷(cid:54)(cid:93)(cid:68)(cid:69)(cid:137)(cid:138)k = (cid:54)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y = x(cid:54)(cid:71)x-2y=0(cid:54) è 2ø l 2 2 (cid:142)(cid:39)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)3x-2y-6=0(cid:63)x-2y=0. æ 3ö (cid:74)(cid:112)(cid:10)(cid:140)l(cid:43)(cid:107)(cid:46)(cid:108)(cid:109)(cid:99)(cid:138)(cid:54)l:x=3,Bç3,- ÷, PB =3,A(cid:69)PB(cid:80)(cid:44)d =3(cid:54) è 2ø 1 9 (cid:137)(cid:138)S = ´3´3= ¹9(cid:108)(cid:150)(cid:151)(cid:152)(cid:153). VABP 2 2 3 (cid:140)l(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:138)(cid:54)(cid:96)PB:y- =k(x-3)(cid:54)(cid:149)Px,y ,Bx ,y (cid:54) 2 1 1 2 2 ì 3 y=k(x-3)+ ï ï í 2 (cid:54)(cid:154)y(cid:72)(cid:68)  4k2+3  x2-  24k2-12k  x+36k2-36k-27=0(cid:54) ïx2 y2 + =1 ïî12 9 Δ=  24k2-12k 2 -4  4k2+3  36k2-36k-27  >0(cid:54)(cid:55)k ¹k (cid:54)(cid:71)k ¹- 1 (cid:54) AP 2 ì 24k2-12k 27 ïx +x = 4 3 k2+1 3k2+9k+ í ï 1 2 4k2+3 , PB = k2+1 x +x 2-4xx = 4 (cid:54) ï 36k2-36k-27 1 2 1 2 4k2+3 xx = ïî 1 2 4k2+3 3 27 3 3k+ 4 3 k2+1 3k2+9k+ 3k+ A(cid:69)(cid:49)(cid:50)PB(cid:80)(cid:44) 2 1 4 2 (cid:54) d = ,S = × × =9 k2+1 VPAB 2 4k2+3 k2+1 1 3 1 3 \k = (cid:63) (cid:54)(cid:155)(cid:150)(cid:151)(cid:21)(cid:128)(cid:54)\l:y= x(cid:63)y= x-3(cid:54)(cid:71)3x-2y-6=0(cid:63)x-2y=0. 2 2 2 2 æ 3ö (cid:74)(cid:116)(cid:10)(cid:140)l(cid:43)(cid:107)(cid:46)(cid:108)(cid:109)(cid:99)(cid:138)(cid:54)l:x=3,Bç3,- ÷, PB =3,A(cid:69)PB(cid:80)(cid:44)d =3(cid:54) è 2ø 1 9 (cid:137)(cid:138)S = ´3´3= ¹9(cid:108)(cid:150)(cid:151)(cid:152)(cid:153). VABP 2 23 (cid:140)(cid:49)(cid:50)l(cid:107)(cid:46)(cid:109)(cid:99)(cid:138)(cid:54)(cid:96)l:y=k(x-3)+ (cid:54) 2 æ 3ö (cid:96)l(cid:117)y(cid:156)(cid:43)(cid:51)(cid:41)(cid:36)Q(cid:54)(cid:149)x=0(cid:54)(cid:93)Qç0,-3k+ ÷(cid:54) è 2ø ì 3 (cid:89)(cid:90) ï í y=kx-3k+ 2(cid:54)(cid:93)(cid:146)  3+4k2 x2-8k æ ç3k- 3ö ÷x+36k2-36k-27=0(cid:54) ï î3x2+4y2 =36 è 2ø  3+4k2 x2-8k æ ç3k- 3ö ÷x+36k2-36k-27=0(cid:54) è 2ø (cid:144)(cid:145)Δ=8k2 æ ç3k- 3ö ÷ 2 -4  3+4k2 36k2-36k-27  >0(cid:54)(cid:55)k ¹- 1 (cid:54) è 2ø 2 36k2-36k-27 12k2-12k-9 (cid:93)3x = ,x = (cid:54) B 3+4k2 B 3+4k2 1 1 3 12k+18 1 3 (cid:93)S = AQ x -x = 3k+ =9(cid:54)(cid:24)(cid:43)k = (cid:63)k= (cid:54)(cid:157)(cid:66)(cid:67)(cid:158)(cid:159)(cid:86)(cid:105)(cid:106)(cid:155)(cid:150)(cid:151)(cid:21)(cid:128). 2 P B 2 2 3+4k2 2 2 1 3 (cid:93)(cid:49)(cid:50)l(cid:36)y = x(cid:63)y= x-3(cid:54)(cid:71)3x-2y-6=0(cid:63)x-2y=0. 2 2 2(cid:26)(cid:27)2024(cid:28)(cid:29)(cid:30)Ⅱ(cid:31)·19(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)C:x2-y2 =mm>0(cid:54)(cid:41)P5,4(cid:99)C(cid:39)(cid:54)k(cid:36)(cid:162)(cid:13)(cid:54)01)(cid:39)(cid:54)(cid:49)(cid:50)l(cid:51)C(cid:52)P(cid:54)Q(cid:40)(cid:41)(cid:54)(cid:49)(cid:50) a2 a2-1 AP,AQ(cid:43)(cid:107)(cid:46)(cid:244)(cid:35)(cid:36)0(cid:26) (1)(cid:42)l(cid:43)(cid:107)(cid:46)(cid:73) (2)(cid:47)tanÐPAQ=2 2(cid:54)(cid:42)(cid:245)PAQ(cid:43)(cid:56)(cid:57)(cid:26) (cid:60)(cid:25)(cid:61)(cid:62)(1)-1(cid:73) 16 2 (2) (cid:26) 9 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:41)A(2,1)(cid:99)(cid:160)(cid:161)(cid:50)(cid:39)(cid:72)(cid:42)(cid:70)a(cid:54)(cid:246)(cid:34)(cid:49)(cid:50)l(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:54)(cid:96)l:y=kx+m(cid:54) Px,y ,Qx ,y (cid:54)(cid:81)(cid:97)(cid:98)k +k =0(cid:54)(cid:71)(cid:72)(cid:24)(cid:70)l(cid:43)(cid:107)(cid:46)(cid:73) 1 1 2 2 AP AQ (cid:27)2(cid:32)(cid:97)(cid:98)(cid:49)(cid:50)AP,AQ(cid:43)(cid:107)(cid:46)(cid:244)(cid:35)(cid:36)0(cid:72)(cid:34)(cid:49)(cid:50)AP,AQ(cid:43)(cid:247)(cid:107)(cid:78)(cid:248)(cid:249)(cid:54)(cid:97)(cid:98)tanÐPAQ=2 2(cid:71)(cid:72)(cid:42)(cid:70)(cid:49)(cid:50) AP,AQ(cid:43)(cid:107)(cid:46)(cid:54)(cid:81)(cid:64)(cid:159)(cid:89)(cid:90)(cid:49)(cid:50)AP,AQ(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:42)(cid:70)(cid:41)P,Q(cid:43)(cid:91)(cid:92)(cid:54)(cid:71)(cid:72)(cid:68)(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:58)(cid:59)(cid:75)(cid:231)PQ (cid:43)(cid:115)(cid:54)(cid:127)(cid:41)(cid:69)(cid:49)(cid:50)(cid:43)(cid:80)(cid:44)(cid:7)(cid:86)(cid:42)(cid:70)(cid:41)A(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44)(cid:54)(cid:71)(cid:72)(cid:68)(cid:70)(cid:245)PAQ(cid:43)(cid:56)(cid:57)(cid:26) x2 y2 4 1 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:250)(cid:36)(cid:41)A(2,1)(cid:99)(cid:160)(cid:161)(cid:50)C: - =1(a>1)(cid:39)(cid:54)(cid:129)(cid:75) - =1(cid:54)(cid:24)(cid:68)a2 =2(cid:54)(cid:71)(cid:160)(cid:161)(cid:50) a2 a2-1 a2 a2-1 x2 C: - y2 =1(cid:26) 2 (cid:246)(cid:34)(cid:49)(cid:50)l(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:54)(cid:96)l:y=kx+m(cid:54)Px,y ,Qx ,y (cid:54) 1 1 2 2 ìy=kx+m (cid:89)(cid:90) ï íx2 (cid:72)(cid:68)(cid:54)  1-2k2 x2-4mkx-2m2-2=0(cid:54) ï -y2 =1 î 2 (cid:129)(cid:75)(cid:54)x +x =- 4mk ,xx = 2m2+2 (cid:54)Δ=16m2k2-4  2m2+2  2k2-1  >0Þm2+1-2k2 >0(cid:55) 1 2 2k2-1 1 2 2k2-1 2 k ¹± (cid:26) 2 y -1 y -1 (cid:129)(cid:75)(cid:127)k +k =0(cid:72)(cid:68)(cid:54) 2 + 1 =0(cid:54) AP AQ x -2 x -2 2 1 (cid:71)x -2kx +m-1+x -2kx +m-1=0(cid:54) 1 2 2 1(cid:71)2kxx +m-1-2kx +x -4m-1=0(cid:54) 1 2 1 2 2m2+2 æ 4mk ö (cid:129)(cid:75)2k´ +m-1-2k ç- ÷-4m-1=0(cid:54) 2k2-1 è 2k2-1ø (cid:16)(cid:251)(cid:68)(cid:54)8k2+4k-4+4mk+1=0(cid:54)(cid:71)k+12k-1+m=0(cid:54) (cid:129)(cid:75)k =-1(cid:63)m=1-2k(cid:54) (cid:140)m=1-2k(cid:138)(cid:54)(cid:49)(cid:50)l:y=kx+m=kx-2+1(cid:48)(cid:41)A2,1(cid:54)(cid:117)(cid:21)(cid:128)(cid:108)(cid:147)(cid:54)(cid:252)(cid:253)(cid:54) (cid:202)k =-1(cid:26) (cid:27)2(cid:32)(cid:254)(cid:58)(cid:74)(cid:22)(cid:255)(cid:10)(cid:60)(cid:256)(cid:257)(cid:24)(cid:62)(cid:162)(cid:258)(cid:259)(cid:16) æ π ö (cid:108)(cid:260)(cid:96)(cid:49)(cid:50)PA,AQ(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)a,bça< 0(cid:54) 1 2 (cid:140)P,Q(cid:155)(cid:99)(cid:160)(cid:161)(cid:50)(cid:171)(cid:172)(cid:138)(cid:54)ÐPAQ=2a(cid:54)(cid:129)(cid:75)tan2a=2 2(cid:54) 2 (cid:71) 2tan2a+tana- 2 =0(cid:54)(cid:24)(cid:68)tana= (cid:27)(cid:261)(cid:200)(cid:252)(cid:253)(cid:32) 2 (cid:137)(cid:138)PA(cid:117)(cid:160)(cid:161)(cid:50)(cid:43)(cid:262)(cid:263)(cid:50)(cid:84)(cid:85)(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:171)(cid:172)(cid:141)(cid:51)(cid:41)(cid:54)(cid:252)(cid:253)(cid:73) (cid:140)P,Q(cid:155)(cid:99)(cid:160)(cid:161)(cid:50)(cid:264)(cid:172)(cid:138)(cid:54) (cid:250)(cid:36)tanÐPAQ=2 2(cid:54)(cid:129)(cid:75)tanb-a=2 2(cid:54)(cid:71)tan2a=-2 2(cid:54) (cid:71) 2tan2a-tana- 2=0 (cid:54)(cid:24)(cid:68)tana= 2(cid:27)(cid:261)(cid:200)(cid:252)(cid:253)(cid:32)(cid:54) (cid:52)(cid:178)(cid:54)(cid:49)(cid:50)PA:y= 2x-2+1(cid:54)(cid:49)(cid:50)QA:y=- 2x-2+1(cid:54) ìy= 2x-2+1 ï 3   (cid:89)(cid:90)íx2 (cid:72)(cid:68)(cid:54) x2+2 2-4 x+10-4 2 =0(cid:54) ï -y2 =1 2 î 2 10-4 2 4 2-5 (cid:250)(cid:36)(cid:58)(cid:59)(cid:146)(cid:22)(cid:221)(cid:97)(cid:36)2(cid:54)(cid:129)(cid:75)x = (cid:54)y = (cid:54) P 3 P 3 10+4 2 -4 2-5 (cid:95)(cid:15)(cid:72)(cid:68)(cid:54)x = (cid:54)y = (cid:26) Q 3 Q 3 5 5 16 2+1- (cid:129)(cid:75)PQ:x+y- =0(cid:54) PQ = (cid:54)(cid:41)A(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44) 3 2 2 (cid:54) 3 3 d = = 2 3 1 16 2 2 16 2 (cid:202)(cid:245)PAQ(cid:43)(cid:56)(cid:57)(cid:36) ´ ´ = (cid:26) 2 3 3 9 (cid:254)(cid:58)(cid:74)(cid:94)(cid:255)(cid:10) (cid:96)(cid:49)(cid:50)AP(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)a(cid:54) æ ç00(cid:54)(cid:55)mn=-1(cid:54)(cid:82)(cid:83)(cid:286)(cid:287)(cid:74)(cid:68) C³çn+ ÷ 1+n2 (cid:54)(cid:96)(cid:288)(cid:13) AB BC 2 è nø 2 f(x)= æ çx+ 1ö ÷  1+x2(cid:54)(cid:82)(cid:83)(cid:289)(cid:13)(cid:42)(cid:70)(cid:144)(cid:256)(cid:226)(cid:200)(cid:54)(cid:93)(cid:68)C(cid:43)(cid:256)(cid:226)(cid:200)(cid:54)(cid:81)(cid:290)(cid:291)(cid:292)(cid:293)(cid:200)(cid:71)(cid:72). è xø 1 (cid:74)(cid:94)(cid:10)(cid:96)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:36)y=k(x-a)+a2+ (cid:54)(cid:130)(cid:144)(cid:117)(cid:294)(cid:14)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:81)(cid:82)(cid:83)(cid:114)(cid:115)(cid:7)(cid:86)(cid:35)(cid:286)(cid:287)(cid:74)(cid:68) 4  1+k23 (cid:54)(cid:82)(cid:83)(cid:295)(cid:296)(cid:74)(cid:35)(cid:42)(cid:289)(cid:71)(cid:72)(cid:42)(cid:70)(cid:284)(cid:115)(cid:256)(cid:200)(cid:54)(cid:81)(cid:290)(cid:291)(cid:292)(cid:293)(cid:200)(cid:71)(cid:72). AB + AD ³ k2 (cid:74)(cid:77)(cid:10)(cid:82)(cid:83)(cid:84)(cid:87)(cid:91)(cid:92)(cid:268)(cid:74)(cid:54)(cid:81)(cid:96)(cid:41)(cid:54)(cid:82)(cid:83)(cid:77)(cid:78)(cid:295)(cid:296)(cid:81)(cid:173)(cid:78)(cid:297)(cid:64)(cid:298)(cid:299)(cid:192)(cid:54)(cid:191)(cid:148)(cid:300)(cid:236)(cid:108)(cid:180)(cid:86)(cid:71)(cid:72)(cid:106)(cid:176).æ 1ö 2 1 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)P(x,y),(cid:93) y = x2+çy- ÷ (cid:54)(cid:40)(cid:292)(cid:95)(cid:84)(cid:58)(cid:16)(cid:251)(cid:68)y=x2+ (cid:54) è 2ø 4 1 (cid:202)W :y=x2+ . 4 æ 1ö æ 1ö æ 1ö (cid:27)2(cid:32)(cid:74)(cid:22)(cid:10)(cid:96)(cid:282)(cid:79)(cid:43)(cid:77)(cid:221)(cid:283)(cid:41)Aça,a2+ ÷,Bçb,b2+ ÷,Cçc,c2+ ÷(cid:99)W(cid:39),(cid:55)a0(cid:54)(cid:55)mn=-1(cid:54)(cid:93)m = - (cid:54) BC n 1 (cid:96)(cid:282)(cid:79)(cid:284)(cid:115)(cid:36)C,(cid:127)(cid:173)(cid:174)(cid:272)(cid:108)(cid:260)(cid:96)|m|³|n|(cid:54)k -k =c-a=n-m=n+ (cid:54) BC AB n 1 æ 1ö æ 1ö (cid:93) C =|AB|+|BC|=(b-a) 1+m2 +(c-b) 1+n2 ³(c-a) 1+n2 =çn+ ÷ 1+n2 (cid:54)(cid:246)(cid:34)çn+ ÷ 1+n2 >0 2 è nø è nø 2 2 (cid:93)(cid:149) f(x)= æ çx+ 1ö ÷  1+x2 ,x>0, f¢(x)=2 æ çx+ 1ö ÷ æ ç2x- 1ö ÷ , è xø è xø è xø 2 (cid:149) f¢(x)=0(cid:54)(cid:24)(cid:68)x= (cid:54) 2 æ 2ö (cid:140)xÎç0, ÷(cid:138)(cid:54) f¢(x)<0(cid:54)(cid:137)(cid:138) f(x)(cid:135)(cid:301)(cid:302)(cid:232)(cid:54) ç ÷ è 2 ø æ 2 ù (cid:140)xÎç ,1ú(cid:54) f¢(x)>0(cid:54)(cid:137)(cid:138) f(x)(cid:135)(cid:301)(cid:302)(cid:303)(cid:54) ç è 2 û æ 2ö 27 (cid:93) f(x) = f ç ÷= (cid:54) min ç è 2 ÷ ø 4 1 27 3 3 (cid:202) C³ = ,(cid:71)C³3 3. 2 4 2 2 (cid:140)C =3 3(cid:138),n= ,m=- 2,(cid:55)(b-a) 1+m2 =(b-a) 1+n2 (cid:54)(cid:71)m=n(cid:138)(cid:180)(cid:9)(cid:304)(cid:90)(cid:54)(cid:305)(cid:306)(cid:54)(cid:202)C >3 3, 2 (cid:68)(cid:106).(cid:74)(cid:94)(cid:10)(cid:108)(cid:260)(cid:96)A,B,D(cid:99)W(cid:39)(cid:54)(cid:55)BA^DA(cid:54) æ 1ö (cid:166)(cid:21)(cid:128)(cid:72)(cid:96)Aça,a2+ ÷(cid:54)(cid:246)(cid:34)(cid:49)(cid:50)BA(cid:54)DA(cid:43)(cid:107)(cid:46)(cid:155)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)0(cid:54) è 4ø 1 (cid:93)(cid:96)BA,DA(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k(cid:35)- (cid:54)(cid:127)(cid:173)(cid:174)(cid:272)(cid:54)(cid:108)(cid:260)(cid:96) k £1(cid:54) k 1 (cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:36)y=k(x-a)+a2+ (cid:54) 4 ì 1 y=x2+ ï ï 4 (cid:93)(cid:89)(cid:90)í (cid:68)x2-kx+ka-a2 =0(cid:54) ï y=k(x-a)+a2+ 1 ïî 4 D=k2-4  ka-a2 =k-2a2 >0(cid:54)(cid:93)k ¹2a (cid:93)|AB|= 1+k2 |k-2a|(cid:54) 1 1 (cid:95)(cid:15)|AD|= 1+ +2a (cid:54) k2 k 1 1 \|AB|+|AD|= 1+k2 |k-2a|+ 1+ +2a k2 k æ 1 ö 1  1+k23 ³ 1+k2 ç k-2a + +2a ÷³ 1+k2 k+ = è k ø k k2 (cid:149)k2 =m(cid:54)(cid:93)mÎ0,1 (cid:54)(cid:96) f(m)= (m+1)3 =m2+3m+ 1 +3(cid:54) m m 1 (2m-1)(m+1)2 1 (cid:93) f¢(m)=2m+3- = (cid:54)(cid:149) f¢(m)=0(cid:54)(cid:24)(cid:68)m= (cid:54) m2 m2 2 æ 1ö (cid:140)mÎç0, ÷(cid:138)(cid:54) f¢(m)<0(cid:54)(cid:137)(cid:138) f(m)(cid:135)(cid:301)(cid:302)(cid:232)(cid:54) è 2ø æ1 ö (cid:140)mÎç ,+¥÷(cid:54) f¢(m)>0(cid:54)(cid:137)(cid:138) f(m)(cid:135)(cid:301)(cid:302)(cid:303)(cid:54) è2 ø æ1ö 27 (cid:93) f(m) = f ç ÷= (cid:54) min è2ø 4 3 3 \|AB|+|AD|³ (cid:54) 21 1 æ 1 ö 2 (cid:307) 1+k2 |k-2a|+ 1+ +2a ³ 1+k2 ç|k-2a|+ +2a ÷(cid:54)(cid:137)(cid:308)(cid:199)(cid:180)(cid:152)(cid:153)(cid:36)k=1(cid:54)(cid:117)(cid:256)(cid:275)(cid:199)(cid:180)(cid:138)k = k2 k è k ø 2 3 3 (cid:108)(cid:22)(cid:118)(cid:54)(cid:202) AB + AD > . 2 1 (cid:74)(cid:77)(cid:10)(cid:36)(cid:309)(cid:187)(cid:188)(cid:58)(cid:310),(cid:311)(cid:312)(cid:130)(cid:294)(cid:14)(cid:50)(cid:134)(cid:143)(cid:87)(cid:279) (cid:221)(cid:135)(cid:136)(cid:68)(cid:294)(cid:14)(cid:50)W¢:y=x2, 4 (cid:282)(cid:79)ABCD(cid:313)(cid:295)(cid:36)(cid:282)(cid:79)A¢B¢C¢D¢,(cid:93)(cid:227)(cid:21)(cid:180)(cid:314)(cid:52)(cid:282)(cid:79)A¢B¢C¢D¢(cid:43)(cid:284)(cid:115)(cid:285)(cid:52)3 3. (cid:96) B¢ t ,t2 ,A¢ t ,t2 ,C¢ t ,t2 , (cid:97)(cid:98)(cid:173)(cid:174)(cid:272)(cid:108)(cid:260)(cid:96) t ³0. 0 0 1 1 2 2 0 (cid:93) k =t +t ,k =t +t , (cid:127)(cid:52) A¢B¢^B¢C¢, (cid:93) t +t t +t =-1. A¢B¢ 1 0 B¢C¢ 2 0 1 0 2 0 (cid:127)(cid:52) A¢B¢ = 1+t +t 2 t -t , B¢C¢ = 1+t +t 2 t -t , (cid:55) t (cid:315)(cid:52) t ,t (cid:244)(cid:316), 1 0 1 0 2 0 2 0 0 1 2 (cid:93) A¢B¢ + B¢C¢ = 1+t +t 2 t -t + 1+t +t 2 t -t . (cid:149) t +t =tanq, 1 0 1 0 2 0 2 0 2 0 æ πö t +t =-cotq,qÎç0, ÷,(cid:93)t =tanq-t ,t =-cotq-t ,(cid:205)(cid:206) 1 0 è 2ø 2 0 1 0 A¢B¢ + B¢C¢ = 1+cot2q2t +cotq+ 1+tan2qtanq-2t  0 0 æ 1 1 ö sinq cosq 2t (cosq-sinq) sin3q+cos3q (cid:202) A¢B¢ + B¢C¢ =2t ç - ÷+ + = 0 + 0èsinq cosqø cos2q sin2q sinqcosq sin2qcos2q æ πù (cid:140)qÎç0, ú (cid:138), è 4û ① sin3q+cos3q sinq cosq 1 2 A¢B¢ + B¢C¢ ³ = + ³2 =2 ³2 2 sin2qcos2q cos2q sin2q sinqcosq sin2q æπ πö (cid:140) qÎç , ÷ (cid:138),(cid:127)(cid:52)t + = + sin2qcos3q sin2qcos2q cosq sin2q 2 2 = = sin2qsin2q×2cos2q  1-cos2q  1-cos2q  ×2cos2q 2 2 3 3 ³ ³ = æ 1-cos2q  +  1-cos2q  +2cos2qö 3 æ2ö 3 2 (cid:54) ç ÷ ç ÷ ç 3 ÷ è3ø è ø 3 3 3 (cid:140)(cid:55)(cid:317)(cid:140)cosq = (cid:138)(cid:180)(cid:9)(cid:304)(cid:90)(cid:54)(cid:202) A¢B¢ + B¢C¢ > (cid:54)(cid:202)(cid:282)(cid:79)(cid:284)(cid:115)(cid:285)(cid:52)3 3. 3 2. 1 æ 1ö (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:43)(cid:267)(cid:94)(cid:221)(cid:43)(cid:3)(cid:235)(cid:178)(cid:216)(cid:48)(cid:286)(cid:287)(cid:68) C =|AB|+|BC|³çn+ ÷ 1+n2 (cid:54)(cid:95)(cid:138)(cid:36)(cid:309)(cid:251)(cid:310)(cid:242) 2 è nø (cid:188)(cid:54)(cid:173)(cid:264)(cid:292)(cid:43)(cid:86)(cid:318)(cid:84)(cid:58)(cid:88)(cid:81)(cid:96)(cid:28)(cid:288)(cid:13)(cid:42)(cid:289)(cid:54)(cid:256)(cid:88)(cid:81)(cid:290)(cid:291)(cid:292)(cid:293)(cid:200)(cid:71)(cid:72). x2 y2 3(cid:26)(cid:27)2022(cid:28)(cid:29)(cid:30)Ⅱ(cid:31)·21(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)C: - =1(a>0,b>0)(cid:43)(cid:264)(cid:319)(cid:41)(cid:36)F(2,0)(cid:54)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:36) a2 b2 y=± 3x(cid:26) (1)(cid:42)C(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:48)F(cid:43)(cid:49)(cid:50)(cid:117)C(cid:43)(cid:40)(cid:152)(cid:262)(cid:263)(cid:50)(cid:64)(cid:159)(cid:51)(cid:52)A(cid:54)B(cid:40)(cid:41)(cid:54)(cid:41)Px,y ,Qx ,y (cid:99)C(cid:39)(cid:54)(cid:55) 1 1 2 2 x > x >0,y >0(cid:26)(cid:48)P(cid:55)(cid:107)(cid:46)(cid:36)- 3(cid:43)(cid:49)(cid:50)(cid:117)(cid:48)Q(cid:55)(cid:107)(cid:46)(cid:36) 3 (cid:43)(cid:49)(cid:50)(cid:51)(cid:52)(cid:41)M.(cid:205)(cid:143)(cid:56) (cid:145)(cid:20)(cid:199)(cid:40)(cid:221) 1 2 1 (cid:170)(cid:36)(cid:152)(cid:153)(cid:54)(cid:106)(cid:176)(cid:53)(cid:320)(cid:22)(cid:221)(cid:304)(cid:90)(cid:10) ①②③ M(cid:99)AB(cid:39)(cid:73) PQ(cid:321)AB(cid:73) |MA|=|MB|(cid:26) (cid:4) ① (cid:10)(cid:47)(cid:20)(cid:278)(cid:108)(cid:95) ② (cid:43)(cid:100)(cid:148)(cid:64)(cid:159)(cid:24)(cid:25) ③ (cid:54)(cid:93)(cid:163)(cid:267)(cid:22)(cid:221)(cid:24)(cid:25)(cid:187)(cid:64). y2 (cid:60)(cid:25)(cid:61)(cid:62)(1)x2- =1 3 (2)(cid:184)(cid:24)(cid:65) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:82)(cid:83)(cid:319)(cid:41)(cid:91)(cid:92)(cid:42)(cid:68)c(cid:43)(cid:200)(cid:54)(cid:82)(cid:83)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:42)(cid:68)a,b(cid:43)(cid:3)(cid:268)(cid:54)(cid:269)(cid:206)(cid:82)(cid:83)a,b,c(cid:43)(cid:84)(cid:58)(cid:3)(cid:268)(cid:42)(cid:68) a,b(cid:43)(cid:200)(cid:54)(cid:68)(cid:69)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32)(cid:104)(cid:64)(cid:65)(cid:68)(cid:69)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)(cid:322)(cid:54)(cid:96)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:36)k, M(x0,y0),(cid:127) |AM|=|BM|(cid:180)(cid:314)(cid:64)(cid:65) 8k2 ③ (cid:68)(cid:69)x +ky = (cid:73)(cid:127)(cid:49)(cid:50)PM (cid:35)QM (cid:43)(cid:107)(cid:46)(cid:68)(cid:69)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54)(cid:191)(cid:148)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:54)(cid:40)(cid:41)(cid:316)(cid:80)(cid:44)(cid:7)(cid:86)(cid:68)(cid:69)(cid:49) 0 0 k2-3 3x (cid:50) PQ (cid:43)(cid:107)(cid:46)m= 0 (cid:54)(cid:127) PQ//AB(cid:180)(cid:314)(cid:259)(cid:16)(cid:36)ky =3x (cid:54)(cid:127) M (cid:99)(cid:49)(cid:50)AB(cid:39)(cid:180)(cid:314)(cid:52)ky =k2x -2(cid:54) y 0 0 0 0 0 ② ① (cid:204)(cid:88)(cid:20)(cid:278)(cid:40)(cid:221)(cid:170)(cid:36)(cid:33)(cid:34)(cid:152)(cid:153)(cid:22)(cid:221)(cid:170)(cid:36)(cid:191)(cid:192)(cid:54)(cid:269)(cid:85)(cid:106)(cid:176)(cid:71)(cid:72). b (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:264)(cid:319)(cid:41)(cid:36)F(2,0)(cid:54) c=2, (cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:36)y=± 3x(cid:54) = 3(cid:54) b= 3a(cid:54) a ∴ ∵ ∴ ∴ c2 =a2+b2 =4a2 =4(cid:54) a=1(cid:54) b= 3(cid:26) ∴ y2 ∴ ∴ C(cid:43)(cid:58)(cid:59)(cid:36)(cid:10)x2- =1(cid:73) 3 ∴(cid:27)2(cid:32)(cid:127)(cid:33)(cid:34)(cid:68)(cid:49)(cid:50)PQ(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)(cid:322)(cid:54)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:108)(cid:36)(cid:322)(cid:54) (cid:47)(cid:20)(cid:127) (cid:323) (cid:63)(cid:20)(cid:127) (cid:323) (cid:10)(cid:127) (cid:304)(cid:90)(cid:72)(cid:34)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)(cid:322)(cid:73) (cid:47)(cid:20) ①② (cid:323) ③ (cid:54)(cid:93)M (cid:36) ② (cid:50) ③ (cid:324)AB① (cid:43)(cid:145)(cid:41) ② (cid:54)(cid:325)(cid:47)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:108)(cid:109)(cid:99)(cid:54)(cid:93)(cid:127)(cid:160)(cid:161)(cid:50)(cid:43)(cid:173)(cid:174)(cid:272)(cid:72)(cid:34)M (cid:99)x(cid:156) (cid:39)(cid:54)①(cid:71)(cid:36)③(cid:319)(cid:41)②F ,(cid:137)(cid:138)(cid:127)(cid:173)(cid:174)(cid:272)(cid:72)(cid:34)P(cid:23)Q(cid:3)(cid:52)x(cid:156)(cid:173)(cid:174)(cid:54)(cid:117)(cid:205)(cid:206)x =x (cid:54)(cid:33)(cid:34)(cid:108)(cid:147)(cid:73) 1 2 (cid:326)(cid:244)(cid:54)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)(cid:322). (cid:96)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:36)k,(cid:49)(cid:50)AB(cid:58)(cid:59)(cid:36)y=kx-2, (cid:93)(cid:152)(cid:153) M (cid:99)AB(cid:39)(cid:54)(cid:180)(cid:314)(cid:52)y =kx -2Ûky =k2x -2(cid:73) 0 0 0 0 (cid:40)(cid:262)(cid:263)①(cid:50)(cid:43)(cid:58)(cid:59)(cid:148)(cid:327)(cid:36)3x2-y2 =0, (cid:89)(cid:90)(cid:154)(cid:253)y(cid:327)(cid:16)(cid:251)(cid:183)(cid:15)(cid:68)(cid:10)  k2-3  x2-4k2x+4k2 =0 (cid:96)Ax ,y ,Bx ,y  ,(cid:50)(cid:324)(cid:145)(cid:41)(cid:36)N  x ,y  ,(cid:93)x = x 3 +x 4 = 2k2 ,y =kx -2= 6k , 3 3 4 4 N N N 2 k2-3 N N k2-3 (cid:96)Mx ,y  , 0 0 (cid:93)(cid:152)(cid:153) AM = BM (cid:180)(cid:314)(cid:52)x -x 2+y -y 2 =x -x 2+y -y 2, 0 3 0 3 0 4 0 4 (cid:87)(cid:233)(cid:327)③(cid:82)(cid:83)(cid:84)(cid:58)(cid:201)(cid:7)(cid:86)(cid:183)(cid:15)(cid:68)(cid:10) x 3 -x 4 é ë2x 0 -x 3 +x 4 ù û +y 3 -y 4 é ë2y 0 -y 3 +y 4 ù û =0(cid:54) y -y ë é2x 0 -x 3 +x 4  û ù+ x 3 -x 4 é ë2y 0 -y 3 +y 4 ù û =0,(cid:71)x 0 -x N +ky 0 -y N =0, 3 4 8k2 (cid:71)x +ky = (cid:73) 0 0 k2-3 (cid:127)(cid:21)(cid:128)(cid:34)(cid:49)(cid:50)PM (cid:43)(cid:107)(cid:46)(cid:36)- 3, (cid:49)(cid:50)QM (cid:43)(cid:107)(cid:46)(cid:36) 3, (cid:127)y -y =- 3x -x ,y -y = 3x -x , 1 0 1 0 2 0 2 0 ∴y -y =- 3x +x -2x , 1 2 1 2 0 ∴ y -y 3x +x -2x  (cid:129)(cid:75)(cid:49)(cid:50)PQ(cid:43)(cid:107)(cid:46)m= 1 2 =- 1 2 0 , x -x x -x 1 2 1 2 (cid:49)(cid:50)PM :y=- 3x-x +y ,(cid:71)y= y + 3x - 3x, 0 0 0 0    (cid:66)(cid:67)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)3x2-y2-3=0,(cid:71) 3x+y 3x-y =3(cid:145)(cid:54) (cid:68)(cid:10)  y + 3x é 2 3x-  y + 3x ù=3, 0 0 ë 0 0 û 1 æ 3 ö (cid:24)(cid:68)P(cid:43)(cid:214)(cid:91)(cid:92)(cid:10)x 1 = 2 3 ç ç è y + 3x +y 0 + 3x 0 ÷ ÷ ø , 0 0 1 æ 3 ö (cid:95)(cid:15)(cid:10)x =- ç +y - 3x ÷(cid:54) 2 2 3 ç è y - 3x 0 0÷ ø 0 01 æ 3y ö 3x x -x = ç 0 +y ÷,x +x -2x =- 0 -x , 1 2 3è y2-3x2 0 ø 1 2 0 y2-3x2 0 0 0 0 0 ∴ 3x m= 0 , y 0 ∴ (cid:152)(cid:153) PQ//AB(cid:180)(cid:314)(cid:52)m=k Ûky =3x (cid:54) 0 0 ∴(cid:142)(cid:39)(cid:129)②(cid:328)(cid:10) (cid:152)(cid:153) M (cid:99)AB(cid:39)(cid:54)(cid:180)(cid:314)(cid:52)ky =k2x -2(cid:73) 0 0 (cid:152)(cid:153)①PQ//AB(cid:180)(cid:314)(cid:52)ky =3x (cid:73) 0 0 ② 8k2 (cid:152)(cid:153) AM = BM (cid:180)(cid:314)(cid:52)x +ky = (cid:73) 0 0 k2-3 ③ (cid:20) (cid:323) : ①② ③ 2k2 8k2 (cid:127) (cid:24)(cid:68)(cid:10)x = ,\x +ky =4x = , (cid:304)(cid:90)(cid:73) 0 k2-3 0 0 0 k2-3 ①② ∴③ (cid:20) (cid:323) (cid:10) ①③ ② 2k2 6k2 (cid:127) (cid:24)(cid:68)(cid:10)x = (cid:54)ky = (cid:54) 0 k2-3 0 k2-3 ①③ ky =3x (cid:54) (cid:304)(cid:90)(cid:73) 0 0 ∴(cid:20) (cid:323) ∴(cid:10)② ②③ ① 2k2 6k2 6 (cid:127) (cid:24)(cid:68)(cid:10)x = (cid:54)ky = (cid:54) x -2= (cid:54) 0 k2-3 0 k2-3 0 k2-3 ②③ ∴ ky =k2x -2(cid:54) (cid:304)(cid:90). 0 0   ∴4(cid:26)(cid:27)2023(cid:28)(cid:29)(cid:30)Ⅱ ∴(cid:31)①·21(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:145)(cid:45)(cid:36)(cid:91)(cid:92)(cid:225)(cid:41)(cid:54)(cid:171)(cid:319)(cid:41)(cid:36) -2 5,0 (cid:54)(cid:44)(cid:45)(cid:46)(cid:36) 5(cid:26) (1)(cid:42)C(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:175)C(cid:43)(cid:171)(cid:23)(cid:264)(cid:283)(cid:41)(cid:64)(cid:159)(cid:36)A(cid:54)A (cid:54)(cid:48)(cid:41)-4,0(cid:43)(cid:49)(cid:50)(cid:117)C(cid:43)(cid:171)(cid:172)(cid:51)(cid:52)M(cid:54)N(cid:40)(cid:41)(cid:54)M(cid:99)(cid:267)(cid:94)(cid:329)(cid:330)(cid:54)(cid:49)(cid:50) 1 2 MA (cid:117)NA (cid:51)(cid:52)(cid:41)P(cid:26)(cid:106)(cid:176):(cid:41)P(cid:99)(cid:189)(cid:49)(cid:50)(cid:39). 1 2 x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) - =1 4 16 (2)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65). (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:42)(cid:68)a,b(cid:43)(cid:200)(cid:71)(cid:72)(cid:331)(cid:189)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:204)(cid:88)(cid:127)(cid:41)(cid:43)(cid:91)(cid:92)(cid:64)(cid:159)(cid:332)(cid:70)(cid:49)(cid:50)MA (cid:117)NA (cid:43)(cid:58)(cid:59)(cid:54)(cid:89)(cid:90)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54) 1 2 x+2 1 (cid:154)(cid:253)y(cid:54)(cid:191)(cid:148)(cid:211)(cid:125)(cid:189)(cid:15)(cid:187)(cid:188)(cid:72)(cid:68) =- (cid:54)(cid:71)(cid:51)(cid:41)(cid:43)(cid:214)(cid:91)(cid:92)(cid:36)(cid:189)(cid:200)(cid:54)(cid:98)(cid:137)(cid:72)(cid:106)(cid:68)(cid:41)P(cid:99)(cid:189)(cid:49)(cid:50)x=-1(cid:39). x-2 3 x2 y2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:36) - =1a>0,b>0(cid:54)(cid:127)(cid:319)(cid:41)(cid:91)(cid:92)(cid:72)(cid:34)c=2 5(cid:54) a2 b2c (cid:93)(cid:127)e= = 5(cid:72)(cid:68)a=2(cid:54) b= c2-a2 =4 (cid:54) a x2 y2 (cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:36) - =1. 4 16 (cid:27)2(cid:32)(cid:127)(1)(cid:72)(cid:68)A -2,0,A 2,0(cid:54)(cid:96)Mx,y ,Nx ,y (cid:54) 1 2 1 1 2 2 1 1 (cid:203)(cid:204)(cid:49)(cid:50)(cid:43)(cid:107)(cid:46)(cid:108)(cid:36)0(cid:54)(cid:129)(cid:75)(cid:96)(cid:49)(cid:50)MN(cid:43)(cid:58)(cid:59)(cid:36)x=my-4(cid:54)(cid:55)- 0(cid:54) 4 16 32m 48 (cid:93)y +y = ,y y = (cid:54) 1 2 4m2-1 1 2 4m2-1 y y (cid:49)(cid:50)MA (cid:43)(cid:58)(cid:59)(cid:36)y= 1 x+2 (cid:54)(cid:49)(cid:50)NA (cid:43)(cid:58)(cid:59)(cid:36)y= 2 x-2 (cid:54) 1 x +2 2 x -2 1 2 (cid:89)(cid:90)(cid:49)(cid:50)MA (cid:117)(cid:49)(cid:50)NA (cid:43)(cid:58)(cid:59)(cid:72)(cid:68)(cid:10) 1 2 x+2 y x +2 y my -2 my y -2y +y +2y = 2 1 = 2 1 = 1 2 1 2 1 x-2 y x -2 y my -6 my y -6y 1 2 1 2 1 2 1 48 32m -16m m× -2× +2y +2y 4m2-1 4m2-1 1 4m2-1 1 1 = = =- (cid:54) 48 48m 3 m´ -6y -6y 4m2-1 1 4m2-1 1 x+2 1 (cid:127) =- (cid:72)(cid:68)x=-1(cid:54)(cid:71)x =-1(cid:54) x-2 3 P (cid:98)(cid:137)(cid:72)(cid:68)(cid:41)P(cid:99)(cid:189)(cid:49)(cid:50)x=-1(cid:39)(cid:242)(cid:279). (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234):(cid:42)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:43)(cid:189)(cid:49)(cid:50)(cid:227)(cid:21)(cid:54)(cid:128)(cid:99)(cid:30)(cid:333)(cid:11)(cid:334)(cid:43)(cid:187)(cid:188)(cid:335)(cid:336)(cid:54)(cid:259)(cid:16)(cid:335)(cid:336)(cid:35)(cid:142)(cid:148)(cid:213)(cid:83)(cid:335)(cid:336)(cid:54) (cid:144)(cid:145)(cid:97)(cid:98)(cid:96)(cid:206)(cid:108)(cid:42)(cid:43)(cid:193)(cid:337)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:68)(cid:69)(cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:72)(cid:75)(cid:251)(cid:16)(cid:242)(cid:188)(cid:54)(cid:178)(cid:24)(cid:21)(cid:43)(cid:3)(cid:235). (cid:22)(cid:23)(cid:49)(cid:50)(cid:35)(cid:161)(cid:50)(cid:89)(cid:90)x2 y2 1(cid:23)(cid:37)(cid:38) + =1(a>b>0)(cid:117)(cid:49)(cid:50)l:y=kx+m(cid:212)(cid:51)(cid:52)AB(cid:40)(cid:41)(cid:54)(cid:96)A(x (cid:54)y )(cid:54)B(x (cid:54)y ) a2 b2 1 1 2 2 ìx2 y2 ï + =1 ía2 b2 (cid:54)(b2 +k2a2)x2 +2a2kmx+a2m2 -a2b2 =0 ï îy=kx+m x2 y2 (cid:37)(cid:38) + =1(a>0(cid:54)b>0)(cid:117)(cid:48)(cid:189)(cid:41)(m(cid:54)0)(cid:43)(cid:49)(cid:50)l(cid:212)(cid:51)(cid:52)AB(cid:40)(cid:41)(cid:54)(cid:96)(cid:36)x=ty+m(cid:54)(cid:165)(cid:137)(cid:154)(cid:253)x(cid:54)(cid:338)(cid:339) a2 b2 ìx2 y2 ï + =1 y(cid:54)(cid:168)(cid:169)(cid:43)(cid:58)(cid:59)(cid:165)(cid:143)(cid:10)ía2 b2 (cid:54)(a2 +t2b2)y2 +2b2tmy+b2m2 -a2b2 =0 ï îx=ty+m (cid:4)(cid:128)(cid:10) (cid:165)(cid:340)(cid:49)(cid:50)(cid:341)(cid:146)(cid:48)(cid:37)(cid:38)(cid:342)(cid:343)(cid:22)(cid:189)(cid:41)(cid:54)(cid:178)(cid:108)(cid:335)(cid:49)(cid:185)(cid:344)(cid:176)(cid:49)(cid:50)(cid:117)(cid:37)(cid:38)(cid:146)(cid:40)(cid:221)(cid:51)(cid:41)(cid:43)(cid:54)(cid:22)(cid:345)(cid:228)(cid:240)(cid:241)(cid:346)(cid:70)D>0(cid:54)(cid:150) (cid:151)(cid:137)(cid:152)(cid:153)(cid:54)(cid:347)(cid:72)(cid:75)(cid:68)(cid:69)(cid:211)(cid:125)(cid:189)(cid:15)(cid:43)(cid:3)(cid:268)(cid:26) ① (cid:319)(cid:41)(cid:99)y(cid:156)(cid:39)(cid:43)(cid:37)(cid:38)(cid:117)(cid:49)(cid:50)(cid:43)(cid:3)(cid:268)(cid:54)(cid:160)(cid:161)(cid:50)(cid:117)(cid:49)(cid:50)(cid:43)(cid:3)(cid:268)(cid:35)(cid:39)(cid:328)(cid:79)(cid:86)(cid:298)(cid:348)(cid:54)(cid:108)(cid:99)(cid:349)(cid:328)(cid:26) 2②(cid:23)(cid:294)(cid:14)(cid:50)y2 =2px(p>0)(cid:117)(cid:49)(cid:50)x=ty+m(cid:212)(cid:51)(cid:52)A(cid:23)B(cid:40)(cid:41)(cid:54)(cid:96)A(x (cid:54)y )(cid:54)B(x (cid:54)y ) 1 1 2 2 ìy + y =2pt (cid:89)(cid:90)(cid:72)(cid:68)y2 =2p(ty+m)(cid:54)D>0(cid:138)(cid:54)í 1 2 îy y =-2pm 1 2 p y2 y 2 1 (cid:350)(cid:351)(cid:352)(cid:54)(cid:140)(cid:49)(cid:50) AB (cid:48)(cid:319)(cid:41)(cid:43)(cid:138)(cid:353)(cid:54)(cid:71)m= (cid:54)y y =-2pm=-p2(cid:54)xx = 1 × 2 = p2(cid:54)(cid:250)(cid:36) AB (cid:36)(cid:216)(cid:354)(cid:43) 2 1 2 1 2 2p 2p 4 (cid:138)(cid:353)(cid:273)(cid:150)(cid:151)(cid:139)(cid:86)(cid:54)(cid:97)(cid:98)(cid:137)(cid:138)A(cid:23)B(cid:91)(cid:92)(cid:355)(cid:175)(cid:356)(cid:26) (cid:294)(cid:14)(cid:50) x2 =2py(p>0) (cid:117)(cid:49)(cid:50)y=kx+m(cid:212)(cid:51)(cid:52) C(cid:23)D (cid:40)(cid:41)(cid:54)(cid:96)C(x (cid:54)y )(cid:54)D(x (cid:54)y ) 1 1 2 2 ìx +x =2pk (cid:89)(cid:90)(cid:72)(cid:68) x2 =2p(kx+m) (cid:54)D>0 (cid:138)(cid:54) í 1 2 îxx =-2pm 1 2 (cid:4)(cid:128)(cid:10)(cid:99)(cid:49)(cid:50)(cid:117)(cid:294)(cid:14)(cid:50)(cid:43)(cid:227)(cid:21)(cid:145)(cid:54)(cid:96)(cid:49)(cid:50)(cid:43)(cid:138)(cid:353)(cid:20)(cid:278)(cid:79)(cid:86)(cid:243)(cid:193)(cid:30)(cid:64)(cid:65)(cid:54)(cid:357)(cid:357)(cid:72)(cid:75)(cid:358)(cid:359)(cid:187)(cid:188)(cid:196)(cid:26)(cid:208)(cid:360)(cid:134)(cid:39)(cid:20) (cid:278)(cid:182)(cid:96)(cid:73)(cid:208)(cid:360)(cid:134)(cid:264)(cid:54)(cid:20)(cid:278)(cid:361)(cid:96)(cid:73)(cid:4)(cid:128)(cid:108)(cid:72)(cid:362)(cid:363)(cid:334)(cid:364)(cid:365)(cid:366)(cid:54)(cid:198)(cid:265)(cid:110)(cid:111)(cid:198)(cid:265)(cid:64)(cid:65)(cid:26) (cid:326)(cid:191)(cid:10)(cid:211)(cid:125)(cid:189)(cid:15)(cid:367)(cid:185)(cid:309)(cid:21)(cid:368)(cid:152)(cid:153)(cid:117)(cid:58)(cid:59)(cid:145)(cid:43)(cid:101)(cid:13)(cid:54)(cid:129)(cid:75)(cid:311)(cid:312)(cid:99)(cid:308)(cid:15)(cid:369)(cid:165)(cid:134)(cid:196)(cid:227)(cid:21)(cid:54)(cid:56)(cid:57)(cid:227)(cid:21)(cid:54)(cid:77)(cid:41)(cid:209)(cid:50)(cid:227) (cid:21)(cid:54)(cid:78)(cid:297)(cid:227)(cid:21)(cid:180)(cid:162)(cid:30)(cid:342)(cid:370)(cid:43)(cid:138)(cid:353)(cid:54)(cid:241)(cid:371)(cid:21)(cid:186)(cid:145)(cid:43)(cid:372)(cid:45)(cid:6)(cid:373)(cid:54)(cid:259)(cid:16)(cid:36)(cid:91)(cid:92)(cid:124)(cid:125)(cid:54)(cid:259)(cid:16)(cid:36)(cid:72)(cid:75)(cid:195)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:43) (cid:79)(cid:86)(cid:54)(cid:218)(cid:273)(cid:178)(cid:186)(cid:230)(cid:30)(cid:374)(cid:256)(cid:162)(cid:30)(cid:43)(cid:58)(cid:86)(cid:26) (cid:94)(cid:23)(cid:97)(cid:43)(cid:158)(cid:159)(cid:86)(cid:35)(cid:211)(cid:125)(cid:189)(cid:15) x2 y2 + =1(a>b>0)(cid:117)y=kx+m(cid:89)(cid:90)(cid:54)(cid:40)(cid:292)(cid:95)(cid:138)(cid:121)(cid:39)a2b2(cid:71)(cid:72)(cid:68)(cid:69)(a2k2 +b2)x2 +2kma2x+a2(m2 -b2)=0(cid:54) a2 b2 (cid:36)(cid:309)(cid:58)(cid:310)(cid:375)(cid:328)(cid:54)(cid:130)(cid:39)(cid:86)(cid:251)(cid:175)(cid:36)Ax2 +Bx+C =0(cid:26)(cid:139)(cid:86)(cid:72)(cid:75)(cid:376)(cid:304)(cid:22)(cid:221)(cid:3)(cid:52)x(cid:43)(cid:22)(cid:296)(cid:94)(cid:167)(cid:58)(cid:59)(cid:54)(cid:158)(cid:159)(cid:86)(cid:36) D=4a2b2(a2k2 +b2 -m2)(cid:72)(cid:251)(cid:135)(cid:175)4a2b2(A-m2)(cid:26) x2 y2 (cid:95)(cid:15) + =1(a>b>0)(cid:35)x=ty+m(cid:89)(cid:90)(a2 +t2b2)y2 +2b2tmy+b2m2 -a2b2 =0(cid:54)(cid:36)(cid:309)(cid:58)(cid:310)(cid:375)(cid:328)(cid:54)(cid:130)(cid:39)(cid:86) a2 b2(cid:251)(cid:175)(cid:36)Ay2 +By+C =0(cid:54)D=4a2b2(a2 +t2b2 -m2)(cid:54)(cid:72)(cid:251)(cid:175)4a2b2(A-m2)(cid:26) l(cid:117)C(cid:212)(cid:44)ÛD<0(cid:73)l(cid:117)C(cid:212)(cid:377)ÛD=0(cid:73)l(cid:117)C(cid:212)(cid:51)ÛD>0(cid:26) B C (cid:4)(cid:128)(cid:10)(cid:27)1(cid:32)(cid:127)(cid:211)(cid:125)(cid:189)(cid:15)(cid:332)(cid:70)x +x =- (cid:54)xx = (cid:54)(cid:4)(cid:128)(cid:378)(cid:379)(cid:152)(cid:153)D>0(cid:26) 1 2 A 1 2 A (cid:27)2(cid:32)(cid:42)(cid:24)(cid:138)(cid:241)(cid:4)(cid:128)(cid:21)(cid:368)(cid:129)(cid:146)(cid:43)(cid:378)(cid:379)(cid:152)(cid:153)(cid:54)(cid:241)(cid:147)(cid:148)(cid:129)(cid:146)(cid:43)(cid:21)(cid:128)(cid:26) (cid:27)3(cid:32)(cid:165)(cid:340)(cid:178)(cid:319)(cid:41)(cid:99)y(cid:156)(cid:39)(cid:43)(cid:37)(cid:38)(cid:54)(cid:380)(cid:240)(cid:241)(cid:371)a2(cid:54)b2(cid:248)(cid:295)(cid:136)(cid:381)(cid:71)(cid:72)(cid:26) (cid:27)4(cid:32)(cid:49)(cid:50)(cid:35)(cid:160)(cid:161)(cid:50)(cid:89)(cid:90)(cid:191)(cid:340)(cid:298)(cid:348)(cid:54)(cid:319)(cid:41)(cid:99)x(cid:156)(cid:43)(cid:160)(cid:161)(cid:50)(cid:54)(cid:380)(cid:241)(cid:371)b2(cid:295)(cid:304)-b2(cid:71)(cid:72)(cid:73) (cid:319)(cid:41)(cid:99)y(cid:156)(cid:43)(cid:160)(cid:161)(cid:50)(cid:54)(cid:371)a2(cid:295)(cid:304)-b2(cid:71)(cid:72)(cid:54)b2(cid:295)(cid:304)a2(cid:71)(cid:72)(cid:26) (cid:27)5(cid:32)(cid:4)(cid:128)(cid:94)(cid:167)(cid:161)(cid:50)(cid:58)(cid:59)(cid:35)(cid:94)(cid:167)(cid:161)(cid:50)(cid:58)(cid:59)(cid:357)(cid:357)(cid:108)(cid:335)(cid:216)(cid:48)(cid:89)(cid:90)(cid:154)(cid:296)(cid:54)(cid:82)(cid:83)D(cid:158)(cid:382)(cid:97)(cid:43)(cid:3)(cid:268)(cid:54)(cid:250)(cid:36)(cid:137)(cid:110)(cid:111)(cid:143)(cid:357)(cid:357) (cid:383)(cid:146)(cid:303)(cid:97)(cid:54)(cid:97)(cid:98)(cid:21)(cid:368)(cid:43)(cid:378)(cid:379)(cid:152)(cid:153)(cid:72)(cid:75)(cid:252)(cid:253)(cid:303)(cid:97)(cid:27)(cid:22)(cid:345)(cid:36)(cid:51)(cid:41)(cid:214)(cid:384)(cid:91)(cid:92)(cid:43)(cid:385)(cid:386)(cid:330)(cid:387)(cid:32)(cid:54)(cid:129)(cid:75)(cid:99)(cid:388)(cid:69)(cid:40)(cid:152)(cid:94)(cid:167) (cid:161)(cid:50)(cid:51)(cid:41)(cid:227)(cid:21)(cid:43)(cid:138)(cid:353)(cid:54)(cid:195)(cid:83)(cid:389)(cid:390)(cid:43)(cid:58)(cid:86)(cid:64)(cid:65)(cid:54)(cid:63)(cid:391)(cid:24)(cid:58)(cid:59)(cid:100)(cid:54)(cid:392)(cid:182)(cid:188)(cid:70)(cid:198)(cid:265)(cid:91)(cid:92)(cid:26) (cid:77)(cid:23)(cid:114)(cid:115)(cid:7)(cid:86) (cid:96)M(x (cid:54)y )(cid:54)N(x (cid:54)y )(cid:97)(cid:98)(cid:40)(cid:41)(cid:80)(cid:44)(cid:7)(cid:86)|MN|= (x -x )2 +(y - y )2 (cid:26) 1 1 2 2 1 2 1 2 1(cid:23)(cid:47)M(cid:23)N (cid:99)(cid:49)(cid:50)y=kx+m(cid:39)(cid:54)(cid:66)(cid:67)(cid:16)(cid:251)(cid:54)(cid:68)|MN|= 1+k2 x 1 -x 2 (cid:73) 2(cid:23)(cid:47)M(cid:23)N (cid:129)(cid:99)(cid:49)(cid:50)(cid:58)(cid:59)(cid:36)x=ty+m(cid:54)(cid:66)(cid:67)(cid:16)(cid:251)(cid:54)(cid:68)|MN|= 1+t2 y - y 1 2 |x -x | | y - y | 3(cid:23)(cid:168)(cid:169)(cid:49)(cid:78)(cid:77)(cid:78)(cid:79)(cid:42)(cid:24)(cid:114)(cid:115)(cid:54)|MN| = 2 1 = 2 1 (cid:26)(cid:144)(cid:145)k(cid:36)(cid:49)(cid:50)MN (cid:107)(cid:46)(cid:54)a(cid:36)(cid:49)(cid:50)(cid:247)(cid:107)(cid:78)(cid:26) |cosa| |sina| (cid:4)(cid:128)(cid:10)(cid:27)1(cid:32)(cid:39)(cid:328)(cid:124)(cid:125)(cid:86)(cid:145)(cid:54)(cid:140)(cid:36)k ¹0(cid:54)m¹0(cid:138)(cid:54)mk =1(cid:73) (cid:27)2(cid:32)(cid:49)(cid:50)(cid:39)(cid:181)(cid:238)(cid:40)(cid:41)(cid:80)(cid:44)(cid:228)(cid:72)(cid:165)(cid:39)(cid:187)(cid:188)(cid:54)(cid:108)(cid:178)(cid:393)(cid:68)(cid:49)(cid:50)(cid:35)(cid:161)(cid:50)(cid:89)(cid:90)(cid:88)(cid:347)(cid:335)(cid:83)(cid:26) (cid:27)3(cid:32)(cid:49)(cid:50)(cid:35)(cid:161)(cid:50)(cid:89)(cid:90)(cid:88)(cid:16)(cid:251)(cid:68)(cid:69)(cid:43)(cid:86)(cid:318)(cid:175)(cid:36)Ax2 +Bx+C =0(A¹0)(cid:54)(cid:158)(cid:159)(cid:86)(cid:36)D=B2 -4AC(cid:54)D>0(cid:138)(cid:54) B C B2 -4AC D x -x = (x +x )2 -4xx = (- )2 -4× = = (cid:54)(cid:82)(cid:83)(cid:42)(cid:97)(cid:7)(cid:86)(cid:323)(cid:289)(cid:273)(cid:394)(cid:58)(cid:310)(cid:54)(cid:195)(cid:83)(cid:137)(cid:58)(cid:74) 1 2 1 2 1 2 A A A A (cid:99)(cid:24)(cid:21)(cid:16)(cid:251)(cid:43)(cid:138)(cid:353)(cid:72)(cid:75)(cid:285)(cid:285)(cid:395)(cid:29)(cid:396)(cid:46)(cid:26) (cid:27)4(cid:32)(cid:49)(cid:50)(cid:35)(cid:38)(cid:212)(cid:51)(cid:43)(cid:138)(cid:353)(cid:54)(cid:48)(cid:38)(cid:45)(cid:397)(cid:49)(cid:50)(cid:43)(cid:133)(cid:50)(cid:54)(cid:82)(cid:83)(cid:49)(cid:78)(cid:77)(cid:78)(cid:79)(cid:43)(cid:3)(cid:268)(cid:42)(cid:24)(cid:114)(cid:115)(cid:383)(cid:398)(cid:399)(cid:251)(cid:135)(cid:26) (cid:27)5(cid:32)(cid:49)(cid:50)(cid:165)(cid:340)(cid:48)(cid:319)(cid:41)(cid:72)(cid:75)(cid:30)(cid:113)(cid:319)(cid:41)(cid:114)(cid:7)(cid:86)(cid:75)(cid:231)(cid:319)(cid:115)(cid:7)(cid:86)(cid:26) (cid:102)(cid:23)(cid:33)(cid:34)(cid:114)AB(cid:43)(cid:145)(cid:41)(cid:54)(cid:400)(cid:401)AB(cid:43)(cid:107)(cid:46)(cid:35)(cid:58)(cid:59) x2 y2 b2x 1(cid:23)AB(cid:178)(cid:37)(cid:38) + =1a>b.0(cid:43)(cid:22)(cid:152)(cid:114)(cid:54)(cid:145)(cid:41)Mx ,y (cid:54)(cid:93)AB(cid:43)(cid:107)(cid:46)(cid:36)- 0 (cid:54) a2 b2 0 0 a2y 0 (cid:242)(cid:83)(cid:41)(cid:201)(cid:74)(cid:42)AB(cid:43)(cid:107)(cid:46)(cid:73)(cid:96)Ax,y (cid:54)Bx ,y x ¹ x (cid:54)A(cid:54)B(cid:228)(cid:99)(cid:37)(cid:38)(cid:39)(cid:54) 1 1 2 2 1 2ìx2 y2 ï 1 + 1 =1 ïa2 b2 x2 -x 2 y2 - y 2 (cid:129)(cid:75)í (cid:54)(cid:40)(cid:86)(cid:212)(cid:232)(cid:68) 1 2 + 1 2 =0 ïx 2 y 2 a2 b2 2 + 2 =1 ïîa2 b2 x +x x -x  y + y y - y  (cid:129)(cid:75) 1 2 1 2 + 1 2 1 2 =0 a2 b2 y - y  b2x +x  b2x b2x (cid:71) 1 2 =- 1 2 =- 0 (cid:54)(cid:202)k =- 0 x -x  a2y + y  a2y AB a2y 1 2 1 2 0 0 x2 y2 b2x 2(cid:23)(cid:242)(cid:83)(cid:298)(cid:348)(cid:43)(cid:58)(cid:74)(cid:72)(cid:75)(cid:323)(cid:70)(cid:73)(cid:47)AB(cid:178)(cid:160)(cid:161)(cid:50) - =1a>b.0(cid:43)(cid:114)(cid:54)(cid:145)(cid:41)Mx ,y (cid:54)(cid:93)k = 0 (cid:73)(cid:47) a2 b2 0 0 AB a2y 0 p (cid:161)(cid:50)(cid:178)(cid:294)(cid:14)(cid:50)y2 =2pxp>0(cid:54)(cid:93)k = (cid:26) AB y 0 (cid:22)(cid:23)(cid:24)(cid:25)(cid:21) x2 y2 2 1(cid:26)(cid:27)2024·(cid:402)(cid:403)(cid:404)(cid:405)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)E: + =1(a>b>0)(cid:43)(cid:171)(cid:319)(cid:41)(cid:36)F (cid:54)(cid:39)(cid:283)(cid:41)(cid:36)B(cid:54)(cid:44)(cid:45)(cid:46)e= (cid:54) a2 b2 2 (cid:49)(cid:50)FB(cid:48)(cid:41)P(1,2). (1)(cid:42)(cid:37)(cid:38)E(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:73) (2)(cid:48)(cid:41)F (cid:43)(cid:49)(cid:50)l(cid:117)(cid:37)(cid:38)E(cid:212)(cid:51)(cid:52)M(cid:54)N(cid:40)(cid:41)(cid:27)M(cid:23)N(cid:228)(cid:108)(cid:99)(cid:91)(cid:92)(cid:156)(cid:39)(cid:32)(cid:54)(cid:47)ÐMPF =ÐNPF (cid:54)(cid:42)(cid:49)(cid:50)l(cid:43) (cid:58)(cid:59). x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) +y2 =1(cid:73) 2 (2)5x+y+5=0. (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:408)(cid:189)(cid:152)(cid:153)(cid:54)(cid:42)(cid:70)a,b,c(cid:71)(cid:68)(cid:37)(cid:38)E(cid:43)(cid:92)(cid:407)(cid:58)(cid:59). (cid:27)2(cid:32)(cid:97)(cid:98)(cid:408)(cid:189)(cid:152)(cid:153)(cid:54)(cid:409)(cid:410)(cid:247)(cid:107)(cid:78)(cid:43)(cid:3)(cid:268)(cid:72)(cid:68)k ×k =1(cid:54)(cid:96)(cid:70)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:54)(cid:117)(cid:37)(cid:38)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125) MP NP (cid:189)(cid:15)(cid:191)(cid:148)(cid:107)(cid:46)(cid:43)(cid:91)(cid:92)(cid:7)(cid:86)(cid:42)(cid:24)(cid:71)(cid:68). c 2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:149)F(-c,0)(cid:54)(cid:127)e= = (cid:54)(cid:68)a= 2c,b=c(cid:54)(cid:93)(cid:49)(cid:50)FB(cid:43)(cid:107)(cid:46)k=1(cid:54) a 2 (cid:127)(cid:49)(cid:50)FB(cid:48)(cid:41)P(1,2)(cid:54)(cid:68)(cid:49)(cid:50)FB(cid:43)(cid:58)(cid:59)(cid:36)y=x+1(cid:54)(cid:250)(cid:137)b=c=1,a= 2(cid:54) x2 (cid:129)(cid:75)(cid:37)(cid:38)C(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:36) +y2 =1. 2 (cid:27)2(cid:32)(cid:96)ÐMPF =ÐNPF =q(cid:54)(cid:49)(cid:50)MP(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)b(cid:54) π (cid:49)(cid:50)NP(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)a(cid:54)(cid:127)(cid:49)(cid:50)FP(cid:43)(cid:107)(cid:46)k=1(cid:34)(cid:49)(cid:50)FP(cid:43)(cid:247)(cid:107)(cid:78)(cid:36) (cid:54) 4π π π π (cid:52)(cid:178)a= +q, =b+q(cid:54)(cid:71)(cid:146)a+b= (cid:54)(cid:203)(cid:204)a,b(cid:155)(cid:108)(cid:180)(cid:52) (cid:54) 4 4 2 2 π sin( -a) sina 2 (cid:93)tanatanb= × =1(cid:54)(cid:71)(cid:49)(cid:50)MP,NP(cid:43)(cid:107)(cid:46)(cid:150)(cid:151)k ×k =1(cid:54) cosa π MP NP cos( -a) 2 (cid:127)(cid:21)(cid:96)(cid:34)(cid:54)(cid:49)(cid:50)l(cid:43)(cid:107)(cid:46)(cid:108)(cid:36)0(cid:54)(cid:96)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)x=my-1,m¹1(cid:54) ìx=my-1 (cid:127)í (cid:54)(cid:154)(cid:253)x(cid:327)(cid:183)(cid:15)(cid:68)(cid:54)(m2+2)y2-2my-1=0(cid:54)(cid:203)(cid:204)D>0(cid:54) îx2+2y2 =2 2m 1 (cid:96)M(x,y ),N(x ,y )(cid:54)(cid:93)y +y = ,y y =- (cid:54) 1 1 2 2 1 2 m2+2 1 2 m2+2 y -2 y -2 (cid:127)k ×k =1(cid:54)(cid:68) 1 × 2 =1(cid:54)(cid:71)(x -1)(x -1)-(y -2)(y -2)=0(cid:54) MP NP x -1 x -1 1 2 1 2 1 2 (cid:93)(my -2)(my -2)-(y -2)(y -2)=0(cid:54)(cid:183)(cid:15)(cid:68)(m2-1)y y -(2m-2)(y +y )=0(cid:54) 1 2 1 2 1 2 1 2 m2-1 (2m-2)×2m 1 (cid:71)- - =0(cid:54)(cid:52)(cid:178)5m2-4m-1=0(cid:54)(cid:206)m¹1(cid:54)(cid:24)(cid:68)(cid:54)m=- (cid:54) m2+2 m2+2 5 1 (cid:129)(cid:75)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)x=- y-1(cid:54)(cid:71)5x+y+5=0. 5 (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:267)2(cid:227)(cid:54)(cid:127)ÐMPF =ÐNPF (cid:54)(cid:191)(cid:148)(cid:49)(cid:50)(cid:247)(cid:107)(cid:78)(cid:231)(cid:107)(cid:46)(cid:43)(cid:128)(cid:190)(cid:42)(cid:68)k ×k =1(cid:178) MP NP (cid:24)(cid:21)(cid:244)(cid:3)(cid:235). y2 2(cid:26)(cid:27)2024·(cid:411)(cid:412)(cid:413)(cid:414)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)G(cid:10)x2- =1(cid:117)(cid:49)(cid:50)l(cid:10)y=x+1(cid:51)(cid:52)A(cid:23)B(cid:40)(cid:41)(cid:27)A(cid:99)B(cid:171)(cid:415)(cid:32)(cid:54) 4 (cid:48)(cid:41)A(cid:43)(cid:40)(cid:152)(cid:3)(cid:52)l(cid:173)(cid:174)(cid:43)(cid:49)(cid:50)l (cid:23)l (cid:64)(cid:159)(cid:51)(cid:160)(cid:161)(cid:50)G(cid:52)C(cid:23)D(cid:40)(cid:41)(cid:27)C(cid:99)(cid:264)(cid:172)(cid:54)D(cid:99)(cid:171)(cid:172)(cid:32)(cid:26) 1 2 (1)(cid:96)(cid:49)(cid:50)l (cid:43)(cid:107)(cid:46)(cid:36)k (cid:54)(cid:49)(cid:50)l (cid:43)(cid:107)(cid:46)(cid:36)k (cid:54)(cid:42)k ×k (cid:43)(cid:200)(cid:73) 1 1 2 2 1 2 (2)(cid:47)(cid:49)(cid:50)CD(cid:117)(cid:160)(cid:161)(cid:50)G(cid:99)(cid:41)B(cid:308)(cid:43)(cid:377)(cid:50)(cid:51)(cid:52)(cid:41)P(cid:54)(cid:42)VABP(cid:43)(cid:56)(cid:57)(cid:26) (cid:60)(cid:25)(cid:61)(cid:62)(1)1 32 (2) (cid:26) 15 π (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:96)(cid:49)(cid:50)l (cid:23)l (cid:43)(cid:247)(cid:107)(cid:78)(cid:64)(cid:159)(cid:36)q(cid:23)q(cid:27)q(cid:23)q Î0,π(cid:32)(cid:54)(cid:93)q+q =2a= (cid:54)(cid:81)(cid:82)(cid:83)(cid:107)(cid:46)(cid:117) 1 2 1 2 1 2 1 2 2 (cid:247)(cid:107)(cid:78)(cid:43)(cid:3)(cid:268)(cid:54)(cid:191)(cid:148)(cid:416)(cid:289)(cid:7)(cid:86)(cid:42)(cid:24)(cid:73)5 2 (cid:27)2(cid:32)(cid:104)(cid:42)(cid:70)(cid:41)B(cid:43)(cid:91)(cid:92)(cid:54)(cid:269)(cid:206)(cid:68)(cid:69)(cid:160)(cid:161)(cid:50)G(cid:99)(cid:41)B(cid:308)(cid:43)(cid:377)(cid:50)(cid:58)(cid:59)(cid:36) x- y=1(cid:54)(cid:108)(cid:260)(cid:96)(cid:49)(cid:50)CD(cid:36) 3 3 mx+1+ny=1(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:191)(cid:148)(cid:211)(cid:125)(cid:189)(cid:15)(cid:35)(cid:77)(cid:78)(cid:79)(cid:56)(cid:57)(cid:7)(cid:86)(cid:42)(cid:24). π (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:34)(cid:49)(cid:50)l(cid:107)(cid:46)(cid:36)1(cid:54)\(cid:49)(cid:50)l(cid:43)(cid:247)(cid:107)(cid:78)a= (cid:54) 4 (cid:96)(cid:49)(cid:50)l (cid:23)l (cid:43)(cid:247)(cid:107)(cid:78)(cid:64)(cid:159)(cid:36)q(cid:23)q(cid:27)q(cid:23)q Î0,π(cid:32)(cid:54) 1 2 1 2 1 2 π (cid:49)(cid:50)l (cid:23)l (cid:3)(cid:52)(cid:49)(cid:50)l(cid:173)(cid:174)(cid:54)\q+q =2a= (cid:54) 1 2 1 2 2 æπ ö sinç -q÷ æπ ö sinq è2 1ø \k ×k =tanq×tanq =tanq×tanç -q÷= 1 × =1(cid:26) 1 2 1 2 1 è2 1ø cosq æπ ö 1 cosç -q÷ è2 1ø ì y2 ïx2- =1 æ5 8ö (cid:27)2(cid:32)(cid:89)(cid:90)í 4 Þ A-1,0,Bç , ÷(cid:54) ï è3 3ø î y=x+1 5 2 \(cid:160)(cid:161)(cid:50)G(cid:99)(cid:41)B(cid:308)(cid:43)(cid:377)(cid:50)(cid:58)(cid:59)(cid:36) x- y=1(cid:26) 3 3 (cid:108)(cid:260)(cid:96)(cid:49)(cid:50)CD(cid:36)mx+1+ny=1(cid:54)Cx,y (cid:54)Dx ,y (cid:54) 1 1 2 2 ì y2 ï x2- =1 ì ï4x+1-12-y2-4=0 (cid:89)(cid:90)í 4 (cid:68)í (cid:54) ï îmx+1+ny=1 ïî mx+1+ny=1 Þ4x+12-8x+1é ëmx+1+nyù û -y2 =0 y2 y y (cid:183)(cid:15)(cid:68) +8n× +8m-4=0(cid:54)(cid:130)(cid:180)(cid:86)(cid:376)(cid:170)(cid:3)(cid:52) (cid:43)(cid:58)(cid:59)(cid:10) x+12 x+1 x+1 y y y y (cid:40)(cid:97)(cid:244)(cid:35) 1 + 2 =-8n(cid:54)(cid:40)(cid:97)(cid:244)(cid:57) 1 × 2 =8m-4(cid:54) x +1 x +1 x +1 x +1 1 2 1 2 y y (cid:206)(cid:144)(cid:145)k ×k =k ×k = 1 × 2 =8m-4(cid:54) 1 2 AC AD x +1 x +1 1 2 5 (cid:127)(cid:27)1(cid:32)(cid:68)k ×k =1(cid:54)\m= 1 2 8 5 æ3 ö \(cid:49)(cid:50)CD(cid:36) x+1+ny=1(cid:54)(cid:48)(cid:189)(cid:41)ç ,0÷(cid:54) 8 è5 ø 5 2 æ3 ö æ3 ö (cid:229)Q(cid:160)(cid:161)(cid:50)G(cid:99)(cid:41)B(cid:308)(cid:43)(cid:377)(cid:50)(cid:58)(cid:59)(cid:36) x- y=1(cid:54)(cid:48)(cid:41)ç ,0÷(cid:54)\Pç ,0÷(cid:54) 3 3 è5 ø è5 ø 3 -0+1 1 1 8 5 32(cid:26) \S = × AB ×d = × 2× × = VABP 2 P-AB 2 3 2 15x2 y2 1 3(cid:26)(cid:27)2024·(cid:417)(cid:418)(cid:419)(cid:420)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)C(cid:10) + =1(a>b>0)(cid:43)(cid:44)(cid:45)(cid:46)(cid:36) (cid:54)(cid:171)､(cid:264)(cid:319)(cid:41)(cid:64)(cid:159)(cid:36)F(cid:54)F (cid:54) a2 b2 2 1 2 (cid:39)､(cid:143)(cid:283)(cid:41)(cid:64)(cid:159)(cid:36)A(cid:54)A (cid:54)(cid:55)(cid:102)(cid:292)(cid:79)AFAF (cid:43)(cid:56)(cid:57)(cid:36)2 3. 1 2 1 1 2 2 (1)(cid:42)(cid:37)(cid:38)C(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:73) (2)(cid:49)(cid:50)l(cid:10)y=kx+m(m>0)(cid:117)(cid:37)(cid:38)C(cid:51)(cid:52)P(cid:54)Q(cid:40)(cid:41)(cid:54)(cid:55)P(cid:54)Q(cid:3)(cid:52)(cid:225)(cid:41)(cid:43)(cid:173)(cid:174)(cid:41)(cid:64)(cid:159)(cid:36)M(cid:54)N(cid:54)(cid:47)OP 2+ OQ 2 (cid:178)(cid:22)(cid:221)(cid:117)m(cid:141)(cid:3)(cid:43)(cid:162)(cid:13)(cid:54)(cid:93)(cid:140)(cid:102)(cid:292)(cid:79)PQMN(cid:56)(cid:57)(cid:256)(cid:285)(cid:138)(cid:54)(cid:42)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59). x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) + =1 4 3 (2)(cid:25)(cid:61)(cid:184)(cid:24)(cid:65) (cid:60)(cid:64)(cid:65)(cid:62) (cid:27)1(cid:32)(cid:127)(cid:37)(cid:38)(cid:43)(cid:272)(cid:421)(cid:231)(cid:33)(cid:34)(cid:152)(cid:153)(cid:72)(cid:68)a(cid:54)b(cid:54)c(cid:43)(cid:3)(cid:268)(cid:54)(cid:205)(cid:206)(cid:72)(cid:42)(cid:70)a(cid:54)b(cid:54)c(cid:43)(cid:200)(cid:54)(cid:205)(cid:206)(cid:72)(cid:68)(cid:37)(cid:38)C(cid:43)(cid:92)(cid:407)(cid:58) (cid:59)(cid:73) (cid:27)2(cid:32)(cid:49)(cid:50)l(cid:58)(cid:59)(cid:117)(cid:37)(cid:38)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:72)(cid:68)(cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:54)(cid:205)(cid:206)(cid:72)(cid:124)(cid:217)(cid:70)|OP|2+|OQ|2(cid:54)(cid:127)|OP|2+|OQ|2(cid:178)(cid:22) (cid:221)(cid:117)m(cid:141)(cid:3)(cid:43)(cid:162)(cid:13)(cid:54)(cid:72)(cid:42)(cid:70)k(cid:43)(cid:200)(cid:54)(cid:124)(cid:217)(cid:70)(cid:102)(cid:292)(cid:79)PQMN(cid:56)(cid:57)(cid:54)(cid:42)(cid:70)(cid:140)(cid:102)(cid:292)(cid:79)PQMN(cid:56)(cid:57)(cid:256)(cid:285)(cid:138)m(cid:43) (cid:200)(cid:54)(cid:71)(cid:72)(cid:42)(cid:24)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:26) c 1 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)e= = (cid:54) a 2 1 S = ×2c×2b=2bc=2 3(cid:54)(cid:129)(cid:75)bc= 3(cid:54) (cid:102)(cid:292)(cid:79)A1F1A2F2 2 (cid:250)(cid:36)a2(cid:422)b2+c2(cid:54)(cid:129)(cid:75)a(cid:422)2(cid:54)b= 3(cid:54)c(cid:422)1(cid:54) x2 y2 (cid:129)(cid:75)(cid:37)(cid:38)(cid:58)(cid:59)(cid:36) + =1(cid:26) 4 3 (cid:27)2(cid:32) (cid:165)(cid:390)(cid:54)(cid:96)P(cid:27)x1(cid:54)y1(cid:32)(cid:54)Q(cid:27)x2(cid:54)y2(cid:32)(cid:54) OP|2 + OQ|2=  x2+y2 +  x2+y2 =x2+3- 3 x2+x2+3- 3 x2 1 1 2 2 1 4 1 2 4 2 =6+ 1 x2+x2 =6+ 1 [  x +x )2-2xx ù(cid:54) 4 1 2 4 1 2 1 2ûìy=kx+m ï (cid:89)(cid:90)íx2 y2 (cid:54)(cid:154)(cid:253)y(cid:183)(cid:15)(cid:68)(cid:27)3+4k2(cid:32)x2+8kmx+4m2﹣12(cid:422)0(cid:54) ï + =1 î 4 3 Δ(cid:422)(cid:27)8km(cid:32)2﹣4(cid:27)4m2﹣12(cid:32)(cid:27)3+4k2(cid:32)(cid:423)0(cid:54)(cid:71)m2(cid:424)3+4k2(cid:54) -8km 4m2-12 (cid:129)(cid:75)x +x = (cid:54)xx = . (cid:54) 1 2 3+4k2 1 2 3+4k2 1 æ -8km 8m2-24ù OP|2 + OQ|2=6+ [ç )2- ú 4 è3+4k2 3+4k2 û 1 32k2m2-24m2+96k2+72 =6+ × (cid:54) 4 (3+4k2)2 3 3 (cid:250)(cid:36)|OP|2+|OQ|2(cid:178)(cid:22)(cid:221)(cid:117)m(cid:141)(cid:3)(cid:43)(cid:162)(cid:13)(cid:54)(cid:129)(cid:75)32k2﹣24(cid:422)0(cid:54)k2 = (cid:54)k =± (cid:54) 4 2 -4km 2m2-6 x +x = (cid:54)xx = (cid:54) 1 2 3 1 2 3 16k2m2 8m2-24 24-4m2 PQ = 1+k2 (x +x )2-4xx = 1+k2 - = 1+k2 1 2 1 2 9 3 3 m (cid:41)O(cid:69)(cid:49)(cid:50)l(cid:43)(cid:80)(cid:44)d = (cid:54) O 1+k2 1 6-m2 1 3 (cid:129)(cid:75)S = PQ d = m = 6-m2 m2 £ = 3(cid:54) VPOQ 2 O 3 3 3 (cid:140)(cid:55)(cid:317)(cid:140) 6-m2 = m2 (cid:54)(cid:71)m2(cid:422)3(cid:54) (cid:250)(cid:36)m(cid:423)0(cid:54)(cid:129)(cid:75) m= 3 (cid:138)(cid:54)(cid:199)(cid:68)(cid:256)(cid:285)(cid:200)(cid:36) 3 (cid:54) (cid:250)(cid:36)S(cid:102)(cid:292)(cid:79)MNPQ(cid:422)4S POQ(cid:54)(cid:129)(cid:75)S POQ(cid:256)(cid:285)(cid:138)(cid:54)S(cid:102)(cid:292)(cid:79)MNPQ(cid:256)(cid:285)(cid:54) 3 △ 3 △ (cid:129)(cid:75)l(cid:10)y= x+ 3(cid:63)y=- x+ 3(cid:26) 2 2 c 4(cid:26)(cid:27)2024·(cid:28)(cid:425)(cid:426)(cid:427)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)E(cid:10)x2-3y2 =3(cid:43)(cid:171)(cid:23)(cid:264)(cid:319)(cid:41)(cid:64)(cid:159)(cid:36)F(cid:54)F (cid:54)A(cid:178)(cid:49)(cid:50)l(cid:10)y=- x 1 2 a2 (cid:27)(cid:144)(cid:145)a(cid:178)(cid:428)(cid:429)(cid:156)(cid:115)(cid:54)c(cid:178)(cid:429)(cid:319)(cid:80)(cid:32)(cid:39)(cid:108)(cid:95)(cid:52)(cid:225)(cid:41)O(cid:43)(cid:22)(cid:221)(cid:279)(cid:41)(cid:54)(cid:107)(cid:46)(cid:36)k (cid:43)(cid:49)(cid:50)AF (cid:117)(cid:160)(cid:161)(cid:50)E(cid:51)(cid:52)M (cid:54) 1 1 N (cid:40)(cid:41)(cid:54)(cid:107)(cid:46)(cid:36)k (cid:43)(cid:49)(cid:50)AF (cid:117)(cid:160)(cid:161)(cid:50)E(cid:51)(cid:52)P(cid:54)Q(cid:40)(cid:41)(cid:26) 2 2 1 1 (1)(cid:42) + (cid:43)(cid:200)(cid:73) k k 1 2 (2)(cid:47)(cid:49)(cid:50)OM (cid:54)ON(cid:54)OP(cid:54)OQ(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k (cid:54)k (cid:54)k (cid:54)k (cid:54)(cid:227)(cid:178)(cid:430)(cid:109)(cid:99)(cid:41)A(cid:54)(cid:150)(cid:151) OM ON OP OQ k OM +k ON +k OP +k OQ =0(cid:54)(cid:47)(cid:109)(cid:99)(cid:54)(cid:42)(cid:70)A(cid:41)(cid:91)(cid:92)(cid:73)(cid:47)(cid:108)(cid:109)(cid:99)(cid:54)(cid:344)(cid:176)(cid:15)(cid:127)(cid:26) (cid:60)(cid:25)(cid:61)(cid:62)(1)-3 æ6 4ö æ 6 4ö (2)(cid:109)(cid:99)(cid:54)Aç ,- ÷(cid:54)(cid:63)Aç- , ÷ è5 5ø è 5 5øæ 2 ö (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:96) Açt,- t÷ t ¹0(cid:54)(cid:82)(cid:83)(cid:107)(cid:46)(cid:7)(cid:86)(cid:42)(cid:24)(cid:73) è 3 ø (cid:27)2(cid:32)(cid:96)Mx,y ,Nx ,y ,Px ,y ,Qx ,y (cid:54)(cid:49)(cid:50)AF (cid:58)(cid:59)(cid:36)y=k x+2(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:191)(cid:148)(cid:211)(cid:125) 1 1 2 2 3 3 4 4 1 1 2k 2k 1 1 (cid:189)(cid:15)(cid:68)(cid:69)k +k = 1 (cid:54)k +k = 2 (cid:54)(cid:191)(cid:148) + =-3(cid:42)(cid:24). OM ON 4k2+1 OP OQ 4k2+1 k k 1 2 1 2 x2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:72)(cid:68)(cid:160)(cid:161)(cid:50)E(cid:10) -y2 =1(cid:54) 3 (cid:93)a2 = 3,b2 = 1,\c2 = a2 +b2 = 4,\c = 2(cid:54) 2 (cid:171)(cid:23)(cid:264)(cid:319)(cid:41)(cid:64)(cid:159)(cid:36)F -2,0(cid:54)F 2,0(cid:54)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)(cid:10)y=- x 1 2 3 ∴ æ 2 ö (cid:96)Açt,- t÷ t ¹0(cid:54) è 3 ø 2 - t-0 2t 3 2t (cid:54)(cid:95)(cid:15)(cid:72)(cid:68)k =- (cid:26) k = =- 2 3t-2 1 t+2 3t+2 1 1 3t+2 3t-2 6t + =- - =- =-3(cid:73) k k 2t 2t 2t 1 2 ∴ (cid:27)2(cid:32)(cid:96)Mx,y ,Nx ,y ,Px ,y ,Qx ,y (cid:54)(cid:165)(cid:390)(cid:54) 1 1 2 2 3 3 4 4 (cid:49)(cid:50)AF (cid:58)(cid:59)(cid:36)y=k x+2(cid:54) 1 1 (cid:66)(cid:67)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:72)(cid:68)(cid:10)  1-3k2 x2-12k2x-12k2-3=0(cid:54) 1 1 1 12k2 -12k2-3 (cid:129)(cid:75)x +x = 1 (cid:54)(cid:93)x x = 1 (cid:54) 1 2 1-3k2 1 2 1-3k2 1 1 y y y x +y x (cid:93)k +k = 1 + 2 = 1 2 2 1 (cid:54) OM ON x x xx 1 2 1 2 k x +2x +k x +2x = 1 1 2 1 2 1 (cid:54) xx 1 2 2k xx +2k x +x  = 1 1 2 1 2 1 (cid:54) xx 1 22k = 1 (cid:26) 4k2+1 1 2k (cid:95)(cid:15)k +k = 2 (cid:54) OP OQ 4k2+1 2 2k 2k (cid:71) 1 + 2 =0(cid:54) 4k2+1 4k2+1 1 2 (cid:71)k +k 4kk +1=0(cid:54) 1 2 1 2 1 k +k =0(cid:63)kk =- (cid:54) 1 2 1 2 4 ∴ 1 1 (cid:229) + =-3(cid:54) k k 1 2 (cid:47)k +k =0(cid:26)(cid:141)(cid:24)(cid:54)(cid:252)(cid:253)(cid:26) 1 2 1 1 1 kk =- (cid:54)(cid:24)(cid:68)k =- (cid:54)k =1(cid:54)(cid:63)k =1(cid:54)k =- (cid:54) 1 2 4 1 4 2 1 2 4 ∴ 1 2 1 (cid:47)k =- (cid:54)k =1(cid:54)(cid:127)A(cid:99)(cid:49)(cid:50)AF (cid:39)(cid:72)(cid:68)(cid:54)- t=- t+2(cid:54) 1 4 2 1 3 4 6 æ6 4ö t = (cid:26)(cid:137)(cid:138)Aç ,- ÷(cid:54) 5 è5 5ø ∴ 1 2 (cid:47)k =1(cid:54)k =- (cid:54)(cid:127)A(cid:99)(cid:49)(cid:50)AF (cid:39)(cid:72)(cid:68)(cid:54)- t =t+2(cid:54) 1 2 4 1 3 6 æ 6 4ö t=- (cid:137)(cid:138)Aç- , ÷ 5 è 5 5ø ∴ æ6 4ö æ 6 4ö (cid:109)(cid:99)(cid:41)Aç ,- ÷(cid:54)(cid:63)Aç- , ÷(cid:54)(cid:150)(cid:151)k OM +k ON +k OP +k OQ =0(cid:26) è5 5ø è 5 5ø ∴ 5(cid:26)(cid:27)2024·(cid:412)(cid:431)(cid:432)(cid:412)·(cid:77)(cid:406)(cid:32)(cid:99)(cid:84)(cid:56)(cid:49)(cid:78)(cid:91)(cid:92)(cid:268)xOy(cid:145)(cid:54)(cid:33)(cid:34)(cid:294)(cid:14)(cid:50)E:y2 =2px(p>0)(cid:43)(cid:319)(cid:41)(cid:36)F,A(cid:178)E(cid:39) π (cid:267)(cid:22)(cid:329)(cid:330)(cid:342)(cid:43)(cid:279)(cid:41).(cid:140)(cid:49)(cid:50)AF(cid:43)(cid:247)(cid:107)(cid:78)(cid:36) (cid:138)(cid:54) AF =4. 3 (1)(cid:42)E(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:33)(cid:34)(cid:41)D2,2,B,C(cid:178)E(cid:39)(cid:108)(cid:95)(cid:40)(cid:41).(cid:47)(cid:102)(cid:292)(cid:79)ABCD(cid:178)(cid:84)(cid:85)(cid:102)(cid:292)(cid:79)(cid:54)(cid:106)(cid:176)(cid:10)(cid:49)(cid:50)AC(cid:48)(cid:189)(cid:41). (cid:60)(cid:25)(cid:61)(cid:62)(1)y2 =4x (2)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:48)(cid:41)A(cid:170)x(cid:156)(cid:43)(cid:133)(cid:50)(cid:54)(cid:407)(cid:50)(cid:43)(cid:133)(cid:50)(cid:54)(cid:191)(cid:148)(cid:294)(cid:14)(cid:50)(cid:43)(cid:189)(cid:190)(cid:72)(cid:68) AH = p+2=4(cid:54)(cid:71)(cid:72)(cid:68)p=2 2 (cid:35)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:49)(cid:50)AC(cid:58)(cid:59)(cid:36)x=my+n(cid:54)(cid:89)(cid:90)(cid:58)(cid:59)(cid:191)(cid:148)(cid:211)(cid:125)(cid:189)(cid:15)(cid:72)(cid:68)B  4m2+2n-2,4m-2  (cid:54)(cid:66)(cid:67)(cid:294)(cid:14)(cid:50)(cid:58)(cid:59)(cid:72)3 (cid:68)n= -2m(cid:54)(cid:71)(cid:72)(cid:68)(cid:191)(cid:340). 2 æ p ö p (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:72)(cid:34)(cid:10)(cid:294)(cid:14)(cid:50)E(cid:43)(cid:319)(cid:41)Fç ,0÷(cid:54)(cid:407)(cid:50)x=- (cid:54) è 2 ø 2 (cid:48)(cid:41)A(cid:170)x(cid:156)(cid:43)(cid:133)(cid:50)(cid:54)(cid:133)(cid:151)(cid:36)H (cid:54)(cid:170)(cid:407)(cid:50)(cid:43)(cid:133)(cid:50)(cid:54)(cid:133)(cid:151)(cid:36)H (cid:54) 1 2 (cid:127)(cid:294)(cid:14)(cid:50)(cid:189)(cid:190)(cid:72)(cid:68) AH = AF =4(cid:54) 2 π (cid:250)(cid:36)(cid:49)(cid:50)AF(cid:43)(cid:247)(cid:107)(cid:78)(cid:36) (cid:54)(cid:93) FH =2(cid:54) 3 1 (cid:72)(cid:68) AH = p+2=4(cid:54)(cid:24)(cid:68)p=2(cid:54) 2 (cid:129)(cid:75)E(cid:43)(cid:58)(cid:59)(cid:36)y2 =4x. (cid:27)2(cid:32)(cid:96)(cid:49)(cid:50)AC(cid:58)(cid:59)(cid:36)x=my+n(cid:54)Ax,y ,Cx ,y ,Bx ,y (cid:54) 1 1 2 2 0 0 ìy2 =4x (cid:89)(cid:90)(cid:58)(cid:59)(cid:100)í (cid:54)(cid:154)(cid:253)x(cid:183)(cid:15)(cid:68)y2-4my-4n=0(cid:54) îx=my+n (cid:93)D>0,y +y =4m,y y =-4n(cid:54) 1 2 1 2 (cid:250)(cid:36)(cid:102)(cid:292)(cid:79)ABCD(cid:178)(cid:84)(cid:85)(cid:102)(cid:292)(cid:79)(cid:54) ìy = y +y -2=4m-2 (cid:93)í 0 1 2 (cid:54)(cid:71)B  4m2+2n-2,4m-2  (cid:54) îx 0 =x 1 +x 2 -2=my 1 +y 2 +2n-2=4m2+2n-2 (cid:66)(cid:67)y2 =4x(cid:145)(cid:68)(4m-2)2 =4  4m2+2n-2  (cid:54)(cid:183)(cid:15)(cid:68)n= 3 -2m(cid:54) 2 3 3 (cid:93)(cid:49)(cid:50)AC(cid:10)x=my+ -2m=my-2+ (cid:54) 2 2æ3 ö (cid:129)(cid:75)(cid:49)(cid:50)AC(cid:48)(cid:189)(cid:41)ç ,2÷. è2 ø x2 y2 6(cid:26)(cid:27)2024·(cid:39)(cid:433)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)C(cid:10) + = 1(cid:54)F(cid:23)F (cid:64)(cid:159)(cid:36)(cid:171)(cid:23)(cid:264)(cid:319)(cid:41)(cid:54)(cid:49)(cid:50)l(cid:48)F (cid:51)(cid:37)(cid:38)(cid:52)A(cid:23)B 1 2 2 8 4 (cid:40)(cid:41). (1)(cid:42)(cid:37)(cid:38)(cid:43)(cid:44)(cid:45)(cid:46)(cid:73) (2)(cid:140)ÐFAB=90°(cid:54)(cid:55)(cid:41)A(cid:99)x(cid:156)(cid:39)(cid:58)(cid:138)(cid:54)(cid:42)A(cid:23)B(cid:40)(cid:41)(cid:43)(cid:91)(cid:92)(cid:73) 1 (3)(cid:47)(cid:49)(cid:50)AF (cid:51)y(cid:156)(cid:52)M (cid:54)(cid:49)(cid:50)BF(cid:51)y(cid:156)(cid:52)N (cid:54)(cid:178)(cid:430)(cid:109)(cid:99)(cid:49)(cid:50)l(cid:54)(cid:195)(cid:68)S =S (cid:434)(cid:47)(cid:109)(cid:99)(cid:54)(cid:42)(cid:70)(cid:49)(cid:50)l 1 1 VF1AB VF1MN (cid:43)(cid:58)(cid:59)(cid:73)(cid:47)(cid:108)(cid:109)(cid:99)(cid:54)(cid:435)(cid:344)(cid:176)(cid:15)(cid:127). 2 (cid:60)(cid:25)(cid:61)(cid:62)(1) 2 æ8 2ö (2)Bç ,- ÷(cid:73)A0,2 è3 3ø (3)(cid:109)(cid:99)(cid:49)(cid:50)x+ 3y-2=0(cid:63)x- 3y-2=0(cid:150)(cid:151)(cid:21)(cid:128) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:37)(cid:38)(cid:58)(cid:59)(cid:49)(cid:185)(cid:42)a,b(cid:54)(cid:71)(cid:72)(cid:68)(cid:44)(cid:45)(cid:46)(cid:73) (cid:27)2(cid:32)(cid:127)(cid:133)(cid:49)(cid:43)(cid:134)(cid:196)(cid:124)(cid:217)(cid:16)(cid:251)(cid:54)(cid:191)(cid:148)(cid:41)(cid:99)(cid:37)(cid:38)(cid:39)(cid:71)(cid:72)(cid:42)(cid:70)A(cid:41)(cid:91)(cid:92)(cid:54)(cid:81)(cid:89)(cid:90)(cid:49)(cid:50)(cid:117)(cid:37)(cid:38)(cid:72)(cid:68)B(cid:41)(cid:91)(cid:92)(cid:73) (cid:27)3(cid:32)(cid:127)(cid:49)(cid:50)(cid:58)(cid:59)(cid:68)(cid:70)y ,y (cid:54)(cid:64)(cid:159)(cid:42)(cid:70)(cid:77)(cid:78)(cid:79)(cid:56)(cid:57)(cid:54)(cid:97)(cid:98)(cid:56)(cid:57)(cid:212)(cid:180)(cid:436)(cid:90)(cid:58)(cid:59)(cid:42)(cid:70)m(cid:71)(cid:72)(cid:68)(cid:24). 3 4 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:37)(cid:38)(cid:58)(cid:59)(cid:34)(cid:54)a=2 2(cid:54)b=2(cid:54) (cid:129)(cid:75) c= a2-b2 =2 (cid:54) c 2 2 (cid:129)(cid:75)(cid:44)(cid:45)(cid:46)e= = = . a 2 2 2 (cid:27)2(cid:32)F -2,0(cid:54)F 2,0(cid:54)(cid:96)Ax,y (cid:54)(cid:55)y >0. 1 2 1 1 1 uuur uuuur (cid:129)(cid:75)AF =-x -2,-y (cid:54)AF =-x +2,-y (cid:54) 1 1 1 2 1 1 uuur uuuur QÐFAB=90°ÐFAF =90°(cid:54)\AF ×AF =x2-4+y2 =0(cid:54) 1 1 2 1 2 1 1 x2 y2 æ x2 ö (cid:229)A(cid:99)(cid:37)(cid:38)(cid:39)(cid:54)(cid:150)(cid:151) 1 + 1 =1(cid:54)(cid:71)y2 =4ç1- 1 ÷(cid:54) 8 4 1 è 8 ø æ x2 ö \x2-4+4ç1- 1 ÷=0(cid:54)(cid:24)(cid:68)x =0(cid:54)(cid:71)A0,2 . 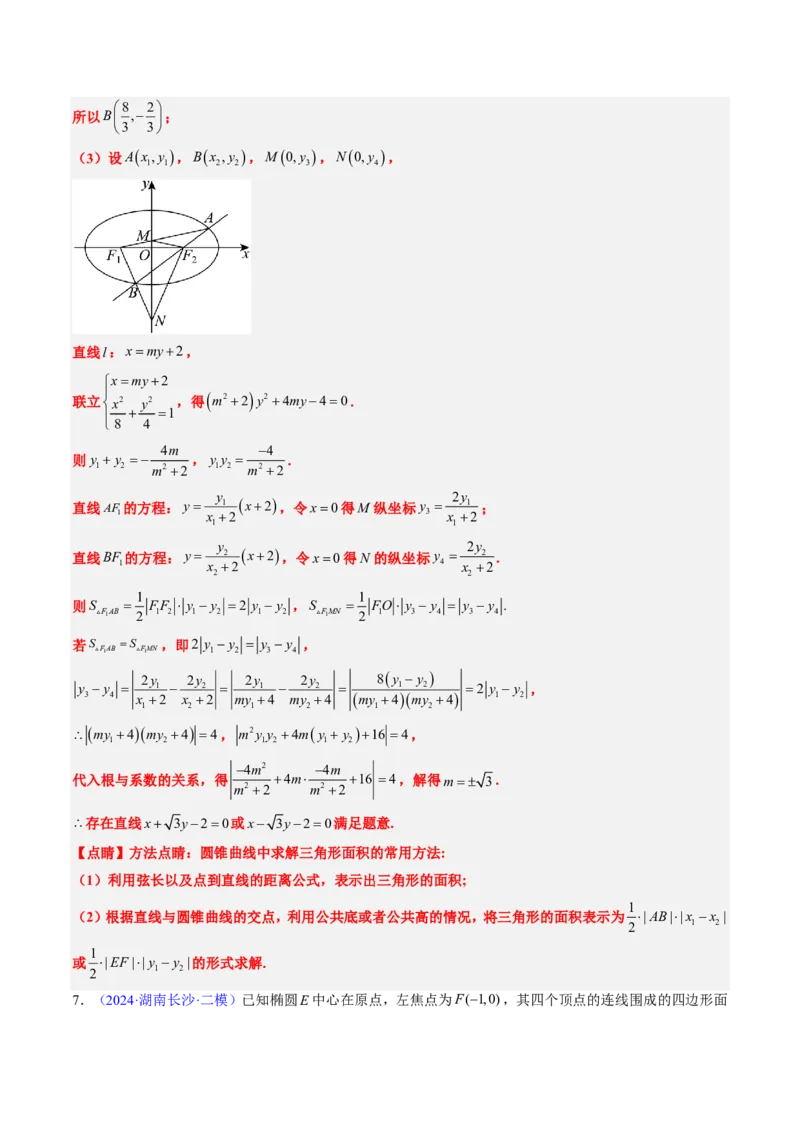1 è 8 ø 1 (cid:129)(cid:75)(cid:49)(cid:50)AB(cid:10)y=-x+2(cid:54) ì 8 ìy=-x+2 x= ï ï ï 3 ìx=0 (cid:89)(cid:90)íx2 y2 (cid:54)(cid:24)(cid:68)í (cid:63)í (cid:54) ï î 8 + 4 =1 ï y=- 2 îy=2 ïî 3æ8 2ö (cid:129)(cid:75)Bç ,- ÷(cid:73) è3 3ø (cid:27)3(cid:32)(cid:96)Ax,y (cid:54)Bx ,y (cid:54)M0,y (cid:54)N0,y (cid:54) 1 1 2 2 3 4 (cid:49)(cid:50)l(cid:10)x=my+2(cid:54) ìx=my+2 (cid:89)(cid:90) ï íx2 y2 (cid:54)(cid:68)  m2+2  y2+4my-4=0. ï + =1 î 8 4 4m -4 (cid:93)y +y =- (cid:54)y y = . 1 2 m2+2 1 2 m2+2 y 2y (cid:49)(cid:50)AF (cid:43)(cid:58)(cid:59)(cid:10)y= 1 x+2 (cid:54)(cid:149)x=0(cid:68)M (cid:384)(cid:91)(cid:92)y = 1 (cid:73) 1 x +2 3 x +2 1 1 y 2y (cid:49)(cid:50)BF(cid:43)(cid:58)(cid:59)(cid:10)y= 2 x+2 (cid:54)(cid:149)x=0(cid:68)N (cid:43)(cid:384)(cid:91)(cid:92)y = 2 . 1 x +2 4 x +2 2 2 1 1 (cid:93)S = FF × y -y =2 y -y (cid:54)S = FO × y -y = y -y . VF1AB 2 1 2 1 2 1 2 VF1MN 2 1 3 4 3 4 (cid:47)S =S (cid:54)(cid:71)2 y -y = y -y (cid:54) VF1AB VF1MN 1 2 3 4 2y 2y 2y 2y 8y -y  y -y = 1 - 2 = 1 - 2 = 1 2 =2 y -y (cid:54) 3 4 x +2 x +2 my +4 my +4 my +4my +4 1 2 1 2 1 2 1 2 \my +4my +4 =4(cid:54) m2y y +4my +y +16 =4(cid:54) 1 2 1 2 1 2 -4m2 -4m (cid:66)(cid:67)(cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:54)(cid:68) +4m× +16 =4(cid:54)(cid:24)(cid:68)m=± 3. m2+2 m2+2 \(cid:109)(cid:99)(cid:49)(cid:50)x+ 3y-2=0(cid:63)x- 3y-2=0(cid:150)(cid:151)(cid:21)(cid:128). (cid:60)(cid:41)(cid:234)(cid:62)(cid:58)(cid:74)(cid:41)(cid:234)(cid:10)(cid:38)(cid:437)(cid:161)(cid:50)(cid:145)(cid:42)(cid:24)(cid:77)(cid:78)(cid:79)(cid:56)(cid:57)(cid:43)(cid:162)(cid:83)(cid:58)(cid:74): (cid:27)1(cid:32)(cid:82)(cid:83)(cid:114)(cid:115)(cid:75)(cid:231)(cid:41)(cid:69)(cid:49)(cid:50)(cid:43)(cid:80)(cid:44)(cid:7)(cid:86)(cid:54)(cid:124)(cid:217)(cid:70)(cid:77)(cid:78)(cid:79)(cid:43)(cid:56)(cid:57); 1 (cid:27)2(cid:32)(cid:97)(cid:98)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:43)(cid:51)(cid:41)(cid:54)(cid:82)(cid:83)(cid:7)(cid:209)(cid:76)(cid:63)(cid:391)(cid:7)(cid:209)(cid:29)(cid:43)(cid:110)(cid:111)(cid:54)(cid:130)(cid:77)(cid:78)(cid:79)(cid:43)(cid:56)(cid:57)(cid:124)(cid:217)(cid:36) ×|AB|×|x -x | 2 1 2 1 (cid:63) ×|EF|×| y -y |(cid:43)(cid:79)(cid:86)(cid:42)(cid:24). 2 1 2 7(cid:26)(cid:27)2024·(cid:438)(cid:439)(cid:115)(cid:440)·(cid:94)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)E(cid:145)(cid:45)(cid:99)(cid:225)(cid:41)(cid:54)(cid:171)(cid:319)(cid:41)(cid:36)F(-1,0)(cid:54)(cid:144)(cid:102)(cid:221)(cid:283)(cid:41)(cid:43)(cid:367)(cid:50)(cid:386)(cid:304)(cid:43)(cid:102)(cid:292)(cid:79)(cid:56)(cid:57)(cid:36)2 2. (1)(cid:42)(cid:37)(cid:38)E(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:73) (2)(cid:48)(cid:37)(cid:38)E(cid:43)(cid:171)(cid:319)(cid:41)F (cid:170)(cid:107)(cid:46)(cid:109)(cid:99)(cid:43)(cid:40)(cid:49)(cid:50)AB(cid:23)CD(cid:64)(cid:159)(cid:51)(cid:37)(cid:38)(cid:52)A(cid:23)B(cid:23)C(cid:23)D(cid:54)(cid:55)AB^CD(cid:54)(cid:50)(cid:324) AB(cid:23)CD(cid:43)(cid:145)(cid:41)(cid:64)(cid:159)(cid:36)M (cid:23)N .(cid:42)(cid:102)(cid:292)(cid:79)BCMN (cid:56)(cid:57)(cid:43)(cid:256)(cid:226)(cid:200). x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) +y2 =1 2 4 (2) 9 x2 y2 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:72)(cid:34)(cid:37)(cid:38)(cid:43)(cid:319)(cid:41)(cid:99)x(cid:156)(cid:39)(cid:54)(cid:92)(cid:407)(cid:58)(cid:59)(cid:72)(cid:96)(cid:36) + =1a>b>0(cid:54)(cid:127)(cid:37)(cid:38)(cid:43)(cid:272)(cid:421)(cid:72)(cid:68)(cid:102) a2 b2 1 (cid:292)(cid:79)(cid:56)(cid:57)(cid:36) ´2a´2b=2 2(cid:54)(cid:127)(cid:319)(cid:41)(cid:91)(cid:92)(cid:72)(cid:34)c=1(cid:54)(cid:89)(cid:90)(cid:58)(cid:59)(cid:71)(cid:72)(cid:42)(cid:70)a(cid:23)b 2 (cid:27)2(cid:32)(cid:127)(cid:41)(cid:107)(cid:86)(cid:96)(cid:70)(cid:49)(cid:50)AB(cid:23)CD(cid:43)(cid:58)(cid:59)(cid:54)(cid:89)(cid:90)(cid:49)(cid:50)AB(cid:117)(cid:37)(cid:38)E(cid:43)(cid:58)(cid:59)(cid:54)(cid:332)(cid:70)(cid:158)(cid:159)(cid:86)(cid:35)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:127)(cid:114)(cid:115) 1 1 1 (cid:7)(cid:86)(cid:68)(cid:69) AB (cid:54)(cid:95)(cid:15)(cid:72)(cid:68) CD (cid:54)(cid:102)(cid:292)(cid:79)BCMN (cid:56)(cid:57)(cid:36) BM ×CN (cid:54)(cid:206) BM = AB (cid:23) CN = CD (cid:54)(cid:82)(cid:83) AB 2 2 2 (cid:35) CD (cid:269)(cid:85)(cid:259)(cid:16)(cid:54)(cid:71)(cid:72)(cid:42)(cid:70)(cid:56)(cid:57)(cid:43)(cid:256)(cid:226)(cid:200). x2 y2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:21)(cid:128)(cid:72)(cid:34)(cid:37)(cid:38)(cid:43)(cid:319)(cid:41)(cid:99)x(cid:156)(cid:39)(cid:54)(cid:96)(cid:37)(cid:38)E(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:36) + =1a>b>0(cid:54) a2 b2 (cid:37)(cid:38)(cid:102)(cid:221)(cid:283)(cid:41)(cid:43)(cid:367)(cid:50)(cid:386)(cid:304)(cid:43)(cid:102)(cid:292)(cid:79)(cid:178)(cid:441)(cid:79)(cid:54)(cid:40)(cid:152)(cid:173)(cid:78)(cid:50)(cid:248)(cid:212)(cid:133)(cid:49)(cid:54)(cid:206)(cid:40)(cid:152)(cid:173)(cid:78)(cid:50)(cid:115)(cid:64)(cid:159)(cid:36)2a(cid:54)2b(cid:54) 1 (cid:127)(cid:33)(cid:34)(cid:68) ´2a´2b=2 2(cid:54)(cid:71)ab= 2(cid:54) 2 (cid:250)(cid:36)(cid:171)(cid:319)(cid:41)(cid:36)F(-1,0)(cid:54)(cid:129)(cid:75)c=1(cid:54)(cid:72)(cid:68)a2-b2 =1(cid:54) ìïab= 2 ìïa= 2 (cid:89)(cid:90)í (cid:54)(cid:24)(cid:68)í (cid:54) ïîa2-b2 =1 ïîb=1 x2 (cid:202)(cid:37)(cid:38)E(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:36) +y2 =1. 2 (cid:27)2(cid:32)(cid:170)(cid:70)(cid:37)(cid:38)E(cid:43)(cid:390)(cid:329)(cid:54)(cid:165)(cid:143)(cid:390)(cid:129)(cid:217)(cid:10) (cid:97)(cid:98)(cid:21)(cid:128)(cid:72)(cid:34)(cid:49)(cid:50)AB(cid:23)CD(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:54)(cid:55)AB^CD(cid:54) (cid:129)(cid:75)(cid:40)(cid:49)(cid:50)AB(cid:23)CD(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)0(cid:54)1 (cid:250)(cid:137)(cid:96)(cid:49)(cid:50)AB(cid:23)CD(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k(cid:23)- (cid:54) k 1 (cid:229)F(-1,0)(cid:54)(cid:96)(cid:49)(cid:50)AB(cid:58)(cid:59)(cid:36)y=k(x+1)(cid:54)(cid:49)(cid:50)CD(cid:58)(cid:59)(cid:36)y=- (x+1)(cid:54) k (cid:96)A(cid:23)B(cid:23)C(cid:23)D(cid:43)(cid:91)(cid:92)(cid:64)(cid:159)(cid:36)x,y (cid:23)x ,y (cid:23)x ,y (cid:23)x ,y (cid:54) 1 1 2 2 3 3 4 4 (cid:96)(cid:102)(cid:292)(cid:79)BCMN (cid:56)(cid:57)(cid:36)S. ìy=k(x+1) (cid:89)(cid:90) ï íx2 (cid:54)(cid:68)  2k2+1  x2+4k2x+  2k2-2  =0(cid:54) ï +y2 =1 î 2 Δ=  4k22 -4´  2k2+1  2k2-2  =8  k2+1  >0(cid:54) ì 4k2 ïx +x =- ï 1 2 2k2+1 (cid:250)(cid:36)x(cid:23)x(cid:178)(cid:139)(cid:58)(cid:59)(cid:40)(cid:97)(cid:54)(cid:127)(cid:211)(cid:125)(cid:189)(cid:15)(cid:72)(cid:68)í (cid:54) 1 2 ï 2k2-2 xx = ïî 1 2 2k2+1 (cid:127)(cid:114)(cid:115)(cid:7)(cid:86)(cid:72)(cid:68) AB = x -x 2+y -y 2 = k2+1 x -x = k2+1× x +x -4xx (cid:54) 2 1 2 1 1 2 1 2 1 2 8k2+8 2 2  k2+1  (cid:93) AB = k2+1 = (cid:54) 2k2+1 2k2+1 æ 1 ö 2 2ç èk2 +1÷ ø 2 2  k2+1  (cid:95)(cid:15)(cid:72)(cid:68)(cid:54) CD = = . 2 k2+2 +1 k2 (cid:250)(cid:36)M (cid:23)N (cid:64)(cid:159)(cid:178)(cid:50)(cid:324)AB(cid:23)CD(cid:43)(cid:145)(cid:41)(cid:54)(cid:55)AB^CD(cid:54) 1 1 (cid:129)(cid:75)BM ^CN (cid:54) BM = AB (cid:54) CN = CD (cid:54) 2 2 1 1 2 2  k2+1  2 2  k2+1   k2+1 2 S = BM ×CN = AB ×CD = × = (cid:54) 2 8 8  2k2+1  k2+2  2k2+1  k2+2  é ù ê ú k4+2k2+1 1æ k2 ö 1 1 1æ 1 ö 4 (cid:129)(cid:75)S = = ç1- ÷= ê1- ú³ ç1- ÷= (cid:54) 2k4+5k2+2 2è 2k4+5k2+2ø 2ê ê ë 2ç è æ k2+ k 1 2 ÷ ø ö +5 ú ú û 2è 2´2+5ø 9 1 (cid:140)(cid:55)(cid:317)(cid:140)k2 = (cid:54)(cid:71)k=±1(cid:138)(cid:54)(cid:180)(cid:9)(cid:304)(cid:90). k2 4 (cid:202)(cid:102)(cid:292)(cid:79)BCMN (cid:56)(cid:57)(cid:43)(cid:256)(cid:226)(cid:200)(cid:36) . 9 x2 y2 8(cid:26)(cid:27)2024·(cid:419)(cid:442)(cid:431)(cid:443)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38) + =1(a>b>0)(cid:43)(cid:171)(cid:283)(cid:41)(cid:36)A(cid:54)(cid:39)(cid:283)(cid:41)(cid:36)B(cid:54)(cid:143)(cid:283)(cid:41)(cid:36)C(cid:54)(cid:47)(cid:37)(cid:38) a2 b2 3 (cid:43)e= (cid:54)(cid:77)(cid:78)(cid:79)ABC(cid:43)(cid:56)(cid:57)(cid:36)2. 2(1)(cid:42)(cid:37)(cid:38)(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:73) (2)(cid:33)(cid:34)(cid:41)D(cid:27)0(cid:54)2(cid:32)(cid:54)(cid:49)(cid:50)AD(cid:51)(cid:37)(cid:38)(cid:52)(cid:41)E(cid:54)(cid:48)(cid:41)D(cid:43)(cid:49)(cid:50)(cid:51)(cid:37)(cid:38)(cid:52)M(cid:54)N(cid:40)(cid:41)(cid:54)(cid:47)(cid:49)(cid:50)CM(cid:117)x(cid:156)(cid:51) |DQ| (cid:52)P(cid:41)(cid:54)(cid:48)E(cid:55)(cid:84)(cid:85)(cid:52)x(cid:156)(cid:43)(cid:49)(cid:50)(cid:117)BN(cid:51)(cid:52)Q(cid:41)(cid:54)(cid:42) (cid:43)(cid:200). |PQ| x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) +y2 =1 4 |DQ| 3 (2) = |PQ| 2 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:37)(cid:38)(cid:43)(cid:300)(cid:236)(cid:196)(cid:71)(cid:72)(cid:42)(cid:24)(cid:73) (cid:27)2(cid:32)(cid:42)(cid:70)(cid:41)E(cid:43)(cid:91)(cid:92)(cid:54)(cid:64)(cid:49)(cid:50)MN(cid:107)(cid:46)(cid:178)(cid:430)(cid:109)(cid:99)(cid:40)(cid:444)(cid:110)(cid:111)(cid:299)(cid:192)(cid:54)(cid:140)(cid:49)(cid:50)MN(cid:107)(cid:46)(cid:109)(cid:99)(cid:138)(cid:54)(cid:96)(cid:70)(cid:49)(cid:50)MN(cid:43) (cid:58)(cid:59)(cid:54)(cid:117)(cid:37)(cid:38)(cid:89)(cid:90)(cid:54)(cid:42)(cid:24)D(cid:54)(cid:97)(cid:98)(cid:51)(cid:41)(cid:221)(cid:13)(cid:177)(cid:70)(cid:3)(cid:52)D(cid:43)(cid:108)(cid:180)(cid:86)(cid:54)(cid:332)(cid:70)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:332)(cid:70)(cid:49)(cid:50)CM (cid:43)(cid:58)(cid:59)(cid:54)(cid:42) (cid:70)(cid:41)P(cid:43)(cid:214)(cid:91)(cid:92)(cid:54)(cid:332)(cid:70)(cid:49)(cid:50)BN(cid:43)(cid:58)(cid:59)(cid:54)(cid:42)(cid:24)(cid:41)Q(cid:43)(cid:214)(cid:91)(cid:92)(cid:54)(cid:332)(cid:70)k -k (cid:71)(cid:72)(cid:68)(cid:77)(cid:41)(cid:209)(cid:50)(cid:54)(cid:269)(cid:206)(cid:42)(cid:24). DQ DP ì ï a2 =b2+c2 ï ï c 3 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:166)(cid:21)(cid:128)(cid:10)í e= = (cid:54)(cid:24)(cid:68)a=2(cid:54)b=1(cid:54)c= 3(cid:54) ï a 2 ï1 ï ´2b´a=2 î2 x2 (cid:37)(cid:38)(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:36) +y2 =1(cid:73) 4 (cid:27)2(cid:32) ì y=x+2 (cid:49)(cid:50)DA(cid:10)y=x+2(cid:54)í (cid:54) îx2+4y2 =4 6 4 (cid:24)(cid:68)x =- (cid:54)y = .(cid:47)(cid:49)(cid:50)MN(cid:10)x=0(cid:54) E 5 E 5 DQ 3 (cid:93) = (cid:54)(cid:47)(cid:49)(cid:50)MN(cid:10)y =kx+2(cid:54) PQ 2 ìy=kx+2 (cid:96)M(x,y)(cid:54)N(x ,y )(cid:54)í (cid:54) 1 1 2 2 îx2+4y2 =4 (cid:183)(cid:15)(cid:68)(1+4k2)x2+16kx+12=0(cid:54)D=256k2-48-192k2 =64k2-48>0(cid:54) 3 3 16k 12 (cid:24)(cid:68)k > (cid:63)k <- (cid:54)x +x =- (cid:54)xx = (cid:54) 2 2 1 2 1+4k2 1 2 1+4k2 y +1 (cid:49)(cid:50)CM(cid:10)y= 1 x-1(cid:54)(cid:149)y=0(cid:54) x 1 x y -1 (cid:68)x = 1 .(cid:49)(cid:50)BN(cid:10)y= 2 x+1(cid:54) P y +1 x 1 2 4 x 6(y -1) 2(y +1) 6(kx +1) 2(kx +3) 8kxx +6(x +x ) (cid:149)y= (cid:54)(cid:68)x =- 2 (cid:54)(cid:250)(cid:36)k -k = 2 + 1 = 2 + 1 = 1 2 1 2 =0(cid:54) 5 Q 5(y -1) DQ DP x x x x xx 2 2 1 2 1 1 2 |DQ| |2-y | 3 (cid:129)(cid:75)D(cid:54)P(cid:54)Q(cid:77)(cid:41)(cid:209)(cid:50)(cid:54)(cid:129)(cid:75) = Q = (cid:54) |PQ| |y -0| 2 Q |DQ| 3 (cid:142)(cid:39)(cid:34)(cid:10) = . |PQ| 2 9(cid:26)(cid:27)2024·(cid:438)(cid:439)(cid:115)(cid:440)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:294)(cid:14)(cid:50)C:y2 =2px(p>0)(cid:54)(cid:48)(cid:41)D0,2(cid:43)(cid:49)(cid:50)l(cid:117)C(cid:51)(cid:52)(cid:108)(cid:95)(cid:43)(cid:40)(cid:41)A,B. (cid:140)(cid:49)(cid:50)l(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)135°(cid:138)(cid:54) AB =4 30. (1)(cid:42)C(cid:43)(cid:58)(cid:59)(cid:73) DA AE (2)(cid:99)(cid:50)(cid:324)AB(cid:39)(cid:199)(cid:445)(cid:52)(cid:41)A,B(cid:43)(cid:41)E(cid:54)(cid:55)(cid:150)(cid:151) = (cid:54)(cid:374)(cid:227)(cid:178)(cid:430)(cid:109)(cid:99)(cid:22)(cid:152)(cid:189)(cid:49)(cid:50)(cid:54)(cid:195)(cid:68)(cid:41)E(cid:446)(cid:99)(cid:218)(cid:152)(cid:189) DB EB (cid:49)(cid:50)(cid:39)(cid:434)(cid:47)(cid:109)(cid:99)(cid:54)(cid:42)(cid:70)(cid:139)(cid:49)(cid:50)(cid:73)(cid:47)(cid:108)(cid:109)(cid:99)(cid:54)(cid:435)(cid:344)(cid:176)(cid:15)(cid:127). (cid:60)(cid:25)(cid:61)(cid:62)(1)y2=12x (2)(cid:41)E(cid:446)(cid:99)(cid:49)(cid:50)y=3x(cid:39). (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:104)(cid:42)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:54)(cid:81)(cid:117)(cid:294)(cid:14)(cid:50)(cid:89)(cid:90)(cid:100)(cid:304)(cid:58)(cid:59)(cid:100)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:231)(cid:40)(cid:41)(cid:80)(cid:44)(cid:7)(cid:86)(cid:54)(cid:42)(cid:114)|AB| (cid:43)(cid:115)(cid:71)(cid:72)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:49)(cid:50)l(cid:58)(cid:59)(cid:54)(cid:81)(cid:117)(cid:294)(cid:14)(cid:50)(cid:89)(cid:90)(cid:100)(cid:304)(cid:58)(cid:59)(cid:100)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:231)(cid:212)(cid:348)(cid:77)(cid:78)(cid:79)(cid:42)(cid:24)(cid:71)(cid:72). (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)Ax,y ,Bx ,y  . 1 1 2 2 (cid:47)(cid:49)(cid:50)l(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)135o(cid:54)(cid:93)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y=-x+2. ìy=-x+2, (cid:89)(cid:90)í (cid:68)x2-4+2px+4=0(cid:54) îy2 =2px, (cid:93)D=(4+2p)2-16=4p2+16p>0(cid:54) (cid:55)x +x =4+2p,xx =4(cid:54) 1 2 1 2 (cid:129)(cid:75) AB = 2 éx +x 2-4xx ù =2 2 p2+4p. ë 1 2 1 2û (cid:250)(cid:36) AB =4 30(cid:54)(cid:129)(cid:75)p=6(cid:54)(cid:202)C(cid:43)(cid:58)(cid:59)(cid:36)y2=12x. (cid:27)2(cid:32)(cid:109)(cid:99)(cid:54)(cid:189)(cid:49)(cid:50)(cid:36)y=3x.(cid:127)(cid:21)(cid:128)(cid:34)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:54) (cid:96)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)y=kx+2k ¹0(cid:54)Ax,y ,Bx ,y  . 1 1 2 2 ìy2 =12x, (cid:89)(cid:90)í (cid:68)k2x2+4k-12x+4=0. îy=kx+2, 3 (cid:127)k ¹0,Δ=(4k-12)2-16k2 >0(cid:54)(cid:68)k < (cid:55)k ¹0(cid:54) 2 12-4k 4 x +x = ,xx = . 1 2 k2 1 2 k2 (cid:108)(cid:260)(cid:96)x b>0(cid:43)(cid:447)(cid:156)(cid:115)(cid:36)2 3(cid:54)(cid:171)(cid:23)(cid:264)(cid:283)(cid:41)(cid:64)(cid:159)(cid:36)C,D(cid:54)(cid:48)(cid:264) a2 b2 (cid:319)(cid:41)F1,0(cid:43)(cid:49)(cid:50)l(cid:51)(cid:37)(cid:38)E(cid:52)A,B(cid:40)(cid:41)(cid:27)(cid:108)(cid:117)C,D(cid:448)(cid:148)(cid:32)(cid:54)(cid:49)(cid:50)AC(cid:117)(cid:49)(cid:50)BD(cid:51)(cid:52)(cid:41)T(cid:26) (1)(cid:42)(cid:37)(cid:38)E(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:42)(cid:106)(cid:10)(cid:41)T(cid:99)(cid:189)(cid:49)(cid:50)(cid:39). x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) + =1(cid:73) 4 3 (2)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65). (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:408)(cid:189)(cid:152)(cid:153)(cid:54)(cid:42)(cid:70)a,b,c(cid:71)(cid:72)(cid:68)(cid:24).(cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)AB(cid:58)(cid:59)(cid:54)(cid:117)(cid:37)(cid:38)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:81)(cid:42)(cid:70)(cid:49)(cid:50)AC(cid:117)(cid:49)(cid:50)BD(cid:43)(cid:51)(cid:41)(cid:214)(cid:91)(cid:92)(cid:54)(cid:327)(cid:191)(cid:148)(cid:211)(cid:125)(cid:189)(cid:15)(cid:187)(cid:188) (cid:71)(cid:68). (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:166)(cid:21)(cid:128)(cid:54)b= 3(cid:54)(cid:429)(cid:319)(cid:80)c=1(cid:54)(cid:93) a= b2+c2 =2 (cid:54) x2 y2 (cid:129)(cid:75)(cid:37)(cid:38)E(cid:43)(cid:58)(cid:59)(cid:36) + =1. 4 3 (cid:27)2(cid:32)(cid:203)(cid:204)(cid:49)(cid:50)AB(cid:108)(cid:133)(cid:49)(cid:52)y(cid:156)(cid:54)(cid:96)(cid:49)(cid:50)AB:x=ty+1(cid:54) ìx=ty+1 (cid:127)í (cid:154)(cid:253)x(cid:327)(cid:183)(cid:15)(cid:68)  3t2+4  y2+6ty-9=0(cid:54) î3x2+4y2 =12 D=36t2+36(3t2+4)=144(t2+1)>0(cid:54)(cid:96)Ax,y ,Bx ,y (cid:54) 1 1 2 2 -6t -9 3 (cid:93)y +y = ,y y = (cid:54)(cid:55)(cid:146)ty y = y +y (cid:54) 1 2 3t2+4 1 2 3t2+4 1 2 2 1 2 y y (cid:49)(cid:50)AC:y= 1 (x+2)(cid:54)(cid:49)(cid:50)BD:y= 2 (x-2)(cid:54) x +2 x -2 1 2 y y y y 2y 2y (cid:89)(cid:90)(cid:154)(cid:253)y(cid:68) 1 (x+2)= 2 (x-2)(cid:54)(cid:71)( 2 - 1 )x= 1 + 2 (cid:54) x +2 x -2 x -2 x +2 x +2 x -2 1 2 2 1 1 2 (cid:183)(cid:15)(cid:68)[y x +2-y x -2]x=2y x -2+2y x +2(cid:54) 2 1 1 2 1 2 2 1 (cid:71)[y ty +3-y ty -1]x=2y ty -1+2y ty +3(cid:54) 2 1 1 2 1 2 2 1 3 (cid:52)(cid:178)3y +y x=4ty y -2y +6y (cid:54)(cid:206)t y y = y +y (cid:54) 2 1 1 2 1 2 1 1 2 2 1 2 6y +y -2y +6y 12y +4y (cid:93)3y +y x=6y +y -2y +6y (cid:54)(cid:250)(cid:137)x= 1 2 1 2 = 2 1 =4(cid:54) 2 1 1 2 1 2 3y +y 3y +y 2 1 2 1 (cid:129)(cid:75)(cid:41)T(cid:99)(cid:189)(cid:49)(cid:50)x=4(cid:39). y2 11(cid:26)(cid:27)2024·(cid:39)(cid:433)(cid:449)(cid:403)(cid:28)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)C:x2- =1(cid:54)(cid:41)F(cid:23)F (cid:64)(cid:159)(cid:36)(cid:160)(cid:161)(cid:50)(cid:43)(cid:171)(cid:23)(cid:264)(cid:319)(cid:41)(cid:54) 1 2 3 Ax,y (cid:23)Bx ,y (cid:36)(cid:160)(cid:161)(cid:50)(cid:39)(cid:43)(cid:41). 1 1 2 2 (1)(cid:42)(cid:264)(cid:319)(cid:41)F (cid:69)(cid:160)(cid:161)(cid:50)(cid:43)(cid:262)(cid:263)(cid:50)(cid:43)(cid:80)(cid:44)(cid:73) 2 uuuur uuuur (2)(cid:47)AF =3FB(cid:54)(cid:42)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:73) 2 2 (3)(cid:47)AF //BF (cid:54)(cid:144)(cid:145)A(cid:23)B(cid:40)(cid:41)(cid:155)(cid:99)x(cid:156)(cid:39)(cid:58)(cid:54)(cid:55)(cid:64)(cid:159)(cid:136)(cid:52)(cid:160)(cid:161)(cid:50)(cid:43)(cid:171)(cid:23)(cid:264)(cid:40)(cid:172)(cid:54)(cid:42)(cid:102)(cid:292)(cid:79)AFF B(cid:43)(cid:56)(cid:57) 1 2 1 2 (cid:43)(cid:199)(cid:200)(cid:385)(cid:386).(cid:60)(cid:25)(cid:61)(cid:62)(1) 3 15 (2)x=± y+2 15 (3) 12,+¥. (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:54)(cid:42)(cid:70)(cid:41)F (cid:43)(cid:91)(cid:92)(cid:35)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:54)(cid:97)(cid:98)(cid:41)(cid:69)(cid:49)(cid:50)(cid:43)(cid:80)(cid:44)(cid:7)(cid:86)(cid:187)(cid:188)(cid:71)(cid:72)(cid:42)(cid:24)(cid:73) 2 (cid:27)2(cid:32)(cid:246)(cid:34)(cid:49)(cid:50)AB(cid:108)(cid:117)x(cid:156)(cid:448)(cid:148)(cid:54)(cid:96)(cid:144)(cid:58)(cid:59)(cid:36)x=my+2(cid:54)(cid:89)(cid:90)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:124)(cid:217) 15 y +y ,y y (cid:54)(cid:191)(cid:148)y =-3y (cid:187)(cid:188)(cid:42)(cid:68)m=± (cid:71)(cid:72)(cid:73) 1 2 1 2 1 2 15 (cid:27)3(cid:32)(cid:165)(cid:390)(cid:54)(cid:127)(cid:27)2(cid:32)(cid:54)(cid:82)(cid:83)(cid:114)(cid:115)(cid:7)(cid:86)(cid:42)(cid:70) BQ (cid:54)(cid:82)(cid:83)(cid:84)(cid:85)(cid:50)(cid:244)(cid:316)(cid:43)(cid:80)(cid:44)(cid:7)(cid:86)(cid:42)(cid:70)(cid:84)(cid:85)(cid:50)AP(cid:117)BQ(cid:244)(cid:316)(cid:43)(cid:80) 1 12 1+m2 (cid:44)(cid:54)(cid:269)(cid:206)(cid:124)(cid:217)S = S = (cid:54)(cid:191)(cid:148)(cid:295)(cid:296)(cid:74)(cid:187)(cid:188)(cid:71)(cid:72)(cid:42)(cid:24). AF1F2B 2 APQB 1-3m2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:54)(cid:264)(cid:319)(cid:41)F 2,0(cid:54)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:36) 3x±y=0(cid:54) 2 2 3 2 3 (cid:250)(cid:137)(cid:319)(cid:41)F 2 (cid:69)(cid:262)(cid:263)(cid:50)(cid:43)(cid:80)(cid:44)(cid:36) d = = = 3. 3+1 2 (cid:27)2(cid:32)(cid:203)(cid:204)(cid:54)(cid:49)(cid:50)AB(cid:108)(cid:117)x(cid:156)(cid:448)(cid:148)(cid:54)(cid:96)(cid:49)(cid:50)AB(cid:58)(cid:59)(cid:36)x=my+2(cid:54) uuuur uuuur (cid:127)AF =3FB(cid:54)(cid:68)y =-3y (cid:54) 2 2 1 2 ìx=my+2 (cid:127) ï í y2 (cid:54)(cid:68)  3m2-1  y2+12my+9=0(cid:54) ïx2- =1 î 3 (cid:144)(cid:145)(cid:54)D=36m2+36>0(cid:446)(cid:304)(cid:90)(cid:54) -12m 9 y +y = (cid:54)y ×y = (cid:54) 1 2 3m2-1 1 2 3m2-1 6m -3 (cid:66)(cid:67)y =-3y (cid:54)(cid:154)(cid:296)(cid:68)y = (cid:54)y2 = (cid:54) 1 2 2 3m2-1 2 3m2-1 -3 æ 6m ö 2 15 (cid:71) =ç ÷ (cid:54)(cid:24)(cid:68)m=± (cid:54) 3m2-1 è3m2-1ø 15 15 (cid:129)(cid:75)(cid:54)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:36)x=± y+2. 15 (cid:27)3(cid:32)(cid:450)(cid:115)AF (cid:51)(cid:160)(cid:161)(cid:50)(cid:52)(cid:41)P(cid:54)(cid:450)(cid:115)BF (cid:51)(cid:160)(cid:161)(cid:50)(cid:52)(cid:41)Q.(cid:93)(cid:127)(cid:173)(cid:174)(cid:272)(cid:68)(cid:54) 1 2 (cid:102)(cid:292)(cid:79)APQB(cid:36)(cid:84)(cid:85)(cid:102)(cid:292)(cid:79)(cid:54)(cid:55)(cid:56)(cid:57)(cid:36)(cid:102)(cid:292)(cid:79)AFF B(cid:56)(cid:57)(cid:43)2(cid:451). 1 2 (cid:127)(cid:21)(cid:54)(cid:96)Qx ,y (cid:54)(cid:49)(cid:50)AP(cid:59)(cid:36)x=my-2(cid:54)(cid:49)(cid:50)BQ(cid:58)(cid:59)x=my+2(cid:54) 3 3 36m2+36 6  m2+1  (cid:127)(cid:267)(cid:27)2(cid:32)(cid:227)(cid:54)(cid:246)(cid:68) BQ = 1+m2 y -y = 1+m2 = (cid:54) 2 3 3m2-1 3m2-16  m2+1  (cid:250)(cid:36)y 2 y 3 <0(cid:54)(cid:68)3m2-1<0(cid:54)(cid:250)(cid:206) BQ = (cid:54) 1-3m2 4 (cid:84)(cid:85)(cid:50)AP(cid:117)BQ(cid:244)(cid:316)(cid:43)(cid:80)(cid:44)(cid:36)h= (cid:54) 1+m2 1 1 12 1+m2 (cid:250)(cid:137)(cid:54)S = S = BQ ×h= . AF1F2B 2 APQB 2 1-3m2 é 2 ö (cid:149) 1+m2 =t (cid:54)(cid:93)tÎ ê 1, 3÷(cid:54) ë 3 ø 12t 12 S = = é 2 ö (cid:68) AF1F2B 4-3t2 4 -3t (cid:99)tÎ ê ë 1, 3 3÷ ø (cid:39)(cid:178)(cid:452)(cid:453)(cid:303)(cid:288)(cid:13)(cid:54) t (cid:202)S ³12(cid:27)(cid:180)(cid:9)(cid:140)(cid:55)(cid:317)(cid:140)t=1(cid:138)(cid:304)(cid:90)(cid:32)(cid:54) AF1F2B (cid:129)(cid:75)(cid:54)(cid:102)(cid:292)(cid:79)AFF B(cid:56)(cid:57)(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:36) 12,+¥ . 1 2 x2 y2 3 12(cid:26)(cid:27)2024·(cid:417)(cid:418)(cid:439)(cid:208)·(cid:94)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)C(cid:10) + =1(cid:27)a> b> 0(cid:32)(cid:43)(cid:44)(cid:45)(cid:46)(cid:36) (cid:54)(cid:55)C(cid:43)(cid:171)(cid:23)(cid:264)(cid:319)(cid:41) a2 b2 2 (cid:117)(cid:447)(cid:156)(cid:43)(cid:40)(cid:221)(cid:454)(cid:41)(cid:168)(cid:304)(cid:43)(cid:102)(cid:292)(cid:79)(cid:43)(cid:56)(cid:57)(cid:36)8 3. (1)(cid:42)(cid:37)(cid:38)C(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:48)(cid:41)P1,0(cid:43)(cid:49)(cid:50)l(cid:117)(cid:37)(cid:38)C(cid:51)(cid:52)A(cid:54)B(cid:40)(cid:41)(cid:54)(cid:48)(cid:41)A(cid:117)x(cid:156)(cid:133)(cid:49)(cid:43)(cid:49)(cid:50)(cid:117)(cid:37)(cid:38)C(cid:43)(cid:53)(cid:22)(cid:221)(cid:51)(cid:41)(cid:36)Q.(cid:140) VBPQ(cid:43)(cid:56)(cid:57)(cid:199)(cid:68)(cid:256)(cid:285)(cid:200)(cid:138)(cid:54)(cid:42)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59). x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) + =1 16 4 (2)x±2y-1=0 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:37)(cid:38)(cid:319)(cid:41)(cid:117)(cid:283)(cid:41)(cid:43)(cid:91)(cid:92)(cid:117)(cid:44)(cid:45)(cid:46)(cid:43)(cid:189)(cid:190)(cid:187)(cid:188)(cid:71)(cid:72)(cid:68)(cid:25)(cid:61)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:54)(cid:89)(cid:90)(cid:161)(cid:50)(cid:58)(cid:59)(cid:88)(cid:72)(cid:68)(cid:117)(cid:91)(cid:92)(cid:146)(cid:3)(cid:43)(cid:211)(cid:125)(cid:189)(cid:15)(cid:124)(cid:125)(cid:86)(cid:54)(cid:191)(cid:148)(cid:77)(cid:78)(cid:79)(cid:56)(cid:57)(cid:7)(cid:86)(cid:124)(cid:217)(cid:70) (cid:56)(cid:57)(cid:88)(cid:409)(cid:410)(cid:300)(cid:236)(cid:108)(cid:180)(cid:86)(cid:187)(cid:188)(cid:71)(cid:72)(cid:68)(cid:25)(cid:61). c 3 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)(cid:37)(cid:38)C(cid:43)(cid:319)(cid:80)(cid:36)2c(cid:54)(cid:166)(cid:21)(cid:128)(cid:54) = (cid:54)2bc=8 3(cid:54)(cid:229)a2 =b2+c2(cid:54) a 2 (cid:24)(cid:68)a=4(cid:54)b=2(cid:54)c=2 3(cid:54)x2 y2 (cid:129)(cid:75)(cid:37)(cid:38)C(cid:43)(cid:58)(cid:59)(cid:36) + =1(cid:73) 16 4 (cid:27)2(cid:32)(cid:127)(cid:21)(cid:128)(cid:72)(cid:68)(cid:49)(cid:50)l(cid:43)(cid:107)(cid:46)(cid:108)(cid:36)0(cid:54)(cid:202)(cid:72)(cid:96)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)x=my+1(cid:54) Ax,y (cid:54)Bx ,y (cid:54)(cid:93)Qx,-y (cid:54) 1 1 2 2 1 1 ì x=my+1 (cid:89)(cid:90)(cid:49)(cid:50)l(cid:117)(cid:37)(cid:38)C(cid:43)(cid:58)(cid:59) ï íx2 y2 (cid:54)(cid:68)  m2+4  y2+2my-15=0(cid:54) ï + =1 î16 4 15 (cid:127)(cid:52)(cid:49)(cid:50)(cid:48)(cid:37)(cid:38)(cid:342)(cid:22)(cid:41)(cid:54)(cid:202)(cid:210)(cid:146)D>0(cid:54)(cid:93)y y =- (cid:26) 1 2 m2+4 1 1 (cid:229)S = ´ 2y ´ x -x (cid:54)S = ´ 2y ´1-x (cid:54) VABQ 2 1 2 1 VAPQ 2 1 1 (cid:246)(cid:34)x -x (cid:117)1-x (cid:95)(cid:9)(cid:54) 2 1 1 (cid:129)(cid:75)S =S -S = y ´ x -x -1-x  VBPQ VABQ VAPQ 1 2 1 1 = y ´x -x -1-x  = y ´ x -1 = y ´ my = my y 1 2 1 1 1 2 1 2 1 2 15m 15 15 15 = = £ = m2+4 4 4 4 (cid:54) m + 2 m´ m m 4 (cid:140)(cid:55)(cid:317)(cid:140) m = (cid:54)(cid:71)m=±2(cid:138)(cid:180)(cid:9)(cid:304)(cid:90)(cid:54) m 15 (cid:129)(cid:75)VBPQ(cid:56)(cid:57)(cid:43)(cid:256)(cid:285)(cid:200)(cid:36) (cid:54)(cid:137)(cid:138)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:36)x±2y-1=0(cid:26) 4 13(cid:26)(cid:27)2024·(cid:455)(cid:456)(cid:116)(cid:457)(cid:119)·(cid:77)(cid:406)(cid:32)(cid:99)(cid:84)(cid:56)(cid:49)(cid:78)(cid:91)(cid:92)(cid:268)xOy(cid:145)(cid:54)(cid:41)A(cid:54)B(cid:64)(cid:159)(cid:178)x(cid:156)(cid:35)y(cid:156)(cid:39)(cid:43)(cid:279)(cid:41)(cid:54)(cid:55)|AB|= 3, uuur uuur uuur (cid:279)(cid:41)P(cid:150)(cid:151) 3OP=2OA+OB(cid:54)(cid:175)P(cid:43)(cid:280)(cid:281)(cid:36)C(cid:26) (1)(cid:42)C(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:96)(cid:161)(cid:50)C(cid:117)x(cid:156)(cid:43)(cid:51)(cid:41)(cid:36)A (cid:54)A (cid:27)A (cid:99)A (cid:43)(cid:171)(cid:292)(cid:32)(cid:54)(cid:48)(cid:41)Q(cid:27)1(cid:54)0(cid:32)(cid:55)(cid:108)(cid:117)x(cid:156)(cid:84)(cid:85)(cid:43)(cid:49)(cid:50)l(cid:117)C(cid:212)(cid:51) 1 2 1 2 k (cid:52)M(cid:54)N(cid:40)(cid:41)(cid:54)(cid:175)(cid:49)(cid:50)A M(cid:54)A N(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k (cid:35)k (cid:54)(cid:42) 1 (cid:43)(cid:200)(cid:26) 1 2 1 2 k 2 x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) +y2 =1 4 k 1 (2) 1 = k 3 2 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:33)(cid:34)(cid:191)(cid:148)(cid:134)(cid:196)(cid:43)(cid:50)(cid:272)(cid:242)(cid:188)(cid:43)(cid:91)(cid:92)(cid:124)(cid:217)(cid:71)(cid:72)(cid:42)(cid:24)(cid:73)(cid:27)2(cid:32)(cid:89)(cid:90)(cid:49)(cid:50)(cid:117)(cid:37)(cid:38)(cid:58)(cid:59)(cid:54)(cid:191)(cid:148)(cid:58)(cid:59)(cid:43)(cid:97)(cid:117)(cid:268)(cid:13)(cid:3)(cid:268)(cid:231)(cid:49)(cid:50)(cid:43)(cid:107)(cid:46)(cid:3)(cid:268)(cid:71)(cid:72)(cid:42)(cid:24)(cid:26) (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:24)(cid:10)(cid:96)Px,y,Ax ,0,B0,y (cid:54) 0 0 (cid:250)(cid:36) AB = 3(cid:54)(cid:129)(cid:75) x2+y2 = 3(cid:54) 0 0 uuur uuur uuur (cid:127) 3OP=2OA+OB(cid:68)(cid:54) 3x,y =2x ,0+0,y (cid:54) 0 0 3x x2 (cid:130)x = (cid:54)y = 3y(cid:66)(cid:67)x2+y2 =3(cid:68)(cid:54) +y2 =1(cid:54) 0 2 0 0 0 4 x2 (cid:129)(cid:75)(cid:279)(cid:41)P(cid:43)(cid:280)(cid:281)C(cid:43)(cid:58)(cid:59)(cid:36) +y2 =1(cid:73) 4 (cid:27)2(cid:32)(cid:127)(cid:27)1(cid:32)(cid:34)A -2,0,A 2,0,Mx,y ,Nx ,y (cid:54) 1 2 1 1 2 2 ìx=my+1 (cid:89)(cid:90) ï íx2 (cid:68)(cid:54)  4+m2 y2+2my-3=0(cid:54) ï +y2 =1 î 4 2m -3 (cid:127)(cid:211)(cid:125)(cid:189)(cid:15)(cid:68)(cid:54)y +y =- ,y ×y = (cid:54) 1 2 4+m2 1 2 4+m2 y +y 2m 3 (cid:52)(cid:178) 1 2 = (cid:54)(cid:205)(cid:206)my y = y +y (cid:54) y ×y 3 1 2 2 1 2 1 2 y y (cid:250)(cid:36)k = 2 (cid:54)k = 2 (cid:54)x =my +1,x =my +1, 1 x +2 2 x -2 1 1 2 2 1 2 y 1 k x +2 y my -1 my y -y 3 (cid:93) 1 = 1 = 1 2 = 1 2 1 (cid:54)my y = y +y (cid:54) k y y my +3 my y +3y 1 2 2 1 2 2 2 2 1 1 2 2 x -2 2 1 3 y + y k 1 = 2 1 2 2 = 1 (cid:54)(cid:129)(cid:75) k 1 = 1 (cid:26) k 3 9 3 k 3 2 y + y 2 2 1 2 2 14(cid:26)(cid:27)2024·(cid:458)(cid:403)(cid:459)(cid:460)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)C(cid:10) x2 - y2 =1a>0,b>0(cid:43)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:36)y=± 3 x(cid:54)(cid:48)(cid:41)4,0 a2 b2 2 (cid:43)(cid:49)(cid:50)l(cid:51)(cid:160)(cid:161)(cid:50)C(cid:52)M (cid:54)N (cid:40)(cid:41)(cid:54)(cid:55)(cid:140)l^x(cid:156)(cid:138)(cid:54) MN =6. (1)(cid:42)C(cid:43)(cid:58)(cid:59)(cid:73) k (2)(cid:175)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:171)(cid:264)(cid:283)(cid:41)(cid:64)(cid:159)(cid:36)A(cid:54)A (cid:54)(cid:49)(cid:50)AM (cid:54)A N(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k (cid:54)k (cid:54)(cid:42) 1 (cid:43)(cid:200). 1 2 1 2 1 2 k 2(3)(cid:461)(cid:401)(cid:38)E(cid:10)x2+y2-4x-4y-1=0(cid:39)(cid:178)(cid:430)(cid:109)(cid:99)(cid:41)S(cid:54)(cid:195)(cid:68)(cid:48)S(cid:170)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)l (cid:54)l (cid:248)(cid:212)(cid:133)(cid:49). 1 2 x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) - =1(cid:73) 4 3 1 (2)- (cid:73) 3 (3)(cid:109)(cid:99). (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:408)(cid:189)(cid:152)(cid:153)(cid:54)(cid:42)(cid:70)a,b(cid:71)(cid:72)(cid:68)C(cid:43)(cid:58)(cid:59). (cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)l(cid:43)(cid:58)(cid:59)(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:191)(cid:148)(cid:107)(cid:46)(cid:91)(cid:92)(cid:7)(cid:86)(cid:42)(cid:24)(cid:71)(cid:68). (cid:27)3(cid:32)(cid:96)(cid:70)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)(cid:58)(cid:59)(cid:54)(cid:117)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:191)(cid:148)(cid:158)(cid:159)(cid:86)(cid:42)(cid:70)(cid:40)(cid:152)(cid:377)(cid:50)(cid:51)(cid:41)(cid:43)(cid:280)(cid:281)(cid:58)(cid:59)(cid:54)(cid:81)(cid:158)(cid:382) (cid:117)(cid:38)E(cid:43)(cid:136)(cid:381)(cid:3)(cid:268)(cid:71)(cid:72)(cid:68)(cid:24). ìb 3 ï ïa = 2 ìïa=2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:173)(cid:174)(cid:272)(cid:34)(cid:54)(cid:160)(cid:161)(cid:50)C(cid:48)(cid:41)(4,3)(cid:54)(cid:93)í (cid:54)(cid:24)(cid:68)í (cid:54) ï16 9 ïîb= 3 - =1 ïîa2 b2 x2 y2 (cid:129)(cid:75)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36) - =1. 4 3 (cid:27)2(cid:32)(cid:127)(cid:27)1(cid:32)(cid:68)A(-2,0),A (2,0)(cid:54)(cid:96)Mx,y ,Nx ,y (cid:54) 1 2 1 1 2 2 (cid:203)(cid:204)(cid:49)(cid:50)MN(cid:108)(cid:133)(cid:49)(cid:52)y(cid:156)(cid:54)(cid:96)(cid:49)(cid:50)MN(cid:43)(cid:58)(cid:59)(cid:36)x=my+4(cid:54) ìx=my+4 (cid:127)í (cid:154)(cid:253)x(cid:68)(3m2-4)y2+24my+36=0(cid:54) î3x2-4y2 =12 -24m 36 (cid:203)(cid:204)3m2-4¹0,D=144(m2+4)>0(cid:54)y +y = ,y y = (cid:54) 1 2 3m2-4 1 2 3m2-4 2m 3 (cid:93)y +y =- y y (cid:54)(cid:71)my y =- y +y (cid:54) 1 2 3 1 2 1 2 2 1 2 (cid:129)(cid:75) k 1 = x 1 y + 1 2 = y 1 x 2 -2 = y 1 my 2 +2 = my 1 y 2 +2y 1 = - 2 3 y 1 +y 2 +2y 1 =- 1 . k 2 y 2 x 1 +2y 2 y 2 my 2 +6 my 1 y 2 +6y 2 - 3 y +y +6y 3 x -2 2 1 2 2 2 (cid:27)3(cid:32)(cid:38)E:x2+y2-4x-4y-1=0(cid:39)(cid:109)(cid:99)(cid:41)S(cid:54)(cid:195)(cid:68)(cid:48)S(cid:170)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)(cid:248)(cid:212)(cid:133)(cid:49). (cid:47)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)(cid:146)(cid:51)(cid:41)(cid:54)(cid:93)(cid:40)(cid:152)(cid:377)(cid:50)(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:55)(cid:108)(cid:36)0(cid:54) (cid:96)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)(cid:64)(cid:159)(cid:36)y=k x+n,y=k x+n (cid:54) 1 1 2 2x2 y2 (cid:130)y=kx+n(cid:66)(cid:67) - =1(cid:154)(cid:253)y(cid:68)(cid:10)(3-4k2)-8knx-4n2-12=0(cid:54) 4 3 (cid:127)D¢=0(cid:68)64k2n2+4  3-4k2 4n2+12  =0(cid:54)(cid:24)(cid:68)n2 =4k2-3(cid:54) (cid:250)(cid:137)n2 =4k2-3,n2 =4k2-3(cid:54)(cid:96)(cid:40)(cid:152)(cid:377)(cid:50)(cid:43)(cid:51)(cid:41)(cid:91)(cid:92)(cid:36)x ,y (cid:54) 1 1 2 2 0 0 ìy -k x =n (cid:93)í 0 1 0 1 (cid:54)(cid:71)(cid:146)y -k x 2 =4k2-3(cid:54)(cid:55)y -k x 2 =4k2-3(cid:54) îy -k x =n 0 1 0 1 0 2 0 2 0 2 0 2 (cid:71)  x2-4  k2-2x y k +y2+3=0,  x2-4  k2-2x y k +y2+3=0(cid:54) 0 1 0 0 1 0 0 2 0 0 2 0 (cid:52)(cid:178)k,k (cid:178)(cid:58)(cid:59)  x 2-4  k2-2x y k+y 2+3=0(cid:43)(cid:40)(cid:97)(cid:54) 1 2 0 0 0 0 y2+3 (cid:206)kk =-1(cid:54)(cid:93) 0 =-1(cid:54)(cid:71)x2+y2 =1(cid:54)(cid:205)(cid:206)(cid:40)(cid:152)(cid:377)(cid:50)(cid:312)(cid:51)(cid:41)(cid:43)(cid:280)(cid:281)(cid:36)(cid:38)x2+y2 =1(cid:54) 1 2 x2-4 0 0 0 (cid:206)x2+y2 =1(cid:43)(cid:38)(cid:45)(cid:36)O(0,0)(cid:54)(cid:429)(cid:354)(cid:36)1(cid:54)(cid:38)E:(x-2)2+(y-2)2 =32(cid:43)(cid:38)(cid:45)E(2,2)(cid:54)(cid:429)(cid:354)(cid:36)3(cid:54) (cid:203)(cid:204)|OE|= 22+22 =2 2(cid:54)(cid:150)(cid:151)3-1<|OE|<3+1(cid:54)(cid:71)(cid:38)O(cid:117)(cid:38)E(cid:212)(cid:51)(cid:54) (cid:129)(cid:75)(cid:38)E:x2+y2-4x-4y-1=0(cid:39)(cid:109)(cid:99)(cid:41)S(cid:54)(cid:195)(cid:68)(cid:48)S(cid:170)(cid:160)(cid:161)(cid:50)(cid:43)(cid:40)(cid:152)(cid:377)(cid:50)(cid:248)(cid:212)(cid:133)(cid:49). (cid:60)(cid:41)(cid:234)(cid:62)(cid:58)(cid:74)(cid:41)(cid:234)(cid:10) (cid:462)(cid:70)(cid:313)(cid:196)(cid:74)(cid:54)(cid:24)(cid:21)(cid:463)(cid:464)(cid:36)(cid:104)(cid:20)(cid:278)(cid:465)(cid:140)(cid:43)(cid:196)(cid:36)(cid:313)(cid:196)(cid:54)(cid:81)(cid:371)(cid:241)(cid:106)(cid:176)(cid:36)(cid:189)(cid:200)(cid:43)(cid:196)(cid:83)(cid:39)(cid:328)(cid:313) (cid:196)(cid:124)(cid:217)(cid:54)(cid:256)(cid:88)(cid:371)(cid:68)(cid:69)(cid:43)(cid:86)(cid:318)(cid:16)(cid:251)(cid:54)(cid:68)(cid:69)(cid:189)(cid:200)(cid:73) (cid:350)(cid:369)(cid:74)(cid:54)(cid:205)(cid:350)(cid:351)(cid:110)(cid:111)(cid:67)(cid:466)(cid:54)(cid:42)(cid:70)(cid:189)(cid:200)(cid:54)(cid:81)(cid:106)(cid:176)(cid:218)(cid:221)(cid:200)(cid:117)(cid:313) ① (cid:196)(cid:141)(cid:3)(cid:26) ② 15(cid:26)(cid:27)2024·(cid:412)(cid:431)(cid:467)(cid:468)·(cid:94)(cid:406)(cid:32)(cid:96)(cid:37)(cid:38)E(cid:10) x2 + y2 =1 a>b>0(cid:157)(cid:48)(cid:41)P2,-1(cid:54)(cid:55)(cid:44)(cid:45)(cid:46)e= 2 (cid:54)(cid:49)(cid:50)m:x=3 a2 b2 2 (cid:133)(cid:49)x(cid:156)(cid:51)x(cid:156)(cid:52)T(cid:54)(cid:48)T(cid:43)(cid:49)(cid:50)l 1 (cid:51)(cid:37)(cid:38)E(cid:52)Ax 1 ,y 1 (cid:54)Bx 2 ,y 2 (cid:40)(cid:41)(cid:54)(cid:367)(cid:185)PA(cid:54)PB(cid:54)PT (cid:26) (1)(cid:42)(cid:37)(cid:38)E(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:96)(cid:49)(cid:50)PA(cid:54)PB(cid:43)(cid:107)(cid:46)(cid:64)(cid:159)(cid:36)k (cid:54)k (cid:26) 1 2 (cid:27)ⅰ(cid:32)(cid:42)k +k (cid:43)(cid:200)(cid:73) 1 2 |MN| (cid:27)ⅱ(cid:32)(cid:165)(cid:390)(cid:10)(cid:48)P(cid:170)x(cid:156)(cid:43)(cid:133)(cid:50)l(cid:54)(cid:48)A(cid:170)PT(cid:43)(cid:84)(cid:85)(cid:50)(cid:64)(cid:159)(cid:51)PB(cid:54)l(cid:52)M(cid:54)N(cid:54)(cid:42) (cid:43)(cid:200)(cid:26) |MA| x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1) + =1 6 3 (2)(cid:27)i(cid:32)2(cid:73)(cid:27)ii(cid:32)1 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:152)(cid:153)(cid:54)(cid:177)(cid:70)(cid:3)(cid:52)a,b,c(cid:43)(cid:58)(cid:59)(cid:100)(cid:54)(cid:82)(cid:83)(cid:469)(cid:189)(cid:268)(cid:13)(cid:74)(cid:54)(cid:71)(cid:72)(cid:42)(cid:24)(cid:73)(cid:27)2(cid:32)(cid:27)ⅰ(cid:32)(cid:103)(cid:104)(cid:96)(cid:49)(cid:50)l (cid:43)(cid:58)(cid:59)(cid:54)(cid:327)(cid:89)(cid:90)(cid:37)(cid:38)(cid:58)(cid:59)(cid:54)(cid:259)(cid:16)(cid:36)(cid:3)(cid:52)(cid:107)(cid:46)(cid:43)(cid:22)(cid:296)(cid:94)(cid:167)(cid:58)(cid:59)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:71)(cid:72) 1 (cid:42)(cid:24)(cid:73) (cid:27)ⅱ(cid:32)(cid:103)(cid:104)(cid:96)(cid:49)(cid:50)PA,PB(cid:43)(cid:247)(cid:107)(cid:78)(cid:64)(cid:159)(cid:36)a,b,(cid:97)(cid:98)(cid:182)(cid:114)(cid:189)(cid:15)(cid:82)(cid:83)(cid:78)(cid:124)(cid:217)(cid:292)(cid:115) MN (cid:54) AN (cid:54)(cid:81)(cid:42)(cid:179)(cid:200)(cid:54)(cid:82)(cid:83) (cid:27)ⅰ(cid:32)(cid:43)(cid:191)(cid:192)(cid:54)(cid:71)(cid:72)(cid:42)(cid:24). ì 4 1 + =1 ï a2 b2 ï ïc 2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:34) í = ïa 2 ïa2 =b2+c2 ï î (cid:24)(cid:68)a= 6(cid:54)b=c= 3 x2 y2 (cid:129)(cid:75)(cid:37)(cid:38)E(cid:43)(cid:58)(cid:59)(cid:36) + =1(cid:73) 6 3 y +1 y +1 (cid:27)2(cid:32)(cid:27)ⅰ(cid:32)(cid:246)(cid:34)T3,0(cid:54)k =1(cid:54)k = 1 (cid:54)k = 2 (cid:54) PT 1 x -2 2 x -2 1 2 (cid:96)(cid:49)(cid:50)l (cid:43)(cid:58)(cid:59)(cid:36)mx-2+ny+1=1(cid:54)(cid:127)(cid:49)(cid:50)l (cid:48)T3,0(cid:34)m+n=1(cid:54) 1 1 ìx2 y2 ï + =1 (cid:89)(cid:90)(cid:58)(cid:59)í 6 3 ï îmx-2+ny+1=0 (cid:68)2-4ny+12+4n-4mx-2y+1+1+4mx-22 =0(cid:54) æ y+1ö 2 y+1 (cid:313)(cid:79)(cid:68)(cid:10)2-4n ç ÷ +4n-4m +1+4m=0(cid:54) èx-2ø x-2 4n-4m 4n-41-n 8n-4 (cid:71)k +k = = = =2(cid:73) 1 2 4n-2 4n-2 4n-2 (cid:27)ⅱ(cid:32)(cid:96)(cid:49)(cid:50)PA,PB(cid:43)(cid:247)(cid:107)(cid:78)(cid:64)(cid:159)(cid:36)a,b, 5π π π π (cid:93)k =tana(cid:54)k =tanb(cid:54)ÐNMP= -b(cid:54)ÐMPN =b- ,ÐPAN =a- (cid:54)ÐAPN = -a(cid:54) 1 2 4 2 4 2 PN PN æ πö MN = sinÐMPN = sinçb- ÷ (cid:99)VPMN(cid:145)(cid:54) sinÐNMP æ πö è 2ø(cid:54) sinçb- ÷ è 4ø PN PN æπ ö AN = sinÐAPN = sinç -a÷ (cid:99)(cid:245)PAN(cid:145)(cid:54) sinÐPAN æ πö è2 ø(cid:54) sinça- ÷ è 4ø æ πö æ πö 2 sinçb- ÷×sinça- ÷ -cosb× sina-cosa MN è 2ø è 4ø 2 tana-1 (cid:129)(cid:75) = = =- AN æ πö æπ ö 2 tanb-1 sinçb- ÷×sinç -a÷ cosa× sinb-cosb è 4ø è2 ø 2tana-1 (cid:127)k +k =2(cid:34)(cid:54)tana+tanb=2(cid:54)(cid:71) =-1(cid:54) 1 2 tanb-1 MN (cid:202) =1. AN . (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:267)(cid:22)(cid:227)(cid:43)(cid:259)(cid:16)(cid:179)(cid:470)(cid:471)(cid:472)(cid:54)(cid:259)(cid:16)(cid:36)(cid:3)(cid:52)(cid:107)(cid:46)(cid:43)(cid:58)(cid:59)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:71)(cid:72)(cid:42)(cid:24)(cid:54)(cid:267) MN (cid:94)(cid:227)(cid:471)(cid:472)(cid:96)(cid:247)(cid:107)(cid:78)(cid:54)(cid:82)(cid:83)(cid:77)(cid:78)(cid:288)(cid:13)(cid:124)(cid:217) (cid:43)(cid:200). AN 16(cid:26)(cid:27)2024·(cid:402)(cid:403)(cid:473)(cid:474)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:294)(cid:14)(cid:50)C(cid:10)y2 =2px(cid:27)p>0(cid:32)(cid:48)(cid:41)1,2(cid:54)F(cid:36)C(cid:43)(cid:319)(cid:41)(cid:54)A(cid:54)B(cid:36)C(cid:39)(cid:108) (cid:95)(cid:52)(cid:225)(cid:41)O(cid:43)(cid:40)(cid:41). (1)(cid:47)OA^OB(cid:54)(cid:374)(cid:461)(cid:401)(cid:49)(cid:50)AB(cid:178)(cid:430)(cid:48)(cid:189)(cid:41)(cid:54)(cid:47)(cid:178)(cid:54)(cid:42)(cid:70)(cid:139)(cid:189)(cid:41)(cid:73)(cid:47)(cid:108)(cid:178)(cid:54)(cid:435)(cid:344)(cid:176)(cid:15)(cid:127)(cid:73) (2)(cid:47)AF ^BF(cid:54)(cid:42)(cid:245)AFB(cid:56)(cid:57)(cid:43)(cid:256)(cid:226)(cid:200). (cid:60)(cid:25)(cid:61)(cid:62)(1)(cid:49)(cid:50)AB(cid:48)(cid:189)(cid:41)4,0   (2)4 3-2 2 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:103)(cid:104)(cid:97)(cid:98)(cid:33)(cid:34)(cid:41)(cid:42)(cid:70)(cid:294)(cid:14)(cid:50)(cid:58)(cid:59)(cid:54)(cid:96)AB:x=my+n(cid:54)Ax,y ,Bx ,y (cid:54)(cid:89)(cid:90)(cid:294)(cid:14)(cid:50)(cid:58)(cid:59)(cid:54) 1 1 2 2 (cid:146)y +y =4m,y y =-4n(cid:54)(cid:191)(cid:148)OA^OB(cid:54)(cid:127)(cid:134)(cid:196)(cid:133)(cid:49)(cid:43)(cid:91)(cid:92)(cid:124)(cid:217)(cid:72)(cid:177)(cid:70)(cid:58)(cid:59)(cid:54)(cid:127)(cid:137)(cid:24)(cid:70)n(cid:54)(cid:269)(cid:22)(cid:463)(cid:475)(cid:105) 1 2 1 2 (cid:158)(cid:159)(cid:86)(cid:71)(cid:72)(cid:68)(cid:24)(cid:73) (cid:27)2(cid:32)(cid:127)AF ^BF(cid:68)(cid:152)(cid:153)(cid:180)(cid:86)n2-6n+1=4m2(cid:54)(cid:269)(cid:22)(cid:463)(cid:68)(cid:70)n(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:178)n³3+2 2(cid:63)00(cid:32)(cid:48)(cid:41)1,2(cid:54) (cid:129)(cid:75)22 =4=2p(cid:54)(cid:129)(cid:75)(cid:294)(cid:14)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36)y2 =2px=4x(cid:54)(cid:49)(cid:50)AB(cid:107)(cid:46)(cid:108)(cid:72)(cid:335)(cid:36)0(cid:54)(cid:430)(cid:93)(cid:49)(cid:50)AB(cid:117)(cid:294)(cid:14)(cid:50)(cid:341)(cid:146)(cid:40)(cid:221)(cid:51)(cid:41)(cid:54) (cid:202)(cid:72)(cid:96)AB:x=my+n(cid:54)Ax,y ,Bx ,y (cid:54) 1 1 2 2 (cid:89)(cid:90)(cid:294)(cid:14)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36)y2 =4x(cid:54)(cid:72)(cid:68) y2-4my-4n=0(cid:54)Δ=16  m2+n  >0(cid:54) (cid:127)(cid:211)(cid:125)(cid:189)(cid:15)(cid:146)y +y =4m,y y =-4n(cid:54) 1 2 1 2 (cid:250)(cid:36)OA^OB(cid:54) uuur uuur y y 2 (cid:129)(cid:75) OA×OB=xx +y y = 1 2 +y y =n2-4n=0 (cid:54) 1 2 1 2 16 1 2 (cid:250)(cid:36)A(cid:54)B(cid:36)C(cid:39)(cid:108)(cid:95)(cid:52)(cid:225)(cid:41)O(cid:43)(cid:40)(cid:41)(cid:54)(cid:129)(cid:75)n¹0(cid:54)(cid:129)(cid:75)n=4(cid:54)(cid:157)(cid:475)(cid:105)(cid:147)(cid:148)(cid:21)(cid:128)(cid:73) (cid:71)AB:x=my+4(cid:54) (cid:129)(cid:75)(cid:49)(cid:50)AB(cid:48)(cid:189)(cid:41)4,0(cid:73) (cid:27)2(cid:32) (cid:203)(cid:204)F1,0(cid:54)(cid:127)(cid:27)1(cid:32)(cid:68)(cid:54)y +y =4m,y y =-4n(cid:54) 1 2 1 2 uuur uuur y y 2 (cid:250)(cid:36)AF ^BF(cid:54)(cid:129)(cid:75) AF×BF =1-x 1-x +y y =1+y y + 1 2 -my +n+my +n 1 2 1 2 1 2 16 1 2 =1-4n+n2-4m2-2n=0(cid:54) (cid:71)(cid:146)(cid:152)(cid:153)(cid:180)(cid:86)n2-6n+1=4m2(cid:304)(cid:90)(cid:54)(cid:206) Δ=16  m2+n  =4  n2-6n+1  +16n=4  n2-2n+1  =4n-12 >0(cid:54) (cid:129)(cid:75)(cid:103)(cid:104)(cid:146)n¹1(cid:54)(cid:144)(cid:167)n2-6n+1=4m2 ³0(cid:54)n³3+2 2(cid:63)n£3-2 2(cid:54) (cid:250)(cid:36)n(cid:36)(cid:49)(cid:50)AB:x=my+n(cid:99)x(cid:156)(cid:39)(cid:43)(cid:476)(cid:80)(cid:54)(cid:55)A,B(cid:117)O(cid:212)(cid:445)(cid:54)(cid:127)(cid:390)(cid:72)(cid:34)n>0(cid:54) (cid:205)(cid:206)n(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:178)n³3+2 2(cid:63)0|BC|(cid:54)\(cid:41)P(cid:43)(cid:280)(cid:281)(cid:178)(cid:75)B,C(cid:36)(cid:319)(cid:41)(cid:43)(cid:37)(cid:38)(cid:54) x2 y2 (cid:206)22-12 =3(cid:54)\(cid:41)P(cid:43)(cid:280)(cid:281)E(cid:43)(cid:58)(cid:59)(cid:36) + =1(cid:73) 4 3 (cid:27)2(cid:32) (cid:127)(cid:27)1(cid:32)(cid:68)D(-2,0),D (2,0)(cid:178)(cid:37)(cid:38)E(cid:43)(cid:171)(cid:264)(cid:283)(cid:41)(cid:54) 1 2 (cid:96)Q1,y ,Gx,y ,Hx ,y (cid:54) 0 1 1 2 2 uuuur uuuur (cid:127)Q,G,D (cid:77)(cid:41)(cid:209)(cid:50)(cid:54)(cid:68)DQ(cid:121)DG(cid:54) 1 1 1 uuuur uuuur (cid:206)DQ=3,y ,DG=x +2,y (cid:54) 1 0 1 1 1 3y \3y = y x +2,\y = 1 (cid:54) 1 0 1 0 x +2 1 uuuur uuuuur (cid:127)Q,H,D (cid:77)(cid:41)(cid:209)(cid:50)(cid:54)(cid:68)DQ(cid:121)D H (cid:54) 2 2 2 uuuur uuuur (cid:206)DQ=-1,y ,DG=x -2,y (cid:54) 1 0 1 2 2 y \-y = y x -2,\y = 2 (cid:54) 1 0 1 0 x -2 2 3y y \ 1 =- 2 (cid:54)(cid:71)3y x -2+y x +2=0(cid:54) x +2 x -2 1 2 2 1 1 2 ì ty=x+m ï (cid:96)GH(cid:43)(cid:58)(cid:59)(cid:36)ty=x+m(cid:54)(cid:89)(cid:90)íx2 y2 (cid:54) ï + =1 î 4 3 (cid:68)  3t2+4  y2-6tmy+3m2-12=0(cid:54) (cid:93)Δ=36t2m2-4  3t2+4  3m2-12  =48  3t2-m2+4  >0(cid:54) 6tm 3m2-12 y +y = ,y y = (cid:54) 1 2 3t2+4 1 2 3t2+4 \2ty y = m2-4 y +y (cid:54)(cid:127)3y x -2+y x +2=0(cid:54) 1 2 m 1 2 1 2 2 1 (cid:68)3y ty -m-2+y ty -m+2=0(cid:54) 1 2 2 1 (cid:71)4ty y -(m-2)y -3(m+2)y =0(cid:54) 1 2 2 1 2  m2-4  \ y +y -(m-2)y -3(m+2)y =0 (cid:54) m 1 2 2 1\(m+4)  (m-2)y -(m+2)y =0(cid:446)(cid:304)(cid:90)(cid:54)\m=-4(cid:54) 2 1 \GH(cid:129)(cid:99)(cid:49)(cid:50)(cid:446)(cid:48)(cid:189)(cid:41)(4,0)(cid:26) (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:27)2(cid:32)(cid:3)(cid:235)(cid:99)(cid:52)(cid:96)(cid:41)Q,G,H(cid:43)(cid:91)(cid:92)(cid:54)(cid:97)(cid:98)Q,G,D (cid:77)(cid:41)(cid:209)(cid:50)(cid:68)(cid:69)(cid:84)(cid:85)(cid:3)(cid:268). 1 x2 18(cid:26)(cid:27)2024·(cid:438)(cid:439)(cid:480)(cid:478)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)C: +y2 =1. 2 (1)(cid:33)(cid:34)VMPQ(cid:43)(cid:283)(cid:41)(cid:155)(cid:99)(cid:37)(cid:38)C(cid:39)(cid:54)(cid:47)(cid:91)(cid:92)(cid:225)(cid:41)O(cid:36)VMPQ(cid:43)(cid:448)(cid:45)(cid:54)(cid:42)(cid:41)O(cid:69)(cid:49)(cid:50)PQ(cid:80)(cid:44)(cid:43)(cid:256)(cid:226)(cid:200)(cid:73) (2)(cid:33)(cid:34)(cid:189)Nx ,y (cid:99)(cid:37)(cid:38)C(cid:39)(cid:54)(cid:49)(cid:50)l(cid:27)(cid:117)x(cid:156)(cid:108)(cid:448)(cid:148)(cid:32)(cid:117)(cid:37)(cid:38)(cid:51)(cid:52)A(cid:23)B(cid:40)(cid:41)(cid:54)(cid:47)(cid:49)(cid:50)AB(cid:54)AN(cid:54)BN(cid:43)(cid:107) 0 0 (cid:46)(cid:155)(cid:109)(cid:99)(cid:54)(cid:55)AN ^BN (cid:54)(cid:106)(cid:176)(cid:10)(cid:49)(cid:50)AB(cid:48)(cid:189)(cid:41)(cid:27)(cid:91)(cid:92)(cid:83)x (cid:54)y (cid:124)(cid:217)(cid:32). 0 0 1 (cid:60)(cid:25)(cid:61)(cid:62)(1) 2 (2)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:96)M(m,n)(cid:54)(cid:140)n=0(cid:138)(cid:54)(cid:42)(cid:70)(cid:225)(cid:41)O(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44)(cid:73)(cid:140)n¹0(cid:54)(cid:41)(cid:201)(cid:74)(cid:42)(cid:70)(cid:49)(cid:50)PQ(cid:43)(cid:107) (cid:46)(cid:54)(cid:68)(cid:49)(cid:50)PQ(cid:43)(cid:58)(cid:59)(cid:54)(cid:124)(cid:217)(cid:225)(cid:41)O(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44)(cid:54)(cid:127)n(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:42)(cid:256)(cid:226)(cid:200). (cid:27)2(cid:32)(cid:96)Ax ,y (cid:54)Bx ,y (cid:54)(cid:127)AN ^BN (cid:54)(cid:68)x x -x x +x +x2+y y -y y +y +y2 =0(cid:54)(cid:96)(cid:49)(cid:50) 3 3 4 4 3 4 0 3 4 0 3 4 0 3 4 0 kx + y l:y=kx+m(cid:54)(cid:66)(cid:67)(cid:37)(cid:38)C(cid:43)(cid:58)(cid:59)(cid:54)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:16)(cid:251)(cid:54)(cid:68)m=- 0 0 (cid:54) (cid:66)(cid:67)(cid:49)(cid:50)(cid:58)(cid:59)(cid:72)(cid:68)(cid:129)(cid:48)(cid:189)(cid:41). 3 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)M(m,n)(cid:54)(cid:175)(cid:50)(cid:324)PQ(cid:145)(cid:41)(cid:36)D(cid:54) uuuur uuur æ m nö (cid:250)(cid:36)O(cid:36)VMPQ(cid:43)(cid:448)(cid:45)(cid:54)(cid:129)(cid:75)MO=2OD(cid:54)(cid:93)(cid:41)D(cid:43)(cid:91)(cid:92)(cid:36)ç- ,- ÷(cid:54) è 2 2ø m 2 (cid:47)n=0(cid:54)(cid:93) m = 2(cid:54)(cid:137)(cid:138)(cid:49)(cid:50)PQ(cid:117)x(cid:156)(cid:133)(cid:49)(cid:54)(cid:202)(cid:225)(cid:41)O(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44)(cid:36) = (cid:73) 2 2 (cid:47)n¹0(cid:54)(cid:137)(cid:138)(cid:49)(cid:50)PQ(cid:43)(cid:107)(cid:46)(cid:109)(cid:99)(cid:54) (cid:96)Px,y (cid:54)Qx ,y (cid:54)(cid:93)x +x =-m,y +y =-n(cid:54) 1 1 2 2 1 2 1 2 ìx2 ï ï 2 1 +y 1 2 =1, x +x x -x  (cid:229)í (cid:40)(cid:86)(cid:212)(cid:232)(cid:68) 1 2 1 2 +y +y y -y =0(cid:54) ïx2 2 1 2 1 2 2 +y2 =1, ïî 2 2 y -y x +x m (cid:72)(cid:68)k = 1 2 =- 1 2 =- . PQ x -x 2y +y  2n 1 2 1 2n m æ mö (cid:202)(cid:49)(cid:50)PQ(cid:43)(cid:58)(cid:59)(cid:36)y+ =- çx+ ÷(cid:54)(cid:71)2mx+4ny+m2+2n2 =0(cid:54) 2 2nè 2 ø m2+2n2 (cid:93)(cid:41)O(cid:69)(cid:49)(cid:50)PQ(cid:43)(cid:80)(cid:44)(cid:36)d = (cid:54) 4m2+16n2 m2 1 2 (cid:130) +n2 =1(cid:66)(cid:67)(cid:68)d = = (cid:54) 2 2n2+2 2 n2+1 1 2 (cid:250)(cid:36)00(cid:54)x +x = -4km (cid:54)x x = 2m2-2 (cid:54) 3 4 1+2k2 3 4 1+2k2 2m m2-2k2 y +y =kx +x +2m= (cid:54)y y =kx +mkx +m=k2x x +kmx +x +m2 = (cid:54) 3 4 3 4 1+2k2 3 4 3 4 3 4 3 4 1+2k2 -4km 2m2-2 2m m2-2k2 (cid:130)(cid:75)(cid:39)4(cid:221)(cid:86)(cid:318)(cid:66)(cid:67) (cid:54)(cid:68)x2-x × + + y2-y × + =0(cid:54) 0 0 1+2k2 1+2k2 0 0 1+2k2 1+2k2 ① (cid:68)2k2x2+4kmx +2m2+x2-2+ y2-2my +m2+2k2y2-2k2 =0(cid:54) 0 0 0 0 0 0 (cid:71)é 2kx +m2+x2-2 ù+éy -m2+2k2 y2-1 ù=0 (cid:54) ë 0 0 û ë 0 0 û (cid:250)(cid:36)(cid:41)Nx ,y (cid:99)(cid:37)(cid:38)C(cid:39)(cid:54)(cid:129)(cid:75)x2-2=-2y2(cid:54)y2 ② -1=- x 0 2 (cid:54) 0 0 0 0 0 2 (cid:66)(cid:67) (cid:68)2 ékx +m2-y2ù+éy -m2-k2x2ù=0(cid:54) ë 0 0û ë 0 0û (cid:68)2② kx +m+y kx +m-y =kx +m-y kx -m+y (cid:54) 0 0 0 0 0 0 0 0(cid:71)kx +m-y kx +3m+y =0(cid:54) 0 0 0 0 (cid:250)(cid:36)AN ^BN (cid:54)(cid:129)(cid:75)N (cid:108)(cid:99)(cid:49)(cid:50)AB(cid:39)(cid:54)(cid:93)kx +m-y ¹0(cid:54) 0 0 kx + y (cid:93)kx + y +3m=0(cid:54)(cid:68)m=- 0 0 (cid:54) 0 0 3 æ x ö y æx y ö (cid:129)(cid:75)(cid:49)(cid:50)AB:y=kçx- 0 ÷- 0 (cid:48)(cid:189)(cid:41)ç 0 ,- 0 ÷. è 3 ø 3 è 3 3 ø (cid:60)(cid:41)(cid:234)(cid:62)(cid:58)(cid:74)(cid:41)(cid:234)(cid:10)(cid:24)(cid:25)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:43)(cid:21)(cid:186)(cid:138)(cid:54)(cid:138)(cid:162)(cid:371)(cid:40)(cid:221)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:154)(cid:253)x((cid:63)y)(cid:436)(cid:90)(cid:22)(cid:296)(cid:94) (cid:167)(cid:58)(cid:59)(cid:54)(cid:204)(cid:88)(cid:409)(cid:410)(cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:54)(cid:327)(cid:191)(cid:148)(cid:21)(cid:96)(cid:152)(cid:153)(cid:436)(cid:90)(cid:146)(cid:3)(cid:101)(cid:313)(cid:196)(cid:43)(cid:180)(cid:196)(cid:3)(cid:268)(cid:54)(cid:481)(cid:231)(cid:69)(cid:49)(cid:50)(cid:58)(cid:59)(cid:43)(cid:96)(cid:74) (cid:138)(cid:54)(cid:482)(cid:210)(cid:30)(cid:113)(cid:363)(cid:56)(cid:54)(cid:108)(cid:241)(cid:483)(cid:484)(cid:49)(cid:50)(cid:107)(cid:46)(cid:36)0(cid:63)(cid:108)(cid:109)(cid:99)(cid:180)(cid:350)(cid:351)(cid:110)(cid:79)(cid:54)(cid:485)(cid:16)(cid:146)(cid:3)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:89)(cid:90)(cid:68)(cid:70)(cid:22)(cid:296) (cid:94)(cid:167)(cid:58)(cid:59)(cid:88)(cid:43)(cid:242)(cid:188)(cid:335)(cid:336)(cid:54)(cid:448)(cid:486)(cid:97)(cid:117)(cid:268)(cid:13)(cid:244)(cid:316)(cid:43)(cid:3)(cid:268)(cid:23)(cid:114)(cid:115)(cid:23)(cid:107)(cid:46)(cid:23)(cid:77)(cid:78)(cid:79)(cid:43)(cid:56)(cid:57)(cid:180)(cid:227)(cid:21)(cid:54)(cid:206)(cid:145)(cid:41)(cid:114)(cid:227)(cid:21)(cid:54) (cid:487)(cid:83)(cid:41)(cid:201)(cid:74)(cid:26) 19(cid:26)(cid:27)2024·(cid:102)(cid:488)(cid:489)(cid:490)(cid:491)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:294)(cid:14)(cid:50)C:x2 =2pyp>0(cid:39)(cid:22)(cid:41)Q(cid:69)(cid:319)(cid:41)F(cid:43)(cid:80)(cid:44)(cid:36)2(cid:54)(cid:41)Q(cid:69)y(cid:156)(cid:43) (cid:80)(cid:44)(cid:36) 3p(cid:26) (1)(cid:42)(cid:294)(cid:14)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:48)F(cid:43)(cid:49)(cid:50)(cid:51)(cid:294)(cid:14)(cid:50)C(cid:52)A(cid:54)B(cid:40)(cid:41)(cid:54)(cid:48)(cid:41)B(cid:170)x(cid:156)(cid:43)(cid:133)(cid:50)(cid:51)(cid:49)(cid:50)AO(cid:27)O(cid:178)(cid:91)(cid:92)(cid:225)(cid:41)(cid:32)(cid:52)D(cid:54)(cid:48)A(cid:170)(cid:49) (cid:122)GD(cid:122) (cid:50)DF(cid:43)(cid:133)(cid:50)(cid:117)(cid:294)(cid:14)(cid:50)C(cid:43)(cid:53)(cid:22)(cid:51)(cid:41)(cid:36)E(cid:54)(cid:49)(cid:50)BD(cid:117)AE(cid:51)(cid:52)(cid:41)G(cid:26)(cid:42) |GB| (cid:60)(cid:25)(cid:61)(cid:62)(1)x2 =2y(cid:73) (2)(1,2) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:54)(cid:96)(cid:70)(cid:41)Q(cid:43)(cid:91)(cid:92)(cid:54)(cid:97)(cid:98)(cid:21)(cid:186)(cid:129)(cid:408)(cid:6)(cid:373)(cid:177)(cid:70)(cid:180)(cid:86)(cid:42)(cid:70)p(cid:43)(cid:200)(cid:54)(cid:269)(cid:206)(cid:72)(cid:68)(cid:294)(cid:14)(cid:50)(cid:43)(cid:58) (cid:59)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:35)A(cid:54)B(cid:40)(cid:41)(cid:43)(cid:91)(cid:92)(cid:54)(cid:130)(cid:49)(cid:50)(cid:58)(cid:59)(cid:117)(cid:294)(cid:14)(cid:50)(cid:58)(cid:59)(cid:89)(cid:90)(cid:54)(cid:191)(cid:148)(cid:211)(cid:125)(cid:189)(cid:15)(cid:42)(cid:70)(cid:41)D(cid:54)G (cid:122)GD(cid:122) (cid:43)(cid:91)(cid:92)(cid:54)(cid:71)(cid:72)(cid:42)(cid:70) (cid:43)(cid:124)(cid:125)(cid:86)(cid:54)(cid:81)(cid:269)(cid:85)(cid:42)(cid:24)(cid:71)(cid:72)(cid:26) |GB| (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:108)(cid:260)(cid:96)Qx ,y (cid:54) 0 0 (cid:250)(cid:36)(cid:294)(cid:14)(cid:50)C(cid:39)(cid:22)(cid:41)Q(cid:69)(cid:319)(cid:41)F(cid:43)(cid:80)(cid:44)(cid:36)4(cid:54)(cid:41)Q(cid:69)y(cid:156)(cid:43)(cid:80)(cid:44)(cid:36) 3p(cid:54) ì p ïy + =2 (cid:129)(cid:75)í 0 2 (cid:54) ï îx 0 = 3p æ pö (cid:183)(cid:15)(cid:68)( 3p)2 =2pç2- ÷(cid:54)(cid:24)(cid:68)p=1(cid:63)p=0(cid:27)(cid:252)(cid:253)(cid:32)(cid:54) è 2ø (cid:93)(cid:294)(cid:14)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36)x2 =2y(cid:73) 1 (cid:27)2(cid:32)(cid:127)(cid:21)(cid:128)(cid:34)(cid:49)(cid:50)AB(cid:43)(cid:107)(cid:46)(cid:210)(cid:109)(cid:99)(cid:54)F(0, )(cid:54) 21 (cid:108)(cid:260)(cid:96)(cid:49)(cid:50)AB(cid:43)(cid:58)(cid:59)(cid:36)y=kx+ (cid:54)Ax,y ,Bx ,y (cid:54) 2 1 1 2 2 ì 1 ïy=kx+ (cid:89)(cid:90)í 2(cid:54)(cid:154)(cid:253)y(cid:327)(cid:183)(cid:15)(cid:68)x2-2kx-1=0(cid:54)D = 4k2 + 4 > 0(cid:54) ï îx2 =2y (cid:127)(cid:211)(cid:125)(cid:189)(cid:15)(cid:68)x +x =2k,xx =-1(cid:54) 1 2 1 2 y x (cid:246)(cid:34)(cid:49)(cid:50)OA(cid:43)(cid:58)(cid:59)(cid:36)y= 1 x= 1 x(cid:54) x 2 1 æ xx ö æ 1ö (cid:250)(cid:36)BD^x(cid:156)(cid:54)(cid:129)(cid:75)Dçx , 1 2 ÷(cid:54)(cid:71)Dçx ,- ÷(cid:54) è 2 2 ø è 2 2ø 1 (cid:129)(cid:75)k =- (cid:54) DF x 2 (cid:250)(cid:36)DF AE(cid:54)(cid:129)(cid:75)k =x (cid:54) AE 2 (cid:93)(cid:49)(cid:50)A⊥E(cid:43)(cid:58)(cid:59)(cid:36)y-y =x x-x (cid:54) 1 2 1 (cid:250)(cid:36)x =x (cid:54)(cid:129)(cid:75)y =2y +y +1(cid:54) G 2 G 2 1 3 2y +y + (cid:137)(cid:138)|GD| 2 1 2(cid:54) = |GB| y +y +1 2 1 xx 2 1 (cid:250)(cid:36) y y = 1 2 = (cid:54) 1 2 4 4 2 3 +y + |GD| 4y 1 2 4y2+6y +2 1 (cid:129)(cid:75) = 1 = 1 1 =1+ (cid:54) |GB| 1 4y2+4y +1 2y +1 +y +1 1 1 1 4y 1 1 (cid:127)(cid:21)(cid:128)(cid:34)y >0(cid:54)(cid:93)2y +1Î1,+¥(cid:54) 1 1 |GD| 1 (cid:129)(cid:75) =1+ Î(1,2)(cid:26) |GB| 2y +1 1 |GD| (cid:202) (cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:36)(1,2)(cid:26) |GB| (cid:60)(cid:41)(cid:266)(cid:62)(cid:246)(cid:492)(cid:41)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:30)(cid:333)(cid:294)(cid:14)(cid:50)(cid:43)(cid:58)(cid:59)(cid:75)(cid:231)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:43)(cid:142)(cid:148)(cid:227)(cid:21)(cid:54)(cid:30)(cid:333)(cid:309)(cid:493)(cid:494)(cid:323)(cid:15)(cid:23)(cid:64)(cid:298)(cid:299) (cid:192)(cid:35)(cid:242)(cid:188)(cid:335)(cid:336)(cid:54)(cid:495)(cid:52)(cid:145)(cid:496)(cid:21)(cid:26)(cid:370)(cid:246)(cid:70)(cid:492)(cid:43)(cid:352)(cid:58)(cid:99)(cid:52)(cid:187)(cid:188)(cid:54)(cid:327)(cid:55)(cid:187)(cid:188)(cid:300)(cid:236)(cid:228)(cid:178)(cid:212)(cid:3)(cid:497)(cid:498)(cid:101)(cid:13)(cid:43)(cid:242)(cid:188)(cid:54)(cid:250)(cid:137)(cid:241)(cid:42)(cid:499)(cid:64)(cid:500)(cid:45)(cid:347)(cid:72)(cid:75). 20(cid:26)(cid:27)2024·(cid:28)(cid:425)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:37)(cid:38)C (cid:10) x2 + y2 =1a>b>0(cid:43)(cid:171)(cid:264)(cid:319)(cid:41)(cid:64)(cid:159)(cid:36)F(cid:54)F (cid:54)(cid:44)(cid:45)(cid:46)(cid:36) 1 (cid:54)(cid:48)(cid:294) 1 a2 b2 1 2 2 (cid:14)(cid:50)C (cid:10)y2 =2ax(cid:319)(cid:41)(cid:43)(cid:49)(cid:50)(cid:51)(cid:294)(cid:14)(cid:50)(cid:52)M(cid:54)N(cid:40)(cid:41)(cid:54) MN (cid:43)(cid:256)(cid:226)(cid:200)(cid:36)4.(cid:367)(cid:185)MO(cid:54)NO(cid:327)(cid:450)(cid:115)(cid:64)(cid:159)(cid:51)C 2 1 (cid:52)A(cid:54)B(cid:40)(cid:41)(cid:54)(cid:55)(cid:41)A(cid:117)(cid:41)M(cid:54)(cid:41)B(cid:117)(cid:41)N(cid:155)(cid:108)(cid:99)(cid:95)(cid:22)(cid:329)(cid:330)(cid:54)VOMN (cid:117)VOAB(cid:43)(cid:56)(cid:57)(cid:64)(cid:159)(cid:175)(cid:36)S (cid:54) OMN △ S . VOAB (1)(cid:42)C (cid:35)C (cid:43)(cid:58)(cid:59)(cid:73) 1 2 S (2)(cid:175)l= (cid:245)OMN (cid:54)(cid:42)l(cid:43)(cid:256)(cid:226)(cid:200). S (cid:245)OAB x2 y2 (cid:60)(cid:25)(cid:61)(cid:62)(1)(cid:37)(cid:38)C (cid:43)(cid:58)(cid:59)(cid:36) + =1(cid:54)(cid:294)(cid:14)(cid:50)C (cid:43)(cid:58)(cid:59)(cid:36)y2 =4x 1 2 4 3 19 (2) . 12 (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:82)(cid:83)(cid:294)(cid:14)(cid:50)(cid:48)(cid:319)(cid:41)(cid:114)(cid:42)(cid:256)(cid:226)(cid:200)(cid:54)(cid:42)(cid:24)(cid:70)a(cid:200)(cid:54)(cid:71)(cid:72)(cid:42)(cid:24)(cid:40)(cid:221)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32)(cid:82)(cid:83)(cid:294)(cid:14)(cid:50)(cid:48)(cid:319)(cid:41)(cid:114)(cid:43)(cid:454)(cid:41)(cid:69)(cid:225)(cid:41)(cid:43)(cid:107)(cid:46)(cid:244)(cid:57)(cid:36)(cid:189)(cid:200)(cid:54)(cid:205)(cid:206)(cid:462)(cid:67)(cid:28)(cid:313)(cid:196)(cid:49)(cid:50)OM (cid:107)(cid:46)(cid:36)m(cid:54)(cid:71)(cid:72)(cid:42)(cid:70) (cid:41)A(cid:91)(cid:92)(cid:54)(cid:95)(cid:15)(cid:273)(cid:72)(cid:75)(cid:42)(cid:70)(cid:41)B(cid:91)(cid:92)(cid:54)(cid:204)(cid:88)(cid:82)(cid:83)(cid:40)(cid:41)(cid:316)(cid:114)(cid:115)(cid:7)(cid:86)(cid:72)(cid:42)(cid:68)OA,OB,OM,ON (cid:43)(cid:115)(cid:297)(cid:54)(cid:71)(cid:72)(cid:187)(cid:188) (cid:40)(cid:77)(cid:78)(cid:79)(cid:56)(cid:57)(cid:179)(cid:43)(cid:84)(cid:58)(cid:54)(cid:256)(cid:88)(cid:259)(cid:16)(cid:69)(cid:313)(cid:196)m(cid:43)(cid:288)(cid:13)(cid:42)(cid:256)(cid:226)(cid:200)(cid:71)(cid:72). ì a a ïx=ty+ (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)(cid:49)(cid:50)MN(cid:43)(cid:58)(cid:59)(cid:36)x=ty+ (cid:54)(cid:96)Mx,y (cid:54)Nx ,y (cid:54)(cid:89)(cid:90)í 2, 2 1 1 2 2 ï î y2 =2ax (cid:183)(cid:15)(cid:68)y2-2aty-a2 =0(cid:54)(cid:129)(cid:75) MN =x +x +a=ty +y +2a=2at2+2a(cid:54) 1 2 1 2 (cid:129)(cid:75)(cid:140)t=0(cid:138)(cid:54) MN (cid:146)(cid:256)(cid:226)(cid:200)2a(cid:54)(cid:129)(cid:75)2a=4(cid:54)(cid:24)(cid:68)a=2(cid:54) c 1 (cid:229)(cid:250)(cid:36)(cid:44)(cid:45)(cid:46)(cid:36)e= = (cid:54)(cid:129)(cid:75)c=1(cid:54)(cid:93) b= a2-c2 = 4-1= 3 (cid:54) a 2 x2 y2 (cid:129)(cid:75)(cid:37)(cid:38)C (cid:43)(cid:58)(cid:59)(cid:36) + =1(cid:54)(cid:294)(cid:14)(cid:50)C (cid:43)(cid:58)(cid:59)(cid:36)y2 =4x. 1 2 4 3 (cid:27)2(cid:32)a2 y y (cid:127)(cid:27)1(cid:32)(cid:72)(cid:68)y y =-a2 =-4(cid:54)xx = =1(cid:54)(cid:129)(cid:75)k ×k = 1× 2 =-4(cid:54) 1 2 1 2 4 OM ON x x 1 2 (cid:96)(cid:49)(cid:50)OM (cid:43)(cid:58)(cid:59)(cid:36)y=mx(cid:54) ìx2 y2 (cid:89)(cid:90) ï í 4 + 3 =1 (cid:54)(cid:183)(cid:15)(cid:68)  3+4m2 x2 =12(cid:54)(cid:24)(cid:68)x2 = 12 (cid:54) ï A 3+4m2 î y=mx -4 12m2 (cid:95)(cid:15)(cid:72)(cid:96)(cid:49)(cid:50)ON(cid:43)(cid:58)(cid:59)(cid:36)y= x(cid:54)(cid:72)(cid:24)(cid:68)x2 = (cid:54) m B 3m2+64 2 l2 = æ ç S VOMN ö ÷ 2 = æ ç ç 1 2 OM ON sinÐMON ö ÷ ÷ 2 = ç æ ç ç 1+m2 x 1 1+ æ ç è - m 4 ö ÷ ø 2 x 2 ÷ ö ÷ ÷ = 1 è S VOAB ø ç è 1 2 OA OB sinÐAOB ÷ ø ç ç è 1+m2 x A 1+ æ ç è - m 4 ö ÷ ø 2 x B ÷ ÷ ø x A 2x B 2 12m4+265m2+192 m2 4 265 m2 4 265 361 = = + + ³2 ´ + = . 144m2 12 3m2 144 12 3m2 144 144 19 (cid:129)(cid:75)(cid:140)m=±2(cid:138)(cid:54)l(cid:146)(cid:256)(cid:226)(cid:200) . 12 (cid:60)(cid:41)(cid:234)(cid:62)(cid:58)(cid:74)(cid:41)(cid:234)(cid:10)(cid:27)1(cid:32)(cid:82)(cid:83)(cid:294)(cid:14)(cid:50)(cid:48)(cid:319)(cid:41)(cid:114)(cid:43)(cid:256)(cid:226)(cid:200)(cid:36)(cid:216)(cid:354)(cid:218)(cid:22)(cid:272)(cid:421)(cid:355)(cid:24)(cid:21)(cid:73) (cid:27)2(cid:32)(cid:82)(cid:83)(cid:294)(cid:14)(cid:50)(cid:48)(cid:319)(cid:41)(cid:114)(cid:43)(cid:454)(cid:41)(cid:69)(cid:225)(cid:41)(cid:43)(cid:107)(cid:46)(cid:244)(cid:57)(cid:36)(cid:189)(cid:200)(cid:54)(cid:355)(cid:462)(cid:67)(cid:107)(cid:46)(cid:313)(cid:196)(cid:54)(cid:42)(cid:70)(cid:41)A,B(cid:91)(cid:92)(cid:73) (cid:27)3(cid:32)(cid:82)(cid:83)(cid:40)(cid:41)(cid:316)(cid:43)(cid:114)(cid:115)(cid:7)(cid:86) PQ = 1+k2 x -x (cid:355)(cid:42)(cid:70)OA,OB,OM,ON (cid:115)(cid:297)(cid:54)(cid:71)(cid:72)(cid:42)(cid:56)(cid:57)(cid:179)(cid:73) P Q (cid:27)4(cid:32)(cid:256)(cid:88)(cid:371)(cid:56)(cid:57)(cid:179)(cid:259)(cid:16)(cid:36)(cid:40)(cid:97)(cid:244)(cid:57)(cid:43)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:75)(cid:231)(cid:107)(cid:46)(cid:313)(cid:196)m(cid:39)(cid:355)(cid:54)(cid:256)(cid:88)(cid:82)(cid:83)(cid:300)(cid:236)(cid:108)(cid:180)(cid:86)(cid:72)(cid:42)(cid:70)(cid:256)(cid:226)(cid:200). x2 y2 21(cid:26)(cid:27)2024·(cid:411)(cid:412)(cid:413)(cid:414)·(cid:77)(cid:406)(cid:32)(cid:96)(cid:160)(cid:161)(cid:50)C(cid:10) - =1(cid:27)a>0(cid:54)b>0(cid:32)(cid:43)(cid:22)(cid:152)(cid:262)(cid:263)(cid:50)(cid:36)x-3y=0(cid:54)(cid:319)(cid:41)(cid:69) a2 b2 (cid:262)(cid:263)(cid:50)(cid:43)(cid:80)(cid:44)(cid:36)1(cid:26)A(cid:54)A (cid:64)(cid:159)(cid:36)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:171)(cid:23)(cid:264)(cid:283)(cid:41)(cid:54)(cid:49)(cid:50)l(cid:48)(cid:41)T2,0(cid:51)(cid:160)(cid:161)(cid:50)(cid:52)(cid:41)M (cid:54)N (cid:54)(cid:175)(cid:49) 1 2 (cid:50)MA (cid:54)NA (cid:43)(cid:107)(cid:46)(cid:36)k (cid:54)k (cid:26) 1 2 1 2 (1)(cid:42)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:73) k (2)(cid:42)(cid:106) 1 (cid:36)(cid:189)(cid:200)(cid:26) k 2 x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) -y2=1 9 (2)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:409)(cid:410)(cid:262)(cid:263)(cid:50)(cid:189)(cid:190)(cid:231)(cid:41)(cid:69)(cid:49)(cid:50)(cid:80)(cid:44)(cid:7)(cid:86)(cid:187)(cid:188)(cid:71)(cid:72)(cid:68)(cid:73) (cid:27)2(cid:32)(cid:96)(cid:70)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54)(cid:89)(cid:90)(cid:161)(cid:50)(cid:72)(cid:68)(cid:117)(cid:51)(cid:41)(cid:384)(cid:91)(cid:92)(cid:146)(cid:3)(cid:211)(cid:125)(cid:189)(cid:15)(cid:54)(cid:170)(cid:501)(cid:71)(cid:72)(cid:68)(cid:129)(cid:96)(cid:101)(cid:13)(cid:117)(cid:384)(cid:91)(cid:92)(cid:43)(cid:3)(cid:268)(cid:54)(cid:409) (cid:410)(cid:107)(cid:46)(cid:7)(cid:86)(cid:124)(cid:217)(cid:70)(cid:107)(cid:46)(cid:88)(cid:54)(cid:154)(cid:253)(cid:129)(cid:96)(cid:101)(cid:13)(cid:71)(cid:72)(cid:68)(cid:106).ìb 1 = ï a 3 ï ìa2 =9 ï c ï (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:72)(cid:68)í =1 (cid:54)(cid:24)(cid:68)íb2 =1 (cid:54) ï 1+32 ï c2 =10 ï c2 =a2+b2 î ï î x2 (cid:202)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36) -y2=1(cid:73) 9 (cid:27)2(cid:32)(cid:127)(cid:160)(cid:161)(cid:50)C(cid:43)(cid:58)(cid:59)(cid:36) x2 -y2=1(cid:54)(cid:93)A -3,0(cid:54)A 3,0(cid:54) 9 1 2 (cid:127)(cid:21)(cid:128)(cid:72)(cid:34)(cid:49)(cid:50)l(cid:107)(cid:46)(cid:108)(cid:36)0(cid:54)(cid:202)(cid:72)(cid:96)l:x=my+2(cid:54)Mx,y (cid:54)Nx ,y (cid:54) 1 1 2 2 ìx=my+2 (cid:89)(cid:90) ï íx2 (cid:54)(cid:154)(cid:253)x(cid:72)(cid:68)  m2-9  y2+4my-5=0(cid:54) ï -y2 =1 î 9 Δ=16m2+20  m2-9  =36m2-180>0(cid:54)(cid:71)m2 >5(cid:54) 4m 5 (cid:93)y +y =- (cid:54)y y =- (cid:54) 1 2 m2-9 1 2 m2-9 4m - (cid:93) y 1 +y 2 = m2-9 = 4m (cid:54)(cid:71)my y = 5 y +y (cid:54) y y 5 5 1 2 4 1 2 1 2 - m2-9 y -0 y y -0 y k = 1 = 1 (cid:54)k = 2 = 2 (cid:54) 1 x --3 x +3 2 x -3 x -3 1 1 2 2 y 1 k x +3 y x -3 y my -1 my y -y (cid:93) 1 = 1 = 1 × 2 = 1 × 2 = 1 2 1 k y x +3 y my +5 y my y +5y 2 2 1 2 1 2 1 2 2 x -3 2 5 y +y -y 4 1 2 1 5y +5y -4y y +5y 1 = = 1 2 1 = 1 2 = (cid:54) 5 y +y +5y 5y 1 +5y 2 +20y 2 5y 1 +5y 2  5 4 1 2 2 k 1 (cid:71) 1 (cid:36)(cid:189)(cid:200) . k 5 2 (cid:60)(cid:41)(cid:234)(cid:62)(cid:58)(cid:74)(cid:41)(cid:234)(cid:10)(cid:82)(cid:83)(cid:211)(cid:125)(cid:189)(cid:15)(cid:74)(cid:24)(cid:502)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:212)(cid:51)(cid:227)(cid:21)(cid:43)(cid:300)(cid:236)(cid:463)(cid:464)(cid:165)(cid:143)(cid:10)(cid:27)1(cid:32)(cid:96)(cid:49)(cid:50)(cid:58)(cid:59)(cid:54)(cid:96)(cid:51)(cid:41)(cid:91)(cid:92)(cid:36)x,y ,x ,y (cid:73) 1 1 2 2 (cid:27)2(cid:32)(cid:89)(cid:90)(cid:49)(cid:50)(cid:117)(cid:38)(cid:437)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:54)(cid:68)(cid:69)(cid:3)(cid:52)x(cid:27)(cid:63)y(cid:32)(cid:43)(cid:22)(cid:296)(cid:94)(cid:167)(cid:58)(cid:59)(cid:54)(cid:4)(cid:128)D(cid:43)(cid:158)(cid:382)(cid:73) (cid:27)3(cid:32)(cid:177)(cid:70)(cid:211)(cid:125)(cid:189)(cid:15)(cid:73) (cid:27)4(cid:32)(cid:130)(cid:129)(cid:42)(cid:227)(cid:21)(cid:63)(cid:21)(cid:145)(cid:43)(cid:3)(cid:268)(cid:259)(cid:16)(cid:36)x +x (cid:23)xx (cid:27)(cid:63)y +y (cid:23)y y (cid:32)(cid:43)(cid:79)(cid:86)(cid:73) 1 2 1 2 1 2 1 2 (cid:27)5(cid:32)(cid:66)(cid:67)(cid:211)(cid:125)(cid:189)(cid:15)(cid:42)(cid:24). x2 y2 22(cid:26)(cid:27)2024·(cid:411)(cid:412)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)G: - =1a>0,b>0(cid:43)(cid:428)(cid:156)(cid:115)(cid:36)4(cid:54)(cid:171)(cid:23)(cid:264)(cid:319)(cid:41)(cid:64)(cid:159)(cid:36)F(cid:23)F (cid:54)(cid:144) a2 b2 1 2 (cid:145)F (cid:69)(cid:144)(cid:262)(cid:263)(cid:50)(cid:43)(cid:80)(cid:44)(cid:36)1(cid:26) 2 (1)(cid:42)(cid:160)(cid:161)(cid:50)G(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:10) (2)(cid:47)(cid:41)P(cid:178)(cid:160)(cid:161)(cid:50)G(cid:99)(cid:267)(cid:22)(cid:329)(cid:330)(cid:43)(cid:279)(cid:41)(cid:54)(cid:160)(cid:161)(cid:50)G(cid:99)(cid:41)P(cid:308)(cid:43)(cid:377)(cid:50)l (cid:117)x(cid:156)(cid:212)(cid:51)(cid:52)(cid:41)T(cid:26) 1 (cid:27)i(cid:32)(cid:106)(cid:176)(cid:10)(cid:503)(cid:50)PT (cid:178)ÐFPF (cid:43)(cid:78)(cid:84)(cid:64)(cid:50)(cid:73) 1 2 (cid:27)ii(cid:32)(cid:48)(cid:91)(cid:92)(cid:225)(cid:41)O(cid:43)(cid:49)(cid:50)l (cid:117)l (cid:133)(cid:49)(cid:54)(cid:117)(cid:49)(cid:50)PF(cid:212)(cid:51)(cid:52)(cid:41)Q(cid:54)(cid:42)△QFF (cid:56)(cid:57)(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:26) 2 1 1 1 2 x2 (cid:60)(cid:25)(cid:61)(cid:62)(1)G: -y2 =1 4 (2)(cid:27)i(cid:32)(cid:106)(cid:176)(cid:184)(cid:24)(cid:65)(cid:73)(cid:27)ii(cid:32)0,2(cid:26) (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:127)(cid:21)(cid:128)(cid:72)(cid:49)(cid:185)(cid:42)(cid:70)a,b(cid:54)(cid:205)(cid:206)(cid:72)(cid:42)(cid:70)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32)(cid:27)i(cid:32)(cid:96)P(x ,y )(cid:54)(cid:377)(cid:50)l :y-y =kx-x (cid:54)(cid:66)(cid:67)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:16)(cid:251)(cid:54)(cid:127)(cid:158)(cid:159)(cid:86)(cid:180)(cid:52)(cid:322)(cid:72)(cid:124)(cid:217)(cid:70)k(cid:54)(cid:205) 0 0 1 0 0 PF TF (cid:206)(cid:72)(cid:124)(cid:217)(cid:70)(cid:377)(cid:50)(cid:58)(cid:59)(cid:54)(cid:124)(cid:217)(cid:70)(cid:41)T(cid:43)(cid:91)(cid:92)(cid:54)(cid:204)(cid:88)(cid:216)(cid:48)(cid:187)(cid:188) 1 , 1 (cid:43)(cid:200)(cid:72)(cid:68)(cid:191)(cid:192)(cid:73)(cid:27)ii(cid:32)(cid:48)F (cid:170)FE^l (cid:54) PF TF 2 2 1 2 2 (cid:96)FEIPF =E(cid:54)(cid:97)(cid:98)(cid:78)(cid:84)(cid:64)(cid:50)(cid:43)(cid:272)(cid:421)(cid:35)(cid:77)(cid:78)(cid:79)(cid:145)(cid:136)(cid:50)(cid:189)(cid:15)(cid:42)(cid:70) FQ (cid:54)(cid:81)(cid:124)(cid:217)(cid:70)△QFF (cid:56)(cid:57)(cid:72)(cid:42)(cid:70)(cid:144)(cid:385) 2 1 1 1 2 (cid:386). (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:250)(cid:36)(cid:428)(cid:156)(cid:115)(cid:36)4 (cid:129)(cid:75)2a=4(cid:54)(cid:71)a=2(cid:54) b (cid:250)(cid:36)(cid:264)(cid:319)(cid:41)F (c,0)(cid:69)(cid:262)(cid:263)(cid:50)y=± x(cid:80)(cid:44)(cid:36)1(cid:54) 2 a bc (cid:129)(cid:75) =b=1(cid:54) a2+b2 x2 (cid:202)(cid:160)(cid:161)(cid:50)G(cid:43)(cid:92)(cid:407)(cid:58)(cid:59)(cid:36)G: -y2 =1(cid:26) 4 (cid:27)2(cid:32)(cid:27)i(cid:32)(cid:96)P(x ,y )(cid:54)(cid:377)(cid:50)l :y-y =kx-x (cid:54)(cid:93)x2-4y2 =4(cid:54) 0 0 1 0 0 0 0 ìx2 ï -y2 =1 (cid:89)(cid:90)í 4 ï îy-y 0 =kx-x 0 æ1 ö (cid:16)(cid:251)(cid:68)ç -k2 ÷x2-2ky -kx x-y -kx 2-1=0(cid:26) è4 ø 0 0 0 0 x (cid:127)Δ=0(cid:54)(cid:24)(cid:68)(cid:10)k = 0 (cid:54) 4y 0 x æ 4 ö (cid:129)(cid:75)(cid:49)(cid:50)PT:y-y = 0 x-x  (cid:54)(cid:149)y=0(cid:54)(cid:68)Tç ,0÷(cid:54) 0 4y 0 0 èx 0 ø 4 4 (cid:202)TF = + 5(cid:54)TF =- + 5(cid:26) 1 x 2 x 0 0  2 5 5 (cid:250)(cid:36) PF = x + 5 +y2 = x2+ 5x +4 =2+ x (cid:54) 1 0 0 4 0 0 2 0 5 (cid:129)(cid:75) PF = PF -4= x -2(cid:54) 2 1 2 0 PF TF (cid:129)(cid:75) PF ×TF = TF × PF (cid:54)(cid:71) 1 = 1 (cid:54) 1 2 1 2 PF TF 2 2 (cid:202)(cid:503)(cid:50)PT(cid:178)ÐFPF (cid:43)(cid:78)(cid:84)(cid:64)(cid:50)(cid:26) 1 2 (cid:27)ii(cid:32)(cid:48)F (cid:170)FE^l (cid:54)(cid:96)FEIPF =E(cid:26) 2 2 1 2 1 (cid:250)(cid:36)l (cid:36)ÐFPF (cid:43)(cid:78)(cid:84)(cid:64)(cid:50)(cid:54)(cid:129)(cid:75) PF = PE 1 1 2 2 (cid:129)(cid:75) FE = PF - PE = PF - PF =4(cid:26) 1 1 1 2 (cid:250)(cid:36)OQ^l (cid:54)FE^l (cid:54)(cid:129)(cid:75)OQ(cid:321)FE(cid:54) 1 2 1 2 (cid:229)(cid:250)(cid:36)O(cid:36)FF (cid:145)(cid:41)(cid:26) 1 2 (cid:93)OQ(cid:178)△FFE(cid:43)(cid:145)(cid:136)(cid:50)(cid:54)(cid:202)Q(cid:178)FE(cid:43)(cid:145)(cid:41)(cid:26) 1 2 1 (cid:129)(cid:75) FQ =2(cid:54)(cid:175)ÐPFF =q(cid:54) 1 1 2 (cid:250)(cid:36)OQ^l (cid:54)(cid:129)(cid:75)ÐPQO(cid:36)(cid:504)(cid:78)(cid:54)(cid:129)(cid:75)ÐFQO(cid:36)(cid:505)(cid:78)(cid:54) 1 1 (cid:129)(cid:75) FQ 2+ OQ 2 < FO 2(cid:54)(cid:129)(cid:75) OQ 2 <1(cid:54)(cid:129)(cid:75) OQ <1(cid:54) 1 1 OQsinÐFQO 1 (cid:127)(cid:182)(cid:114)(cid:189)(cid:15)(cid:68)sinq= 1 < (cid:54) 5 5 æ 5ö (cid:129)(cid:75)sinqÎç0, ÷(cid:54) ç ÷ è 5 ø 1 (cid:93)S = FQ FF ×sinq=2 5sinqÎ0,2(cid:26) VOF1F2 2 1 1 2(cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234)(cid:10)(cid:137)(cid:21)(cid:30)(cid:333)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:43)(cid:42)(cid:74)(cid:54)(cid:30)(cid:333)(cid:49)(cid:50)(cid:117)(cid:160)(cid:161)(cid:50)(cid:43)(cid:136)(cid:381)(cid:3)(cid:268)(cid:54)(cid:30)(cid:333)(cid:160)(cid:161)(cid:50)(cid:145)(cid:43)(cid:56)(cid:57) (cid:227)(cid:21)(cid:54)(cid:267)(cid:27)2(cid:32)(cid:227)(cid:24)(cid:21)(cid:43)(cid:3)(cid:235)(cid:178)(cid:97)(cid:98)(cid:160)(cid:161)(cid:50)(cid:43)(cid:272)(cid:421)(cid:191)(cid:148)(cid:78)(cid:84)(cid:64)(cid:50)(cid:43)(cid:272)(cid:421)(cid:42)(cid:24)(cid:54)(cid:30)(cid:333)(cid:13)(cid:11)(cid:259)(cid:16)(cid:193)(cid:337)(cid:35)(cid:187)(cid:188)(cid:335)(cid:336)(cid:54) (cid:495)(cid:52)(cid:470)(cid:506)(cid:21). 3   23(cid:26)(cid:27)2024·(cid:507)(cid:508)(cid:509)(cid:510)·(cid:77)(cid:406)(cid:32)(cid:33)(cid:34)(cid:160)(cid:161)(cid:50)E(cid:43)(cid:262)(cid:263)(cid:50)(cid:36)y=± x(cid:54)(cid:171)(cid:283)(cid:41)(cid:36)A - 3,0 (cid:26) 3 (1)(cid:42)(cid:160)(cid:161)(cid:50)E(cid:43)(cid:58)(cid:59)(cid:73) (2)(cid:49)(cid:50)l:x=t(cid:51)x(cid:156)(cid:52)(cid:41)D(cid:54)(cid:48)D(cid:41)(cid:43)(cid:49)(cid:50)(cid:51)(cid:160)(cid:161)(cid:50)E(cid:52)B(cid:54)C(cid:54)(cid:49)(cid:50)AB(cid:54)AC(cid:64)(cid:159)(cid:51)l(cid:52)G(cid:54)H(cid:54)(cid:47)O(cid:54) A(cid:54)G(cid:54)H(cid:155)(cid:99)(cid:38)P(cid:39)(cid:54) (cid:42)k ×k (cid:43)(cid:200)(cid:54)(cid:327)(cid:42)(cid:41)D(cid:43)(cid:214)(cid:91)(cid:92)(cid:73) AG OH ①(cid:42)(cid:38)P(cid:56)(cid:57)(cid:43)(cid:199)(cid:200)(cid:385)(cid:386)(cid:26) ② x2 (cid:60)(cid:25)(cid:61)(cid:62)(1) -y2 =1 3 æ 3 ö æ27π 7πö æ7π ö (2) 1(cid:73)ç ç ,0÷ ÷ (cid:73) ç , ÷Èç ,+¥÷ è 4 ø è 16 4 ø è 4 ø ① ② (cid:60)(cid:64)(cid:65)(cid:62)(cid:27)1(cid:32)(cid:97)(cid:98)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:231)(cid:283)(cid:41)(cid:42)(cid:70)a,b(cid:68)(cid:160)(cid:161)(cid:50)(cid:58)(cid:59)(cid:73) (cid:27)2(cid:32) (cid:96)Dt,0(cid:54)(cid:127)(cid:102)(cid:41)(cid:209)(cid:38)(cid:72)(cid:68)k ×k =1(cid:54)(cid:97)(cid:98)(cid:107)(cid:46)(cid:7)(cid:86)(cid:259)(cid:16)(cid:36)B,C(cid:41)(cid:91)(cid:92)(cid:124)(cid:217)(cid:79)(cid:86)(cid:54)(cid:127)(cid:49)(cid:50)(cid:117)(cid:160) AG OH (cid:161)(cid:50)(cid:89)①(cid:90)(cid:68)(cid:70)(cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:54)(cid:98)(cid:137)(cid:16)(cid:251)(cid:71)(cid:72)(cid:42)(cid:70)t(cid:73) (cid:42)(cid:70)G(cid:41)(cid:91)(cid:92)(cid:68)(cid:70)OG(cid:54)(cid:82)(cid:83)(cid:182)(cid:114)(cid:189)(cid:15)(cid:42)(cid:70)(cid:320)(cid:185)(cid:38) (cid:43)(cid:429)(cid:354)(cid:54)(cid:97)(cid:98)(cid:155)(cid:200)(cid:108)(cid:180)(cid:86)(cid:42)(cid:70)(cid:429)(cid:354)(cid:43)(cid:256)(cid:200)(cid:54)(cid:71)(cid:72)(cid:68)(cid:70)(cid:38)(cid:56)(cid:57)(cid:43)(cid:256)(cid:200). ② x2 y2 (cid:60)(cid:126)(cid:24)(cid:62)(cid:27)1(cid:32)(cid:96)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:36) - =1(cid:27)a>0(cid:54)b>0(cid:32)(cid:54) a2 b2 b b 3 (cid:205)(cid:206)(cid:262)(cid:263)(cid:50)(cid:58)(cid:59)(cid:36)(cid:10)y=± x(cid:54)(cid:127)(cid:21)(cid:152)(cid:153)(cid:34)(cid:10) = (cid:26) a a 3   (cid:250)(cid:36)(cid:160)(cid:161)(cid:50)(cid:43)(cid:171)(cid:283)(cid:41)(cid:36)A - 3,0 (cid:54)(cid:129)(cid:75)a= 3(cid:54)b=1(cid:54) x2 (cid:129)(cid:75)(cid:160)(cid:161)(cid:50)(cid:43)(cid:58)(cid:59)(cid:36)(cid:10) -y2 =1(cid:26) 3(cid:27)2(cid:32) (cid:165)(cid:390)(cid:54)Dt,0(cid:54)(cid:96)(cid:49)(cid:50)BC(cid:43)(cid:58)(cid:59)(cid:36)(cid:10)my=x-t(cid:54) (cid:130)x=①my+t(cid:66)(cid:67)(cid:58)(cid:59)(cid:10)x2-3y2-3=0(cid:54)(cid:68)  m2-3  y2+2mty+t2-3=0(cid:54) (cid:140)m2-3¹0(cid:55)Δ=12  t2+m2-3  >0(cid:138)(cid:54) (cid:96)Bx,y (cid:54)Cx ,y (cid:54)(cid:93)y+y =- 2mt (cid:54)y y = t2-3 (cid:26) 1 1 2 2 1 2 m2-3 1 2 m2-3 π π (cid:96)(cid:49)(cid:50)AG(cid:43)(cid:247)(cid:107)(cid:78)(cid:36)a(cid:54)(cid:108)(cid:260)(cid:96)00(cid:138)(cid:54) tana> (cid:73) 4 4tana 5 3 3 (cid:47)G(cid:54)H(cid:99)x(cid:156)(cid:143)(cid:58)(cid:138)(cid:54)(cid:71)tana < 0(cid:138)(cid:54) tana< (cid:54) 4 4tana 5 5 (cid:129)(cid:75)tana> (cid:63)tana<- (cid:26) 5 5 3 (cid:229)(cid:49)(cid:50)AG(cid:117)(cid:262)(cid:263)(cid:50)(cid:108)(cid:84)(cid:85)(cid:54)(cid:129)(cid:75)tana¹± (cid:26) 3 5 5 3 (cid:129)(cid:75)0 (cid:63)tana< (cid:55)tana¹± (cid:26) 5 5 3 2 2 (cid:250)(cid:36)OG= æ ç 3ö ÷ + æ ç 5 3tanaö ÷ = 1 3  1+25tan2a (cid:54) ç ÷ ç ÷ è 4 ø è 4 ø 4 1 3  1+25tan2a  (cid:96)(cid:38)P(cid:43)(cid:429)(cid:354)(cid:36)R(cid:54)(cid:56)(cid:57)(cid:36)S(cid:54)(cid:93) OG 4 (cid:54) 2R= = sina sina 3  1+25×tan2a  1  1+25tan2a  sin2a+cos2a  (cid:129)(cid:75) R2 = ´ = ´ 64 sin2a 64 sin2a 3  1+25tan2a  1+tan2a  3 æ 1 ö = ´ = ç25tan2a+ +26÷ 64 tan2a 64è tan2a ø 3 æ 1 ö 27 ³ ç2 25tan2a× +26÷= (cid:54) 64 ç è tan2a ÷ ø 16 1 5 (cid:140)(cid:55)(cid:317)(cid:140)25tan2a= (cid:71)tana=± (cid:138)(cid:54)(cid:39)(cid:328)(cid:108)(cid:180)(cid:86)(cid:199)(cid:180)(cid:9)(cid:54) tan2a 5 5 5 3 tana> (cid:63)tana<- (cid:55)tana¹± (cid:26) 5 5 3 27 7 27π 7π (cid:129)(cid:75)R2 > (cid:55)R2 ¹ (cid:54)(cid:205)(cid:206)S > (cid:55)S ¹ (cid:26) 16 4 16 4 (cid:60)(cid:41)(cid:234)(cid:62)(cid:3)(cid:235)(cid:41)(cid:41)(cid:234)(cid:10)(cid:236)(cid:21)(cid:43)(cid:3)(cid:235)(cid:41)(cid:99)(cid:52)(cid:82)(cid:83)(cid:49)(cid:50)(cid:43)(cid:247)(cid:107)(cid:78)(cid:117)(cid:38)(cid:43)(cid:342)(cid:185)(cid:102)(cid:292)(cid:79)(cid:43)(cid:78)(cid:43)(cid:3)(cid:268)(cid:54)(cid:68)(cid:70) æπ ö sinç -a÷ æπ ö sina è2 ø k ×k =tana×tanç -a÷= ´ =1(cid:218)(cid:22)(cid:3)(cid:235)(cid:13)(cid:196)(cid:3)(cid:268)(cid:54)(cid:81)(cid:259)(cid:16)(cid:36)(cid:49)(cid:50)(cid:117)(cid:160)(cid:161)(cid:50)(cid:212)(cid:51)(cid:54)(cid:82)(cid:83) AG OH è2 ø cosa æπ ö cosç -a÷ è2 ø (cid:97)(cid:117)(cid:268)(cid:13)(cid:43)(cid:3)(cid:268)(cid:16)(cid:251)(cid:42)(cid:101)(cid:13)(cid:43)(cid:162)(cid:258)(cid:227)(cid:21).