四川省成都市树德中学2024届高三上学期11月阶段性测试文科数学(1)_2023年11月_01每日更新_18号_2024届四川省成都市树德中学高三上学期11月阶段性测试

1 1 树德中学高 2021 级高三上学期 11 月阶段性测试数学（文科）试题 10. 数列{a }满足：a 2，  1(nN*)，记数列{a a }的前n项和为S ，若S m恒成立，则 n 1 a a n n1 n n n1 n 命题人：李波波 审题人：王钊、朱琨、唐颖君 实数m的取值范围是( ) 第I卷 (选择题，共60分) 2 4 A．[1，) B．[ ,) C．[2，) D．[ ,) 一、选择题:本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目 3 3 要求的. 11.设 f(x),g(x)是定义在R上的两个周期函数，f(x)的周期为4，g(x)的周期为2，且 f(x)是奇函数. 1. 已知集合A  x∣y lg  x1  ,B   y∣y 2x,xR  ，则AB （ ） k(x1),0x„1,  A. 1,0 B. 1, C. R D. ,0  当x(0,2]时，f(x) 1(x1)2 ，g(x) 1 ，其中k 0.若在区间(0，5]上，关于x的   ,1 x„2  2 2. 若复数z满足z 1i 23i，则复数z的虚部是（ ） 方程 f(x) g(x)有5个不同的实数根，则k的取值范围是（ ） 1 1 5 5 A.  B.  i C. D. i 2 2 2 2 A．(0, 3 ) B．[ 1 , 3 ) C．( 1 , 3 ) D．[ 1 , 2 ) 1 1 3 2 3 2 3 3 4 3. 已知命题 p:xR，x2 x10，命题q：若ab，则  ，下列命题为真命题的是( ) a b 12. 已知A(2,2)，B，C是抛物线y2 2px上的三点，如果直线AB，AC被圆(x2)2  y2 3截得的两段 A． pq B．(p)q C．(p)q D．(p)(q) 4．在区间[0,  ]上随机取一个数x，则sinx的值介于0到 3 之间的概率为( ) 弦长都等于2 2，则直线BC的方程为( ) 2 2 A．x2y10 B．3x6y40 C．2x6y30 D．x3y20 2 1 1 1 A． B． C． D． 3 2 3 6 5．已知a，b，c为直线，，，为平面，下列说法正确的是( ) 第II卷(非选择题,共90分) A．若ac，bc，则a//b B．若，，则// 二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上. C．若a//，b//，则a//b D．若//，//，则// y x1 6. 已知双曲线C: x2  y2 1(a0,b0)的左焦点为F c,0，坐标原点为O，若在双曲线右支上存在一 13．若x，y满足 y„2x ，则2yx的最小值是 ． a2 b2 1    1 3 点P满足 PF  3c，且 PO c，则双曲线C的离心率为（ ） 14．已知在平行四边形ABCD中，点E满足AE AC，DE  AB AD，则实数 ． 1 4 4 21 31  A． 2 B． 31 C． 2 D． 31 15. 函数 f(x)    3 (1log 2 x),x1 ，其中常数(0,  )，且sin 1 ．若 f(f( 2)) 6 ，则实数 7．已知四棱锥S  ABCD 的所有顶点都在同一圆面上，底面ABCD是正方形且和球心O在同一平面内，若  sin(2x  )a,x„1 2 3 3 此四棱锥的最大体积为18，则球O的表面积等于( )  3 A．18 B．36 C．54 D．72 a ． 8．已知a  (x,y)，b  (x1,9)(x0,y0)，若a  //b  ，则x y的最小值为( ) 16. 将函数 f(x)2sinx图象上所有点的纵坐标不变，横坐标缩短到原来的 1 ，得到h(x)的图像，再将 2  A．6 B．9 C．16 D．18 函数h(x)的图象左移 个单位，得到g(x)的图象，已知直线 y a与函数g(x)的图象相交，记 y轴右侧 9. 深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的．在神经网络优化中， 8 G 指数衰减的学习率模型为L＝L DG 0 ，其中L表示每一轮优化时使用的学习率，L 表示初始学习率，D表 从左到右的前三个交点的横坐标依次为a 1 、a 2 、a 3 ，若a 1 、a 2 、a 3 成等比数列，则公比q=______． 0 0 示衰减系数，G表示训练迭代轮数，G 表示衰减速度．已知某个指数衰减的学习率模型的初始学习率为0.5， 0 衰减速度为22，且当训练迭代轮数为22时，学习率衰减为0.45，则学习率衰减到0.05以下(不含0.05)所 需的训练迭代轮数至少为(参考数据：lg3≈0.477)( ) A．477 B．478 C．479 D．480 高三数学（文科） 2023-11 第 1 页 共 2 页三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. x2 y2 2 20.（12分）椭圆C:  1(ab0)左、右顶点分别为A，B，离心率为 ，点M( 2,1)在椭圆C a2 b2 2 17．（12分）在ABC 中，角A，B，C 所对的边分别是a，b，c．若 3bsinAa(2cosB)． 上． （1）求角B的大小； （1）求椭圆C 的方程； 1 （2）D为边AB上一点，且满足CD2，AC 4，锐角三角形ACD的面积为 15，求BC的长． （2）直线l交椭圆C于P,Q两点，记直线BP的斜率为k ，直线BQ的斜率为k ，满足k k  .过 1 2 1 2 4 左顶点A作直线PQ的垂线，垂足为H，问：在平面内是否存在定点T,使得TH 为定值，若存在，求出点T 18．（12分）某体育频道为了解某地电视观众对卡塔尔世界杯的收看情况，随机抽取了该地200名观众进 行调查，下表是根据所有调查结果制作的观众日均收看世界杯时间（单位：时）的频率分布表： 的坐标；若不存在，试说明理由. 日均收看世界杯时间（时) [0.5，1] (1，1.5] (1.5，2] (2，2.5] (2.5，3] (3，3.5] 频率 0.1 0.18 0.22 0.25 0.2 0.05 21.（12分）已知函数 f(x)(xa)lnxax2 2x(a 0)，其导函数为g(x)． 如果把日均收看世界杯的时间高于2.5小时的观众称为“足球迷”． （1）根据已知条件完成下面的22列联表，并判断是否有99.9%的把握认为该地的电视观众是否为 （1）若a0，直线ykx1与曲线y f(x)相切，求k的值； “足球迷”与性别有关； （2）若函数g(x)有且仅有两个零点，求实数a的取值范围． 非足球迷 足球迷 合计 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/10/2923:31:48；用户：李波波；邮箱：muziqingtian11@163.com；学号：1391 女 70 男 40 合计 请考生在第22、23题中任选择一题作答,如果多做，则按所做的第一题记分.作答时,用2B铅笔在答题 （2）从样本中为“足球迷”的观众中，先按性别比例用分层抽样的方法抽出5人，再从这5人中随 卡上把所选题目对应的标号涂黑. 机抽取3人进行交流，求3人都是男性观众的概率． xcos 22．（10分）在直角坐标系xOy中，曲线C 的方程为x2  y2 4x0．曲线C 的参数方程为 ( 参考公式：K2  n(ad bc)2 ，其中nabcd ． 1 2 y1sin (ab)(cd)(ac)(bd) 参考数据： 为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系． （1）求曲线C 和曲线C 的极坐标方程； P(K2 k ) 0.10 0.05 0.025 0.010 0.005 0.001 1 2 0   （2）若射线( 0,0 )交曲线C 于点P，直线 (R)与曲线C 和曲线C 分别交 k 2.706 3.841 5.024 6.635 7.879 10.828 2 1 2 1 2 0 于点M 、N，且点P、M 、N均异于点O，求MPN面积的最大值． 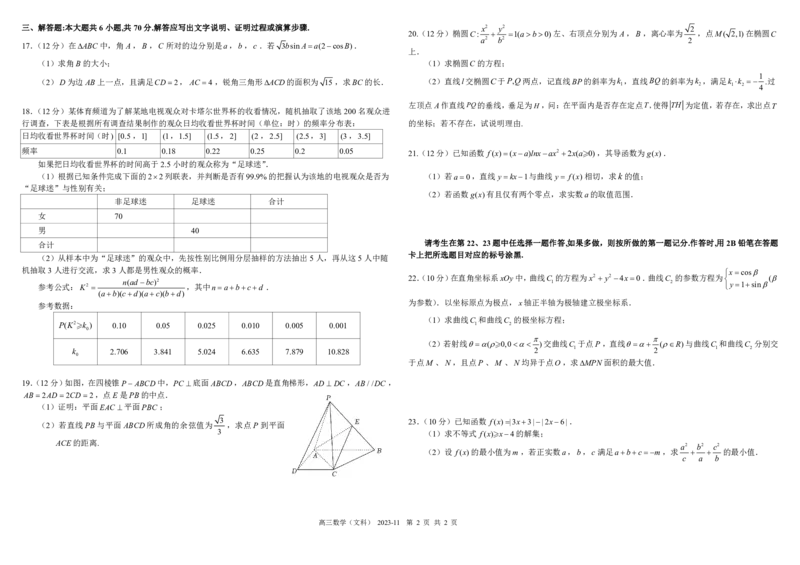19．（12分）如图，在四棱锥P ABCD中，PC 底面ABCD，ABCD是直角梯形，AD DC，AB//DC ， AB2AD2CD2，点E是PB的中点． （1）证明：平面EAC 平面PBC ； （2）若直线PB与平面 ABCD所成角的余弦值为 3 ，求点P到平面 23．（10分）已知函数 f(x)|3x3||2x6|． 3 （1）求不等式 f(x) x4的解集； ACE的距离. a2 b2 c2 （2）设 f(x)的最小值为m，若正实数a，b，c满足abcm，求   的最小值． c a b 高三数学（文科） 2023-11 第 2 页 共 2 页4 2 树德中学高 2021 级高三上学期 11 月阶段性测试数学（文科）试题 答案 所以3人都是男性观众的概率为  ．…………12分 10 5 一、选择题：1-6ACDADD 7-12BCCCBB 19.解：（1）证明：PC 平面ABCD，AC 平面ABCD，PC  AC， 1 1 9 AB2，由ADCD1，ADDC且ABCD是直角梯形， 二、填空题：13. 3 14. 15. 16. 或5 4 6 5  AC AD2 DC2  2,BC AD2 (ABDC)2  2，AC2BC2  AB2 ， 17解：（1）由正弦定理得 3sinBsinAsinA(2cosB)．sinA0， 3sinB2cosB．……2分 AC  BC，又PC  AC，PCBC C，PC平面PBC ，BC平面PBC ，AC 平面PBC ，   即 3sinBcosB2，即2sin(B )2，即sin(B )1．…………4分 6 6 AC 平面PBC ，又AC 平面EAC ，平面EAC 平面PBC ；…………5分     （2）方法一：因为PC 平面ABCD，所以PBC即为直线PB与平面ABCD所成角， 0B，B  ，即B ，即角B的大小为 …………5分 6 2 3 3 BC 2 3 所以cosPBC   ，所以PB 6 ，则PC 2．…………7分 1 15 PB PB 3 （2）ACD的面积为S  24sinACD 15 ，即sinACD ，…………6分 2 4 因为PC 底面ABCD，点E是PB的中点， 1 1 1 1 1 1 ACD是锐角三角形cosACD 1sin2ACD  ， 所以V  V  ( ( 12)2) ，…………9分 4 PACE 2 PACB 2 3 2 3 1 6 1 6 3 由余弦定理得AD2 22 42 224 416416，…………8分 在RtPCB中CE ，又由（1）知AC 平面PBC ，则RtACE的面积S   2  ， 4 2 ACE 2 2 2 15 1 1 3 1 2 3 则AD4，ACD为等腰三角形，sinBDC sinADC sinACD …………10分 设点P到平面ACE的距离为h，则由V  S h  h 得h ， 4 PACE 3 ACE 3 2 3 3 BC CD 2 3 则BCD中，  ，得BC  5 …………12分 所以点P到平面ACE的距离为h .…………12分 sinBDC sinB 3 18.解：（1）由频率分布表可知，“足球迷”对应的频率为0.20.050.25． 方法二：因为PC 平面ABCD，所以PBC即为直线PB与平面ABCD所成角， 所以在抽取的200人中，“足球迷”有2000.2550人． BC 2 3 所以cosPBC   ，所以PB 6 ，则PC 2．…………7分 故22列联表如下： PB PB 3 非足球迷 足球迷 合计 因为AC 平面PBC ，所以点A到平面PCE的距离为AC  2， 女 70 10 80 1 1 男 80 40 120 设点P到平面ACE的距离为h，因为V V ，所以 S h S AC …………9分 PACE APCE 3 ACE 3 PCE 合计 150 50 200 6 1 6 3 在RtPCB中CE ，又由（1）知AC 平面PBC ，则RtACE的面积S   2  ， …………2分 2 ACE 2 2 2 200(70408010)2 100 K2   11.11110.828，…………4分 可求得S  2 1505080120 9 PCE 2 所以有99.9%的把握认为该地的电视观众是否为“足球迷”与性别有关．…………5分 1 1 2 3 2 3 所以 S h S AC ，得h ，所以点P到平面ACE的距离为h .…………12分 （2）样本中为“足球迷”的观众有50人，男、女人数之比为4:1． 3 ACE 3 PCE 3 3 故用分层抽样方法从中抽出5人，男性有4人，记为A，A ，A ，A ，女性有1人，记为B，……7分 c 2 1 2 3 4   a 2 a2 4 从这5人中再随机抽取3人，有(A 1 ，A 2 ，A 3 )，(A 1 ，A 2 ，A 4 )，(A 2 ，A 3 ，A 4 )，(A 1 ，A 3 ，A 4 )，(A 1 ， 20.解：（1）依题意，   2  1 1 ，解得  b2 2，所以椭圆C的方程为 x2  y2 1；…………4分 a2 b2  4 2 c2 2 a2 b2 c2  A ，B)，(A ，A ，B)，(A ，A ，B)，(A ，A ，B)，(A ，A ，B)，(A ，A ，B)共10个结果，  2 1 3 1 4 2 3 2 4 3 4  其中3人都是男性观众的结果有4个，…………11分 高三数学（文科） 2023-11 第 3 页 共 2 页（2）依题意A2，0，B2，0，设Px,y ，Qx ,y ， ①当a0时，g(x)lnx3在(0,)递增，由g(x)0，可得xe3，不合题意；…………6分 1 1 2 2 若直线PQ的斜率为0，则P，Q关于y轴对称，必有 k k 0 ，不合题意； ②当a0时，设h(x)2ax2 xa，因为h(0)a0，且2a0，所以存在x 0，使得h(x ) g(x )0， 1 2 0 0 0 所以直线PQ斜率必不为0，设其方程为xtyn n2， 当0xx 时，h(x)0，即g(x)0，g(x)递增；当xx 时，h(x)0，即g(x)0，g(x)递减， 0 0 x22y2 4 x0,g(x);x,g(x) .…………8分 与椭圆C联立 ，整理得：  t22  y22tnyn240， xtyn 若g(x)有且只有两个零点，即g(x) 0 max  2tn y y  所以4t2n24  t22  n24  8  2t2n24  0，且    1 2 t2 2 ，…………6分 x 2  y y  n24 因为2ax 0 2 x 0 a0，所以a 2x 2 0 1 0，即x 0  2 ，  1 2 t22 0 1 y y 1 1 2 因为k k  ，所以 1  2  ， 得4y y x 2x 20…………7分 则g(x)  g(x )lnx a(2x  )3lnx  2， 1 2 4 x 2 x 2 4 1 2 1 2 max 0 0 0 x 0 2x 2 1 1 2 0 0 即 2 2 1 8x 设m(x)lnx 2(x ) ，m(x)  0 ，所以m(x)递增， 4y y ty n2ty n2  t24  y y tn2y y n22 2x2 1 2 x (2x2 1)2 1 2 1 2 1 2 1 2   t2 4    n24 tn2    2tn    n22 若g(x)有且只有两个零点，即g(x) max 0，因为m（1）0，所以当x 0 1时，m(x 0 )0…………10分 t22   t22 x 1 所以x 1,此时a 0  (0,1)， 0 2x 2 1 1   4t2 n24  2t2nn2n22 t22  0 ， 0 2x 0  x 0 t22 故g(x)有且只有两个零点时，0a1．…………12分 因为n2，  4t2n22t2nn2 t22  0，4n8t2n2t22t2nnt22n2t240 22.解：（1）把xcos，ysin代入x2  y2 4x0， 2  2  整理得6n40，解得n ，直线PQ恒过定点N ，0.…………10分 得曲线C 的极坐标方程为2 4cos，即4cos．…………2分 3  3  1 因为AH PQ ，所以点H在以AN为直径的圆上，.…………11分 xcos 将 中的参数消去，得曲线C 的普通方程为x2  y2 2y0， y1sin 2  4  故存在点T ，0为AN的中点，满足题意.…12分  3  把xcos，ysin代入，得曲线C 的极坐标方程为2 2sin，即2sin．…………5分 21.解：（1）当a0时， f(x)xlnx2x，则 f(x)lnx3， 2 3  设切点为(x ， f(x ))，则切线方程为y(lnx 3)(xx )x lnx 2x ，整理得y(lnx 3)xx ，…3分 （2）由题得|OP|4cos，|OM |4cos( )4sin，|ON|2sin( )2cos， 0 0 0 0 0 0 0 0 0 2 2 |NM ||OM ||ON|4sin2cos，…………7分 直线ykx1与曲线y f(x)相切，所以切线y(lnx 3)xx 过点0,1，所以x 1， 0 0 0 1 1 因为OPMN ，所以S  |MN||OP| (4sin2cos)4cos2(4sincos2cos2) MPN 2 2 k lnx 33…………5分 0 2(2sin2cos21)2 5sin(2)2„2 52 ， a 1 a 2ax2 xa （2）g(x) f(x)lnx2ax 3，则g(x) 2a  ， x x x2 x2 高三数学（文科） 2023-11 第 4 页 共 2 页1     其中tan ，0 ，当2 ，即  时，MPN的面积取得最大值2 52．…10分 2 2 2 4 2 5 23.解：（1）当x„ 1时，原不等式等价于(3x3)2x6 x4，解得x„  ； 2 1 当1 x3时，原不等式等价于3x32x6 x4，解得 „x3； 4 当x 3时，原不等式等价于3x3(2x6) x4，解得x 3． 5 1 综上所述，原不等式的解集是(, ][ ,)．…………5分 2 4 x9,x„ 1  （2）由（1）得 f(x)5x3,1x3，所以 f(x)  f(1)8，则abc8．…………7分 min  x9,x 3 a2 b2 c2 a2 b2 c2 因为 c 2a， a 2b， b 2c，所以   abc 2(abc)16， c a b c a b a2 b2 c2 8 a2 b2 c2 即   8，当且仅当abc 时等号成立，故   的最小值为8．…………10分 c a b 3 c a b 高三数学（文科） 2023-11 第 5 页 共 2 页