专题16双曲线（1大考向真题解读）-解析版_2024-2025高三（6-6月题库）_2024年08月试卷_08202025版《真题题源解密-专题分类》数学

专题 16 双曲线 命题解读 考向 考查统计 1.高考对双曲线的考查，重点是 （1）双曲线的定义、几何图形和标准 方程。 2023·新高考Ⅰ卷，16 （2）双曲线的几何性质（范围、对称 双曲线的离心率 2024·新高考Ⅰ卷，12 性、顶点、离心率、渐近线）。 （3）直线和双曲线的位置关系及综合 应用。 命题分析 2024年高考新高考Ⅰ卷考查应用定义求解双曲线的离心率，难度较易。Ⅱ卷是双曲线与数列的综合问题， 后续专题会解读。双曲线是圆雉曲线的重要内容，但从总体上看，双曲线的考试要求要比椭圆和抛物线低， 在双曲线的试题中，最为重要的是三点是：方程、渐近线、离心率。预计2025年高考还是主要考查双曲线 的定义和离心率、渐近线。 试题精讲 (cid:22)(cid:23)(cid:24)(cid:25)(cid:21) 1(cid:26)(cid:27)2024(cid:28)(cid:29)(cid:30)Ⅰ(cid:31)·12(cid:32)(cid:33)(cid:34)(cid:35)(cid:36)C: x2 - y2 =1(a>0,b>0)(cid:37)(cid:38)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F(cid:23)F (cid:45)(cid:46)F (cid:47)(cid:48)(cid:49)(cid:50)y(cid:51)(cid:37) a2 b2 1 2 2 (cid:52)(cid:36)(cid:53)C(cid:50)A(cid:45)B(cid:54)(cid:41)(cid:45)(cid:55)|FA|=13,|AB|=10(cid:45)(cid:56)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) (cid:26) 1 3 (cid:60)(cid:61)(cid:62)(cid:63) 2 (cid:60)(cid:42)(cid:64)(cid:63)(cid:65)(cid:21)(cid:66)(cid:67)(cid:68)(cid:34)(cid:35)(cid:36)(cid:69)(cid:70)(cid:71)(cid:72)(cid:45)(cid:73)(cid:68) AF (cid:45)(cid:74)(cid:75)(cid:34)(cid:35)(cid:36)(cid:76)(cid:22)(cid:77)(cid:78)(cid:73)(cid:68) AF (cid:45)(cid:79)(cid:80)(cid:81)(cid:82)a,b,c(cid:37)(cid:83)(cid:45) 2 1 (cid:84)(cid:85)(cid:73)(cid:68)(cid:57)(cid:58)(cid:59). x2 y2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:65)(cid:21)(cid:80)(cid:88)A,B,F (cid:89)(cid:41)(cid:90)(cid:91)(cid:92)(cid:93)(cid:94)(cid:45)(cid:33)A(cid:95)(cid:76)(cid:22)(cid:72)(cid:96)(cid:45)(cid:97)x=c(cid:98)(cid:99) - =1 2 a2 b2 b2 æ b2 ö æ b2 ö 2b2 b2 (cid:81)y=± (cid:45)(cid:79)Açc, ÷,Bçc,- ÷(cid:45)(cid:100) AB = =10(cid:45) AF = =5(cid:45) a è a ø è a ø a 2 ab2 (cid:101) AF - AF =2a(cid:45)(cid:81) AF = AF +2a=2a+5=13(cid:45)(cid:87)(cid:81)a=4(cid:45)(cid:98)(cid:99) =5(cid:81)b2 =20(cid:45) 1 2 1 2 a c 6 3 (cid:100)c2 =a2+b2 =36,(cid:45)(cid:79)c=6(cid:45)(cid:102)(cid:103)e= = = . a 4 2 3 (cid:100)(cid:61)(cid:62)(cid:44)(cid:10) 2 (cid:22)(cid:23)(cid:24)(cid:25)(cid:21) x2 y2 1(cid:26)(cid:27)2023(cid:28)(cid:29)(cid:30)Ⅰ(cid:31)·16(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(a>0,b>0)(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F,F (cid:26)(cid:41)A(cid:95)C(cid:105)(cid:45)(cid:41)B a2 b2 1 2 uuur uuur uuuur 2uuuur (cid:95)y(cid:51)(cid:105)(cid:45)FA^FB,F A=- F B(cid:45)(cid:56)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) (cid:26) 1 1 2 3 2 3 5 3 (cid:60)(cid:61)(cid:62)(cid:63) / 5 5 5 (cid:60)(cid:42)(cid:64)(cid:63)(cid:106)(cid:107)(cid:22)(cid:10)(cid:108)(cid:109)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:110)(cid:111)(cid:112)(cid:13)(cid:113)(cid:37)(cid:114)(cid:115)(cid:66)(cid:78)(cid:81)(cid:82) AF , BF , BF , AF (cid:3)(cid:50)a,m(cid:37)(cid:116)(cid:117)(cid:118)(cid:45) 2 2 1 1 (cid:84)(cid:85)(cid:108)(cid:109)(cid:119)(cid:120)(cid:77)(cid:15)(cid:73)(cid:81)a=m(cid:45)(cid:121)(cid:85)(cid:108)(cid:109)(cid:122)(cid:123)(cid:77)(cid:15)(cid:81)(cid:82)a,c(cid:37)(cid:124)(cid:125)(cid:106)(cid:126)(cid:45)(cid:84)(cid:85)(cid:81)(cid:87). 5 2 (cid:106)(cid:107)(cid:127)(cid:10)(cid:128)(cid:21)(cid:66)(cid:33)(cid:68)(cid:129)(cid:41)(cid:91)(cid:92)(cid:45)(cid:84)(cid:85)(cid:65)(cid:111)(cid:112)(cid:91)(cid:92)(cid:130)(cid:131)(cid:73)(cid:81)x = c,y =- t(cid:45)t2 =4c2(cid:45)(cid:97)(cid:41)A(cid:98)(cid:99)(cid:34)(cid:35)(cid:36)C 0 3 0 3 (cid:81)(cid:82)(cid:3)(cid:50)a,b,c(cid:37)(cid:124)(cid:125)(cid:106)(cid:126)(cid:45)(cid:84)(cid:85)(cid:81)(cid:87)(cid:132) (cid:60)(cid:86)(cid:87)(cid:63)(cid:106)(cid:107)(cid:22)(cid:10) (cid:128)(cid:21)(cid:66)(cid:45)(cid:33) AF =2m(cid:45)(cid:56) BF =3m= BF , AF =2a+2m(cid:45) 2 2 1 1 (cid:95)RtVABF (cid:133)(cid:45)9m2+(2a+2m)2 =25m2(cid:45)(cid:56)(a+3m)(a-m)=0(cid:45)(cid:100)a=m(cid:134)a=-3m(cid:27)(cid:135)(cid:136)(cid:32)(cid:45) 1 (cid:102)(cid:103) AF =4a, AF =2a(cid:45) BF = BF =3a(cid:45)(cid:56) AB =5a(cid:45) 1 2 2 1 AF 4a 4 (cid:100)cosÐFAF = 1 = = (cid:45) 1 2 AB 5a 5 16a2+4a2-4c2 4 (cid:102)(cid:103)(cid:95)(cid:137)AFF (cid:133)(cid:45)cosÐFAF = = (cid:45)(cid:138)(cid:15)(cid:81)5c2 =9a2(cid:45) 1 2 1 2 2´4a´2a 5c 3 5 (cid:100)e= = . a 5 (cid:106)(cid:107)(cid:127): (cid:128)(cid:21)(cid:66)(cid:45)(cid:81)F(-c,0),F (c,0)(cid:45)(cid:139)Ax ,y ,B(0,t)(cid:45) 1 2 0 0 uuuur 2uuuur 2 5 2 (cid:140)(cid:44)F A=- F B(cid:45)(cid:102)(cid:103)x -c,y =- -c,t(cid:45)(cid:56)x = c,y =- t(cid:45) 2 3 2 0 0 3 0 3 0 3 uuur uuur uuur uuur æ8 2 ö 8 2 (cid:101)FA^FB(cid:45)(cid:102)(cid:103)FA×FB=ç c,- t÷×c,t = c2- t2 =0(cid:45)(cid:56)t2 =4c2(cid:45) 1 1 1 1 è3 3 ø 3 3 25 4 c2 t2 25c2 4t2 25c2 16c2 (cid:101)(cid:41)A(cid:95)C(cid:105)(cid:45)(cid:56) 9 9 (cid:45)(cid:138)(cid:15)(cid:81) - =1(cid:45)(cid:56) - =1(cid:45) - =1 9a2 9b2 9a2 9b2 a2 b2 (cid:102)(cid:103)25c2b2-16c2a2 =9a2b2(cid:45)(cid:79)25c2 c2-a2 -16a2c2 =9a2 c2-a2 (cid:45) (cid:138)(cid:15)(cid:81)25c4-50a2c2+9a4 =0(cid:45)(cid:56)  5c2-9a2 5c2-a2 =0(cid:45)(cid:87)(cid:81)5c2 =9a2(cid:134)5c2 =a2(cid:45) 3 5 5 3 5 (cid:101)e>1(cid:45)(cid:102)(cid:103)e= (cid:134)e= (cid:27)(cid:135)(cid:136)(cid:32)(cid:45)(cid:100)e= . 5 5 5 3 5 (cid:100)(cid:61)(cid:62)(cid:44)(cid:10) . 5 (cid:22)(cid:23)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78) (cid:48)(cid:141)(cid:142)(cid:110)(cid:54)(cid:143)(cid:77)(cid:41)F,F (cid:37)(cid:144)(cid:57)(cid:37)(cid:145)(cid:37)(cid:146)(cid:147)(cid:83)(cid:94)(cid:50)(cid:148)(cid:13)(cid:27)(cid:69)(cid:50)(cid:149)(cid:150)(cid:151)(cid:50) FF (cid:32)(cid:37)(cid:41)(cid:37)(cid:152)(cid:153)(cid:154)(cid:155)(cid:34)(cid:35)(cid:36)(cid:27)(cid:156)(cid:54) 1 2 1 2 (cid:143)(cid:77)(cid:41)(cid:154)(cid:34)(cid:35)(cid:36)(cid:37)(cid:40)(cid:41)(cid:32)(cid:26)(cid:109)(cid:157)(cid:75)(cid:116)(cid:158)(cid:44) M MF - MF =2a(0<2a< FF )  1 2 1 2 (cid:26) (cid:4)(cid:66)(cid:10)(cid:27)1(cid:32)(cid:55)(cid:77)(cid:78)(cid:118)(cid:133)(cid:136)(cid:159)(cid:146)(cid:147)(cid:83)(cid:45)(cid:56)(cid:35)(cid:36)(cid:160)(cid:44)(cid:34)(cid:35)(cid:36)(cid:133)(cid:37)(cid:22)(cid:161)(cid:26) (cid:27)2(cid:32)(cid:162)2a= FF (cid:163)(cid:45)(cid:41)(cid:37)(cid:152)(cid:153)(cid:164)(cid:103)F (cid:165)F (cid:44)(cid:166)(cid:41)(cid:37)(cid:54)(cid:167)(cid:168)(cid:36)(cid:132)(cid:162)2a=0(cid:163)(cid:45)(cid:41)(cid:37)(cid:152)(cid:153)(cid:164)(cid:36)(cid:169)FF (cid:37)(cid:170)(cid:52) 1 2 1 2 1 2 (cid:48)(cid:42)(cid:36)(cid:26) (cid:27)3(cid:32)2a> FF (cid:163)(cid:45)(cid:41)(cid:37)(cid:152)(cid:153)(cid:171)(cid:172)(cid:95)(cid:26) 1 2(cid:95)(cid:173)(cid:109)(cid:77)(cid:78)(cid:165)(cid:92)(cid:174)(cid:106)(cid:126)(cid:87)(cid:21)(cid:163)(cid:4)(cid:66)(cid:103)(cid:175)(cid:54)(cid:41)(cid:10) (cid:167)(cid:176)“ FF >2a”(cid:164)(cid:177)(cid:178)(cid:179)(cid:132) (cid:180)(cid:181)(cid:77)(cid:182)(cid:27)(cid:40)(cid:41)(cid:95)(cid:183)(cid:143)(cid:51)(cid:105)(cid:32)(cid:45)(cid:184)(cid:77)(cid:112)(cid:27)(cid:185)(cid:77)a2(cid:45)b2(cid:37)(cid:83)(cid:32)(cid:45)(cid:4)(cid:66)a2 +b2 =c2 1 2 ①(cid:37)(cid:173)(cid:109)(cid:26) ② (cid:127)(cid:23)(cid:34)(cid:35)(cid:36)(cid:37)(cid:106)(cid:126)(cid:23)(cid:71)(cid:186)(cid:187)(cid:188)(cid:189) x2 y2 y2 x2 (cid:92)(cid:174)(cid:106)(cid:126) - =1(a>0,b>0) - =1(a>0,b>0) a2 b2 a2 b2 (cid:71)(cid:186) A 2 (cid:40)(cid:41)(cid:91)(cid:92) F(-c,0)(cid:45)F (c,0) F(0,-c)(cid:45)F (0,c) 1 2 1 2 (cid:147)(cid:190)(cid:188) (cid:3)(cid:50)x(cid:45)y(cid:51)(cid:178)(cid:51)(cid:147)(cid:190)(cid:45)(cid:3)(cid:50)(cid:191)(cid:41)(cid:178)(cid:133)(cid:58)(cid:147)(cid:190) (cid:192)(cid:41)(cid:91)(cid:92) A(-a,0)(cid:45)A (a,0) A(0,a)(cid:45)A (0,-a) 1 2 1 2 (cid:193)(cid:194) x ³a y ³a (cid:195)(cid:51)(cid:23)(cid:196)(cid:51) (cid:195)(cid:51)(cid:197)(cid:44)2a(cid:45)(cid:196)(cid:51)(cid:197)(cid:44)2b c b2 (cid:57)(cid:58)(cid:59) e= = 1+ (e>1) a a2 x2 y2 b y2 x2 a (cid:139) - =0Þ y=± x(cid:45) (cid:139) - =0Þ y=± x(cid:45) (cid:198)(cid:199)(cid:36)(cid:106)(cid:126) a2 b2 a a2 b2 b (cid:40)(cid:41)(cid:82)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:44)b (cid:40)(cid:41)(cid:82)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:44)b ì>1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:142) ì>1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:142) 0 0 0 0 ï ï (cid:41)(cid:165)(cid:34)(cid:35)(cid:36) x2 y2 ï (cid:27)(cid:203)(cid:40)(cid:41)(cid:204)(cid:42)(cid:32) y2 x2 ï (cid:27)(cid:203)(cid:40)(cid:41)(cid:204)(cid:42)(cid:32) - í - í (cid:37)(cid:200)(cid:201)(cid:3)(cid:202) a2 b2 ï =1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:105) a2 b2 ï =1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:105) 0 0 0 0 ï î<1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:205) ï î<1,(cid:41)(x ,y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:205) 0 0 0 0 (cid:206)(cid:40)(cid:41)(cid:37)(cid:34) x2 y2 y2 x2 - =1(-a2 2c) ï 1 2 ï 1 í S = PF × PF sinÐFPF ï DPF1F2 2 1 2 1 2 ï FF 2 = PF 2 + PF 2 -2 PF PF cosÐFPF î 1 2 1 2 1 2 1 2 (cid:94)(cid:51)(cid:34)(cid:35)(cid:36)(cid:226)(cid:227)(cid:228)(cid:175)(cid:229)(cid:180)(cid:167)(cid:176)(cid:10)(cid:34)(cid:35)(cid:36)(cid:44)(cid:94)(cid:51)(cid:34)(cid:35)(cid:36)Ûa=bÛ(cid:57)(cid:58)(cid:59)e= 2 Û(cid:54)(cid:198) (cid:94)(cid:51)(cid:34)(cid:35)(cid:36) (cid:199)(cid:36)(cid:230)(cid:93)(cid:170)(cid:52)Û(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=±xÛ(cid:106)(cid:126)(cid:80)(cid:33)(cid:44)x2 - y2 =l(l¹0)(cid:26) (cid:60)(cid:34)(cid:35)(cid:36)(cid:148)(cid:109)(cid:74)(cid:231)(cid:63) 1(cid:23)(cid:34)(cid:35)(cid:36)(cid:37)(cid:218)(cid:219) 2b2 (cid:46)(cid:34)(cid:35)(cid:36)(cid:37)(cid:40)(cid:41)(cid:150)(cid:110)(cid:34)(cid:35)(cid:36)(cid:195)(cid:51)(cid:170)(cid:52)(cid:37)(cid:52)(cid:36)(cid:232)(cid:34)(cid:35)(cid:36)(cid:233)(cid:81)(cid:37)(cid:36)(cid:169)(cid:45)(cid:190)(cid:44)(cid:34)(cid:35)(cid:36)(cid:37)(cid:218)(cid:219)(cid:26)(cid:218)(cid:219)(cid:197)(cid:44) (cid:26) a2(cid:23)(cid:41)(cid:110)(cid:34)(cid:35)(cid:36)(cid:37)(cid:200)(cid:201)(cid:3)(cid:202) x2 y2 x2 y2 (cid:147)(cid:50)(cid:34)(cid:35)(cid:36) - =1(a>b>0)(cid:45)(cid:41)P(x (cid:45)y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:142)(cid:204)(cid:45)(cid:94)(cid:234)(cid:50) 0 - 0 >1(cid:26) a2 b2 0 0 a2 b2 x2 y2 (cid:41)P(x (cid:45)y )(cid:95)(cid:34)(cid:35)(cid:36)(cid:205)(cid:204)(cid:45)(cid:94)(cid:234)(cid:50) 0 - 0 <1 (cid:74)(cid:75)(cid:36)(cid:188)(cid:235)(cid:236)(cid:37)(cid:88)(cid:237)(cid:41)(cid:238)(cid:42)(cid:64)(cid:26) 0 0 a2 b2 3(cid:23)(cid:34)(cid:35)(cid:36)(cid:148)(cid:30)(cid:188)(cid:189) ab (cid:188)(cid:189)1(cid:10)(cid:34)(cid:35)(cid:36)(cid:37)(cid:40)(cid:41)(cid:82)(cid:54)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:44)(cid:148)(cid:13)b(cid:132)(cid:192)(cid:41)(cid:82)(cid:54)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:44)(cid:148)(cid:13) (cid:132) c a2b2 (cid:188)(cid:189)2(cid:10)(cid:34)(cid:35)(cid:36)(cid:105)(cid:37)(cid:239)(cid:66)(cid:41)P(cid:82)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:54)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:37)(cid:240)(cid:113)(cid:164)(cid:22)(cid:143)(cid:148)(cid:13) (cid:132) c2 b2 4(cid:23)(cid:34)(cid:35)(cid:36)(cid:40)(cid:41)(cid:89)(cid:223)(cid:186)(cid:141)(cid:113)(cid:44) (cid:27)(cid:80)(cid:103)(cid:156)(cid:241)(cid:15)(cid:87)(cid:45)(cid:192)(cid:41)(cid:242)(cid:29)(cid:45)(cid:243)(cid:223)(cid:242)(cid:151)(cid:45)(cid:42)(cid:244)(cid:242)(cid:151)(cid:45)(cid:141)(cid:113)(cid:242)(cid:69)(cid:32) q tan 2 5(cid:23)(cid:34)(cid:35)(cid:36)(cid:37)(cid:207)(cid:36) x2 y2 x x y y (cid:41)M(x (cid:45)y )(cid:95)(cid:34)(cid:35)(cid:36) - =1(a>0(cid:45)b>0)(cid:105)(cid:45)(cid:46)(cid:41)M (cid:47)(cid:34)(cid:35)(cid:36)(cid:37)(cid:207)(cid:36)(cid:106)(cid:126)(cid:44) 0 - 0 =1(cid:26)(cid:55)(cid:41) 0 0 a2 b2 a2 b2 x2 y2 x x y y M(x (cid:45)y )(cid:95)(cid:34)(cid:35)(cid:36) - =1(a>0(cid:45)b>0)(cid:205)(cid:45)(cid:56)(cid:41)M (cid:147)(cid:173)(cid:207)(cid:41)(cid:123)(cid:106)(cid:126)(cid:44) 0 - 0 =1 0 0 a2 b2 a2 b2 (cid:22)(cid:23)(cid:245)(cid:20)(cid:21) y2 x2 1(cid:26)(cid:27)2024·(cid:246)(cid:247)(cid:248)(cid:249)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(m>0)(cid:37)(cid:195)(cid:51)(cid:197)(cid:94)(cid:50)(cid:196)(cid:51)(cid:197)(cid:37)2(cid:251)(cid:45)(cid:56)C(cid:37)(cid:198)(cid:199)(cid:36) 3m+2 m (cid:106)(cid:126)(cid:44)(cid:27) (cid:32) 1 2 A(cid:26)y=± x B(cid:26)y=± x C(cid:26)y=±2x D(cid:26)y=± 2x 2 2 (cid:60)(cid:61)(cid:62)(cid:63)C (cid:60)(cid:42)(cid:64)(cid:63)(cid:181)(cid:81)(cid:82)(cid:106)(cid:126)(cid:45)(cid:73)(cid:68)m=2(cid:45)(cid:81)(cid:82)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:165)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126). (cid:60)(cid:86)(cid:87)(cid:63)(cid:65)(cid:21)(cid:66)(cid:81) 3m+2 =2 m(cid:45)(cid:87)(cid:81)m=2(cid:45) y2 x2 C: - =1(cid:45)(cid:100)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=±2x. 8 2 (cid:100)(cid:20)(cid:10)C x2 y2 2(cid:26)(cid:27)2024·(cid:252)(cid:253)(cid:254)(cid:255)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)F(cid:45)F (cid:44)(cid:35)(cid:36)C(cid:10) + =1m¹4(cid:37)(cid:40)(cid:41)(cid:45)(cid:56)(cid:175)(cid:256)(cid:257)(cid:107)(cid:258)(cid:259)(cid:37)(cid:164)(cid:27) (cid:32) 1 2 4 m 3 A(cid:26)(cid:55)m=1(cid:45)(cid:56)(cid:35)(cid:36)C(cid:37)(cid:57)(cid:58)(cid:59)e= 25 B(cid:26)(cid:55)m=-1(cid:45)(cid:56)(cid:35)(cid:36)C(cid:37)(cid:57)(cid:58)(cid:59)e= 2 C(cid:26)(cid:55)(cid:35)(cid:36)C(cid:105)(cid:260)(cid:261)(cid:54)(cid:143)(cid:171)(cid:220)(cid:37)(cid:41)P(cid:45)(cid:262)(cid:81)ÐFPF =90°(cid:45)(cid:56)m=2 1 2 D(cid:26)(cid:55)m<0(cid:45)(cid:56)(cid:35)(cid:36)C(cid:105)(cid:172)(cid:95)(cid:263)(cid:143)(cid:171)(cid:220)(cid:37)(cid:41)P(cid:45)(cid:262)(cid:81)ÐFPF =90° 1 2 (cid:60)(cid:61)(cid:62)(cid:63)C (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:266)(cid:77)(cid:37)(cid:106)(cid:126)(cid:45)(cid:74)(cid:75)(cid:267)(cid:268)(cid:23)(cid:34)(cid:35)(cid:36)(cid:37)(cid:188)(cid:189)(cid:269)(cid:270)(cid:42)(cid:64)(cid:271)(cid:272)(cid:79)(cid:80)(cid:81)(cid:87). 4-1 3 (cid:60)(cid:86)(cid:87)(cid:63)(cid:147)(cid:50)A(cid:45)(cid:162)m=1(cid:163)(cid:45)(cid:35)(cid:36)C(cid:164)(cid:267)(cid:268)(cid:45)(cid:57)(cid:58)(cid:59)e= = (cid:45)A(cid:273)(cid:185)(cid:132) 2 2 4+1 5 (cid:147)(cid:50)B(cid:45)(cid:162)m=-1(cid:163)(cid:45)(cid:35)(cid:36)C(cid:164)(cid:34)(cid:35)(cid:36)(cid:45)(cid:57)(cid:58)(cid:59)e= = (cid:45)B(cid:273)(cid:185)(cid:132) 2 2 (cid:147)(cid:50)C(cid:45)(cid:162)m=8(cid:163)(cid:45)(cid:35)(cid:36)C(cid:164)(cid:267)(cid:268)(cid:45)(cid:214)(cid:222)(cid:274)(cid:51)(cid:197)b=2(cid:45)(cid:274)(cid:40)(cid:144)c= m-4 =2(cid:45) (cid:275)(cid:276)(cid:103)(cid:36)(cid:169)FF (cid:44)(cid:52)(cid:219)(cid:37)(cid:268)(cid:260)(cid:46)(cid:156)(cid:143)(cid:267)(cid:268)(cid:222)(cid:51)(cid:166)(cid:41)(cid:45)(cid:79)(cid:277)(cid:75)(cid:167)(cid:176)(cid:37)m(cid:80)(cid:103)(cid:164)8(cid:45)C(cid:258)(cid:259)(cid:132) 1 2 (cid:147)(cid:50)D(cid:45)(cid:162)m<0(cid:163)(cid:45)(cid:56)(cid:35)(cid:36)(cid:164)(cid:40)(cid:41)(cid:95)x(cid:105)(cid:37)(cid:34)(cid:35)(cid:36)(cid:45)(cid:56)|FF |>4(cid:45) 1 2 (cid:103)(cid:36)(cid:169)FF (cid:44)(cid:52)(cid:219)(cid:37)(cid:268)(cid:110)(cid:34)(cid:35)(cid:36)(cid:261)4(cid:143)(cid:53)(cid:41)(cid:45)(cid:79)(cid:277)(cid:75)(cid:167)(cid:176)(cid:37)(cid:41)P(cid:261)4(cid:143)(cid:45)D(cid:273)(cid:185). 1 2 (cid:100)(cid:20)(cid:10)C y2 x2 3(cid:26)(cid:27)2024·(cid:278)(cid:279)·(cid:89)(cid:250)(cid:32)(cid:46)(cid:34)(cid:35)(cid:36)C: - =1(a>b>0)(cid:37)(cid:175)(cid:192)(cid:41)F (cid:47)(cid:280)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:170)(cid:36)(cid:45)(cid:42)(cid:43)(cid:110)(cid:54)(cid:167)(cid:198) a2 b2 uuur uuuur (cid:199)(cid:36)(cid:93)(cid:53)(cid:50)M,N(cid:54)(cid:41)(cid:45)(cid:55)NF =2FM ,(cid:56)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44)(cid:27) (cid:32) 2 3 A(cid:26) B(cid:26) 3 C(cid:26)2 3 D(cid:26)3 3 (cid:60)(cid:61)(cid:62)(cid:63)A a (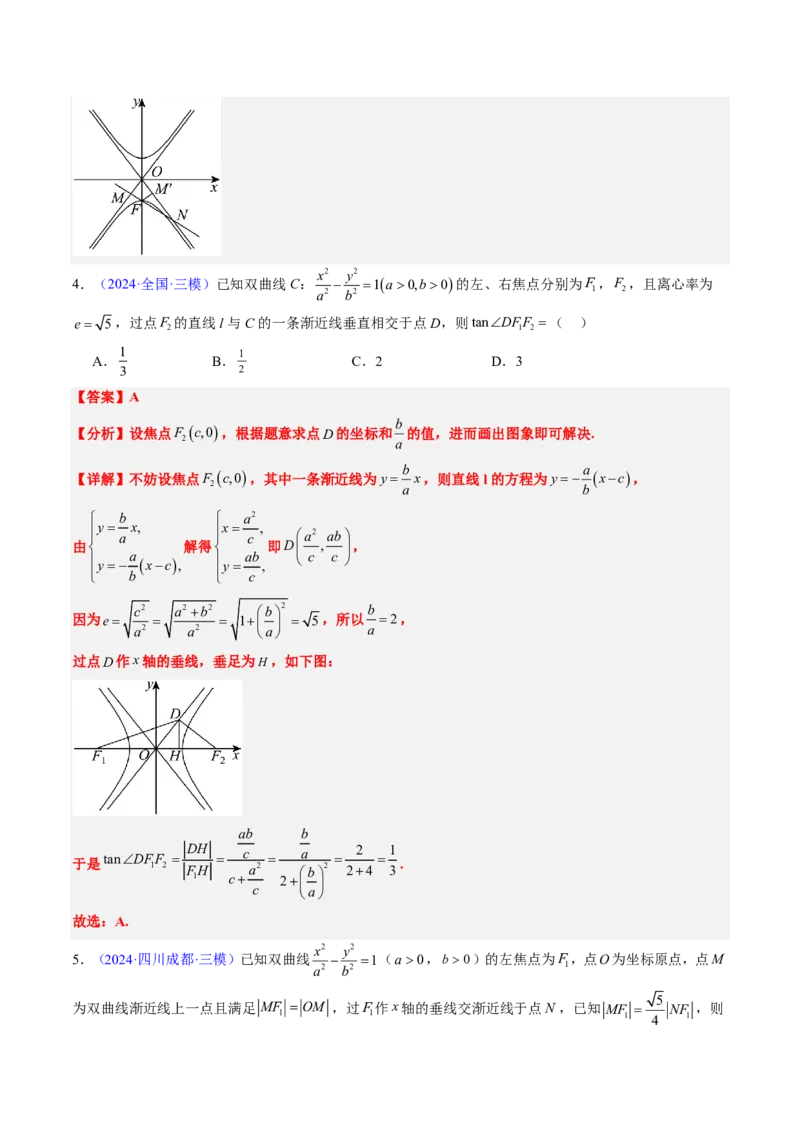cid:60)(cid:42)(cid:64)(cid:63)(cid:46)(cid:41)F (cid:47)(cid:281)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:170)(cid:36)FM¢(cid:50)M¢(cid:45)(cid:282)(cid:283)(cid:34)(cid:35)(cid:36)(cid:37)(cid:147)(cid:190)(cid:188)(cid:284)(cid:131)(cid:80)(cid:81) (cid:45)(cid:79)(cid:80)(cid:81)(cid:57)(cid:58)(cid:59). b (cid:60)(cid:86)(cid:87)(cid:63)(cid:46)(cid:41)F (cid:47)(cid:281)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:37)(cid:170)(cid:36)FM¢(cid:50)M¢(cid:45)(cid:65)(cid:147)(cid:190)(cid:188)(cid:80)(cid:81) FM = FM¢(cid:45) uuur uuuur π (cid:65)NF =2FM (cid:45)(cid:56)(cid:261) NF =2 FM¢ (cid:45)(cid:56)ÐFNM¢= (cid:45) 6 π π a æπ πö π (cid:100)ÐNOM = (cid:45)(cid:100)ÐNOF = (cid:45)(cid:100) =tanç - ÷=tan = 3(cid:45) 3 6 b è2 6ø 3 2 c b2 æ 3ö 2 3 (cid:79)e= = 1+ = 1+ç ÷ = . a a2 ç è 3 ÷ ø 3 (cid:100)(cid:20)(cid:10)A.x2 y2 4(cid:26)(cid:27)2024·(cid:285)(cid:286)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C(cid:10) - =1a>0,b>0(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F(cid:45)F (cid:45)(cid:150)(cid:57)(cid:58)(cid:59)(cid:44) a2 b2 1 2 e= 5(cid:45)(cid:46)(cid:41)F (cid:37)(cid:52)(cid:36)l(cid:110)C(cid:37)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:170)(cid:52)(cid:93)(cid:53)(cid:50)(cid:41)D(cid:45)(cid:56)tanÐDFF =(cid:27) (cid:32) 2 1 2 1 1 A(cid:26) B(cid:26) C(cid:26)2 D(cid:26)3 3 2 (cid:60)(cid:61)(cid:62)(cid:63)A b (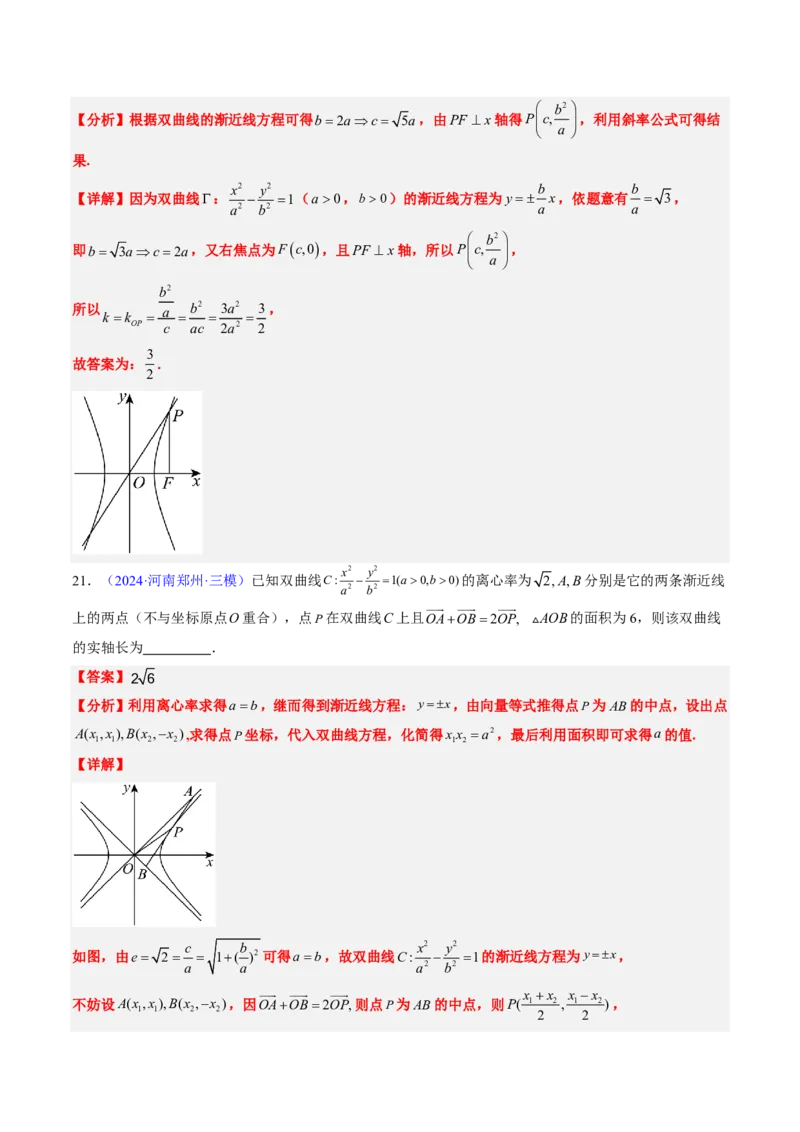cid:60)(cid:42)(cid:64)(cid:63)(cid:33)(cid:40)(cid:41)F c,0(cid:45)(cid:264)(cid:265)(cid:21)(cid:66)(cid:73)(cid:41)D(cid:37)(cid:91)(cid:92)(cid:165) (cid:37)(cid:83)(cid:45)(cid:121)(cid:85)(cid:67)(cid:68)(cid:71)(cid:72)(cid:79)(cid:80)(cid:87)(cid:287). 2 a b a (cid:60)(cid:86)(cid:87)(cid:63)(cid:171)(cid:288)(cid:33)(cid:40)(cid:41)F c,0(cid:45)(cid:214)(cid:133)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:44)y= x(cid:45)(cid:56)(cid:52)(cid:36)l(cid:37)(cid:106)(cid:126)(cid:44)y=- x-c(cid:45) 2 a b ì b ì a2 ï ï y= a x, ï ï x= c , æa2 abö (cid:65)í (cid:87)(cid:81)í (cid:79)Dç , ÷(cid:45) ï y=- a x-c, ï y= ab , è c c ø ïî b ïî c c2 a2+b2 æbö 2 b (cid:140)(cid:44)e= = = 1+ç ÷ = 5(cid:45)(cid:102)(cid:103) =2(cid:45) a2 a2 èaø a (cid:46)(cid:41)D(cid:47)x(cid:51)(cid:37)(cid:170)(cid:36)(cid:45)(cid:170)(cid:227)(cid:44)H(cid:45)(cid:228)(cid:175)(cid:71)(cid:10) ab b DH c a 2 1 (cid:50)(cid:164)tanÐDFF = = = = = . 1 2 FH a2 æbö 2 2+4 3 1 c+ 2+ç ÷ c èaø (cid:100)(cid:20)(cid:10)A. x2 y2 5(cid:26)(cid:27)2024·(cid:263)(cid:289)(cid:178)(cid:290)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36) - =1(cid:27)a>0(cid:45)b>0(cid:32)(cid:37)(cid:38)(cid:40)(cid:41)(cid:44)F(cid:45)(cid:41)O(cid:44)(cid:91)(cid:92)(cid:191)(cid:41)(cid:45)(cid:41)M a2 b2 1 5 (cid:44)(cid:34)(cid:35)(cid:36)(cid:198)(cid:199)(cid:36)(cid:105)(cid:22)(cid:41)(cid:150)(cid:226)(cid:227) MF = OM (cid:45)(cid:46)F(cid:47)x(cid:51)(cid:37)(cid:170)(cid:36)(cid:53)(cid:198)(cid:199)(cid:36)(cid:50)(cid:41)N (cid:45)(cid:104)(cid:88) MF = NF (cid:45)(cid:56) 1 1 1 4 1(cid:214)(cid:57)(cid:58)(cid:59)(cid:44)(cid:27) (cid:32) A(cid:26)2 B(cid:26) 3 C(cid:26) 5 D(cid:26) 5 2 (cid:60)(cid:61)(cid:62)(cid:63)D (cid:60)(cid:42)(cid:64)(cid:63)(cid:33)M,N(cid:54)(cid:41)(cid:37)(cid:91)(cid:92)(cid:45)(cid:276)(cid:216)(cid:108)(cid:109)(cid:54)(cid:41)(cid:213)(cid:144)(cid:57)(cid:7)(cid:118)(cid:256)(cid:106)(cid:126)(cid:73)(cid:87)(cid:79)(cid:80). (cid:60)(cid:86)(cid:87)(cid:63) MF = OM (cid:45)(cid:100)(cid:41)M (cid:95)OF (cid:37)(cid:170)(cid:52)(cid:48)(cid:42)(cid:36)(cid:105)(cid:45) 1 1 c (cid:56)(cid:41)M (cid:37)(cid:90)(cid:91)(cid:92)(cid:44)- (cid:45)(cid:150)(cid:46)F(cid:47)x(cid:51)(cid:37)(cid:170)(cid:36)(cid:53)(cid:198)(cid:199)(cid:36)(cid:50)(cid:41)N (cid:45) 2 1 æ c ö (cid:100)(cid:33)(cid:41)Mç- ,y ÷,N-c,y (cid:45) è 2 1ø 2 b bc bc (cid:171)(cid:288)(cid:33)M,N(cid:291)(cid:95)y= x(cid:105)(cid:45)(cid:56)y =- ,y =- (cid:45) a 1 2a 2 a QMF = 5 NF (cid:45)F-c,0(cid:45) 1 4 1 \ æ ç- c +c ö ÷ 2 + æ ç- bcö ÷ 2 = 5 é ê -c+c2+ æ ç- bcö ÷ 2ù ú(cid:45)(cid:79) c2 = 1 æ ç bcö ÷ 2 (cid:45)4a2 =b2(cid:45) è 2 ø è 2aø 16êë è a ø úû 4 16è a ø b c æbö 2 \ =2(cid:45)(cid:100)(cid:57)(cid:58)(cid:59)(cid:44)e= = 1+ç ÷ = 1+4 = 5. a a èaø (cid:100)(cid:20)(cid:10)D. x2 y2 6(cid:26)(cid:27)2024·(cid:292)(cid:293)(cid:294)(cid:295)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(a>0,b>0)(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F,F (cid:45)(cid:34)(cid:35)(cid:36)(cid:37)(cid:39)(cid:161)(cid:105) a2 b2 1 2 π (cid:261)(cid:22)(cid:41)A,AF (cid:110)(cid:34)(cid:35)(cid:36)(cid:37)(cid:38)(cid:161)(cid:53)(cid:50)(cid:41)B(cid:45)(cid:36)(cid:169)AF (cid:37)(cid:133)(cid:41)(cid:44)M (cid:45)(cid:150)(cid:226)(cid:227)BM ^ AF (cid:45)(cid:55)ÐFAF = (cid:45)(cid:56)(cid:34)(cid:35) 1 2 2 1 2 3 (cid:36)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44)(cid:27) (cid:32) A(cid:26)2 B(cid:26) 6 C(cid:26) 7 D(cid:26) 13 (cid:60)(cid:61)(cid:62)(cid:63)C (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:167)(cid:176)(cid:81)(cid:137)ABF (cid:164)(cid:94)(cid:296)(cid:89)(cid:223)(cid:186)(cid:45)(cid:33)(cid:137)ABF (cid:37)(cid:296)(cid:197)(cid:44)m(cid:45)(cid:74)(cid:75)(cid:34)(cid:35)(cid:36)(cid:77)(cid:78)(cid:81) 2 2 AF =6a, AF =4a(cid:45)(cid:95)(cid:137)AFF (cid:133)(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:73)(cid:81)(cid:57)(cid:58)(cid:59). 1 2 1 2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:140)(cid:44)M (cid:164)(cid:36)(cid:169)AF (cid:37)(cid:133)(cid:41)(cid:45)(cid:150)BM ^ AF (cid:45)(cid:102)(cid:103) AB = BF (cid:45) 2 2 2 π (cid:101)ÐFAF = (cid:45)(cid:102)(cid:103)(cid:137)ABF (cid:164)(cid:94)(cid:296)(cid:89)(cid:223)(cid:186)(cid:45) 1 2 3 2 (cid:33)(cid:137)ABF (cid:37)(cid:296)(cid:197)(cid:44)m(cid:45)(cid:65)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:88)(cid:45) AF - AF =2a(cid:45) BF - BF =2a(cid:45) 2 1 2 2 1 (cid:102)(cid:103) AF =m+2a, BF =m-2a(cid:45) 1 1 (cid:101) AF - BF = AB =m(cid:45)(cid:102)(cid:103)m+2a-(m-2a)=m(cid:45)(cid:79)m=4a(cid:45) 1 1 (cid:102)(cid:103) AF =6a, AF =4a(cid:45) 1 2 π (cid:95)(cid:137)AFF (cid:133)(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:88)(cid:45) FF 2 = AF 2+ AF 2-2 AF AF cos (cid:45) 1 2 1 2 1 2 1 2 3 1 (cid:102)(cid:103)(2c)2 =36a2+16a2-2´6a´4a´ =28a2 2 c (cid:79)c= 7a(cid:45)(cid:102)(cid:103)(cid:57)(cid:58)(cid:59)e= = 7. a (cid:100)(cid:20)(cid:10)C x2 y2 7(cid:26)(cid:27)2024·(cid:297)(cid:298)(cid:299)(cid:289)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)E(cid:10) - =1a>0,b>0(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F(cid:45)F (cid:45)(cid:46)(cid:41)F (cid:37) a2 b2 1 2 2 (cid:52)(cid:36)(cid:110)(cid:34)(cid:35)(cid:36)E(cid:37)(cid:39)(cid:161)(cid:53)(cid:50)A(cid:45)B(cid:54)(cid:41)(cid:45)(cid:55) AB = AF (cid:45)(cid:150)(cid:34)(cid:35)(cid:36)E(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 2(cid:45)(cid:56)cosÐBAF =(cid:27) (cid:32) 1 1 3 7 3 1 1 A(cid:26) B(cid:26)- C(cid:26) D(cid:26)- 8 4 8 8 (cid:60)(cid:61)(cid:62)(cid:63)D (cid:60)(cid:42)(cid:64)(cid:63)(cid:65)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:74)(cid:75)(cid:104)(cid:88)(cid:167)(cid:176)(cid:73)(cid:81) BF =2a(cid:45)(cid:84)(cid:85)(cid:184)(cid:81) BF =4a(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:73)(cid:81)cosÐBF F(cid:45) 2 1 2 1 (cid:65)(cid:300)(cid:301)(cid:7)(cid:118)(cid:81)cosÐAF F(cid:45)(cid:33) AF =m(cid:45)(cid:56) AF =m+2a(cid:45)(cid:184)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:73)(cid:81)m(cid:45)(cid:84)(cid:85)(cid:108)(cid:109)(cid:122)(cid:123)(cid:77)(cid:15)(cid:73)(cid:87)(cid:79) 2 1 2 1 (cid:80). (cid:60)(cid:86)(cid:87)(cid:63)(cid:140)(cid:44)(cid:34)(cid:35)(cid:36)E(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 2(cid:45)(cid:102)(cid:103)c= 2a(cid:45)(cid:140)(cid:44) AB = AF (cid:45) 1 (cid:102)(cid:103) BF = AB - AF = AF - AF =2a(cid:45) 2 2 1 2 (cid:65)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:80)(cid:81) BF - BF = BF -2a=2a(cid:45) 1 2 1 (cid:102)(cid:103) BF =4a=2 BF (cid:45) 1 2(cid:95)(cid:137)BFF (cid:133)(cid:45) 1 2 BF 2+ FF 2- BF 2 4a2+8a2-16a2 2 (cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:81)cosÐBF F = 2 1 2 1 = =- (cid:45) 2 1 2 BF × FF 2´2a´2 2a 4 2 1 2 2 (cid:95)(cid:137)AFF (cid:133)(cid:45)cosÐFF A=-cosÐFF B= (cid:45) 1 2 1 2 1 2 4 (cid:33) AF =m(cid:45)(cid:56) AF =m+2a(cid:45) 2 1 (cid:65) AF 2 = FF 2+ AF 2-2 FF AF cosÐFF A(cid:81) 1 1 2 2 1 2 2 1 2 2 2 8a (2a+m)2 =(2 2a)2+m2-2´2 2a×m× (cid:45)(cid:87)(cid:81)m= a(cid:45)(cid:102)(cid:103) AF = (cid:45) 4 3 1 3 64a2 64a2 (cid:102)(cid:103)cosÐBAF = AF 1 2+ AB 2- BF 1 2 = 9 + 9 -16a2 =- 1 . 1 2 AF × AB 8a 8a 8 1 2´ ´ 3 3 (cid:100)(cid:20)(cid:10)D. . x2 y2 8(cid:26)(cid:27)2024·(cid:302)(cid:303)(cid:304)(cid:249)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)F(cid:45)F (cid:42)(cid:43)(cid:164)(cid:34)(cid:35)(cid:36) - =1a>0(cid:45)b>0(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:45)(cid:41)O(cid:44)(cid:91)(cid:92) 1 2 a2 b2 uuur uuuur (cid:191)(cid:41)(cid:45)(cid:46)F(cid:37)(cid:52)(cid:36)(cid:42)(cid:43)(cid:53)(cid:34)(cid:35)(cid:36)(cid:38)(cid:23)(cid:39)(cid:54)(cid:161)(cid:50)A(cid:45)B(cid:54)(cid:41)(cid:45)(cid:41)C(cid:95)x(cid:51)(cid:105)(cid:45)CB=3F A(cid:45)BF (cid:48)(cid:42)ÐFBC(cid:45) 1 2 2 1 (cid:214)(cid:133)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:110)(cid:36)(cid:169)AB(cid:53)(cid:50)(cid:41)P(cid:45)(cid:56)sinÐPOF =(cid:27) (cid:32) 2 41 42 43 2 11 A(cid:26) B(cid:26) C(cid:26) D(cid:26) 7 7 7 7 (cid:60)(cid:61)(cid:62)(cid:63)B uuur uuuur (cid:60)(cid:42)(cid:64)(cid:63)(cid:65)CB=3F A(cid:80)(cid:81)VFAF ~VFBC(cid:45)(cid:74)(cid:75)(cid:223)(cid:48)(cid:42)(cid:36)(cid:37)(cid:188)(cid:189)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:80)(cid:81) 2 1 2 1 BF = AF = AB =4a (cid:45)(cid:84)(cid:85)(cid:80)(cid:81)ÐABF =60°(cid:45)(cid:95)VFBF (cid:133)(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:80)(cid:81)c= 7a(cid:45)(cid:121)(cid:85)(cid:80)(cid:81) 2 2 2 1 2 b 42 b = (cid:45)(cid:85)tanÐPOF = (cid:45)(cid:84)(cid:85)(cid:80)(cid:73)(cid:87). c 7 2 a (cid:60)(cid:86)(cid:87)(cid:63)uuur uuuur (cid:228)(cid:71)QCB=3F A , \VFAF ~VFBC , |FF |=2c , |CF |=4c(cid:45) 2 1 2 1 1 2 2 (cid:33)|AF |=t,(cid:56)|BF |=3t,|AB|=2t(cid:45) 1 1 |BC| |FC| QBF (cid:48)(cid:42)ÐFBC ,\ = 2 =2 , 2 1 |BF | |FF | 1 1 2 1 \|BC|=2|BF |=6t , AF = BC =2t , 1 2 3 (cid:65)(cid:34)(cid:35)(cid:36)(cid:77)(cid:78)(cid:80)(cid:88)(cid:305)AF(cid:305)-(cid:305)AF(cid:305)=t=2a(cid:45) BF - BF =2a, 2 1 1 2 \BF = AF = AB =4a (cid:45)(cid:79)ÐABF =60°, 2 2 2 (cid:95)VFBF (cid:133)(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:88) 1 2 FB|2 + F B|2 -|FF |2 (6a)2+(4a)2-(2c)2 cosÐFBF = 1 2 1 2 = 1 2 2 FB × F B 2×6a×4a 1 2 b 42 (cid:16)(cid:306)(cid:81)c= 7a , (cid:65)a2+b2 =c2(cid:81) = , c 7 b b 42 (cid:171)(cid:288)(cid:139)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:110)(cid:36)(cid:169)AB(cid:37)(cid:53)(cid:41)P(cid:95)(cid:76)(cid:22)(cid:72)(cid:96)(cid:45)(cid:56)tanÐPOF = , \sinÐPOF = = . 2 a 2 c 7 (cid:100)(cid:20)(cid:10)B uuur uuuur (cid:60)(cid:41)(cid:307)(cid:63)(cid:3)(cid:308)(cid:41)(cid:41)(cid:307)(cid:10)(cid:156)(cid:309)(cid:21)(cid:37)(cid:3)(cid:308)(cid:164)(cid:65)CB=3F A(cid:80)(cid:81)VFAF ~VFBC(cid:45)(cid:74)(cid:75)(cid:223)(cid:48)(cid:42)(cid:36)(cid:37)(cid:188)(cid:189)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37) 2 1 2 1 (cid:77)(cid:78)(cid:80)(cid:81) BF = AF = AB =4a (cid:45)(cid:84)(cid:85)(cid:80)(cid:81)ÐABF =60°. 2 2 2 9(cid:26)(cid:27)2024·(cid:310)(cid:311)(cid:312)(cid:293)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)F(cid:45)F (cid:164)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:7)(cid:206)(cid:40)(cid:41)(cid:45)P(cid:164)(cid:313)(cid:314)(cid:37)(cid:22)(cid:143)(cid:7)(cid:206)(cid:41)(cid:45)(cid:150) 1 2 π ÐFPF = (cid:45)(cid:55)(cid:267)(cid:268)(cid:37)(cid:57)(cid:58)(cid:59)(cid:44)e (cid:45)(cid:34)(cid:35)(cid:36)(cid:37)(cid:57)(cid:58)(cid:59)(cid:44)e (cid:45)(cid:56)e2+e2(cid:37)(cid:221)(cid:151)(cid:83)(cid:44)(cid:27) (cid:32) 1 2 3 1 2 1 2 5+ 3 2+ 3 A(cid:26)3+ 3 B(cid:26) C(cid:26) D(cid:26)4 2 2 (cid:60)(cid:61)(cid:62)(cid:63)C x2 y2 x2 y2 (cid:60)(cid:42)(cid:64)(cid:63)(cid:33)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:106)(cid:126)(cid:42)(cid:43)(cid:44)(cid:10) + =1(cid:45) - =1(cid:45)(cid:315)(cid:81)a2-b2 =a2+b2 =c2(cid:45)(cid:33) a2 b2 a2 b2 1 1 2 2 1 1 2 2 PF =m, PF =n(cid:45)(cid:108)(cid:109)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:81)(cid:82)m=a -a ,n=a +a (cid:45)(cid:276)(cid:216)(cid:95)(cid:137)PFF (cid:133)(cid:45)(cid:108)(cid:109)(cid:122)(cid:123)(cid:77)(cid:15) 1 2 1 2 1 2 1 2 1 3 (cid:81)(cid:82) + =4(cid:45)(cid:276)(cid:216)(cid:108)(cid:109)(cid:316)(cid:317)(cid:171)(cid:94)(cid:118)(cid:73)(cid:87). e2 e2 1 2(cid:60)(cid:86)(cid:87)(cid:63)(cid:87)(cid:10)(cid:228)(cid:71)(cid:102)(cid:158)(cid:10) x2 y2 x2 y2 (cid:33)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:106)(cid:126)(cid:42)(cid:43)(cid:44)(cid:10) + =1(cid:45) - =1(cid:45) a2 b2 a2 b2 1 1 2 2 (cid:65)(cid:21)(cid:66)(cid:81)a2-b2 =a2+b2 =c2(cid:45) 1 1 2 2 (cid:33) PF =m, PF =n(cid:45)(cid:56)m+n=2a,n-m=2a (cid:45) 1 2 1 2 (cid:87)(cid:81)m=a -a ,n=a +a (cid:45) 1 2 1 2 (cid:95)(cid:137)PFF (cid:133)(cid:45)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:81)(cid:10) FF 2 = PF 2+ PF 2-2 PF × PF ×cosÐFPF (cid:45) 1 2 1 2 1 2 1 2 1 2 (cid:79)2c2 =a -a 2+a +a 2-a -a a +a (cid:45)(cid:16)(cid:306)(cid:81)4c2 =a2+3a2(cid:45) 1 2 1 2 1 2 1 2 1 2 1 3 (cid:56) + =4(cid:45) e2 e2 1 2 (cid:102)(cid:103)e2+e2 = 1 e2+e2 æ ç 1 + 3 ö ÷= 1æ ç e 2 2 + 3e 1 2 +4 ö ÷(cid:45) 1 2 4 1 2 èe2 e2 ø 4èe2 e2 ø 1 2 1 2 1 æ e2 3e2 ö 2+ 3 ³ ç2 2 × 1 +4÷= (cid:45) 4ç e2 e2 ÷ 2 è 1 2 ø e2 3e2 (cid:162)(cid:150)(cid:160)(cid:162) 2 = 1 (cid:45)(cid:79)e2 = 3e2(cid:163)(cid:45)(cid:94)(cid:9)(cid:178)(cid:179)(cid:132) e2 e2 2 1 1 2 (cid:100)(cid:20)(cid:10)C x2 y2 10(cid:26)(cid:27)2024·(cid:252)(cid:253)(cid:318)(cid:249)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36) - =1a,b>0(cid:105)(cid:172)(cid:95)(cid:3)(cid:50)(cid:191)(cid:41)(cid:133)(cid:58)(cid:147)(cid:190)(cid:37)(cid:54)(cid:41)A(cid:45)B(cid:45)(cid:103)(cid:187)(cid:34) a2 b2 (cid:35)(cid:36)(cid:105)(cid:37)(cid:281)(cid:22)(cid:41)C(cid:45)(cid:262)(cid:81)VABC(cid:44)(cid:273)(cid:89)(cid:223)(cid:186)(cid:45)(cid:56)(cid:319)(cid:34)(cid:35)(cid:36)(cid:57)(cid:58)(cid:59)(cid:37)(cid:320)(cid:83)(cid:193)(cid:194)(cid:164)(cid:27) (cid:32) A(cid:26)  2,+¥  B(cid:26)  3,+¥  C(cid:26)2,+¥ D(cid:26) æ ç 2 3 ,+¥ ö ÷ ç ÷ è 3 ø (cid:60)(cid:61)(cid:62)(cid:63)A (cid:60)(cid:42)(cid:64)(cid:63)(cid:33)(cid:41)Ax,y(cid:45)(cid:56)(cid:80)(cid:320)C  - 3y, 3x  (cid:45)(cid:98)(cid:99)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:138)(cid:15)(cid:80)(cid:81) y2 = 3a2+b2 (cid:45)(cid:74)(cid:75)(cid:198)(cid:199)(cid:36)(cid:256)(cid:118)(cid:73) x2 a2+3b2 (cid:87)(cid:79)(cid:80). b (cid:60)(cid:86)(cid:87)(cid:63)(cid:65)(cid:21)(cid:66)(cid:80)(cid:88)(cid:10)(cid:34)(cid:35)(cid:36)(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=± x(cid:45) a(cid:33)(cid:41)Ax,y(cid:45)(cid:56)(cid:80)(cid:320)C  - 3y, 3x  (cid:45) ìx2 y2 ï - =1 ïa2 b2 y2 3a2+b2 b2 (cid:56)í (cid:45)(cid:138)(cid:15)(cid:81) = < (cid:45) ï3y2 3x2 x2 a2+3b2 a2 - =1 ïî a2 b2 c2 c c2 (cid:87)(cid:81)b2 >a2(cid:45)(cid:79)c2-a2 >a2(cid:45)(cid:80)(cid:81) >2(cid:45)(cid:56)e= = > 2(cid:45) a2 a a2   (cid:102)(cid:103)(cid:319)(cid:34)(cid:35)(cid:36)(cid:57)(cid:58)(cid:59)(cid:37)(cid:320)(cid:83)(cid:193)(cid:194)(cid:164) 2,+¥ (cid:26) (cid:100)(cid:20)(cid:10)A. (cid:60)(cid:41)(cid:307)(cid:63)(cid:3)(cid:308)(cid:41)(cid:41)(cid:307)(cid:10)1.(cid:321)(cid:322)(cid:33)(cid:41)(cid:10)(cid:33)(cid:41)Ax,y(cid:45)(cid:264)(cid:265)(cid:170)(cid:52)(cid:165)(cid:197)(cid:323)(cid:3)(cid:202)(cid:80)(cid:320)C  - 3y, 3x  (cid:132) y2 b2 2.(cid:264)(cid:265)(cid:198)(cid:199)(cid:36)(cid:37)(cid:114)(cid:115)(cid:66)(cid:78)(cid:80)(cid:81)(cid:10) < . x2 a2 (cid:127)(cid:23)(cid:324)(cid:20)(cid:21) x2 y2 11(cid:26)(cid:27)2024·(cid:312)(cid:325)(cid:326)(cid:327)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(cid:45)(cid:56)(cid:27) (cid:32) l+6 3-l A(cid:26)l(cid:37)(cid:320)(cid:83)(cid:193)(cid:194)(cid:164)(-6,3) B(cid:26)C(cid:37)(cid:40)(cid:41)(cid:80)(cid:95)x(cid:51)(cid:105)(cid:328)(cid:80)(cid:95)y(cid:51)(cid:105) C(cid:26)C(cid:37)(cid:40)(cid:144)(cid:44)6 D(cid:26)C(cid:37)(cid:57)(cid:58)(cid:59)e(cid:37)(cid:320)(cid:83)(cid:193)(cid:194)(cid:44)(1,3) (cid:60)(cid:61)(cid:62)(cid:63)AC (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:37)(cid:329)(cid:330)(cid:45)(cid:315)(cid:50)(cid:73)(cid:81)-60(cid:45)(cid:87)(cid:81)-60,3-l>0(cid:45)\C(cid:37)(cid:40)(cid:41)(cid:208)(cid:331)(cid:95)x(cid:51)(cid:105)(cid:45)(cid:100)B(cid:258)(cid:259)(cid:132) (cid:147)(cid:50)C(cid:45)(cid:33)C(cid:37)(cid:274)(cid:40)(cid:144)(cid:44)c(c>0)(cid:45)(cid:56)c2 =l+6+3-l=9(cid:45)\c=3(cid:45)(cid:79)(cid:40)(cid:144)(cid:44)2c=6(cid:45)(cid:100)C(cid:273)(cid:185)(cid:132) 3 (cid:147)(cid:50)D(cid:45)(cid:57)(cid:58)(cid:59)e= (cid:45)Q-60,b>0(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F(cid:45)F (cid:45)(cid:46)(cid:41)F a2 b2 1 2 1 (cid:37)(cid:52)(cid:36)(cid:110)C(cid:37)(cid:38)(cid:161)(cid:93)(cid:53)(cid:50)P(cid:45)Q(cid:54)(cid:41)(cid:45)(cid:55)PQ^PF (cid:45)(cid:150)4 PQ =3 PF (cid:45)(cid:56)(cid:27) (cid:32) 2 2 uuur uuur A(cid:26) PQ =2a B(cid:26)PF =-2QF 1 1 17 C(cid:26)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) D(cid:26)(cid:52)(cid:36)PQ(cid:37)(cid:333)(cid:59)(cid:44)±4 3 (cid:60)(cid:61)(cid:62)(cid:63)ACD (cid:60)(cid:42)(cid:64)(cid:63)(cid:33) PF =x(cid:45) QF = y(cid:45)(cid:74)(cid:75)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:110)(cid:119)(cid:120)(cid:77)(cid:15)(cid:80)(cid:103)(cid:73)(cid:81)x,y(cid:37)(cid:83)(cid:45)(cid:79)(cid:80)(cid:271)(cid:272)(cid:68)A(cid:45)B(cid:20)(cid:270)(cid:132) 1 1 (cid:184)(cid:74)(cid:75)(cid:119)(cid:120)(cid:77)(cid:15)(cid:80)(cid:103)(cid:73)(cid:81)a,c(cid:37)(cid:3)(cid:202)(cid:45)(cid:184)(cid:73)(cid:68)(cid:57)(cid:58)(cid:59)(cid:132)(cid:73)(cid:52)(cid:36)(cid:37)(cid:333)(cid:59)(cid:45)(cid:95)(cid:52)(cid:223)(cid:89)(cid:223)(cid:186)(cid:133)(cid:45)(cid:109)(cid:333)(cid:59)(cid:37)(cid:77)(cid:78)(cid:73)(cid:273) (cid:207)(cid:83)(cid:80)(cid:103)(cid:73)(cid:81)(cid:52)(cid:36)(cid:37)(cid:333)(cid:59). (cid:60)(cid:86)(cid:87)(cid:63)(cid:228)(cid:71)(cid:45)(cid:65)4 PQ =3 PF (cid:45)(cid:80)(cid:33) PQ =3m(cid:45) PF =4m. 2 2 (cid:140)(cid:44)PQ^PF (cid:45)(cid:102)(cid:103) QF =5m. 2 2 2a (cid:33) PF =x(cid:45) QF = y(cid:45)(cid:56)4m-x=2a(cid:45)5m-y=2a(cid:45)x+y=3m(cid:45)(cid:87)(cid:81)m= (cid:45) 1 1 3 2a 4a (cid:56)x= (cid:45)y= (cid:45) 3 3 uuur uuur (cid:102)(cid:103) PQ =2a(cid:45)(cid:100)A(cid:20)(cid:270)(cid:273)(cid:185)(cid:132)QF =2FP(cid:45)(cid:100)B(cid:20)(cid:270)(cid:258)(cid:259)(cid:132) 1 1 4a2 64a2 c2 17 (cid:95)(cid:137)PFF (cid:133)(cid:45)(cid:65) PF 2+ PF 2 = FF 2(cid:45)(cid:81) + =4c2(cid:45)(cid:56) = (cid:45) 1 2 1 2 1 2 9 9 a2 9 17 (cid:84)(cid:85)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) (cid:45)(cid:100)C(cid:20)(cid:270)(cid:273)(cid:185). 3 PF (cid:101)tanÐPFF = 2 =4(cid:45)(cid:102)(cid:103)(cid:52)(cid:36)PQ(cid:37)(cid:333)(cid:59)(cid:44)±4(cid:45)(cid:100)D(cid:20)(cid:270)(cid:273)(cid:185). 1 2 PF 1 (cid:100)(cid:20)(cid:10)ACD. x2 y2 13(cid:26)(cid:27)2024·(cid:334)(cid:249)(cid:334)(cid:294)·(cid:89)(cid:250)(cid:32)(cid:34)(cid:35)(cid:36)C: - =1(a>0,b>0)(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)(cid:41)F,F (cid:45)(cid:333)(cid:59)(cid:44)(cid:273)(cid:37)(cid:198)(cid:199) a2 b2 1 2 (cid:36)(cid:44)l (cid:45)(cid:46)(cid:41)F (cid:47)(cid:52)(cid:36)l (cid:37)(cid:170)(cid:36)(cid:45)(cid:170)(cid:227)(cid:44)(cid:41)A(cid:45)(cid:53)(cid:34)(cid:35)(cid:36)(cid:50)(cid:41)P(cid:45)(cid:33)(cid:41)M (cid:164)(cid:34)(cid:35)(cid:36)C(cid:105)(cid:239)(cid:66)(cid:22)(cid:41)(cid:45)(cid:55) 1 2 1 2 4 PF = AF ,S = (cid:45)(cid:56)(cid:27) (cid:32) 2 3 2 VPF1F2 3 A(cid:26)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 5x2 B(cid:26)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:206)(cid:335)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:44)y2- =1 4 MF æ 3+ 5ù C(cid:26)(cid:162)(cid:41)M (cid:200)(cid:50)(cid:34)(cid:35)(cid:36)C(cid:39)(cid:161)(cid:163)(cid:45) 1 Îç1, ú MF è 2 û 2 4 D(cid:26)(cid:41)M (cid:82)(cid:54)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:212)(cid:113)(cid:44) 5 (cid:60)(cid:61)(cid:62)(cid:63)ACD (cid:60)(cid:42)(cid:64)(cid:63)(cid:108)(cid:109)(cid:89)(cid:223)(cid:186)(cid:141)(cid:113)(cid:7)(cid:118)(cid:81)ab=2(cid:45)(cid:184)(cid:108)(cid:109)(cid:122)(cid:123)(cid:77)(cid:15)(cid:81)b=2a(cid:45)(cid:56)(cid:87)(cid:68)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:45)(cid:184)(cid:108)(cid:109)(cid:57)(cid:58)(cid:59)(cid:77)(cid:78) MF 2 (cid:165)(cid:206)(cid:335)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:37)(cid:203)(cid:78)(cid:79)(cid:80)(cid:271)(cid:272)AB(cid:132)(cid:147)C(cid:45)(cid:284)(cid:131)(cid:81) 1 =1+ (cid:45)(cid:184)(cid:264)(cid:265) MF ³ 5-1(cid:37)(cid:193)(cid:194)(cid:79)(cid:80)(cid:271) MF MF 2 2 2 (cid:272)(cid:132)(cid:147)D(cid:45)Mx ,y (cid:45)(cid:108)(cid:109)(cid:41)(cid:82)(cid:52)(cid:36)(cid:37)(cid:144)(cid:57)(cid:7)(cid:118)(cid:336)(cid:74)(cid:75)(cid:41)(cid:34)(cid:35)(cid:36)(cid:105)(cid:16)(cid:306)(cid:79)(cid:80). 0 0 2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:228)(cid:71)(cid:45)(cid:140)(cid:44) AF =b(cid:45)(cid:102)(cid:103) PF = b(cid:45) 2 2 3 2 a 2ab y = PF sinÐPF F = b× = (cid:45) P 2 2 1 3 c 3c 1 2ab 4 2 (cid:56)S = ×2c× = (cid:45)(cid:102)(cid:103)ab=2(cid:45)(cid:101) PF = b+2a(cid:45) VPF1F2 2 3c 3 1 3 2 2 æ2 ö æ2 ö (cid:95)VPFF(cid:133)(cid:45) cosÐPF F = F 2 F 1 2+ PF 2 2- PF 1 2 = 4c2+ç è3 b÷ ø -ç è3 b+2a÷ ø = b (cid:45) 2 1 2 1 2 F F PF 2 c 2 1 2 2×2c b 3 y2 (cid:16)(cid:306)(cid:81)b=2a(cid:45)(cid:102)(cid:103)a=1,b=2,c= 5(cid:45)(cid:34)(cid:35)(cid:36)C(cid:106)(cid:126)(cid:44)x2- =1(cid:45) 4 c (cid:147)(cid:50)A(cid:45)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) = 5(cid:45)A(cid:273)(cid:185)(cid:132) a y2 (cid:147)(cid:50)B(cid:45)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:206)(cid:335)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:44) -x2 =1(cid:45)B(cid:258)(cid:259)(cid:132) 4 MF MF +2 2 (cid:147)(cid:50)C(cid:45) 1 = 2 =1+ (cid:45)(cid:140)(cid:44) MF ³ 5-1(cid:45) MF MF MF 2 2 2 2 2 3+ 5 MF æ 3+ 5ù (cid:56)1<1+ £ (cid:45)(cid:79) 1 Îç2, ú(cid:45)C(cid:273)(cid:185)(cid:132) ç MF 2 MF è 2 û 2 2 (cid:147)(cid:50)D(cid:45)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=±2x(cid:45)(cid:33)Mx ,y (cid:45) 0 0æ y2 ö 4ç1+ 0 ÷-y2 (cid:41)M (cid:82)(cid:54)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:212)(cid:113)(cid:44) 2x -y -2x -y 4x2-y2 è 4 ø 0 4 (cid:45)D(cid:273)(cid:185)(cid:45) 0 0 × 0 0 = 0 0 = = 5 5 5 5 5 (cid:100)(cid:20)(cid:10)ACD. x2 y2 x2 y2 14(cid:26)(cid:27)2024·(cid:292)(cid:293)(cid:337)(cid:338)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:267)(cid:268) + =1a >b >0(cid:37)(cid:57)(cid:58)(cid:59)(cid:44)e (cid:45)(cid:34)(cid:35)(cid:36) - =1a >0,b >0 a2 b2 1 1 1 a2 b2 2 2 1 1 2 2 (cid:37)(cid:57)(cid:58)(cid:59)(cid:44)e (cid:45)(cid:54)(cid:35)(cid:36)(cid:261)(cid:7)(cid:206)(cid:40)(cid:41)F,F ,P(cid:164)(cid:267)(cid:268)(cid:110)(cid:34)(cid:35)(cid:36)(cid:37)(cid:22)(cid:143)(cid:7)(cid:206)(cid:41)(cid:45)ÐFPF =60o(cid:45)(cid:103)(cid:175)(cid:74)(cid:231)(cid:273)(cid:185)(cid:37) 2 1 2 1 2 (cid:164)(cid:27) (cid:32) A(cid:26)a2-a2 =b2-b2 1 2 1 2 1 3 B(cid:26) + =1 4e2 4e2 1 2 C(cid:26)b2 =3b2 1 2 é2 13 3ù D(cid:26)(cid:55)e Îé 3,2ù(cid:45)(cid:56)e Îê , ú 2 ë û 1 ë 13 3 û (cid:60)(cid:61)(cid:62)(cid:63)BCD (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:40)(cid:144)(cid:93)(cid:94)(cid:80)(cid:271)(cid:272)A(cid:132)(cid:264)(cid:265)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:77)(cid:78)(cid:45)(cid:74)(cid:75)(cid:122)(cid:123)(cid:77)(cid:15)(cid:138)(cid:15)(cid:80)(cid:271)(cid:272)B(cid:132)(cid:264)(cid:265)B(cid:133) 4c2 =a2+3a2(cid:339)(cid:186)(cid:80)(cid:271)(cid:272)C(cid:132)(cid:65)B(cid:133)(cid:74)(cid:231)(cid:45)(cid:74)(cid:75)e (cid:37)(cid:193)(cid:194)(cid:80)(cid:271)(cid:272)D. 1 2 2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:264)(cid:265)(cid:21)(cid:66)(cid:45)(cid:33)F -c,0,F c,0(cid:45) 1 2 ìa2-b2 =c2 (cid:147)(cid:50)A(cid:133)(cid:45)(cid:140)(cid:44)(cid:267)(cid:268)(cid:110)(cid:34)(cid:35)(cid:36)(cid:261)(cid:7)(cid:206)(cid:40)(cid:41)(cid:45)(cid:80)(cid:81)í 1 1 (cid:45)(cid:102)(cid:103)a2-b2 =a2+b2(cid:45) îa2+b2 =c2 1 1 2 2 2 2 (cid:79)a2-a2 =b2+b2(cid:45)(cid:102)(cid:103)A(cid:258)(cid:259)(cid:132) 1 2 1 2 ìïPF - PF =2a (cid:147)(cid:50)B(cid:133)(cid:45)(cid:171)(cid:288)(cid:33)(cid:41)P(cid:95)(cid:76)(cid:22)(cid:72)(cid:96)(cid:45)(cid:65)(cid:267)(cid:268)(cid:165)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:45)(cid:80)(cid:81)í 1 2 2 (cid:45) ïîPF 1 + PF 2 =2a 1 (cid:102)(cid:103) PF =a +a , PF =a -a (cid:45) 1 1 2 2 1 2 (cid:101)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:81) FF 2 = PF 2+ PF 2-2 PF × PF cos60o(cid:45) 1 2 1 2 1 2 (cid:80)(cid:81)4c2 =2a2+2a2-  a2-a 2 =a2+3a2(cid:45) 1 2 1 2 1 2 1 3 a2 3a2 4c2 (cid:102)(cid:103) + = 1 + 2 = =1(cid:45)(cid:102)(cid:103)B(cid:273)(cid:185)(cid:132) 4e2 4e2 4c2 4c2 4c2 1 2 (cid:147)(cid:50)C(cid:133)(cid:45)(cid:65)a2-c2 =3c2-3a2(cid:45)(cid:80)(cid:81)b2 =3b2(cid:45)(cid:102)(cid:103)C(cid:273)(cid:185)(cid:132) 1 2 1 2 1 é1 1ù (cid:147)(cid:50)D(cid:133)(cid:45)(cid:140)(cid:44)e 2 Îé ë 3,2ù û (cid:45)(cid:102)(cid:103) e2 Î ê ë4 , 3 ú û (cid:45) 2 1 3 1 é 13ù é2 13 3ù (cid:65) 4e 1 2 + 4e 2 2 =1(cid:80)(cid:81) e 1 2 Î ê ë 3, 4 ú û (cid:45)(cid:102)(cid:103)e 1 Îê ë 13 , 3 ú û (cid:45)(cid:102)(cid:103)D(cid:273)(cid:185).(cid:100)(cid:20)(cid:10)BCD. x2 y2 15(cid:26)(cid:27)2024·(cid:340)(cid:341)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(a>0)(cid:37)(cid:38)(cid:45)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F,F ,P(cid:44)(cid:34)(cid:35)(cid:36)C(cid:105)(cid:41)(cid:45)(cid:150) a2 16 1 2 (cid:137)PFF (cid:37)(cid:142)(cid:207)(cid:268)(cid:268)(cid:58)(cid:44)I(3,1)(cid:45)(cid:56)(cid:175)(cid:256)(cid:257)(cid:107)(cid:273)(cid:185)(cid:37)(cid:164)(cid:27) (cid:32) 1 2 1 A(cid:26)a=3 B(cid:26)(cid:52)(cid:36)PF (cid:37)(cid:333)(cid:59)(cid:44) 1 4 64 65 C(cid:26)VPFF (cid:37)(cid:342)(cid:197)(cid:44) D(cid:26)(cid:137)PFF (cid:37)(cid:205)(cid:343)(cid:268)(cid:274)(cid:219)(cid:44) 1 z 3 1 2 12 (cid:60)(cid:61)(cid:62)(cid:63)ACD (cid:60)(cid:42)(cid:64)(cid:63)(cid:147)(cid:50)A(cid:45)(cid:264)(cid:265)(cid:89)(cid:223)(cid:186)(cid:110)(cid:214)(cid:142)(cid:207)(cid:268)(cid:188)(cid:189)(cid:74)(cid:75)(cid:34)(cid:35)(cid:36)(cid:77)(cid:78)(cid:79)(cid:80)(cid:73)(cid:87)(cid:132)(cid:264)(cid:265)(cid:104)(cid:88)(cid:167)(cid:176)FA(cid:23)F A(cid:23)IA(cid:103) 1 2 (cid:187)(cid:110)(cid:129)(cid:143)(cid:102)(cid:209)(cid:112)(cid:37)(cid:3)(cid:202)(cid:79)(cid:80)(cid:73)(cid:68)ÐPFA=2ÐIFA(cid:23)ÐPF A=2ÐIF A(cid:165)ÐF PF (cid:45)(cid:121)(cid:85)(cid:80)(cid:128)(cid:125)(cid:73)(cid:68)(cid:52)(cid:36)PF1 1 1 2 2 2 1 PF +PF +FF r (cid:37)(cid:333)(cid:59)(cid:23)(cid:74)(cid:75)(cid:40)(cid:89)(cid:223)(cid:186)(cid:141)(cid:113)(cid:7)(cid:118)S = 1 2 1 2 (cid:81)VPFF (cid:37)(cid:342)(cid:197)(cid:23)(cid:74)(cid:75)(cid:273)(cid:123)(cid:77)(cid:15)(cid:81)(cid:137)PFF (cid:37)(cid:205) VF1PF2 2 1 z 1 2 (cid:343)(cid:268)(cid:274)(cid:219). (cid:60)(cid:86)(cid:87)(cid:63)(cid:228)(cid:71)1(cid:45)(cid:65)(cid:167)(cid:176)(cid:45)(cid:41)P(cid:173)(cid:95)(cid:34)(cid:35)(cid:36)C(cid:37)(cid:39)(cid:161)(cid:105)(cid:45) (cid:33)(cid:268)I (cid:42)(cid:43)(cid:110)(cid:137)PFF (cid:37)(cid:89)(cid:296)(cid:207)(cid:50)(cid:41)M､N､A(cid:45)(cid:56)(cid:65)(cid:21)A3,0(cid:45) 1 2 (cid:150) PM = PN , FM = FA (cid:45) F N = F A (cid:45) 1 1 2 2 (cid:101)Q PF - PF = FM - F N = AF - F A =x +c-c-x =2x =2a 1 2 1 2 1 2 A A A \a=x =3(cid:45)A(cid:20)(cid:270)(cid:273)(cid:185)(cid:132) A IA 1 (cid:65)(cid:20)(cid:270)A(cid:81)F -5,0,F 5,0(cid:45)(cid:344)(cid:343)IF(cid:23)IF (cid:23)IA(cid:45)(cid:56)tanÐIFA= = (cid:45) 1 2 1 2 1 AF 8 12tanÐIFA 16 (cid:102)(cid:103)k =tanÐPFA=tan2ÐIFA= 1 = (cid:45)B(cid:20)(cid:270)(cid:258)(cid:259)(cid:132) PF1 1 1 1-tan2ÐIFA 63 1 4 (cid:220)(cid:15)(cid:45)tanÐPF A=tan2ÐIF A= (cid:45) 2 2 3 12 \tanÐFPF =-tanÐPFA+ÐPF A=- (cid:45) 1 2 1 2 5 ÐFPF 3 \Þtan 1 2 = (cid:45) 2 2 b2 32 S = = (cid:102)(cid:103)(cid:65)(cid:40)(cid:89)(cid:223)(cid:141)(cid:113)(cid:7)(cid:118)(cid:81) VF1PF2 ÐFPF 3 (cid:45) tan 1 2 2 PF +PF +FF r 64 (cid:101)S = 1 2 1 2 (cid:45)(cid:100)(cid:81) PF + PF + FF = (cid:45) VF1PF2 2 1 2 1 2 3 64 \(cid:137)PFF (cid:37)(cid:342)(cid:197)(cid:44) (cid:45)C(cid:20)(cid:270)(cid:273)(cid:185)(cid:132) 1 2 3 12 12 (cid:65)tanÐFPF =- ÞsinÐFPF = (cid:45) 1 2 5 1 2 13 FF 65 (cid:65)(cid:273)(cid:123)(cid:77)(cid:15) 1 2 =2R(cid:81)R= (cid:45)D(cid:20)(cid:270)(cid:273)(cid:185). sinÐFPF 12 1 2 (cid:100)(cid:20)(cid:10)ACD. (cid:60)(cid:41)(cid:307)(cid:63)(cid:3)(cid:308)(cid:41)(cid:307)(cid:10)(cid:73)(cid:52)(cid:36)PF1(cid:37)(cid:333)(cid:59)(cid:23)VPFF (cid:37)(cid:342)(cid:197)(cid:23)(cid:137)PFF (cid:37)(cid:205)(cid:343)(cid:268)(cid:274)(cid:219)(cid:37)(cid:3)(cid:308)(cid:164)(cid:264)(cid:265)(cid:104)(cid:88)(cid:167)(cid:176) 1 z 1 2 FA(cid:23)F A(cid:23)IA(cid:103)(cid:187)(cid:110)(cid:129)(cid:143)(cid:102)(cid:209)(cid:112)(cid:37)(cid:3)(cid:202)(cid:79)(cid:80)(cid:73)(cid:68)ÐPFA=2ÐIFA(cid:23)ÐPF A=2ÐIF A(cid:165)ÐF PF . 1 2 1 1 2 2 2 1 (cid:89)(cid:23)(cid:24)(cid:25)(cid:21) x2 16(cid:26)(cid:27)2024·(cid:302)(cid:325)(cid:345)(cid:249)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: -y2 =1(a>0)(cid:346)(cid:46)(cid:41)(2,1)(cid:45)(cid:56)C(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44) (cid:26) a2 2 (cid:60)(cid:61)(cid:62)(cid:63)y=± x 2 (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:46)(cid:41)(2,1)(cid:73)(cid:68)a(cid:45)(cid:276)(cid:216)(cid:80)(cid:81). x2 4 (cid:60)(cid:86)(cid:87)(cid:63)(cid:140)(cid:44)(cid:34)(cid:35)(cid:36)C: -y2 =1(a>0)(cid:346)(cid:46)(cid:41)(2,1)(cid:45)(cid:102)(cid:103) -1=1(cid:45)(cid:87)(cid:81)a= 2(cid:45) a2 a2b 2 (cid:101)b=1(cid:45)(cid:102)(cid:103)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=± x=± x. a 2 2 (cid:100)(cid:61)(cid:62)(cid:44)(cid:10)y=± x. 2 x2 y2 17(cid:26)(cid:27)2024·(cid:297)(cid:298)(cid:347)(cid:348)(cid:292)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(a>0,b>0)(cid:37)(cid:38)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F(cid:23)F (cid:45)(cid:35)(cid:36)C(cid:105)(cid:37)(cid:41) a2 b2 1 2 uuuur uuuur π M (cid:226)(cid:227)(cid:45)FM×FM =0(cid:45)ÐMFF = (cid:45)(cid:56)(cid:34)(cid:35)(cid:36)(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) (cid:26) 1 2 1 2 6 (cid:60)(cid:61)(cid:62)(cid:63) 3+1/1+ 3 (cid:60)(cid:42)(cid:64)(cid:63)(cid:108)(cid:109) (cid:45)(cid:80)(cid:81) (cid:45) (cid:45)(cid:74)(cid:75)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:45)(cid:79)(cid:80)(cid:73)(cid:81)(cid:34)(cid:35)(cid:36)(cid:37)(cid:57)(cid:58)(cid:59). uuuur uuuur π (cid:60)(cid:86)(cid:87)(cid:63)(cid:140)(cid:44)FM×FM =0(cid:45)ÐMFF = (cid:45)(cid:102)(cid:103)MF ^MF (cid:45) 1 2 1 2 6 1 2 (cid:101)FF = 2c(cid:45)(cid:102)(cid:103)|MF |= 3c(cid:45)|MF |=c(cid:45) 1 2 1 2 (cid:102)(cid:103)|MF |-|MF |= 3c-c=2a(cid:45) 1 2 c 2 (cid:56)e= = = 3+1(cid:45)(cid:79)(cid:34)(cid:35)(cid:36)(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 3+1. a 3-1 (cid:100)(cid:61)(cid:62)(cid:44)(cid:10) 3+1. x2 y2 18(cid:26)(cid:27)2024·(cid:278)(cid:279)(cid:349)(cid:350)(cid:292)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)G: - =1(a>0,b>0)(cid:37)(cid:38)(cid:23)(cid:39)(cid:40)(cid:41)(cid:42)(cid:43)(cid:44)F，F (cid:45)(cid:46)(cid:41)F a2 b2 1 2 2 (cid:37)(cid:52)(cid:36)(cid:110)G(cid:37)(cid:39)(cid:161)(cid:53)(cid:50)A，B(cid:54)(cid:41)(cid:45)(cid:55) AF =8, BF =5,ÐAFB=60°(cid:45)(cid:56)a= (cid:26) 1 1 1 3 (cid:60)(cid:61)(cid:62)(cid:63) /1.5 2 (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:37)(cid:77)(cid:78)(cid:116)(cid:158)(cid:68) AF (cid:45) BF (cid:45)(cid:79)(cid:80)(cid:81)(cid:82) AB (cid:45)(cid:184)(cid:65)(cid:122)(cid:123)(cid:77)(cid:15)(cid:284)(cid:131)(cid:80)(cid:81). 2 2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:128)(cid:21)(cid:66)(cid:46)(cid:41)F (cid:37)(cid:52)(cid:36)(cid:110)G(cid:37)(cid:39)(cid:161)(cid:53)(cid:50)A(cid:45)B(cid:54)(cid:41)(cid:45) 2 (cid:150) AF =8(cid:45) BF =5(cid:45)ÐAFB=60°(cid:45) 1 1 1 (cid:56)00,b>0(cid:37)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:233) a2 b2 (cid:81)(cid:37)(cid:123)(cid:197)(cid:44)2(cid:45)(cid:56)(cid:34)(cid:35)(cid:36)E(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) . (cid:60)(cid:61)(cid:62)(cid:63) 5 5 |b´0±a´ | (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:167)(cid:176)(cid:45)(cid:97)(cid:123)(cid:197)(cid:353)(cid:16)(cid:44)(cid:268)(cid:58)(cid:82)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57) 2 5(cid:45)(cid:121)(cid:85)(cid:80)(cid:81)(cid:68)a(cid:110)c(cid:37)(cid:3)(cid:202)(cid:45) d = = a2+b2 2 (cid:73)(cid:87)(cid:79)(cid:80). x2 y2 (cid:60)(cid:86)(cid:87)(cid:63)(cid:147)(cid:50)(cid:34)(cid:35)(cid:36) - =1(cid:45)(cid:214)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)bx±ay=0(cid:45) a2 b2 5 9 (cid:147)(cid:50)(cid:268)x2+y2-5y+4=0(cid:45)(cid:261)x2+(y- )2 = (cid:45) 2 4 5 3 (cid:268)(cid:58)(cid:44)(0(cid:45))(cid:45)(cid:274)(cid:219)r= (cid:45) 2 2 3 5 (cid:198)(cid:199)(cid:36)(cid:232)(cid:268)(cid:233)(cid:81)(cid:37)(cid:123)(cid:197)(cid:44)2(cid:45)(cid:102)(cid:103)(cid:268)(cid:58)(cid:82)(cid:198)(cid:199)(cid:36)(cid:37)(cid:144)(cid:57)(cid:44) ( )2-12 = (cid:45) 2 2 5 |b´0±a´ | (cid:65)(cid:41)(cid:82)(cid:52)(cid:36)(cid:144)(cid:57)(cid:7)(cid:118)(cid:81)(cid:10) d = 2 = 5(cid:45)(cid:102)(cid:103)4a2 =b2(cid:45) a2+b2 2 c (cid:102)(cid:103)4a2 =c2-a2(cid:45)(cid:87)(cid:81)e= = 5(cid:45)(cid:102)(cid:103)(cid:34)(cid:35)(cid:36)E(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 5. a (cid:100)(cid:61)(cid:62)(cid:44)(cid:10) 5. x2 y2 20(cid:26)(cid:27)2024·(cid:292)(cid:354)(cid:355)(cid:356)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)G(cid:10) - =1(cid:27)a>0(cid:45)b>0(cid:32)(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=± 3x(cid:45)(cid:214)(cid:39) a2 b2 (cid:40)(cid:41)(cid:44)F(cid:45)(cid:55)(cid:52)(cid:36)y=kx(cid:110)G(cid:95)(cid:76)(cid:22)(cid:72)(cid:96)(cid:37)(cid:53)(cid:41)(cid:44)P(cid:150)PF ^x(cid:51)(cid:45)(cid:56)(cid:195)(cid:13)k(cid:37)(cid:83)(cid:44) . 3 (cid:60)(cid:61)(cid:62)(cid:63) 2æ b2 ö (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:80)(cid:81)b=2aÞc= 5a(cid:45)(cid:65)PF ^x(cid:51)(cid:81)Pçc, ÷(cid:45)(cid:108)(cid:109)(cid:333)(cid:59)(cid:7)(cid:118)(cid:80)(cid:81)(cid:74) è a ø (cid:357). x2 y2 b b (cid:60)(cid:86)(cid:87)(cid:63)(cid:140)(cid:44)(cid:34)(cid:35)(cid:36)G(cid:10) - =1(cid:27)a>0(cid:45)b>0(cid:32)(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=± x(cid:45)(cid:128)(cid:21)(cid:66)(cid:261) = 3(cid:45) a2 b2 a a æ b2 ö (cid:79)b= 3aÞc=2a(cid:45)(cid:101)(cid:39)(cid:40)(cid:41)(cid:44)Fc,0(cid:45)(cid:150)PF ^x(cid:51)(cid:45)(cid:102)(cid:103)Pçc, ÷(cid:45) è a ø b2 (cid:102)(cid:103) a b2 3a2 3(cid:45) k =k = = = = OP c ac 2a2 2 3 (cid:100)(cid:61)(cid:62)(cid:44)(cid:10) . 2 x2 y2 21(cid:26)(cid:27)2024·(cid:312)(cid:303)(cid:358)(cid:249)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:34)(cid:35)(cid:36)C: - =1(a>0,b>0)(cid:37)(cid:57)(cid:58)(cid:59)(cid:44) 2,A,B(cid:42)(cid:43)(cid:164)(cid:313)(cid:37)(cid:54)(cid:167)(cid:198)(cid:199)(cid:36) a2 b2 uuur uuur uuur (cid:105)(cid:37)(cid:54)(cid:41)(cid:27)(cid:171)(cid:110)(cid:91)(cid:92)(cid:191)(cid:41)O(cid:340)(cid:75)(cid:32)(cid:45)(cid:41)P(cid:95)(cid:34)(cid:35)(cid:36)C(cid:105)(cid:150)OA+OB=2OP, VAOB(cid:37)(cid:141)(cid:113)(cid:44)6(cid:45)(cid:56)(cid:319)(cid:34)(cid:35)(cid:36) (cid:37)(cid:195)(cid:51)(cid:197)(cid:44) (cid:26) (cid:60)(cid:61)(cid:62)(cid:63)2 6 (cid:60)(cid:42)(cid:64)(cid:63)(cid:108)(cid:109)(cid:57)(cid:58)(cid:59)(cid:73)(cid:81)a=b(cid:45)(cid:359)(cid:85)(cid:81)(cid:82)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:10)y=±x(cid:45)(cid:65)(cid:111)(cid:112)(cid:94)(cid:118)(cid:360)(cid:81)(cid:41)P(cid:44)AB(cid:37)(cid:133)(cid:41)(cid:45)(cid:33)(cid:68)(cid:41) A(x,x ),B(x ,-x ),(cid:73)(cid:81)(cid:41)P(cid:91)(cid:92)(cid:45)(cid:98)(cid:99)(cid:34)(cid:35)(cid:36)(cid:106)(cid:126)(cid:45)(cid:16)(cid:306)(cid:81)xx =a2(cid:45)(cid:221)(cid:216)(cid:108)(cid:109)(cid:141)(cid:113)(cid:79)(cid:80)(cid:73)(cid:81)a(cid:37)(cid:83). 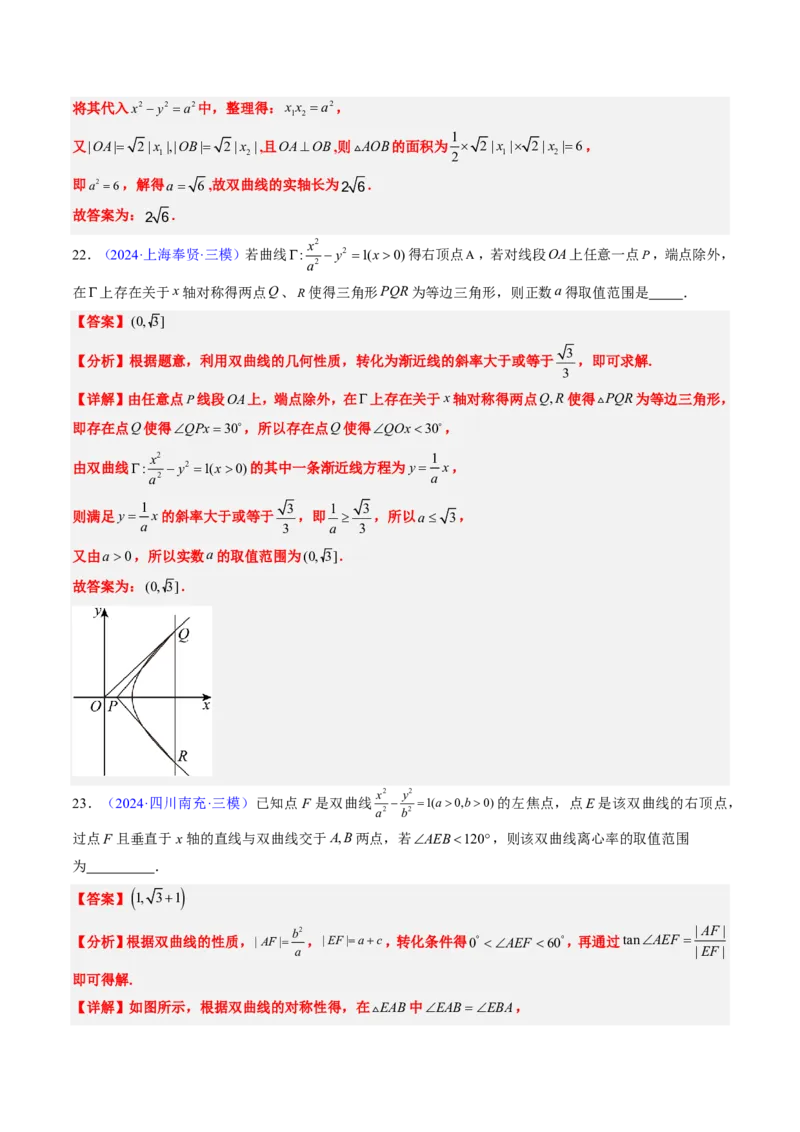1 1 2 2 1 2 (cid:60)(cid:86)(cid:87)(cid:63) c b x2 y2 (cid:228)(cid:71)(cid:45)(cid:65)e= 2 = = 1+( )2 (cid:80)(cid:81)a=b(cid:45)(cid:100)(cid:34)(cid:35)(cid:36)C: - =1(cid:37)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y=±x(cid:45) a a a2 b2 uuur uuur uuur x +x x -x (cid:171)(cid:288)(cid:33)A(x,x ),B(x ,-x )(cid:45)(cid:140)OA+OB=2OP,(cid:56)(cid:41)P(cid:44)AB(cid:37)(cid:133)(cid:41)(cid:45)(cid:56)P( 1 2, 1 2)(cid:45) 1 1 2 2 2 2(cid:97)(cid:214)(cid:98)(cid:99)x2-y2 =a2(cid:133)(cid:45)(cid:138)(cid:15)(cid:81)(cid:10)xx =a2(cid:45) 1 2 1 (cid:101)|OA|= 2|x |,|OB|= 2|x |,(cid:150)OA^OB,(cid:56)VAOB(cid:37)(cid:141)(cid:113)(cid:44) ´ 2|x |´ 2|x |=6(cid:45) 1 2 2 1 2 (cid:79)a2 =6(cid:45)(cid:87)(cid:81)a= 6,(cid:100)(cid:34)(cid:35)(cid:36)(cid:37)(cid:195)(cid:51)(cid:197)(cid:44)2 6. (cid:100)(cid:61)(cid:62)(cid:44)(cid:10)2 6. x2 22(cid:26)(cid:27)2024·(cid:105)(cid:361)(cid:362)(cid:363)·(cid:89)(cid:250)(cid:32)(cid:55)(cid:35)(cid:36)G: -y2 =1(x>0)(cid:81)(cid:39)(cid:192)(cid:41)A(cid:45)(cid:55)(cid:147)(cid:36)(cid:169)OA(cid:105)(cid:239)(cid:66)(cid:22)(cid:41)P(cid:45)(cid:166)(cid:41)(cid:364)(cid:205)(cid:45) a2 (cid:95)G(cid:105)(cid:172)(cid:95)(cid:3)(cid:50)x(cid:51)(cid:147)(cid:190)(cid:81)(cid:54)(cid:41)Q(cid:23)R(cid:262)(cid:81)(cid:89)(cid:223)(cid:186)PQR(cid:44)(cid:94)(cid:296)(cid:89)(cid:223)(cid:186)(cid:45)(cid:56)(cid:273)(cid:13)a(cid:81)(cid:320)(cid:83)(cid:193)(cid:194)(cid:164) (cid:26) (cid:60)(cid:61)(cid:62)(cid:63)(0, 3] 3 (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:21)(cid:66)(cid:45)(cid:108)(cid:109)(cid:34)(cid:35)(cid:36)(cid:37)(cid:114)(cid:115)(cid:188)(cid:189)(cid:45)(cid:353)(cid:16)(cid:44)(cid:198)(cid:199)(cid:36)(cid:37)(cid:333)(cid:59)(cid:69)(cid:50)(cid:134)(cid:94)(cid:50) (cid:45)(cid:79)(cid:80)(cid:73)(cid:87). 3 (cid:60)(cid:86)(cid:87)(cid:63)(cid:65)(cid:239)(cid:66)(cid:41)P(cid:36)(cid:169)OA(cid:105)(cid:45)(cid:166)(cid:41)(cid:364)(cid:205)(cid:45)(cid:95)G(cid:105)(cid:172)(cid:95)(cid:3)(cid:50)x(cid:51)(cid:147)(cid:190)(cid:81)(cid:54)(cid:41)Q,R(cid:262)(cid:81)VPQR(cid:44)(cid:94)(cid:296)(cid:89)(cid:223)(cid:186)(cid:45) (cid:79)(cid:172)(cid:95)(cid:41)Q(cid:262)(cid:81)ÐQPx=30o(cid:45)(cid:102)(cid:103)(cid:172)(cid:95)(cid:41)Q(cid:262)(cid:81)ÐQOx<30o(cid:45) x2 1 (cid:65)(cid:34)(cid:35)(cid:36)G: -y2 =1(x>0)(cid:37)(cid:214)(cid:133)(cid:22)(cid:167)(cid:198)(cid:199)(cid:36)(cid:106)(cid:126)(cid:44)y= x(cid:45) a2 a 1 3 1 3 (cid:56)(cid:226)(cid:227)y= x(cid:37)(cid:333)(cid:59)(cid:69)(cid:50)(cid:134)(cid:94)(cid:50) (cid:45)(cid:79) ³ (cid:45)(cid:102)(cid:103)a£ 3(cid:45) a 3 a 3 (cid:101)(cid:65)a>0(cid:45)(cid:102)(cid:103)(cid:195)(cid:13)a(cid:37)(cid:320)(cid:83)(cid:193)(cid:194)(cid:44)(0, 3]. (cid:100)(cid:61)(cid:62)(cid:44)(cid:10)(0, 3]. x2 y2 23(cid:26)(cid:27)2024·(cid:263)(cid:289)(cid:303)(cid:229)·(cid:89)(cid:250)(cid:32)(cid:104)(cid:88)(cid:41)F(cid:164)(cid:34)(cid:35)(cid:36) - =1(a>0,b>0)(cid:37)(cid:38)(cid:40)(cid:41)(cid:45)(cid:41)E(cid:164)(cid:319)(cid:34)(cid:35)(cid:36)(cid:37)(cid:39)(cid:192)(cid:41)(cid:45) a2 b2 (cid:46)(cid:41)F (cid:150)(cid:170)(cid:52)(cid:50)x(cid:51)(cid:37)(cid:52)(cid:36)(cid:110)(cid:34)(cid:35)(cid:36)(cid:53)(cid:50)A,B(cid:54)(cid:41)(cid:45)(cid:55)ÐAEB<120°(cid:45)(cid:56)(cid:319)(cid:34)(cid:35)(cid:36)(cid:57)(cid:58)(cid:59)(cid:37)(cid:320)(cid:83)(cid:193)(cid:194) (cid:44) (cid:26)   (cid:60)(cid:61)(cid:62)(cid:63) 1, 3+1 b2 |AF| (cid:60)(cid:42)(cid:64)(cid:63)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:37)(cid:188)(cid:189)(cid:45)|AF|= (cid:45)|EF|=a+c(cid:45)(cid:353)(cid:16)(cid:167)(cid:176)(cid:81)0° <ÐAEF <60°(cid:45)(cid:184)(cid:218)(cid:46)tanÐAEF = a |EF| (cid:79)(cid:80)(cid:81)(cid:87). (cid:60)(cid:86)(cid:87)(cid:63)(cid:228)(cid:71)(cid:102)(cid:158)(cid:45)(cid:264)(cid:265)(cid:34)(cid:35)(cid:36)(cid:37)(cid:147)(cid:190)(cid:188)(cid:81)(cid:45)(cid:95)VEAB(cid:133)ÐEAB=ÐEBA(cid:45)(cid:101)(cid:140)(cid:44)ÐAEB<120°, (cid:102)(cid:103)(cid:95)RtVAEF(cid:133)(cid:45)ÐAEF <60°, |AF| (cid:79)tanÐAEF = < 3 |EF| (cid:102)(cid:103)|AF|< 3|EF|(cid:45) b2 (cid:101)(cid:140)(cid:44)AB(cid:44)(cid:218)(cid:219)(cid:45)(cid:79)|AF|= (cid:45)|EF|=a+c(cid:45) a b2 (cid:102)(cid:103) < 3(a+c)(cid:45)(cid:150)c2 =a2 +b2(cid:45) a (cid:102)(cid:103)c2-a2 < 3(a2+ac)(cid:45) (cid:79)c2- 3ac-(1+ 3)a2 <0(cid:45)   (cid:79)e2- 3e- 1+ 3 <0(cid:45) (cid:87)(cid:81)-11(cid:45) (cid:102)(cid:103)(cid:319)(cid:34)(cid:35)(cid:36)(cid:37)(cid:57)(cid:58)(cid:59)(cid:320)(cid:83)(cid:193)(cid:194)(cid:44)(cid:10)1