专题16分解法模型和最短路径问题_2024-2025高三（6-6月题库）_2024年08月试卷_0816新高考数学题型全归纳之排列组合（20个专题）

专题 分解法模型和最短路径问题 16 类型 ：分解模型 1 例 ．对 分解质因数得 33000 2335311 ，则33000的正偶数因数的个数是（ ） 1 33000 ． ． ． ． A 48 B 72 C 64 D 96 例 ． 的正约数有（ ）个 2 5400 ． ． ． ． A例 48 能被多少B个不4同6的偶数整除 C 36 D 38 3. 30030 类型 ：最短路径问题 2 例 ．有一种走 方格迷宫 游戏，游戏规则是每次水平或竖直走动一个方格，走过的方格不能重复，只要有 1 “ ” 一个方格不同即为不同走法．现有如图的方格迷宫，图中的实线不能穿过，则从入口走到出口共有多少种 不同走法？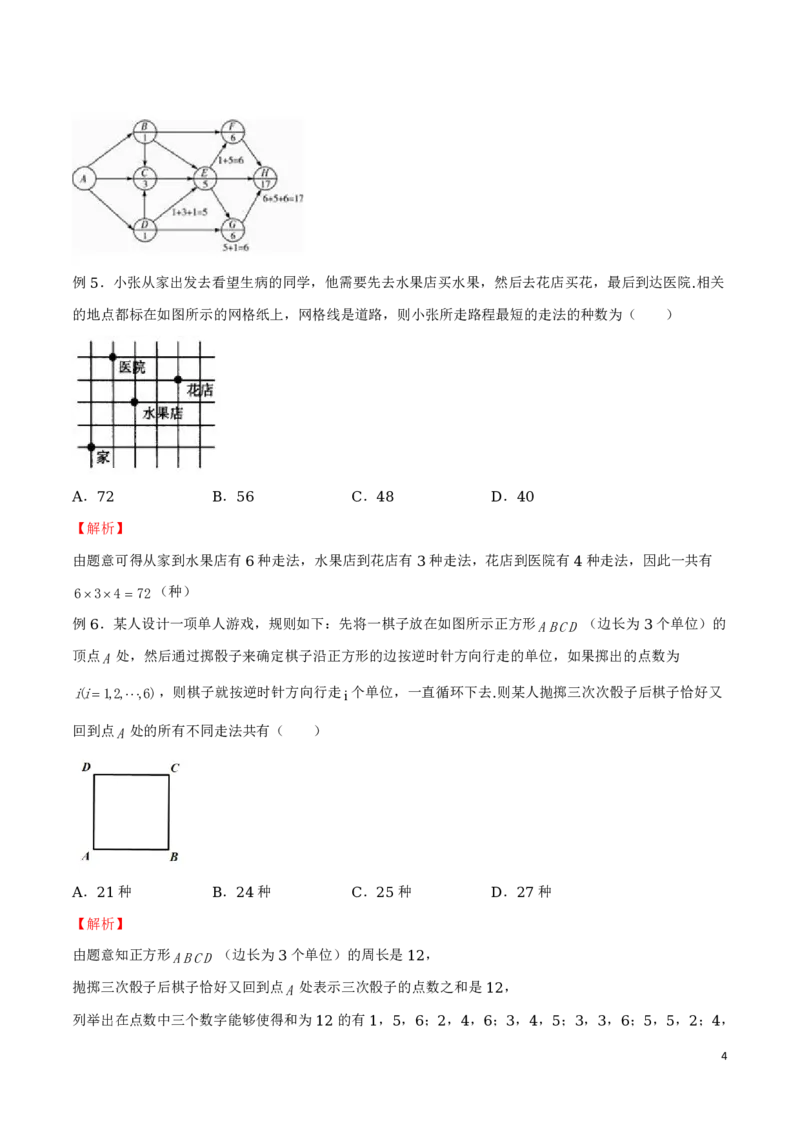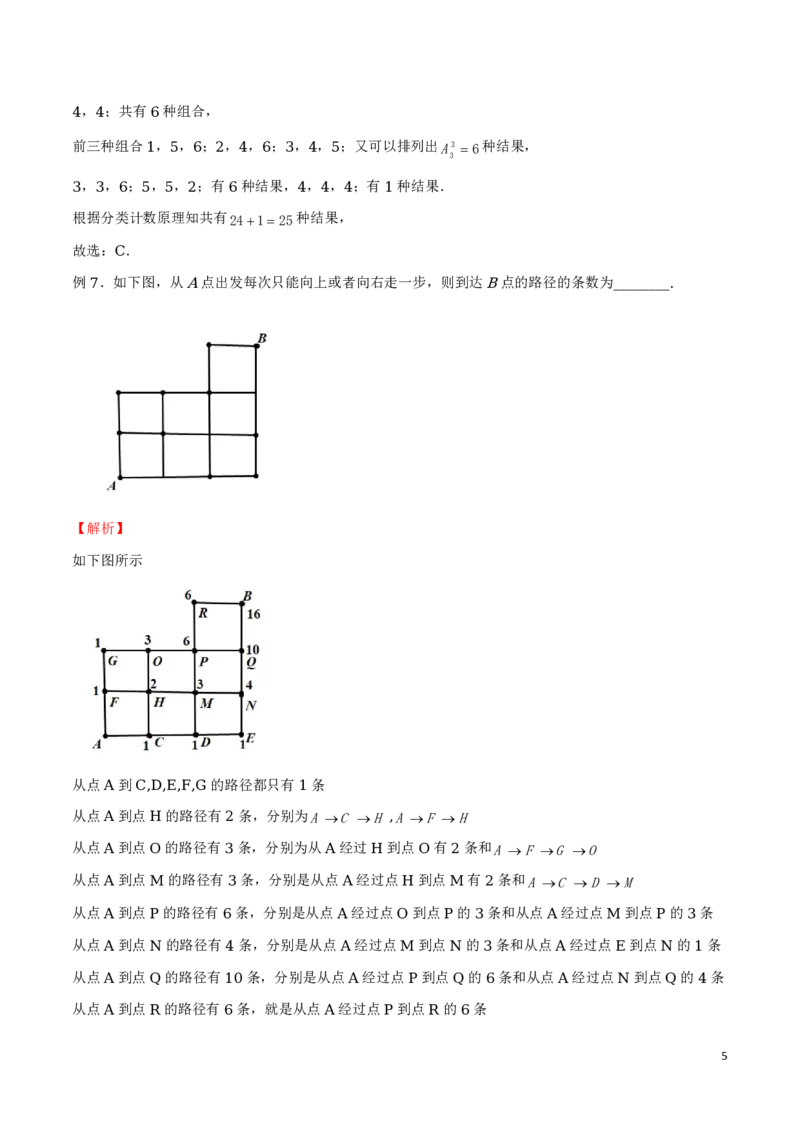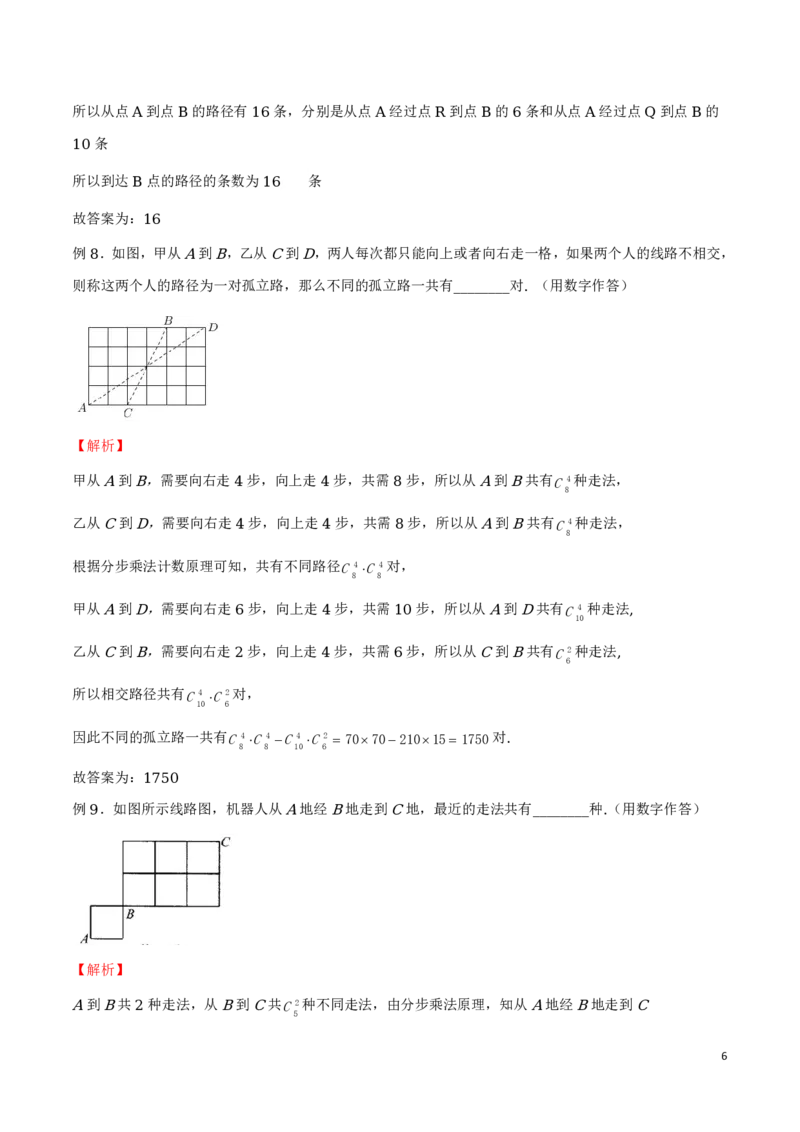（ ） ． ． ． ． A 6 B 8 C 10 D 12 例 ．如图，某城市中，M 、N 两地有整齐的道路网，若规定只能向东或向北两个方向沿途中路线前进， 2 则从M 到N 不同的走法共有（ ） ． ． ． ． A 10 B 13 C 15 D 25 例 ．如图，蚂蚁从 沿着长方体的棱以 的方向行走至 ，不同的行走路线有 3 A B ( ) 1． 条 ． 条 ． 条 ． 条 A 6 B 7 C 8 D 9 例 ．如图所示为某市各旅游景点的分布图，图中一支箭头表示一段有方向的路，试计算顺着箭头方向，从 4 到 可走的不同的旅游路线的条数为（ ） A H ． ． ． ． A 14 B 15 C 16 D 17 例 ．小张从家出发去看望生病的同学，他需要先去水果店买水果，然后去花店买花，最后到达医院 相关 5 . 的地点都标在如图所示的网格纸上，网格线是道路，则小张所走路程最短的走法的种数为（ ） ． ． ． ． A 72 B 56 C 48 D 40 例 ．某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形ABCD （边长为 个单位）的 6 3 顶点A处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为 i(i1,2,,6)，则棋子就按逆时针方向行走 i 个单位，一直循环下去 则某人抛掷三次次骰子后棋子恰好又 . 回到点A处的所有不同走法共有（ ） ． 种 ． 种 ． 种 ． 种 A 21 B 24 C 25 D 27 例 ．如下图，从 点出发每次只能向上或者向右走一步，则到达 点的路径的条数为 7 A B ________. 2例 ．如图，甲从 到 ，乙从 到 ，两人每次都只能向上或者向右走一格，如果两个人的线路不相交， 8 A B C D 则称这两个人的路径为一对孤立路，那么不同的孤立路一共有 对 （用数字作答） ________ . 例 ．如图所示线路图，机器人从 地经 地走到 地，最近的走法共有 种 （用数字作答） 9 A B C ________ . 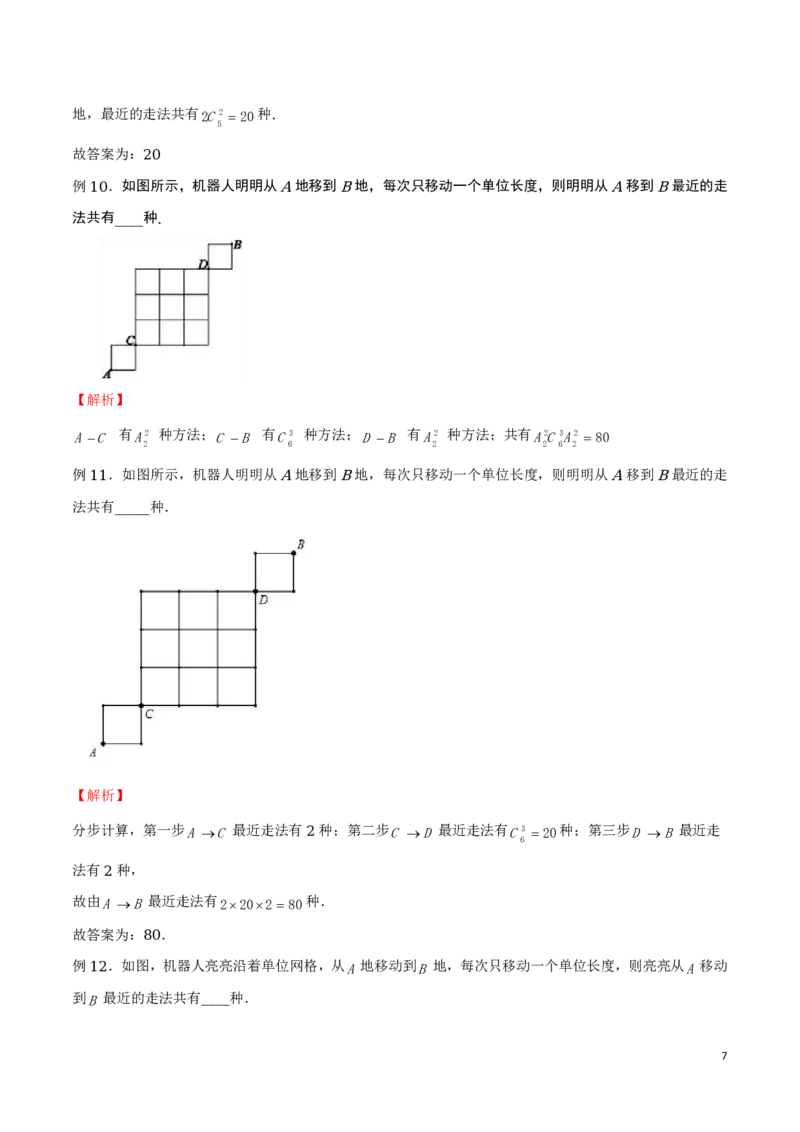例 ．如图所示，机器人明明从 地移到 地，每次只移动一个单位长度，则明明从 移到 最近的走 10 A B A B 法共有 种 ____ . 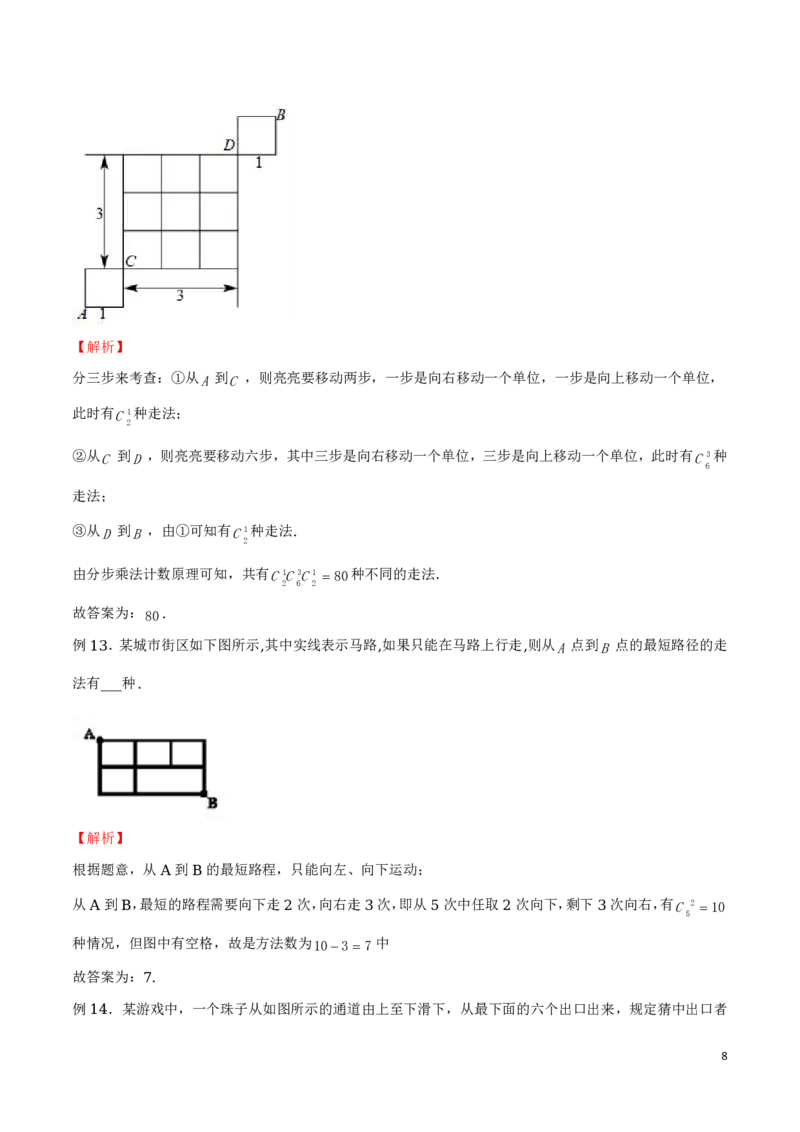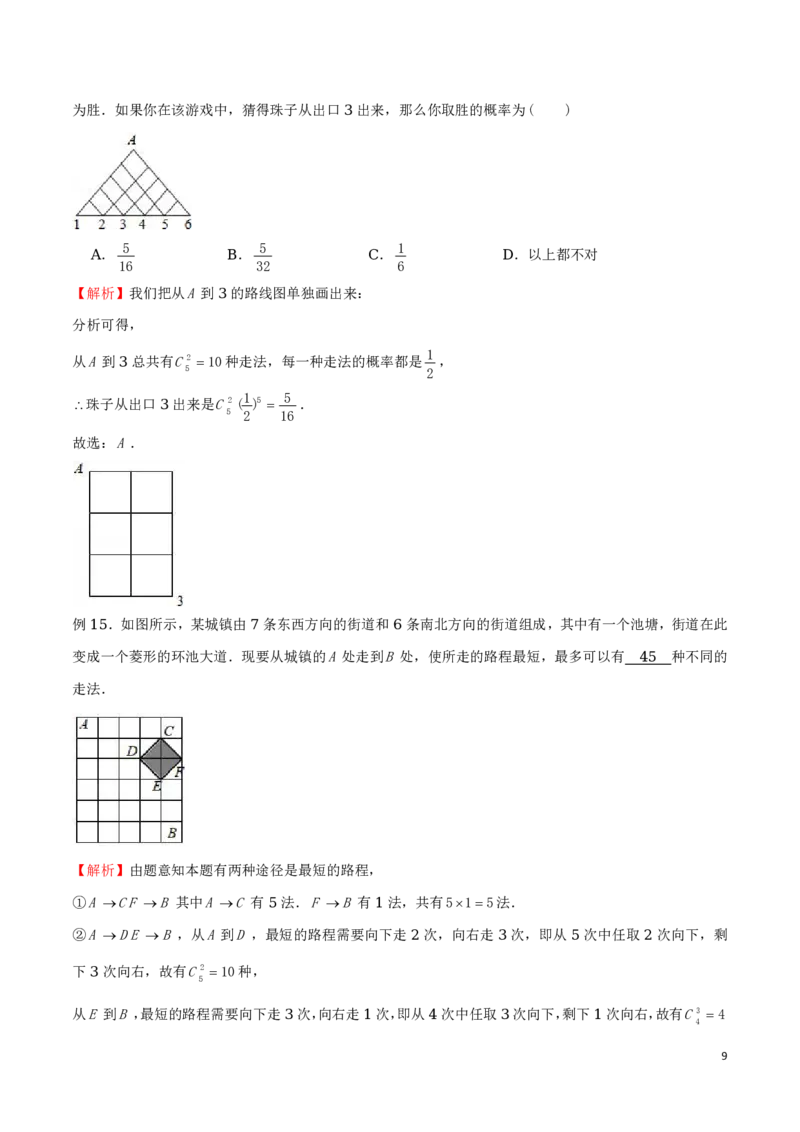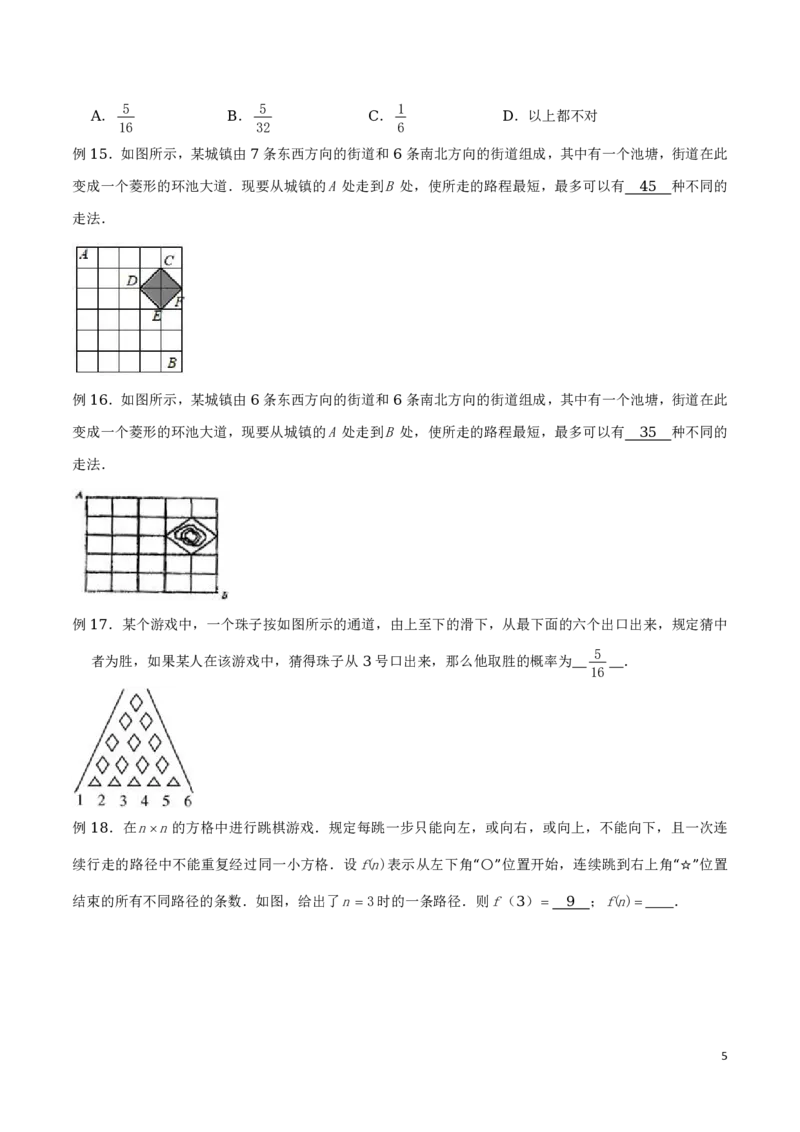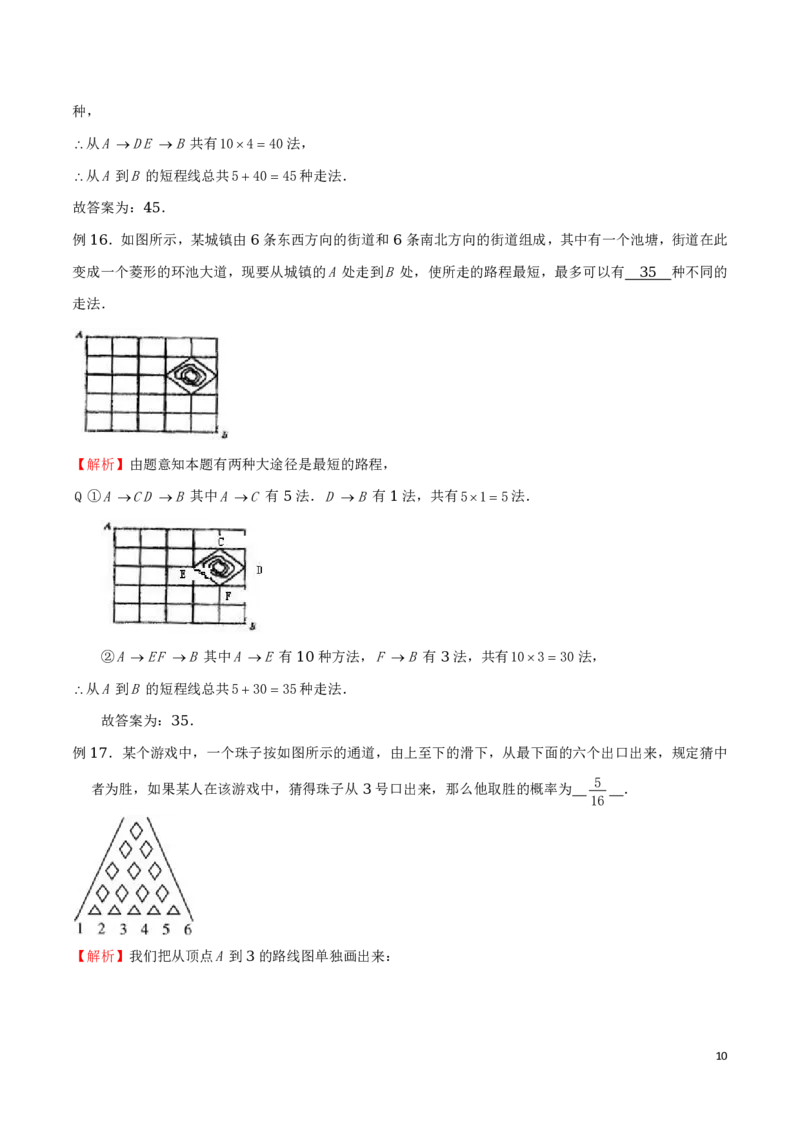例 ．如图所示，机器人明明从 地移到 地，每次只移动一个单位长度，则明明从 移到 最近的走 11 A B A B 法共有 种． _____ 3例 ．如图，机器人亮亮沿着单位网格，从A地移动到B地，每次只移动一个单位长度，则亮亮从A移动 12 到B最近的走法共有 种． ____ 例 ．某城市街区如下图所示 其中实线表示马路 如果只能在马路上行走 则从A点到B点的最短路径的走 13 , , , 法有 种． ___ 例 ．某游戏中，一个珠子从如图所示的通道由上至下滑下，从最下面的六个出口出来，规定猜中出口者 14 为胜．如果你在该游戏中，猜得珠子从出口 出来，那么你取胜的概率为( ) 3 45 5 1 ． ． ． ．以上都不对 16 32 6 A B C D 例 ．如图所示，某城镇由 条东西方向的街道和 条南北方向的街道组成，其中有一个池塘，街道在此 15 7 6 变成一个菱形的环池大道．现要从城镇的A处走到B处，使所走的路程最短，最多可以有 种不同的 45 走法． 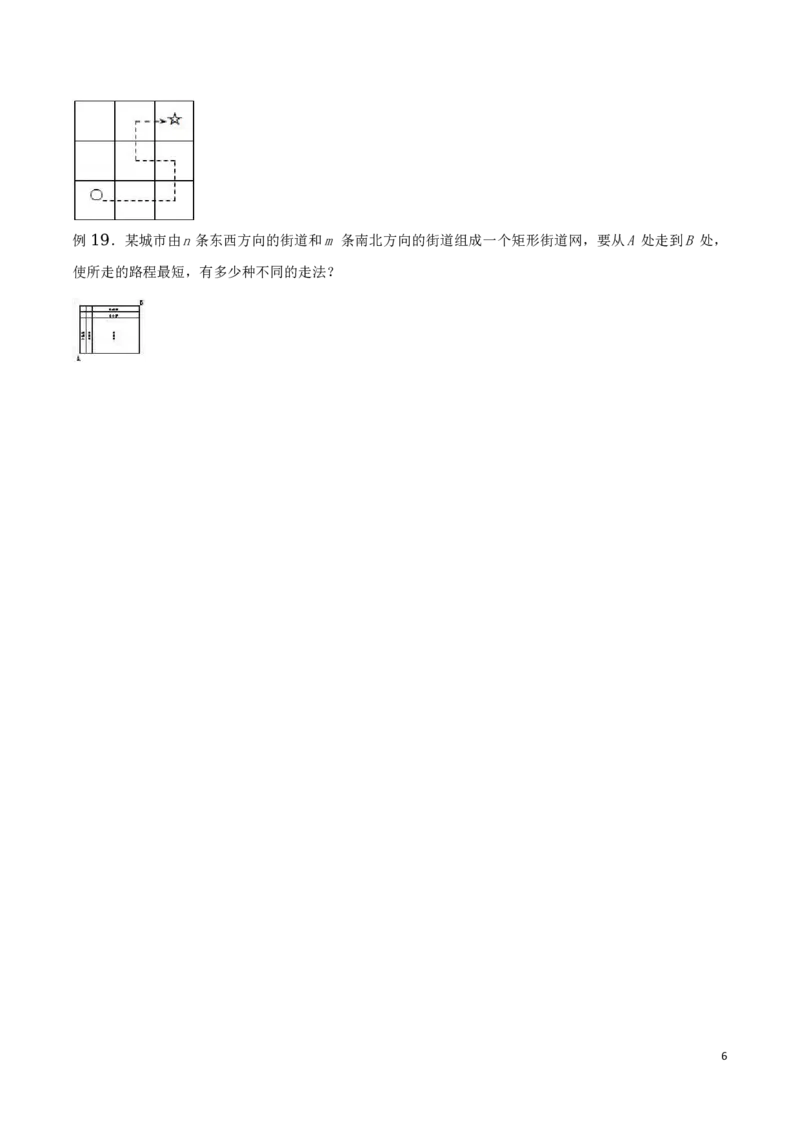例 ．如图所示，某城镇由 条东西方向的街道和 条南北方向的街道组成，其中有一个池塘，街道在此 16 6 6 变成一个菱形的环池大道，现要从城镇的A处走到B处，使所走的路程最短，最多可以有 种不同的 35 走法． 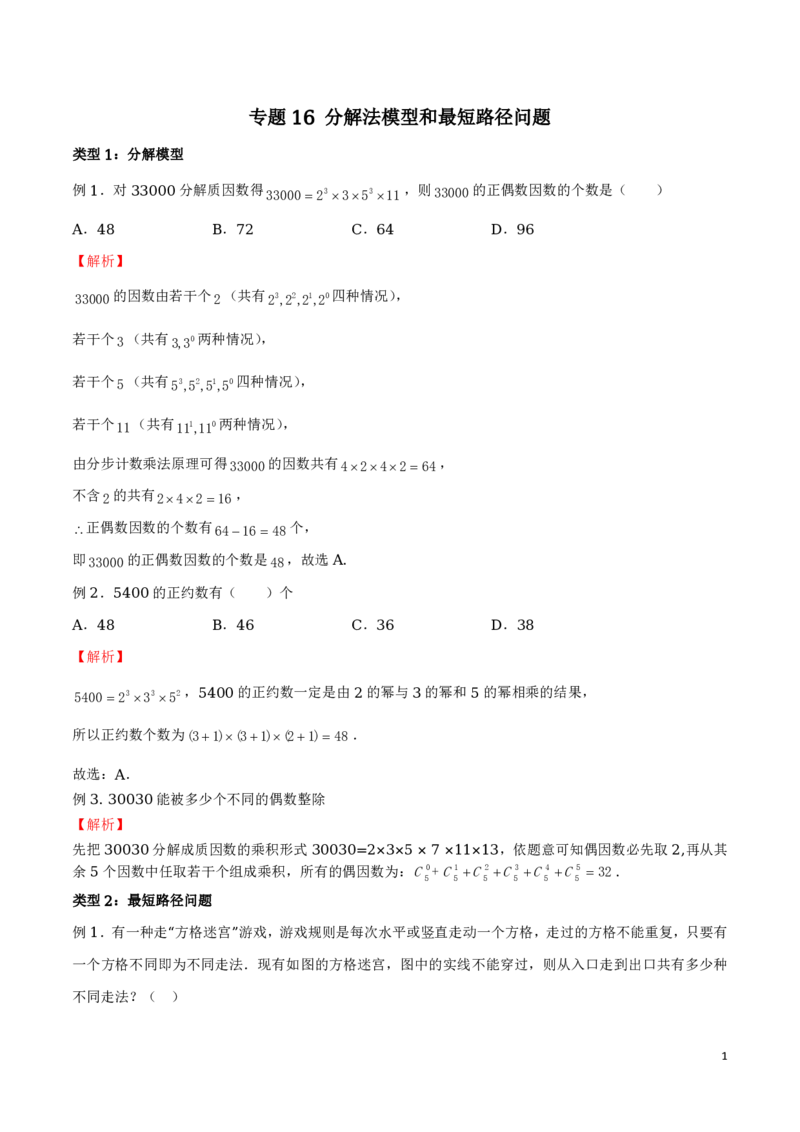例 ．某个游戏中，一个珠子按如图所示的通道，由上至下的滑下，从最下面的六个出口出来，规定猜中 17 5 者为胜，如果某人在该游戏中，猜得珠子从 号口出来，那么他取胜的概率为 ． 16 3 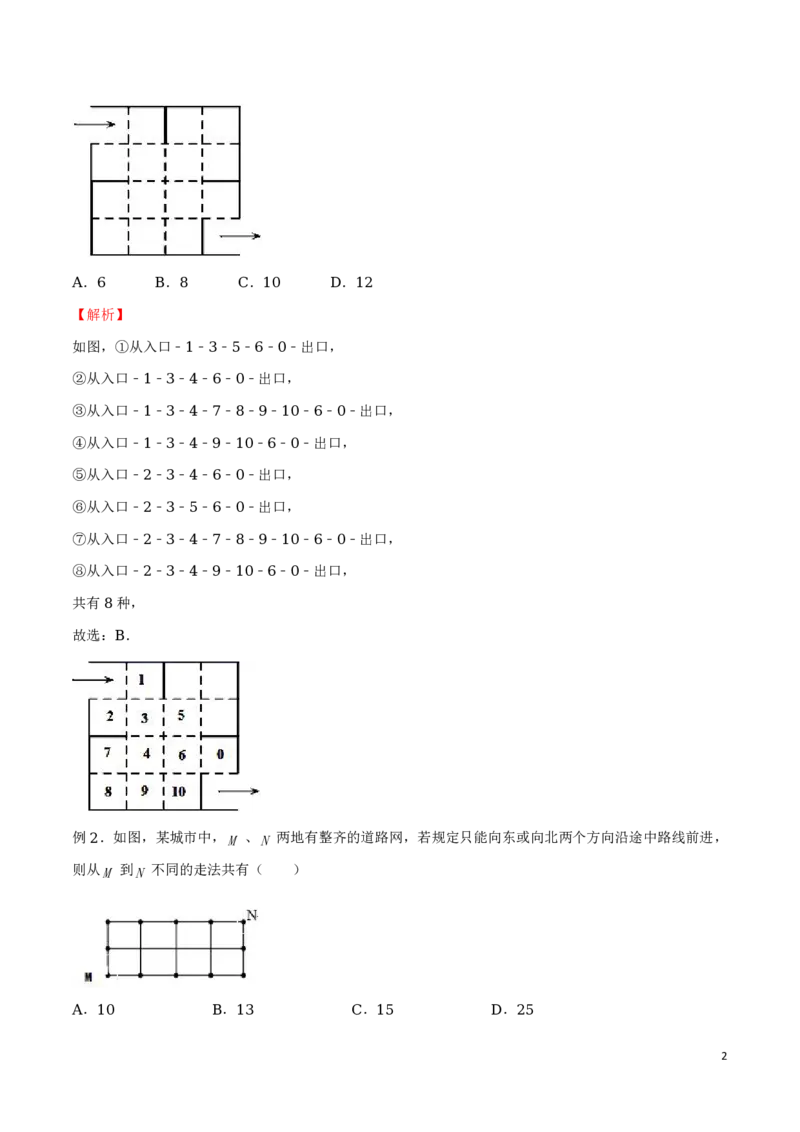例 ．在nn的方格中进行跳棋游戏．规定每跳一步只能向左，或向右，或向上，不能向下，且一次连 18 续行走的路径中不能重复经过同一小方格．设f(n)表示从左下角 〇 位置开始，连续跳到右上角 位置 ☆ “ ” “ ” 结束的所有不同路径的条数．如图，给出了n 3时的一条路径．则f（ ） ；f(n) ． 3 9 5例 ．某城市由n条东西方向的街道和m 条南北方向的街道组成一个矩形街道网，要从A处走到B处， 19 使所走的路程最短，有多少种不同的走法？ 6专题 分解法模型和最短路径问题 16 类型 ：分解模型 1 例 ．对 分解质因数得 33000 2335311 ，则33000的正偶数因数的个数是（ ） 1 33000 ． ． ． ． A 48 B 72 C 64 D 96 【解析】 33000的因数由若干个2（共有23,22,21,20四种情况）， 若干个3（共有3,30两种情况）， 若干个5（共有53,52,51,50四种情况）， 若干个11（共有111,110两种情况）， 由分步计数乘法原理可得33000的因数共有4242 64， 不含2的共有242 16， 正偶数因数的个数有6416 48个， 即33000的正偶数因数的个数是48，故选 A. 例 ． 的正约数有（ ）个 2 5400 ． ． ． ． A 48 B 46 C 36 D 38 【解析】 5400 233352， 的正约数一定是由 的幂与 的幂和 的幂相乘的结果， 5400 2 3 5 所以正约数个数为(31)(31)(21)48． 故选： ． 例 A 能被多少个不同的偶数整除 【解3.析3】0030 先把 分解成质因数的乘积形式 ，依题意可知偶因数必先取 再从其 余 个30因0数30中任取若干个组成乘积，所3有0的03偶0=因2数×为3×：5C×07+C×11 1C×123C3 C4 C5 32 2, 5 5 5 5 5 5 5 . 类型 ：最短路径问题 2 例 ．有一种走 方格迷宫 游戏，游戏规则是每次水平或竖直走动一个方格，走过的方格不能重复，只要有 1 “ ” 一个方格不同即为不同走法．现有如图的方格迷宫，图中的实线不能穿过，则从入口走到出口共有多少种 不同走法？（ ） 1． ． ． ． A 6 B 8 C 10 D 12 【解析】 如图，①从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 1 3 5 6 0 ②从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 1 3 4 6 0 ③从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 1 3 4 7 8 9 10 6 0 ④从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 1 3 4 9 10 6 0 ⑤从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 2 3 4 6 0 ⑥从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 2 3 5 6 0 ⑦从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 2 3 4 7 8 9 10 6 0 ⑧从入口﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣ ﹣出口， 2 3 4 9 10 6 0 共有 种， 8 故选： ． B 例 ．如图，某城市中，M 、N 两地有整齐的道路网，若规定只能向东或向北两个方向沿途中路线前进， 2 则从M 到N 不同的走法共有（ ） ． ． ． ． A 10 B 13 C 15 D 25 2【解析】 因为只能向东或向北两个方向 向北走的路有 条，向东走的路有 条 5 3 走路时向北走的路有 种结果，向东走的路有 种结果 5 3 根据分步计数原理知共有35 15种结果，选 C 例 ．如图，蚂蚁从 沿着长方体的棱以 的方向行走至 ，不同的行走路线有 3 A B ( ) ． 条 ． 条 ． 条 ． 条 A 6 B 7 C 8 D 9 【解析】 共有 个顶点与A点相邻，经过每个相邻顶点，按规定方向都有 条路径到达B点，所以，蚂蚁从A沿着 3 2 长方体的棱以规定的方向行走至B，不同的行走路线有：32 6（条），故选 A. 例 ．如图所示为某市各旅游景点的分布图，图中一支箭头表示一段有方向的路，试计算顺着箭头方向，从 4 到 可走的不同的旅游路线的条数为（ ） A H ． ． ． ． A 14 B 15 C 16 D 17 【解析】 要到 点，需从 、 、 走过来， 、 、 各点又可由哪些点走过来，这样一步步倒推，最后归结到 ， H F E G F E G A 然后再反推过去得到如下的计算方法： 至 、 、 的路数记在 、 、 的圆圈内， 、 、 分别到 、 A B C D B C D B C D F 、 的路数亦记在圈内，最后 、 、 各路数之和，即得到至 的总路数，如下图所示，易得到 条 E G F E G H 17 路线，故选 ． D 3例 ．小张从家出发去看望生病的同学，他需要先去水果店买水果，然后去花店买花，最后到达医院 相关 5 . 的地点都标在如图所示的网格纸上，网格线是道路，则小张所走路程最短的走法的种数为（ ） ． ． ． ． A 72 B 56 C 48 D 40 【解析】 由题意可得从家到水果店有 种走法，水果店到花店有 种走法，花店到医院有 种走法，因此一共有 6 3 4 634 72（种） 例 ．某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形ABCD （边长为 个单位）的 6 3 顶点A处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为 i(i1,2,,6)，则棋子就按逆时针方向行走 i 个单位，一直循环下去 则某人抛掷三次次骰子后棋子恰好又 . 回到点A处的所有不同走法共有（ ） ． 种 ． 种 ． 种 ． 种 A 21 B 24 C 25 D 27 【解析】 由题意知正方形ABCD （边长为 个单位）的周长是 ， 3 12 抛掷三次骰子后棋子恰好又回到点A处表示三次骰子的点数之和是 ， 12 列举出在点数中三个数字能够使得和为 的有 ， ， ； ， ， ； ， ， ； ， ， ； ， ， ； ， 12 1 5 6 2 4 6 3 4 5 3 3 6 5 5 2 4 4， ；共有 种组合， 4 4 6 前三种组合 ， ， ； ， ， ； ， ， ；又可以排列出A3 6种结果， 3 1 5 6 2 4 6 3 4 5 ， ， ； ， ， ；有 种结果， ， ， ；有 种结果． 3 3 6 5 5 2 6 4 4 4 1 根据分类计数原理知共有24125种结果， 故选： ． C 例 ．如下图，从 点出发每次只能向上或者向右走一步，则到达 点的路径的条数为 7 A B ________. 【解析】 如下图所示 从点 到 的路径都只有 条 A C,D,E,F,G 1 从点 到点 的路径有 条，分别为AC H AF H A H 2 , 从点 到点 的路径有 条，分别为从 经过 到点 有 条和AF G O A O 3 A H O 2 从点 到点 的路径有 条，分别是从点 经过点 到点 有 条和AC D M A M 3 A H M 2 从点 到点 的路径有 条，分别是从点 经过点 到点 的 条和从点 经过点 到点 的 条 A P 6 A O P 3 A M P 3 从点 到点 的路径有 条，分别是从点 经过点 到点 的 条和从点 经过点 到点 的 条 A N 4 A M N 3 A E N 1 从点 到点 的路径有 条，分别是从点 经过点 到点 的 条和从点 经过点 到点 的 条 A Q 10 A P Q 6 A N Q 4 从点 到点 的路径有 条，就是从点 经过点 到点 的 条 A R 6 A P R 6 5所以从点 到点 的路径有 条，分别是从点 经过点 到点 的 条和从点 经过点 到点 的 A B 16 A R B 6 A Q B 条 10 所以到达 点的路径的条数为 条 B 16 故答案为： 16 例 ．如图，甲从 到 ，乙从 到 ，两人每次都只能向上或者向右走一格，如果两个人的线路不相交， 8 A B C D 则称这两个人的路径为一对孤立路，那么不同的孤立路一共有 对 （用数字作答） ________ . 【解析】 甲从 到 ，需要向右走 步，向上走 步，共需 步，所以从 到 共有C4种走法， 8 A B 4 4 8 A B 乙从 到 ，需要向右走 步，向上走 步，共需 步，所以从 到 共有C4种走法， 8 C D 4 4 8 A B 根据分步乘法计数原理可知，共有不同路径C4 C4对， 8 8 甲从 到 ，需要向右走 步，向上走 步，共需 步，所以从 到 共有C4 种走法 10 A D 6 4 10 A D , 乙从 到 ，需要向右走 步，向上走 步，共需 步，所以从 到 共有C2种走法 6 C B 2 4 6 C B , 所以相交路径共有C4 C2对， 10 6 因此不同的孤立路一共有C4 C4 C4 C2  707021015 1750对 8 8 10 6 . 故答案为： 1750 例 ．如图所示线路图，机器人从 地经 地走到 地，最近的走法共有 种 （用数字作答） 9 A B C ________ . 【解析】 到 共 种走法，从 到 共C2种不同走法，由分步乘法原理，知从 地经 地走到 5 A B 2 B C A B C 6地，最近的走法共有2C2 20种 5 . 故答案为： 20 例 ．如图所示，机器人明明从 地移到 地，每次只移动一个单位长度，则明明从 移到 最近的走 10 A B A B 法共有 种 ____ . 【解析】 AC 有A2 种方法；C B 有C3 种方法；DB 有A2 种方法；共有A2C3A2  80 2 6 2 2 6 2 例 ．如图所示，机器人明明从 地移到 地，每次只移动一个单位长度，则明明从 移到 最近的走 11 A B A B 法共有 种． _____ 【解析】 分步计算，第一步AC 最近走法有 种；第二步C D最近走法有C3 20种；第三步D B最近走 6 2 法有 种， 2 故由AB最近走法有2202  80种． 故答案为： ． 80 例 ．如图，机器人亮亮沿着单位网格，从A地移动到B地，每次只移动一个单位长度，则亮亮从A移动 12 到B最近的走法共有 种． ____ 7【解析】 分三步来考查：①从A到C ，则亮亮要移动两步，一步是向右移动一个单位，一步是向上移动一个单位， 此时有C1种走法； 2 ②从C 到D，则亮亮要移动六步，其中三步是向右移动一个单位，三步是向上移动一个单位，此时有C3种 6 走法； ③从D到B，由①可知有C1种走法 2 . 由分步乘法计数原理可知，共有C1C3C1  80种不同的走法 2 6 2 . 故答案为：80 . 例 ．某城市街区如下图所示 其中实线表示马路 如果只能在马路上行走 则从A点到B点的最短路径的走 13 , , , 法有 种． ___ 【解析】 根据题意，从 到 的最短路程，只能向左、向下运动； A B 从 到 ，最短的路程需要向下走 次，向右走 次，即从 次中任取 次向下，剩下 次向右，有C 2 10 5 A B 2 3 5 2 3 种情况，但图中有空格，故是方法数为103 7 中 故答案为： 7. 例 ．某游戏中，一个珠子从如图所示的通道由上至下滑下，从最下面的六个出口出来，规定猜中出口者 14 8为胜．如果你在该游戏中，猜得珠子从出口 出来，那么你取胜的概率为( ) 3 5 5 1 ． ． ． ．以上都不对 16 32 6 A B C D 【解析】我们把从A到 的路线图单独画出来： 3 分析可得， 1 从A到 总共有C2 10种走法，每一种走法的概率都是 ， 5 2 3 1 5 珠子从出口 出来是C2 ( )5  ． 5 2 16 3 故选：A． 例 ．如图所示，某城镇由 条东西方向的街道和 条南北方向的街道组成，其中有一个池塘，街道在此 15 7 6 变成一个菱形的环池大道．现要从城镇的A处走到B处，使所走的路程最短，最多可以有 种不同的 45 走法． 【解析】由题意知本题有两种途径是最短的路程， ①ACF B其中AC 有 法．F B有 法，共有515法． 5 1 ②ADE B，从A到D，最短的路程需要向下走 次，向右走 次，即从 次中任取 次向下，剩 2 3 5 2 下 次向右，故有C2 10种， 5 3 从E到B，最短的路程需要向下走 次，向右走 次，即从 次中任取 次向下，剩下 次向右，故有C3  4 4 3 1 4 3 1 9种， 从ADE B共有104 40法， 从A到B的短程线总共540  45种走法． 故答案为： ． 45 例 ．如图所示，某城镇由 条东西方向的街道和 条南北方向的街道组成，其中有一个池塘，街道在此 16 6 6 变成一个菱形的环池大道，现要从城镇的A处走到B处，使所走的路程最短，最多可以有 种不同的 35 走法． 【解析】由题意知本题有两种大途径是最短的路程， Q ①ACD B其中AC 有 法．D B有 法，共有515法． 5 1 ②AEF B其中AE有 种方法，F B有 法，共有103 30法， 10 3 从A到B的短程线总共530  35种走法． 故答案为： ． 35 例 ．某个游戏中，一个珠子按如图所示的通道，由上至下的滑下，从最下面的六个出口出来，规定猜中 17 5 者为胜，如果某人在该游戏中，猜得珠子从 号口出来，那么他取胜的概率为 ． 16 3 【解析】我们把从顶点A到 的路线图单独画出来： 3 10分析可得， 1 从顶点A到 总共有C2 10种走法，每一种走法的概率都是 ， 5 2 3 1 5 珠子从出口 出来是C2( )5  ． 5 2 16 3 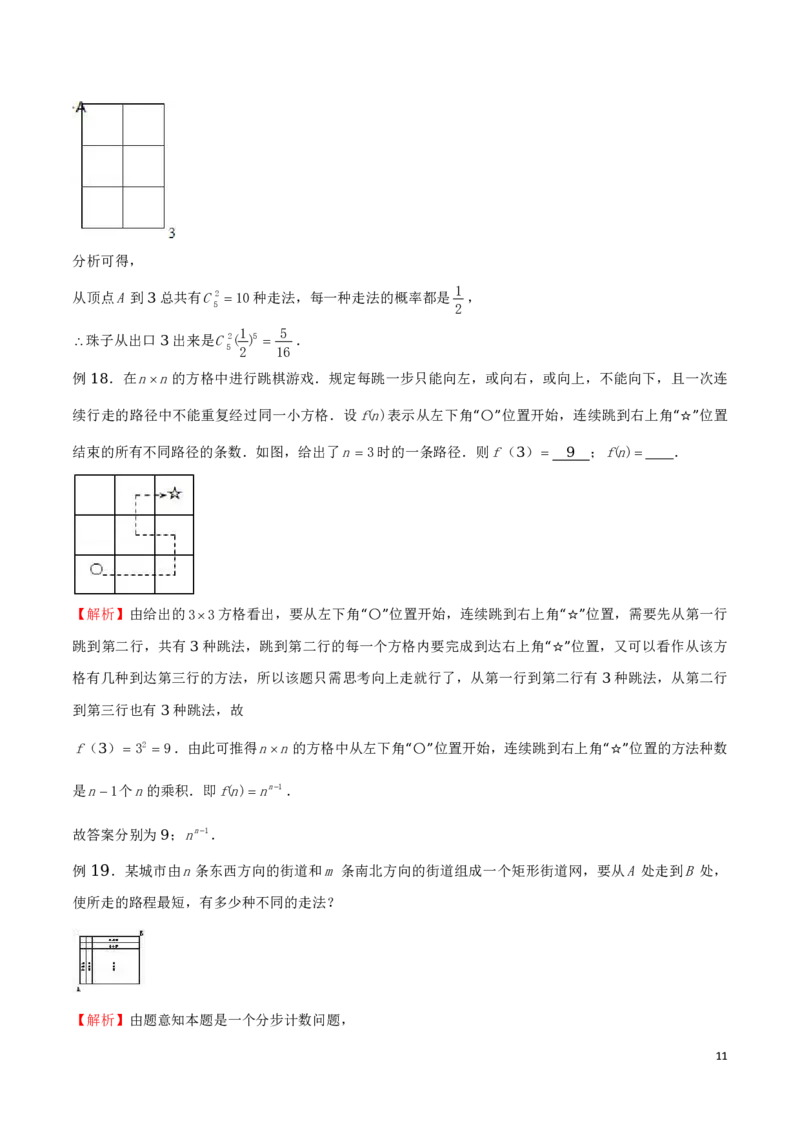例 ．在nn的方格中进行跳棋游戏．规定每跳一步只能向左，或向右，或向上，不能向下，且一次连 18 续行走的路径中不能重复经过同一小方格．设f(n)表示从左下角 〇 位置开始，连续跳到右上角 位置 ☆ “ ” “ ” 结束的所有不同路径的条数．如图，给出了n 3时的一条路径．则f（ ） ；f(n) ． 3 9 【解析】由给出的33方格看出，要从左下角 〇 位置开始，连续跳到右上角 位置，需要先从第一行 ☆ “ ” “ ” 跳到第二行，共有 种跳法，跳到第二行的每一个方格内要完成到达右上角 位置，又可以看作从该方 ☆ 3 “ ” 格有几种到达第三行的方法，所以该题只需思考向上走就行了，从第一行到第二行有 种跳法，从第二行 3 到第三行也有 种跳法，故 3 f（ ） 32 9．由此可推得nn的方格中从左下角 〇 位置开始，连续跳到右上角 位置的方法种数 ☆ 3 “ ” “ ” 是n1个n的乘积．即f(n)nn1． 故答案分别为 ；nn1． 9 例 ．某城市由n条东西方向的街道和m 条南北方向的街道组成一个矩形街道网，要从A处走到B处， 19 使所走的路程最短，有多少种不同的走法？ 【解析】由题意知本题是一个分步计数问题， 11将相邻两个交点之间的街道称为一段，那么从A到B需要走(nm 2)段， 而这些段中，必须有东西方向的(n1)段，其余的为南北方向的(m 1)段， 共有Cm1 Cn1 种走法． mn2 mn2 12