专题14立体几何综合（5大考向真题解读）-解析版_2024-2025高三（6-6月题库）_2024年08月试卷_08202025版《真题题源解密-专题分类》数学

专题 14 立体几何综合 命题解读 考向 考查统计 1.(cid:8)(cid:9)(cid:25)(cid:26)(cid:27)(cid:28)(cid:29)(cid:30)(cid:31)(cid:19)(cid:9)(cid:32)(cid:11)(cid:33)(cid:16)(cid:34) 2023·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)18(cid:12)1(cid:13) (cid:12)1(cid:13)(cid:35)(cid:36)(cid:37)(cid:38)(cid:39)(cid:40)(cid:19)(cid:41)(cid:42)(cid:11)(cid:35)(cid:36)(cid:37)(cid:38) (cid:3)(cid:4)(cid:5)(cid:6) 2024·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)17(cid:12)1(cid:13) (cid:39)(cid:40)(cid:19)(cid:43)(cid:44)(cid:45)(cid:46)(cid:47)(cid:48)(cid:49)(cid:50)(cid:11)(cid:51)(cid:52)(cid:37)(cid:38)(cid:39) 2022·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)20(cid:12)1(cid:13) (cid:40)(cid:19)(cid:53)(cid:54)(cid:55)(cid:36)(cid:47)(cid:48)(cid:56)(cid:57)(cid:58)(cid:59)(cid:60) 2023·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)20(cid:12)1(cid:13) (cid:14)(cid:15)(cid:5)(cid:6) (cid:12)2(cid:13)(cid:51)(cid:52)(cid:37)(cid:38)(cid:39)(cid:40)(cid:19)(cid:61)(cid:62)(cid:63)(cid:64)(cid:47)(cid:48)(cid:56) 2024·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)17(cid:12)1(cid:13) (cid:57)(cid:58)(cid:59)(cid:11)(cid:51)(cid:52)(cid:37)(cid:38)(cid:39)(cid:40)(cid:19)(cid:65)(cid:40)(cid:66)(cid:47)(cid:48)(cid:56) (cid:16)(cid:17)(cid:18)(cid:19)(cid:20)(cid:21) 2022·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)19(cid:12)1(cid:13) (cid:57)(cid:58)(cid:59)(cid:11)(cid:67)(cid:68)(cid:39)(cid:40)(cid:19)(cid:65)(cid:40)(cid:66)(cid:69)(cid:70)(cid:39)(cid:40)(cid:19) 2022·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)19(cid:12)2(cid:13) (cid:71)(cid:61)(cid:72)(cid:14)(cid:15)(cid:60) 2022·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)20(cid:12)2(cid:13) (cid:22)(cid:23)(cid:18)(cid:24) (cid:12)3(cid:13)(cid:68)(cid:28)(cid:29)(cid:73)(cid:74)(cid:4)(cid:3)(cid:4)(cid:75)(cid:14)(cid:15)(cid:5)(cid:6)(cid:19) 2023·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)20(cid:12)2(cid:13) (cid:76)(cid:77)(cid:11)(cid:78)(cid:47)(cid:67)(cid:68)(cid:39)(cid:40)(cid:73)(cid:76)(cid:77)(cid:26)(cid:27)(cid:28)(cid:29)(cid:79) 2024·(cid:7)(cid:8)(cid:9)Ⅱ(cid:10)(cid:11)17(cid:12)2(cid:13) (cid:80)(cid:5)(cid:61)(cid:18)(cid:81)(cid:82)(cid:5)(cid:6)(cid:19)(cid:83)(cid:84)(cid:85)(cid:86)(cid:45)(cid:46)(cid:60) (cid:12)4(cid:13)(cid:67)(cid:68)(cid:39)(cid:40)(cid:73)(cid:36)(cid:87)(cid:88)(cid:18)(cid:15)(cid:61)(cid:75)(cid:15)(cid:61) 2023·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)18(cid:12)2(cid:13) (cid:89)(cid:3)(cid:18)(cid:75)(cid:3)(cid:18)(cid:89)(cid:3)(cid:18)(cid:19)(cid:90)(cid:24)(cid:91)(cid:92)(cid:11)(cid:93)(cid:67) (cid:105)(cid:106)(cid:23)(cid:18)(cid:24)(cid:22)(cid:48)(cid:107)(cid:40) 2024·(cid:7)(cid:8)(cid:9)Ⅰ(cid:10)(cid:11)17(cid:12)2(cid:13) (cid:94)(cid:95)(cid:36)(cid:87)(cid:96)(cid:83)(cid:97)(cid:91)(cid:92)(cid:19)(cid:98)(cid:99)(cid:11)(cid:27)(cid:100)(cid:39)(cid:40) (cid:73)(cid:101)(cid:102)(cid:103)(cid:37)(cid:38)(cid:24)(cid:91)(cid:92)(cid:79)(cid:19)(cid:104)(cid:68)(cid:60) 命题分析 2024年高考新高考Ⅰ卷考查了线面平行关系的证明和已知二面角求长度问题。Ⅱ卷考查了线线垂直关系 的证明和二面角正弦值的求解。难度适中，不过解题的证明方法还是比较少见的，大家要注意。例如Ⅰ卷是 利用垂直关系的性质来考查平行，二面角既可以用定义法也可以建系解决。预计2025年高考第（1）问还 是主要考查平行与垂直的判定与性质，第（2）问主要考查利用空间向量的相关知识解决空间角的问题(cid:22) 试题精讲 (cid:23)(cid:24)(cid:25)(cid:26)(cid:21) 1(cid:27)(cid:28)2024(cid:29)(cid:30)(cid:31)Ⅰ(cid:32)·17(cid:33)(cid:34)(cid:35)(cid:36)(cid:37)(cid:38)(cid:39)P-ABCD(cid:40)(cid:36)PA^(cid:41)(cid:42)ABCD(cid:36)PA= AC =2(cid:36) BC =1,AB= 3(cid:27)(1)(cid:43)AD^PB(cid:36)(cid:44)(cid:45)(cid:10)AD//(cid:46)(cid:42)PBC(cid:47) 42 (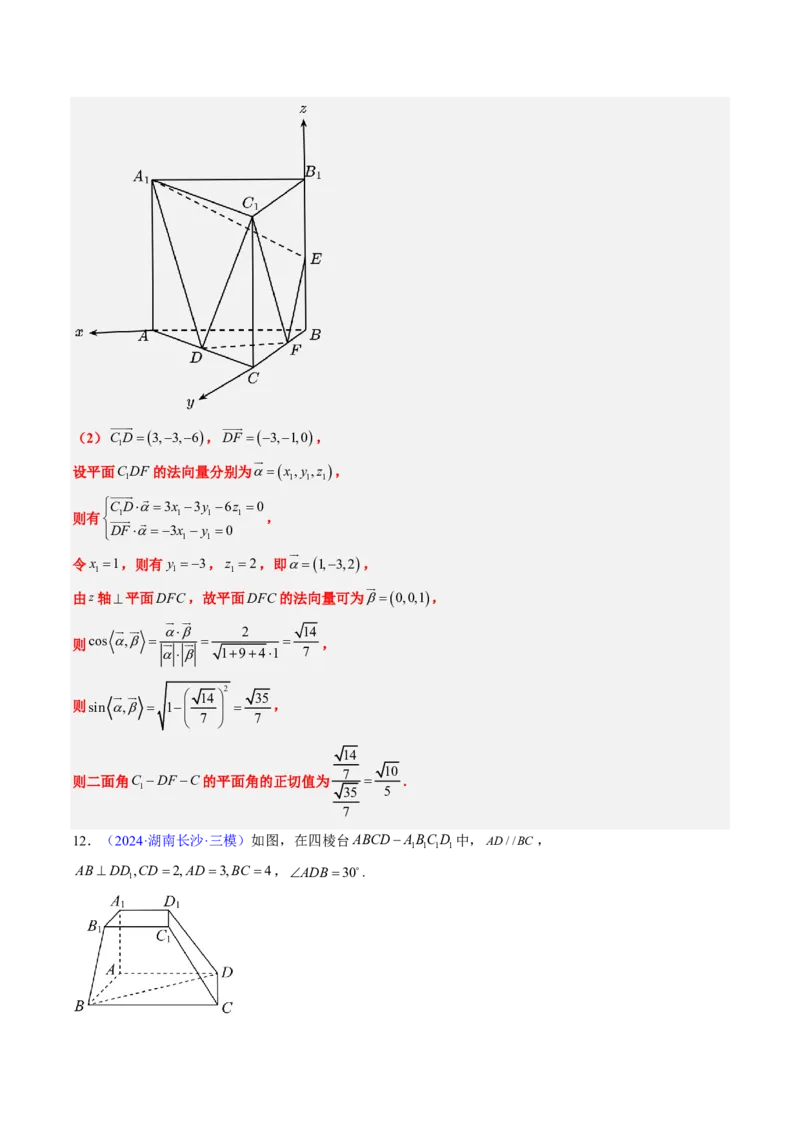2)(cid:43)AD^DC(cid:36)(cid:48)(cid:49)(cid:42)(cid:50)A-CP-D(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) (cid:36)(cid:56)AD(cid:27) 7 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) (2) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:63)(cid:44)(cid:64)AD^(cid:46)(cid:42)PAB(cid:36)(cid:65)(cid:66)(cid:67)AD^AB(cid:36)(cid:68)(cid:69)(cid:70)(cid:71)(cid:15)(cid:72)(cid:71)(cid:15)(cid:66)(cid:67)BC ^ AB(cid:36)(cid:73)(cid:74) AD//BC(cid:36)(cid:75)(cid:76)(cid:77)(cid:78)(cid:42)(cid:46)(cid:79)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:65)(cid:66)(cid:44)(cid:64)(cid:47) (cid:28)2(cid:33)(cid:81)(cid:82)D(cid:83)DE^AC(cid:84)E(cid:36)(cid:75)(cid:81)(cid:82)E(cid:83)EF ^CP(cid:84)F (cid:36)(cid:85)(cid:86)DF(cid:36)(cid:76)(cid:77)(cid:87)(cid:88)(cid:78)(cid:89)(cid:66)(cid:90)(cid:36)ÐDFE(cid:65)(cid:55)(cid:49) (cid:42)(cid:50)A-CP-D(cid:51)(cid:46)(cid:42)(cid:50)(cid:36)(cid:65)(cid:66)(cid:56)(cid:67)tanÐDFE= 6(cid:36)(cid:75)(cid:62)(cid:91)(cid:92)AD(cid:51)(cid:93)(cid:94)(cid:95)(cid:96)(cid:64)DE,EF(cid:36)(cid:65)(cid:66)(cid:25)(cid:97)(cid:98)(cid:56)(cid:64) AD(cid:27) (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:28)1(cid:33)(cid:100)(cid:55)PA^(cid:46)(cid:42)ABCD(cid:36)(cid:74)ADÌ(cid:46)(cid:42)ABCD(cid:36)(cid:101)(cid:102)PA^ AD(cid:36) (cid:103)AD^PB(cid:36)PBIPA=P(cid:36)PB,PAÌ(cid:46)(cid:42)PAB(cid:36)(cid:101)(cid:102)AD^(cid:46)(cid:42)PAB(cid:36) (cid:74)ABÌ(cid:46)(cid:42)PAB(cid:36)(cid:101)(cid:102)AD^AB. (cid:100)(cid:55)BC2+ AB2 = AC2(cid:36)(cid:101)(cid:102)BC ^ AB(cid:36) (cid:76)(cid:77)(cid:46)(cid:42)(cid:90)(cid:104)(cid:66)(cid:90)AD//BC(cid:36) (cid:103)ADË(cid:46)(cid:42)PBC(cid:36)BCÌ(cid:46)(cid:42)PBC(cid:36)(cid:101)(cid:102)AD//(cid:46)(cid:42)PBC(cid:27) (cid:28)2(cid:33)(cid:34)(cid:35)(cid:101)(cid:96)(cid:36)(cid:81)(cid:82)D(cid:83)DE^AC(cid:84)E(cid:36)(cid:75)(cid:81)(cid:82)E(cid:83)EF ^CP(cid:84)F (cid:36)(cid:85)(cid:86)DF(cid:36) (cid:100)(cid:55)PA^(cid:46)(cid:42)ABCD(cid:36)(cid:101)(cid:102)(cid:46)(cid:42)PAC ^(cid:46)(cid:42)ABCD(cid:36)(cid:74)(cid:46)(cid:42)PACI(cid:46)(cid:42)ABCD= AC(cid:36) (cid:101)(cid:102)DE^(cid:46)(cid:42)PAC(cid:36)(cid:103)EF ^CP(cid:36)(cid:101)(cid:102)CP^(cid:46)(cid:42)DEF (cid:36) (cid:76)(cid:77)(cid:49)(cid:42)(cid:50)(cid:51)(cid:71)(cid:105)(cid:66)(cid:90)(cid:36)ÐDFE(cid:65)(cid:55)(cid:49)(cid:42)(cid:50)A-CP-D(cid:51)(cid:46)(cid:42)(cid:50)(cid:36) 42 (cid:65)sinÐDFE= (cid:36)(cid:65)tanÐDFE= 6(cid:27) 7 x 4-x2 (cid:100)(cid:55)AD^DC(cid:36)(cid:106)AD = x(cid:36)(cid:107) CD= 4-x2 (cid:36)(cid:68)(cid:108)(cid:42)(cid:109)(cid:89)(cid:66)(cid:67)(cid:36)DE= (cid:36) 2 (cid:103) CE=  4-x2 - x2 4-x2 = 4-x2 (cid:36)(cid:74)VEFC(cid:55)(cid:108)(cid:110)(cid:111)(cid:50)(cid:87)(cid:50)(cid:112)(cid:36)(cid:101)(cid:102)EF = 4-x2 (cid:36) 4 2 2 2x 4-x2 2 (cid:113)tanÐDFE= = 6(cid:36)(cid:25)(cid:67)x= 3(cid:36)(cid:65)AD= 3(cid:27) 4-x2 2 2 2(cid:27)(cid:28)2024(cid:29)(cid:30)(cid:31)Ⅱ(cid:32)·17(cid:33)(cid:34)(cid:35)(cid:36)(cid:46)(cid:42)(cid:37)(cid:114)(cid:112)ABCD(cid:40)(cid:36)AB=8(cid:36)CD=3(cid:36)AD=5 3(cid:36)ÐADC =90°(cid:36)  2  1 ÐBAD=30°(cid:36)(cid:82)E(cid:36)F(cid:115)(cid:116)AE= AD(cid:36)AF = AB(cid:36)(cid:117)△AEF (cid:118)EF(cid:119)(cid:120)(cid:121) !PEF(cid:36)(cid:122)(cid:67)PC =4 3(cid:27) 5 2 (1)(cid:44)(cid:45)(cid:10)EF ^PD(cid:47) (2)(cid:56)(cid:42)PCD(cid:123)(cid:42)PBF(cid:101)(cid:124)(cid:51)(cid:49)(cid:42)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 8 65 (2) 65 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:68)(cid:21)(cid:125)(cid:36)(cid:76)(cid:77)(cid:126)(cid:53)(cid:71)(cid:15)(cid:56)(cid:67)EF =2(cid:36)(cid:127)(cid:92)(cid:69)(cid:70)(cid:71)(cid:15)(cid:51)(cid:72)(cid:71)(cid:15)(cid:66)(cid:44)(cid:67)EF^AD(cid:36)(cid:107)EF ^PE,EF ^DE(cid:36) (cid:128)(cid:129)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:123)(cid:130)(cid:131)(cid:65)(cid:66)(cid:44)(cid:45)(cid:47) (cid:28)2(cid:33)(cid:68)(cid:28)1(cid:33)(cid:36)(cid:76)(cid:77)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:123)(cid:130)(cid:131)(cid:66)(cid:44)(cid:45)PE^ED(cid:36)(cid:132)(cid:133)(cid:34)(cid:35)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)E-xyz(cid:36)(cid:127)(cid:92) (cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:56)(cid:25)(cid:42)(cid:42)(cid:50)(cid:65)(cid:66).  2  1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:68)AB=8,AD=5 3,AE= AD,AF = AB(cid:36) 5 2 (cid:67)AE=2 3,AF =4(cid:36)(cid:103)ÐBAD=30°(cid:36)(cid:141)△AEF (cid:40)(cid:36) (cid:68)(cid:126)(cid:53)(cid:71)(cid:15)(cid:67) EF = AE2+AF2-2AE×AFcosÐBAD = 16+12-2×4×2 3× 3 =2, 2 (cid:101)(cid:102)AE2+EF2 = AF2(cid:36)(cid:107)AE^EF(cid:36)(cid:65)EF^AD(cid:36) (cid:101)(cid:102)EF ^PE,EF ^DE(cid:36)(cid:103)PEIDE=E,PE(cid:24)DEÌ(cid:46)(cid:42)PDE(cid:36)(cid:101)(cid:102)EF^(cid:46)(cid:42)PDE(cid:36)(cid:103)PDÌ(cid:46)(cid:42)PDE(cid:36) (cid:113)EF^PD(cid:47) (cid:28)2(cid:33)(cid:85)(cid:86)CE(cid:36)(cid:68)ÐADC=90°,ED=3 3,CD=3(cid:36)(cid:107)CE2 =ED2+CD2 =36(cid:36) (cid:141)VPEC(cid:40)(cid:36)PC=4 3,PE=2 3,EC=6(cid:36)(cid:67)EC2+PE2 =PC2(cid:36) (cid:101)(cid:102)PE^EC(cid:36)(cid:68)(cid:28)1(cid:33)(cid:90)PE^EF(cid:36)(cid:103)ECIEF =E,EC(cid:24)EFÌ(cid:46)(cid:42)ABCD(cid:36) (cid:101)(cid:102)PE^(cid:46)(cid:42)ABCD(cid:36)(cid:103)EDÌ(cid:46)(cid:42)ABCD(cid:36) (cid:101)(cid:102)PE^ED(cid:36)(cid:107)PE,EF,ED(cid:142)(cid:142)(cid:88)(cid:111)(cid:36)(cid:132)(cid:133)(cid:34)(cid:35)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)E-xyz(cid:36) (cid:107)E(0,0,0),P(0,0,2 3),D(0,3 3,0),C(3,3 3,0),F(2,0,0),A(0,-2 3,0)(cid:36) (cid:68)F (cid:143)AB(cid:51)(cid:40)(cid:82)(cid:36)(cid:67)B(4,2 3,0)(cid:36)     (cid:101)(cid:102)PC=(3,3 3,-2 3),PD=(0,3 3,-2 3),PB=(4,2 3,-2 3),PF =(2,0,-2 3)(cid:36)   (cid:106)(cid:46)(cid:42)PCD(cid:144)(cid:46)(cid:42)PBF(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:62)(cid:91)(cid:55)n=(x,y ,z ),m=(x ,y ,z )(cid:36) 1 1 1 2 2 2     ì ïn×PC =3x +3 3y -2 3z =0 ì ïm×PB=4x +2 3y -2 3z =0 (cid:107)í   1 1 1 (cid:36)í   2 2 2 (cid:36) ïîn×PD=3 3y -2 3z =0 ïîm×PF =2x -2 3z =0 1 1 2 2 (cid:146)y =2,x = 3(cid:36)(cid:67)x =0,z =3,y =-1,z =1(cid:36) 1 2 1 1 2 2   (cid:101)(cid:102)n=(0,2,3),m=( 3,-1,1)(cid:36)     m×n 1 65 (cid:101)(cid:102) cosm,n =   = = (cid:36) m n 5× 13 65 8 65 (cid:106)(cid:46)(cid:42)PCD(cid:144)(cid:46)(cid:42)PBF(cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)(cid:107)sinq= 1-cos2q= (cid:36) 65 8 65 (cid:65)(cid:46)(cid:42)PCD(cid:144)(cid:46)(cid:42)PBF(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 65 (cid:23)(cid:24)(cid:25)(cid:26)(cid:21) 1(cid:27)(cid:28)2022(cid:29)(cid:30)(cid:31)Ⅰ(cid:32)·19(cid:33)(cid:34)(cid:35)(cid:36)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:51)(cid:148)(cid:109)(cid:55)4(cid:36)VABC(cid:51)(cid:42)(cid:109)(cid:55)2 2(cid:27) 1 1 1 1(1)(cid:56)A(cid:149)(cid:46)(cid:42)ABC(cid:51)(cid:150)(cid:151)(cid:47) 1 (2)(cid:106)D(cid:55)AC(cid:51)(cid:40)(cid:82)(cid:36)AA = AB(cid:36)(cid:46)(cid:42)ABC ^(cid:46)(cid:42)ABBA (cid:36)(cid:56)(cid:49)(cid:42)(cid:50)A-BD-C(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) 1 1 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1) 2 3 (2) 2 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:68)(cid:108)(cid:148)(cid:109)(cid:89)(cid:152)(cid:153)(cid:65)(cid:66)(cid:67)(cid:25)(cid:47) (cid:28)2(cid:33)(cid:68)(cid:42)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:154)(cid:80)(cid:71)(cid:66)(cid:67)BC^(cid:46)(cid:42)ABBA (cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:65)(cid:66)(cid:67)(cid:25). 1 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)(cid:106)(cid:82)A(cid:149)(cid:46)(cid:42)ABC(cid:51)(cid:150)(cid:151)(cid:55)h(cid:36) 1 1 1 1 1 2 2 1 1 4 (cid:107)V = S ×h= h=V = S ×AA= V = (cid:36) A-A1BC 3 VA1BC 3 A1 -ABC 3 VABC 1 3 ABC-A1B1C1 3 (cid:25)(cid:67)h= 2(cid:36) (cid:101)(cid:102)(cid:82)A(cid:149)(cid:46)(cid:42)ABC(cid:51)(cid:150)(cid:151)(cid:55) 2(cid:47) 1 (cid:28)2(cid:33)(cid:155)AB(cid:51)(cid:40)(cid:82)E,(cid:85)(cid:86)AE,(cid:34)(cid:35)(cid:36)(cid:100)(cid:55)AA = AB(cid:36)(cid:101)(cid:102)AE^ AB, 1 1 1 (cid:103)(cid:46)(cid:42)ABC ^(cid:46)(cid:42)ABBA (cid:36)(cid:46)(cid:42)ABCÇ(cid:46)(cid:42)ABBA = AB(cid:36) 1 1 1 1 1 1 1 (cid:48)AEÌ(cid:46)(cid:42)ABBA (cid:36)(cid:101)(cid:102)AE^(cid:46)(cid:42)ABC(cid:36) 1 1 1 (cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)BB ^(cid:46)(cid:42)ABC(cid:36) 1 1 1 1 (cid:68)BCÌ(cid:46)(cid:42)ABC(cid:36)BCÌ(cid:46)(cid:42)ABC(cid:66)(cid:67)AE^BC(cid:36)BB ^BC(cid:36) 1 1 (cid:103)AE,BB Ì(cid:46)(cid:42)ABBA (cid:48)(cid:156)(cid:157)(cid:36)(cid:101)(cid:102)BC^(cid:46)(cid:42)ABBA (cid:36) 1 1 1 1 1 (cid:101)(cid:102)BC,BA,BB (cid:142)(cid:142)(cid:88)(cid:111)(cid:36)(cid:102)B(cid:55)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:34)(cid:35)(cid:36) 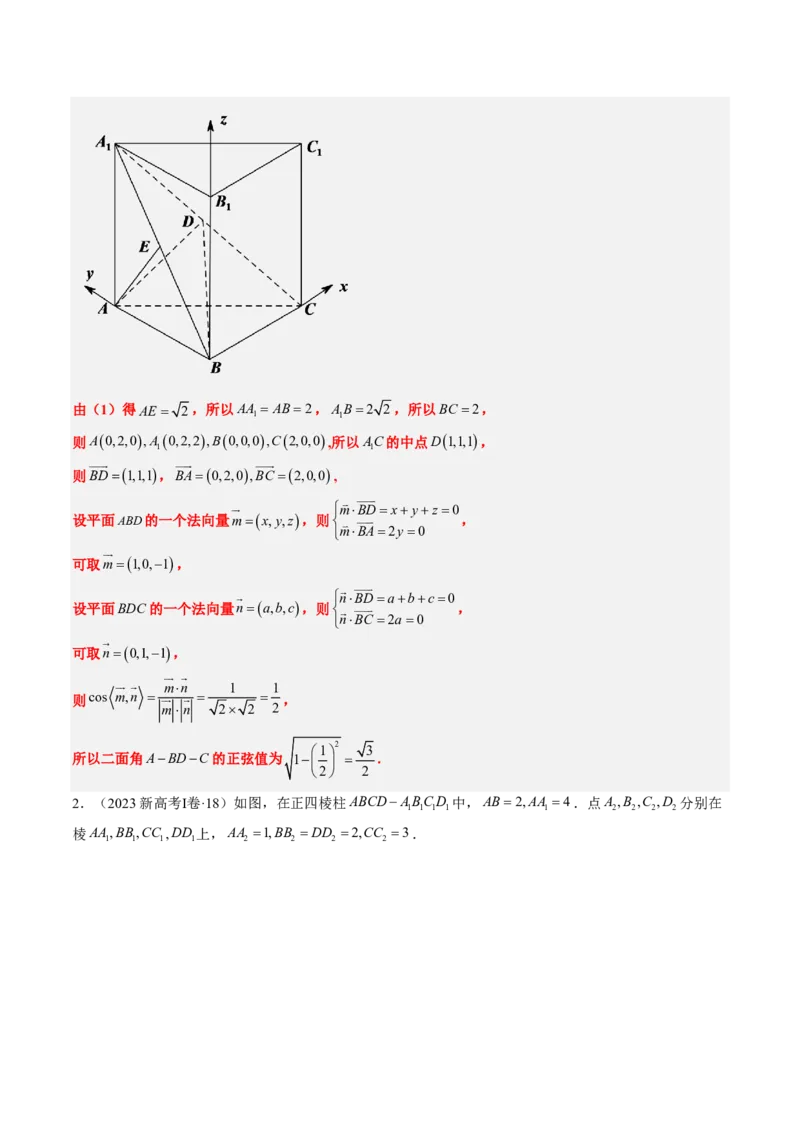1(cid:68)(cid:28)1(cid:33)(cid:67)AE= 2(cid:36)(cid:101)(cid:102)AA = AB=2(cid:36)AB=2 2(cid:36)(cid:101)(cid:102)BC =2(cid:36) 1 1 (cid:107)A0,2,0,A 0,2,2,B0,0,0,C2,0,0,(cid:101)(cid:102)AC(cid:51)(cid:40)(cid:82)D1,1,1(cid:36) 1 1    (cid:107)BD=1,1,1(cid:36)BA=0,2,0,BC =2,0,0, v v  ìm×BD=x+y+z=0 (cid:106)(cid:46)(cid:42)ABD(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)m=x,y,z(cid:36)(cid:107)ív v (cid:36) îm×BA=2y=0  (cid:66)(cid:155)m=1,0,-1(cid:36)  v  ìn×BD=a+b+c=0 (cid:106)(cid:46)(cid:42)BDC(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)n=a,b,c(cid:36)(cid:107)í v (cid:36) în×BC =2a=0 r (cid:66)(cid:155)n=0,1,-1(cid:36)     m×n 1 1 (cid:107)cos m,n =   = = (cid:36) m× n 2´ 2 2 2 æ1ö 3 (cid:101)(cid:102)(cid:49)(cid:42)(cid:50)A-BD-C(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) 1-ç ÷ = . è2ø 2 2(cid:27)(cid:28)2023(cid:29)(cid:30)(cid:31)Ⅰ(cid:32)·18(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:52)(cid:37)(cid:38)(cid:147)ABCD-ABCD (cid:40)(cid:36)AB=2,AA =4(cid:27)(cid:82)A ,B ,C ,D (cid:62)(cid:91)(cid:141) 1 1 1 1 1 2 2 2 2 (cid:38)AA,BB,CC ,DD (cid:159)(cid:36)AA =1,BB =DD =2,CC =3(cid:27) 1 1 1 1 2 2 2 2(1)(cid:44)(cid:45)(cid:10)BC(cid:160)AD (cid:47) 2 2 2 2 (2)(cid:82)P(cid:141)(cid:38)BB (cid:159)(cid:36)(cid:161)(cid:49)(cid:42)(cid:50)P-AC -D (cid:55)150°(cid:162)(cid:36)(cid:56)B P(cid:27) 1 2 2 2 2 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)(cid:47) (2)1 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:136)(cid:137)(cid:156)(cid:108)(cid:44)(cid:45)(cid:47) (cid:28)2(cid:33)(cid:106)P(0,2,l)(0£l£4)(cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:89)(cid:56)(cid:49)(cid:42)(cid:50)(cid:36)(cid:132)(cid:133)(cid:97)(cid:98)(cid:56)(cid:64)l(cid:65)(cid:66)(cid:67)(cid:25). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:102)C(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)CD,CB,CC (cid:101)(cid:141)(cid:111)(cid:78)(cid:55)x,y,z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:34)(cid:35)(cid:36) 1 (cid:107)C(0,0,0),C (0,0,3),B (0,2,2),D (2,0,2),A (2,2,1)(cid:36) 2 2 2 2   \BC =(0,-2,1),A D =(0,-2,1)(cid:36) 2 2 2 2   \BC(cid:160)A D (cid:36) 2 2 2 2 (cid:103)BC(cid:36)A D (cid:164)(cid:141)(cid:165)(cid:23)(cid:166)(cid:111)(cid:78)(cid:159)(cid:36) 2 2 2 2 \BC(cid:160)A D . 2 2 2 2 (cid:28)2(cid:33)(cid:106)P(0,2,l)(0£l£4)(cid:36)    (cid:107)AC =(-2,-2,2),PC =(0,-2,3-l),DC =(-2,0,1)(cid:36) 2 2 2 2 2  (cid:106)(cid:46)(cid:42)PAC (cid:51)(cid:89)(cid:139)(cid:140)n=(x,y,z)(cid:36) 2 2  ì ïn×AC =-2x-2y+2z=0 (cid:107)í   2  2 (cid:36) ïîn×PC =-2y+(3-l)z=0 2 (cid:146) z=2(cid:36)(cid:67)y=3-l,x=l-1(cid:36)  \n=(l-1,3-l,2)(cid:36)  (cid:106)(cid:46)(cid:42)AC D (cid:51)(cid:89)(cid:139)(cid:140)m=(a,b,c)(cid:36) 2 2 2   ì ïm×AC =-2a-2b+2c=0 (cid:107)í   2  2  (cid:36) ïîm×DC =-2a+c=0 2 2 (cid:146) a=1(cid:36)(cid:67)b=1,c=2(cid:36)  \m=(1,1,2)(cid:36)     n×m 6 3 \cos n,m =   = = cos150° = (cid:36) n m 6 4+(l-1)2+(3-l)2 2 (cid:16)(cid:167)(cid:66)(cid:67)(cid:36)l2-4l+3=0(cid:36) (cid:25)(cid:67)l=1(cid:168)l=3(cid:36) \P(0,2,1)(cid:168)P(0,2,3)(cid:36) \B P=1. 2 3(cid:27)(cid:28)2022(cid:29)(cid:30)(cid:31)Ⅱ(cid:32)·20(cid:33)(cid:34)(cid:35)(cid:36)PO(cid:143)(cid:87)(cid:38)(cid:39)P-ABC(cid:51)(cid:30)(cid:36)PA=PB(cid:36)AB^AC(cid:36)E(cid:143)PB(cid:51)(cid:40)(cid:82)(cid:27) (1)(cid:44)(cid:45)(cid:10)OE//(cid:46)(cid:42)PAC(cid:47) (2)(cid:43)ÐABO=ÐCBO=30°(cid:36)PO=3(cid:36)PA=5(cid:36)(cid:56)(cid:49)(cid:42)(cid:50)C-AE-B(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 11 (2) 13 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)BO(cid:169)(cid:170)(cid:93)(cid:157)AC(cid:84)(cid:82)D(cid:36)(cid:85)(cid:86)OA(cid:24)PD(cid:36)(cid:76)(cid:77)(cid:87)(cid:50)(cid:112)(cid:171)(cid:108)(cid:67)(cid:149)OA=OB(cid:36)(cid:75)(cid:76)(cid:77)(cid:111)(cid:50) (cid:87)(cid:50)(cid:112)(cid:51)(cid:130)(cid:131)(cid:67)(cid:149)AO=DO(cid:36)(cid:65)(cid:66)(cid:67)(cid:149)O(cid:55)BD(cid:51)(cid:40)(cid:82)(cid:73)(cid:74)(cid:67)(cid:149)OE//PD(cid:36)(cid:65)(cid:66)(cid:67)(cid:44)(cid:47) (cid:28)2(cid:33)(cid:132)(cid:133)(cid:172)(cid:161)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:56)(cid:64)(cid:49)(cid:42)(cid:50)(cid:51)(cid:126)(cid:53)(cid:51)(cid:173)(cid:119)(cid:54)(cid:36)(cid:75)(cid:76)(cid:77)(cid:165)(cid:50)(cid:87)(cid:50)(cid:174)(cid:13)(cid:51)(cid:175) (cid:176)(cid:3)(cid:138)(cid:177)(cid:153)(cid:66)(cid:67). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:44)(cid:45)(cid:10)(cid:85)(cid:86)BO(cid:169)(cid:170)(cid:93)(cid:157)AC(cid:84)(cid:82)D(cid:36)(cid:85)(cid:86)OA(cid:24)PD(cid:36) (cid:100)(cid:55)PO(cid:143)(cid:87)(cid:38)(cid:39)P-ABC(cid:51)(cid:30)(cid:36)(cid:101)(cid:102)PO^(cid:46)(cid:42)ABC(cid:36)AO,BOÌ(cid:46)(cid:42)ABC(cid:36)(cid:101)(cid:102)PO^ AO(cid:24)PO^BO(cid:36) (cid:103)PA=PB(cid:36)(cid:101)(cid:102)(cid:178)POA@(cid:178)POB(cid:36)(cid:65)OA=OB(cid:36)(cid:101)(cid:102)ÐOAB=ÐOBA(cid:36) (cid:103)AB^AC(cid:36)(cid:65)ÐBAC =90°(cid:36)(cid:101)(cid:102)ÐOAB+ÐOAD=90°(cid:36)ÐOBA+ÐODA=90°(cid:36) (cid:101)(cid:102)ÐODA=ÐOAD (cid:101)(cid:102)AO=DO(cid:36)(cid:65)AO=DO=OB(cid:36)(cid:101)(cid:102)O(cid:55)BD(cid:51)(cid:40)(cid:82)(cid:36)(cid:103)E(cid:55)PB(cid:51)(cid:40)(cid:82)(cid:36)(cid:101)(cid:102)OE//PD(cid:36) (cid:103)OEË(cid:46)(cid:42)PAC(cid:36)PDÌ(cid:46)(cid:42)PAC(cid:36) (cid:101)(cid:102)OE//(cid:46)(cid:42)PAC (cid:28)2(cid:33)(cid:25)(cid:10)(cid:81)(cid:82)A(cid:83)Az//OP(cid:36)(cid:34)(cid:35)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:100)(cid:55)PO=3(cid:36)AP=5(cid:36)(cid:101)(cid:102) OA= AP2-PO2 =4 (cid:36) (cid:103)ÐOBA=ÐOBC =30°(cid:36)(cid:101)(cid:102)BD=2OA=8(cid:36)(cid:107)AD=4(cid:36)AB=4 3(cid:36)       (cid:101)(cid:102)AC =12(cid:36)(cid:101)(cid:102)O 2 3,2,0 (cid:36)B 4 3,0,0 (cid:36)P 2 3,2,3 (cid:36)C0,12,0(cid:36) æ 3ö (cid:101)(cid:102)Eç3 3,1, ÷(cid:36) è 2ø  æ 3ö     (cid:107)AE=ç3 3,1, ÷(cid:36)AB= 4 3,0,0 (cid:36)AC =0,12,0(cid:36) è 2ø ìv v 3  ïn×AE=3 3x+y+ z=0 (cid:106)(cid:46)(cid:42)AEB(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36)(cid:107)í 2 (cid:36)(cid:146)z=2(cid:36)(cid:107)y=-3(cid:36)x=0(cid:36)(cid:101)(cid:102) ïv v în×AB=4 3x=0  n=0,-3,2(cid:47) ìv v 3  ïm×AE=3 3a+b+ c=0 (cid:106)(cid:46)(cid:42)AEC(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)m=a,b,c(cid:36)(cid:107)í 2 (cid:36) ï îm v ×  A  C v =12b=0    (cid:146)a= 3(cid:36)(cid:107)c=-6(cid:36)b=0(cid:36)(cid:101)(cid:102)m= 3,0,-6 (cid:47)     n×m -12 4 3 (cid:101)(cid:102)cos n,m =   = =- . n m 13´ 39 13   4 3 (cid:106)(cid:49)(cid:42)(cid:50)C-AE-B(cid:51)(cid:179)(cid:180)(cid:55)q(cid:36)(cid:107) cosq= cos n,m = (cid:36) 13 11 11 (cid:101)(cid:102)sinq= 1-cos2q= (cid:36)(cid:65)(cid:49)(cid:42)(cid:50)C-AE-B(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 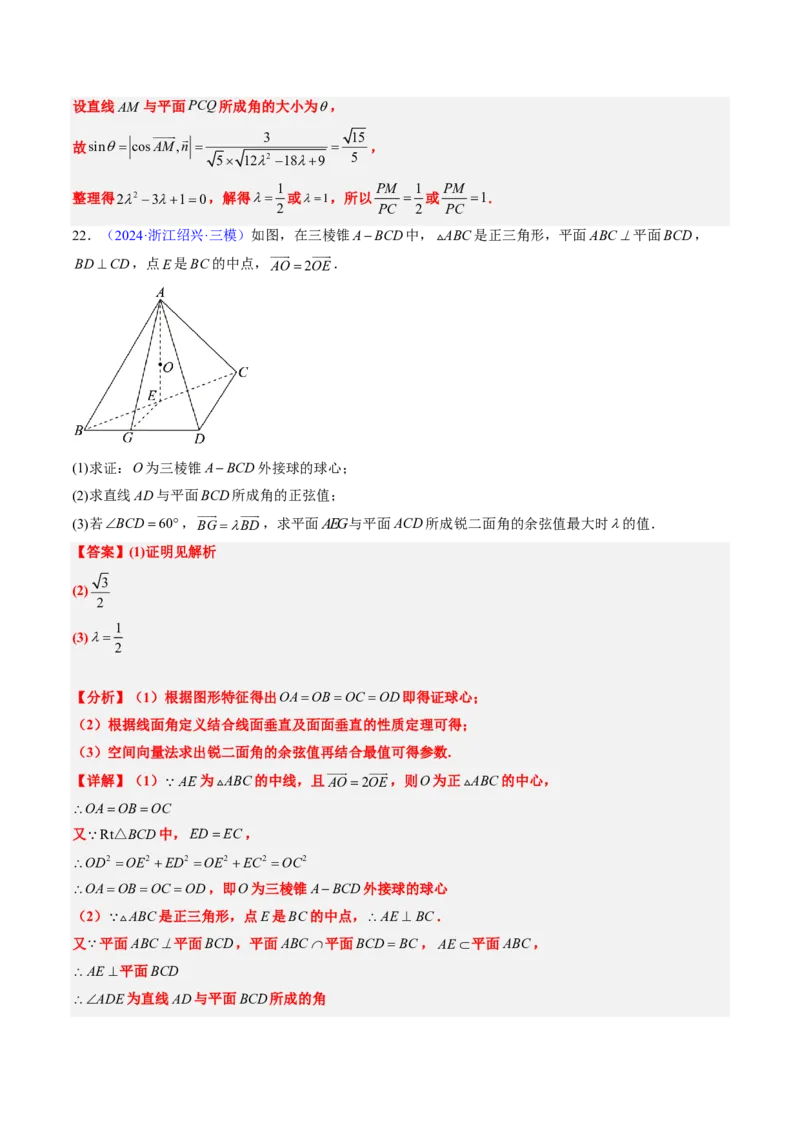13 134(cid:27)(cid:28)2023 (cid:29)(cid:30)(cid:31)Ⅱ(cid:32)·20(cid:33)(cid:34)(cid:35)(cid:36)(cid:87)(cid:38)(cid:39)A-BCD(cid:40)(cid:36)DA=DB=DC(cid:36)BD^CD(cid:36)ÐADB=ÐADC =60o(cid:36) E(cid:55)BC(cid:51)(cid:40)(cid:82)(cid:27) (1)(cid:44)(cid:45)(cid:10)BC ^DA(cid:47)   (2)(cid:82)F(cid:115)(cid:116)EF =DA(cid:36)(cid:56)(cid:49)(cid:42)(cid:50)D-AB-F(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)(cid:47) 3 (2) (cid:27) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:76)(cid:77)(cid:21)(cid:125)(cid:181)(cid:44)BC^(cid:46)(cid:42)ADE(cid:36)(cid:73)(cid:74)(cid:44)(cid:67)BC ^DA(cid:47) (cid:28)2(cid:33)(cid:68)(cid:21)(cid:66)(cid:44)AE^(cid:46)(cid:42)BCD(cid:36)(cid:101)(cid:102)(cid:102)(cid:82)E(cid:55)(cid:158)(cid:82)(cid:36)ED,EB,EA(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x,y,z(cid:163)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50) (cid:136)(cid:137)(cid:138)(cid:36)(cid:75)(cid:56)(cid:64)(cid:46)(cid:42)ABD,ABF (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:36)(cid:76)(cid:77)(cid:49)(cid:42)(cid:50)(cid:51)(cid:139)(cid:140)(cid:7)(cid:182)(cid:102)(cid:154)(cid:165)(cid:50)(cid:87)(cid:50)(cid:174)(cid:13)(cid:3)(cid:138)(cid:65)(cid:66)(cid:25)(cid:64)(cid:27) (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)AE,DE(cid:36)(cid:100)(cid:55)E(cid:55)BC(cid:40)(cid:82)(cid:36)DB=DC(cid:36)(cid:101)(cid:102)DE^BC (cid:36) (cid:100)(cid:55)DA=DB=DC(cid:36)ÐADB=ÐADC =60o(cid:36)(cid:101)(cid:102)VACD(cid:123)△ABD(cid:183)(cid:55)(cid:108)(cid:114)(cid:87) ① (cid:50)(cid:112)(cid:36) \AC = AB(cid:36)(cid:73)(cid:74)AE^BC (cid:36)(cid:68) (cid:36)AEIDE=E(cid:36)AE,DEÌ(cid:46)(cid:42)ADE(cid:36) (cid:101)(cid:102)(cid:36)BC^(cid:46)(cid:42)ADE(cid:36)(cid:74) ②ADÌ(cid:46) ① (cid:42) ②ADE(cid:36)(cid:101)(cid:102)BC ^DA(cid:27) (cid:28)2(cid:33)(cid:164)(cid:184)(cid:106)DA=DB=DC =2(cid:36)QBD^CD(cid:36)\BC =2 2,DE= AE= 2(cid:27) \AE2+DE2 =4= AD2(cid:36)\AE^DE(cid:36)(cid:103)QAE^BC,DEIBC =E(cid:36)DE,BCÌ(cid:46)(cid:42)BCD\AE^(cid:46)(cid:42) BCD(cid:27) (cid:102)(cid:82)E(cid:55)(cid:158)(cid:82)(cid:36)ED,EB,EA(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x,y,z(cid:163)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:34)(cid:35)(cid:101)(cid:96)(cid:10)(cid:106)D( 2,0,0),A(0,0, 2),B(0, 2,0),E(0,0,0)(cid:36)   (cid:106)(cid:46)(cid:42)DAB(cid:123)(cid:46)(cid:42)ABF (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:62)(cid:91)(cid:55)n =x,y ,z ,n =x ,y ,z (cid:36) 1 1 1 1 2 2 2 2    (cid:49)(cid:42)(cid:50)D-AB-F(cid:46)(cid:42)(cid:50)(cid:55)q,(cid:74)AB= 0, 2,- 2 (cid:36)          (cid:100)(cid:55)EF =DA= - 2,0, 2 (cid:36)(cid:101)(cid:102)F - 2,0, 2 (cid:36)(cid:65)(cid:185)AF = - 2,0,0 (cid:36) ï ì- 2x + 2z =0  \í 1 1 (cid:36)(cid:155)x =1(cid:36)(cid:101)(cid:102)n =(1,1,1)(cid:47) ïî 2y - 2z =0 1 1 1 1 ï ì 2y - 2z =0  í 2 2 (cid:36)(cid:155)y =1(cid:36)(cid:101)(cid:102)n =(0,1,1)(cid:36) ïî- 2x =0 2 2 2   n ×n 1 2 2 6 6 3 (cid:101)(cid:102)(cid:36) cosq=   = = (cid:36)(cid:73)(cid:74)sinq= 1- = (cid:27) n n 3´ 2 3 9 3 1 2 3 (cid:101)(cid:102)(cid:49)(cid:42)(cid:50)D-AB-F(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) (cid:27) 3 (cid:23)(cid:24)(cid:111)(cid:78)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140) 1(cid:24)(cid:111)(cid:78)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)  (cid:34)(cid:35)8-153(cid:101)(cid:96)(cid:36)l(cid:55)(cid:186)(cid:81)(cid:187)(cid:90)(cid:82)A(cid:48)(cid:46)(cid:79)(cid:84)(cid:187)(cid:90)(cid:188)(cid:189)(cid:139)(cid:140)a(cid:51)(cid:111)(cid:78)(cid:27)(cid:119)(cid:134)(cid:135)(cid:190)(cid:125)(cid:23)(cid:82)O(cid:36)(cid:82)P(cid:141)(cid:111)(cid:78)l(cid:159)       (cid:51)(cid:191)(cid:192)(cid:166)(cid:193)(cid:143)(cid:194)(cid:141)(cid:195)(cid:13)t(cid:36)(cid:122)OP=OA+ta (cid:36)(cid:196)(cid:40)(cid:139)(cid:140)a(cid:197)(cid:198)(cid:111)(cid:78)l(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:36)(cid:141)l(cid:159)(cid:155)AB=a(cid:36)(cid:107)(cid:182)         (cid:66)(cid:16)(cid:55)OP=OA+tAB=OA+t  OB-OA  =①1-tOA+tOB ① 1 ②  1    (cid:144) (cid:199)(cid:200)(cid:55)(cid:134)(cid:135)(cid:111)(cid:78)(cid:51)(cid:139)(cid:140)(cid:95)(cid:201)(cid:182)(cid:36)(cid:161)t = (cid:36)(cid:65)(cid:82)P(cid:143)(cid:78)(cid:202)AB(cid:51)(cid:40)(cid:82)(cid:162)(cid:36)OP= OA+OB (cid:36)(cid:203)(cid:182)(cid:197) 2 2 ① ② (cid:198)(cid:78)(cid:202)AB(cid:51)(cid:40)(cid:82)(cid:7)(cid:182)(cid:27) 2(cid:24)(cid:204)(cid:42)(cid:139)(cid:140)    (cid:34)(cid:35)8-154(cid:101)(cid:96)(cid:36)(cid:187)(cid:90)(cid:46)(cid:42)a(cid:123)(cid:139)(cid:140)a(cid:36)(cid:83)OA=a(cid:36)(cid:34)(cid:205)(cid:111)(cid:78)OA(cid:46)(cid:79)(cid:84)(cid:46)(cid:42)a(cid:168)(cid:141)(cid:46)(cid:42)a(cid:206)(cid:36)(cid:107)(cid:207)(cid:45)(cid:139)(cid:140)  a(cid:46)(cid:79)(cid:84)(cid:46)(cid:42)a(cid:27)(cid:46)(cid:79)(cid:84)(cid:165)(cid:23)(cid:46)(cid:42)(cid:51)(cid:139)(cid:140)(cid:36)(cid:197)(cid:198)(cid:204)(cid:42)(cid:139)(cid:140)(cid:27)a O A a a 3(cid:24)(cid:204)(cid:42)(cid:139)(cid:140)(cid:71)(cid:15)      (cid:34)(cid:205)(cid:142)(cid:145)(cid:139)(cid:140)a(cid:36)b(cid:164)(cid:204)(cid:78)(cid:36)(cid:208)(cid:209)(cid:139)(cid:140)p(cid:123)(cid:139)(cid:140)a(cid:36)b(cid:204)(cid:42)(cid:51)(cid:191)(cid:192)(cid:166)(cid:193)(cid:143)(cid:194)(cid:141)(cid:210)(cid:23)(cid:51)(cid:185)(cid:211)(cid:195)(cid:13)(cid:119)x,y(cid:36)(cid:122)    p=xa+ yb(cid:27)    (cid:212)(cid:213)(cid:10) (cid:134)(cid:135)(cid:23)(cid:82)P(cid:214)(cid:84)(cid:46)(cid:42)ABC(cid:206)(cid:51)(cid:191)(cid:192)(cid:166)(cid:193)(cid:143)(cid:194)(cid:141)(cid:185)(cid:211)(cid:195)(cid:13)(cid:119)x,y(cid:36)(cid:122)AP=xAB+ yAC(cid:47)(cid:168)(cid:119)(cid:134)(cid:135)     (cid:190)(cid:125)(cid:23)①(cid:82)O(cid:36)(cid:185)OP-OA=xAB+ yAC(cid:36)(cid:215)(cid:182)(cid:200)(cid:55)(cid:134)(cid:135)(cid:46)(cid:42)ABC(cid:51)(cid:139)(cid:140)(cid:95)(cid:201)(cid:182)(cid:27)     (cid:187)(cid:90)(cid:134)(cid:135)(cid:190)(cid:125)(cid:23)(cid:82)O(cid:144)(cid:164)(cid:204)(cid:78)(cid:51)(cid:87)(cid:82)A(cid:36)B(cid:36)C(cid:36)(cid:115)(cid:116)(cid:139)(cid:140)(cid:3)(cid:138)(cid:182)OP=xOA+ yOB+zOC (cid:28)(cid:196)(cid:40) ②x+ y+z=1(cid:33)(cid:51)(cid:82)P(cid:123)(cid:82)A(cid:36)B(cid:36)C(cid:204)(cid:42)(cid:47)(cid:216)(cid:217)(cid:218)(cid:124)(cid:133)(cid:27) (cid:49)(cid:24)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:13)(cid:140)(cid:109)(cid:152)(cid:153) 1(cid:24)(cid:142)(cid:139)(cid:140)(cid:219)(cid:50)         (cid:187)(cid:90)(cid:142)(cid:145)(cid:188)(cid:189)(cid:139)(cid:140)a(cid:36)b(cid:36)(cid:141)(cid:134)(cid:135)(cid:190)(cid:155)(cid:23)(cid:82)O(cid:36)(cid:83)OA=a(cid:36)OB=b(cid:36)(cid:107)ÐAOB(cid:197)(cid:198)(cid:139)(cid:140)a(cid:36)b(cid:51)(cid:219)(cid:50)(cid:36)(cid:220)(cid:83)       p     a,b (cid:36)(cid:221)(cid:222)(cid:223)(cid:71)0£ a,b £p(cid:36)(cid:34)(cid:205) a,b = (cid:36)(cid:208)(cid:209)(cid:139)(cid:140)a(cid:36)b(cid:224)(cid:156)(cid:88)(cid:111)(cid:36)(cid:220)(cid:83)a^b(cid:27) 2 2(cid:24)(cid:13)(cid:140)(cid:109)(cid:71)(cid:105)                 (cid:187)(cid:90)(cid:142)(cid:145)(cid:188)(cid:189)(cid:139)(cid:140)a(cid:36)b(cid:36)(cid:107) a bcos a,b (cid:197)(cid:198)a(cid:36)b(cid:51)(cid:13)(cid:140)(cid:109)(cid:36)(cid:220)(cid:83)a×b(cid:36)(cid:65)a×b= a b cos a,b (cid:27)(cid:189)(cid:139)(cid:140)    2 (cid:123)(cid:190)(cid:225)(cid:139)(cid:140)(cid:51)(cid:13)(cid:140)(cid:109)(cid:55)0(cid:36)(cid:226)(cid:91)(cid:227)(cid:36)a×a= a (cid:27) 3(cid:24)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:13)(cid:140)(cid:109)(cid:115)(cid:116)(cid:51)(cid:152)(cid:153)(cid:228)(cid:10)             la ×b=l a×b (cid:36)a×b=b×a(cid:28)(cid:157)(cid:229)(cid:228)(cid:33)(cid:47)          a× b+c =a×b+a×c(cid:28)(cid:62)(cid:230)(cid:228)(cid:33)(cid:27) (cid:87)(cid:24)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:136)(cid:137)(cid:152)(cid:153)(cid:154)(cid:231)(cid:92)     1(cid:24)(cid:106)a=a,a ,a (cid:36)b=b,b ,b (cid:36)(cid:107)a+b=a +b,a +b ,a +b (cid:47) 1 2 3 1 2 3 1 1 2 2 3 3   a-b=a -b,a -b ,a -b (cid:47) 1 1 2 2 3 3  la=la ,la ,la (cid:47) 1 2 3   a×b=ab +a b +ab (cid:47) 1 1 2 2 3 3       a//b b¹0 Þa =lb,a =lb ,a =lb (cid:47) 1 1 2 2 3 3  a^bÞab +a b +ab =0(cid:27) 1 1 2 2 3 3    2(cid:24)(cid:106)Ax,y ,z (cid:36)Bx ,y ,z (cid:36)(cid:107)AB=OB-OA=x -x,y - y ,z -z (cid:27) 1 1 1 2 2 2 2 1 2 1 2 1 (cid:232)(cid:233)(cid:143)(cid:207)(cid:36)(cid:23)(cid:145)(cid:139)(cid:140)(cid:141)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:40)(cid:51)(cid:136)(cid:137)(cid:108)(cid:84)(cid:95)(cid:96)(cid:215)(cid:139)(cid:140)(cid:51)(cid:185)(cid:139)(cid:78)(cid:202)(cid:51)(cid:234)(cid:82)(cid:51)(cid:136)(cid:137)(cid:235)(cid:236)(cid:82)(cid:51)(cid:136)(cid:137)(cid:27) 3(cid:24)(cid:142)(cid:145)(cid:139)(cid:140)(cid:51)(cid:219)(cid:50)(cid:154)(cid:142)(cid:82)(cid:135)(cid:51)(cid:150)(cid:151)(cid:7)(cid:182)(cid:27)     (cid:187)(cid:90)a=a,a ,a (cid:36)b=b,b ,b (cid:36)(cid:107) a = a 2 = a2 +a 2 +a2 (cid:47) 1 2 3 1 2 3 1 2 3 ①  b = b 2 = b2 +b2 +b2 (cid:47) 1 2 3   a×b=ab +a b +ab (cid:47) 1 1 2 2 3 3   ab +a b +ab cos a,b = 1 1 2 2 3 3 (cid:47) a2 +a 2 +a2 b2 +b2 +b2 1 2 3 1 2 3  (cid:187)(cid:90)Ax,y ,z (cid:36)Bx ,y ,z (cid:36)(cid:107) AB = x -x 2 +y - y 2 +z -z 2 (cid:36) 1 1 1 2 2 2 1 2 1 2 1 2  (cid:168) ② (cid:237)dA,B= AB (cid:27)(cid:196)(cid:40)dA,B(cid:95)(cid:96)A(cid:123)B(cid:142)(cid:82)(cid:135)(cid:51)(cid:150)(cid:151)(cid:36)(cid:232)(cid:233)(cid:143)(cid:134)(cid:135)(cid:142)(cid:82)(cid:51)(cid:150)(cid:151)(cid:7)(cid:182)(cid:27)        a×b 4(cid:24)(cid:139)(cid:140)a(cid:141)(cid:139)(cid:140)b(cid:159)(cid:51)(cid:238)(cid:239)(cid:55) a cos a,b =  (cid:27) b (cid:37)(cid:24)(cid:89)(cid:139)(cid:140)(cid:51)(cid:56)(cid:25)(cid:123)(cid:167)(cid:240)(cid:231)(cid:92) 1(cid:24)(cid:46)(cid:42)(cid:51)(cid:89)(cid:139)(cid:140)(cid:10)    (cid:34)(cid:205)(cid:95)(cid:96)(cid:139)(cid:140)n(cid:51)(cid:185)(cid:139)(cid:78)(cid:202)(cid:101)(cid:141)(cid:111)(cid:78)(cid:88)(cid:111)(cid:84)(cid:46)(cid:42)a(cid:36)(cid:107)(cid:200)(cid:232)(cid:145)(cid:139)(cid:140)(cid:88)(cid:111)(cid:84)(cid:46)(cid:42)a(cid:36)(cid:220)(cid:83)n^a(cid:36)(cid:34)(cid:205)n^a(cid:36)  (cid:208)(cid:209)(cid:139)(cid:140)n(cid:197)(cid:198)(cid:46)(cid:42)a(cid:51)(cid:89)(cid:139)(cid:140)(cid:27) (cid:241)(cid:82)(cid:4)(cid:125)(cid:10)   (cid:89)(cid:139)(cid:140)(cid:23)(cid:71)(cid:143)(cid:188)(cid:189)(cid:139)(cid:140)(cid:47) (cid:23)(cid:145)(cid:46)(cid:42)(cid:51)(cid:101)(cid:185)(cid:89)(cid:139)(cid:140)(cid:199)(cid:224)(cid:156)(cid:46)(cid:79)(cid:47) (cid:139)(cid:140)n(cid:143)(cid:46)(cid:42)(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:139)(cid:140)m(cid:143)(cid:123)   ①(cid:46)(cid:42)(cid:46)(cid:79)(cid:168)(cid:141)(cid:46)(cid:42)(cid:206)(cid:36)(cid:107)(cid:185)②m×n=0(cid:27) ③   (cid:242)(cid:23)(cid:243)(cid:10)(cid:244)(cid:64)(cid:46)(cid:42)(cid:206)(cid:142)(cid:145)(cid:164)(cid:46)(cid:79)(cid:51)(cid:139)a=x (cid:36)y (cid:36)z (cid:36)b=x (cid:36)y (cid:36)z (cid:47) 1 1 1 2 2 2    ïìn×a=0 ìxx + yy +zz =0 (cid:242)(cid:49)(cid:243)(cid:10)(cid:208)(cid:209)(cid:46)(cid:42)(cid:89)(cid:139)(cid:140)n=x(cid:36)y(cid:36)z (cid:36)(cid:115)(cid:116)í  Þí 1 1 1 (cid:27) ïîn×b=0 îxx 2 + yy 2 +zz 2 =0 2(cid:24)(cid:80)(cid:71)(cid:111)(cid:78)(cid:24)(cid:46)(cid:42)(cid:135)(cid:51)(cid:214)(cid:245)(cid:3)(cid:138)   (cid:111)(cid:78)(cid:123)(cid:111)(cid:78)(cid:51)(cid:214)(cid:245)(cid:3)(cid:138)(cid:10)(cid:164)(cid:246)(cid:129)(cid:51)(cid:142)(cid:166)(cid:111)(cid:78)a(cid:36)b(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:62)(cid:91)(cid:55)a(cid:36)b (cid:27)     (cid:43)①a b (cid:36)(cid:65)a=lb(cid:36)(cid:107)a(cid:160)b(cid:47)     (cid:43)a(cid:247)∥ b(cid:36)(cid:65)a×b=0(cid:36)(cid:107)a(cid:247)b(cid:27)   (cid:111)(cid:78)(cid:123)(cid:46)(cid:42)(cid:51)(cid:214)(cid:245)(cid:3)(cid:138)(cid:10)(cid:111)(cid:78)l(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:55)a(cid:36)(cid:46)(cid:42)a(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n (cid:36)(cid:48)l(cid:247)a(cid:27)     (cid:43)②a n (cid:36)(cid:65)a=ln(cid:36)(cid:107)l(cid:247)a(cid:47) ∥     (cid:43)a(cid:247)n(cid:36)(cid:65)a×n=0(cid:36)(cid:107)a(cid:160)a(cid:27) 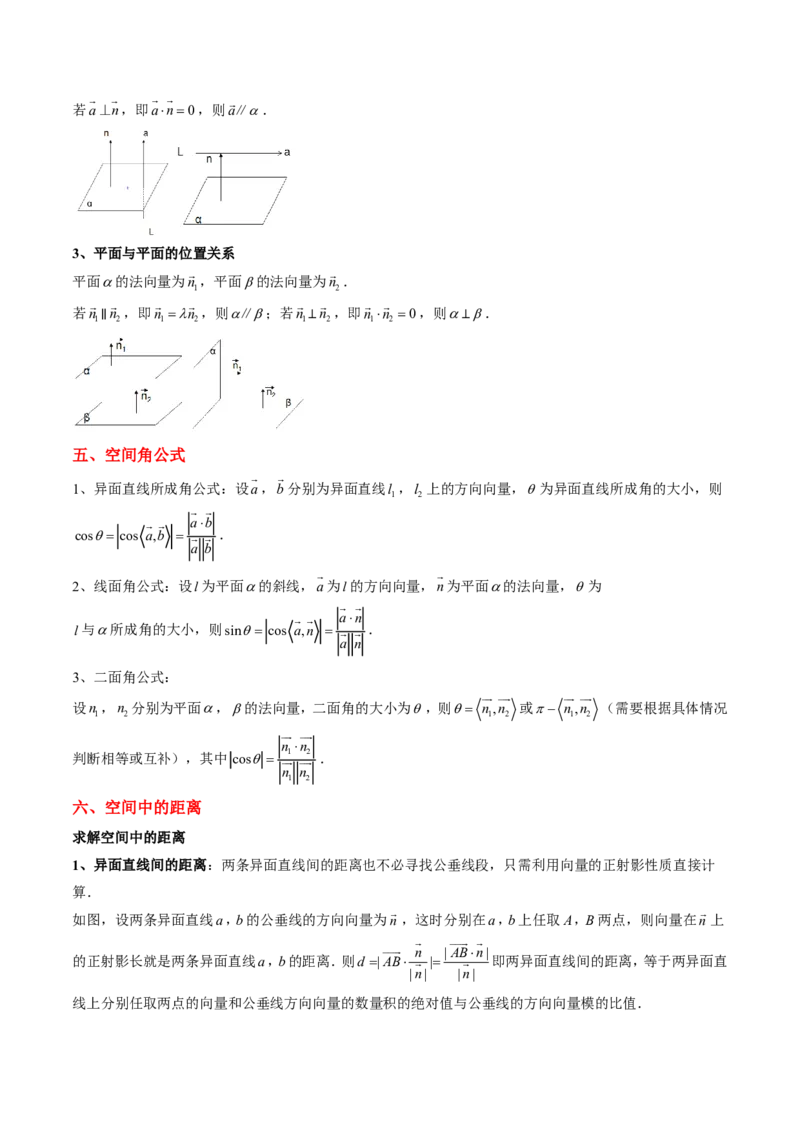3(cid:24)(cid:46)(cid:42)(cid:123)(cid:46)(cid:42)(cid:51)(cid:214)(cid:245)(cid:3)(cid:138)   (cid:46)(cid:42)a(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n (cid:36)(cid:46)(cid:42)b(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n (cid:27) 1 2         (cid:43)n n (cid:36)(cid:65)n =ln (cid:36)(cid:107)a(cid:160)b(cid:47)(cid:43)n n (cid:36)(cid:65)n ×n =0(cid:36)(cid:107)a b(cid:27) 1 2 1 2 1 2 1 2 ∥ ⊥ ⊥ (cid:248)(cid:24)(cid:134)(cid:135)(cid:50)(cid:7)(cid:182)   1(cid:24)(cid:249)(cid:42)(cid:111)(cid:78)(cid:101)(cid:124)(cid:50)(cid:7)(cid:182)(cid:10)(cid:106)a(cid:36)b(cid:62)(cid:91)(cid:55)(cid:249)(cid:42)(cid:111)(cid:78)l (cid:36)l (cid:159)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:36)q(cid:55)(cid:249)(cid:42)(cid:111)(cid:78)(cid:101)(cid:124)(cid:50)(cid:51)(cid:179)(cid:180)(cid:36)(cid:107) 1 2     a×b cosq= cos a,b =   (cid:27) a b   2(cid:24)(cid:78)(cid:42)(cid:50)(cid:7)(cid:182)(cid:10)(cid:106)l(cid:55)(cid:46)(cid:42)a(cid:51)(cid:250)(cid:78)(cid:36)a(cid:55)l(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:36)n(cid:55)(cid:46)(cid:42)a(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)q(cid:55)     a×n l(cid:123)a(cid:101)(cid:124)(cid:50)(cid:51)(cid:179)(cid:180)(cid:36)(cid:107)sinq= cos a,n =   (cid:27) a n 3(cid:24)(cid:49)(cid:42)(cid:50)(cid:7)(cid:182)(cid:10)     (cid:106)n (cid:36)n (cid:62)(cid:91)(cid:55)(cid:46)(cid:42)a(cid:36)b(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:49)(cid:42)(cid:50)(cid:51)(cid:179)(cid:180)(cid:55)q(cid:36)(cid:107)q= n,n (cid:168)p- n,n (cid:28)(cid:251)(cid:192)(cid:76)(cid:77)(cid:252)(cid:148)(cid:253)(cid:254) 1 2 1 2 1 2   n ×n (cid:80)(cid:255)(cid:156)(cid:108)(cid:168)(cid:224)(cid:256)(cid:33)(cid:36)(cid:196)(cid:40) cosq=  1  2 (cid:27) n n 1 2 (cid:257)(cid:24)(cid:134)(cid:135)(cid:40)(cid:51)(cid:150)(cid:151) (cid:56)(cid:25)(cid:134)(cid:135)(cid:40)(cid:51)(cid:150)(cid:151) 1(cid:24)(cid:249)(cid:42)(cid:111)(cid:78)(cid:135)(cid:51)(cid:150)(cid:151)(cid:10)(cid:142)(cid:166)(cid:249)(cid:42)(cid:111)(cid:78)(cid:135)(cid:51)(cid:150)(cid:151)(cid:218)(cid:164)(cid:258)(cid:259)(cid:260)(cid:7)(cid:88)(cid:78)(cid:202)(cid:36)(cid:261)(cid:251)(cid:127)(cid:92)(cid:139)(cid:140)(cid:51)(cid:52)(cid:262)(cid:239)(cid:130)(cid:131)(cid:111)(cid:86)(cid:177) (cid:153)(cid:27)   (cid:34)(cid:35)(cid:36)(cid:106)(cid:142)(cid:166)(cid:249)(cid:42)(cid:111)(cid:78)a(cid:36)b(cid:51)(cid:7)(cid:88)(cid:78)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:55)n (cid:36)(cid:232)(cid:162)(cid:62)(cid:91)(cid:141)a(cid:36)b(cid:159)(cid:190)(cid:155)A(cid:36)B(cid:142)(cid:82)(cid:36)(cid:107)(cid:139)(cid:140)(cid:141)n (cid:159)     n |AB×n| (cid:51)(cid:52)(cid:262)(cid:239)(cid:93)(cid:233)(cid:143)(cid:142)(cid:166)(cid:249)(cid:42)(cid:111)(cid:78)a(cid:36)b(cid:51)(cid:150)(cid:151)(cid:27)(cid:107)d =|AB×  |=  (cid:65)(cid:142)(cid:249)(cid:42)(cid:111)(cid:78)(cid:135)(cid:51)(cid:150)(cid:151)(cid:36)(cid:108)(cid:84)(cid:142)(cid:249)(cid:42)(cid:111) |n| |n| (cid:78)(cid:159)(cid:62)(cid:91)(cid:190)(cid:155)(cid:142)(cid:82)(cid:51)(cid:139)(cid:140)(cid:144)(cid:7)(cid:88)(cid:78)(cid:97)(cid:139)(cid:139)(cid:140)(cid:51)(cid:13)(cid:140)(cid:109)(cid:51)(cid:173)(cid:119)(cid:54)(cid:123)(cid:7)(cid:88)(cid:78)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:263)(cid:51)(cid:264)(cid:54)(cid:27)2(cid:24)(cid:82)(cid:149)(cid:46)(cid:42)(cid:51)(cid:150)(cid:151)  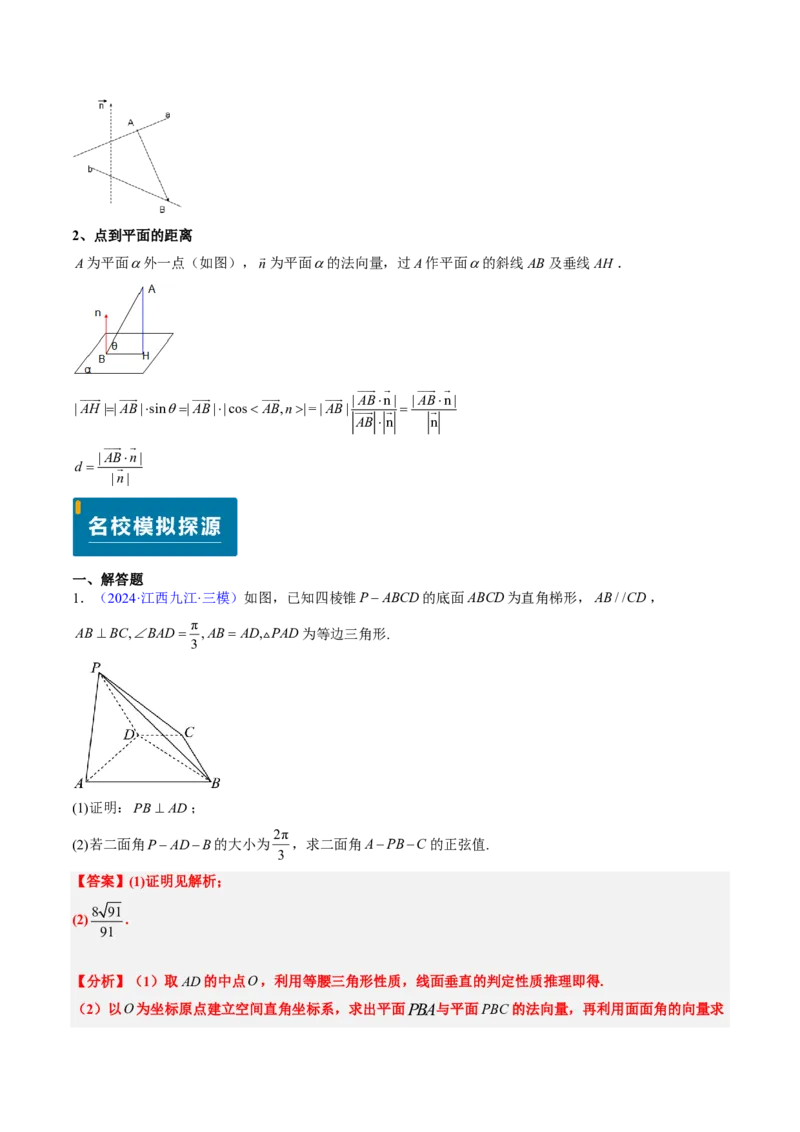A(cid:55)(cid:46)(cid:42)a(cid:265)(cid:23)(cid:82)(cid:28)(cid:34)(cid:35)(cid:33)(cid:36)n (cid:55)(cid:46)(cid:42)a(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:81)A(cid:83)(cid:46)(cid:42)a(cid:51)(cid:250)(cid:78)AB(cid:154)(cid:88)(cid:78)AH (cid:27)          |AB×n| |AB×n| |AH |=|AB|×sinq=|AB|×|cos< AB,n>|=|AB|   =  AB × n n   |AB×n| d =  |n| (cid:23)(cid:24)(cid:25)(cid:26)(cid:21) 1(cid:27)(cid:28)2024·(cid:266)(cid:267)(cid:268)(cid:266)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:187)(cid:90)(cid:37)(cid:38)(cid:39)P-ABCD(cid:51)(cid:41)(cid:42)ABCD(cid:55)(cid:111)(cid:50)(cid:269)(cid:112)(cid:36)AB//CD(cid:36) π AB^BC,ÐBAD= ,AB= AD,VPAD(cid:55)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112). 3 (1)(cid:44)(cid:45)(cid:10)PB^ AD(cid:47) 2π (2)(cid:43)(cid:49)(cid:42)(cid:50)P-AD-B(cid:51)(cid:179)(cid:180)(cid:55) (cid:36)(cid:56)(cid:49)(cid:42)(cid:50)A-PB-C(cid:51)(cid:52)(cid:53)(cid:54). 3 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)(cid:47) 8 91 (2) . 91 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)AD(cid:51)(cid:40)(cid:82)O(cid:36)(cid:127)(cid:92)(cid:108)(cid:110)(cid:87)(cid:50)(cid:112)(cid:130)(cid:131)(cid:36)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:130)(cid:131)(cid:212)(cid:15)(cid:65)(cid:67). (cid:28)2(cid:33)(cid:102)O(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:46)(cid:42)PBA(cid:123)(cid:46)(cid:42)PBC(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:75)(cid:127)(cid:92)(cid:42)(cid:42)(cid:50)(cid:51)(cid:139)(cid:140)(cid:56)(cid:89)(cid:56)(cid:25)(cid:65)(cid:67). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:155)AD(cid:51)(cid:40)(cid:82)O(cid:36)(cid:85)(cid:86)(cid:78)(cid:202)PO,BO,BD(cid:36)(cid:68)PA=PD(cid:36)(cid:67)AD^PO(cid:36) π (cid:68)AB=AD,ÐBAD= (cid:36)(cid:67)△ABD(cid:55)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36)(cid:107)AD^BO(cid:36) 3 (cid:103)POÇBO=O,PO,BOÌ(cid:46)(cid:42)POB(cid:36)(cid:84)(cid:143)AD^(cid:46)(cid:42)POB(cid:36)(cid:103)PBÌ(cid:46)(cid:42)POB(cid:36) (cid:101)(cid:102)PB^ AD. 2π (cid:28)2(cid:33)(cid:68)(cid:28)1(cid:33)(cid:90)ÐPOB(cid:55)(cid:49)(cid:42)(cid:50)(cid:51)(cid:46)(cid:42)(cid:50)(cid:36)(cid:65)ÐPOB= (cid:36) 3 (cid:141)(cid:46)(cid:42)POB(cid:206)(cid:81)O(cid:83)Oz^OB(cid:36)(cid:270)(cid:271)(cid:111)(cid:78)OA,OB,Oz(cid:142)(cid:142)(cid:88)(cid:111)(cid:36) (cid:102)O(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)(cid:111)(cid:78)OA,OB,Oz(cid:62)(cid:91)(cid:55)x,y,z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:164)(cid:184)(cid:106)AB=2(cid:36)(cid:107) PO = BO = 3(cid:36)A1,0,0,B  0, 3,0  ,P æ ç ç 0,- 3 , 3ö ÷ ÷ ,D-1,0,0(cid:36) è 2 2ø 1 1  1 æ 1 3 ö æ 3 3 ö (cid:68)AB//CD,AB^BC(cid:36)(cid:67)DC = BD= AB(cid:36)DC = AB=ç- , ,0÷(cid:36)Cç- , ,0÷(cid:36) ç ÷ ç ÷ 2 2 2 è 2 2 ø è 2 2 ø   3 3 3  (cid:106)(cid:46)(cid:42)PBA(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)m=(x,y ,z )(cid:36)PB=(0, ,- ),AB=(-1, 3,0)(cid:36) 1 1 1 2 2 ì   3 3 3 ïm×PB= y - z =0   3 3 í 2 1 2 1 (cid:36)(cid:155)y =1(cid:36)(cid:67)m=( 3,1, 3)(cid:36)(cid:74)CB=( , ,0)(cid:36) ï  1 2 2 îm×AB=-x + 3y =0 1 1 ì   3 3 3 ïn×PB= y - z =0  ï 2 2 2 2  (cid:106)(cid:46)(cid:42)PBC(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=(x ,y ,z )(cid:36)(cid:107)í (cid:36)(cid:155)x =1(cid:36)(cid:67)n=(1,- 3,-3)(cid:36) 2 2 2 ï  3 3 2 n×CB= x + y =0 ï î 2 2 2 2     |m×n| 3 3 3 3 (cid:106)(cid:49)(cid:42)(cid:50)A-PB-C(cid:51)(cid:46)(cid:42)(cid:50)(cid:55)q(cid:36)(cid:107)|cosq|=|cosám,nñ|=   = = (cid:36) |m||n| 7´ 13 91 8 91 8 91 (cid:100)(cid:203)sinq= (cid:36)(cid:101)(cid:102)(cid:49)(cid:42)(cid:50)A-PB-C(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 91 91 2(cid:27)(cid:28)2024·(cid:272)(cid:273)(cid:274)(cid:275)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:87)(cid:38)(cid:39)ABCD(cid:40)(cid:36)(cid:46)(cid:42)ABD^(cid:46)(cid:42)ACD(cid:36)(cid:46)(cid:42)ABD^(cid:46)(cid:42)BCD(cid:36)(cid:46)(cid:42) ACD^(cid:46)(cid:42)BCD(cid:36)(1)(cid:56)(cid:44)(cid:10)AD,BD,CD(cid:142)(cid:142)(cid:88)(cid:111)(cid:47) (2)(cid:43)DA=1,DB=2,DC =3,P(cid:55)AB(cid:40)(cid:82)(cid:36)Q(cid:55)AC(cid:40)(cid:82)(cid:36)(cid:56)BQ(cid:123)(cid:46)(cid:42)PDC(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 3 130 (2) 65 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:141)BC(cid:159)(cid:190)(cid:155)(cid:23)(cid:82)E(cid:36)(cid:83)EF ^BD(cid:157)BD(cid:84)F (cid:36)(cid:83)EG^DC(cid:157)DC(cid:84)G(cid:36)(cid:44)(cid:45)EF^(cid:46)(cid:42) ABD(cid:36)(cid:73)(cid:74)(cid:44)(cid:45)EF^AD(cid:36)(cid:276)(cid:74)(cid:212)(cid:64)EG^ AD(cid:36)(cid:65)(cid:66)(cid:44)(cid:45)AD^(cid:46)(cid:42)BCD(cid:36)(cid:276)(cid:74)(cid:66)(cid:44)(cid:45)(cid:128)(cid:213)(cid:47) (cid:28)2(cid:33)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:156)(cid:3)(cid:82)(cid:136)(cid:137)(cid:36)(cid:56)(cid:64)(cid:46)(cid:42)PDC(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:76)(cid:77)(cid:134)(cid:135)(cid:50)(cid:51)(cid:139)(cid:140)(cid:56)(cid:89)(cid:277)(cid:36)(cid:65)(cid:66) (cid:56)(cid:67)(cid:26)(cid:58). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:141)BC(cid:159)(cid:190)(cid:155)(cid:23)(cid:82)E(cid:36)(cid:83)EF ^BD(cid:157)BD(cid:84)F (cid:36)(cid:83)EG^DC(cid:157)DC(cid:84)G(cid:36) (cid:68)(cid:46)(cid:42)ABD^(cid:46)(cid:42)BCD(cid:157)(cid:84)BD(cid:36)EF Ì(cid:42)BCD(cid:36)EF ^BD(cid:36)(cid:107)EF^(cid:46)(cid:42)ABD(cid:36) (cid:103)ADÌ(cid:46)(cid:42)ABD(cid:36)(cid:107)EF^AD(cid:36)(cid:165)(cid:15)EG^ AD(cid:36) (cid:103)(cid:68)EF,EGÌ(cid:46)(cid:42)BCD(cid:36)EFIEG=E(cid:66)(cid:67)AD^(cid:46)(cid:42)BCD(cid:36) BD,CDÌ(cid:46)(cid:42)BCD(cid:36)(cid:107)AD^BD,AD^CD(cid:27) (cid:165)(cid:15)(cid:66)(cid:67)BD^CD(cid:36)(cid:65)AD,BD,CD(cid:142)(cid:142)(cid:88)(cid:111)(cid:27) (cid:28)2(cid:33)(cid:62)(cid:91)(cid:102)DB(cid:36)DC(cid:36)DA(cid:101)(cid:141)(cid:111)(cid:78)(cid:55)x(cid:163)(cid:24)y(cid:163)(cid:24)z(cid:163)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) æ 3 1ö æ 1ö (cid:181)(cid:67)B2,0,0,Qç0, , ÷,Pç1,0, ÷,C0,3,0(cid:36) è 2 2ø è 2ø  æ 1ö   æ 3 1ö (cid:185)DP=ç1,0, ÷,DC =0,3,0,BQ=ç-2, , ÷(cid:36) è 2ø è 2 2ø    ì ïDP×n=0 (cid:106)(cid:42)PDC(cid:51)(cid:89)(cid:139)(cid:140)n=x,y,z(cid:36)(cid:107)(cid:68)í  (cid:36) ïîDC×n=0 ì 1 ïx+ z=0  (cid:65)í 2 (cid:36)(cid:66)(cid:155)n=1,0,-2(cid:27) ï î3y=0π (cid:106)BQ(cid:123)(cid:46)(cid:42)PDC(cid:101)(cid:124)(cid:50)(cid:55)q,qÎ[0, ](cid:36) 2     BQ×n 3 3 130 (cid:107) sinq= cosBQ,n =   = = (cid:36) BQ n 9 1 65 4+ + × 5 4 4 3 130 (cid:107)BQ(cid:123)(cid:46)(cid:42)PDC(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) 65 3(cid:27)(cid:28)2024·(cid:37)(cid:278)(cid:124)(cid:199)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:101)(cid:185)(cid:38)(cid:93)(cid:199)(cid:55)2(cid:36)ÐBBC =60°(cid:36)D(cid:55)AC(cid:123)AC (cid:157) 1 1 1 1 1 1 (cid:82)(cid:27) (1)(cid:44)(cid:45)(cid:10)(cid:46)(cid:42)BCD^(cid:46)(cid:42)ABC (cid:47) 1 1 13 (2)(cid:43)DB = (cid:36)(cid:56)(cid:49)(cid:42)(cid:50)A -CB -C (cid:51)(cid:126)(cid:53)(cid:54)(cid:27) 1 2 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 13 (2) 13 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:68)(cid:42)(cid:42)(cid:88)(cid:111)(cid:80)(cid:71)(cid:71)(cid:15)(cid:44)(cid:45)(cid:36)(cid:65) (cid:63)(cid:44)(cid:45)AB ^(cid:46)(cid:42)BCD(cid:36)(cid:75)(cid:44)(cid:45)(cid:42)BCD^(cid:46)(cid:42)ABC . 1 1 1   (cid:28)2(cid:33)(cid:63)(cid:132)(cid:138)(cid:36)(cid:271)(cid:279)(cid:56)(cid:25)(cid:64)(cid:46)(cid:42)ACB (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)n(cid:144)(cid:46)(cid:42)CCB (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)m(cid:36)(cid:280)(cid:281)(cid:7)(cid:182) 1 1 1 1     m×n cosq= cosm,n =   (cid:65)(cid:66). m× n (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:155)BC(cid:40)(cid:82)O(cid:36)(cid:155)AB (cid:40)(cid:82)E(cid:36)(cid:85)(cid:86)DE(cid:36)BE(cid:36)OE(cid:36) 1 (cid:100)(cid:55)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:101)(cid:185)(cid:38)(cid:93)(cid:199)(cid:55)2(cid:36)ÐBBC =60°(cid:36) 1 1 1 1 (cid:185)AO=BO= 3(cid:36)AB=BB (cid:36)E(cid:55)AB (cid:51)(cid:40)(cid:82)(cid:36)BCDE(cid:37)(cid:82)(cid:204)(cid:42)(cid:36) 1 1 1 (cid:101)(cid:102)OE^ AB (cid:36)(cid:48)BE^ AB (cid:36)BE(cid:24)OEÌ(cid:46)(cid:42)BCD(cid:36)OEIBE=E(cid:36) 1 1 (cid:101)(cid:102)AB ^(cid:46)(cid:42)BCD(cid:36)(cid:103)AB Ì(cid:46)(cid:42)ABC (cid:36)(cid:113)(cid:46)(cid:42)BCD^(cid:46)(cid:42)ABC (cid:27) 1 1 1 1 1 1 (cid:28)2(cid:33)(cid:100)(cid:55)BC//BC (cid:36)(cid:101)(cid:102)BC ^(cid:46)(cid:42)AOB (cid:36)AB Ì(cid:46)(cid:42)AOB (cid:36) 1 1 1 1 1 1 1 (cid:101)(cid:102)BC ^ AB (cid:36)(cid:101)(cid:102)(cid:178)ABC (cid:55)(cid:111)(cid:50)(cid:87)(cid:50)(cid:112)(cid:36)(cid:101)(cid:102)AC =2DB = 13(cid:36) 1 1 1 1 1 1 1 3+3-9 1 (cid:101)(cid:102)AB = AC2-BC2 =3(cid:36)(cid:141)VAOB (cid:40)(cid:36)cosÐAOB = =- (cid:27) 1 1 1 1 1 1 2´3 2    (cid:102)O(cid:55)(cid:158)(cid:82)(cid:36)(cid:83)Oz^(cid:46)(cid:42)BCCB (cid:36)(cid:102)OB(cid:36)OB (cid:36)Oz(cid:97)(cid:139)(cid:55)x(cid:36)y(cid:36)z(cid:163)(cid:52)(cid:97)(cid:139)(cid:36) 1 1 1(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:34)(cid:35)(cid:101)(cid:96)(cid:36) (cid:107)C-1,0,0(cid:36)B  0, 3,0  (cid:36)C  -2, 3,0  (cid:36)A æ ç0,- 3 , 3ö ÷(cid:36) 1 1 ç è 2 2 ÷ ø   æ 3 3ö  æ 3 3ö    (cid:68)AA =CC (cid:36)(cid:101)(cid:102)A ç-1, , ÷(cid:36)(cid:101)(cid:102)CA =ç0, , ÷(cid:36)CB = 1, 3,0 (cid:36) 1 1 1ç è 2 2 ÷ ø 1 ç è 2 2 ÷ ø 1   ìx+ 3y=0  ì ïCB ×n=0 ï (cid:106)(cid:46)(cid:42)A 1 CB 1 (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=(x,y,z)(cid:36)(cid:107)í 1  (cid:36)(cid:65)í 3 3 (cid:36) ïîCA ×n=0 ï y+ z=0 1 î 2 2   (cid:146)z=1(cid:36)(cid:25)(cid:67)n=(3,- 3,1)(cid:36)(cid:101)(cid:102)(cid:46)(cid:42)CCB (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)m=(0,0,1)(cid:36) 1 1 (cid:220)(cid:49)(cid:42)(cid:50)A -CB -C (cid:51)(cid:179)(cid:180)(cid:55)q(cid:36)(cid:48)q(cid:55)(cid:282)(cid:50)(cid:36) 1 1 1     m×n 13 (cid:107)cosq= cosm,n =   = (cid:36) m× n 13 13 (cid:65)(cid:49)(cid:42)(cid:50)A -CB -C (cid:51)(cid:46)(cid:42)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:55) (cid:27) 1 1 1 13 π 4(cid:27)(cid:28)2024·(cid:266)(cid:267)(cid:283)(cid:284)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)1(cid:36)(cid:37)(cid:114)(cid:112)ABCD(cid:55)(cid:285)(cid:112)(cid:36)ÐABC = (cid:36)E(cid:36)F (cid:62)(cid:91)(cid:55)AD(cid:36)DC(cid:51)(cid:40)(cid:82)(cid:36) 3 (cid:34)(cid:35)2(cid:27)(cid:117)VABC(cid:118)AC(cid:139)(cid:159)(cid:120)(cid:286)(cid:36)(cid:122)(cid:67)(cid:46)(cid:42)ABC^(cid:46)(cid:42)ACFE(cid:36)(cid:117)VDEF(cid:118)EF (cid:139)(cid:159)(cid:120)(cid:286)(cid:27)(cid:122)(cid:67)(cid:46)(cid:42)DEF ^ (cid:46)(cid:42)ACFE(cid:36)(cid:85)(cid:86)BD. (1)(cid:56)(cid:44)(cid:10)A(cid:36)B(cid:36)D(cid:36)E(cid:37)(cid:82)(cid:204)(cid:42)(cid:10) (2)(cid:56)(cid:46)(cid:42)AEDB(cid:123)(cid:46)(cid:42)FDBC(cid:101)(cid:124)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54). (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)1 (2) 5 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:127)(cid:92)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:67)(cid:149)BM//DN (cid:36)(cid:128)(cid:129)(cid:40)(cid:214)(cid:78)(cid:71)(cid:15)(cid:67)(cid:149)AB//DE(cid:36)(cid:287)(cid:279)(cid:44)(cid:45)(cid:37)(cid:82)(cid:204)(cid:42)(cid:65) (cid:66). (cid:28)2(cid:33)(cid:260)(cid:149)(cid:119)(cid:231)(cid:49)(cid:42)(cid:50)(cid:51)(cid:46)(cid:42)(cid:50)(cid:36)(cid:288)(cid:281)(cid:87)(cid:50)(cid:112)(cid:40)(cid:36)(cid:127)(cid:92)(cid:126)(cid:53)(cid:71)(cid:15)(cid:56)(cid:25)(cid:65)(cid:66). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:155)AC(cid:36)EF (cid:51)(cid:40)(cid:82)(cid:62)(cid:91)(cid:55)M (cid:36)N (cid:36)(cid:85)(cid:86)BM (cid:36)DN (cid:36) (cid:155)AM (cid:36)BM (cid:51)(cid:40)(cid:82)(cid:62)(cid:91)(cid:55)G(cid:36)H(cid:36)(cid:85)(cid:86)GH(cid:36)HD(cid:36)GE(cid:36) (cid:68)(cid:21)(cid:125)(cid:90)VABC(cid:36)VDEF(cid:199)(cid:143)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36) (cid:101)(cid:102)BM ^ AC(cid:36)DN ^EF (cid:36) (cid:100)(cid:55)(cid:46)(cid:42)ABC^(cid:46)(cid:42)ACFE(cid:36)(cid:46)(cid:42)DEF ^(cid:46)(cid:42)ACFE(cid:36) (cid:101)(cid:102)BM ^(cid:46)(cid:42)ACFE(cid:36)DN^(cid:46)(cid:42)ACFE(cid:36)(cid:101)(cid:102)BM//DN (cid:36) (cid:100)(cid:55)AM (cid:36)BM (cid:51)(cid:40)(cid:82)(cid:62)(cid:91)(cid:55)G(cid:36)H(cid:36)(cid:101)(cid:102)GE//MN (cid:101)(cid:102)HM =DN(cid:36)(cid:101)(cid:102)DH//MN(cid:36) (cid:101)(cid:102)DH//GE(cid:36)(cid:103)(cid:100)(cid:55)DH =GE(cid:36) (cid:101)(cid:102)GH//DE(cid:36) (cid:100)(cid:55)AM (cid:36)BM (cid:51)(cid:40)(cid:82)(cid:62)(cid:91)(cid:55)G(cid:36)H(cid:36) (cid:101)(cid:102)GH//AB(cid:36) (cid:101)(cid:102)AB//DE(cid:36)(cid:101)(cid:102)A(cid:36)B(cid:36)D(cid:36)E(cid:37)(cid:82)(cid:204)(cid:42)(cid:47) (cid:28)2(cid:33)(cid:85)(cid:86)AD(cid:36)DC(cid:36)(cid:48)(cid:170)(cid:93)AE,CF(cid:157)(cid:84)(cid:82)P(cid:36)(cid:68)(cid:21)(cid:125)(cid:90)AP= AB(cid:36)BD=DP(cid:36)(cid:101)(cid:102)AD^BD(cid:36)(cid:165)(cid:15)CD^BD(cid:36) (cid:101)(cid:102)ÐADC(cid:233)(cid:143)(cid:49)(cid:42)(cid:50)A-DB-C(cid:51)(cid:46)(cid:42)(cid:50)(cid:36) 3 7 (cid:106)AB=2a(cid:36)(cid:107)AC =2a(cid:36)DN= a(cid:36)AN = a(cid:36) 2 2 10 10 (cid:101)(cid:102)DA= a(cid:36)(cid:165)(cid:15)DC = a(cid:36) 2 2 10 10 a2+ a2-4a2 4 4 1 (cid:101)(cid:102)cosÐADC = = (cid:36) 10 10 5 2´ a´ a 2 2 1 (cid:101)(cid:102)(cid:46)(cid:42)AEDB(cid:123)(cid:46)(cid:42)FDBC(cid:101)(cid:124)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:55) . 5 5(cid:27)(cid:28)2024·(cid:289)(cid:290)(cid:291)(cid:105)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:141)(cid:241)(cid:225)(cid:148)ABCDFE(cid:40)(cid:36)(cid:41)(cid:42)ABCD(cid:55)(cid:285)(cid:112)(cid:36)ÐABC =60°(cid:36)AE∥DF(cid:36) AE^ AD(cid:36)AB= AE=2DF =4. (1)(cid:80)(cid:255)AD(cid:143)(cid:292)(cid:46)(cid:79)(cid:84)(cid:46)(cid:42)CEF(cid:36)(cid:169)(cid:44)(cid:45)(cid:47) (2)(cid:43)(cid:42)EAB^(cid:42)ABCD(cid:47)(cid:56)(cid:10) (cid:28)ⅰ(cid:33)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)(cid:51)(cid:179)(cid:180)(cid:47) (cid:28)ⅱ(cid:33)(cid:56)(cid:82)A(cid:149)(cid:46)(cid:42)CEF(cid:51)(cid:150)(cid:151). (cid:57)(cid:26)(cid:58)(cid:59)(1)AD(cid:123)(cid:46)(cid:42)CEF(cid:164)(cid:46)(cid:79)(cid:36)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) π (2)(cid:28)i(cid:33) (cid:47)(cid:28)ii(cid:33)2 2 4 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)AE(cid:40)(cid:82)G(cid:36)(cid:44)(cid:45)AD//GF (cid:36)(cid:293)(cid:106)AD//(cid:46)(cid:42)CEF(cid:36)(cid:76)(cid:77)(cid:78)(cid:42)(cid:46)(cid:79)(cid:130)(cid:131)(cid:71)(cid:15)(cid:44)(cid:45) AD//EF(cid:36)(cid:212)(cid:64)(cid:294)(cid:295)(cid:36)(cid:66)(cid:67)(cid:128)(cid:213)(cid:47) (cid:28)2(cid:33)(cid:28)i(cid:33)(cid:44)(cid:45)(cid:78)(cid:78)(cid:88)(cid:111)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:136)(cid:137)(cid:152)(cid:153)(cid:56)(cid:25)(cid:46)(cid:42)(cid:123)(cid:46)(cid:42)(cid:51)(cid:50)(cid:36)(cid:28)ii(cid:33)(cid:127)(cid:92) (cid:139)(cid:140)(cid:97)(cid:89)(cid:56)(cid:82)(cid:149)(cid:46)(cid:42)(cid:150)(cid:151). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)AD(cid:164)(cid:46)(cid:79)(cid:84)(cid:46)(cid:42)CEF(cid:36)(cid:15)(cid:68)(cid:34)(cid:296)(cid:10) (cid:155)AE(cid:40)(cid:82)G(cid:36)(cid:100)(cid:55)AE(cid:160)DF,AE=2DF(cid:36)(cid:101)(cid:102)AG//DF,AG=DF (cid:107)(cid:37)(cid:114)(cid:112)AGFD(cid:55)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)(cid:101)(cid:102)AD//GF (cid:36) (cid:103)GFÇEF =F (cid:36)(cid:101)(cid:102)AD(cid:164)(cid:46)(cid:79)(cid:84)EF (cid:36) (cid:293)(cid:106)AD//(cid:46)(cid:42)CEF(cid:36) (cid:100)(cid:55)(cid:46)(cid:42)CEFÇ(cid:46)(cid:42)ADFE=EF(cid:36)ADÌ(cid:46)(cid:42)ADFE (cid:101)(cid:102)AD//EF(cid:36)(cid:123)AD(cid:164)(cid:46)(cid:79)(cid:84)EF (cid:294)(cid:295)(cid:36) (cid:101)(cid:102)(cid:293)(cid:106)(cid:164)(cid:124)(cid:133)(cid:36)(cid:65)AD(cid:164)(cid:46)(cid:79)(cid:84)(cid:46)(cid:42)CEF(cid:47) (cid:28)2(cid:33)(cid:155)CD(cid:40)(cid:82)M (cid:36)(cid:85)(cid:86)AM (cid:100)(cid:55)(cid:285)(cid:112)ABCD,ÐABC =60°(cid:36) (cid:101)(cid:102)VACD(cid:55)(cid:52)(cid:87)(cid:50)(cid:112)(cid:36)(cid:103)M (cid:55)CD(cid:40)(cid:82)(cid:36)(cid:101)(cid:102)AM ^CD(cid:36) (cid:68)(cid:84)AB//CD(cid:36)(cid:101)(cid:102)AM ^ AB(cid:36) (cid:103)(cid:42)EAB^(cid:42)ABCD(cid:36)(cid:42)EABÇ(cid:42)ABCD= AB(cid:36)AM Ì(cid:42)ABCD (cid:101)(cid:102)AM ^(cid:42)EAB(cid:36)(cid:100)(cid:55)AEÌ(cid:42)EAB(cid:36)(cid:101)(cid:102)AM ^ AE (cid:103)(cid:100)(cid:55)AE^ AD(cid:36)AM IAD= A,AM,ADÌ(cid:42)ABCD(cid:36) (cid:101)(cid:102)AE^(cid:42)ABCD(cid:36)(cid:74)AB,AM Ì(cid:42)ABCD(cid:36)(cid:101)(cid:102)AE^ AB(cid:36)    (cid:101)(cid:102)(cid:34)(cid:35)(cid:36)(cid:102)A(cid:55)(cid:158)(cid:82)(cid:36)AB,AM,AE(cid:101)(cid:141)(cid:111)(cid:78)(cid:55)x,y,z(cid:163)(cid:51)(cid:52)(cid:97)(cid:139)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:107)A0,0,0,B4,0,0,C  2,2 3,0  ,E0,0,4,F  -2,2 3,2   (cid:28)i(cid:33)(cid:100)(cid:55)AE^(cid:42)ABCD(cid:36)(cid:101)(cid:102)AE=0,0,4(cid:55)(cid:46)(cid:42)ABCD(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140) (cid:106)(cid:46)(cid:42)CEF(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n  =x,y,z(cid:36)(cid:100)(cid:55)C  E  =  -2,-2 3,4  ,C  F  =-4,0,2  ì ïn×CE=-2x-2 3y+4z=0 ìïy= 3x    (cid:101)(cid:102)í   Þí (cid:36)(cid:146)x=1(cid:36)n= 1, 3,2 ïîn×CF =-4x+2z=0 ïîz=2x (cid:106)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)     n×AE 8 2 π (cid:101)(cid:102)cosq= cos =   = = (cid:36)(cid:107)q= n × AE 2 2´4 2 4 π (cid:65)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)(cid:179)(cid:180)(cid:55) (cid:47) 4       (cid:28)ii(cid:33)(cid:100)(cid:55)AC = 2,2 3,0 (cid:36)(cid:68)(cid:28)i(cid:33)(cid:90)(cid:46)(cid:42)(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n= 1, 3,2   AC×n 2+6+0 (cid:101)(cid:102)(cid:82)A(cid:149)(cid:46)(cid:42)CEF(cid:51)(cid:150)(cid:151)(cid:55)  = =2 2. n 2 2 6(cid:27)(cid:28)2024·(cid:272)(cid:273)(cid:129)(cid:297)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:23)(cid:10)(cid:108)(cid:110)(cid:111)(cid:50)VABC(cid:40)AC ^ AB(cid:48)AC =2(cid:36)(cid:62)(cid:91)(cid:118)(cid:87)(cid:50)(cid:112)(cid:87)(cid:114)(cid:139)(cid:265)(cid:83)(cid:108)(cid:110) π (cid:269)(cid:112)ABB A ,BCC B ,CAAC (cid:122)(cid:67)AA =BB =CC =1,ÐCAA =ÐBAA = (cid:36)(cid:118)(cid:87)(cid:114)AB,BC,CA(cid:120)(cid:286)(cid:36)(cid:122)(cid:67) 2 2 2 3 3 3 2 2 2 3 2 3 A A,B B ,C C (cid:36)(cid:246)(cid:129)(cid:84)A,B,C (cid:36)(cid:34)(cid:35)(cid:49) 2 3 2 3 2 3 1 1 1 (1)(cid:56)(cid:44)(cid:10)AA ^BC (cid:27) 1 1 1 (2)(cid:56)(cid:111)(cid:78)CC (cid:123)(cid:46)(cid:42)AABB(cid:101)(cid:124)(cid:50)q(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 6 (2) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:256)(cid:171)(cid:35)(cid:112)(cid:67)(cid:149)(cid:87)(cid:38)(cid:39)P-ABC(cid:36)(cid:68)(cid:78)(cid:42)(cid:88)(cid:111)(cid:44)(cid:67)AA ^BC (cid:47) 1 1 1 (cid:28)2(cid:33)(cid:298)(cid:299)(cid:23)(cid:10)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:152)(cid:92)(cid:139)(cid:140)(cid:56)(cid:25)(cid:78)(cid:42)(cid:50)(cid:47) (cid:298)(cid:299)(cid:49)(cid:10)(cid:108)(cid:148)(cid:109)(cid:89)(cid:56)(cid:67)C(cid:149)(cid:46)(cid:42)PAB(cid:51)(cid:150)(cid:151)(cid:36)(cid:75)(cid:92)(cid:241)(cid:225)(cid:89)(cid:56)(cid:67)(cid:78)(cid:42)(cid:50). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:170)(cid:93)AA,CC (cid:157)(cid:84)(cid:82)P,(cid:81)C (cid:83)CM ^ AC(cid:84)M (cid:36)(cid:81)A(cid:83)AN ^ AC(cid:84)N (cid:36) 1 1 1 1 1 1 1 π (cid:103)(cid:37)(cid:114)(cid:112)AACC(cid:55)(cid:108)(cid:110)(cid:269)(cid:112)(cid:36)(cid:107)AC = AC-2AA cos =1(cid:36)(cid:107)AC =2AC (cid:36) 1 1 1 1 1 3 1 1 (cid:103)QAC //AC(cid:36)(cid:101)(cid:102)PA = AA (cid:36)C (cid:55)PC(cid:51)(cid:40)(cid:82)(cid:36) 1 1 1 1 1 1 1(cid:170)(cid:93)AA,BB (cid:157)(cid:84)(cid:82)P (cid:36)(cid:107)PA = AA (cid:36)B (cid:55)PB(cid:51)(cid:40)(cid:82)(cid:36)(cid:107)PA =PA (cid:36) 1 1 2 2 1 1 1 2 1 1 2 1 \P(cid:123)P (cid:246)(cid:129)(cid:84)(cid:82)P(cid:36)P-ABC(cid:55)(cid:87)(cid:38)(cid:39)(cid:36) 1 2 (cid:106)O(cid:55)BC(cid:40)(cid:82)(cid:36)(cid:108)(cid:110)(cid:111)(cid:50)VABC(cid:40)AC = AB,\AO^BC(cid:36) (cid:103)QC (cid:55)PC(cid:51)(cid:40)(cid:82)(cid:36)B (cid:55)PB(cid:51)(cid:40)(cid:82)(cid:36)CC =BB =1(cid:36) PB=PC=2(cid:36) 1 1 1 1 \PO^BC(cid:36)(cid:103)QAOIPO=O,AO,POÌ(cid:46)(cid:42)PAO\BC∴ ^(cid:46)(cid:42)PAO(cid:36) (cid:103)AA Ì(cid:46)(cid:42)PAO(cid:36)\BC ^ AA,QBC//BC,\BC ^ AA . 1 1 1 1 1 1 1 (cid:28)2(cid:33)(cid:97)(cid:89)(cid:23)(cid:10) QBC = 22+22 =2 2,PB=PC =2,\PB2+PC2 =BC2,\PC ^PB, 1 QO(cid:55)(cid:40)(cid:82)(cid:36)\PO= BC = 2(cid:36) 2 (cid:103)QAO= 2,PA=2AA =2,\PO2+AO2 =PA2,\PO^ AO(cid:36) 1 (cid:102)O(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)OA,OB,OP(cid:55)x,y,z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)         (cid:107)A 2,0,0 ,B 0, 2,0 ,P 0,0, 2 ,C 0,- 2,0 (cid:36)          \CP= 0, 2, 2 (cid:36)AP= - 2,0, 2 (cid:36)BP= 0,- 2, 2 (cid:36)    ì ïAP×n=0 ì ï- 2x+ 2z=0 (cid:106)(cid:46)(cid:42)PAB(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36)(cid:107)í  Þí (cid:36) ïîBP×n=0 ïî- 2y+ 2z=0 (cid:155)x=1(cid:36)(cid:107)n  =1,1,1(cid:36)(cid:101)(cid:102) sinq= cosC  P  ,n  = 2+ 2 = 6 . 2 3 3 6 (cid:101)(cid:102)(cid:111)(cid:78)CC (cid:123)(cid:46)(cid:42)AABB(cid:101)(cid:124)(cid:50)q(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 1 1 1 3 (cid:97)(cid:89)(cid:49)(cid:10) QBC = 22+22 =2 2,PB=PC =2,\PB2+PC2 =BC2,\PC ^PB, 1 QO(cid:55)(cid:40)(cid:82)(cid:36)\PO= BC = 2(cid:36)PO^BC(cid:36) 2 (cid:103)QAO= 2,PA=2AA =2,\PO2+AO2 =PA2,\PO^ AO(cid:36) 1 (cid:103)BCÇAO=O(cid:36)BC,AOÌ(cid:46)(cid:42)ABC(cid:36) PO^(cid:46)(cid:42)ABC(cid:36) PA=PB= AB=2(cid:36)VPAB(cid:55)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36) ∴ (cid:106)C(cid:149)(cid:46)(cid:42)PAB(cid:51)(cid:150)(cid:151)(cid:55)h(cid:36)1 1 1 1 π QV =V , ´ ´2´2´ 2 = ´ ´2´2´sin ´h(cid:36) P-ABC C-PAB 3 2 3 2 3 ∴ 2 6 h 6 \h= ,\sinq= = . 3 PC 3 6 (cid:101)(cid:102)(cid:111)(cid:78)CC (cid:123)(cid:46)(cid:42)AABB(cid:101)(cid:124)(cid:50)q(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 1 1 1 3 7(cid:27)(cid:28)2024·(cid:300)(cid:289)(cid:301)(cid:302)(cid:303)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)CA=CB(cid:36)(cid:37)(cid:114)(cid:112)ABBA (cid:55)(cid:285)(cid:112)(cid:36) 1 1 1 1 1 p ÐABB = (cid:36)AC ^BC. 1 3 1 1 (1)(cid:44)(cid:45)(cid:10)BC =BB . 1 (2)(cid:187)(cid:90)(cid:46)(cid:42)ABC^(cid:46)(cid:42)ABBA (cid:36)(cid:56)(cid:49)(cid:42)(cid:50)B-CC -A(cid:51)(cid:52)(cid:53)(cid:54). 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)(cid:47) 4 (2) . 5 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:221)(cid:81)(cid:78)(cid:42)(cid:24)(cid:42)(cid:42)(cid:51)(cid:214)(cid:245)(cid:3)(cid:138)(cid:44)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)BCCB (cid:55)(cid:285)(cid:112)(cid:65)(cid:66)(cid:47) 1 1 (cid:28)2(cid:33)(cid:63)(cid:44)BO^(cid:46)(cid:42)ABC(cid:36)(cid:76)(cid:77)(cid:21)(cid:125)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:97)(cid:89)(cid:65)(cid:66)(cid:56)(cid:25). 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33) (cid:106)O(cid:55)AB(cid:51)(cid:40)(cid:82)(cid:36)(cid:85)(cid:86)CO(cid:36)BO(cid:36)AB (cid:36)BC (cid:36) 1 1 1 (cid:100)(cid:55)CA=CB(cid:36)(cid:101)(cid:102)AB^OC(cid:36) π (cid:100)(cid:55)(cid:37)(cid:114)(cid:112)ABBA (cid:55)(cid:285)(cid:112)(cid:36)ÐABB = (cid:36)(cid:101)(cid:102)VABB (cid:55)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36)(cid:107)AB^OB (cid:36) 1 1 1 3 1 1 (cid:103)OCÌ(cid:46)(cid:42)OBC(cid:36)OB Ì(cid:46)(cid:42)OBC(cid:36)OCIOB =O(cid:36)(cid:101)(cid:102)AB^(cid:46)(cid:42)OBC(cid:36) 1 1 1 1 1 (cid:100)(cid:55)BCÌ(cid:46)(cid:42)OBC(cid:36)(cid:101)(cid:102)AB^BC(cid:36) 1 1 1 (cid:100)(cid:55)AC ^BC(cid:36)ABÌ(cid:46)(cid:42)ABC (cid:36)AC Ì(cid:46)(cid:42)ABC (cid:36) 1 1 1 1 1AC IAB= A(cid:36)(cid:101)(cid:102)BC^(cid:46)(cid:42)ABC (cid:36) 1 1 1 (cid:100)(cid:55)BC Ì(cid:46)(cid:42)ABC (cid:36)(cid:101)(cid:102)BC ^BC(cid:36)(cid:101)(cid:102)(cid:37)(cid:114)(cid:112)BCCB (cid:55)(cid:285)(cid:112)(cid:36)(cid:65)BC =BB . 1 1 1 1 1 1 1 (cid:28)2(cid:33) (cid:100)(cid:55)(cid:46)(cid:42)ABC^(cid:46)(cid:42)ABBA (cid:36)(cid:48)(cid:46)(cid:42)ABCÇ(cid:46)(cid:42)ABBA = AB(cid:36)AB^OB (cid:36)OB Ì(cid:46)(cid:42)ABBA (cid:36) 1 1 1 1 1 1 1 1 (cid:101)(cid:102)BO^(cid:46)(cid:42)ABC(cid:47) 1 (cid:102)O(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)OC(cid:36)OA(cid:36)OB (cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x(cid:36)y(cid:36)z(cid:163)(cid:36) 1 (cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:106)AB=2. (cid:107)O0,0,0(cid:36)C  3,0,0  (cid:36)B0,-1,0(cid:36)B  0,0, 3  (cid:36)A0,1,0(cid:36) 1           (cid:66)(cid:67)AC = 3,-1,0 (cid:36)BB =CC = 0,1, 3 (cid:36)BC = 3,1,0 . 1 1    ì ïm×BC = 3x+y=0, (cid:106)(cid:46)(cid:42)BCC 1 (cid:51)(cid:89)(cid:139)(cid:140)(cid:55)m=x,y,z(cid:36)(cid:107)í   ïîm×CC = y+ 3z=0, 1    (cid:146)x=1(cid:36)(cid:107)y=- 3(cid:36)z=1(cid:36)(cid:66)(cid:67)m= 1,- 3,1 .    ì ïn×AC = 3a-b=0, (cid:106)(cid:46)(cid:42)ACC 1 (cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=a,b,c(cid:36)(cid:107)í   ïîn×CC =b+ 3c=0, 1    (cid:146)a=1(cid:36)(cid:107)b= 3(cid:36)c=-1(cid:36)(cid:66)(cid:67)n= 1, 3,-1 .     m×n 3 4 cosm,n =   = (cid:36)(cid:113)(cid:49)(cid:42)(cid:50)B-CC -A(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 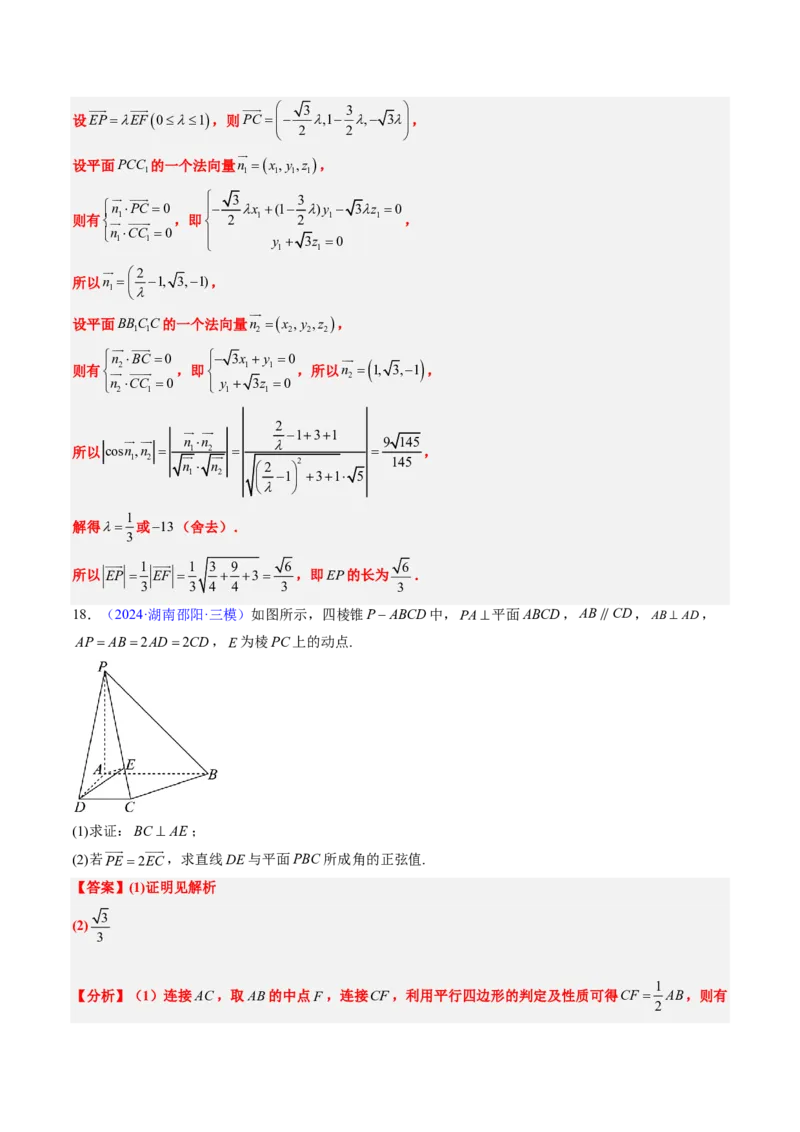m n 5 1 5 8(cid:27)(cid:28)2024·(cid:300)(cid:283)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)D(cid:143)(cid:38)BC(cid:159)(cid:23)(cid:82)(cid:28)(cid:82)D(cid:123)(cid:82)C(cid:164)(cid:246)(cid:129)(cid:33)(cid:36)(cid:48) 1 1 AD^DC(cid:36)(cid:81)A(cid:83)(cid:46)(cid:42)BCCB (cid:51)(cid:88)(cid:78)l(cid:27) 1 1 1(1)(cid:44)(cid:45)(cid:10)l//AD(cid:47) (2)(cid:43)AC =CC =2(cid:36)(cid:161)(cid:87)(cid:38)(cid:39)C -ACD(cid:51)(cid:148)(cid:109)(cid:287)(cid:179)(cid:162)(cid:36)(cid:56)AC(cid:123)(cid:46)(cid:42)ADC (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:27) 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 3 (2) (cid:27) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:63)(cid:44)(cid:45)AD^(cid:46)(cid:42)BCCB (cid:36)(cid:75)(cid:76)(cid:77)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:65)(cid:66)(cid:44)(cid:67)(cid:47) 1 1 (cid:28)2(cid:33)(cid:89)1(cid:10)(cid:68)(cid:87)(cid:38)(cid:39)C -ACD(cid:51)(cid:148)(cid:109)(cid:287)(cid:179)(cid:212)(cid:15)(cid:67)(cid:149)S (cid:287)(cid:179)(cid:36)(cid:127)(cid:92)(cid:175)(cid:176)(cid:164)(cid:108)(cid:182)(cid:67)AD=CD= 2(cid:36)(cid:83) 1 VACD CH ^DC (cid:84)H(cid:36)(cid:66)(cid:212)(cid:67)CH ^(cid:46)(cid:42)ADC (cid:36)(cid:67)(cid:149)AC(cid:123)(cid:46)(cid:42)ADC (cid:101)(cid:124)(cid:51)(cid:50)(cid:108)(cid:84)ÐCAH(cid:36)(cid:25)(cid:87)(cid:50)(cid:112)(cid:65)(cid:67)(cid:47) 1 1 1  (cid:89)2(cid:10)(cid:304)(cid:21)(cid:132)(cid:138)(cid:36)(cid:62)(cid:91)(cid:56)(cid:67)AC(cid:144)(cid:46)(cid:42)ADC (cid:51)(cid:89)(cid:139)(cid:140)(cid:51)(cid:136)(cid:137)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:51)(cid:219)(cid:50)(cid:7)(cid:182)(cid:177)(cid:153)(cid:65)(cid:67). 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)CC ^(cid:46)(cid:42)ABC(cid:36)(cid:100)(cid:55)ADÌ(cid:46)(cid:42)ABC(cid:36)(cid:101)(cid:102)CC ^ AD(cid:27) 1 1 1 1 1 (cid:103)AD^DC,CC ÇDC =C,CC,DCÌ(cid:46)(cid:42)BCCB (cid:36)(cid:101)(cid:102)AD^(cid:46)(cid:42)BCCB (cid:27) 1 1 1 1 1 1 (cid:103)(cid:100)(cid:55)l^(cid:46)(cid:42)BCCB (cid:36)(cid:101)(cid:102)l//AD(cid:27) 1 1 1 (cid:28)2(cid:33)(cid:100)(cid:55)V = S ×CC (cid:36)(cid:101)(cid:102)(cid:161)(cid:87)(cid:38)(cid:39)C -ACD(cid:148)(cid:109)(cid:287)(cid:179)(cid:162)(cid:36)S (cid:287)(cid:179)(cid:27) C1 -ACD 3 VACD 1 1 VACD (cid:68)(cid:28)1(cid:33)(cid:66)(cid:90)AD^(cid:46)(cid:42)BCCB (cid:36)(cid:100)(cid:55)CDÌ(cid:42)BCCB (cid:36)(cid:101)(cid:102)AD^CD(cid:27) 1 1 1 1 (cid:103)AC =2(cid:36)(cid:101)(cid:102)4= AC2 = AD2 +DC2 ³2AD×CD =4S (cid:36) VACD (cid:161)(cid:48)(cid:305)(cid:161)AD=CD= 2(cid:162)(cid:155)(cid:108)(cid:9)(cid:36)(cid:65)(cid:161)S (cid:287)(cid:179)(cid:162)(cid:36)AD=CD= 2(cid:27) VACD (cid:89)1(cid:10)(cid:306)(cid:129)(cid:89) (cid:34)(cid:35)(cid:36)(cid:83)CH ^DC (cid:84)H(cid:36)(cid:85)(cid:128)AH. 1 (cid:68)(cid:28)1(cid:33)(cid:66)(cid:90)AD^(cid:46)(cid:42)BCCB (cid:36)(cid:100)(cid:55)CH Ì(cid:42)BCCB (cid:36)(cid:101)(cid:102)AD^CH(cid:27) 1 1 1 1 (cid:103)DC ÇAD=D,AD,DC Ì(cid:46)(cid:42)ADC (cid:36)(cid:101)(cid:102)CH ^(cid:46)(cid:42)ADC (cid:27) 1 1 1 1 (cid:100)(cid:203)(cid:36)AC(cid:123)(cid:46)(cid:42)ADC (cid:101)(cid:124)(cid:51)(cid:50)(cid:108)(cid:84)ÐCAH(cid:27) 1 (cid:100)(cid:55)CH ^(cid:46)(cid:42)ADC,AH Ì(cid:46)(cid:42)ADC (cid:36)(cid:101)(cid:102)CH ^ AH (cid:27) 1 1 2 2 2 (cid:141)RtVCDC (cid:40)(cid:36)CD = 2,CC = 2(cid:36)(cid:101)(cid:102)DC = 6(cid:36)(cid:100)(cid:203)CH = = , 1 1 1 6 32 (cid:141)RtVACH (cid:40)(cid:36)sinÐCAH = CH 3 3 (cid:27) = = AC 2 3 3 (cid:101)(cid:102)AC(cid:123)(cid:46)(cid:42)ADC (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54) (cid:27) 1 3 (cid:89)2(cid:10)(cid:139)(cid:140)(cid:89) (cid:141)(cid:46)(cid:42)BCCB (cid:206)(cid:36)(cid:83)DE//CC,DE(cid:157)BC (cid:84)E(cid:36)(cid:100)(cid:55)CC ^(cid:46)(cid:42)ABC(cid:36)(cid:101)(cid:102)DE^(cid:46)(cid:42)ABC(cid:27) 1 1 1 1 1 1 (cid:62)(cid:91)(cid:102)DC(cid:36)DA(cid:36)DE(cid:55)x(cid:36)y(cid:36)z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:34)(cid:35).(cid:107)A(0, 2,0),C( 2,0,0),C ( 2,0,2)(cid:27) 1    (cid:106)(cid:46)(cid:42)ADC (cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=(x,y,z)(cid:36)(cid:181)(cid:67)DA=(0, 2,0),DC =( 2,0,2)(cid:36) 1 1   ì ï DA×n= 2y=0,  í  (cid:66)(cid:155)n=( 2,0,-1)(cid:27) ïîDC 1 ×n= 2x+2z=0,      2 3 (cid:100)AC = 2,- 2,0 (cid:36)(cid:107)cosáAC,nñ= = (cid:36) 2 3 3   3 (cid:101)(cid:102)AC(cid:123)(cid:46)(cid:42)ADC (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:108)(cid:84)|cosáAC,nñ|= (cid:27) 1 3 9(cid:27)(cid:28)2024·(cid:266)(cid:307)(cid:308)(cid:309)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:241)(cid:225)(cid:148)(cid:143)(cid:68)(cid:108)(cid:30)(cid:51)(cid:111)(cid:87)(cid:38)(cid:147)(cid:144)(cid:310)(cid:145)(cid:311)(cid:147)(cid:312)(cid:129)(cid:74)(cid:124)(cid:36)BC (cid:55)(cid:310)(cid:145)(cid:311)(cid:147) 1 1 (cid:159)(cid:41)(cid:42)(cid:51)(cid:111)(cid:313)(cid:36)ÐACB=90°(cid:36)AC =BC =2(cid:36)(cid:82)E(cid:36)F (cid:62)(cid:91)(cid:55)AC(cid:36)AB(cid:51)(cid:40)(cid:82)(cid:36)(cid:82)D(cid:55)BC (cid:51)(cid:40)(cid:82)(cid:27) 1 1 (1)(cid:44)(cid:45)(cid:10)(cid:46)(cid:42)BCD//(cid:46)(cid:42)CEF(cid:47) 1 (2)(cid:43)P(cid:143)(cid:78)(cid:202)CF(cid:159)(cid:23)(cid:145)(cid:314)(cid:82)(cid:36)(cid:161)CC =2(cid:162)(cid:36)(cid:56)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:51)(cid:287)(cid:179)(cid:54)(cid:27) 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)2 6 (2) 5 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:63)(cid:44)(cid:45)CD//FB(cid:36)FB=CD(cid:36)(cid:315)(cid:74)(cid:44)(cid:45)FBDC (cid:55)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)(cid:66)(cid:67)BD//FC (cid:36)(cid:75)(cid:44)(cid:45) 1 1 1 1 EF∥BC(cid:36)(cid:68)(cid:42)(cid:42)(cid:46)(cid:79)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:67)(cid:44)(cid:47) (cid:28)2(cid:33)(cid:97)(cid:89)1(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:89)(cid:56)(cid:25)(cid:47)(cid:97)(cid:89)2(cid:36)(cid:63)(cid:44)(cid:45)(cid:46)(cid:42)EFC ^(cid:46)(cid:42)AACC(cid:36)(cid:81)A(cid:83) 1 1 1 1 AH ^EC (cid:157)EC (cid:84)H(cid:36)(cid:107)ÐAPH (cid:233)(cid:143)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:36)(cid:127)(cid:92)(cid:46)(cid:42)(cid:241)(cid:225)(cid:56)(cid:64)AP(cid:287)(cid:180)(cid:36)(cid:67)(cid:25). 1 1 1 1 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)CD(cid:36)(cid:68)(cid:82)D(cid:55)BC (cid:51)(cid:40)(cid:82)(cid:36)BC (cid:55)(cid:310)(cid:145)(cid:311)(cid:147)(cid:159)(cid:41)(cid:42)(cid:51)(cid:111)(cid:313)(cid:90)ÐDCB =45°(cid:36) 1 1 1 1 1 1 1 (cid:68)ÐACB=90°(cid:36)AC =BC =2(cid:36)(cid:90)ÐCBA =45°(cid:36)CD= 2(cid:36) 1 1 1 1 (cid:107)ÐDCB =ÐCBA(cid:36)(cid:103)A,B,D,C (cid:37)(cid:82)(cid:204)(cid:42)(cid:36)(cid:101)(cid:102)AB //CD(cid:36) 1 1 1 1 1 1 1 1 1 1 1 (cid:68)AABB (cid:55)(cid:111)(cid:87)(cid:38)(cid:147)(cid:51)(cid:316)(cid:42)(cid:90)AB //AB(cid:36)(cid:65)AB //FB(cid:36)(cid:107)CD//FB(cid:36) 1 1 1 1 1 1 1 (cid:68)F (cid:55)AB(cid:51)(cid:40)(cid:82)AC =BC =2(cid:67)FB= 2=CD(cid:36) 1 (cid:101)(cid:102)(cid:37)(cid:114)(cid:112)FBDC (cid:55)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)(cid:107)BD//FC (cid:36) 1 1 (cid:103)BDÌ(cid:46)(cid:42)BCD(cid:36)FC Ë(cid:46)(cid:42)BCD(cid:36)(cid:36)(cid:107)FC //(cid:46)(cid:42)BCD(cid:36) 1 1 (cid:100)(cid:55)E(cid:36)F (cid:62)(cid:91)(cid:55)AC(cid:36)AB(cid:51)(cid:40)(cid:82)(cid:36)(cid:101)(cid:102)EF//BC(cid:36) (cid:103)EF Ë(cid:46)(cid:42)BCD(cid:36)(cid:36)BCÌ(cid:46)(cid:42)BCD(cid:36)(cid:36)(cid:101)(cid:102)EF//(cid:46)(cid:42)BCD(cid:36) (cid:103)EFIFC =F, EF,FC Ì(cid:46)(cid:42)EFC (cid:36)(cid:101)(cid:102)(cid:46)(cid:42)BCD//(cid:46)(cid:42)CEF(cid:27) 1 1 1 1    (cid:28)2(cid:33)(cid:28)(cid:89)(cid:23)(cid:33)(cid:102) CA,CB,CC (cid:55)(cid:23)(cid:312)(cid:134)(cid:135)(cid:52)(cid:157)(cid:175)(cid:41)(cid:36)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)O-xyz(cid:36) (cid:107)E(1,0,0),F(1,1,0),C(0,0,2),A(2,0,2)(cid:36) 1 1    (cid:101)(cid:102)EF =(0,1,0),EC =(-1,0,2),AF =(-1,1,-2)(cid:36)FC =(-1,-1,2)(cid:36) 1 1 1   (cid:106)FP=lFC =(-l,-l,2l), lÎ[0,1](cid:36) 1    (cid:107)AP=AF+FP=(-l-1,-l+1,2l-2)(cid:36) 1 1 (cid:68)(cid:46)(cid:42)BCD//(cid:46)(cid:42)CEF(cid:90)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:65)(cid:55)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)(cid:36) 1 1 1 1  (cid:106)(cid:46)(cid:42)CEF(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36) 1   ì ïn×EF = y=0 (cid:68)í   (cid:36)(cid:155)z=1(cid:36)(cid:67)x=2(cid:36) ïîn×EC =-x+2z=0 1  (cid:107)(cid:46)(cid:42)CEF(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=2,0,1(cid:36) 1 (cid:106)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)(cid:107) 1 1     AP×n 4 sinq= cos AP,n = 1  = (cid:36) 1 AP n 2 10 1 5 6(l- )2+ 3 3 2 2 6 (cid:103)lÎ[0,1](cid:36)(cid:107)l= (cid:162)(cid:36)sinq(cid:51)(cid:287)(cid:179)(cid:54)(cid:55) (cid:27) 3 5 2 6 (cid:101)(cid:102)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:51)(cid:287)(cid:179)(cid:54)(cid:55) (cid:27) 1 5 (cid:28)(cid:89)(cid:49)(cid:33)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)CC ^(cid:41)(cid:42)ABC(cid:36) 1 1 1 1 (cid:100)(cid:55)EF Ì(cid:41)(cid:42)ABC(cid:36)(cid:101)(cid:102)CC ^EF (cid:36) 1 (cid:68)(cid:28)1(cid:33)(cid:90)EF//BC(cid:36)BC ^ AC(cid:36)(cid:101)(cid:102)EF^AC(cid:36) (cid:103)ACICC =C, AC,CC Ì(cid:46)(cid:42)AACC(cid:36) 1 1 1 1 (cid:101)(cid:102)EF^(cid:46)(cid:42)AACC(cid:36) 1 1 (cid:100)(cid:55)EF Ì(cid:46)(cid:42)EFC (cid:36) 1 (cid:101)(cid:102)(cid:46)(cid:42)EFC ^(cid:46)(cid:42)AACC(cid:36) 1 1 1 (cid:81)A(cid:83)AH ^EC (cid:157)EC (cid:84)H(cid:36) 1 1 1 1 (cid:100)(cid:55)(cid:46)(cid:42)EFC Ç(cid:46)(cid:42)AACC=CE(cid:36)(cid:101)(cid:102)AH ^(cid:46)(cid:42)CEF(cid:36) 1 1 1 1 1 1(cid:103)(cid:46)(cid:42)BCD//(cid:46)(cid:42)CEF(cid:36) 1 (cid:107)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:65)(cid:55)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)CEF(cid:101)(cid:124)(cid:50)ÐAPH (cid:36) 1 1 (cid:100)(cid:55)Rt(cid:178)CEC Rt(cid:178)AHC (cid:36)(cid:48)(cid:52)(cid:97)(cid:112)ABCD(cid:51)(cid:114)(cid:93)(cid:55)2(cid:36) 1 1 1 (cid:101)(cid:102) A 1 H = 2 ∽ (cid:36)(cid:107)AH = 4 (cid:36) 2 5 1 5 4 (cid:103) AH 5 (cid:36)(cid:192)(cid:122)sinÐAPH (cid:54)(cid:287)(cid:179)(cid:36) sinÐAPH = 1 = 1 1 AP AP 1 1 (cid:107)AP(cid:287)(cid:180)(cid:36)(cid:141)(cid:178)AFC (cid:40)AF =FC = 6,AC =2(cid:36) 1 1 1 1 1 1 1 30 2 6 (cid:81)A(cid:83)AP^CF (cid:157)FC (cid:84)P(cid:36)(cid:68)(cid:108)(cid:42)(cid:109)(cid:66)(cid:56)(cid:64)AP= (cid:36)(cid:203)(cid:162)sinÐAPH = (cid:27) 1 1 1 1 1 3 1 5 2 6 (cid:101)(cid:102)(cid:111)(cid:78)AP(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:51)(cid:287)(cid:179)(cid:54)(cid:55) (cid:27) 1 5 10(cid:27)(cid:28)2024·(cid:317)(cid:318)(cid:319)(cid:320)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:37)(cid:38)(cid:39)P-ABCD(cid:40)(cid:36)(cid:41)(cid:42)ABCD(cid:143)(cid:114)(cid:93)(cid:55)2(cid:51)(cid:52)(cid:97)(cid:112)(cid:36)PA^(cid:46)(cid:42)ABCD(cid:36) PA=2(cid:36)M (cid:143)BC(cid:40)(cid:82)(cid:36)N (cid:143)PD(cid:40)(cid:82). (1)(cid:44)(cid:45)(cid:10)(cid:111)(cid:78)MN //(cid:46)(cid:42)PAB(cid:47)   (2)(cid:43)PG=3GC(cid:36)(cid:56)(cid:46)(cid:42)PCD(cid:123)(cid:46)(cid:42)GMN(cid:51)(cid:219)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54). (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61)(cid:47) 3 (2) . 6 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)PA(cid:51)(cid:40)(cid:82)Q(cid:36)(cid:321)(cid:322)(cid:87)(cid:50)(cid:112)(cid:40)(cid:214)(cid:78)(cid:154)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:130)(cid:131)(cid:36)(cid:127)(cid:92)(cid:78)(cid:42)(cid:46)(cid:79)(cid:51)(cid:80)(cid:255)(cid:212)(cid:15)(cid:65)(cid:67). (cid:28)2(cid:33)(cid:102)A(cid:55)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:46)(cid:42)PCD(cid:123)(cid:46)(cid:42)GMN(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:75)(cid:127)(cid:92)(cid:42)(cid:42)(cid:50)(cid:51)(cid:139)(cid:140)(cid:56)(cid:89) (cid:56)(cid:25)(cid:65)(cid:67). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:141)(cid:37)(cid:38)(cid:39)P-ABCD(cid:40)(cid:36)(cid:155)PA(cid:51)(cid:40)(cid:82)Q(cid:36)(cid:85)(cid:86)QB(cid:36)QN(cid:36)1 (cid:68)N (cid:55)PD(cid:51)(cid:40)(cid:82)(cid:36)(cid:67)QN = AD(cid:36)QN //AD(cid:36) 2 1 (cid:141)(cid:52)(cid:97)(cid:112)ABCD(cid:40)(cid:36)M (cid:143)BC(cid:40)(cid:82)(cid:36)(cid:67)BM = AD(cid:36)BM //AD(cid:36) 2 (cid:107)QN =BM (cid:48)QN //BM (cid:36)(cid:65)(cid:37)(cid:114)(cid:112)BMNQ(cid:55)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36) (cid:100)(cid:203)MN //BQ(cid:36)(cid:103)MNË(cid:46)(cid:42)PAB,BQÌ(cid:46)(cid:42)PAB(cid:36) (cid:101)(cid:102)(cid:111)(cid:78)MN //(cid:46)(cid:42)PAB. (cid:28)2(cid:33)(cid:68)PA^(cid:41)(cid:42)ABCD(cid:36)(cid:48)(cid:37)(cid:114)(cid:112)ABCD(cid:55)(cid:52)(cid:97)(cid:112)(cid:36)(cid:67)(cid:111)(cid:78)AB,AD,AP(cid:142)(cid:142)(cid:88)(cid:111)(cid:36) (cid:102)A(cid:55)(cid:158)(cid:82)(cid:36)(cid:111)(cid:78)AB,AD,AP(cid:62)(cid:91)(cid:55)x,y,z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:34)(cid:35)(cid:36)   (cid:107)B(2,0,0),C(2,2,0),D(0,2,0),A(0,0,0),P(0,0,2),N(0,1,1),M(2,1,0)(cid:36)PD=(0,2,-2),CD=(-2,0,0)(cid:36)    ì ïn ×PD=2y-2z=0  (cid:106)(cid:46)(cid:42)PCD(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n =x,y,z(cid:36)(cid:107)í 1  (cid:36)(cid:146)y=1(cid:36)(cid:67)n =(0,1,1)(cid:36) 1 ïîn ×CD=-2x=0 1 1   (cid:106)Gx,y ,z (cid:36)(cid:107)PG=(x,y ,z -2)(cid:36)GC =(2-x,2-y ,-z )(cid:36) 1 1 1 1 1 1 1 1 1   3 3 1  1 1 1  (cid:68)PG=3GC(cid:36)(cid:67)G( , , )(cid:36)GM =( ,- ,- )(cid:36)(cid:74)MN =(-2,0,1)(cid:36) 2 2 2 2 2 2   ìn ×MN =-2x +z =0  ï 2 2 2  (cid:106)(cid:46)(cid:42)GMN(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n 2 =x 2 ,y 2 ,z 2 (cid:36)(cid:107)í ïn  ×G  M  = 1 x - 1 y - 1 z =0 (cid:36)(cid:155)x 2 =1(cid:36)(cid:67)n 2 =(1,-1,2)(cid:36) î 2 2 2 2 2 2 2     |n ×n | 1 3 (cid:106)(cid:46)(cid:42)PCD(cid:123)(cid:46)(cid:42)GMN(cid:51)(cid:219)(cid:50)(cid:51)(cid:55)q(cid:36) cosq=|cosán,n ñ|= 1 2 = = (cid:36) 1 2 |n ||n | 2´ 6 6 1 2 3 (cid:101)(cid:102)(cid:46)(cid:42)PCD(cid:123)(cid:46)(cid:42)GMN(cid:51)(cid:219)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:55) . 611(cid:27)(cid:28)2024·(cid:323)(cid:266)(cid:324)(cid:325)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)AB^BC(cid:36)AB=BC =BB =6(cid:36)D(cid:24)E(cid:62) 1 1 1 1 (cid:91)(cid:55)AC(cid:24)BB (cid:51)(cid:40)(cid:82)(cid:36)(cid:106)(cid:46)(cid:42)ADE(cid:157)(cid:38)BC(cid:84)(cid:82)F (cid:27) 1 1 (1)(cid:56)BF(cid:47) (2)(cid:56)(cid:49)(cid:42)(cid:50)C -DF-C(cid:51)(cid:46)(cid:42)(cid:50)(cid:51)(cid:52)(cid:326)(cid:54)(cid:27) 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)2 10 (2) 5     (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:132)(cid:133)(cid:172)(cid:161)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:279)(cid:36)(cid:66)(cid:67)(cid:46)(cid:42)ADE(cid:51)(cid:89)(cid:139)(cid:140)m(cid:36)(cid:68) EF Ì(cid:46)(cid:42)ADE(cid:36)(cid:66)(cid:67) EF (cid:123)m 1 1 (cid:88)(cid:111)(cid:36)(cid:177)(cid:153)(cid:65)(cid:66)(cid:67)(cid:25)(cid:47) (cid:28)2(cid:33)(cid:56)(cid:64)(cid:46)(cid:42)CDF(cid:123)(cid:46)(cid:42)DFC(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:321)(cid:322)(cid:219)(cid:50)(cid:7)(cid:182)(cid:177)(cid:153)(cid:196)(cid:219)(cid:50)(cid:126)(cid:53)(cid:54)(cid:279)(cid:65)(cid:66)(cid:67)(cid:196)(cid:52)(cid:326)(cid:54). 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:102)B(cid:55)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:107)(cid:185)B0,0,0(cid:24)B 0,0,6(cid:24)A6,0,0(cid:24)C0,6,0(cid:24)A 6,0,6(cid:24) 1 1 D3,3,0(cid:24)E0,0,3(cid:24)C 0,6,6(cid:36)(cid:106)F0,m,0(cid:36) 1    (cid:107)AD=-3,3,-6(cid:24)AE=-6,0,-3(cid:36)EF =0,m,-3(cid:36) 1 1  (cid:106)(cid:46)(cid:42)ADE(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)m=x,y,z(cid:36) 1   ì ïAD×m=-3x+3y-6z=0 (cid:107)(cid:185)í 1   (cid:36) ïîAE×m=-6x-3z=0 1  (cid:146)x=1(cid:36)(cid:107)(cid:185)y=-3(cid:36)z=-2(cid:36)(cid:65)m=x,y,z(cid:36)   (cid:68)EF Ì(cid:46)(cid:42)ADE(cid:36)(cid:107)EF×m=m´-3+-3´-2=0(cid:36)(cid:25)(cid:67)m=2(cid:36) 1 (cid:113)BF =2(cid:47)  (cid:28)2(cid:33)CD=3,-3,-6(cid:36)DF =-3,-1,0(cid:36) 1  (cid:106)(cid:46)(cid:42)CDF(cid:51)(cid:89)(cid:139)(cid:140)(cid:62)(cid:91)(cid:55)a=x,y ,z (cid:36) 1 1 1 1   ì ïCD×a=3x -3y -6z =0 (cid:107)(cid:185)í 1   1 1 1 (cid:36) ïîDF×a=-3x -y =0 1 1  (cid:146)x =1(cid:36)(cid:107)(cid:185)y =-3(cid:36)z =2(cid:36)(cid:65)a=1,-3,2(cid:36) 1 1 1  (cid:68)z(cid:163)^(cid:46)(cid:42)DFC(cid:36)(cid:113)(cid:46)(cid:42)DFC(cid:51)(cid:89)(cid:139)(cid:140)(cid:66)(cid:55)b=0,0,1(cid:36)     a×b 2 14 (cid:107)cos a,b =   = = (cid:36) a×b 1+9+4×1 7 2   æ 14ö 35 (cid:107)sin a,b = 1-ç ÷ = (cid:36) ç ÷ è 7 ø 7 14 7 10 (cid:107)(cid:49)(cid:42)(cid:50)C -DF-C(cid:51)(cid:46)(cid:42)(cid:50)(cid:51)(cid:52)(cid:326)(cid:54)(cid:55) = . 1 35 5 7 12(cid:27)(cid:28)2024·(cid:275)(cid:283)(cid:93)(cid:327)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:40)(cid:36)AD//BC(cid:36) 1 1 1 1 AB^DD,CD=2,AD=3,BC =4(cid:36)ÐADB=30o. 1(1)(cid:44)(cid:45)(cid:10)(cid:46)(cid:42)ADDA ^(cid:46)(cid:42)ABCD(cid:47) 1 1 49 3 (2)(cid:43)AA ^AD(cid:36)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:148)(cid:109)(cid:55) ,BC =2(cid:36)(cid:56)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CDDC (cid:219)(cid:50)(cid:51)(cid:126)(cid:53) 1 1 1 1 1 12 1 1 1 1 (cid:54). (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 3 273 (2) . 91 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:68)(cid:187)(cid:90)(cid:36)(cid:141)△BCD(cid:40)(cid:36)(cid:68)(cid:52)(cid:53)(cid:71)(cid:15)(cid:36)(cid:66)(cid:67)ÐBDC =90o(cid:36)(cid:141)△ABD(cid:40)(cid:36)(cid:68)(cid:126)(cid:53)(cid:71)(cid:15)(cid:36) (cid:66)(cid:67)AB= 3(cid:36)(cid:68)(cid:69)(cid:70)(cid:71)(cid:15)(cid:51)(cid:72)(cid:71)(cid:15)(cid:66)(cid:67)AB^AD(cid:36)(cid:107)AB^(cid:46)(cid:42)ADDA(cid:36)(cid:107)(cid:67)(cid:46)(cid:42)ADDA ^(cid:46)(cid:42)ABCD(cid:47) 1 1 1 1 (cid:28)2(cid:33)(cid:68)(cid:28)1(cid:33)(cid:144)(cid:187)(cid:90)(cid:36)(cid:66)(cid:67)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:159)(cid:24)(cid:296)(cid:41)(cid:42)(cid:42)(cid:109)(cid:36)(cid:75)(cid:68)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:148) 1 1 1 1 1 1 1 1 (cid:109)(cid:7)(cid:182)(cid:56)(cid:64)(cid:30)(cid:36)(cid:68)(cid:28)1(cid:33)(cid:66)(cid:67)AA ^(cid:46)(cid:42)ABCD(cid:36)(cid:102)A(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36) 1 (cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:106)(cid:46)(cid:42)CDDC (cid:144)(cid:46)(cid:42)ABCD(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:107)(cid:68)(cid:136)(cid:137)(cid:152)(cid:153)(cid:67)(cid:149)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42) 1 1 CDDC (cid:219)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54). 1 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33) (cid:100)(cid:55)AD//BC(cid:36)(cid:101)(cid:102)ÐDBC =ÐADB=30o(cid:36) (cid:141)△BCD(cid:40)(cid:36)(cid:68)(cid:52)(cid:53)(cid:71)(cid:15)(cid:36) CD BC (cid:67) = (cid:36) sinÐDBC sinÐBDC BCsinÐDBC (cid:101)(cid:102)sinÐBDC = =1(cid:36) CD (cid:101)(cid:102)ÐBDC =90o(cid:36) (cid:107)(cid:68)(cid:69)(cid:70)(cid:71)(cid:15)(cid:36)(cid:67)BD= BC2-CD2 =2 3(cid:36) (cid:141)△ABD(cid:40)(cid:36)(cid:68)(cid:126)(cid:53)(cid:71)(cid:15)(cid:36) (cid:67) AB= AD2+BD2-2AD×BDcos30o = 3 (cid:36) (cid:101)(cid:102)AB2+AD2 =BD2(cid:36)(cid:101)(cid:102)ÐBAD=90o(cid:36)(cid:65)AB^AD(cid:36) (cid:103)AB^DD,ADÇDD =D,AD,DD Ì(cid:46)(cid:42)ADDA(cid:36) 1 1 1 1 1 (cid:101)(cid:102)AB^(cid:46)(cid:42)ADDA(cid:36) 1 1(cid:103)ABÌ(cid:46)(cid:42)ABCD(cid:36) (cid:101)(cid:102)(cid:46)(cid:42)ADDA ^(cid:46)(cid:42)ABCD. 1 1 (cid:28)2(cid:33)(cid:68)(cid:28)1(cid:33)(cid:90)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:296)(cid:41)(cid:42)(cid:42)(cid:109) 1 1 1 1 1 1 7 3 S =S +S = ´ 3´3+ ´2´2 3= (cid:36) VABD VBCD 2 2 2 BC 1 7 3 (cid:100)(cid:55) 1 1 = (cid:36)(cid:101)(cid:102)(cid:159)(cid:41)(cid:42)(cid:42)(cid:109)S¢= (cid:36) BC 2 8 (cid:106)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:30)(cid:55)h(cid:36) 1 1 1 1 (cid:107)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:148)(cid:109)(cid:55) 1 h  S¢+ S¢S +S  = 49 3 (cid:36) 1 1 1 1 3 12 (cid:101)(cid:102)h=2(cid:36) (cid:100)(cid:55)(cid:46)(cid:42)ADDA ^(cid:46)(cid:42)ABCD,AA ^ AD(cid:36) 1 1 1 (cid:46)(cid:42)ADDA Ç(cid:46)(cid:42)ABCD= AD(cid:36) 1 1 (cid:101)(cid:102)AA ^(cid:46)(cid:42)ABCD(cid:36)(cid:101)(cid:102)AB,AD,AA(cid:142)(cid:142)(cid:88)(cid:111). 1 1 (cid:102)A(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)AB,AD,AA(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x(cid:163)(cid:36)y(cid:163)(cid:36)z(cid:163)(cid:36) 1 (cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:107) æ 3 ö D(0,3,0),C( 3,4,0),D ç0, ,2÷ 1è 2 ø  æ 3 ö    (cid:101)(cid:102)DD =ç0,- ,2÷,DC = 3,1,0 (cid:36) 1 è 2 ø  (cid:106)(cid:46)(cid:42)CDDC (cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36) 1 1   ì 3 ì ïn×DD =0 ï- y+2z=0 (cid:107)í   1 (cid:36)(cid:65)í 2 (cid:36) ïîn×DC =0 ï î 3x+y=0 3 3 (cid:146)x=1(cid:36)(cid:67)y=- 3,z=- (cid:36) 4  æ 3 3ö (cid:101)(cid:102)(cid:46)(cid:42)CDDC (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=ç1,- 3,- ÷(cid:36) 1 1 ç è 4 ÷ ø  (cid:68)(cid:21)(cid:66)(cid:90)(cid:46)(cid:42)ABCD(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)m=0,0,1(cid:36) (cid:106)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CDDC (cid:51)(cid:219)(cid:50)(cid:55)q(cid:36) 1 1 3 3 -   (cid:107) cosq= cosm  ,n  = m  ×n  = 4 = 3 273 (cid:36) m n 91 91 43 273 (cid:101)(cid:102)(cid:46)(cid:42)ABCD(cid:123)(cid:46)(cid:42)CDDC (cid:219)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:55) . 1 1 91 13(cid:27)(cid:28)2024·(cid:329)(cid:318)(cid:330)(cid:328)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)AB=BC =BB =2(cid:36)M(cid:36)N(cid:62)(cid:91)(cid:55)BB (cid:36)AC 1 1 1 1 1 (cid:40)(cid:82)(cid:36)(cid:48)CM ^AB(cid:27) 1 (1)(cid:44)(cid:45)(cid:10)CM ^ AN (cid:47) 1 1 (2)(cid:43)D(cid:55)(cid:38)AB (cid:159)(cid:51)(cid:314)(cid:82)(cid:36)(cid:161)DN (cid:123)(cid:46)(cid:42)ABC(cid:101)(cid:124)(cid:50)(cid:287)(cid:179)(cid:162)(cid:36)(cid:56)(cid:49)(cid:42)(cid:50)A-DM -N (cid:51)(cid:126)(cid:53)(cid:54). 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:81)(cid:98)(cid:60)(cid:25)(cid:61) 6 (2) 3   (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:132)(cid:133)(cid:172)(cid:161)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:44)(cid:45)CM×AN =0(cid:65)(cid:66)(cid:47) 1 1 (cid:28)2(cid:33)(cid:161)DN (cid:123)(cid:46)(cid:42)ABC(cid:101)(cid:124)(cid:50)(cid:287)(cid:179)(cid:162)(cid:36)(cid:56)(cid:64)(cid:203)(cid:162)(cid:82)D(cid:51)(cid:214)(cid:245)(cid:36)(cid:75)(cid:56)(cid:64)(cid:49)(cid:42)(cid:50)(cid:101)(cid:119)(cid:231)(cid:51)(cid:142)(cid:145)(cid:46)(cid:42)(cid:51)(cid:89)(cid:139)(cid:140)(cid:36) (cid:128)(cid:129)(cid:139)(cid:140)(cid:219)(cid:50)(cid:7)(cid:182)(cid:65)(cid:66)(cid:152)(cid:153)(cid:56)(cid:25). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:141)(cid:111)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)BB ^(cid:46)(cid:42)ABC(cid:36)(cid:74)ABÌ(cid:46)(cid:42)ABC(cid:36)BCÌ(cid:46)(cid:42)ABC(cid:36) 1 1 1 1 (cid:101)(cid:102)BB ^AB(cid:36)BB ^BC(cid:36) 1 1 (cid:100)(cid:55)CM ^AB(cid:36)CM ÇBB =M (cid:36)CM Ì(cid:46)(cid:42)BBCC (cid:36)BB Ì(cid:46)(cid:42)BBCC (cid:36) 1 1 1 1 1 1 1 1 1 (cid:101)(cid:102)AB^(cid:46)(cid:42)BBCC (cid:36) 1 1 (cid:100)(cid:55)BCÌ(cid:46)(cid:42)BBCC (cid:36) 1 1 (cid:101)(cid:102)AB^BC(cid:36) (cid:100)(cid:55)BB ^AB(cid:36)BB ^BC(cid:36) 1 1 (cid:101)(cid:102)BC,BA,BB (cid:142)(cid:142)(cid:224)(cid:156)(cid:88)(cid:111)(cid:36) 1 (cid:102)(cid:82)B(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)BC,BA,BB (cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x,y,z(cid:163)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) 1(cid:100)(cid:55)AB=BC =BB =2(cid:36)M(cid:36)N(cid:62)(cid:91)(cid:55)BB (cid:36)AC(cid:40)(cid:82)(cid:36) 1 1 (cid:101)(cid:102)B0,0,0,C2,0,0,A0,2,0,B 0,0,2(cid:36)C 0,2,2,A 0,2,2,M0,0,1,N1,1,0(cid:36) 1 1 1   (cid:101)(cid:102)CM =-2,0,-1,AN =1,-1,-2(cid:36) 1 1   (cid:101)(cid:102)CM×AN =-2+2=0(cid:36) 1 1   (cid:101)(cid:102)CM ^ AN (cid:36)(cid:65)CM ^ AN (cid:47) 1 1 1 1 (cid:28)2(cid:33) (cid:68)(cid:28)1(cid:33)(cid:67)B0,0,0,C2,0,0,A0,2,0,B 0,0,2(cid:36)C 0,2,2,A 0,2,2,M0,0,1,N1,1,0(cid:36) 1 1 1 (cid:106)D0,d,2,0£d £2(cid:36)  (cid:101)(cid:102)DN =1,1-d,-2(cid:36) (cid:100)(cid:55)BB ^(cid:46)(cid:42)ABC(cid:36) 1   BB (cid:101)(cid:102)(cid:155)(cid:46)(cid:42)ABC(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n= 1 =0,0,1 (cid:36) BB 1 æ é πùö (cid:106)DN (cid:123)(cid:46)(cid:42)ABC(cid:101)(cid:124)(cid:50)(cid:55)q,çqÎ ê 0, ú÷(cid:36) è ë 2ûø     n×DN 2 (cid:101)(cid:102)DN (cid:123)(cid:46)(cid:42)ABC(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55)sinq= cosn,DN =   = (cid:36) n DN 5+1-d2 2 sinq= (cid:43)(cid:192)DN (cid:123)(cid:46)(cid:42)ABC(cid:101)(cid:124)(cid:50)(cid:287)(cid:179)(cid:36)(cid:107)(cid:161)(cid:48)(cid:305)(cid:161) (cid:287)(cid:179)(cid:36) 5+1-d22 (cid:101)(cid:102)(cid:161)(cid:48)(cid:305)(cid:161)d =1(cid:162)(cid:36) sinq= (cid:287)(cid:179)(cid:36)(cid:203)(cid:162)D0,1,2(cid:36) 5+1-d2 (cid:100)(cid:55)BC ^BA,BC ^BB (cid:36)BAÇBB =B(cid:36)BAÌ(cid:46)(cid:42)BAAB (cid:36)BB Ì(cid:46)(cid:42)BAAB (cid:36) 1 1 1 1 1 1 1 (cid:101)(cid:102)BC^(cid:46)(cid:42)BAAB (cid:36) 1 1 (cid:100)(cid:55)DÎ(cid:46)(cid:42)BAAB (cid:36)MÎ(cid:46)(cid:42)BAAB (cid:36)AÎ(cid:46)(cid:42)BAAB (cid:36) 1 1 1 1 1 1 (cid:101)(cid:102)(cid:46)(cid:42)DMA(cid:144)(cid:46)(cid:42)BAAB (cid:143)(cid:165)(cid:23)(cid:145)(cid:46)(cid:42)(cid:36) 1 1 (cid:101)(cid:102)BC^(cid:46)(cid:42)DMA(cid:36)   BC (cid:101)(cid:102)(cid:66)(cid:155)(cid:46)(cid:42)DMA(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n =  =1,0,0 (cid:36) 1 BC (cid:43)D(cid:51)(cid:136)(cid:137)(cid:55)0,1,2(cid:36)(cid:48)(cid:4)(cid:125)(cid:149)M0,0,1,N1,1,0(cid:36)   (cid:101)(cid:102)DM =0,-1,-1,DN =1,0,-2(cid:36)  (cid:106)(cid:46)(cid:42)DMN(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n =x ,y ,z (cid:36) 2 2 2 2   ì ïDM×n =0 ì-y -z =0 (cid:68)í  2 (cid:36)(cid:66)(cid:67)í 2 2 (cid:36)(cid:146)z =1(cid:36)(cid:25)(cid:67)x =2,y =-1(cid:36) ïîDN×n 2 =0 îx 2 -2z 2 =0 2 2 2  (cid:101)(cid:102)(cid:155)(cid:46)(cid:42)DMN(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n =2,-1,1(cid:36) 2 (cid:68)(cid:35)(cid:66)(cid:90)(cid:49)(cid:42)(cid:50)A-DM -N (cid:143)(cid:282)(cid:50)(cid:36)     n 1 ×n 2 2 6 (cid:101)(cid:102)(cid:49)(cid:42)(cid:50)A-DM -N (cid:51)(cid:126)(cid:53)(cid:54)(cid:55) cosn,n =   = = (cid:36) 1 2 n n 4+1+1 3 1 2 6 (cid:306)(cid:159)(cid:101)(cid:331)(cid:36)(cid:49)(cid:42)(cid:50)A-DM -N (cid:51)(cid:126)(cid:53)(cid:54)(cid:55) . 3 14(cid:27)(cid:28)2024·(cid:37)(cid:278)(cid:124)(cid:199)·(cid:87)(cid:263)(cid:33)(cid:40)(cid:332)(cid:143)(cid:333)(cid:334)(cid:51)(cid:113)(cid:335)(cid:36)(cid:283)(cid:97)(cid:200)“(cid:336)”(cid:36)(cid:289)(cid:97)(cid:200)“(cid:337)”.(cid:34)(cid:35)(cid:36)(cid:338)(cid:339)(cid:333)(cid:334)(cid:51)(cid:340)(cid:341)(cid:263)(cid:342)(cid:143)(cid:37) (cid:38)(cid:39)P-ABCD(cid:36)(cid:196)(cid:40)AB= AD= AP=2(cid:36)CB=CD=CP=4(cid:36)AC(cid:157)BD(cid:84)(cid:82)O. (1)(cid:56)(cid:44)(cid:10)(cid:46)(cid:42)PAC ^(cid:46)(cid:42)PBD(cid:47) 2π (2)(cid:43)AC=2 5(cid:36)(cid:48)(cid:49)(cid:42)(cid:50)P-AC-B(cid:55) (cid:36)(cid:56)(cid:111)(cid:78)PB(cid:123)(cid:46)(cid:42)PAD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54). 3 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:81)(cid:98)(cid:60)(cid:25)(cid:61) 1 (2) 2(cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:261)(cid:251)(cid:128)(cid:129)(cid:187)(cid:90)(cid:62)(cid:91)(cid:44)(cid:45)AC^BD(cid:36)PO^ AC(cid:36)(cid:128)(cid:129)(cid:78)(cid:42)(cid:88)(cid:111)(cid:24)(cid:42)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:65)(cid:66)(cid:67) (cid:44)(cid:47) (cid:28)2(cid:33)(cid:132)(cid:133)(cid:172)(cid:161)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:111)(cid:78)(cid:51)(cid:97)(cid:139)(cid:139)(cid:140)(cid:24)(cid:46)(cid:42)(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:68)(cid:139)(cid:140)(cid:219)(cid:50)(cid:7)(cid:182)(cid:65)(cid:66)(cid:56)(cid:25). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:100)(cid:55)AB= AD(cid:36)CB=CD(cid:36) (cid:101)(cid:102)A,C(cid:183)(cid:141)BD(cid:51)(cid:88)(cid:111)(cid:46)(cid:62)(cid:78)(cid:159)(cid:36)(cid:101)(cid:102)AC^BD(cid:36)BO=OD(cid:36) (cid:100)(cid:55)AB= AP,BC =PC,AC = AC(cid:36) (cid:101)(cid:102)VABC @ APC(cid:36) (cid:100)(cid:55)BO^AC(cid:36)(cid:101)(cid:102)PO^ AC(cid:36) (cid:103)(cid:100)(cid:55)AC^BD(cid:36)POIBD=O(cid:36)POÌ(cid:46)(cid:42)PBD(cid:36)BDÌ(cid:46)(cid:42)PBD(cid:36) (cid:101)(cid:102)AC ^(cid:46)(cid:42)PBD(cid:36) (cid:100)(cid:55)ACÌ(cid:46)(cid:42)PAC(cid:36) (cid:101)(cid:102)(cid:46)(cid:42)PAC ^(cid:46)(cid:42)PBD(cid:47) (cid:28)2(cid:33)(cid:68)(cid:28)1(cid:33)(cid:66)(cid:90)OB^OC(cid:36) (cid:102)O(cid:55)(cid:158)(cid:82)(cid:36)OB,OC(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x,y(cid:163)(cid:36)(cid:81)(cid:82)O(cid:88)(cid:111)(cid:84)(cid:41)(cid:42)OBC(cid:51)(cid:111)(cid:78)(cid:55)z(cid:163)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111) (cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:100)(cid:55)AB=2,BC =4,AC =2 5(cid:36) (cid:101)(cid:102)AB2+BC2 = AC2(cid:36)(cid:101)(cid:102)ÐABC =90o(cid:36) 8 4 5 16 2 5 (cid:73)(cid:74)(cid:68)(cid:108)(cid:42)(cid:109)(cid:89)(cid:36)(cid:66)(cid:90)BO= = (cid:36)(cid:68)(cid:69)(cid:70)(cid:71)(cid:15)(cid:36)(cid:66)(cid:90)AO= 4- = (cid:36) 2 5 5 5 5 4 5 (cid:68)(cid:28)1(cid:33)(cid:66)(cid:90)BO=OD=OP(cid:36)(cid:101)(cid:102)OD=OP= (cid:36) 5 (cid:68)(cid:28)1(cid:33)(cid:66)(cid:90)PO^ AC,BO^ AC(cid:36)(cid:74)(cid:46)(cid:42)ABCÇ(cid:46)(cid:42)APC = AC(cid:36)OBÌ(cid:46)(cid:42)ABC(cid:36)OPÌ(cid:46)(cid:42)APC(cid:36)(cid:48) 2π (cid:49)(cid:42)(cid:50)P-AC-B(cid:55) (cid:36) 3 2π (cid:101)(cid:102)ÐPOB= (cid:36) 3 π (cid:101)(cid:102)PO(cid:123)z(cid:163)(cid:101)(cid:141)(cid:111)(cid:78)(cid:51)(cid:219)(cid:50)(cid:55) (cid:36) 6æ 2 5 2 15ö (cid:101)(cid:102)Pç- ,0, ÷(cid:36) ç ÷ è 5 5 ø æ4 5 ö æ 2 5 ö æ 4 5 ö (cid:100)(cid:55)Bç ,0,0÷,Aç0,- ,0÷,Dç- ,0,0÷(cid:36) ç ÷ ç ÷ ç ÷ è 5 ø è 5 ø è 5 ø  æ6 5 2 15ö  æ2 5 2 5 2 15ö  æ 2 5 2 15ö (cid:101)(cid:102)PB=ç ,0,- ÷,PA=ç ,- ,- ÷,PD=ç- ,0,- ÷(cid:36) ç ÷ ç ÷ ç ÷ è 5 5 ø è 5 5 5 ø è 5 5 ø  (cid:106)(cid:46)(cid:42)PAD(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36) ì  2 5 2 5 2 15 ïPA×n= x- y- z=0 ï 5 5 5 (cid:107)í (cid:36) ï  2 5 2 15 PD×n=- x- z=0 ï î 5 5 (cid:146)z=-1(cid:36)(cid:25)(cid:67)x= 3,y=2 3(cid:36)    (cid:101)(cid:102)(cid:46)(cid:42)PAD(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n= 3,2 3,-1 (cid:36) (cid:106)(cid:111)(cid:78)PB(cid:123)(cid:46)(cid:42)PAD(cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)   8 15   n×PB 5 1 (cid:107)sinq= cosn,PB =   = = (cid:36) n × PB 4 15 2 4´ 5 1 (cid:101)(cid:102)(cid:111)(cid:78)PB(cid:123)(cid:46)(cid:42)PAD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 2 15(cid:27)(cid:28)2024·(cid:329)(cid:318)(cid:343)(cid:303)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:101)(cid:96)(cid:36)(cid:344)(cid:42)(cid:148)ABCDEF(cid:36)(cid:41)(cid:42)ABCD(cid:143)(cid:52)(cid:97)(cid:112)(cid:36)(cid:82)O(cid:55)(cid:41)(cid:42)(cid:51)(cid:40)(cid:345)(cid:36)(cid:82)M (cid:55)EF (cid:51)(cid:40)(cid:82)(cid:36)(cid:316)(cid:42)ADEF (cid:123)BCEF(cid:143)(cid:171)(cid:108)(cid:51)(cid:108)(cid:110)(cid:269)(cid:112)(cid:36)EF =4(cid:36)(cid:196)(cid:126)(cid:38)(cid:93)(cid:183)(cid:55)2. (1)(cid:44)(cid:45):MO^(cid:46)(cid:42)ABCD(cid:47) 2 42 (2)(cid:43)(cid:82)P(cid:141)(cid:38)CE(cid:159)(cid:36)(cid:111)(cid:78)BP(cid:123)(cid:46)(cid:42)ABM (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) (cid:36)(cid:56)EP. 21 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) (2)1 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)AB,CD(cid:40)(cid:82)K,Q(cid:36)(cid:221)(cid:81)(cid:44)(cid:45)AB^(cid:46)(cid:42)FKQE(cid:36)(cid:46)(cid:42)FKQE^(cid:46)(cid:42)ABCD(cid:36)(cid:67)(cid:44)MO^(cid:46) (cid:42)ABCD.  (cid:28)2) (cid:102)O(cid:55)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:106)CP=lCE0£l£1(cid:36)(cid:68)(cid:111)(cid:78)BP(cid:123)(cid:46)(cid:42)ABM (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54) 2 42 (cid:55) (cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:89)(cid:56)(cid:64)l(cid:51)(cid:54)(cid:65)(cid:66). 21 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:155)AB,CD(cid:40)(cid:82)K,Q(cid:36)(cid:85)(cid:86)FK,KQ,QE(cid:36)(cid:107)O(cid:55)KQ(cid:51)(cid:40)(cid:82)(cid:36) (cid:100)(cid:55)(cid:316)(cid:42)ADEF (cid:143)(cid:108)(cid:110)(cid:269)(cid:112)(cid:36)(cid:101)(cid:102)EF//AD(cid:36)(cid:103)KQ//AD(cid:36)(cid:101)(cid:102)KQ//EF(cid:36) △ABF (cid:144)(cid:178)DCE(cid:199)(cid:143)(cid:114)(cid:93)(cid:55)2(cid:51)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36)(cid:67)FK =EQ(cid:36)(cid:101)(cid:102)(cid:37)(cid:114)(cid:112)FKQE(cid:55)(cid:108)(cid:110)(cid:269)(cid:112)(cid:36) (cid:100)(cid:55)(cid:82)M (cid:55)EF (cid:51)(cid:40)(cid:82)(cid:36)O(cid:55)KQ(cid:51)(cid:40)(cid:82)(cid:36)(cid:101)(cid:102)MO^KQ. (cid:100)(cid:55)△ABF (cid:143)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36)(cid:101)(cid:102)AB^FK(cid:36) (cid:103)AB^KQ(cid:36)KQ,FK Ì(cid:46)(cid:42)FKQE(cid:36)KQIFK =K (cid:36) (cid:101)(cid:102)AB^(cid:46)(cid:42)FKQE(cid:36)ABÌ(cid:46)(cid:42)ABCD(cid:36)(cid:101)(cid:102)(cid:46)(cid:42)FKQE^(cid:46)(cid:42)ABCD(cid:36) (cid:46)(cid:42)FKQEI(cid:46)(cid:42)ABCD=KQ(cid:36)MO Ì(cid:46)(cid:42)FKQE(cid:36)MO^KQ(cid:36) (cid:113)MO^(cid:46)(cid:42)ABCD. (cid:28)2(cid:33)(cid:141)(cid:269)(cid:112)FKQE(cid:40)(cid:36)EF =4(cid:36)KQ=2(cid:36)FK =EQ= 3(cid:36)(cid:108)(cid:110)(cid:269)(cid:112)(cid:40)(cid:68)(cid:69)(cid:70)(cid:71)(cid:15)(cid:67)MO = 2(cid:36) (cid:155)BC(cid:40)(cid:82)N (cid:36)(cid:68)(cid:28)1(cid:33)(cid:90)(cid:36)OK(cid:36)ON(cid:36)OM (cid:142)(cid:142)(cid:88)(cid:111)(cid:36) (cid:102)O(cid:55)(cid:158)(cid:82)(cid:36)(cid:62)(cid:91)(cid:102)OK(cid:36)ON(cid:36)OM (cid:101)(cid:141)(cid:111)(cid:78)(cid:55)x(cid:163)(cid:36)y(cid:163)(cid:36)z(cid:163)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:107)O0,0,0,M  0,0, 2  ,K1,0,0,C-1,1,0,A1,-1,0,B1,1,0,E  -2,0, 2  (cid:36) (cid:106)(cid:46)(cid:42)ABM (cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n  =x,y,z,  A  B  =0,2,0,  A  M  =  -1,1, 2  (cid:36)   ì ïn×AB=2y=0    (cid:107)í   (cid:36)(cid:146)z=1(cid:36)(cid:107)x= 2,y=0(cid:36)(cid:67)n= 2,0,1 ïîn×AM =-x+y+ 2z=0          (cid:106)CP=lCE0£l£1(cid:36)BP=BC+CP=BC+lCE= -2-l,-l, 2l (cid:36) (cid:106)(cid:111)(cid:78)BP(cid:123)(cid:46)(cid:42)ABM (cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)     BP×n 2 2 2 42 (cid:101)(cid:102)sinq= cosn,BP =   = = . BP × n 3 4l2+4l+4 21 1 (cid:25)(cid:67)l= (cid:28)(cid:346)(cid:54)(cid:347)(cid:348))(cid:36)(cid:101)(cid:102)(cid:82)P(cid:55)(cid:38)CE(cid:51)(cid:40)(cid:82)(cid:36)(cid:101)(cid:102)EP(cid:51)(cid:93)(cid:55)1. 2 16(cid:27)(cid:28)2024·(cid:29)(cid:349)(cid:350)(cid:351)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:52)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:40)(cid:36)ÐBBA=60°(cid:36)AB=2AB =4(cid:36)E(cid:143)CD 1 1 1 1 1 1 1(cid:51)(cid:40)(cid:82)(cid:27) (1)(cid:56)(cid:44)(cid:10)(cid:111)(cid:78)AC ^(cid:46)(cid:42)BDDB (cid:47) 1 1 (2)(cid:56)(cid:111)(cid:78)ED (cid:123)(cid:46)(cid:42)ABBA (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54) 1 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 6 (2) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)AC(cid:157)BD(cid:84)O(cid:36)(cid:85)(cid:86)AC (cid:157)BD(cid:84)O (cid:36)(cid:85)(cid:86)OO (cid:36)(cid:304)(cid:21)(cid:125)(cid:67)OO ^(cid:46)(cid:42)ABCD(cid:36)(cid:65)(cid:66) 1 1 1 1 1 1 1 (cid:67)(cid:149)OO ^ AC(cid:36)(cid:75)(cid:68)AC^BD(cid:36)(cid:65)(cid:66)(cid:67)(cid:44)(cid:47) 1 (cid:28)2(cid:33)(cid:352)(cid:63)(cid:56)(cid:64)AA (cid:102)(cid:154)OO (cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:177)(cid:153)(cid:66)(cid:67). 1 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)AC(cid:157)BD(cid:84)O(cid:36)(cid:85)(cid:86)AC (cid:157)BD(cid:84)O (cid:36)(cid:85)(cid:86)OO (cid:36) 1 1 1 1 1 1 (cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:143)(cid:52)(cid:37)(cid:38)(cid:328)(cid:36) 1 1 1 1 ∵OO ^(cid:46)(cid:42)ABCD(cid:36)(cid:103)ACÌ(cid:46)(cid:42)ABCD(cid:36) 1 ∴OO ^ AC(cid:36)(cid:103)AC^BD(cid:36)OO ÇBD=O(cid:36)OO,BDÌ(cid:46)(cid:42)BDDB (cid:36) 1 1 1 1 1 ∴AC ^(cid:46)(cid:42)BDDB (cid:27) 1 1 ∴(cid:28)2(cid:33)(cid:141)(cid:108)(cid:110)(cid:269)(cid:112)ABBA (cid:40)(cid:36)ÐBBA=60o(cid:36)AB=2AB =4(cid:36) 1 1 1 1 1 4-2 (cid:101)(cid:102) (cid:36) 2 AA =BB = =2 1 1 cos60° (cid:141)(cid:108)(cid:110)(cid:269)(cid:112)BDDB (cid:40)(cid:36)BD= 4 2,BD = 2 2,BB = DD = 2(cid:36) 1 1 1 1 1 1 2 æ4 2-2 2ö (cid:101)(cid:102)OO = 22-ç ÷ = 2(cid:36) 1 ç è 2 ÷ ø QOB,OC,OO(cid:142)(cid:142)(cid:224)(cid:156)(cid:88)(cid:111)(cid:36)(cid:34)(cid:35)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) 1     (cid:107)A(0,-2 2,0),B(2 2,0,0),B( 2,0, 2),C(0,2 2,0),D(-2 2,0,0), E - 2, 2,0 ,D - 2,0, 2 (cid:36) 1 1® ® ® (cid:36) \AB= (2 2,2 2,0),BB = (- 2,0, 2),DE= (0, 2,- 2) 1 1    ì ïn×AB=0 (cid:106)(cid:46)(cid:42)ABB 1 A 1 (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36)(cid:107)í   (cid:36) ïîn×BB =0 1 ì ï2 2x+2 2y=0  \í (cid:36)(cid:155)n=1,-1,1(cid:36) ïî - 2x+ 2z=0     D 1 E×n 2 2 6 (cid:106)(cid:111)(cid:78)ED 1 (cid:123)(cid:46)(cid:42)ABB 1 A 1 (cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)(cid:107)sinq= cosD 1 E,n =  D  E  n  = 3´2 = 3 (cid:36) 1 6 (cid:111)(cid:78)ED (cid:123)(cid:46)(cid:42)ABBA (cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54) (cid:27) 1 1 1 3 ∴ 17(cid:27)(cid:28)2024·(cid:323)(cid:266)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:87)(cid:38)(cid:147)ABC-ABC (cid:40)(cid:36)(cid:41)(cid:42)ABC(cid:143)(cid:114)(cid:93)(cid:55)2(cid:51)(cid:52)(cid:87)(cid:50)(cid:112)(cid:36)(cid:46)(cid:42)ACC A ^ 1 1 1 1 1 π (cid:41)(cid:42)ABC(cid:36)ÐAAC = (cid:36)AA =2(cid:36)E(cid:36)F(cid:62)(cid:91)(cid:143)AC(cid:36)BC (cid:51)(cid:40)(cid:82)(cid:36)P(cid:143)(cid:78)(cid:202)EF (cid:159)(cid:51)(cid:314)(cid:82)(cid:27) 1 3 1 1 1 (1)(cid:161)P(cid:143)(cid:78)(cid:202)EF (cid:51)(cid:40)(cid:82)(cid:162)(cid:36)(cid:56)(cid:82)P(cid:149)(cid:46)(cid:42)ABBA (cid:51)(cid:150)(cid:151)(cid:47) 1 1 9 145 (2)(cid:161)(cid:46)(cid:42)PCC (cid:123)(cid:46)(cid:42)BBCC(cid:51)(cid:219)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:55) (cid:162)(cid:36)(cid:56)EP(cid:27) 1 1 1 145 15 (cid:57)(cid:26)(cid:58)(cid:59)(1) (cid:27) 5 6 (2) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:127)(cid:92)(cid:108)(cid:148)(cid:109)(cid:353)(cid:16)(cid:51)(cid:97)(cid:89)(cid:315)(cid:79)(cid:177)(cid:153)(cid:150)(cid:151)(cid:47) (cid:28)2(cid:33)(cid:127)(cid:92)(cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:177)(cid:153)(cid:150)(cid:151)(cid:47) (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:83)AB (cid:51)(cid:40)(cid:82)D(cid:36)(cid:85)(cid:86)DF(cid:36)DA(cid:36)(cid:85)(cid:86)AE(cid:36)AB(cid:36)EB(cid:36) 1 1 1 1 (cid:100)(cid:55)(cid:82)D(cid:36)F(cid:62)(cid:91)(cid:55)AB (cid:36)BC (cid:51)(cid:40)(cid:82)(cid:36) 1 1 1 1 1 (cid:101)(cid:102)DF(cid:160)AC (cid:36)(cid:48)DF = AC (cid:36) 1 1 2 1 1 (cid:103)(cid:68)(cid:87)(cid:38)(cid:147)(cid:51)(cid:71)(cid:105)(cid:36)(cid:128)(cid:129)(cid:82)E(cid:55)AC(cid:51)(cid:40)(cid:82)(cid:66)(cid:90)(cid:10) DF∥AE(cid:36)(cid:48)DF = AE(cid:36) (cid:101)(cid:102)(cid:37)(cid:114)(cid:112)DFEA(cid:143)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)(cid:101)(cid:102)EF∥AD(cid:36)(cid:103)EF Ë(cid:46)(cid:42)ABBA (cid:36)ADÌ(cid:46)(cid:42)ABBA (cid:36)(cid:101)(cid:102)EFP(cid:46)(cid:42)ABBA (cid:36) 1 1 1 1 1 1 (cid:101)(cid:102)(cid:161)P(cid:143)(cid:78)(cid:202)EF (cid:51)(cid:40)(cid:82)(cid:162)(cid:36)(cid:82)P(cid:149)(cid:46)(cid:42)ABBA (cid:51)(cid:150)(cid:151)(cid:108)(cid:84)(cid:82)E(cid:149)(cid:46)(cid:42)ABBA (cid:51)(cid:150)(cid:151)(cid:47) 1 1 1 1 π 1 1 (cid:100)(cid:55)ÐAAC = (cid:36) AE= AC = AA =1(cid:36) 1 3 2 2 1 1 AE= AA2+AE2-2´AA ´AE´cosÐAAC = 22+12-2´2´1´ = 3 1 1 1 1 2 (cid:100)(cid:55)AE2+AE2 = AA2(cid:36)(cid:101)(cid:102)AE^ AC(cid:36) 1 1 1 (cid:68)(cid:46)(cid:42)ACC A ^(cid:46)(cid:42)ABC(cid:36)(cid:48)(cid:46)(cid:42)ACC A I(cid:46)(cid:42)ABC = AC(cid:36) 1 1 1 1 (cid:100)(cid:55)AEÌ(cid:46)(cid:42)ACC A (cid:36)(cid:101)(cid:102)AE^(cid:46)(cid:42)ABC(cid:36) 1 1 1 1 (cid:103)BEÌ(cid:46)(cid:42)ABC(cid:36)(cid:101)(cid:102)AE^BE(cid:36)(cid:101)(cid:102)AE(cid:143)(cid:87)(cid:38)(cid:39)A -ABE(cid:51)(cid:30)(cid:36) 1 1 1 1 1 3 1 (cid:101)(cid:102)V = S ×AE= ´ ´ 3= (cid:36) A1 -ABE 3 △ABE 1 3 2 2 (cid:141)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)ABC(cid:40)(cid:36) BE= AB2-AE2 = 22-12 = 3, (cid:100)(cid:55)AE^BE(cid:36)(cid:101)(cid:102)(cid:111)(cid:50)(cid:87)(cid:50)(cid:112)AEB(cid:40) 1 1 (cid:103)AB= AE2+BE2 = 6(cid:36) 1 1 2 1 æ1 ö 15 (cid:87)(cid:50)(cid:112)A 1 AB(cid:143)(cid:108)(cid:110)(cid:87)(cid:50)(cid:112)(cid:36)S VA1BA = 2 ´A 1 B´ AB2-ç è2 A 1 B÷ ø = 2 (cid:36) 1 15 (cid:106)(cid:82)E(cid:149)(cid:46)(cid:42)ABA(cid:51)(cid:150)(cid:151)(cid:55)d(cid:36)(cid:107)V =V = S ×d (cid:36)(cid:25)(cid:67)d = (cid:27) 1 A1 -ABE E-A1BA 3 A1BA 5 15 (cid:65)(cid:82)P(cid:149)(cid:46)(cid:42)ABBA (cid:51)(cid:150)(cid:151)(cid:55) (cid:27) 1 1 5 (cid:28)2(cid:33) (cid:102)EB(cid:55)x(cid:163)(cid:36)EC(cid:55)y(cid:163)(cid:36)EA(cid:55)z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) 1 E0,0,0(cid:36)B  3,0,0  (cid:36)B  3,1, 3  (cid:36)C  0,2, 3  (cid:36)C0,1,0(cid:36) 1 1 æ 3 3 ö        æ 3 3 ö (cid:101)(cid:102)Fç , , 3÷(cid:36)BC = - 3,1,0 (cid:36)CC = 0,1, 3 (cid:36)EF =ç , , 3÷(cid:36) ç è 2 2 ÷ ø 1 ç è 2 2 ÷ ø   æ 3 3 ö (cid:106)EP=lEF0£l£1(cid:36)(cid:107)PC =ç- l,1- l,- 3l÷(cid:36) ç ÷ è 2 2 ø  (cid:106)(cid:46)(cid:42)PCC (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)n =x,y ,z (cid:36) 1 1 1 1 1   ì 3 3 ì ïn ×PC =0 ï- lx +(1- l)y - 3lz =0 (cid:107)(cid:185)í 1  (cid:36)(cid:65)í 2 1 2 1 1 (cid:36) ïîn ×CC =0 ï 1 1 î y + 3z =0 1 1  æ2 (cid:101)(cid:102)n =ç -1, 3,-1)(cid:36) 1 èl  (cid:106)(cid:46)(cid:42)BBCC(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)n =x ,y ,z (cid:36) 1 1 2 2 2 2   ï ìn ×BC =0 ì ï- 3x +y =0    (cid:107)(cid:185)í 2  (cid:36)(cid:65)í 1 1 (cid:36)(cid:101)(cid:102)n = 1, 3,-1 (cid:36) 2 ïîn ×CC =0 ïî y + 3z =0 2 1 1 1 2   -1+3+1   n ×n l 9 145 (cid:101)(cid:102) cosn,n =  1 2  = = (cid:36) 1 2 n × n æ2 ö 2 145 1 2 ç -1÷ +3+1× 5 èl ø 1 (cid:25)(cid:67)l= (cid:168)-13(cid:28)(cid:347)(cid:348)(cid:33)(cid:27) 3  1  1 3 9 6 6 (cid:101)(cid:102) EP = EF = + +3= (cid:36)(cid:65)EP(cid:51)(cid:93)(cid:55) (cid:27) 3 3 4 4 3 3 18(cid:27)(cid:28)2024·(cid:275)(cid:283)(cid:354)(cid:355)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:101)(cid:96)(cid:36)(cid:37)(cid:38)(cid:39)P-ABCD(cid:40)(cid:36)PA^(cid:46)(cid:42)ABCD(cid:36)ABPCD(cid:36)AB^AD(cid:36) AP= AB=2AD=2CD(cid:36)E(cid:55)(cid:38)PC(cid:159)(cid:51)(cid:314)(cid:82). (1)(cid:56)(cid:44)(cid:10)BC ^ AE(cid:47)   (2)(cid:43)PE=2EC(cid:36)(cid:56)(cid:111)(cid:78)DE(cid:123)(cid:46)(cid:42)PBC(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54). (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 3 (2) 3 1 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)AC(cid:36)(cid:155)AB(cid:51)(cid:40)(cid:82)F (cid:36)(cid:85)(cid:86)CF(cid:36)(cid:127)(cid:92)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:51)(cid:80)(cid:71)(cid:154)(cid:130)(cid:131)(cid:66)(cid:67)CF = AB(cid:36)(cid:107)(cid:185) 2AC^BC(cid:36)(cid:271)(cid:279)(cid:76)(cid:77)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:154)(cid:130)(cid:131)(cid:71)(cid:15)(cid:65)(cid:66)(cid:44)(cid:45). (cid:28)2(cid:33)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:56)(cid:64)(cid:46)(cid:42)PBC(cid:51)(cid:89)(cid:139)(cid:140)(cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:89)(cid:56)(cid:67)(cid:78)(cid:42)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54). 1 (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:85)(cid:86)AC(cid:36)(cid:155)AB(cid:51)(cid:40)(cid:82)F (cid:36)(cid:85)(cid:86)CF(cid:36)(cid:107)AF = AB=CD. 2 1 (cid:103)QAB∥CD(cid:36)\AF∥CD(cid:36)\(cid:37)(cid:114)(cid:112)ADCF(cid:55)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)\CF = AD= AB(cid:36) 2 \ÐACB=90°(cid:36)(cid:65)AC^BC(cid:36) (cid:103)PA^(cid:46)(cid:42)ABCD(cid:36)BCÌ(cid:46)(cid:42)ABCD(cid:36)\PA^BC(cid:36) (cid:103)QACIPA= A(cid:36)ACÌ(cid:46)(cid:42)PAC(cid:36)PAÌ(cid:46)(cid:42)PAC(cid:36)\BC ^(cid:46)(cid:42)PAC(cid:36) (cid:103)AEÌ(cid:46)(cid:42)PAC(cid:36)\BC ^ AE. (cid:28)2(cid:33)(cid:102)A(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)AD,AB,AP(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x(cid:163)(cid:36)y(cid:163)(cid:36)z(cid:163) (cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:106)AD=CD=a.(cid:107)AP= AB=2AD=2a(cid:36) (cid:304)(cid:21)(cid:125)(cid:67)Da,0,0(cid:36)Ca,a,0(cid:36)B0,2a,0(cid:36)P0,0,2a(cid:36)   (cid:107)BP=0,-2a,2a(cid:36)CP=-a,-a,2a(cid:36)    2 1 æ a 2a 2aö QPE=2EC(cid:36)\DE= DC+ DP=ç- , , ÷. 3 3 è 3 3 3 ø  (cid:106)(cid:46)(cid:42)PBC(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n=x ,y ,z (cid:36) 0 0 0   ì ïn×BP=-2ay +2az =0, (cid:107)í   0 0 ïîn×CP=-ax -ay +2az =0, 0 0 0  (cid:155)y =1(cid:36)(cid:67)z =1(cid:36)x =1(cid:27)\n=1,1,1 . 0 0 0    DE×n a 3 (cid:106)(cid:111)(cid:78)DE(cid:123)(cid:46)(cid:42)PBC(cid:101)(cid:124)(cid:50)(cid:55)q(cid:36)(cid:107)(cid:185)sinq= cos DE,n =   = = . DE n 3 a 3 3 \(cid:111)(cid:78)DE(cid:123)(cid:46)(cid:42)PBC(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) . 3 19(cid:27)(cid:28)2024·(cid:266)(cid:267)(cid:29)(cid:126)·(cid:49)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:37)(cid:38)(cid:39)P-ABCD(cid:40)(cid:36)(cid:41)(cid:42)ABCD(cid:143)(cid:111)(cid:50)(cid:269)(cid:112)(cid:36)ABPCD(cid:36) ÐABC =90°(cid:36)(cid:48)PA=PD= AD(cid:36)PC =PB. (1)(cid:43)O(cid:55)AD(cid:51)(cid:40)(cid:82)(cid:36)(cid:44)(cid:45)(cid:10)(cid:46)(cid:42)POC ^(cid:46)(cid:42)ABCD(cid:47) 1   (2)(cid:43)ÐCDA=60°(cid:36)AB= CD=1(cid:36)(cid:78)(cid:202)PD(cid:159)(cid:51)(cid:82)M (cid:115)(cid:116)DM =lDP(cid:36)(cid:48)(cid:46)(cid:42)PCB(cid:123)(cid:46)(cid:42)ACM(cid:219)(cid:50)(cid:51)(cid:126) 2 42 (cid:53)(cid:54)(cid:55) (cid:36)(cid:56)(cid:195)(cid:13)l(cid:51)(cid:54). 7 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 2 (2) 3 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)BC(cid:40)(cid:82)(cid:55)E(cid:36)(cid:127)(cid:92)(cid:111)(cid:50)(cid:269)(cid:112)(cid:40)(cid:214)(cid:78)(cid:51)(cid:130)(cid:131)(cid:36)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:80)(cid:71)(cid:212)(cid:15)(cid:65)(cid:66)(cid:47) (cid:28)2(cid:33)(cid:221)(cid:81)(cid:52)(cid:87)(cid:50)(cid:112)(cid:44)(cid:45)CO^ AD(cid:36)(cid:102)O(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:49)(cid:42)(cid:50)(cid:67)(cid:139)(cid:140)(cid:56)(cid:89)(cid:177)(cid:153) (cid:56)(cid:25)(cid:65)(cid:66). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:155)BC(cid:40)(cid:82)(cid:55)E(cid:36)(cid:68)(cid:166)(cid:193)(cid:66)(cid:67)OE(cid:55)(cid:269)(cid:112)ABCD(cid:51)(cid:40)(cid:214)(cid:78)(cid:36)(cid:107)OE^BC(cid:36) (cid:103)PB=PC(cid:36)(cid:107)PE^BC(cid:36) (cid:48)PEIOE=E(cid:36)PEÌ(cid:46)(cid:42)POE(cid:36)OEÌ(cid:46)(cid:42)POE(cid:36) (cid:76)(cid:77)(cid:78)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:36)(cid:67)BC^(cid:46)(cid:42)POE(cid:36) QPOÌ(cid:46)(cid:42)POE(cid:36)\BC ^PO. (cid:68)PA=PD(cid:36)(cid:107)PO^ AD(cid:36)(cid:103)AD(cid:36)BC(cid:55)(cid:269)(cid:112)(cid:51)(cid:142)(cid:110)(cid:36)(cid:107)AD(cid:123)BC(cid:156)(cid:157)(cid:36) \PO^(cid:46)(cid:42)ABCD(cid:36) (cid:103)POÍ(cid:46)(cid:42)POC(cid:36)(cid:101)(cid:102)(cid:46)(cid:42)POC ^(cid:46)(cid:42)ABCD. 1 (cid:28)2(cid:33)(cid:155)CD(cid:51)(cid:40)(cid:82)(cid:55)Q(cid:36)(cid:68)AB= CD=1(cid:36)ÐCDA=60°(cid:36) 2 (cid:107)AQ^CD(cid:36)AD=CD=2QD=2(cid:36) (cid:100)(cid:203) ACD(cid:55)(cid:108)(cid:114)(cid:87)(cid:50)(cid:112)(cid:36)CO^ AD. △(cid:68)(cid:28)1(cid:33)(cid:90)PO^(cid:46)(cid:42)ABCD(cid:36)OP(cid:36)OA(cid:36)OC(cid:142)(cid:142)(cid:88)(cid:111)(cid:36)    (cid:34)(cid:35)(cid:36)(cid:102)OC(cid:36)OA(cid:36)OP(cid:62)(cid:91)(cid:55)x(cid:36)y(cid:36)z(cid:163)(cid:52)(cid:97)(cid:139)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) (cid:68)CD=DA=PA=PD=2(cid:36)ÐCDA=60°(cid:36)(cid:107)OP=OC = 3(cid:36) A0,1,0(cid:36)B æ ç 3 , 3 ,0 ö ÷(cid:36)C  3,0,0  (cid:36)P  0,0, 3  (cid:36)D0,-1,0 ç ÷ è 2 2 ø     (cid:68)DM =lDPÞM 0,l-1, 3l (cid:36)     æ 3 3 ö       (cid:101)(cid:102)PC = 3,0,- 3 (cid:36)BC =ç ,- ,0÷(cid:36)AC = 3,-1,0 (cid:36)AM = 0,l-2, 3l (cid:36) ç ÷ è 2 2 ø  (cid:106)(cid:46)(cid:42)PCB(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n =a,b,c(cid:36) 1 ì  ì 3a- 3c=0, ïn ×PC =0, ï (cid:68)í 1  Þí 3 3 ïn ×BC =0, ï a- b=0, î 1 î 2 2    (cid:155)a= 3(cid:36)(cid:67)b=1(cid:36)c= 3(cid:36)(cid:67)n = 3,1, 3 . 1  (cid:106)(cid:46)(cid:42)ACM(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n =x,y,z(cid:36) 2   ì ïn ×AC =0, ï ì 3x-y=0, (cid:68)í 2  Þí ïî n 2 ×AM =0, ïî l-2y+ 3lz=0, (cid:155)y= 3l(cid:36)(cid:67)x=λ(cid:36)z=2-l(cid:36)    (cid:65)(cid:46)(cid:42)ACM(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n = l, 3l,2-l . 2 (cid:220)(cid:46)(cid:42)PCB(cid:123)(cid:46)(cid:42)ACM(cid:219)(cid:50)(cid:51)(cid:179)(cid:180)(cid:55)q(cid:36)   (cid:101)(cid:102)cosq=  n 1 ×n 2 = 42 (cid:36)(cid:16)(cid:167)(cid:67)3l-22 =0(cid:36)(cid:65)l= 2 (cid:36)(cid:101)(cid:102)(cid:195)(cid:13)l(cid:51)(cid:54)(cid:55) 2 . n × n 7 3 3 1 2 20(cid:27)(cid:28)2024·(cid:356)(cid:357)(cid:257)(cid:358)(cid:359)·(cid:87)(cid:263)(cid:33)(cid:187)(cid:90)(cid:37)(cid:38)(cid:328)ABCD-ABCD (cid:51)(cid:159)(cid:24)(cid:296)(cid:41)(cid:42)(cid:62)(cid:91)(cid:143)(cid:114)(cid:93)(cid:55)2(cid:144)4(cid:51)(cid:52)(cid:97)(cid:112)(cid:36)(cid:46) 1 1 1 1 2 13 (cid:42)ADDA ^(cid:46)(cid:42)ABCD(cid:36)AA =3(cid:36)DD = 13(cid:36)cosÐADD=- (cid:36)(cid:82)P(cid:55)DD (cid:51)(cid:40)(cid:82)(cid:36)(cid:82)Q(cid:141)(cid:38)BC 1 1 1 1 1 1 13 1 (cid:159)(cid:36)(cid:48)BQ=3QC(cid:27)(1)(cid:44)(cid:45)(cid:10)PQ//(cid:46)(cid:42)ABBA (cid:47) 1 1 (2)(cid:56)(cid:49)(cid:42)(cid:50)Q-AP-D (cid:51)(cid:52)(cid:53)(cid:54)(cid:27) 1 1 (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 4 445 (2) 89 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:155)AA (cid:51)(cid:40)(cid:82)(cid:55)M (cid:36)(cid:85)(cid:128)MP(cid:36)MB(cid:36)(cid:63)(cid:44)(cid:37)(cid:114)(cid:112)BMPQ(cid:143)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)(cid:66)(cid:67)PQ//MB(cid:36)(cid:75) 1 (cid:68)(cid:78)(cid:42)(cid:46)(cid:79)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:36)(cid:65)(cid:66)(cid:67)(cid:44)(cid:47) (cid:28)2(cid:33)(cid:128)(cid:129)(cid:126)(cid:53)(cid:71)(cid:15)(cid:123)(cid:69)(cid:70)(cid:71)(cid:15)(cid:66)(cid:44)AA ^AD(cid:36)(cid:127)(cid:92)(cid:42)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:71)(cid:15)(cid:90)AA ^(cid:46)(cid:42)ABCD(cid:36)(cid:75)(cid:102)A(cid:55)(cid:136) 1 1 (cid:137)(cid:158)(cid:82)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36)(cid:127)(cid:92)(cid:139)(cid:140)(cid:89)(cid:56)(cid:49)(cid:42)(cid:50)(cid:36)(cid:65)(cid:66)(cid:67)(cid:25)(cid:27) (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:44)(cid:45)(cid:10)(cid:155)AA (cid:51)(cid:40)(cid:82)(cid:55)M (cid:36)(cid:85)(cid:128)MP(cid:36)(cid:100)(cid:55)P(cid:55)DD (cid:40)(cid:82)(cid:36) 1 1 AD +AD (cid:107)MP= 1 1 =3(cid:36)(cid:48)MP//AD(cid:36) 2 (cid:100)(cid:55)AD//BQ(cid:36)BQ=3QC(cid:36)BC =4(cid:36)(cid:101)(cid:102)BQ=3 (cid:101)(cid:102)MP//BQ(cid:36)MP=BQ(cid:36) (cid:101)(cid:102)(cid:37)(cid:114)(cid:112)BMPQ(cid:143)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36) (cid:101)(cid:102)PQ//MB(cid:36) (cid:100)(cid:55)MBÌ(cid:46)(cid:42)ABBA (cid:36)PQË(cid:46)(cid:42)ABBA (cid:36) 1 1 1 1 (cid:101)(cid:102)PQ//(cid:46)(cid:42)ABBA ; 1 1 æ 2 13ö (cid:28)2(cid:33)(cid:141)VADD(cid:40)(cid:36)AD2 = AD2+DD2-2AD ×DD cosÐADD=4+13-2´2´ 13´ç- ÷=25(cid:36)(cid:101)(cid:102) 1 1 1 1 1 1 1 1 1 1 1 ç è 13 ÷ ø AD=5(cid:36) 1 (cid:141)VAAD(cid:40)(cid:36)AA2+AD2 =32+42 =25= AD2(cid:36)(cid:65)AA ^AD(cid:36) 1 1 1 1 (cid:100)(cid:55)(cid:46)(cid:42)ADDA (cid:46)(cid:42)ABCD(cid:36)(cid:46)(cid:42)ADDA Ç(cid:46)(cid:42)ABCD= AD(cid:36)AA Ì(cid:46)(cid:42)ADDA(cid:36) 1 1 1 1 1 1 1 (cid:101)(cid:102)AA ^(cid:46)(cid:42)A⊥BCD(cid:36) 1 (cid:113)(cid:102)A(cid:55)(cid:136)(cid:137)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)(cid:36) æ 3ö (cid:107)Pç0,3, ÷(cid:36)A 0,0,3(cid:36)Q4,3,0 è 2ø 1 æ 3ö  æ 3ö (cid:101)(cid:102)PA =ç0,-3, ÷(cid:36)PQ=ç4,0,- ÷(cid:36) 1 è 2ø è 2ø ì  3 n×PA =-3y+ z=0 (cid:106)(cid:46)(cid:42)APQ(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)m  =x,y,z(cid:36)(cid:107) ï ï í 1 2 (cid:36) 1 ï m  ×  P  Q  =4x- 3 z=0 ïî 2  (cid:146)z=8(cid:36)(cid:67)x=3(cid:36)y=4(cid:36)(cid:101)(cid:102)m=3,4,8(cid:36)  (cid:181)(cid:90)(cid:46)(cid:42)APD (cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=1,0,0(cid:36) 1 1 (cid:106)(cid:49)(cid:42)(cid:50)Q-AP-D (cid:55)q(cid:36)(cid:68)(cid:35)(cid:90)q(cid:55)(cid:360)(cid:50)(cid:36) 1 1   m·n 3 (cid:101)(cid:102)cosq=-   =- (cid:36) m n 89 4 445 (cid:101)(cid:102)sinq= 1-cos2q= (cid:36) 89 4 445 (cid:113)(cid:49)(cid:42)(cid:50)Q-AP-D (cid:51)(cid:52)(cid:53)(cid:54)(cid:55) (cid:27) 1 1 89 21(cid:27)(cid:28)2024·(cid:29)(cid:349)·(cid:87)(cid:263)(cid:33)(cid:187)(cid:90)(cid:41)(cid:42)ABCD(cid:143)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)PA^(cid:46)(cid:42)ABCD(cid:36)PA∥DQ(cid:36)PA=3DQ=3(cid:36) AD=2AB=2(cid:36)(cid:48)ÐABC =60°. (1)(cid:56)(cid:44)(cid:10)(cid:46)(cid:42)PAC ^(cid:46)(cid:42)CDQ(cid:47) 15 PM (2)(cid:78)(cid:202)PC(cid:159)(cid:143)(cid:292)(cid:194)(cid:141)(cid:82)M (cid:36)(cid:122)(cid:67)(cid:111)(cid:78)AM (cid:123)(cid:46)(cid:42)PCQ(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:143) .(cid:43)(cid:194)(cid:141)(cid:36)(cid:56)(cid:64) (cid:51)(cid:54)(cid:47)(cid:43) 5 PC (cid:164)(cid:194)(cid:141)(cid:36)(cid:207)(cid:45)(cid:15)(cid:68). (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 1 (2)(cid:194)(cid:141)(cid:36) (cid:168)1. 2(cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:68)BC2 = AB2+AC2(cid:36)(cid:67)(cid:149)AB^AC(cid:36)(cid:75)(cid:68)PA^(cid:46)(cid:42)ABCD(cid:36)(cid:44)(cid:67)AB^ AP(cid:36)(cid:315)(cid:74)(cid:44)(cid:67)AB^ (cid:46)(cid:42)PAC(cid:36)(cid:128)(cid:129)CD//AB(cid:36)(cid:67)(cid:149)CD^(cid:46)(cid:42)PAC(cid:36)(cid:127)(cid:92)(cid:42)(cid:42)(cid:88)(cid:111)(cid:51)(cid:80)(cid:71)(cid:71)(cid:15)(cid:36)(cid:65)(cid:66)(cid:44)(cid:67)(cid:46)(cid:42)PAC ^(cid:46)(cid:42) CDQ.        (cid:28)2(cid:33)(cid:102)A(cid:55)(cid:158)(cid:82)(cid:36)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)A-xyz(cid:36)(cid:106)PM =lPC =l 0, 3,-3 (cid:36)(cid:56)(cid:67)(cid:139)(cid:140)AM = 0, 3l,3-3l    (cid:144)(cid:46)(cid:42)PCQ(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n= 1, 3,1) (cid:36)(cid:128)(cid:129)(cid:139)(cid:140)(cid:51)(cid:219)(cid:50)(cid:7)(cid:182)(cid:36)(cid:361)(cid:64)(cid:97)(cid:98)(cid:36)(cid:65)(cid:66)(cid:56)(cid:25). (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)(cid:44)(cid:45)(cid:10)(cid:141)VABC(cid:40)(cid:36)BC =2(cid:36)AB=1(cid:36)ÐABC =60°(cid:36) (cid:107)AC2 =BC2+AB2-2BC×ABcosÐABC =3(cid:36)(cid:66)(cid:67)AC = 3(cid:36) (cid:101)(cid:102)BC2 = AB2+AC2(cid:36)(cid:101)(cid:102)AB^AC. (cid:100)(cid:55)PA^(cid:46)(cid:42)ABCD(cid:36)ABÌ(cid:46)(cid:42)ABCD(cid:36)(cid:101)(cid:102)AB^ AP(cid:36) (cid:103)(cid:100)(cid:55)ACIAP= A(cid:36)ACÌ(cid:46)(cid:42)PAC(cid:36)APÌ(cid:46)(cid:42)PAC(cid:36)(cid:101)(cid:102)AB^(cid:46)(cid:42)PAC(cid:36) (cid:100)(cid:55)CD//AB(cid:36)(cid:101)(cid:102)CD^(cid:46)(cid:42)PAC(cid:36) (cid:103)(cid:100)(cid:55)CDÌ(cid:46)(cid:42)CDQ(cid:36)(cid:101)(cid:102)(cid:46)(cid:42)PAC ^(cid:46)(cid:42)CDQ. (cid:28)2(cid:33) ABCD(cid:143)(cid:46)(cid:79)(cid:37)(cid:114)(cid:112)(cid:36)PA^(cid:46)(cid:42)ABCD(cid:36)PA∥DQ(cid:36)PA=3DQ=3(cid:36) AD=2AB=2(cid:36)(cid:48)ÐABC =60°. 15 (cid:293)(cid:106)(cid:78)(cid:202)PC(cid:159)(cid:194)(cid:141)(cid:82)M (cid:36)(cid:122)(cid:67)(cid:111)(cid:78)AM (cid:123)(cid:46)(cid:42)PCQ(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:143) (cid:36) 5 (cid:102)A(cid:55)(cid:158)(cid:82)(cid:36)AB,AC,AP(cid:101)(cid:141)(cid:111)(cid:78)(cid:62)(cid:91)(cid:55)x(cid:163)(cid:24)y(cid:163)(cid:24)z(cid:163)(cid:132)(cid:133)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)A-xyz(cid:36) (cid:34)(cid:35)(cid:101)(cid:96)(cid:36)(cid:107)A(0,0,0),P(0,0,3),C(0, 3,0),Q(-1, 3,1)(cid:36)       (cid:66)(cid:67)PC = 0, 3,-3 (cid:36)PQ= -1, 3,-2 (cid:36)   (cid:106)PM =lPC =l  0, 3,-3  =  0, 3l,-3l 0£l£1(cid:36)      (cid:107)M 0, 3l,3-3l (cid:36)(cid:101)(cid:102)AM = 0, 3l,3-3l (cid:36)    ì ïn×PC = 3y-3z=0 (cid:106)(cid:46)(cid:42)PCQ(cid:51)(cid:23)(cid:145)(cid:89)(cid:139)(cid:140)(cid:55)n=x,y,z(cid:36)(cid:107)í   (cid:36) ïîn×PQ=-x+ 3y-2z=0    (cid:146)y= 3(cid:36)(cid:66)(cid:67)x=1,z=1(cid:36)(cid:101)(cid:102)n= 1, 3,1 (cid:36)(cid:106)(cid:111)(cid:78)AM (cid:123)(cid:46)(cid:42)PCQ(cid:101)(cid:124)(cid:50)(cid:51)(cid:179)(cid:180)(cid:55)q(cid:36)   3 15 (cid:113)sinq= cosAM,n = = (cid:36) 5´ 12l2-18l+9 5 1 PM 1 PM (cid:362)(cid:15)(cid:67)2l2-3l+1=0(cid:36)(cid:25)(cid:67)l= (cid:168)l=1(cid:36)(cid:101)(cid:102) = (cid:168) =1. 2 PC 2 PC 22(cid:27)(cid:28)2024·(cid:323)(cid:266)(cid:324)(cid:325)·(cid:87)(cid:263)(cid:33)(cid:34)(cid:35)(cid:36)(cid:141)(cid:87)(cid:38)(cid:39)A-BCD(cid:40)(cid:36)VABC(cid:143)(cid:52)(cid:87)(cid:50)(cid:112)(cid:36)(cid:46)(cid:42)ABC^(cid:46)(cid:42)BCD(cid:36)   BD^CD(cid:36)(cid:82)E(cid:143)BC(cid:51)(cid:40)(cid:82)(cid:36)AO=2OE(cid:27) (1)(cid:56)(cid:44)(cid:10)O(cid:55)(cid:87)(cid:38)(cid:39)A-BCD(cid:265)(cid:86)(cid:363)(cid:51)(cid:363)(cid:345)(cid:47) (2)(cid:56)(cid:111)(cid:78)AD(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:47)   (3)(cid:43)ÐBCD=60°(cid:36)BG=lBD(cid:36)(cid:56)(cid:46)(cid:42)AEG(cid:123)(cid:46)(cid:42)ACD(cid:101)(cid:124)(cid:282)(cid:49)(cid:42)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:287)(cid:179)(cid:162)l(cid:51)(cid:54)(cid:27) (cid:57)(cid:26)(cid:58)(cid:59)(1)(cid:44)(cid:45)(cid:60)(cid:25)(cid:61) 3 (2) 2 1 (3)l= 2 (cid:57)(cid:62)(cid:61)(cid:59)(cid:28)1(cid:33)(cid:76)(cid:77)(cid:35)(cid:112)(cid:226)(cid:364)(cid:67)(cid:64)OA=OB=OC =OD(cid:65)(cid:67)(cid:44)(cid:363)(cid:345)(cid:47) (cid:28)2(cid:33)(cid:76)(cid:77)(cid:78)(cid:42)(cid:50)(cid:71)(cid:105)(cid:128)(cid:129)(cid:78)(cid:42)(cid:88)(cid:111)(cid:154)(cid:42)(cid:42)(cid:88)(cid:111)(cid:51)(cid:130)(cid:131)(cid:71)(cid:15)(cid:66)(cid:67)(cid:47) (cid:28)3(cid:33)(cid:134)(cid:135)(cid:139)(cid:140)(cid:89)(cid:56)(cid:64)(cid:282)(cid:49)(cid:42)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:75)(cid:128)(cid:129)(cid:287)(cid:54)(cid:66)(cid:67)(cid:365)(cid:13).   (cid:57)(cid:99)(cid:25)(cid:59)(cid:28)1(cid:33)QAE(cid:55)VABC(cid:51)(cid:40)(cid:78)(cid:36)(cid:48)AO=2OE(cid:36)(cid:107)O(cid:55)(cid:52)VABC(cid:51)(cid:40)(cid:345)(cid:36) \OA=OB=OC (cid:103)QRt(cid:178)BCD(cid:40)(cid:36)ED=EC(cid:36) \OD2 =OE2+ED2 =OE2+EC2 =OC2 \OA=OB=OC =OD(cid:36)(cid:65)O(cid:55)(cid:87)(cid:38)(cid:39)A-BCD(cid:265)(cid:86)(cid:363)(cid:51)(cid:363)(cid:345) (cid:28)2(cid:33)QVABC(cid:143)(cid:52)(cid:87)(cid:50)(cid:112)(cid:36)(cid:82)E(cid:143)BC(cid:51)(cid:40)(cid:82)(cid:36)\AE^BC(cid:27) (cid:103)Q(cid:46)(cid:42)ABC^(cid:46)(cid:42)BCD(cid:36)(cid:46)(cid:42)ABCÇ(cid:46)(cid:42)BCD=BC(cid:36)AEÌ(cid:46)(cid:42)ABC(cid:36) \AE^(cid:46)(cid:42)BCD \ÐADE(cid:55)(cid:111)(cid:78)AD(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:51)(cid:50)3 1 AE π (cid:103)QAE= BC(cid:36)ED= BC(cid:36)\tanÐADE= = 3(cid:36)ÐADE= (cid:36) 2 2 ED 3 3 (cid:65)(cid:111)(cid:78)AD(cid:123)(cid:46)(cid:42)BCD(cid:101)(cid:124)(cid:50)(cid:51)(cid:52)(cid:53)(cid:54)(cid:55) 2 (cid:28)3(cid:33)(cid:141)(cid:46)(cid:42)BCD(cid:40)(cid:36)(cid:81)(cid:82)E(cid:83)EH ^BD(cid:36)EF^CD(cid:36)(cid:88)(cid:116)(cid:62)(cid:91)(cid:55)H(cid:36)F (cid:36) (cid:106)BC =4(cid:36)(cid:107)DF = FC =1(cid:36)EA=2 3(cid:36)EF= 3(cid:27) (cid:132)(cid:133)(cid:34)(cid:35)(cid:101)(cid:96)(cid:51)(cid:134)(cid:135)(cid:111)(cid:50)(cid:136)(cid:137)(cid:138)E-xyz(cid:36) (cid:107)E0,0,0(cid:36)A  0,0,2 3  (cid:36)C  -1, 3,0  (cid:36)D  1, 3,0  (cid:36) (cid:106)G1,y,0(cid:36)(cid:107)  E  A  =  0,0,2 3  (cid:36)  A  D  =  1, 3,-2 3  (cid:36)C  D  =2,0,0(cid:36)  E  G  =1,y,0(cid:27)  (cid:106)(cid:46)(cid:42)AEG(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n =x,y ,z (cid:36) 1 1 1 1   ì ïn ×EA=0 ìï2 3z =0  (cid:68)í 1  (cid:36)(cid:67)í 1 (cid:36)(cid:146)y =-1(cid:36)(cid:113)n =y,-1,0(cid:36) ïîn 1 ×EG=0 ïîx 1 +yy 1 =0 1 1  (cid:106)(cid:46)(cid:42)ACD(cid:51)(cid:89)(cid:139)(cid:140)(cid:55)n =x ,y ,z (cid:36) 2 2 2 2   ì ïn ×CD=0 ìï2x =0  (cid:107)í 2  (cid:36)(cid:65)í 2 (cid:36)(cid:146)z =1(cid:36)(cid:107)n =0,2,1(cid:27) ïîn 2 ×AD=0 ïîx 2 + 3y 2 -2 3z 2 =0 2 2 (cid:106)(cid:46)(cid:42)AEG(cid:123)(cid:46)(cid:42)ACD(cid:101)(cid:124)(cid:282)(cid:49)(cid:42)(cid:50)(cid:51)(cid:46)(cid:42)(cid:50)(cid:55)q(cid:36)   -2 2 \cosq= cosn,n = = (cid:36) 1 2 5× y2+1 5× y2+1 2 5 (cid:161)y=0(cid:162)(cid:36)cosq= (cid:36)(cid:203)(cid:162)(cid:126)(cid:53)(cid:54)(cid:287)(cid:179)(cid:36) 5 1 (cid:65)(cid:161)l= (cid:162)(cid:36)(cid:46)(cid:42)AEG(cid:123)(cid:46)(cid:42)ACD(cid:101)(cid:124)(cid:282)(cid:49)(cid:42)(cid:50)(cid:51)(cid:126)(cid:53)(cid:54)(cid:287)(cid:179)(cid:27) 2