文档内容
仁寿县 2023 级高二上学期半期联考
数学试卷
第I卷(选择题)
一、选择题(本题共8道小题,每小题0分,共0分)
1. 已知直线 的倾斜角为 ,则实数 ( )
A. B. C. D.
2. 甲、乙、丙三位同学在学校举办的建党100周年党史知识竞赛活动中获得优胜奖,颁奖时甲、乙、丙三
位同学随机站成一排,则甲乙两人恰好相邻而站的概率为( )
A. B. C. D.
3. 已知 , ,且 ,则向量 与 的夹角为( )
A. B. C. D.
4. 设 ,则两圆 与 的位置关系不可能是( )
A. 相切 B. 相交 C. 内切和内含 D. 外切和外离
的
5. 甲、乙两个雷达独立工作,它们发现飞行目标 概率分别是0.9和0.8,飞行目标被雷达发现的概率为(
)
A. 0.02 B. 0.28 C. 0.72 D. 0.98
6. 已知直线 与直线 平行,且 在 轴上的截距为 ,则
的值为( )
.
A B. C. D.7. 已知向量 , ,则下列向量中,使 能构成空间的一个基底的向量是
( )
A. B. C. D.
8. 在正三棱柱 中,侧棱长为 ,底面三角形的边长为1,则 与侧面 所成角的
正弦值为( )
A. B. C. D.
二、多选题(本题共3道小题,每小题0分,共0分)
9. 已知事件 , ,且 , ,则下列结论正确的是( )
.
A 如果 ,那么 ,
B. 如果 与 互斥,那么 ,
C. 如果 与 相互独立,那么 ,
D. 如果 与 相互独立,那么 ,
10. 下面四个结论正确的是( )
A. 空间向量 ,若 ,则
B. 若空间四个点 , ,则 三点共线C. 已知向量 ,若 ,则 为钝角
D. 任意向量 满足
11. 圆 ,直线 ,点 在圆 上,点 在直线 上,则下列结
论正确的是( )
A. 圆 关于直线 对称
B. 的最大值是9
的
C. 从 点向圆 引切线,切线长 最小值是3
D. 直线 被圆 截得的弦长取值范围为
第II卷(非选择题)
三、填空题(本题共3道小题,每小题0分,共0分)
12. 某人投篮命中的概率为0.3,投篮15次,最有可能命中______次.
13. 直线xcosθ+ y+2=0的倾斜角的范围是________.
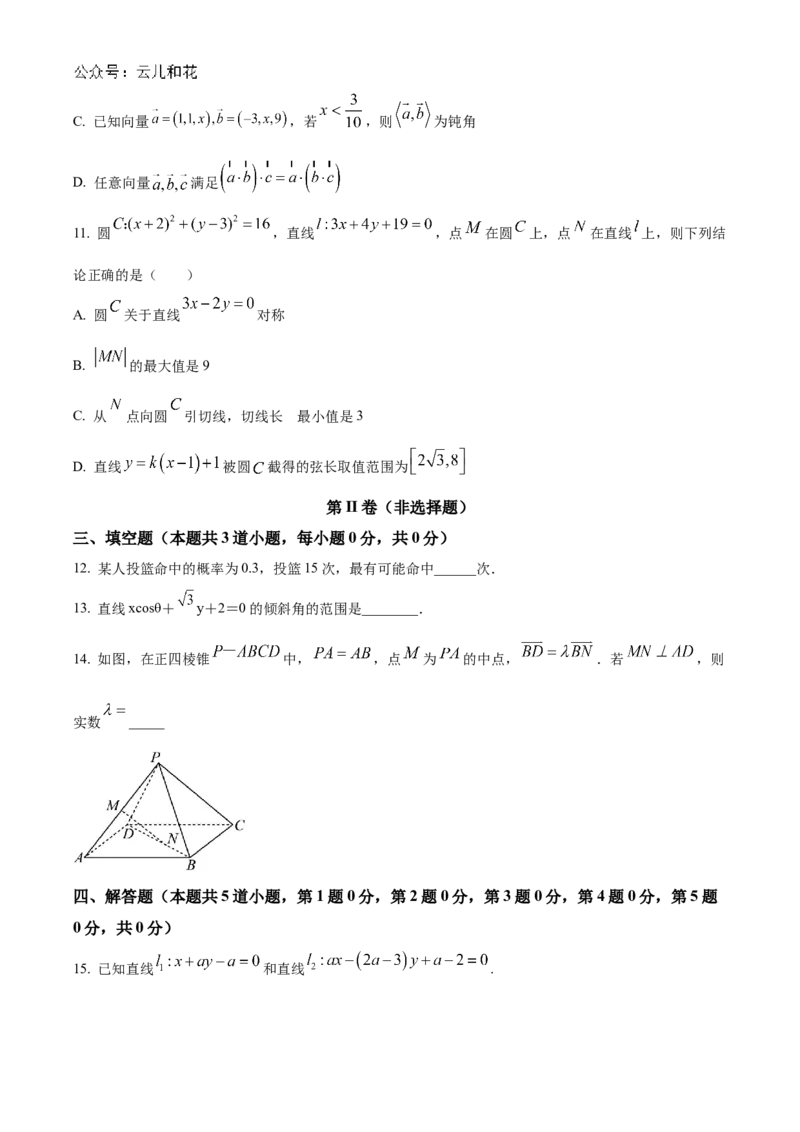
14. 如图,在正四棱锥 中, ,点 为 的中点, .若 ,则
实数 _____
四、解答题(本题共5道小题,第1题0分,第2题0分,第3题0分,第4题0分,第5题
0分,共0分)
15. 已知直线 和直线 .(1)若 ,求实数 的值;
(2)若 ,求实数 的值.
16. 从2名男生(记为 和 )和3名女生(记为 , ,和 )组成的总体中,任意依次抽取2名学生.
(1)分别写出有放回简单随机抽样和不放回简单随机抽样的样本空间;
(2)在(1)中的两种抽样方式下,分别求出抽到的2人为1名男生和1名女生的概率.
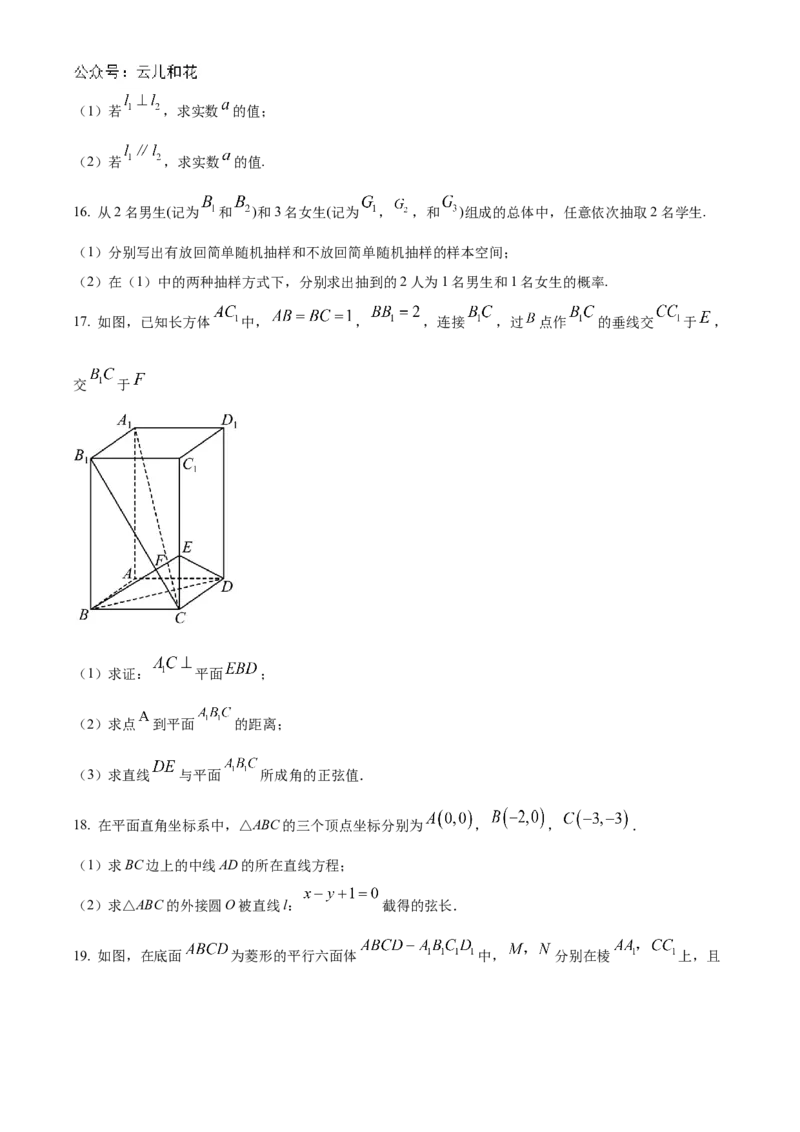
17. 如图,已知长方体 中, , ,连接 ,过 点作 的垂线交 于 ,
交 于
(1)求证: 平面 ;
(2)求点 到平面 的距离;
(3)求直线 与平面 所成角的正弦值.
18. 在平面直角坐标系中,△ABC的三个顶点坐标分别为 , , .
(1)求BC边上的中线AD的所在直线方程;
(2)求△ABC的外接圆O被直线l: 截得的弦长.
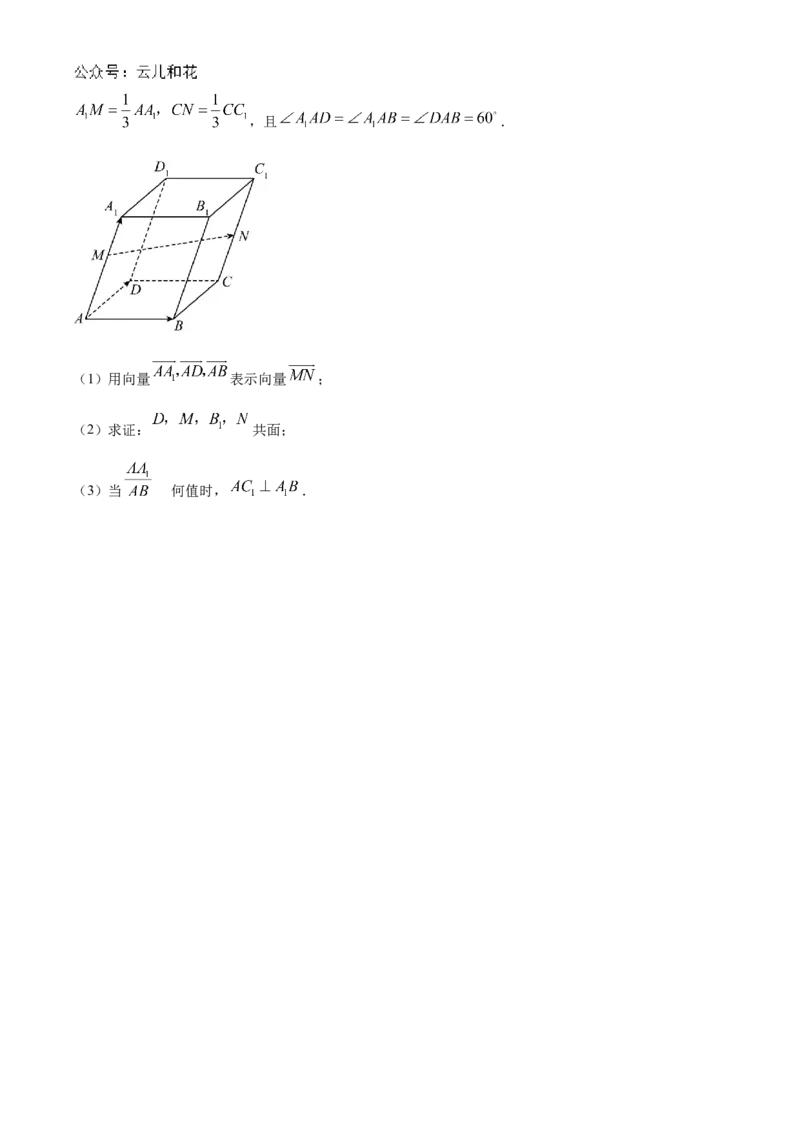
19. 如图,在底面 为菱形的平行六面体 中, 分别在棱 上,且,且 .
(1)用向量 表示向量 ;
(2)求证: 共面;
(3)当 何为值时, .