文档内容
仁寿县 2023 级高二上学期半期联考
数学试卷
第I卷(选择题)
一、选择题(本题共8道小题,每小题0分,共0分)
1. 已知直线 的倾斜角为 ,则实数 ( )
A. B. C. D.
【答案】B
【解析】
【分析】由题意可得直线 的斜率为 ,解方程即可得出答案.
【详解】已知直线 的倾斜角为 ,
则直线 的斜率为 ,
则 .
故选:B.
2. 甲、乙、丙三位同学在学校举办的建党100周年党史知识竞赛活动中获得优胜奖,颁奖时甲、乙、丙三
位同学随机站成一排,则甲乙两人恰好相邻而站的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】先求出甲、乙、丙三位同学随机站成一排的排法总数,再计算甲乙两人恰好相邻而站的排法数,
利用古典概率公式即可求解.
【详解】甲、乙、丙三位同学随机站成一排有:(甲、乙、丙),(甲、丙、乙),(乙、甲、丙),
(乙、丙、甲),(丙、甲、乙),(丙、乙、甲),共 种
甲乙两人恰好相邻而站有:
(甲、乙、丙),(乙、甲、丙),(丙、甲、乙),(丙、乙、甲)共 种,
所以甲乙两人恰好相邻而站的概率为 ,
故选:D.
3. 已知 , ,且 ,则向量 与 的夹角为( )
A. B. C. D.
【答案】A
【解析】
【分析】先由 求出 ,再利用空间向量的夹角公式求解即可
【详解】设向量 与 的夹角为 ,
因为 , ,且 ,
所以 ,得 ,
所以 ,
所以 ,
因为 ,所以 ,
故选:A
4. 设 ,则两圆 与 的位置关系不可能是( )
A. 相切 B. 相交 C. 内切和内含 D. 外切和外离
【答案】D【解析】
的
【分析】求出两圆 圆心和半径,计算圆心距与半径比较即可求解.
【详解】圆 的圆心为 ,半径为4;
圆 的圆心为 ,半径为 .
两圆心之间的距离为 ,
又因为 ,所以两圆不可能外切和外离.
故选:D.
5. 甲、乙两个雷达独立工作,它们发现飞行目标的概率分别是0.9和0.8,飞行目标被雷达发现的概率为(
)
A. 0.02 B. 0.28 C. 0.72 D. 0.98
【答案】D
【解析】
【分析】设事件 表示“甲雷达发现飞行目标”,事件 表示“乙雷达发现飞行目标”,飞行目标被雷达
发现的概率为 ,从而即可求解.
【详解】设事件 表示“甲雷达发现飞行目标”,事件 表示“乙雷达发现飞行目标”,
的
因为甲乙两个雷达独立工作,它们发现飞行目标 概率分别是 和 ,
所以 ,
所以飞行目标被雷达发现的概率为
.
故选:D
6. 已知直线 与直线 平行,且 在 轴上的截距为 ,则
的值为( )A. B. C. D.
【答案】A
【解析】
【详解】分析:根据两条直线平行,得到 的等量关系,根据直线在 轴上的截距,可得 所满足的等
量关系式,联立方程组求得结果.
详解:因为直线 与直线 平行,
所以 ,又直线 在 轴上的截距为 ,
所以 ,解得 ,所以 ,
所以 ,故选A.
点睛:该题考查的是有关直线的问题,在解题的过程中,涉及到的知识点有两条直线平行时系数所满足的
条件,以及直线在y轴上的截距的求法,根据题中的条件,列出相应的等量关系式,求得结果.
7. 已知向量 , ,则下列向量中,使 能构成空间的一个基底的向量是
( )
A. B. C. D.
【答案】D
【解析】
【分析】根据向量共面基本定理只需 无解即可满足 构成空间向量基底,据此检验各
选项即可得解.
【详解】因为 ,所以A中的向量 不能与 , 构成基底;
因为 ,所以B中的向量 不能与 , 构成基底;对于 ,设 ,则 ,解得 , ,
所以 ,故 , , 为共面向量,所以C中的向量 不能与 , 构成基底;
对于 ,设 ,则 ,此方程组无解,所以 , , 不共面,故D
中的向量 与 , 可以构成基底.
故选:D
的
8. 在正三棱柱 中,侧棱长为 ,底面三角形 边长为1,则 与侧面 所成角的
正弦值为( )
A. B. C. D.
【答案】D
【解析】
【分析】作 的中点 ,连接 , , ,根据题意可知 与侧面 所成角即为
,根据已知条件求解即可.
【详解】作 的中点 ,连接 , , ,根据题意,易得 平面 ,
故 与侧面 所成角即为 ,
因侧棱长为 ,底面三角形的边长为1,
所以 , ,
故 ,
即 与侧面 所成角的正弦值为 .
故选:D.
二、多选题(本题共3道小题,每小题0分,共0分)
9. 已知事件 , ,且 , ,则下列结论正确的是( )
A. 如果 ,那么 ,
B. 如果 与 互斥,那么 ,
C. 如果 与 相互独立,那么 ,
D. 如果 与 相互独立,那么 ,
【答案】BD
【解析】【分析】A选项在 前提下,计算出 , ,即可判断;B选项在 与
互斥前提下,计算出 , ,即可判断;C、D选项在 与 相互独立前提下,
计算出 , , , ,
即可判断.
【详解】解:A选项:如果 ,那么 , ,故A选项错误;
B选项:如果 与 互斥,那么 , ,故B选项正确;
C选项:如果 与 相互独立,那么 , ,故C选项错误;
D选项:如果 与 相互独立,那么 , ,故D
选项正确.
故选:BD.
【点睛】本题考查在包含关系,互斥关系,相互独立的前提下的和事件与积事件的概率,是基础题.
10. 下面四个结论正确的是( )
A. 空间向量 ,若 ,则
B. 若空间四个点 , ,则 三点共线
C. 已知向量 ,若 ,则 为钝角
D. 任意向量 满足
【答案】AB
【解析】
【分析】由空间向量的数量积及其运算性质可判断ACD,由空间向量的基本定理与共线定理可判断B
【详解】对于A:因为 , ,则 ,故A正确;对于B:因为 ,则 ,即 ,
又 与 有公共点,所以 三点共线,故B正确;
对于C: ,
若 为钝角:则 ,且 与 不共线,
由 得 ,
当 时, ,即 ,由 与 不共线得 ,
于是得当 且 时, 为钝角,故C错误;
对于D: 是 的共线向量,而 是 的共线向量,故D错误,
故选:AB
11. 圆 ,直线 ,点 在圆 上,点 在直线 上,则下列结
论正确的是( )
A. 圆 关于直线 对称
B. 的最大值是9
C. 从 点向圆 引切线,切线长的最小值是3
D. 直线 被圆 截得的弦长取值范围为
【答案】CD
【解析】
【分析】根据 不在直线 上判断A;根据 判断B;根据 时,切线长最小求解判断C;根据直线 过定点 ,再结合弦长公式判断D.
【详解】解:对于A选项, 圆 ,∴圆心 ,半径 ,
∵ ,∴圆 不关于直线 对称,故A选项错误;
对于B选项,由圆心 到直线 的距离为: ,
的最小值是 ,故 ,故B选项错误;
对于C选项,从 点向圆 引切线,当 时,切线长最小,最小值是 ,故C正确;
对于D选项,直线 过定点 ,该定点在圆C内,
所以直线 被圆 截得的弦长最长时,所截弦长为过点 和圆心的圆 的直径,即弦长
的最大值为8,
最短的弦长为垂直与该直径的弦长, 和圆心 的距离为 ,最短
弦长为 ,
故直线 被圆 截得的弦长取值范围为 ,D正确.
故选:CD.
第II卷(非选择题)
三、填空题(本题共3道小题,每小题0分,共0分)
12. 某人投篮命中的概率为0.3,投篮15次,最有可能命中______次.
【答案】4
【解析】
【分析】易知投篮命中次数服从二项分布,设最有可能命中m次,于是 ,解
出不等式即可得到答案.
【详解】投篮命中次数 ,设最有可能命中 次,则
, , .
最有可能命中4次.
故答案为:4.
13. 直线xcosθ+ y+2=0的倾斜角的范围是________.
【答案】
【解析】
【详解】由题知k=- cosθ,故k∈ ,结合正切函数的图象,当k∈ 时,直线倾斜
角 α∈ ,当 k∈ 时,直线倾斜角 α∈ ,故直线的倾斜角的范围是 ∪
.
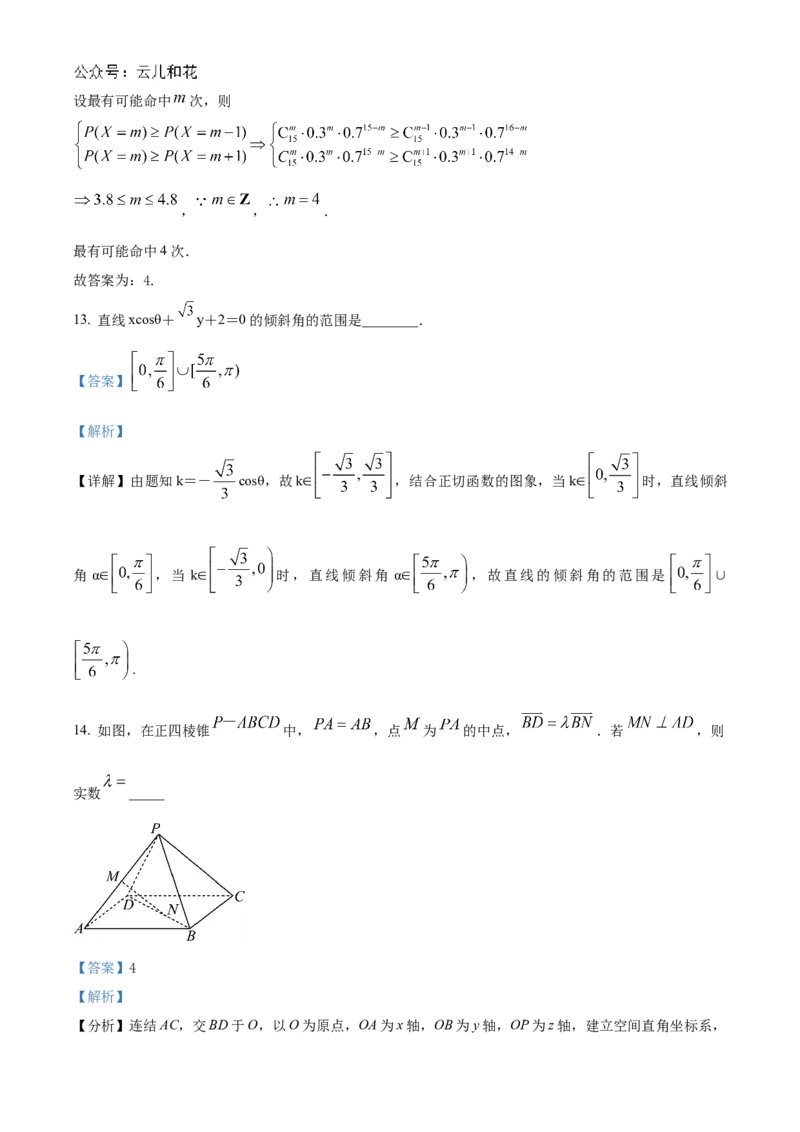
14. 如图,在正四棱锥 中, ,点 为 的中点, .若 ,则
实数 _____
【答案】4
【解析】
【分析】连结AC,交BD于O,以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出实数λ.
【详解】解:连结AC,交BD于O,以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标
系,
设PA=AB=2,则A(√2,0,0),D(0, ,0),P(0,0,√2),M( ,0, ),B
(0,√2,0),
(0,﹣2√2,0),设N(0,b,0),则 (0,b ,0),
∵ λ ,∴﹣2 ,∴b ,
∴N(0, ,0), ( , , ), ( ,0),
∵MN⊥AD,∴ 1 0,
解得实数λ=4.
故答案为4.
【点睛】本题考查实数值的求法,考查空间向量、正四棱锥的结构牲等基础知识,考查运算求解能力,是
中档题.
四、解答题(本题共5道小题,第1题0分,第2题0分,第3题0分,第4题0分,第5题
0分,共0分)
15. 已知直线 和直线 .
(1)若 ,求实数 的值;(2)若 ,求实数 的值.
【答案】(1)0或2 (2)
【解析】
【分析】(1)根据两直线垂直的公式 ,即可求解;
(2)根据两直线平行, ,求解 ,再代回直线验证.
【小问1详解】
若 ,则
,解得 或2;
【小问2详解】
若 ,则
,解得 或1.
时, ,满足 ,
时, ,此时 与 重合,
所以 .
16. 从2名男生(记为 和 )和3名女生(记为 , ,和 )组成的总体中,任意依次抽取2名学生.
(1)分别写出有放回简单随机抽样和不放回简单随机抽样的样本空间;
(2)在(1)中的两种抽样方式下,分别求出抽到的2人为1名男生和1名女生的概率.
【答案】(1)见详解;(2)有放回简单随机抽样下,抽到的2人为1名男生和1名女生的概率为 ;不
放回简单随机抽样下,抽到的2人为1名男生和1名女生的概率为 .
【解析】【分析】
的
(1)用列举法,分别写出两种抽取方法对应 基本事件,即可得出结果;
(2)先列举出两种抽样方式下,“抽到的2人为1名男生和1名女生”所包含的基本事件,确定基本事件
个数,再由古典概型的概率计算公式,即可求出结果.
【详解】(1)由题意,有放回简单随机抽样的样本空间为 , , ,
, , , , , , , , ,
, , , , , , , , ,
, , , ;共包含 个基本事件;
不放回简单随机抽样的样本空间为: , , , , ,
, , , , , , , , ,
, , , , , ;共包含 个基本事件;
(2)由(1)可得,两种抽样方式下,抽到的2人为1名男生和1名女生,所包含的基本事件都是:
, , , , , , , , ,
, , ;共 个,
有放回简单随机抽样下,抽到的2人为1名男生和1名女生的概率为 ;
不放回简单随机抽样下,抽到的2人为1名男生和1名女生的概率为 .
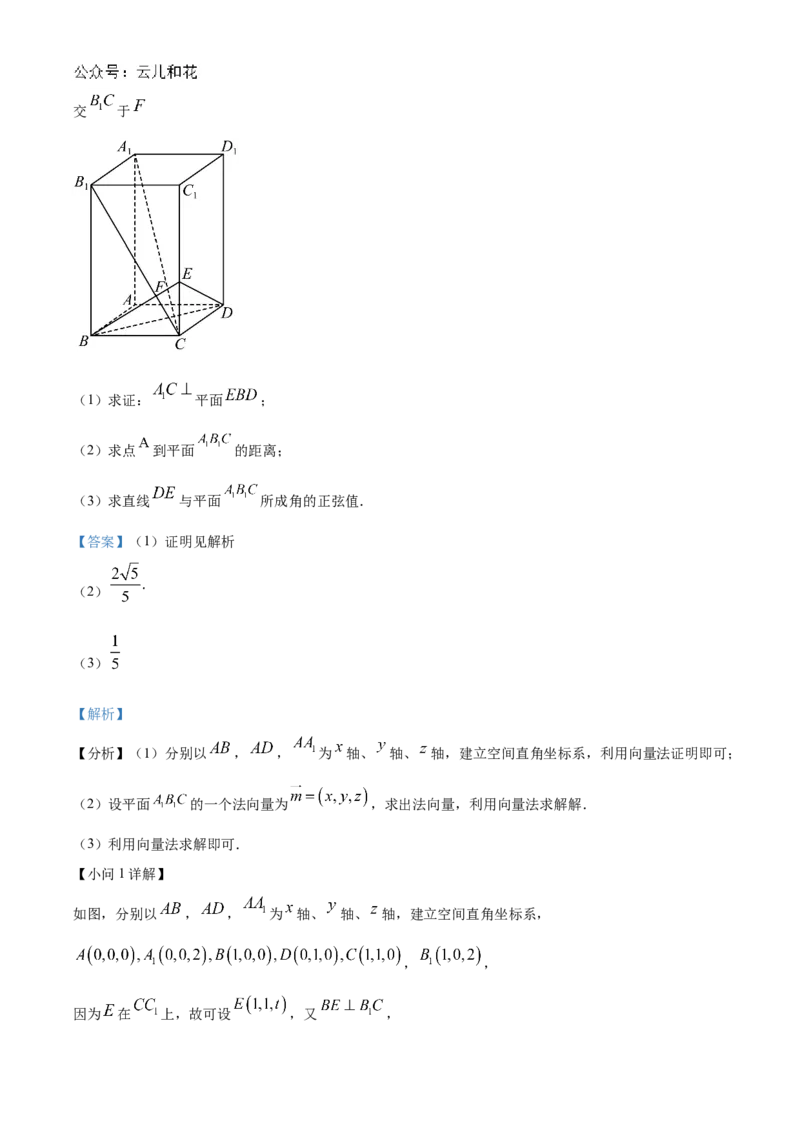
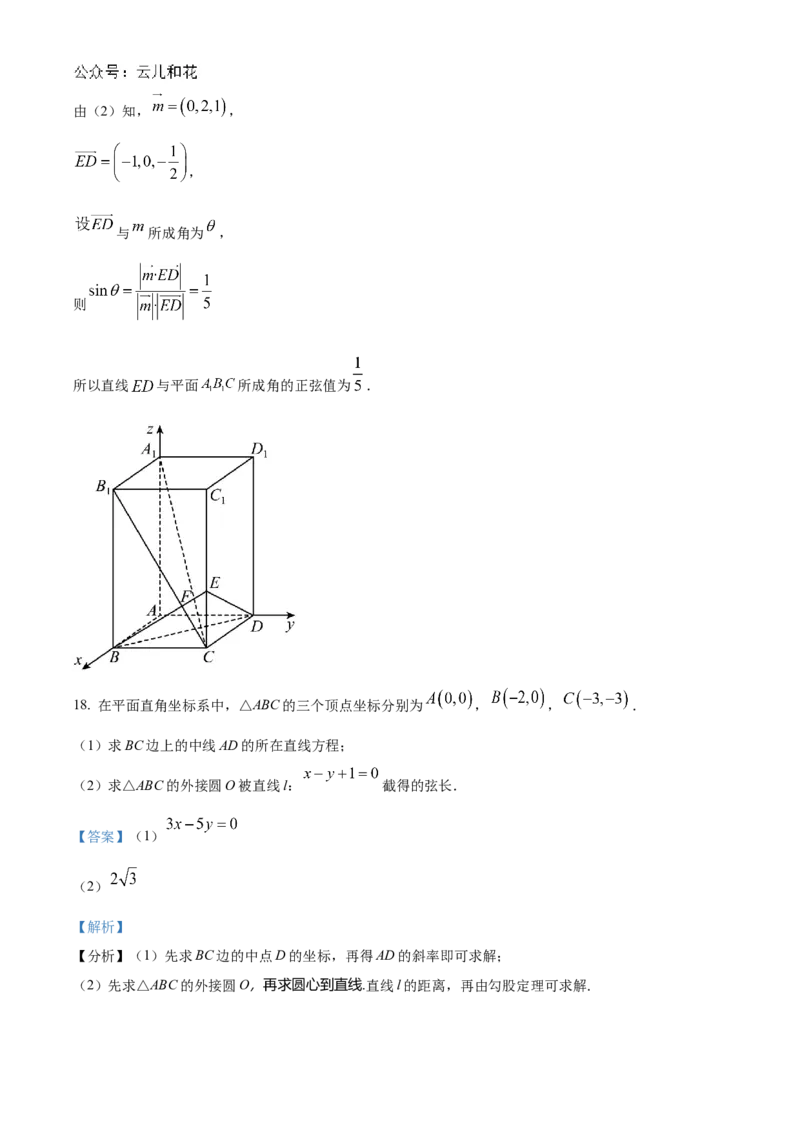
17. 如图,已知长方体 中, , ,连接 ,过 点作 的垂线交 于 ,交 于
(1)求证: 平面 ;
(2)求点 到平面 的距离;
(3)求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】(1)分别以 , , 为 轴、 轴、 轴,建立空间直角坐标系,利用向量法证明即可;
(2)设平面 的一个法向量为 ,求出法向量,利用向量法求解解.
(3)利用向量法求解即可.
【小问1详解】
如图,分别以 , , 为 轴、 轴、 轴,建立空间直角坐标系,
, ,
因为 在 上,故可设 ,又 ,所以 ,解得 ,
所以 ,
,
,即
, 平面 .
所以 平面 .
【小问2详解】
设平面 的一个法向量为 ,
,
则 ,
,
令 ,得 ,
,
所以所求的距离为 ;
【小问3详解】由(2)知, ,
,
与 所成角为 ,
则
所以直线 与平面 所成角的正弦值为 .
18. 在平面直角坐标系中,△ABC的三个顶点坐标分别为 , , .
(1)求BC边上的中线AD的所在直线方程;
(2)求△ABC的外接圆O被直线l: 截得的弦长.
【答案】(1)
(2)
【解析】
【分析】(1)先求BC边的中点D的坐标,再得AD的斜率即可求解;
(2)先求△ABC的外接圆O,再求圆心到直线.直线l的距离,再由勾股定理可求解.【
小问1详解】
∵ ,
∴BC边的中点D的坐标为 ,
∴中线AD的斜率为 ,
∴中线AD的直线方程为: ,即
【小问2详解】
设△ABC的外接圆O的方程为 ,
∵A、B、C三点在圆上,
∴
解得:
∴外接圆O的方程为 ,即 ,
其中圆心O为 ,半径 ,
又圆心O到直线l的距离为 ,
∴被截得的弦长的一半为 ,
∴被截得的弦长为 .
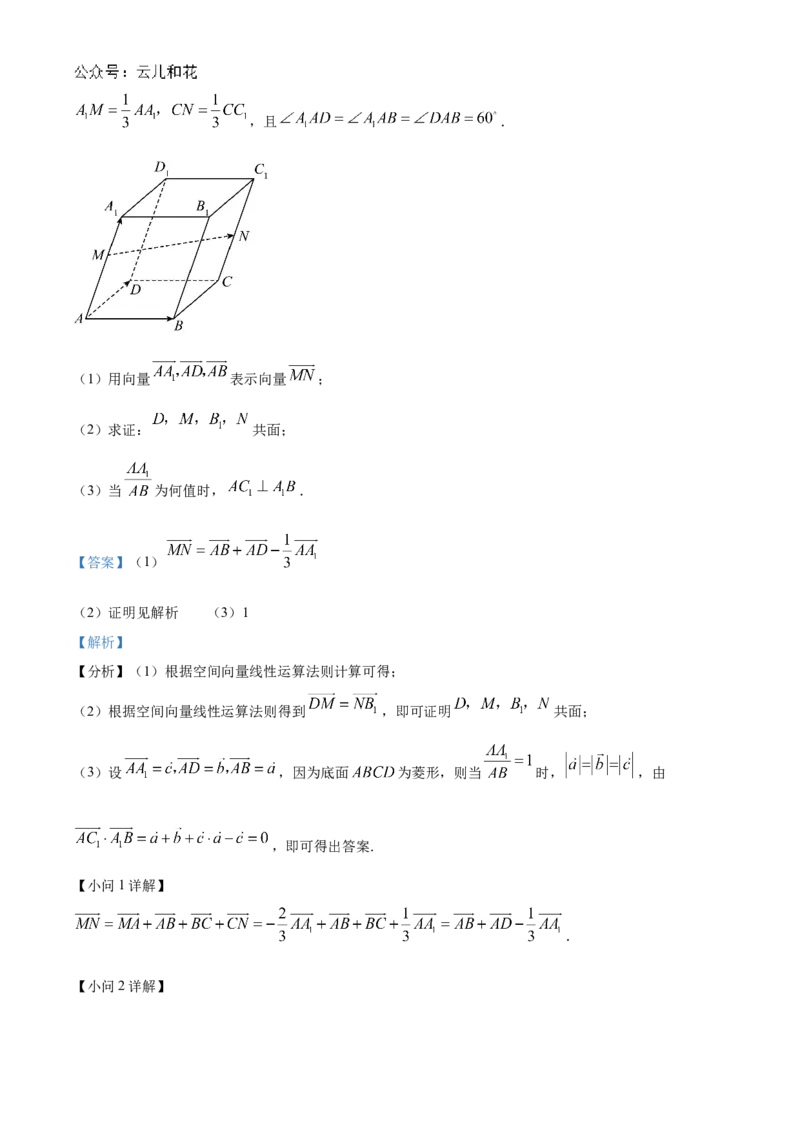
19. 如图,在底面 为菱形的平行六面体 中, 分别在棱 上,且,且 .
(1)用向量 表示向量 ;
(2)求证: 共面;
(3)当 为何值时, .
【答案】(1)
(2)证明见解析 (3)1
【解析】
【分析】(1)根据空间向量线性运算法则计算可得;
(2)根据空间向量线性运算法则得到 ,即可证明 共面;
(3)设 ,因为底面 为菱形,则当 时, ,由
,即可得出答案.
【小问1详解】
.
【小问2详解】证明: , ,
, 共面.
【小问3详解】
当 , ,
证明:设 ,
底面 为菱形,则当 时, ,
, ,
,
,
.