文档内容
彭州市 2023~2024 学年度上期高三期中教学质量调研
文科数学参考答案及评分标准
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1 2 3 4 5 6 7 8 9 10 11 12
A A D B B C D D D A B C
二、填空题:本题共4小题,每小题5分,共20分。
13.2 14. 15. 16.①②③
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(12分)
解:(1) ,
由正弦定理得 , …………………………2分
,可得 , ,即 .………………4分
,所以 ; …………………………6分
(2)解法1:由正弦定理 ,
, …………………………8分
可得 , ,……9分
, ,所以 ,…………………………10分
的面积为 . …………………………12分
解法2:因为 ,且 ,
, …………………………7分
可得 ,
,
, …………………………9分
, ,可得 , ,
, ,
,由余弦定理得 ,即 ,
解得 ,即 , …………………………10分
学科网(北京)股份有限公司的面积为 .………………………12分
18.(12分)
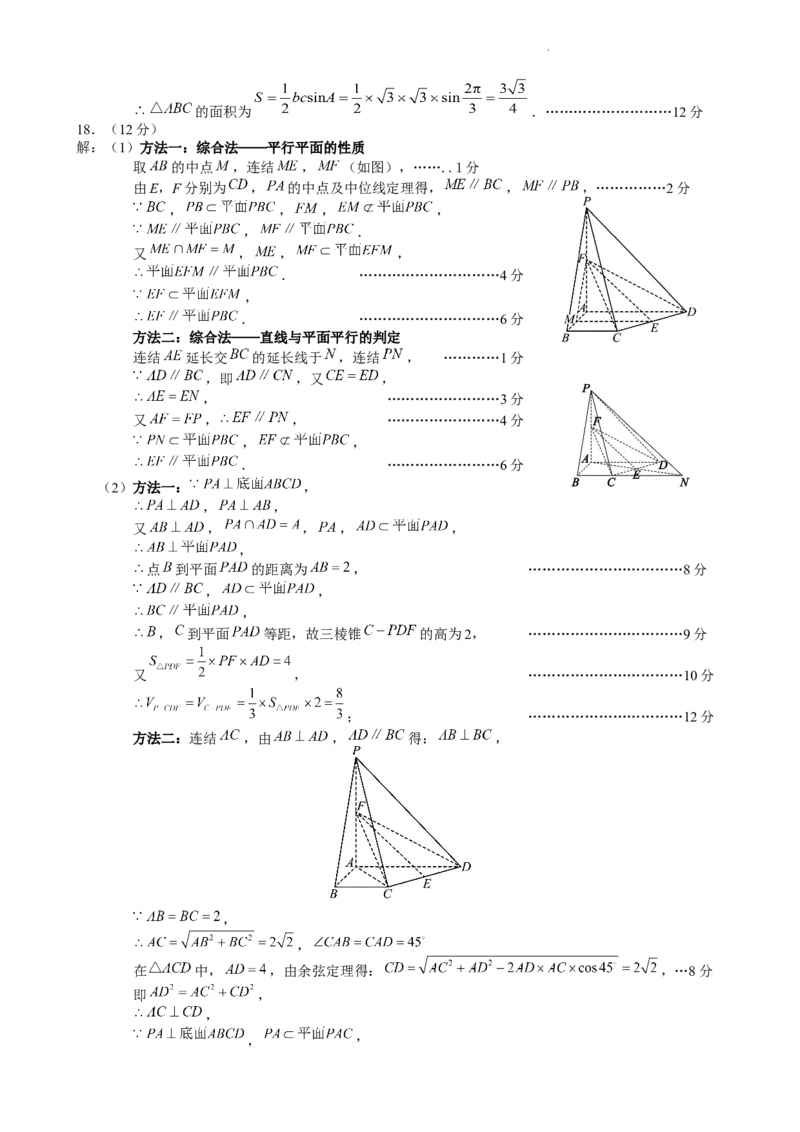
解:(1)方法一:综合法——平行平面的性质
取 的中点 ,连结 , (如图),……..1分
由E,F分别为 , 的中点及中位线定理得, , ,……………2分
, , , ,
, .
又 , , ,
. …………………………4分
,
. …………………………6分
方法二:综合法——直线与平面平行的判定
连结 延长交 的延长线于 ,连结 , …………1分
,即 ,又 ,
, ……………………3分
又 , , ……………………4分
, ,
. ……………………6分
(2)方法一: ,
, ,
又 , , , ,
,
点 到平面 的距离为 , ……………………………8分
, ,
,
, 到平面 等距,故三棱锥 的高为2, ……………………………9分
又 , ……………………………10分
; ……………………………12分
方法二:连结 ,由 , 得: ,
,
,
在 中, ,由余弦定理得: ,…8分
即 ,
,
,
,
学科网(北京)股份有限公司, , ……………………………9分
, ,
……………………………10分
……………12分
19.(12分)
解: (1)由直方图可得 学科良好的人数为 (人),…1
分
所以 列联表如下:
B学科不够良
B学科良好 合计
好
A学科良好 40 30 70
A学科不够良
10 20 30
好
合计 50 50 100
………………………4分
假设 : 学科良好与 学科良好无关,
,………………5分
所以有95%把握认为 学科良好与 学科良好有关; ………………………6分
(2)由题意知, 学科不够良好的学生中, 学科良好和不够良好的学生比为
所抽 学科良好人数为2人, 学科不够良好人数为4人, ………………………7分
记“其中恰有1人为 学科良好”为事件 ,
设 学科良好为 , , 学科不够良好分别为 , , , ,
则所有结果为共15种.事件 包含的基本事件为共8种; ………………………11分
由古典概型的概率公式得: . ………………………12分
20.(12分)
解:(1)由题意知 , ,
又 ,则 , , ………………………1分
,解得 (负值舍去), ………………………3分
由 在椭圆 上及 得 ,解得 , ………………………4分
椭圆 的方程为 ; ………………………5分
(2)由(1)知,右焦点为 ,
据题意设直线 的方程为 , , ,
则 , ,
学科网(北京)股份有限公司于是由 得 ,化简得 (*)……………………7分
由 ,消去 整理得 ,
,
由根与系数的关系得: , ,
代入(*)式得: ,解得 ,
直线 的方程为 , ………………………9分
方法一: , , ,
由求根公式与弦长公式得: ,……………………10分
设点 到直线 的距离为 ,则 , ……………………11分
……………………12分
方法二:由题意可知
, ……………………10分
代入 消去 得 ,
, , , ……………………11分
. …………………………12分
21.(12分)
解:(1)已知 ,函数定义域为 ,
当 时, ,
可得 , ……………………2分
当 时, , ……………………3分
所以函数 的在区间[1,2]上单调递增, ……………………4分
则当 时,函数 取得最大值,最大值 ; ……………………5分
(2)易知 ,
若 ,
当 时, , 单调递减;
当 时, , 单调递增,
所以当 时,函数 取得极小值,不符合题意; …………………………7分
若 ,
学科网(北京)股份有限公司f(x)0
令 ,
解得 或 ,
当 ,即 时,
由(1)知,函数 在 上单调递减,在 上单调递增,
所以当 时,函数 取得极小值,不符合题意; ……………………………8分
若 ,即 时,
当 时, , 单调递增,
当 时, , 单调递减;
当 时, , 单调递增,
所以当 时,函数 取得极大值,
若 存在极大值点 ,且 ,
则 且 ,符合题意; …………………………9分
若 ,即 时,
当 时, , 单调递增;
当 时, , 单调递减;
当 时, , 单调递增,
所以当 时,函数 取得极大值,
此时 且 ,
解得 ,…..11分
综上,满足条件的 的取值范围为 . …………………………12分
22.(10分)
解:(1)曲线 的极坐标方程为: , …………………………2分
曲线 的普通方程为: , ,…………………………4分
曲线 的极坐标方程为 ;…….5分
(2)由(1)得:点 的极坐标为 ,点 的极坐标为 , ………………7分
, …………………………10分
23.(10分)
解:(1)方法一:当 时, ,
① ,无解; …………………………1分
② ,解得 ; …………………………3分
③ ,解得 ; …………………………4分
综上:原不等式的解集为 ; …………………………5分
学科网(北京)股份有限公司方法二:原不等式等价于: , …………………………1分
由绝对值的几何意义知 的几何意义为:
数轴上实数 对应的点到 所对点的距离与其到原点的距离之差大于1,………………3分
又 的解为 , …………………………4分
原不等式的解集为 ; …………………………5分
(2)当 时, ,
原不等式等价于: ,即 ,则 ,…………6分
,故 ,解得 , …………………………9分
的取值范围为 .……10分
学科网(北京)股份有限公司