四川省绵阳市2024-2025学年高二上学期期末教学质量测试数学试题参考答案_2024-2025高二（7-7月题库）_2025年02月试卷_0210四川省绵阳市2024-2025学年高二上学期期末考试试题

高中 2023 级第三学期末教学质量测试 数学参考答案及评分标准 一、选择题：本题共8小题，每小题5分，共40分． 1．B 2．A 3．C 4．D 5．B 6．C 7．B 8．D 二、选择题：本大题共3小题，每小题6分，共18分。在每小题给出的四个选项中， 有多项符合题目要求。全部选对的得6分，选对但不全的得部分分，有选错的得0 分． 9．BD 10．ACD 11．BCD 三、填空题：本题共3个小题，每小题5分，共15分． 11 15 12．3； 13． （或0.275）； 14． 40 3 四、解答题：本题共5小题，第15题13分，第16、17小题15分，第18、19小题17 分，共77分．解答应写出文字说明、证明过程或演算步骤． 15．解：（1）由概率之和为1，可得100a+0.12+0.18+0.3+0.12+0.06=1··············2分 解得a0.0022，···········································································4分 估计平均数为： 0.121000.182000.33000.224000.12500+0.06600 322；··7分 （2）(M 350)0.00220.120.180.30.71，·······························10分 ∴M 35050，解得M 400．····················································13分 16．解：（1）∵C(6，5)，D(6，5)都在圆E上，线段CD的中垂线即x轴， ∴不妨设圆心E(x，0)，·································································2分 又∵半径r  AE CE ，即 (x1)2  (x6)2 52 ，·······················4分 可解x 6，r 5，·······································································6分 ∴圆E的标准方程为(x6)2  y2 25；···········································7分 （2）不妨设点N(x，y)，则 x2  y2 2 (x3)2  y2 ，························9分 化简可得(x4)2  y2 4，··························································12分 所以点N的轨迹为以F(4，0)为圆心，以2为半径的圆F，··················13分 ∵EF 642523，······················································· 14分 ∴圆E与圆F两圆内含，即两圆不存在公共点N满足题意．················15分 高二数学参考答案 第1页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}17．解：（1）抛掷骰子两次，样本空间基本事件总数为36，························· 2分 事假A=“两次点数之和大于9”，包含6个基本事件， 分别是(4，6)，(5，5)，(5，6)，(6，4)，(6，5)，(6，6)，······················4分 6 1 ∴P(A)  ；·······································································6分 36 6 （2）闯第1关时，抛掷骰子一次，样本空间基本事件总数为6，············7分 点数之和大于M=3n n2的基本事件为2，3，4，5，6，·················· 8分 5 故闯过第1关的概率为P  ；·······················································9分 1 6 闯第2关时，抛掷骰子两次，样本空间基本事件总数为36， 点数之和大于M=3n n7的基本事件为： (1，6)，(2，5)，(2，6)，(3，4)，(3，5)，(3，6)，(4，3)，(4，4)，(4，5)， (4，6)，(5，2)，(5，3)，(5，4)，(5，5)，(5，6)，(6，1)，(6，2)，(6，3)， (6，4)，(6，5)，(6，6)，·······························································11分 21 7 共计14个，故闯过第2关的概率为P   ；····························12分 2 36 12 因每次闯关互不影响，则闯过第1关和闯过第2关两个事件相互独立，故由独立 5 7 35 1 事件乘法公式得概率为    ，·········································· 14分 6 12 72 2 所以甲胜的概率小于乙胜的概率，游戏不公平．································15分 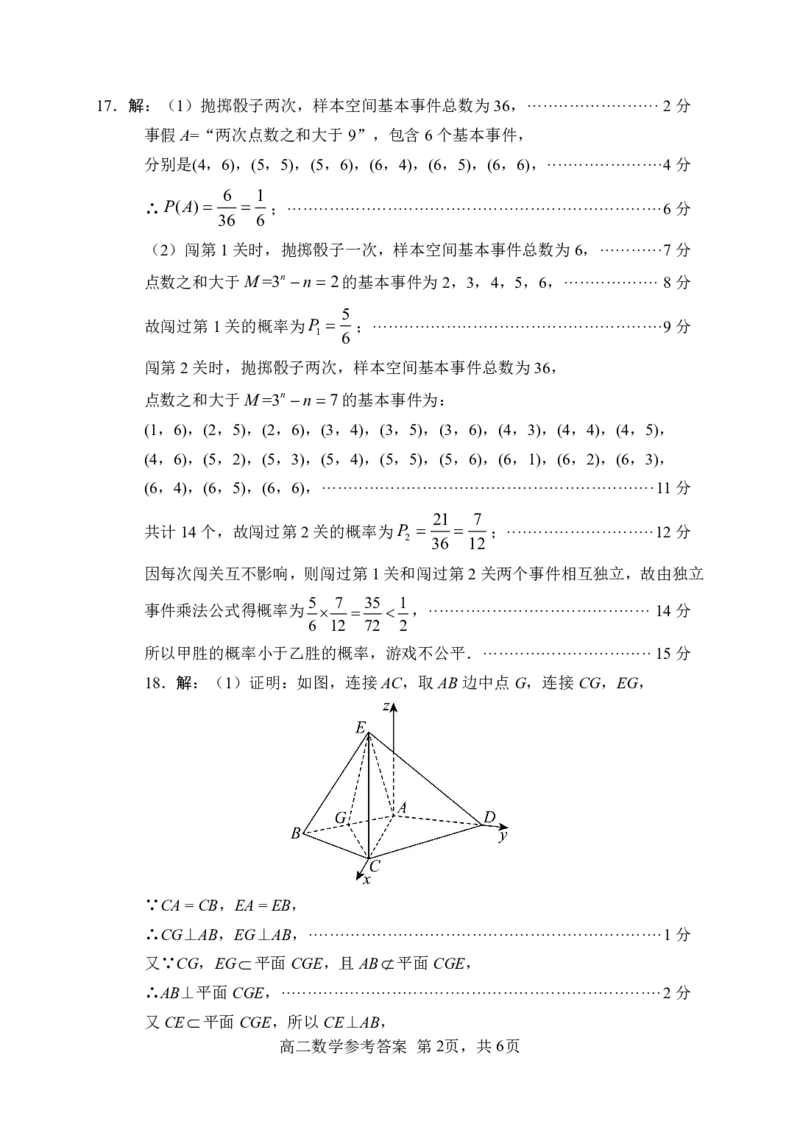18．解：（1）证明：如图，连接AC，取AB边中点G，连接CG，EG， ∵CA=CB，EA=EB， ∴CG⊥AB，EG⊥AB，···································································1分 又∵CG，EG平面CGE，且AB平面CGE， ∴AB⊥平面CGE，········································································2分 又CE平面CGE，所以CE⊥AB， 高二数学参考答案 第2页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}易知△ABC为等边三角形，因此AC=2， 在△ACD中，AC2  AD2 CD2，且AC=AD， ∴△ACD是等腰直角三角形，且AC⊥AD．········································3分 又因为AE⊥AD，且AE，AC平面ACE，AD平面ACE， ∴AD⊥平面ACE， 又CE平面ACE，所以AD⊥CE，··················································4分 又因为AB，AD平面ABCD，且CE平面ABCD， 所以CE⊥平面ABCD；··································································5分 方法二：如上图，在△ACD中，AC2  AD2 CD2，且AC=AD， ∴△ACD是等腰直角三角形，且AC⊥AD，········································1分 又AE⊥AD，则DE=4， 以点A为坐标原点，AC，AD所在的直线分别为x，y轴，建立空间直角坐标系， ∴A(0，0，0)，B(1，− 3，0)，C(2，0，0)，D(0，2，0)， 设E(x，y，z)，由DE=4，AE=BE=2 3，··········································2分 x2  y2 z2 12  ∴(x1)2 (y 3)2 z2 12，解得：E(2，0，2 2)，······················3分   x2 (y2)2 z2 16    ∴CE (0，0，2 2)，又AB(1， 3，0)，AC (2，0，0)，     ∴CEAB0，CEAC 0，则CE⊥AB，CE⊥AC，·························4分 又因为AB，AD平面ABCD，且CE平面ABCD， 所以CE⊥平面ABCD；··································································5分 （2）以点A为坐标原点，AC、AD所在的直线分别为x，y轴，建立空间直角坐标 系，A(0，0，0)，B(1，− 3，0)，C(2，0，0)，D(0，2，0)，E(2，0，2 2)， M(1，0， 2 )，············································································7分   ∴CM (1，0，2)，BC (1， 3，0)，············································8分   ∴M到直线BC的距离为： C  M  2 ( CM    BC )2  3( 1 )2  11 ；···10分 |BC| 2 2   （3）令EN ED=(2，2，2 2)(2，2，2 2)，    则AN  AEEN (22，2，2 22 2)，·································11分 高二数学参考答案 第3页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}由（1）可知，平面ACE的一个法向量为n=(0，1，0)，······················12分 设直线AN与平面ACE所成角为θ，  |ANn| |2| 13 ∴sinθ=    ··········· 13分 ， |AN||n| (22)2 (2)2 (2 22 2)2 13 1 解得 ，···············································································14分 3   4 2 4 2 4 2 4 2 ∴N( ， ， )，AN ( ， ， )，AC (2，0，0)， 3 3 3 3 3 3 设平面ACN的法向量为n (x，y，z)， 1 4 2 4 2  x y+ z0 ∴3 3 3 ，不妨设z1，则y2 2，  2x0 ∴平面ACN的一个法向量n (0，2 2，1)，····································15分 1 又平面ACE的一个法向量为n=(0，1，0)， 设二面角E-AC-N的平面角为α， |n n| 2 2 2 2 ∴|cos| 1   ，················································· 16分 |n ||n| 31 3 1 2 2 ∴二面角E-AC-N的平面角的余弦值 ．·····································17分 3 b2 3 b2 1 19．解：（1）由e 1  ，可得  ，即a2 4b2，·························2分 a2 2 a2 4 x2 y2 ∴椭圆C方程为：  1，·························································3分 4b2 b2 4b21 令x1时，y2  ，MN  4b21 3 ，解得：b2 1，···················4分 4 x2 故椭圆C的方程为： y2 1；························································5分 4 （2）设直线l：x=ty+1，M(x，y )，N(x ，y ) ，P(1，0)， 1 1 2 2   ∴x ty 1，x ty 1，PM=(x 1,y )，PN=(x 1,y ) ，·························6分 1 1 2 2 1 1 2 2   则|PM||PN|PMPN (x 1)(x 1)y y =(t21)y y ，·······················7分 1 2 1 2 1 2 x2 联立直线PM：x=ty−1，与椭圆C方程： y2 1， 4 高二数学参考答案 第4页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}xty1  x2 ，整理得到：(t24)y22ty30 ，·····································8分  y2 1  4 3 3(t21) 3 由韦达定理可得：y y  ，代入得：  ， 1 2 t24 t24 2 解得：t2 2，t  2，···································································9分 故直线l 的方程为x 2y10或x 2y10；································10分 y x 2 （3）设Q(x，y )，则k  0 ，则直线QA方程可设为：x 0 y2， 0 0 QA x 2 y 0 0  x 2 x 0 y2  y (x 2)2 x 2 联立 0 ，可得：( 0 4)y24 0 y0 ， x2 y2 1 y 0 2 y 0   4 4(x 2) 0 y 解得点S的纵坐标为：y  0 ，············································11分 S (x 2)2 0 4 y2 0 x2 y2 又点Q(x，y )在椭圆C ：  1上，则x24y2 8，代入化简得到： 0 0 1 8 2 0 0 4(x 2) 0 y 4(x 2)y (x 2)y x 2 x22x 2 y  0 = 0 0  0 0 ，则x  0 y 2= 0 0 S (x 2)2 (x 2)24y2 x 3 S y S x 3 0 4 0 0 0 0 0 y2 0 x22x 2 (x 2)y x22x 2 (x 2)y 故S( 0 0 ， 0 0)， 同理：T( 0 0 ， 0 0) ················13分 x 3 x 3 x 3 x 3 0 0 0 0   设OS (x，y )，OT (x ，y ) ，则 1 1 2 2         1 1 S  OS OT sinOS，OT  OS OT  1cos2OS，OT  OST 2 2   1   OSOT  OS OT  1(  )2 2 OS OT 1 xx y y = x2y2  x2y2  1( 1 2 1 2 )2 2 1 1 2 2 x2y2  x2y2 1 1 2 2 1 (x2y2)(x2y2)(xx y y )2 1  x2 y2 x2 y2 1 1 2 2 1 2 1 2 = x y x y ·········15分 2 1 1 2 2 (x2y2)(x2y2) 2 1 2 2 1 1 1 2 2 高二数学参考答案 第5页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}1 x22x 2 (x 2)y x22x 2 (x 2)y 4 y 4 y = 0 0  0 0  0 0  0 0  0  0 2 x 3 x 3 x 3 x 3 x29 84y29 0 0 0 0 0 0 = 4 y 0  4  4 =1 ，················································16分 4y2 1 1 1 0 4 y  2 4 y  0 y 0 y 0 0 1 1 (当且仅当4|y | ，即| y | 时，等号成立) 0 |y | 0 2 0 综上所述：△OST面积的最大值为1．················································17分 高二数学参考答案 第6页，共6页 {#{QQABJYCQggggAgAAABhCAQmiCEAQkBCCCYgORAAUoAAAiQFABAA=}#}