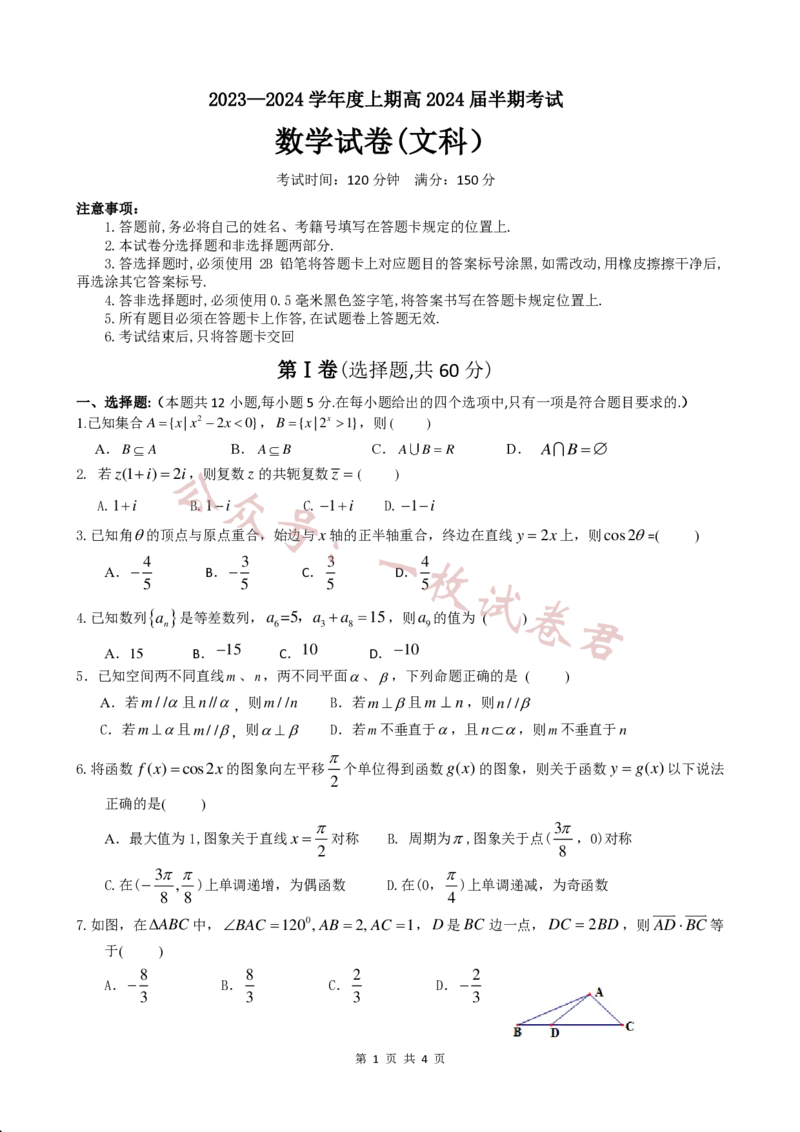文档内容
2023—2024 学年度上期高 2024 届半期考试
数学试卷(文科)
考试时间:120分钟 满分:150分
注意事项:
1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上.
2.本试卷分选择题和非选择题两部分.
3.答选择题时,必须使用 2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,
再选涂其它答案标号.
4.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定位置上.
5.所有题目必须在答题卡上作答,在试题卷上答题无效.
6.考试结束后,只将答题卡交回
第Ⅰ卷(选择题,共 60 分)
一、选择题:(本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合A={x|x2 −2x0},B={x|2x 1},则
第 1 页 共 4 页
( )
A. B A B. A B C.A B=R D. A B =
2. 若 z (1 + i ) = 2 i ,则复数z 的共轭复数 z = ( )
A. 1 + i B. 1 − i C. − 1 + i D. − 1 − i
3.已知角的顶点与原点重合,始边与x轴的正半轴重合,终边在直线 y = 2 x 上,则 c o s 2 =( )
A. −
4
5
3
B.− C.
5
3
5
D.
4
5
4.已知数列 a
n
是等差数列, a
6
= 5 , a
3
+ a
8
= 1 5 ,则a 的值为 ( )
9
A.15 B.
− 1 5
C.
1 0
D.
− 1 0
5.已知空间两不同直线m、n,两不同平面、,下列命题正确的是 ( )
A.若m//且n// ,则m//n B.若 m ⊥ 且m ⊥ n,则 n / /
C.若 m ⊥ 且m//,则⊥ D.若 m 不垂直于,且 n ,则 m 不垂直于 n
6.将函数 f ( x ) = c o s 2 x 的图象向左平移
2
个单位得到函数 g ( x ) 的图象,则关于函数 y = g ( x ) 以下说法
正确的是( )
3
A.最大值为1,图象关于直线x= 对称 B. 周期为,图象关于点( ,0)对称
2 8
3
C.在(− , )上单调递增,为偶函数 D.在(0,
8 8 4
)上单调递减,为奇函数
7.如图,在 中, , 是 边一点, ,则 等
于( )
A. B. C. D.
A B C B A C = 1 2 0 0 , A B = 2 , A C = 1 D B C D C = 2 B D A D B C
公
众
号
:
一
枚
试
卷
君
8 8 2 2
− −
3 3 3 3
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}公
众
号
:
一
枚
试
卷
君
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}三、解答题:(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
在
第 3 页 共 4 页
A B C 中 , 内 角 A 、 B 、 C 所 对 的 边 分 别 为 a、b、c , 其 外 接 圆 半 径 为 1 ,
b
=4,sin A+sinC =1.
1−cosB
(1)求cosB;
(2)求ABC的面积.
18.(本小题满分12分)
某家庭记录了未使用节水龙头 5 0 天的日用水量数据(单位: m 3 )和使用了节水龙头 5 0 天的日用水量数
据,得到频数分布表如下:
未使用节水龙头 5 0 天的日用水量频数分布表
日用
水量
0 , 0 . 1 ) 0 .1 , 0 .2 ) 0 .2 , 0 .3 ) 0 .3 , 0 .4 ) 0 .4 , 0 .5 ) 0.5,0.6) 0 .6 , 0 .7 )
频数 1 3 2 4 9 26 5
使用了节水龙头 5 0 天的日用水量频数分布表
日用水量 0 , 0 . 1 ) 0.1,0.2) 0 .2 , 0 .3 ) 0.3,0.4) 0 .4 , 0 .5 ) 0 .5 , 0 .6 )
频数 1 5 1 3 10 1 6 5
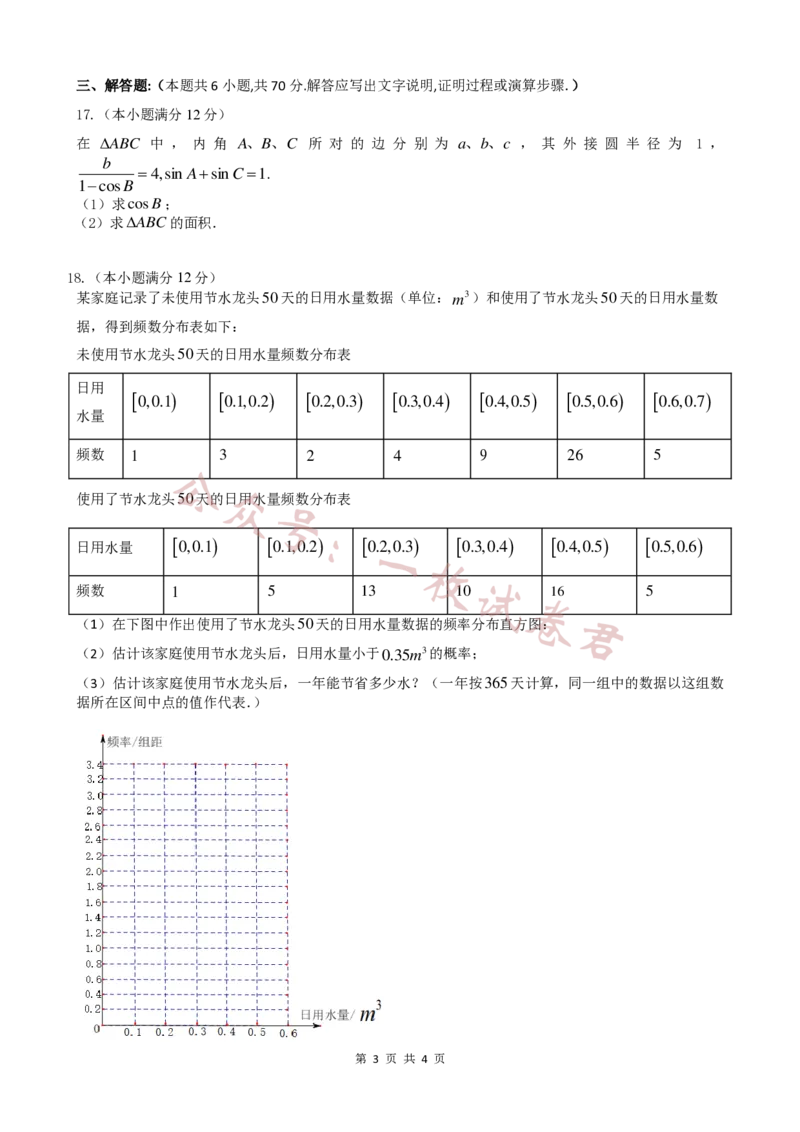
(1)在下图中作出使用了节水龙头 5 0 天的日用水量数据的频率分布直方图:
(2)估计该家庭使用节水龙头后,日用水量小于 0 .3 5 m 3 的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 3 6 5
公
众
号
:
一
枚
试
卷
君
天计算,同一组中的数据以这组数
据所在区间中点的值作代表.)
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}19.(本小题满分12分)
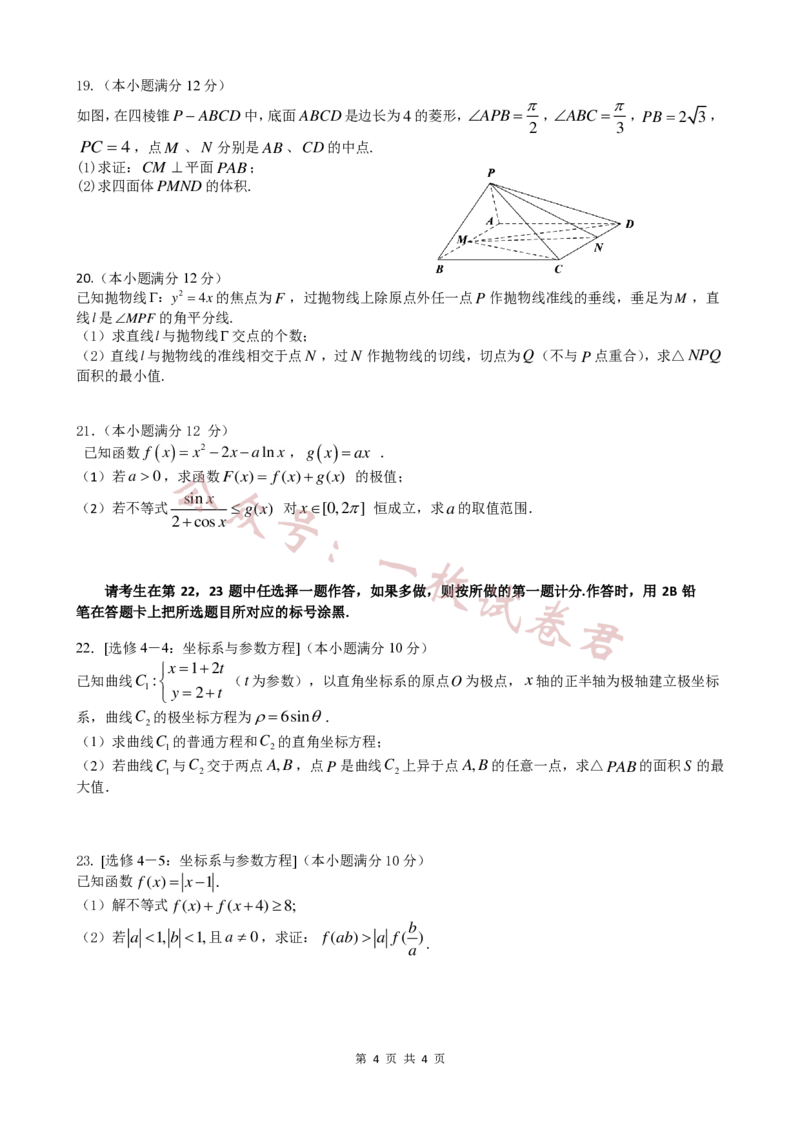
如图,在四棱锥
第 4 页 共 4 页
P − A B C D 中,底面 A B C D 是边长为 4 的菱形, A P B
2
=
,ABC = ,
3
P B = 2 3 ,
PC =4,点 M 、 N 分别是AB、CD的中点.
(1)求证:CM ⊥平面PAB;
(2)求四面体 P M N D 的体积.
20.(本小题满分12分)
已知抛物线 : y 2 = 4 x 的焦点为 F ,过抛物线上除原点外任一点 P 作抛物线准线的垂线,垂足为M ,直
线l是MPF的角平分线.
(1)求直线 l 与抛物线 交点的个数;
(2)直线 l 与抛物线的准线相交于点 N ,过 N 作抛物线的切线,切点为Q(不与P点重合),求△ N P Q
面积的最小值.
21.(本小题满分12 分)
已知函数 , g ( x ) = a x .
(1)若 a 0 ,求函数 F ( x ) = f ( x ) + g ( x ) 的极值;
(2)若不等式
2
s
+
i n
c o
x
s x
g ( x ) 对x[0,2] 恒成立,求 a 的取值范围.
请考生在第 22,23 题中任选择一题作答,如果多做,则按所做的第一题计分.作答时,用 2B 铅
笔在答题卡上把所选题目所对应的标号涂黑.
22.[选修4-4:坐标系与参数方程](本小题满分10分)
已知曲线 C
1
:
x
y
=
=
1
2
+
+
2 t
t
( t 为参数),以直角坐标系的原点 O 为极点, x 轴的正半轴为极轴建立极坐标
系,曲线 C
2
的极坐标方程为 6 s i n = .
(1)求曲线C 的普通方程和
1
C
2
的直角坐标方程;
(2)若曲线C 与
1
C
2
交于两点 A , B ,点 P 是曲线 C
2
上异于点 A , B 的任意一点,求△PAB的面积 S 的最
大值.
23. [选修4-5:坐标系与参数方程](本小题满分10分)
已知函数 f(x)= x−1.
(1)解不等式 f(x)+ f(x+4)8;
(2)若 a 1,b 1,且 a 0
b
,求证: f(ab) a f( )
.
a
f ( x ) = x 2 − 2 x − a l n x
公
众
号
:
一
枚
试
卷
君
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}