B000544519_2数学72C答案_2024-2025高三（6-6月题库）_2024年10月试卷_1022广东茂名区域2025届高三10月金太阳联考（25-72C）

茂名区域高三１０月份联考 数学参考答案 １．Ｃ 狕＝－槡２ｉ（１＋槡２ｉ）＝２－槡２ｉ，所以狕的虚部为－槡２． ｛犪＋１＝３， ２．Ｄ 因为犕＝｛犪＋１，犪－１｝，所以 解得犪＝２． 犪－１＝１， ７－１ ３．Ａ 当犛＝７，狀＝ｅ３ 时，水的质量为 ＝２． ｌｎｅ３ ｓｉｎ狓 ４．Ｄ 当狓＜０时，槡狓２＝｜狓｜＝－狓，所以狆是假命题，瓙狆是真命题．因为ｔａｎ狓＝ ＝ ｃｏｓ狓 ｓｉｎ狓，所以ｃｏｓ狓＝１或ｓｉｎ狓＝０，当狓∈（０，π）时，ｃｏｓ狓≠１，ｓｉｎ狓≠０，所以狇是假命题，瓙狇 是真命题． → １→ １→ １→ １→ １→ １→ １ １ ５．Ｂ 犃犇＝ 犃犅＋ 犃犆＝ 犃犗＋ 犗犅＋ 犃犗＋ 犗犆＝－犪＋ 犫＋ 犮． ２ ２ ２ ２ ２ ２ ２ ２ （ １） 犳（狓） ６．Ｄ 依题意可得犳（０）＝０，犳（狓）在（－∞，０）上单调递增，且犳 － ＝０．由 ≤０，得 ３ 狓２－２ ｛犳（狓）≤０， ｛犳（狓）≥０， ［ １ ］ ［１ ） 或 则狓∈（－∞，－槡２）∪ － ，０ ∪ ，槡２ ． 狓２－２＞０ 狓２－２＜０， ３ ３ ｛犃＋犫＝３， ｛犃＝２， １ ７．Ｄ 因为犃＞０，所以 解得 所以犳（０）＝２ｓｉｎφ＋１＝２，则ｓｉｎφ＝ ．因 －犃＋犫＝－１， 犫＝１， ２ π π （ π） （π） （ωπ π） 为｜φ｜＜ ，所以 φ＝ ，可得犳（狓）＝２ｓｉｎω狓＋ ＋１．因为犳 ＝２ｓｉｎ ＋ ＋１＝ ２ ６ ６ １８ １８ ６ ωπ π π ３，所以 ＋ ＝ ＋２犽π，犽∈犣，即ω＝６＋３６犽，犽∈犣．因为０＜ω＜１０，所以ω＝６． １８ ６ ２ （ １ ） （ ｅ） ８．Ａ 依题意可设犘犿， ｅ犿 ，犙犿，－ ，其中犿＞０． ２ ２犿 （１ ） １ （ ｅ） ｅ １ ｅ狓′＝ ｅ狓，－ ′＝ ，则曲线犆 在点犘处的切线斜率为 ｅ犿，曲线犆 在点犙处 ２ ２ ２狓 ２狓２ １ ２ ２ ｅ １ ｅ 的切线斜率为 ，所以 ｅ犿＝ ，即犿２ｅ犿＝ｅ（犿＞０）．设函数犳（狓）＝狓２ｅ狓（狓＞０），则 ２犿２ ２ ２犿２ （ ｅ） 犳′（狓）＝（狓２＋２狓）ｅ狓＞０，所以犳（狓）为增函数，又犳（１）＝ｅ，所以犿＝１，所以犘 １， ， ２ （ ｅ） 犙１，－ ，故｜犘犙｜＝ｅ． ２ ９．ＡＣＤ 由｜２犪－犫｜＝｜２犪＋犫｜，得４犪２＋犫２－４犪·犫＝４犪２＋犫２＋４犪·犫，解得犪·犫＝０，即 犪⊥犫，反之亦成立，故“｜２犪－犫｜＝｜２犪＋犫｜”是“犪⊥犫”的充要条件．若｜２犪－犫｜＝１，则４犪２＋犫２ 犪·犫 －４犪·犫＝１，解得犪·犫＝１，则ｃｏｓ〈犪，犫〉＝ ＝１，所以〈犪，犫〉＝０，即犪∥犫，若犪∥犫，则 ｜犪｜｜犫｜ 【高三数学·参考答案 第 １页（共５页）】 ·２５－７２犆· 书书书犪·犫＝１或－１，所以｜２犪－犫｜＝１或３，故“｜２犪－犫｜＝１”是“犪∥犫”的充分不必要条件． １０．ＡＢＤ 犳′（狓）＝２狓（狓－６）＋狓２＝３狓（狓－４），当狓∈（０，４）时，犳′（狓）＜０，当狓∈（－∞，０）∪ （４，＋∞）时，犳′（狓）＞０，所以犳（狓）在（－∞，０）和（４，＋∞）上单调递增，在（０，４）上单调递 减，故狓＝４是犳（狓）的极小值点，Ａ正确． 犳（狓）＋犳（－狓）＝狓２（狓－６）＋狓２（－狓－６）＝－１２狓２≤０，Ｂ正确． 当０＜狓＜１时，０＜狓２＜狓＜１，又犳（狓）在（０，１）上单调递减，所以犳（狓）＜犳（狓２），Ｃ错误． 当０＜狓＜１时，犳（４＋狓）－犳（４－狓）＝（４＋狓）２（４＋狓－６）－（４－狓）２（４－狓－６）＝２狓３＞０， 所以犳（４＋狓）＞犳（４－狓），Ｄ正确． （ １）２ ９ １ １１．ＢＣ 犳（狓）＝｜ｓｉｎ２狓｜＋１－２｜ｓｉｎ２狓｜２＝－２｜ｓｉｎ２狓｜－ ＋ ，当｜ｓｉｎ２狓｜＝ 时， ４ ８ ４ ９ 犳（狓）取得最大值，且最大值为 ，Ａ错误．因为狔＝｜ｓｉｎ２狓｜，狔＝ｃｏｓ４狓的最小正周期均为 ８ π π （犽π ） （犽π ） （犽π ，所以犳（狓）的最小正周期为 ，Ｂ正确．因为犳 －狓 ＝ ｓｉｎ２ －狓 ＋ｃｏｓ４ － ２ ２ ２ ２ ２ ） 犽π 狓 ＝｜ｓｉｎ２狓｜＋ｃｏｓ４狓（犽∈犣），所以曲线狔＝犳（狓）关于直线狓＝ （犽∈犣）轴对称，Ｃ正确． ４ １７ １ 槡２ 令犵（狓）＝１６犳（狓）－１７＝０，得犳（狓）＝ ，则｜ｓｉｎ２狓｜＝ ± ，结合函数狔＝｜ｓｉｎ２狓｜（０≤ １６ ４ ８ １ 槡２ 狓≤π）的图象（图略），可知方程｜ｓｉｎ２狓｜＝ ± 在［０，π］上有８个不同的实根，Ｄ错误． ４ ８ 槡３ ３ （３） （３π π） π 槡３ １２．－ 犳（－１）＝２－１＋１＝ ，犳（犳（－１））＝犳 ＝ｓｉｎ ＋ ＝－ｃｏｓ ＝－ ． ２ ２ ２ ２ ６ ６ ２ ２ １３．２槡２ ｌｇ犪＋ｌｏｇ１００＝ｌｇ犪＋ ≥２槡２，当且仅当犪＝１０槡２时，等号成立． 犪 ｌｇ犪 ３ （ １） 槡５ １４．－ 因为２ｓｉｎ狓＋ｃｏｓ狓＝槡５ｓｉｎ（狓＋φ ）＝１ｔａｎφ＝ ，所以ｓｉｎ（狓＋φ ）＝ ． ５ ２ ５ 槡５ 槡５ 由题意可得ｓｉｎ（α＋φ ）＝ ，ｓｉｎ（ β＋φ ）＝ ． ５ ５ 因为α≠β ，α∈［０，２π）， β∈［０，２π），所以α＋φ＋β＋φ＝π，即α－β＝π－２（ β＋φ ）． ３ ｃｏｓ（α－β ）＝ｃｏｓ［π－２（ β＋φ ）］＝－ｃｏｓ２（ β＋φ ）＝２ｓｉｎ２（ β＋φ ）－１＝－ ． ５ 犪２＋犫２－犮２ １ １５．解：（１）因为犪２＋犫２＝犪犫＋犮２，所以ｃｏｓ犆＝ ＝ ，…………………………… ４分 ２犪犫 ２ π 因为犆∈（０，π），所以犆＝ ．……………………………………………………………… ５分 ３ （２）因为犫犮ｓｉｎ犃＝ｓｉｎ犆，所以犪犫犮＝犮，…………………………………………………… ７分 所以犪犫＝１．………………………………………………………………………………… ８分 由犪２＋犫２＝犪犫＋犮２，得犮２＝犪２＋犫２－犪犫≥２犪犫－犪犫＝犪犫＝１，则犮≥１，………………… １０分 当且仅当犪＝犫＝１时，等号成立．………………………………………………………… １１分 【高三数学·参考答案 第 ２页（共５页）】 ·２５－７２犆·犮 １ ２ １ 设△犃犅犆外接圆的半径为犚，则２犚＝ ≥ ＝ ，则犚≥ ， ｓｉｎ犆 π 槡３ 槡３ ｓｉｎ ３ π 所以△犃犅犆外接圆的面积的最小值为 ．……………………………………………… １３分 ３ １６．解：（１）因 为｜犘犉 ｜＝槡７＋１，｜犘犉 ｜＝槡７－１，犘犉 ⊥犘犉 ，所 以｜犉犉 ｜＝ １ ２ １ ２ １ ２ 槡｜犘犉｜２＋｜犘犉｜２＝４， １ ２ 记犉 （－犮，０），犉 （犮，０），则犮＝２．………………………………………………………… ２分 １ ２ 由椭圆的定义可得，２犪＝｜犘犉｜＋｜犘犉｜＝２槡７，犪＝槡７，犫２＝犪２－犮２＝３． …………… ５分 １ ２ 由双曲线的定义可得，２犿＝｜犘犉｜－｜犘犉｜＝２，犿＝１，狀２＝犮２－犿２＝３． …………… ８分 １ ２ 狓２ 狔２ 狔２ 所以犆 的方程为 ＋ ＝１，犆 的方程为狓２－ ＝１． ……………………………… ９分 １ ７ ３ ２ ３ （２）由题意得犃（０，槡３），犅（－１，０），则直线犃犅的方程为狔＝槡３狓＋槡３．设犇（狓，狔）． … １ １ ………………………………………………………………………………………… １１分 烄狔＝槡３狓＋槡３， ７ 联立烅狓２ ＋ 狔２ ＝１， 得４狓２＋７狓＝０，所以狓 １ ＝－ ４ ．………………………………… １３分 烆７ ３ ７ ７ ｜犃犇｜＝槡１＋犽２｜狓－狓｜＝槡１＋３× － －０ ＝ ．……………………………… １５分 １ 犃 ４ ２ １７．（１）证明：因为四边形犃犅犆犇为菱形，所以犅犆∥犃犇， 又犃犇平面犃犃犇犇 ，犅犆平面犃犃犇犇 ， １ １ １ １ 所以犅犆∥平面犃犃犇犇 ．………………………………………………………………… ２分 １ １ 又犅犅∥犃犃 ，犃犃 平面犃犃犇犇 ，犅犅 平面犃犃犇犇 ，所以犅犅∥平面犃犃犇犇 ．… １ １ １ １ １ １ １ １ １ １ １ …………………………………………………………………………………………… ３分 因为犅犅 ∩犅犆＝犅，所以平面犅犆犆犅∥平面犃犃犇犇 ．……………………………… ４分 １ １ １ １ １ 因为平面犃犅犆犇 ∩平面犅犆犆犅 ＝犅犆 ，平面犃犅犆犇 ∩平面犃犃犇犇 ＝犃犇 ， １ １ １ １ １ １ １ １ １ １ １ １ １ １ １ １ 所以犅犆∥犃犇 ，………………………………………………………………………… ５分 １ １ １ １ 同理可得犃犅∥犆犇 ，所以四边形犃犅犆犇 为平行四边形．……………………… ６分 １ １ １ １ １ １ １ １ → → （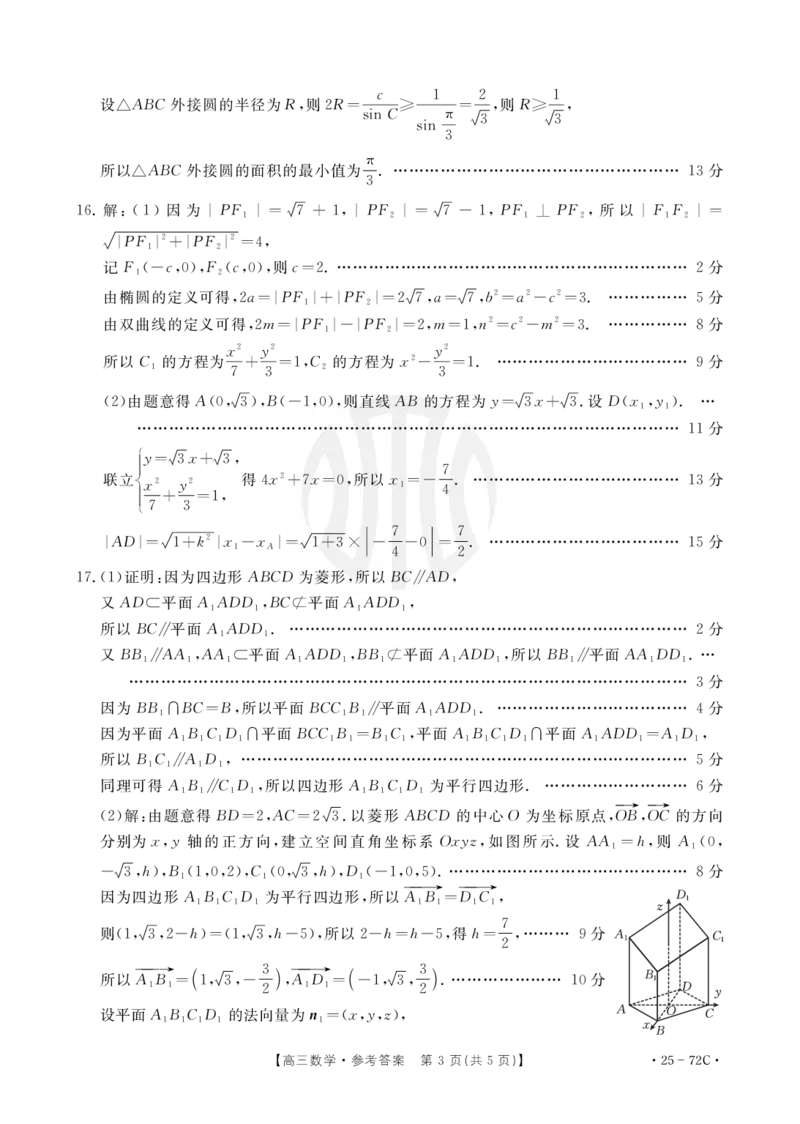２）解：由题意得犅犇＝２，犃犆＝２槡３．以菱形犃犅犆犇的中心犗为坐标原点，犗犅，犗犆的方向 分别为狓，狔轴的正方向，建立空间直角坐标系犗狓狔狕，如图所示．设犃犃 ＝犺，则犃 （０， １ １ －槡３，犺），犅 （１，０，２），犆 （０，槡３，犺），犇 （－１，０，５）．……………………………………… ８分 １ １ １ → → 因为四边形犃犅犆犇 为平行四边形，所以犃犅 ＝犇犆 ， １ １ １ １ １ １ １ １ ７ 则（１，槡３，２－犺）＝（１，槡３，犺－５），所以２－犺＝犺－５，得犺＝ ，……… ９分 ２ → （ ３）→ （ ３） 所以犃犅 ＝ １，槡３，－ ，犃犇 ＝ －１，槡３， ．………………… １０分 １ １ ２ １ １ ２ 设平面犃犅犆犇 的法向量为狀＝（狓，狔，狕）， １ １ １ １ １ 【高三数学·参考答案 第 ３页（共５页）】 ·２５－７２犆·→ → 则犃犅·狀＝０，犃犇 ·狀＝０， １ １ １ １ １ １ 烄 ３ 狓＋槡３狔－ 狕＝０， ２ 即烅 ………………………………………………………………… １１分 ３ －狓＋槡３狔＋ 狕＝０， 烆 ２ 令狕＝２，得狀＝（３，０，２）．………………………………………………………………… １２分 １ 易知平面犃犅犆犇的一个法向量为狀＝（０，０，１），……………………………………… １３分 ２ 狀·狀 ２ ２槡１３ 则ｃｏｓ〈狀，狀〉＝ １ ２ ＝ ＝ ，………………………………………… １４分 １ ２ ｜狀 １ ｜｜狀 ２ ｜ 槡１３×１ １３ ３槡１３ 所以平面犃犅犆犇 与平面犃犅犆犇所成二面角的正弦值为 ．………………… １５分 １ １ １ １ １３ １８．解：（１）第１次换球后甲口袋有２个黑球，即从甲口袋取出的球为白球且从乙口袋取出的球 ２ １ ２ 为黑球，则狆 ＝ × ＝ ．……………………………………………………………… １分 １ ３ ３ ９ 第１次换球后甲口袋有１个黑球，即从甲、乙口袋取出的球同为白球或同为黑球， ２ ２ １ １ ５ 则狇＝ × ＋ × ＝ ．……………………………………………………………… ３分 １ ３ ３ ３ ３ ９ （２）若第２次换球后甲口袋有２个黑球，则分２种情况： ①当第１次换球后甲口袋有１个黑球时，第２次甲口袋取白球且乙口袋取黑球； ②当第１次换球后甲口袋有２个黑球时，第２次甲、乙口袋同取白球． ２ １ １ ５ ２ ２ １ １６ 所以狆 ＝狇× × ＋狆 × ＝ × ＋ × ＝ ． ……………………………… ５分 ２ １ ３ ３ １ ３ ９ ９ ９ ３ ８１ 若第２次换球后甲口袋有１个黑球，则分３种情况： ①当第１次换球后甲口袋有０个黑球时，第２次甲口袋取白球且乙口袋取黑球； ②当第１次换球后甲口袋有１个黑球时，第２次甲、乙口袋同取白球或同取黑球； ③当第１次换球后甲口袋有２个黑球时，第２次甲口袋取黑球且乙口袋取白球． ２ （２ ２ １ １） ２ ４９ 所以狇＝（１－狇－狆）× ＋狇× × ＋ × ＋狆 × ＝ ．………………… ７分 ２ １ １ ３ １ ３ ３ ３ ３ １ ３ ８１ （３）第狀次换球后，甲口袋黑球的个数为１的情况： ①若第狀－１次换球后甲口袋有２个黑球，则第狀次甲口袋取黑球且乙口袋取白球； ②若第狀－１次换球后甲口袋有１个黑球，则第狀次甲、乙口袋同取黑球或同取白球； ③若第狀－１次换球后甲口袋有０个黑球，则第狀次甲口袋取白球且乙口袋取黑球． ２ （１ １ ２ ２） （ ） ２ ２ １ 所以狇＝狆 × ＋狇 × × ＋ × ＋ １－狆 －狇 × ＝ － 狇 ，… 狀 狀－１ ３ 狀－１ ３ ３ ３ ３ 狀－１ 狀－１ ３ ３ ９ 狀－１ ………………………………………………………………………………………… １１分 ３ １（ ３） 即狇－ ＝－ 狇 － ．…………………………………………………………… １３分 狀 ５ ９ 狀－１ ５ ３ ２ ｛ ３｝ ２ １ 又因为狇－ ＝－ ，所以 狇－ 是以－ 为首项，－ 为公比的等比数列，…… １５分 １ ５ ４５ 狀 ５ ４５ ９ 【高三数学·参考答案 第 ４页（共５页）】 ·２５－７２犆·３ ２（ １）狀－１ ３ ２（ １）狀－１ 所以狇－ ＝－ － ，即狇＝ － － ．…………………………… １７分 狀 ５ ４５ ９ 狀 ５ ４５ ９ １９．（１）证明：令函数犺（狓）＝狓－ｓｉｎ狓，则犺′（狓）＝１－ｃｏｓ狓＞０， （ π） 所以犺（狓）在 ０， 上单调递增，犺（狓）＞犺（０）＝０，即狓＞ｓｉｎ狓．……………………… ２分 ２ 令函数犽（狓）＝ｓｉｎ狓－狓ｃｏｓ狓，则犽′（狓）＝ｃｏｓ狓－ｃｏｓ狓＋狓ｓｉｎ狓＝狓ｓｉｎ狓． （ π） （ π） 当狓∈ ０， 时，犽′（狓）＞０，所以犽（狓）在 ０， 上单调递增，犽（狓）＞犽（０）＝０，即ｓｉｎ狓＞ ２ ２ 狓ｃｏｓ狓． （ π） 故当狓∈ ０， 时，狓＞ｓｉｎ狓＞狓ｃｏｓ狓． ………………………………………………… ５分 ２ （２）解：令函数狌（狓）＝犪ｓｉｎ２狓－狓２ｃｏｓ狓，则狌′（狓）＝犪ｓｉｎ２狓－２狓ｃｏｓ狓＋狓２ｓｉｎ狓． 令函数狏（狓）＝狌′（狓），则狏′（狓）＝２犪ｃｏｓ２狓＋（狓２－２）ｃｏｓ狓＋４狓ｓｉｎ狓，狏′（０）＝２犪－２． … …………………………………………………………………………………………… ７分 （ π） ①当２犪－２＜０，即犪＜１时，存在狓∈ ０， ，使得当狓∈（０，狓）时，狏′（狓）＜０， ０ ２ ０ 所以函数狏（狓）＝狌′（狓）在（０，狓）上单调递减．…………………………………………… ８分 ０ 因为狌′（０）＝０，所以当狓∈（０，狓）时，狌′（狓）＜０，所以狌（狓）在（０，狓）上单调递减． … ９分 ０ ０ 因为狌（０）＝０，所以当狓∈（０，狓）时，狌（狓）＜０，不符合题意．………………………… １０分 ０ ②当２犪－２≥０，即犪≥１时，犪ｓｉｎ２狓－狓２ｃｏｓ狓≥ｓｉｎ２狓－狓２ｃｏｓ狓． …………………… １１分 （ π） 令函数犵（狓）＝ｓｉｎ２狓－狓２ｃｏｓ狓，狓∈ ０， ， ２ 则犵′（狓）＝２ｓｉｎ狓ｃｏｓ狓－２狓ｃｏｓ狓＋狓２ｓｉｎ狓＞２ｓｉｎ狓ｃｏｓ狓－２ｓｉｎ狓＋狓２ｓｉｎ狓 （ 狓） （狓 狓）（狓 狓） ＝［狓２－２（１－ｃｏｓ狓）］ｓｉｎ狓＝ 狓２－４ｓｉｎ２ ｓｉｎ狓＝４ ＋ｓｉｎ －ｓｉｎ ｓｉｎ狓．… ２ ２ ２ ２ ２ ………………………………………………………………………………………… １３分 （ π） 狓 狓 狓 狓 （ π） 当狓∈ ０， 时， ＋ｓｉｎ ＞０， －ｓｉｎ ＞０，ｓｉｎ狓＞０，所以犵′（狓）＞０，犵（狓）在 ０， ２ ２ ２ ２ ２ ２ 上单调递增，所以犵（狓）＞犵（０）＝０，即ｓｉｎ２狓－狓２ｃｏｓ狓＞０， （ π） 所以当狓∈ ０， 时，犪ｓｉｎ２狓－狓２ｃｏｓ狓＞０．…………………………………………… １５分 ２ 当狓＝０时，犪ｓｉｎ２狓－狓２ｃｏｓ狓＝０． 因为狌（－狓）＝狌（狓），所以狌（狓）是偶函数， （ π ） 所以当狓∈ － ，０ 时，犪ｓｉｎ２狓－狓２ｃｏｓ狓＞０． ２ （ π π） 故当犪≥１时，犪ｓｉｎ２狓－狓２ｃｏｓ狓≥０在 － ， 上恒成立． ２ ２ 综上，犪的取值范围为［１，＋∞）．………………………………………………………… １７分 【高三数学·参考答案 第 ５页（共５页）】 ·２５－７２犆·