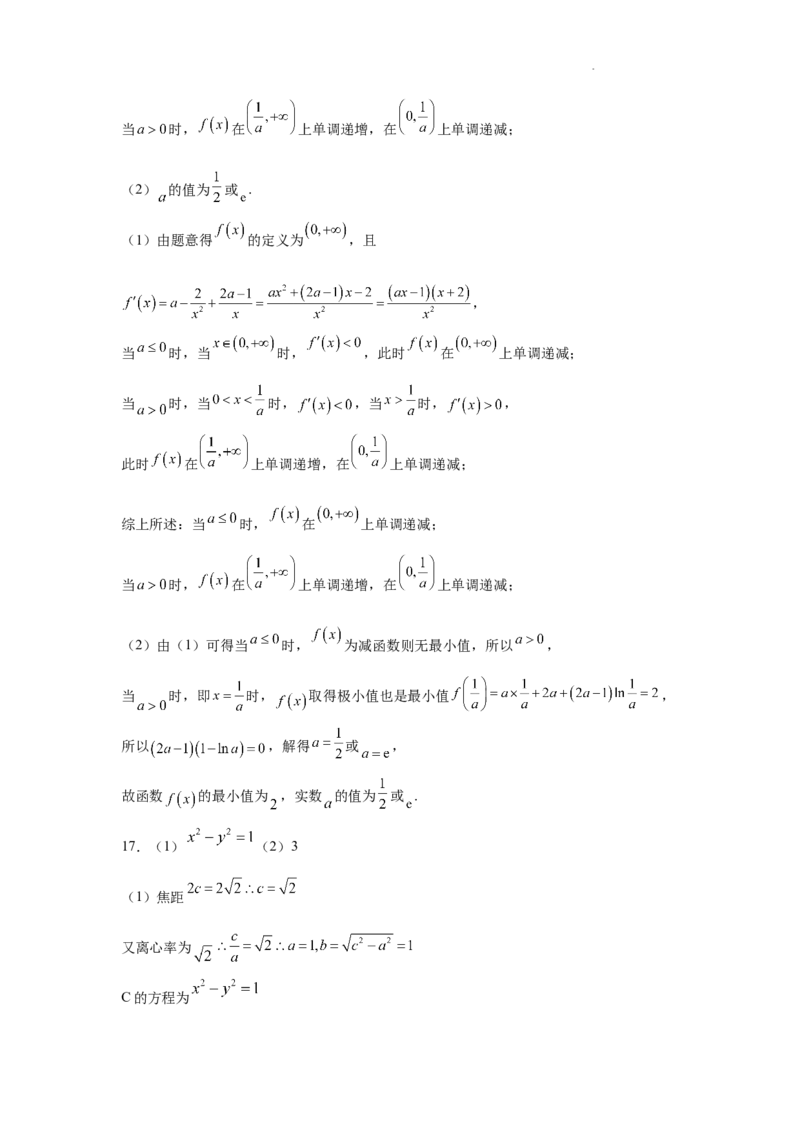哈尔滨师范大学附属中学2025-2026学年度上学期高二期末考试数学答案_2024-2025高二（7-7月题库）_2026年1月高二_260116黑龙江省哈尔滨师范大学附属中学2025-2026学年高二上学期期末（全）

哈尔滨师范大学附属中学2025-2026学年度上学期高二期末考试 数学试题答案 一、选择题 1.C 2.B 3.B 4.B 5.C 6.D 7.A 8.A 二、多选题 9.AB 10.ABC 11.BCD 三、填空题 12. 13. 14. 四、解答题 15．（1）由 ，得 ， 所以 ，又 , 故 是首项为1，公比为2的等比数列； （2）由（1）得 ，则， ． 所以 ， 所以 ． 两式相减，得 ， 所以 ， 解得 ． 16.（1）当 时， 在 上单调递减； 学科网（北京）股份有限公司当 时， 在 上单调递增，在 上单调递减； （2） 的值为 或 . （1）由题意得 的定义为 ，且 ， 当 时，当 时， ，此时 在 上单调递减； 当 时，当 时， ，当 时， ， 此时 在 上单调递增，在 上单调递减； 综上所述：当 时， 在 上单调递减； 当 时， 在 上单调递增，在 上单调递减； （2）由（1）可得当 时， 为减函数则无最小值，所以 ， 当 时，即 时， 取得极小值也是最小值 ， 所以 ，解得 或 ， 故函数 的最小值为 ，实数 的值为 或 . 17．（1） （2）3 （1）焦距 又离心率为 C的方程为 学科网（北京）股份有限公司（2）当曲线C的焦点在 轴上时，C为 设直线MN： ， 与 联立得 由韦达定理 18. （1） ，直线AB： ， 联立得 ， ∴ 的方程为 （2）MN： ， 与 联立得 由韦达定理 学科网（北京）股份有限公司或 ， 当 时， ，过定点D 当 时， ，过定点D 所有定点D的坐标为 或 19.（1） 的极小值为 ，无极大值 当 ，定义域为 当 递减， 当 递增， 的极小值为 ，无极大值 （2）若 ， ∴ （否则 ） 学科网（北京）股份有限公司当 时， 递增， 当 时， 时， 递减， 矛盾 当 时， ，矛盾 综上所述， 的取值范围为 （3）若 有两个极值点 ， 有两个零点 令 ，则 有两个解，不妨令 ， ， 在 递减， 递增 ∴t >1>t >0 2 1 要证x +x >0⇔t +t >2⇔t >2−t >1 1 2 1 2 2 1 由 在 递增，只要证 令 ，则 在 递减， ， 又 在 递增， 学科网（北京）股份有限公司