文档内容
2024 学年第一学期奉贤区高三学科质量调研
数学
(完卷时间120分钟,满分150分)
一、填空题(本大题满分54分)本大题共有12题,考生应在答题纸相应编号
的空格内直接写结果,1~6题每个空格填对得 4分,7~12题每个空格填对得 5
分.
1.设全集 ,集合 ,则 _______.
2.若直线 : 与直线 : 互相垂直,则 _______.
3.已知 ,则不等式 的解集为_______.
4.设 若 ,则 _______.
5.若 , , , , 五人站成一排,如果 , 必须相邻,那么排法共_______种.
6. 的二项展开式中的常数项为_______.(用数字作答)
7.已知抛物线 上有一点 到准线的距离为 ,点 到 轴的距离为 ,则
抛物线的焦点坐标为_______.
8.在复平面内, 为坐标原点,复数 , 对应的点分别为 、
,其中 为虚数单位,则 的大小为 _______.
9. 、 两人下棋,每局两人获胜的可能性一样.某一天两人要进行一场三局两胜的比
赛,
最终胜者赢得100元奖金.第一局比赛 胜,后因为有其他要事中止比赛.为求公平,
则 应该分得______元奖金.
10.申辉中学高一(8)班设计了一个“水滴状”班徽的平面图(如图),徽
章
由等腰三角形 及以弦 和劣弧 所围成的弓形所组成,其中
,劣弧 所在的圆为三角形的外接圆,圆心为 .
已知 , ,外接圆的半径是 ,则该图形的面积为
_______.(用含 的表达式表示)
11.上海市奉贤区奉城镇的古建筑万佛阁(左图1)的屋檐下常系挂风铃(中间图2),风吹铃动,悦耳清脆,亦称惊鸟铃.一般一个惊鸟铃由铜铸造而成,由铃身和铃舌组成.
为了知道一个惊鸟铃的质量,可以通过计算该惊鸟铃的体积,然后由物理学知识计算
出该惊鸟铃的质量.因此我们需要作出一些合理的假设:
假设1:铃身且可近似看作由一个较大的圆锥挖去一个较小的圆锥;
假设2:两圆锥的轴在同一条直线上;
假设3:铃身内部有一个挂铃舌的部位的体积忽略不计.
截 面 图 如 下 ( 右 图 3 ) , 其 中 ,
, ,则制作 100 个这样的惊鸟铃 的
铃身至少需要_______千克铜.(铜的密度为 )
(结果精确到个位)
12.已知集合 , 是由函数 , 的图像
上两两不相同的点构成的点集,集合 ,其中
、 .若集合 中的 元素按照 从 小
到大的顺序排列能构成公差为 的等 差 数 列 , 当
时,计算符合条件的点集 的个数为____________.
二、选择题(本大题满分18分)本大题共有4题,每题有且只有一个正确答案,
考生应在答题纸的相应编号上,将代表答案的小方格涂黑,13-14选对每个得4
分,15-16选对每个得5分,否则一律零分.
13.在 中,“ ”是“ ”的( )
A.充分非必要条件; B.必要非充分条件;
C.充要条件; D.既非充分又非必要条件.
14.函数 ,则下列命题正确的是( )
A.函数是偶函数; B.函数定义域是 ;
C.函数最大值 ; D.函数的最小正周期为 .
15.在四棱锥 中,若 ,则实数组 可能是( )
A. ; B. ; C. ; D. .
16.已知数列 不是常数列,前 项和为 , .若对任意正整数 ,存在正整数 ,使得 ,则称 是“可控数列”.现给出两个命题:
①若各项均为正整数的等差数列 满足: ,则 是“可控数列”;
②若等比数列 是“可控数列”,则其公比为 .
则下列判断正确的是( )
A.①与②均为真命题; B.①与②均为假命题;
C.①为假命题,②为真命题; D.①为真命题,②为假命题.
三、解答题(第17~19题每题14分,第20~21题每题18分,满分78分)
17.已知函数 ,其中 .
(1)若函数 的图像过点 ,求关于 的不等式 的解集;
(2)存在 ,使得数列 、 、 是等比数列,求实数 的取
值
范围.
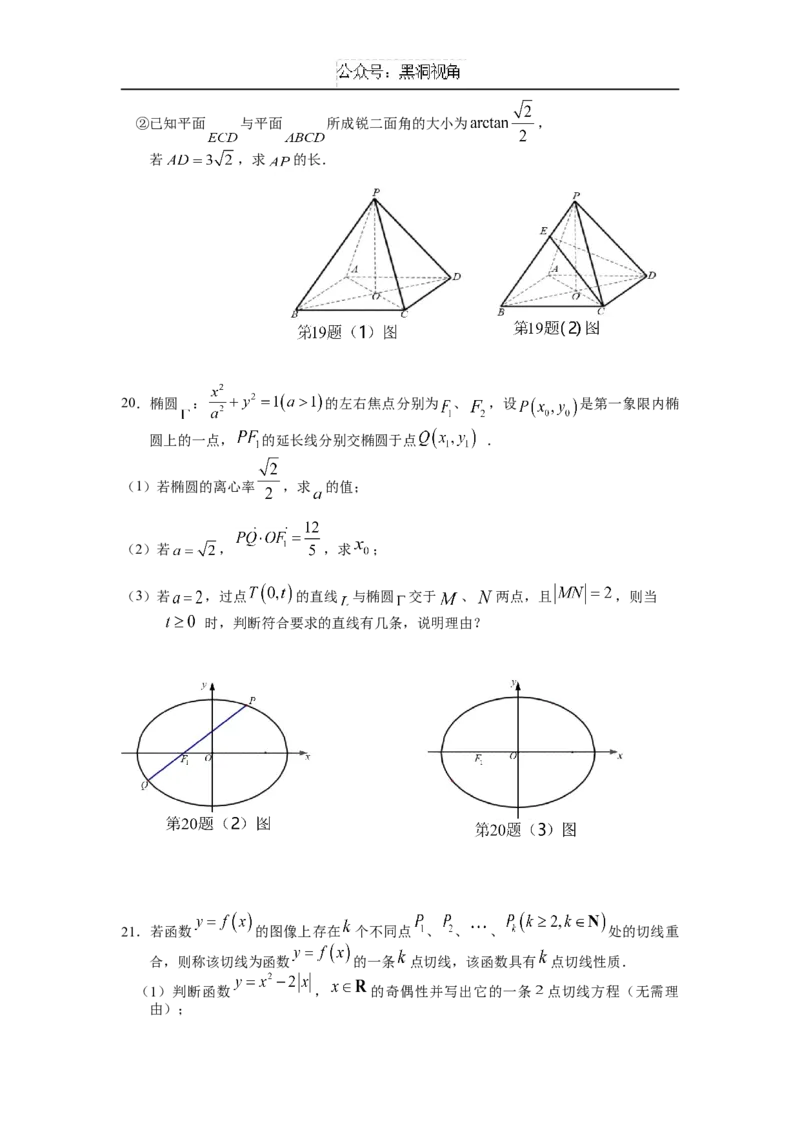
18.某芯片代工厂生产甲、乙两种型号的芯片,为了解芯片的某项指标,从这两种芯片中
各抽取100件进行检测,获得该项指标的频率分布直方图,如图所示:
假设数据在组内均匀分布,以样本估计总体,以事件发生的频率作为相应事件发生的
概率.
(1)求频率分布直方图中 的值并估计乙型芯片该项指标的平均值(同一组中的数据用该
组区间的中点值为代表);
(2)已知甲型芯片指标在 为航天级芯片,乙型芯片指标在标在 为航天
为航天级芯片.现分别采用分层抽样的方式,从甲型芯片指标在 内取2件,
乙型芯片指标在 内取4件,再从这6件中任取2件,求至少有一件为航天级
芯片的概率.
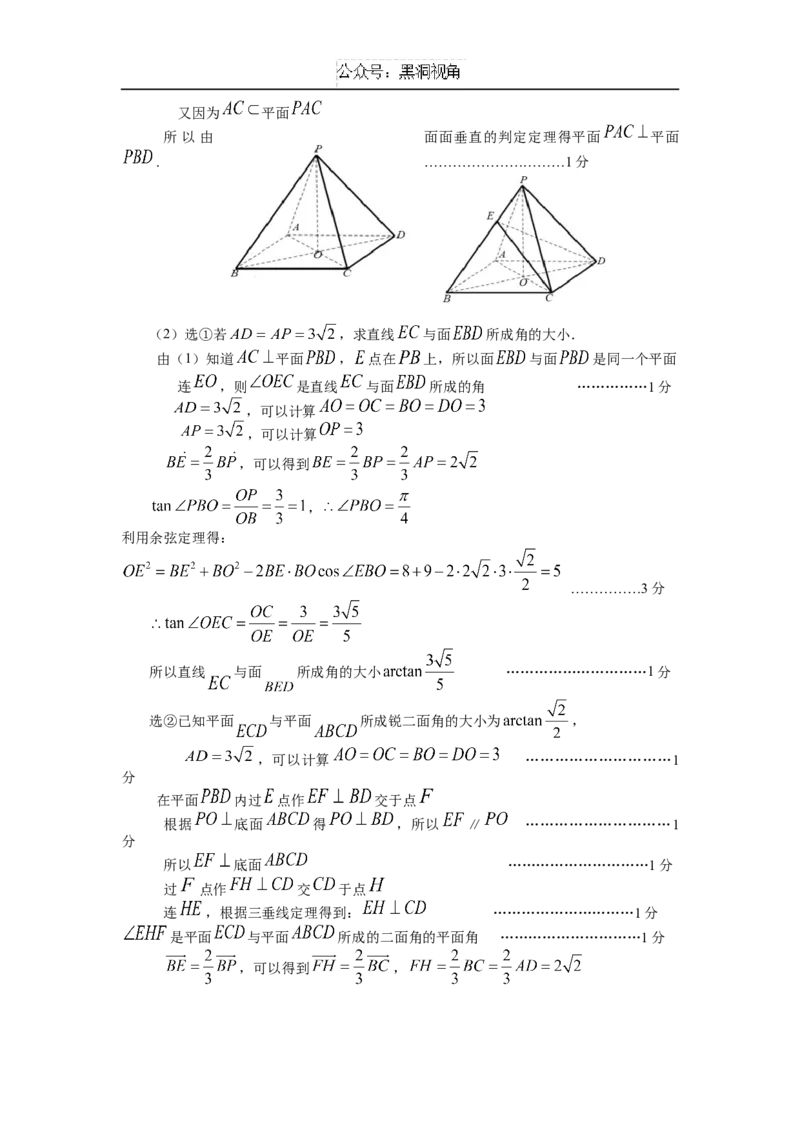
19.如图为正四棱锥 , 为底面 的中心.
(1)求证: ∥面 ,平面 ⊥平面 ;
(2)设 为 上的一点, .
在下面两问中选一个,若都选,只按第①问阅卷,第①问满分5分,第②问满分7分
①若 ,求直线 平面 所成角的大小.②已知平面 与平面 所成锐二面角的大小为 ,
若 ,求 的长.
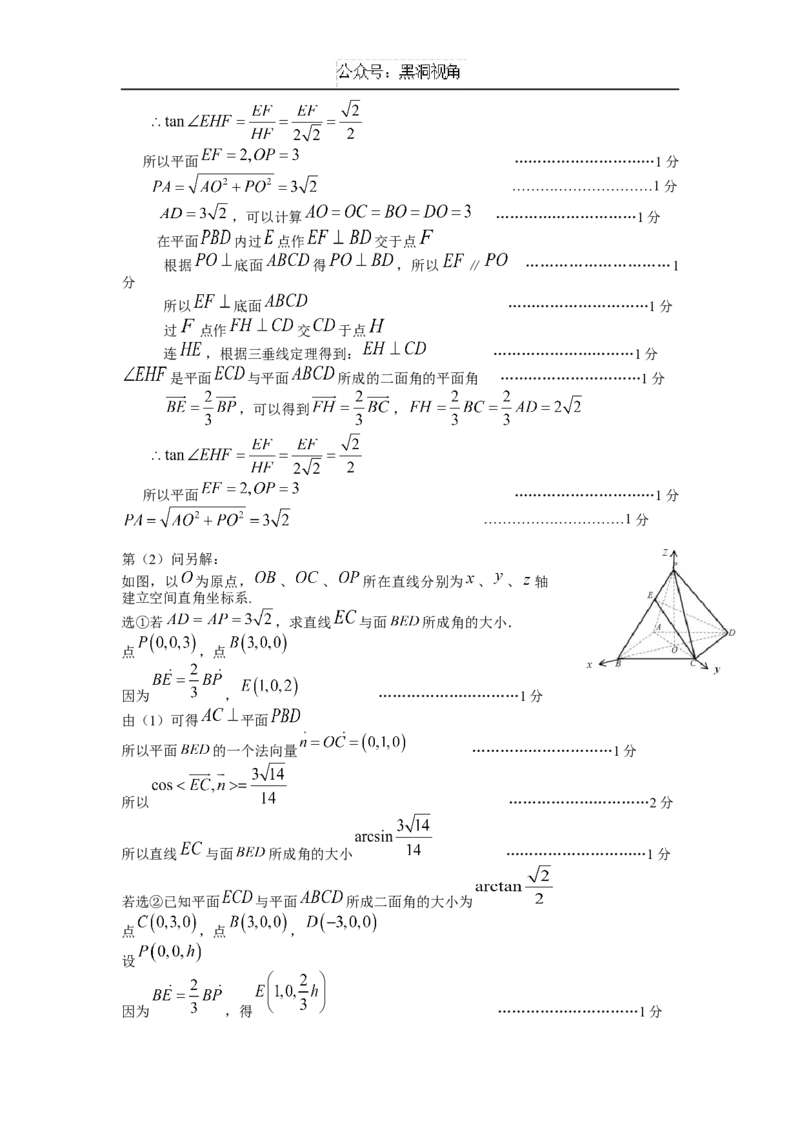
20.椭圆 : 的左右焦点分别为 、 ,设 是第一象限内椭
圆上的一点, 的延长线分别交椭圆于点 .
(1)若椭圆的离心率 ,求 的值;
(2)若 , ,求 ;
(3)若 ,过点 的直线 与椭圆 交于 、 两点,且 ,则当
时,判断符合要求的直线有几条,说明理由?
21.若函数 的图像上存在 个不同点 、 、 、 处的切线重
合,则称该切线为函数 的一条 点切线,该函数具有 点切线性质.
(1)判断函数 , 的奇偶性并写出它的一条 点切线方程(无需理
由);(2)设 ,判断函数 是否具有 点切线性质,并说明理由;
(3)设 ,证明:对任意的 ,函数 具有 点切
线性质,并求出所有相应的切线方程.参考答案
一、填空题
1. 2.
3. 4.
5. 6.
7. 8. (或 )
9. 10.
11.120(119也可以) 12.
二、选择题
13.A 14.C 15.A 16.D
三、解答题(第17~19题每题14分,第20~21题每题18分,满分78分)
17.解:(1)将点 代入函数解析式,得: ,
因为 ,所以 . …………………………2分
因为 在 上是严格增函数,
所以 , …………………………3
分
解得 或 ,
所以原不等式的解集为 . …………………………2分
(2)由题意,数列 、 、 是等比数列,
…………………………2
得: ,
分
即: ,化简得 …………………………1分
,所以 …………………………1分因为 在 上是严格减函数, …………………………1
分
所以 ,所以 的取值范围是 . …………………………2分
若 ,化简得 的解法最多扣一分 …………………1
分
18. 解:(1)由题意 ,
解得: . …………………………3
分
乙型芯片该项指标的平均值为
………3分
(2)由题意:甲型芯片根据分层抽样 取1件, 取1件; ……………2
分
乙型芯片根据分层抽样 取3件, 取1件. ……………2
分
从6件中任取2件的情况有 ……………2分
则至少有一件为航天级芯片的概率为 . ……………2分
19.解:(1)证明: ∥ , 平面 , 不在平面 内,…………2
分
由线面平行判定定理得
∥面 …………………………1分
由题意:四棱锥 为正四棱锥, 为底面 的中心
所以 底面 ,
所以 , …………………………1分
,
又因为 (这一步必需有) …………………………1
分
由线面垂直的判定定理得 平面 …………………………1分又因为 平面
所以由 面面垂直的判定定理得平面 平面
. …………………………1分
(2)选①若 ,求直线 与面 所成角的大小.
由(1)知道 平面 , 点在 上,所以面 与面 是同一个平面
连 ,则 是直线 与面 所成的角 ……………1分
,可以计算
,可以计算
,可以得到
,
利用余弦定理得:
……………3分
所以直线 与面 所成角的大小 …………………………1分
选②已知平面 与平面 所成锐二面角的大小为 ,
,可以计算 …………………………1
分
在平面 内过 点作 交于点
根据 底面 得 ,所以 ∥ …………………………1
分
所以 底面 …………………………1分
过 点作 交 于点
连 ,根据三垂线定理得到: …………………………1分
是平面 与平面 所成的二面角的平面角 …………………………1分
,可以得到 ,所以平面 …………………………1分
…………………………1分
,可以计算 …………………………1分
在平面 内过 点作 交于点
根据 底面 得 ,所以 ∥ …………………………1
分
所以 底面 …………………………1分
过 点作 交 于点
连 ,根据三垂线定理得到: …………………………1分
是平面 与平面 所成的二面角的平面角 …………………………1分
,可以得到 ,
所以平面 …………………………1分
…………………………1分
第(2)问另解:
如图,以 为原点, 、 、 所在直线分别为 、 、 轴
建立空间直角坐标系.
选①若 ,求直线 与面 所成角的大小.
点 ,点
因为 , …………………………1分
由(1)可得 平面
所以平面 的一个法向量 …………………………1分
所以 …………………………2分
所以直线 与面 所成角的大小 …………………………1分
若选②已知平面 与平面 所成二面角的大小为
点 ,点 ,
设
因为 ,得 …………………………1分易得 ,
设平面 的一个法向量为 得: ,
求得: …………………………2分
又平面 的一个法向量为
所以 , …………………………2
分
又因为平面 与平面 所成二面角的大小为
所以 ,解得 …………………………1分
…………………………1分
20.解:(1)椭圆的离心率 …………………………2
分
所以 …………………………2分
(2)显然直线 的斜率是存在的,
…………………………1分
…………………………1分
直线 ,过点 的直线方程为 , ……………………1分
它与椭圆 联立得到
, ……………………1分
…………………………1分
…………………………1分(3) 时,椭圆方程为
斜率不存在时,过任意点 的唯一的直线 : 与椭圆交于 、 两点坐
标 ,此时 恒成立 …………………………………2分
斜率存在时,设过任意点 的直线 的方程为
联立它与椭圆 联立得到
……………………………1分
…………………………………1分
时,方程 方程无解…………………………………1分
时,
当 时,存在直线斜率为 的直线 ,使得使得 ………………1分
当 时,即
存在 的两条直线,使得 ………………………………………1分
所以: 存在3条直线,使得
存在2条直线,使得 ………………………1分
或 存在1条直线,使得
21.解:(1)函数 , 是偶函数 …………………………2分
其一条 点切线方程为: …………………………2分
(2)因为 ,所以 . …………………………2分
记 ,则
由 ,知函数 在 上为严格增函数. ……………………2分因此,对于函数 的图像上任意两点, , ,
,所以其切线斜率不相等,切线不可能重合,
因此函数 不具有 点切线性质. …………………………2分
(3) , ,…………………………1分
故函数在 处的切线方程为: ,
即 ……………1分
一方面取 个点 、 、 、…、 ,在
该 个点处的切线方程均为:
所以该函数具有 点切线性质.…………………………2分
另一方面,若在点 ( )处的切线重合.
则有 .
由 可以知道角 与 终边相同或关于 轴对称、角 与 终边相
同或关于 轴对称、角 与 终边相同或关于 轴对称,
因 中至少2个角终边相同,不妨设角 与 终边相同,则 (
) . 此 时 , 且
,
则 ,故 ,则 或 ……………2分
此时切线方程为 或 .…………………………2分