云南省昆明市第三中学2024-2025学年高三上学期11月月考数学_2024-2025高三（6-6月题库）_2024年12月试卷_1206云南省昆明市第三中学2024-2025学年高三上学期11月月考

昆明三中高 2025 届高三年级上学期第三次综合测试 数学试卷 注意事项： 1．答题前，考生务必用黑色碳素笔将自己的姓名、考号、考场号、座位号填写在答题卡上，并用铅笔 认真填涂考号。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡 皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 3．考试结束后，将答题卡交回。 一、单选题：本大题共8小题，每小题5分，共40分。 1．集合A  a,a21,1  ，B2a，若B A，则实数a 1 A．1 B．0 C． D．1 2 1 2．已知复数z在复平面内的对应点为(1,1)，则z 的虚部为 z 1 3 1 3 A． i B． C． D． i 2 2 2 2 2 3．已知x1，则2x 的最大值是 x1 A．2 B．4 C．6 D．7 4．投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏，在春秋战国时期较为盛行.如图为一幅唐朝的投 壶图，甲、乙、丙是唐朝的三位投壶游戏参与者，假设甲、乙、丙每次投壶时，投中的概率均为0.6且投壶 结果互不影响.若甲、乙、丙各投壶1次，则这3人中至少有2人投中的概率为 A．0.648 B．0.432 C．0.36 D．0.312 试卷第1页，共5页 {#{QQABKYQUogAIAABAAAgCAQ1yCkMQkgAACYgGxEAAoAABCQFABAA=}#}      5．如图，在四边形ABCD中， AC 4, AD 2,CAD60，E为线段AC中点， DE 2EB ，则DBDC 3 3 A． B．15 C．18 D．9 2 6．已知直线l :xay10与圆C:xa2y12 1相交于A，B两点，当VABC面积最大时，实数a的 1 值为 1 1 A．1或1 B． 3 或 3 C． 或1 D． 或 3 7 7 1 5  1 7．已知asin ,bln ,c2 2，则 2 3 A．cba B．abc C．acb D．bac 8．如果数列a 对任意的nN*,a a a a ，则称a 为“速增数列”，若数列a 为“速增数列”， n n2 n1 n1 n n n 且任意项a Z,a 1,a 3,a 2023，则正整数k的最大值为 n 1 2 k A．62 B．63 C．64 D．65 二、多项选择题：本大题共3小题，每小题6分，共18分。全部选对的得6分，选对但不全的得部分分， 有选错或不选的得0分。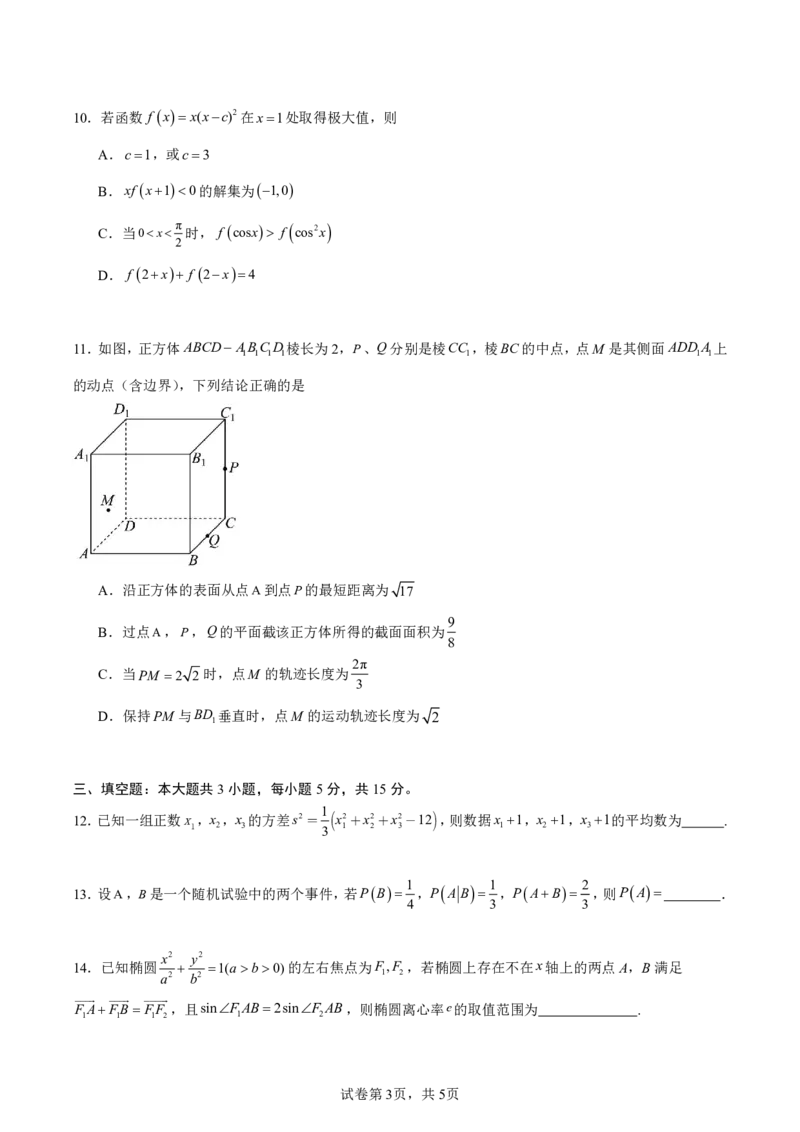 1 9．已知函数 f x tanx(0,0π)的部分图象如图所示，则 2 A．2 π B． 3  3 C． f x的图象与y轴的交点坐标为0,     3  7π D．函数y f x 的图象关于直线x 对称 12 试卷第2页，共5页 {#{QQABKYQUogAIAABAAAgCAQ1yCkMQkgAACYgGxEAAoAABCQFABAA=}#}10．若函数 f xx(xc)2在x1处取得极大值，则 A．c1，或c3 B．xf x10的解集为1,0 C．当0x π 时， f cosx f  cos2x  2 D． f 2x f 2x4 11．如图，正方体ABCD ABCD棱长为2，P、Q分别是棱CC ，棱BC的中点，点M 是其侧面ADDA上 1 1 1 1 1 1 1 的动点（含边界），下列结论正确的是 A．沿正方体的表面从点A到点P的最短距离为 17 9 B．过点A，P，Q的平面截该正方体所得的截面面积为 8 2π C．当PM 2 2 时，点M 的轨迹长度为 3 D．保持PM 与BD 垂直时，点M 的运动轨迹长度为 2 1 三、填空题：本大题共3小题，每小题5分，共15分。 1 12．已知一组正数x，x ，x 的方差s2 = (x2+x2+x2-12)，则数据x 1，x 1，x 1的平均数为 . 1 2 3 3 1 2 3 1 2 3 13．设A，B是一个随机试验中的两个事件，若PB 1 ，P  A B  1 ，PAB 2 ，则PA ． 4 3 3 x2 y2 14．已知椭圆  1(ab0)的左右焦点为F,F ，若椭圆上存在不在x轴上的两点A，B满足 a2 b2 1 2    FAFB FF ，且sinFAB2sinF AB，则椭圆离心率e的取值范围为 . 1 1 1 2 1 2 试卷第3页，共5页 {#{QQABKYQUogAIAABAAAgCAQ1yCkMQkgAACYgGxEAAoAABCQFABAA=}#}四、解答题：共77分。 15．（本小题13分）已知a、b、c分别为VABC的内角A、B、C的对边，S为VABC的面积，且满足 4 3S b2(ac)2. (1)求B；  1 2  7 (2)若BD BA BC ，且|BD| ,ca2，求ABD的余弦值. 3 3 3 16．（本小题15分）如图，AB是半球O的直径，AB4，M,N是底面半圆弧AB 上的两个三等分点，P是 半球面上一点，且PON 60. (1)求四边形OMNB的面积； (2)证明：PB平面PAM ； (3)若点P在底面圆内的射影恰在ON上，求直线PM 与平面PAB所成角的正弦值. 17．（本小题15分）已知函数 f xxeax（a0）. (1)求 f x在区间1,1 上的最大值与最小值； (2)当a1时，求证： f xlnxx1. 试卷第4页，共5页 {#{QQABKYQUogAIAABAAAgCAQ1yCkMQkgAACYgGxEAAoAABCQFABAA=}#}x2 y2 2 18．（本小题17分）已知椭圆C：  1（ab0）的左、右焦点分别为F ，F ，离心率e ， a2 b2 1 2 2   点P 2, 2 在椭圆C上，直线l过F 交椭圆于A，B两点. 1 （1）求椭圆C的标准方程； （2）当F AB90时，点A在x轴上方时，求点A，B的坐标； 2 （3）若直线AF 交y轴于点M，直线BF 交y轴于点N，是否存在直线l，使得ABF 与MNF 的面积满足 2 2 2 1 S 2S ，若存在，求出直线l的方程；若不存在，请说明理由. ABF2 MNF1 19．（本小题17分）某游泳馆为给顾客更好的体验，推出了A和B两个套餐服务，顾客可选择A和B两个 套餐之一，并在App平台上推出了优惠券活动，下表是该游泳馆在App平台10天销售优惠券情况． 日期t 1 2 3 4 5 6 7 8 9 10 销售量 千张 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 0.4 1 10 10 10 经计算可得：y y 2.2,t y 118.73,t2 385. 10 i i i i i1 i1 i1 (1)因为优惠券购买火爆，App平台在第10天时系统出现异常，导致当天顾客购买优惠券数量大幅减少，已 知销售量y和日期t呈线性关系，现剔除第10天数据，求y关于t的经验回归方程 结果中的数值用分数表 示 ； 1 3 (2)若购买优惠券的顾客选择A套餐的概率为 ，选择B套餐的概率为 ，并且A套餐可以用一张优惠券， 4 4 B套餐可以用两张优惠券，记App平台累计销售优惠券为n张的概率为P，求P； n n (3)记（2）中所得概率P的值构成数列P nN . n n ①求P的最值； n ②数列收敛的定义：已知数列a ，若对于任意给定的正数，总存在正整数N ，使得当n N 时，a a ， n 0 0 n （a是一个确定的实数），则称数列a 收敛于a.根据数列收敛的定义证明数列P收敛． n n  n  x x  y y   n x y nxy i i i i 参考公式： b ˆ i1  i1 ,aˆ yb ˆ x .  n  x x 2  n x 2nx 2 i i i1 i1 试卷第5页，共5页 {#{QQABKYQUogAIAABAAAgCAQ1yCkMQkgAACYgGxEAAoAABCQFABAA=}#}