文档内容
冲刺2024年高考数学真题重组卷
真题重组卷02
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.(2023全国甲卷数学(理))若复数 ,则 ( )
A.-1 B.0 · C.1 D.2
2.(2023新课标全国Ⅱ卷)设集合 , ,若 ,则 ( ).
A.2 B.1 C. D.
3.(2023新课标全国Ⅰ卷)已知向量 ,若 ,则( )
A. B.
C. D.
4.(2023新课标全国Ⅱ卷)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽
样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,
则不同的抽样结果共有( ).
A. 种 B. 种
C. 种 D. 种
5.(2023•新高考Ⅱ)若 为偶函数,则
A. B.0 C. D.1
6.(2023新课标全国Ⅰ卷)已知 ,则 ( ).
A. B. C. D.7.(2021•新高考Ⅰ)若过点 可以作曲线 的两条切线,则
A. B. C. D.
8.(2023全国乙卷数学(文)(理))设A,B为双曲线 上两点,下列四个点中,可为线段AB中点
的是( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分。
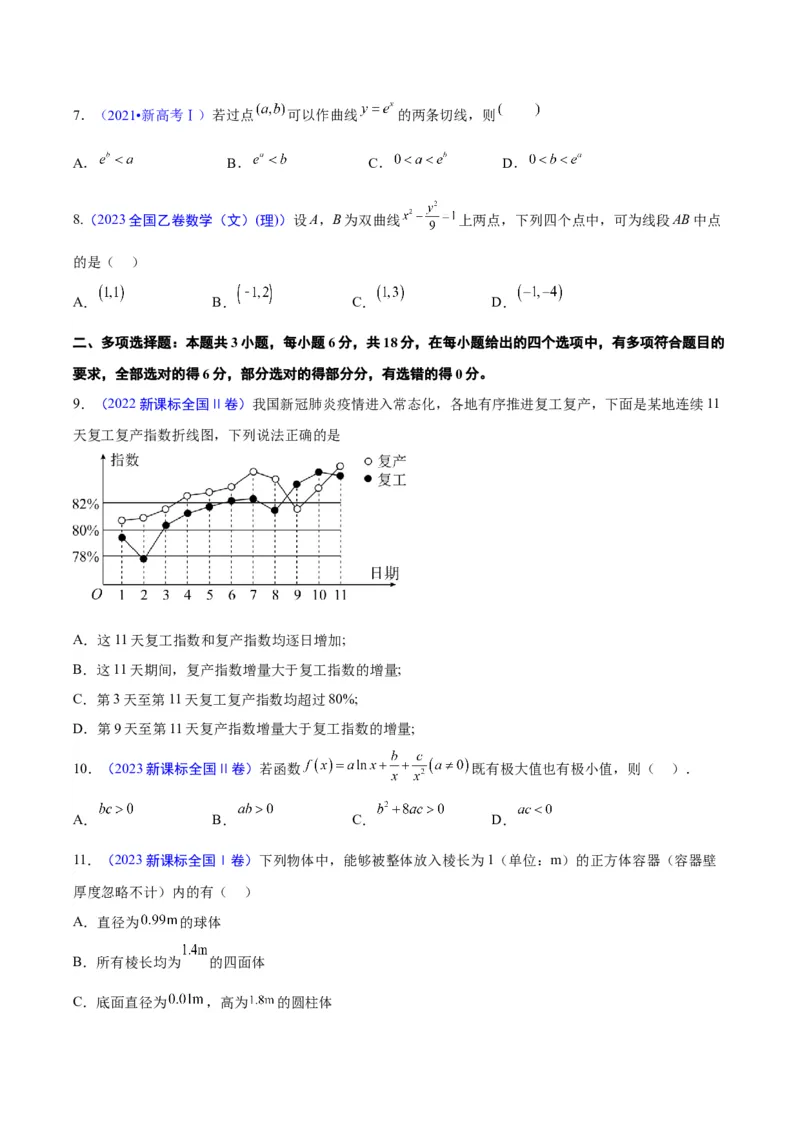
9.(2022新课标全国Ⅱ卷)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11
天复工复产指数折线图,下列说法正确的是
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
10.(2023新课标全国Ⅱ卷)若函数 既有极大值也有极小值,则( ).
A. B. C. D.
11.(2023新课标全国Ⅰ卷)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁
厚度忽略不计)内的有( )
A.直径为 的球体
B.所有棱长均为 的四面体
C.底面直径为 ,高为 的圆柱体D.底面直径为 ,高为 的圆柱体
第 II 卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.(2023·北京卷)已知函数 ,则 ____________.
13.(2023全国乙卷数学(文))已知 为等比数列, , ,则 ______.
14.(2023新课标全国Ⅰ卷)在正四棱台 中, ,则该棱台的体积
为________.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
15.(本小题满分13分)(新题型)在平面直角坐标系 中,点 分别在 轴, 轴上运动,且
,动点 满足 .
(1)求动点 的轨迹 的方程;
(2)设直线 与曲线 交于 , 两点,且 ,求实数 的值.
16.(本小题满分15分)(2023新课标全国Ⅱ卷)如图,三棱锥 中, , ,
,E为BC的中点.
(1)证明: ;
(2)点F满足 ,求二面角 的正弦值.17.(本小题满分15分)(2021•新高考Ⅰ)某学校组织“一带一路”知识竞赛,有 , 两类问题.每
位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;
若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束. 类问题
中的每个问题回答正确得20分,否则得0分; 类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答 类问题的概率为0.8,能正确回答 类问题的概率为0.6,且能正确回答问题的概率
与回答次序无关.
(1)若小明先回答 类问题,记 为小明的累计得分,求 的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
18.(本小题满分17分)(2023•甲卷(理))已知 , .
(1)若 ,讨论 的单调性;
(2)若 恒成立,求 的取值范围.
19.(本小题满分17分)(新题型)若存在 使得 对任意 恒成立,则称 为函数
在 上的最大值点,记函数 在 上的所有最大值点所构成的集合为
(1)若 ,求集合 ;
(2)若 ,求集合 ;
(3)设 为大于1的常数,若 ,证明,若集合 中有且仅有两个元素,则所有满
足条件的 从小到大排列构成一个等差数列.