石家庄三模数学答案_2024年5月_01按日期_13号_2024届河北省石家庄市高三教学质量检测（三）_2024届河北省石家庄市普通高中学校毕业年级教学质量检测（三）数学

2023-2024 年度石家庄市高中毕业年级质量检测（三） 数学答案 一、选择题： 1-4 BCAB 5-10 DDCC 二、选择题： 9.ABD 10.ACD 11.BD 三、填空题：本题共3小题，每小题5分，共15分  1 12. 0.015 13. 0,  2, 14. 2 40  4 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 c b a 15.解：（1）   6,.......................................................................2分 sinC sinB sinA a b sinA ,sinB , ............................................................................4分 6 6 a b 9 1 sinAsinB    ..................................................................6分 6 6 36 4 (2)ab9, a2b2 2ab18, a2 b2 c2 2ab16 1 cosC    ,.......................................................8分 2ab 18 9 1  cosC 1, 9 80 01cosC2  ,.................................................................................10分 81 . 4 5 0sinC ,...........................................................................................12分 9 1 9 S  absinC  sinC 2 5, 2 2 当且仅当ab3时，等号成立.....................................................................13分 16.解：(1) 经验回归方程②的残差数据如下表： x 5 7 9 11 y 200 298 431 609 eˆ 20 －18 －21 21 .....................................4分（说明：以上每空1分） 经验回归方程②的残差图如图所示： 1经验回归方程①更适宜作为y关于x 的回归方程．.......................5分 （以下理由或其他合理的理由，说出一条即可得分）： 理由1：经验回归方程①这4个样本点的残差的绝对值都比经验回归方程②的小． 理由2：经验回归方程①这4个样本的残差点落在的带状区域比经验回归方程②的带状区域更窄． 理由3：经验回归方程①这4个样本的残差点比经验回归方程②的残差点更贴近x 轴．.........6分 60 （2）（i）由题意知，每件产品为优等品的概率P  0.6 …………………8分 0 100 则X B(12,0.6),因此E(X)120.67.2……………………………………10分 由Y 20X 15(12X)1805X 则E(Y)5E(X)180216………………………………………………………12分 123 （ii）由（i）知总利润为216万元，总成本估计值yˆ  173749（万元）……13分 1 3 216 则 p  0.29……………………………………………………………15分 749 a x2 (a1)xa 17．解：（1） f(x) x(a1)  x x (x1)(xa) f(x) ……………………………………………………………………2分 x 当0a1时， 当x(0,a)，x(1,)时， f(x)0， f (x)单调递增； 当x(a,1)时， f(x)0， f (x)单调递减．………………………………………4分 当a1时， 当x(0,1)，x(a,)时， f(x)0， f (x)单调递增； 当x(1,a)时， f(x)0， f (x)单调递减；………………………………………6分 当a1时， f(x)0， f (x)在(0,)单调递增．……………………………………………7分 2 （2）a2时，g(x)ex13x2lnx，g(x)ex13 ， x 2 2 设h(x)ex13 ，h(x)ex1 ，h(x)在区间(0,)单调递增．………9分 x x2 1 因为h(1)10，h(2)e 0， 2 2所以存在唯一x (1,2)使得h(x )0， 0 0 当x(0,x )时，h(x)0，h(x)单调递减，即g(x)单调递减； 0 当x(x ,)时，h(x)0，h(x)单调递增，即g(x)单调递增．……………11分 0 g(1)0，且g(x)在(1,x )单调递减，所以g(x )0，又g(2)e10 0 0 因此g(x)在区间(x ,2)存在唯一零点t………………………………………13分 0 当x(0,1)，x(t,)时，g(x)0，g(x)单调递增； 当x(1,t)时，g(x)0，g(x)单调递减；所以g(x)极值点为1,t ， 因此g(x)极值点个数为2……………………………………………15分 18．（1）证明： 因为平面SAE 平面AED，DEEA， DE 平面AED， 平面SAE 平面AED AE 所以DE平面SAE，…………………………………………………………………2分 又SE 平面SAE，所以DESE，………………………………………………………4分 又因为SE  AD，ED ADD，且AD,DE 平面AED 所以SE 平面AED．…………………………………………………………………6分 （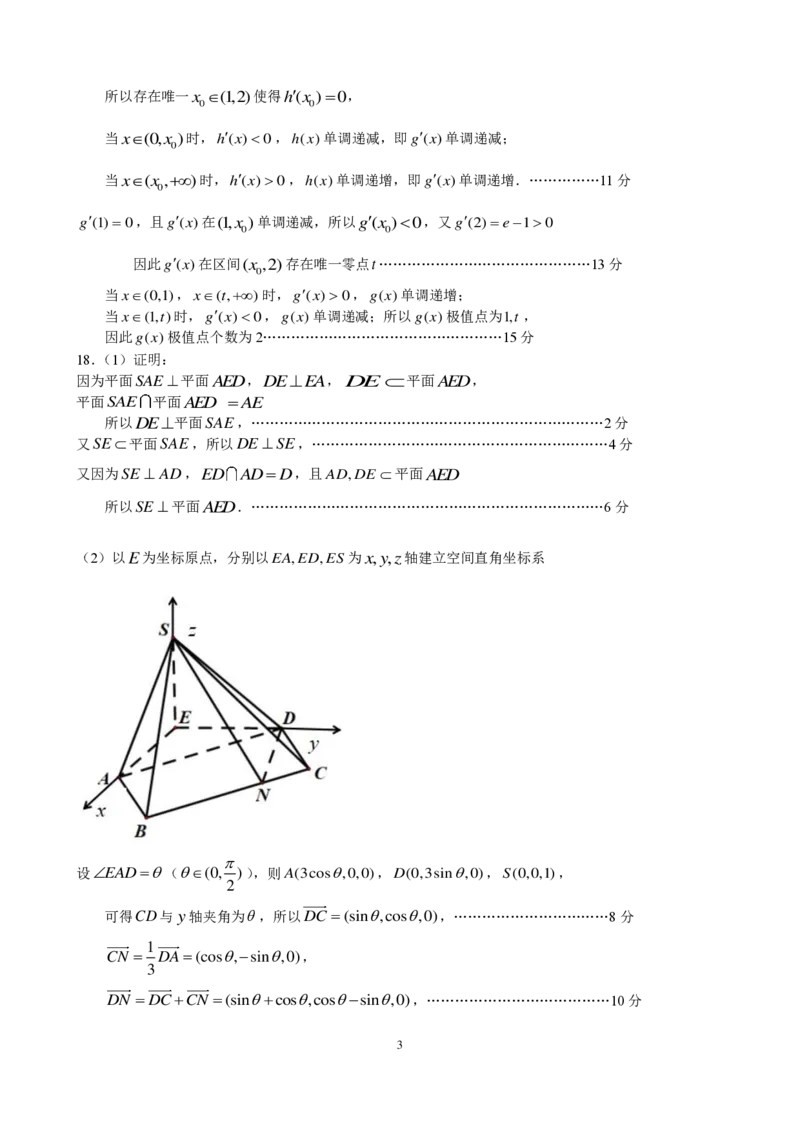2）以E为坐标原点，分别以EA,ED,ES 为x,y,z轴建立空间直角坐标系  设EAD（(0, )），则A(3cos,0,0)，D(0,3sin,0)，S(0,0,1)， 2 可得CD与y轴夹角为，所以DC (sin,cos,0)，……………………………8分 1 CN  DA(cos,sin,0)， 3 DN DCCN (sincos,cossin,0)，…………………………………10分 3SA(3cos,0,1),SD(0,3sin,1)，平面SAD的法向量记为n(x,y,z)  nSA0 3xcosz 0 由 得 nSD0 3ysinz 0 令z 3sincos，得n(sin,cos,3sincos)………………………………12分 sin2sincoscos2sincos cos DN,n 2 19sin2cos2 1 26 即cos DN,n  ，………………………………………………14分 9 13 2 1 sin22 4  当 时，等号成立， 4 此时，直线DN 与平面SAD的所成的角取得最小值，……………………………………15分 1 1 9 3 此时V  S SE   1 ……………………………………………………17分 DSAE 3 ADE 3 4 4 1 1 1 19．解：（1）当l垂直x 轴时，由直线OA与直线OB的斜率之积为 ，故OA:y x,OB:y x， 4 2 2 3 设 A  2t,t  ,B  2t,t  t 0  ， 则 FAF B4t2 3t2 3t2 3 ， 解 得 1 2 2 2 t  ，………………………………………………………………2分 2  2 1  2   1 即 A 2,  ， 则 a2 2b2 ， 解 得 a2 4,b2 1 ， 故 C 的 方 程 为   2    a2 b2 3 x2  y2 1；………………………………………………………………4分 4 2x x ① （2）①设l:xmyn,A  x,y  ,B  x ,y  ,P  2,0  ，由OPOAOB知 1 2 ，将 1 1 2 2 0y y ② 1 2 ①24②2得  x x 2 4  y y 2 4，………………………………………………6分 1 2 1 2 即 2  x24y2  2  x24y2  2  xx 4y y  4 . 由 A,B 为 C 上 点 ， 则 1 1 2 2 1 2 1 2 1 y y 1 x24y2 4,x24y2 4.又直线OA与直线OB的斜率之积为 ，故 1 2  ，即x x 4y y 0. 1 1 2 2 4 x x 4 1 2 1 2 1 2 因此22 1；………………………………………………………………………………8分 4x2 4y2 4     ②由①联立  ，消去 x 得 m24 y22mnyn240， 16m24n2 0 ， xmyn 2mn n2 4 y  y  ,y y  ，…………………………………………………9分 1 2 m2 4 1 2 m2 4    由xx 4y y  my n my n 4y y 0， 1 2 1 2 1 2 1 2 即  my n  my n  4y y   m24  y y mn  y y  n2 0 ， 即 2n2 m2 4 . 因 此 有 1 2 1 2 1 2 1 2 m n2 4 4 y  y  ,y y  ，  y  y 2   y  y 2 4y y  .…………………………………11分 1 2 n 1 2 2n2 1 2 1 2 1 2 n2 1 1 AOB 面积S  OAOB sinAOB ，四边形AB AB的面积S  AA BB sinAOB ，即若要 1 2 1 1 2 2 1 1 证S 2S ，只需证 AA BB 2OAOB. 2 1 1 1     设A x ,y ,B x ,y ，故只需证 y y  y y 2y  y 即可.…………………………………13分 1 3 3 1 4 4 3 1 4 2 1 2 x 2 x 2y y 2y y 直线PA:x 1 y2,OB:x 2 y，联立解得 y  1 2  1 2 ，同理得 y y 4 x y 2y x y n  y y  2y 1 2 1 2 2 2 1 2 1 2 2y y 2y y y  1 2  1 2 .…………………………………………………………………15分 3 x y 2y x y n  y y  2y 2 1 1 1 2 1 2 1 故 4  n2 2  n2 2  y y 2 n2 y y  y y  y  y  1 2  y  y  2y  y 3 1 4 2 1 2 n2 y y 2 2n  y y 2 4y y 1 2 4n8 2n2 8 1 2 1 2 1 2 1 2   n n2 ，故问题得证.……………………………………………………………………………………………17分 5