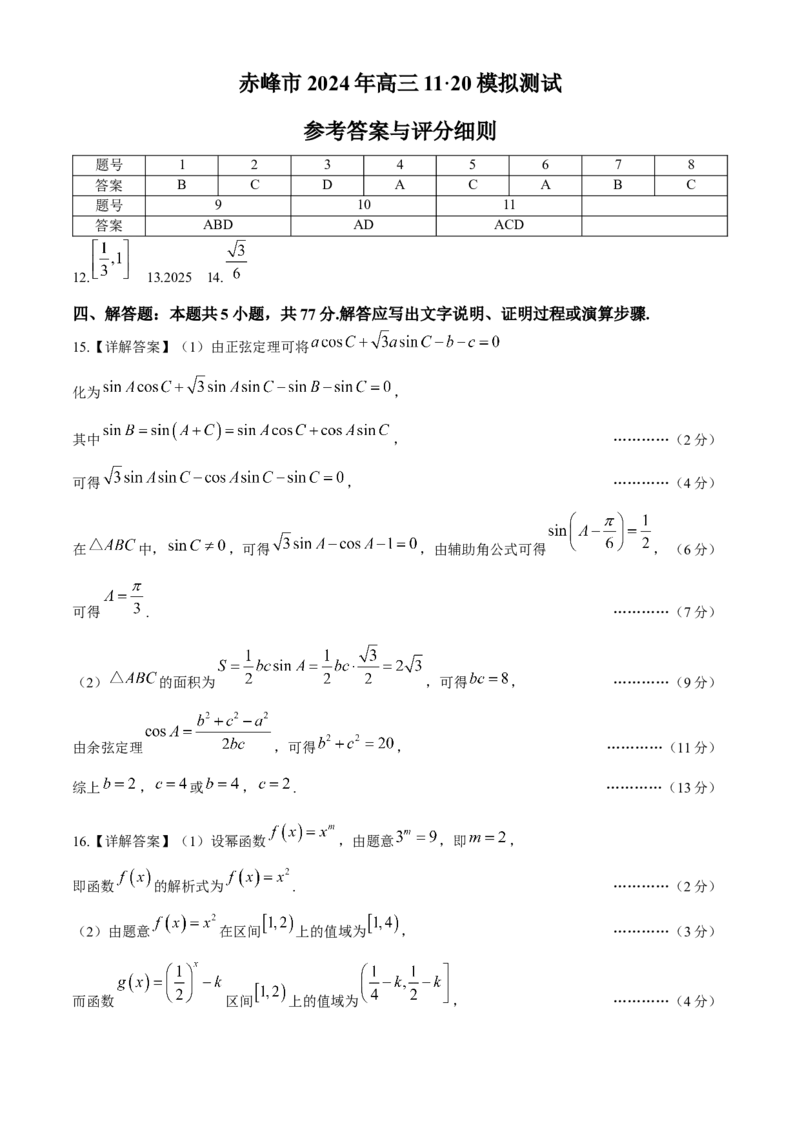文档内容
赤峰市高三年级 11·20 模拟考试试题
数学
2024.11
本试卷共6页。考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名和准考证号填写清楚,将条形码准确粘贴在考生
信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工
整、笔迹清楚。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草
稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只
有一项符合题目要求,选对得5分,选错得0分.
1.已知 , 是两个实数, , ,则 是 的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.结合不等式的性质,下列说法中正确的是
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
3.已知 , , ,则 的最小值为
A. B. C. D.
4.已知 , ,则 的值为
A.-2 B.2 C.-3 D.3
5.已知集合 ,集合 ,集合 ,则以
下元素属于集合 的是
A. B. C. D.
学科网(北京)股份有限公司6.已知 , , ,则 , , 的大小关系是
A. B. C. D.
7.已知函数 在区间 上存在极值点,则 的取值范围是
A. B. C. D.
8.在锐角三角形 中,角 , , 所对的边分别为 , , ,已知 ,点 为 的
中点,则中线 的取值范围是
A. B. C. D.
二、多项选择题:本题共3小题,每小题满分6分,共18分.在每小题给出的选项中,有多项
符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
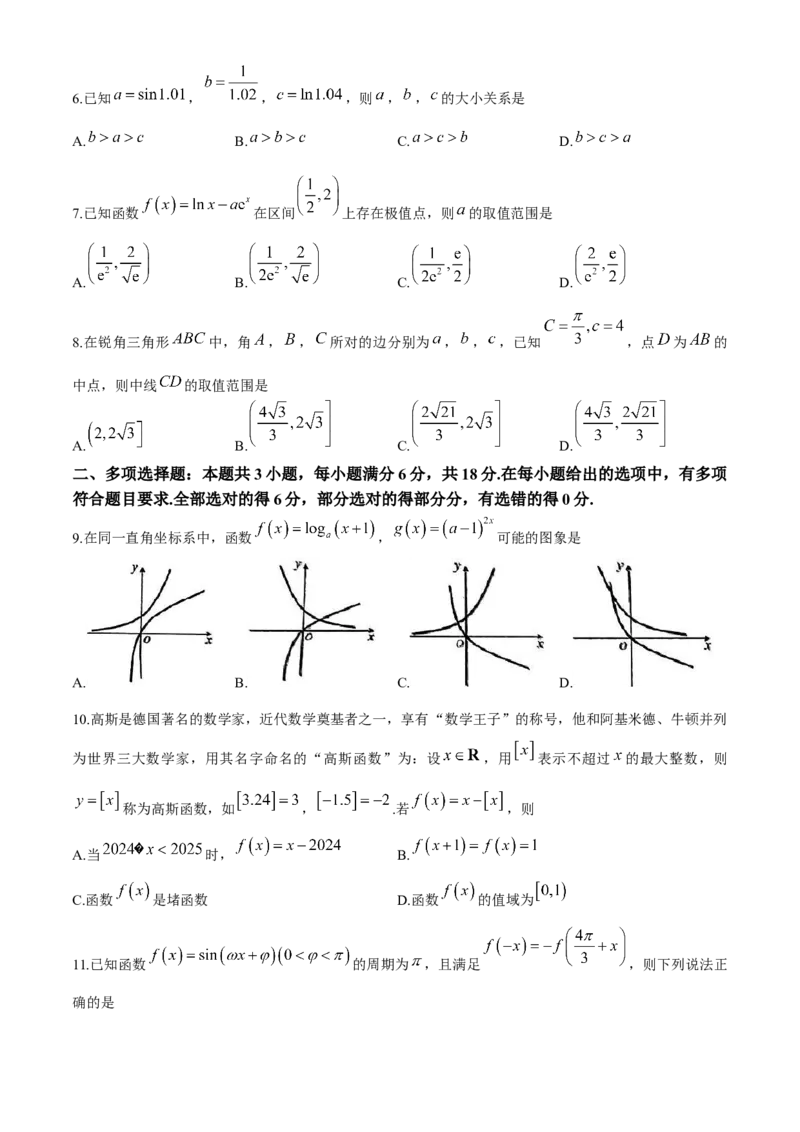
9.在同一直角坐标系中,函数 , 可能的图象是
A. B. C. D.
10.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列
为世界三大数学家,用其名字命名的“高斯函数”为:设 ,用 表示不超过 的最大整数,则
称为高斯函数,如 , .若 ,则
A.当 时, B.
C.函数 是堵函数 D.函数 的值域为
11.已知函数 的周期为 ,且满足 ,则下列说法正
确的是
学科网(北京)股份有限公司A. 在区间 上单调递减
B.直线 是函数 图象的对称轴
C. 在区间 上有两个对称中心
D.若 在区间 上有2024个根,则 的最小值为
三、填空题:本题共3小题,每小题5分,共15分,把答案填在答题卡中的横线上.
12.已知函数 ,则不等式 的解集是________.
13.函数 在 上的导数为 ,若 ,且 ,则
________.
14.在半径为1,圆心角为 的扇形中, 是弧上的动点, 是扇形的内接矩形,则矩形 面
积的最大值为________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
已知 , , 分别为 三个内角 , , 的对边, .
(1)求 ;
(2)若 , 的面积为 ,求 , .
16.(本小题满分15分)已知幂函数 的图象过点 , .
(1)求 的解析式;
(2)记 , 在区间 上的值域分别为 , ,若 是 的必要条件,求实数 的取
值范围;
(3)设 ,对 , 使得 成立,求正实数 的
最小值.
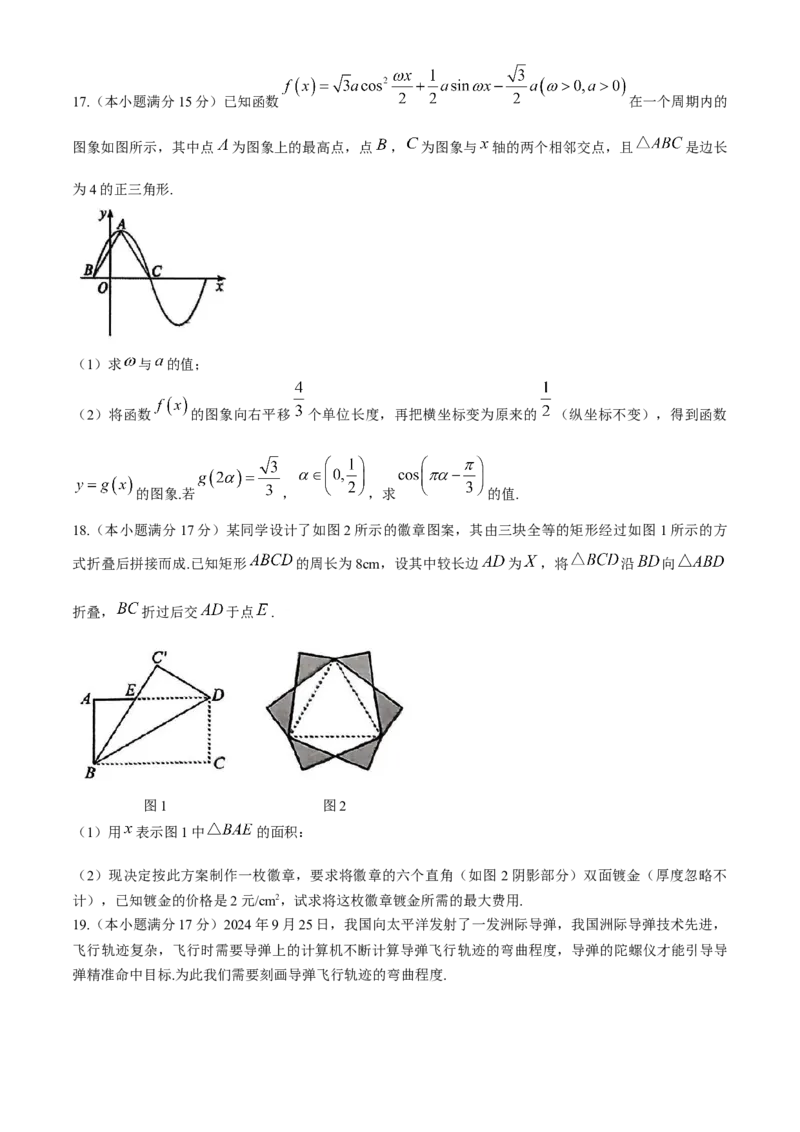
学科网(北京)股份有限公司17.(本小题满分15分)已知函数 在一个周期内的
图象如图所示,其中点 为图象上的最高点,点 , 为图象与 轴的两个相邻交点,且 是边长
为4的正三角形.
(1)求 与 的值;
(2)将函数 的图象向右平移 个单位长度,再把横坐标变为原来的 (纵坐标不变),得到函数
的图象.若 , ,求 的值.
18.(本小题满分17分)某同学设计了如图2所示的徽章图案,其由三块全等的矩形经过如图 1所示的方
式折叠后拼接而成.已知矩形 的周长为8cm,设其中较长边 为 ,将 沿 向
折叠, 折过后交 于点 .
图1 图2
(1)用 表示图1中 的面积:
(2)现决定按此方案制作一枚徽章,要求将徽章的六个直角(如图 2阴影部分)双面镀金(厚度忽略不
计),已知镀金的价格是2元/cm2,试求将这枚徽章镀金所需的最大费用.
19.(本小题满分17分)2024年9月25日,我国向太平洋发射了一发洲际导弹,我国洲际导弹技术先进,
飞行轨迹复杂,飞行时需要导弹上的计算机不断计算导弹飞行轨迹的弯曲程度,导弹的陀螺仪才能引导导
弹精准命中目标.为此我们需要刻画导弹飞行轨迹的弯曲程度.
学科网(北京)股份有限公司如图所示的光滑曲线 上的曲线段 ,其弧长为 ,当动点从 沿曲线段 运动到 点
时, 点的切线 也随着转动到 点的切线 ,记这两条切线之间的夹角为 (它等于 的倾斜角与
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则
弯曲程度越大,因此可以定义 为曲线段 的平均曲率;显然当 越接近 ,即 越小,
y
K lim
s0 s
1
y2 3
2
就越能精确刻画曲线 在点 处的弯曲程度,因此定义 (若极限存在)为曲线
在点 处的曲率.(其中 , 分别表示 在点 处的一阶、二阶导数)
(1)求函数 在点 处的曲率;
(2)已知函数 ,求函数 的曲率 的最大值.
(3)设函数 , ,若存在 , 使得 的曲率为 0,求证:
.
学科网(北京)股份有限公司赤峰市 2024 年高三 11·20 模拟测试
参考答案与评分细则
题号 1 2 3 4 5 6 7 8
答案 B C D A C A B C
题号 9 10 11
答案 ABD AD ACD
12. 13.2025 14.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.【详解答案】(1)由正弦定理可将
化为 ,
其中 , …………(2分)
可得 , …………(4分)
在 中, ,可得 ,由辅助角公式可得 ,(6分)
可得 . …………(7分)
(2) 的面积为 ,可得 , …………(9分)
由余弦定理 ,可得 , …………(11分)
综上 , 或 , . …………(13分)
16.【详解答案】(1)设幂函数 ,由题意 ,即 ,
即函数 的解析式为 . …………(2分)
(2)由题意 在区间 上的值域为 , …………(3分)
而函数 区间 上的值域为 , …………(4分)
学科网(北京)股份有限公司由 是 的必要条件可知 , …………(6分)
即 且 ,解得 . …………(8分)
(3)由题意 , …………(9分)
对 , 使得 成立,可得 , …………(11分)
在区间 上, 的最大值为 , …………(12分)
在区间 上, 的最大值为 , …………(13分)
令 ,可得 ,解得 (舍)或 ,即 ,
即正实数 的最小值为1. …………(15分)
17.【详解答案】
(1)由已知可得 , …………(3分)
由题图可知,正三角形 的高即为函数 的最大值 ,则 . …………(6分)
(2)由(1)可知 ,由函数 的图象向右平移 个单位长度,
再把横坐标变为原来的 ,得 图象可知: , …………(10分)
由 得, , …………(11分)
由 得, ,
从而 , …………(13分)
学科网(北京)股份有限公司故 . …………(15分)
18.【详解答案】(1)因为 ,所以 ,
又因为 为较长边,所以 ,即 . …………(3分)
设 ,则
因为 , ,
所以 ,所以 , …………(5分)
在 中,由勾股定理得 ,
即 ,解得 , …………(7分)
所以 , …………(8分)
所以 的面积 (单位: )
…………(10分)
(2)设一枚徽章的镀金费用为 元,则 …………(13分)
由基本不等式可知: ,当且仅当 ,即 时等号成立, …………(15分)
所以当 时,一枚徽章的镀金部分所需的最大费用为 元. …………(17分)
19. 【 详 解 答 案 】 ( 1 ) , , , ,
,(2分)
所以函数 在点 处的曲率为 . …………(3分)
(2) , , ,
学科网(北京)股份有限公司由 定义知 为非负数,由题意得,
,
, ,
…………(5分)
令 , ,令 , …………(6分)
则 在 上恒成立, …………(8分)
在 上单调递增,即 ,
,当且仅当 时取到,所以曲率 的最大值为 . …………(9分)
(3)证明:由题意可得 , ,
若 曲率为0,则 ,即 ,即 , …………(10分)
令 ,则 ,得 , …………(11分)
所以在 上, , 单调递增,且 ;
在 上, , 单调递减,且 .
又 ,所以 有两个解.
设为 , , , …………(13分)
又 ,所以 ,可设 , ,
学科网(北京)股份有限公司所以 , , ,
化简可得 ,则 . …………(15分)
要证 ,即证 ,
需要证 ,即证 , …………(16分)
令 ,
所以 在 上单调递增,
所以 ,得证. …………(17分)
学科网(北京)股份有限公司