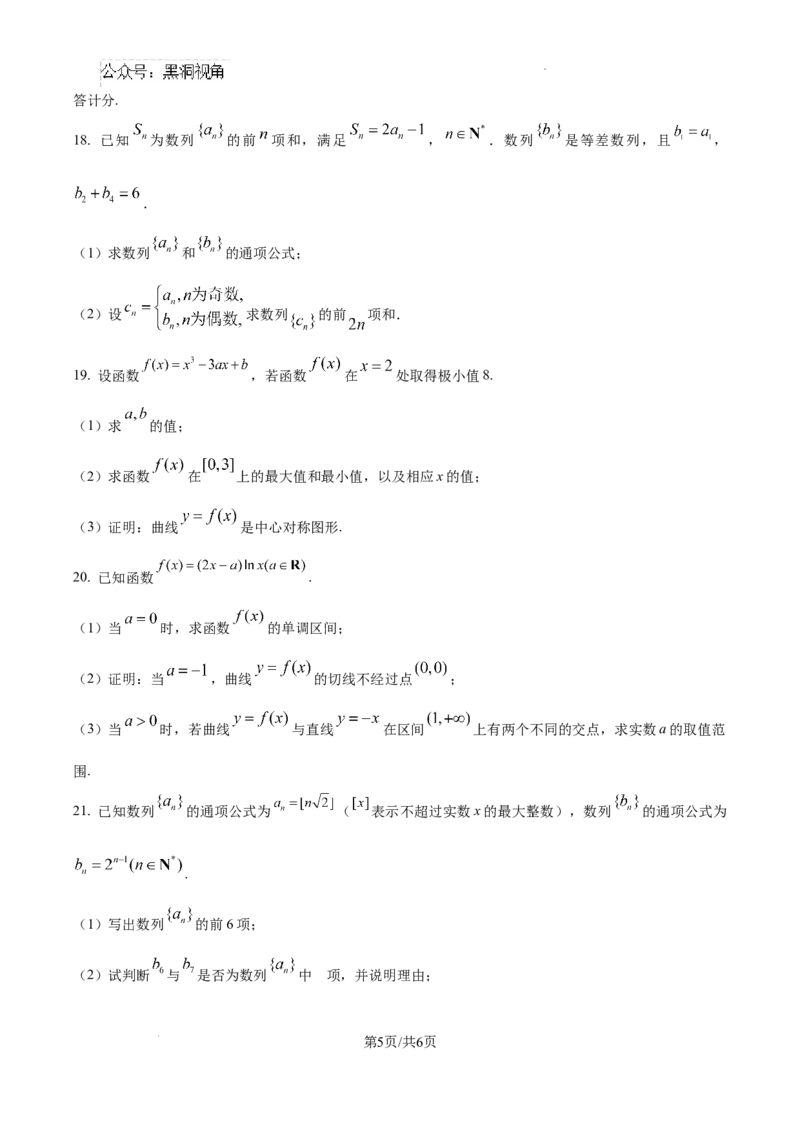文档内容
通州区 2024—2025 学年第一学期高三年级期中质量检测
数学试卷
2024年11月
本试卷共4页,共150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作
答无效.考试结束后,请将答题卡交回.
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要
求的一项.
1. 已知集合 ,集合 ,则 ( )
A. B.
C. D.
2. 设复数 ,则复数 在复平面内对应的点的坐标是( )
A. B.
C. D.
3. 下列函数中,在 上单调递增的是( )
A. B.
C. D.
4. 已知角 终边经过点 ,且 ,则 ( )
A. B. C. D.
第1页/共6页
学科网(北京)股份有限公司5. 设 , 为非零向量,则“ ”是“ ”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
6. 在中, , , ,则 ( )
A. B. C. D.
7. 沙漏也叫做沙钟,是一种测量时间的装置.现有一个沙漏(如图)上方装有 的细沙,细沙从中间小
孔由上方慢慢漏下,经过 时剩余的细沙量为 ,且 (b为常数),经过 时,上方
还剩下一半细沙,要使上方细沙是开始时的 ,需经过的时间为( )
A. B. C. D.
8. 设函数 ,已知 , ,则 的最小值为( )
A. B. C. D.
9. 设集合 ,则( )
A. 对任意实数a, B. 对任意实数a,
第2页/共6页
学科网(北京)股份有限公司C. 当且仅当 时, D. 当且仅当 时,
10. 已知 是 的重心,过点 作一条直线与边 , 分别交于点 , (点 , 与所在边
的端点均不重合),设 , ,则 的最小值是( )
A. 1 B. C. 2 D. 4
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分.
11. 函数 的定义域是___________.
12. 已知向量 在正方形网格中的位置如图所示.若网格中每个小正方形的边长均为 ,则
________.
13. 已知等差数列 的首项为 ,设其前 项和为 ,且 ,则过点 和 ,且
满足 的直线的斜率是________.
14. 设函数
①若 ,则函数 的零点个数有________个.
②若函数 有最小值,则实数a的取值范围是________.
第3页/共6页
学科网(北京)股份有限公司15. 已知无穷数列 满足 , ,给出下列四个结论:
① , ;
②数列 为单调递减数列;
③ ,使得 ;
④ ,均有 .
其中正确结论的序号是________.
三、解答题共6小题,共85分.解答应写出文字说明、演算步骤或证明过程.
16. 已知函数 , .
(1)求 的最小正周期及 的值;
(2)直线 与函数 , 图象分别交于 两点,求 的最大值.
的
17. 记 的内角 的对边分别为 ,已知 , .
(1)求 及 ;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使 存在且唯一,求
的面积.
条件①: ;
条件②: ;
条件③: .
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别作答,按第一个解
第4页/共6页
学科网(北京)股份有限公司答计分.
18. 已知 为数列 的前 项和,满足 , .数列 是等差数列,且 ,
.
(1)求数列 和 的通项公式;
(2)设 求数列 的前 项和.
19. 设函数 ,若函数 在 处取得极小值8.
(1)求 的值;
(2)求函数 在 上的最大值和最小值,以及相应x的值;
(3)证明:曲线 是中心对称图形.
20. 已知函数 .
(1)当 时,求函数 的单调区间;
(2)证明:当 ,曲线 的切线不经过点 ;
(3)当 时,若曲线 与直线 在区间 上有两个不同的交点,求实数a的取值范
围.
21. 已知数列 的通项公式为 ( 表示不超过实数x的最大整数),数列 的通项公式为
.
(1)写出数列 的前6项;
的
(2)试判断 与 是否为数列 中 项,并说明理由;
第5页/共6页
学科网(北京)股份有限公司(3)证明:数列 与数列 的公共项有无数多个.
第6页/共6页
学科网(北京)股份有限公司