答案(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_九省联考模式填空题100题（含答案）

参考答案，仅供参考哦 1 1． 5 b1np 【分析】利用换元法可得 ，进而根据不等式的性质，分  a1mnp 情况讨论求解. 【解析】令bam,cbn,1c p,其中m,n,p0， b1np 所以 ，  a1mnp 若b2a，则b1n p21mn p，故2mn p1， 令M=maxba,cb,1cmaxm,n,p， 2M 2m  1 因此M n ,故4M 2mn p1,则M  ，  4 M  p 若ab1，则1n p1mn p1，即m2n2p1， M=maxba,cb,1cmaxm,n,p， M m  1 则2M 2n ,故5M m2n2p1,则M  ，  5 2M 2p 1 当且仅当m2n2p1且maxm,n,p 时等号成立， 5 1 如取mn p 时可满足等号成立， 5 1 综上可知maxba,cb,1c的最小值为 ， 5 1 故答案为： 5 【点评】本题的关键是利用换元法，在b2a和ab1前提下进行合理 分类讨论，根据题意得到相对应的不等式组，注意题目的条件关键词 是“或”. 第 14 页 共 90 页4 2． 9 【分析】由题，先求得 M 最大值时，x 和 y 的关系范围，再画出图像， 分别求得不同范围的的最小值即可求得答案. 【解析】由题，当xy xyxy1yx1 3(xy)2 4 当xy x y2xy，解得 xy3xy  yx 4 3 4 所以当yx 时，M  xy，即图像的区域 1 3 3(xy)2 当xyxy1 x y2xy，即 2(xy)13xy1 3 2 2 解得yx ，所以当yx ，M  xyxy1，即图像的区域 3 3 3 所以当在区域 2 时，M  x y2xy 综上可得：在区域 1 中，M  xy；在区域 2 中，M  x y2xy；在区域 3 中， M  xyxy1 2 4 在区域 1 中，当且紧当x y 时，M  xy取最小值为 3 9 1 4 在区域 2 中，当且紧当x y 时，M  x y2xy取最小值为 3 9 1 4 在区域 3 中，当且紧当x y 时，M  xyxy1取最小值为 3 9 第 15 页 共 90 页4 综上所述，可得 M 的最小值为 9 【点评】本题考查了函数与不等式综合，熟悉理解题意，求最值是解 题的关键，属于难题. 3． 2 1 1 【分析】先根据c的范围，讨论 bc, b的大小关系，在每种情况中 a ac 分别用均值不等式和不等式的性质确定 的范围，即可得解． M  1 1 a  【解析】设M max b, bc, c ， ac a b  1 1 a 则由题意可得M  b 0,M  bc 0,M  c 0 ， ac a b  1  1 因为  bc bc，所以 ac  a 1 1 ①当 c1 时， bc b 0， a ac 1 a 只需考虑M  bc,M  c ， a b 1 1 b a a a 所以 M  bc b 2 ， M  c 1 2 ， a a a b b b b a 所以 M2 2 2 4 ，可得 M 2 ，当且仅当abc1时取等号； a b 1 1 1 a ②当0c1时，0 bc b，只需考虑M  b,M  c ， a ac ac b 第 16 页 共 90 页 1  a  1 1 1 1 所以M2  b ca  bc 2 a  2 bc  4 ， ac b  a bc a bc 可得 M 2 ，当且仅当a1,bc1时取等号. 综上所述， M 的最小值为 2. 故答案为：2. 【点评】关键点点睛：本题的关键点是在利用均值不等式和不等式的 性质时，特别注意同向不等式的应用和均值不等式成立的条件. 4． 2 2 2 5 【解析】分类讨论，结合均值不等式，注意取等验证是否满足即可． 1 2 2 【解析】（1）若x ,  y时，即1 xy2时，A x 2 2，当 x 2,y1 y x x 时可取等号， 1 2 若x ,y 时，即xy2时，Axy 2 xy  2 2 ， y x 1 2 2 若 x,  y时，即0 xy1时，由0 xy1知 2， y x xy 1 2 2 所以A  2 2 2， y x xy 综上可知 A 的最小值为 2 2 ； 2当z 3 时，B x 2 z 5 z2 5，当 z 5,x 3 5 ,y 2 5 时可取等号； x z z 5 5 当z 3 时，B x 3  2  x 3  2x  5x  3 2 5，当 z 5,x 3 5 ,y 2 5 时可 x x z x 3 3 x 5 5 取等号； 综上所述， ， 3 5 2 5 时可取等号； B2 5 z 5,x ,y 5 5 故答案为： ， ． 2 2 2 5 【点评】本题考查代数式的最值求法，考涉及均值不等式及分类讨论 思想，属于中档题． 第 17 页 共 90 页16 5． 7 【分析】先求出切线方程，再结合函数的新定义和函数图像找到最小 值点，代入横坐标即可求出最小值. x1  x1  x2x1 3 【解析】因为y ，所以y    ， x2 x2 x22 x22 所以y13，在点1,2处的切线方程为y23x1 y3x1， p,pq, 设gx4 x1, f x3x1，由maxp,q 和函数图像可知， q,pq, 当x1时，最小值为两函数的交点， 3 3 16 所以3x141x x ，此时 f x gx3 1 ， 7 7 7 16 故答案为： 7 6． 5 【分析】根据题意，将函数 f(x)写成分段函数的形式，将问题转化为 求分段函数的最小值问题. x5,x5x24x5, x5,0x5, 【解析】由题意知 f x  x24x5,x5x24x5,  x24x5,x 0或x 5, 当0x5时， f xx5单调递增， f xx5 f 05， 当 x0 时， f xx24x5在,0单调递减，  f xx24x5 f 05， 第 18 页 共 90 页当x5时， f xx24x5在5,单调递增，  f xx24x5 f 510， 综上， f x的最小值为 5. 故答案为： 5. 7．1 【分析】首先求解函数hx的解析式，再求解函数的最小值. 1 【解析】令 f xgx，x0，即 x  ，x0，得x1， x 当x0,1 ， x  x 1 ，当x1,， x  x 1 ， x x 1  ,x0,1 所以hxx  x,x1, 当x0,1 时，hx单调递减，当x1,时，函数hx单调递增， 所以当x1时，hx 1． min 故答案为： 1 8． 3 3 【分析】作出函数Mx的图象，可得出函数Mx的最小值及其对应的 x的值. 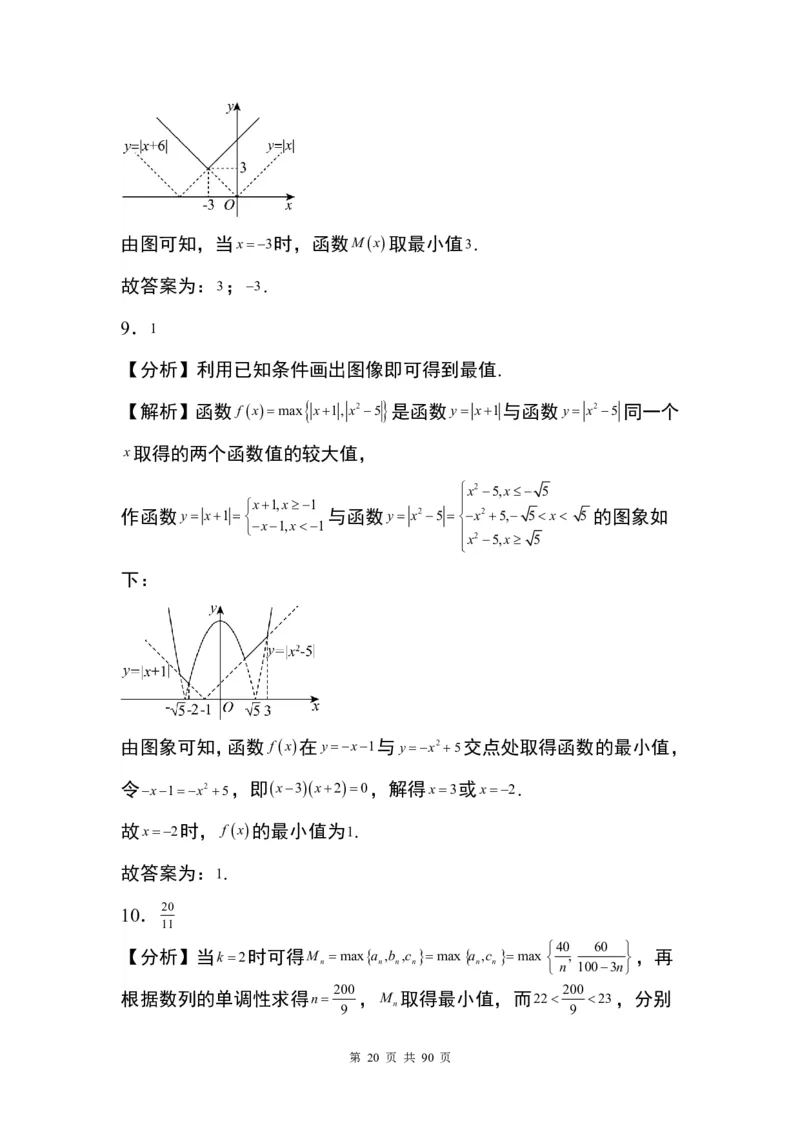【解析】由 x  x6 可得 x2 x212x36 ，解得 x3 ， 由 x  x6 可得 x2 x212x36 ，解得 x3 ， x ,x3 故Mxmax  x , x6  ， x6,x3 作出函数Mx的图象如下图中的实线部分所示： 第 19 页 共 90 页由图可知，当x3时，函数Mx取最小值3. 故答案为：3；3. 9． 1 【分析】利用已知条件画出图像即可得到最值. 【解析】函数 f xmax  x1, x25  是函数y x1与函数y x25 同一个 x取得的两个函数值的较大值， x25,x 5 x1,x1   作函数y x1  与函数y x25  x25, 5x 5 的图象如 x1,x1   x25,x 5 下： 由图象可知，函数 f x在yx1与 yx25 交点处取得函数的最小值， 令 x1x25 ，即x3x20，解得x3或x2. 故x2时， f x的最小值为 1. 故答案为： 1. 10．20 11 40 60  【分析】当k 2时可得M maxa ,b ,c maxa ,c max  ,  ，再 n n n n n n  n 1003n 200 200 根据数列的单调性求得n ，M 取得最小值，而22 23，分别 9 n 9 第 20 页 共 90 页求出M 、M ，比较可得k 2时M 的最小值；然后当k1、k3时，根 44 45 n 据数列的单调性，分别求出可能取得最小值时的值，比较即可得答案. 40 60  【解析】当k 2时可得M maxa ,b ,c maxa ,c max  ,  ， n n n n n n  n 1003n 因为数列a 是单调递减数列，数列c 为单调递增数列， n n 40 60 200 所以当  时，M 取得最小值，此时n ， n 1003n n 9 400 40 60  20 因为22 23，而M maxa ,c max  ,  ， 9 22 22 22 22 100322 11 40 60  60 M maxa ,c max  ,  ， 23 23 23 23 100323 31 又 20  60 ，所以当k 2时，M 的最小值为20； 11 31 n 11 80 60  当k1时，M maxa ,b ,c maxb ,c max  ,  ， n n n n n n  n 1002n 因为数列b 为单调递减数列，数列c 为单调递增数列， n n 80 60 400 所以当  时，M 取得最小值，此时n ， n 1002n n 11 400 80 60  20 因为36 37，而M maxb ,c  max ,   ， 11 36 36 36 36 100236 9 80 60  30 M maxb ,c max  ,  ， 37 37 37 37 100237 13 20 20 20 此时M 的最小值为 ，而  ； n 9 9 11 60 60 15 当k3时，c    ，a b ， n 1001kn 1004n 25n n n 40 15  所以M maxa ,b ,c maxa,c max  ,  ， n n n n n n  n 25n 40 15  令H max ,  ， n  n 25n  15  因为数列a 为单调递减数列，数列   为单调递增数列， n 25n 40 15 40 15  200 所以  时，H max ,  取得最小值，此时n ， n 25n n  n 25n 11 200 40 15  20 因为18 19，H max ,   ， 11 18 18 2518 9 40 15  5 H max ,   ， 19 19 2519 2 20 5 20 又因为  ，此时M 的最小值为 . 9 2 n 9 第 21 页 共 90 页综上所述，M 的最小值为20 . n 11 故答案为：20 . 11 11．4 4 【分析】根据题意分析可得2tx2 ，结合基本不等式运算求解， y(xy) 注意等号成立的条件. 4 【解析】由题意可知：tx2,t ， y(xy) 4 且x y0，则x2 0, 0， y(x y) 4 4 则2tx2 ，当且仅当x2  时，等号成立， y(xy) y(xy) 4 4 16 2tx2 x2 x2 可得 y(xy) y(xy) 2 x 2 ，    2  当且仅当y xy，即x2y时，等号成立， 16 16 16 且 2t x2 2 x2 8 ，当且仅当x2  ，即 x2 时，等号成立， x2 x2 x2 4 综上所述：当x2y2时，可得2t8，即t4，此时x2   4， y(xy) 所以t的最小值为 4. 故答案为：4. 10 12． 11 40 60  【分析】当k 2时可得M maxa ,b ,c maxa ,c max ,  ，再 n n n n n n  n 2003n 400 400 根据数列的单调性求得n ，M 取得最小值，而44 45，分别 9 n 9 求出M 、M ，比较可得k 2时M 的最小值；然后当k1、k3时，根 44 45 n 据数列的单调性，分别求出可能取得最小值时的值，比较即可得答案. 40 60  【解析】解﹔当k 2时可得M maxa ,b ,c maxa ,c max ,  ， n n n n n n  n 2003n 因为数列a 是单调递减数列，数列c 为单调递增数列， n n 第 22 页 共 90 页40 60 400 所以当  时，M 取得最小值，此时n ， n 2003n n 9 400 40 60  10 因为44 45，而M maxa ,c max  ,  ， 9 44 44 44 44 200344 11 40 60  12 M maxa ,c max  ,  ， 45 45 45 45 200345 13 10 12 10 又  ，所以当k 2时，M 的最小值为 ； 11 13 n 11 80 30  当k1时，M maxa ,b ,c maxb ,c max  ,  ， n n n n n n  n 100n 因为数列b 为单调递减数列，数列c 为单调递增数列， n n 80 30 800 所以当  时，M 取得最小值，此时n ， n 100n n 11 800 80 30  10 因为72 73，而M maxb ,c max ,  ， 11 72 72 72 72 10072 9 80 30  10 M maxb ,c max  ,  ， 73 73 73 73 10073 9 此时M 的最小值为10，而 10  10 ， n 9 9 11 60 60 15 当k3时，c    ，a b ， n 2001kn 2004n 50n n n 40 15  所以M maxa ,b ,c maxa ,c max ,  ， n n n n n n  n 50n 40 15  令H max ,  ， n  n 50n  15  因为数列a 为单调递减数列，数列   为单调递增数列， n 50n 40 15 40 15  400 所以  时，H max ,  取得最小值，此时n ， n 50n n  n 50n 11 400 40 15  10 40 15  15 因为36 37，H max ,   ，H max ,  ， 11 36 36 5036 9 37 37 5037 13 又因为 10  15 ，此时M 的最小值为10 . 9 13 n 9 10 综上所述，M 的最小值为 . n 11 10 故答案为： . 11 【点评】关键点点睛：本题考查数列最值的求解，解题的关键在于根 据分析出数列的单调性，找出临界值点，通过比较大小后得出结果. 13．40 第 23 页 共 90 页ax(x) 【分析】根据题意，设g(x)sinx ，利用分离常数法和配方法 cx(x)b2 a ab2 1 化简得g(x)sinx c  c2   c4b ，分类讨论当c4b 2[0 ， 2 ] 时 f(a， (x )2 2 4c 4 2 4c b，c)无意义，当c4b 2[0 ， 2 ] 时，对gx进行求导，再利用导数研 4c 4  究函数的单调性，从而可确定当g(x)在 x 处取最大值，所以 2 2 a f a,b,c|1 4 |1 a ，取最小值时，结合条件a，b，c为不超过 2 4bc c b2 4 20 的正整数，得出a，b，c的值，即可求出 abc 的值． ax(x) 【解析】解：根据题意，令g(x)sinx ， cx(x)b2 化简得 b2 g(x)sinx a (1 c )sinx a  ab2  1 sinx a  ab2  1 c b2 c c 2  1 b c c 2  c 4b x(x) (x )22(  ) (x )2 2 c 2 4 c 2 4c ， 当c4b 2[0 ， 2 ] 时，即当 4bc0 时，g(x)在[0，1]上无最大值，所以 f(a， 4c 4 b，c)无意义，  当c4b 2[0 ， 2 ] 时，即当 4bc0 时， g(x)cosx 2ab2( 2 x) ， 4c 4 (cx(x)b2)2  当x[0， ) 时，g(x)0，g(x)单调递增，又因为g(0)0，所以g(x)0， 2  当 x( ，]时，g(x)0，g(x)单调递减，又因为g()0，所以g(x)0， 2 2 a 所以g(x)在 x  处取最大值，所以 f a,b,c|1 4 |1 a ， 2 2 4bc c b2 4 因为要求a，b，c不相同，为不超过 20 的正整数， 所以当a1， b20 ，c2时， f(a，b，c)取最小值， 第 24 页 共 90 页所以 abc120240 ， 故答案为：40． 1 14． 3 【分析】由x x 和x x 的地位上相同，同时x x 和x x 的地位上也 1 2 4 5 2 3 3 4 相同，分类讨论，即可求解. 【解析】由题意知，x x 和x x 的地位上相同，类似的：x x 和x x 1 2 4 5 2 3 3 4 的地位上也相同， （1）若x x 最大，设x x a， 2 3 2 3 要使得a最小，则其余的数尽可能的大，其中x x 最大取a，此时x x ， 1 2 1 3 剩下x x 也要尽可能大，取x x a，则ax a1， 4 5 4 5 3 因为x x a，要使得x 尽可能大，则x a,x 0， 2 3 3 3 2 1 此时aaa1，解得a ； 3 （2）若x x 最大，设x x a， 1 2 1 2 与（1）中类似，x  x,x x a时，a最小， 3 1 4 5 同样2ax 1，要使得a最小，则x最大，此时x a,x 0， 1 1 1 2 1 可得2aa1，解得a . 3 综上可得min  maxx x ,x x ,x x ,x x  1 . 1 2 2 3 3 4 4 5 3 1 故答案为： . 3 【点评】本题主要考查了多项式的和的应用，以及不等式和函数的最 值问题，着重考查了分类讨论，转化与回归思想，以及推理与运算能 力.  1 5 15． 1 1,    2  第 25 页 共 90 页【解析】（1）分三种abc、abc和abc三种情况加以讨论，分 a b c a b c 别求出max , ,  和min , ,  的值，即可算出总有t1成立，得到本 b c a b c a 题答案； 1 ,cb2  a b c a b c b （2）根据题意，可得max , , c，且min , ,  ，因此对 cb2 b c a b c a b ,cb2 c 和 cb2两种情况加以讨论，利用三角形两边之和大于第三边和不等式 的性质进行推导，解不等式组可得t的取值范围. a b c a b c 【解析】（1）①若abc，则max , , min , , 1 ， b c a b c a a b c a b c 此时，t max , , min , , 1 ； b c a b c a a b c c a b c b ②若abc，则max , ,  ，min , ,  ， b c a a b c a c a b c a b c 此时，t max , , min , , 1 ； b c a b c a a b c b a b c a ③若abc，则max , ,  ，min , ,  ， b c a a b c a b a b c a b c 此时，t max , , min , , 1 . b c a b c a 综上所述，若ABC为等腰三角形，则t 1； a b c 1 b  （2） a1 ，abc，max , ,  max , ,cc， b c a b c  1 ,cb2  a b c 1 b  b min , , min , , c . b c a b c  b ,cb2 c 1 c ①当 cb2时，t c  ，则ctbt1，由abc，即1btb， b b 1 当t 1时，b ， t1 ctbb2，tb，可得t 1 ，即 t2t10 ，解得 1t 1 5 . t1 2  1 5 当t1时，bca1，合乎题意，此时，t的取值范围是 1, ；   2  第 26 页 共 90 页b ②当 cb2时，t c b，由abc且 cb2，得 1bb2，即 t2t10 ， c 解得 1t 1 5 . 2  1 5 当t1时，cba也成立，此时，t的取值范围是 1, .   2   1 5 综上所述，当a1时，t的取值范围是 1, .   2   1 5 故答案为： 1 ； 1, .   2  【点评】本题给出三角形三边中任意两边的比值，求它们的最大值与 最小值之积的取值范围，着重考查了三角形两边之和大于第三边、不 等式的基本性质和不等式的解法等知识，属于难题． 16．①③ x24x，x＜0 【分析】g（x） ，F（x）＝max{f（x），g（x）}（x∈R） x24x，x0 x24x，x2  2x，2＜x＜6 ．画出图象，数形结合即可得出．  x24x，x6  【解析】由gx为偶函数，且当 x0 时，gxx24x， ∴令 x0 ，则x0 ，则gx(x)24x gx， 即当 x0 时，gx x24x， x24x，x＜0 ∴g（x） ， x24x，x0 x24x，x2  F（x）＝max{f（x），g（x）}（x∈R）2x，2＜x＜6 ．  x24x，x6  画出图象， 由图象可得：①当 x≥6 时，∵x2﹣4x≥2x，∴F（x）＝x2﹣4x，因此正 第 27 页 共 90 页确． ②由图象可得：函数 F（x）不为奇函数，因此不正确． ③﹣2≤x≤6 时，2x＞x2﹣4x，可得函数 F（x）＝2x，因此函数 F（x） 在[﹣2，6]上为增函数，所以函数 F（x）在[﹣2，2]上为增函数是正 确的． ④x≤﹣2 时，g（x）＝x2+4x≥2x，可得 F（x）＝x2+4x≥﹣4，综合可得 函数 F（x）的最小值为﹣4，无最大值，④不正确． 其中正确的是 ①③． 故答案为①③． 【点评】本题考查了函数的图象与 性质、不等式的解法，考查了数形结合方法、推理能力与计算能力， 属于中档题． 17．（2）（3）（4） 【分析】依次判断每个选项的正误：（1）等号成立的条件不满足；（2） 两式相减恒大于 0；（3）利用均值不等式再累加得到证明；（4）ab， 根据范围大小得到分段函数求在最值，判断得到答案. 第 28 页 共 90 页1 1 【解析】（1）y x22 2，当 x22  ，即 x2 1 时成立， x22 x22 错误； （2）a0,b0且 a¹b ，则 a3b3ab2a2babab2 0 ， 故 a3b3 ab2a2b 恒成立，正确； b c a （3）a0,b0,c0  a 2 b;  b 2 c;  c 2 a，不等式累加得 a b c b c a 到    a b c ，当abc时等号成立，正确； a b c 1 1  1  1  （4）不妨设ab，则hmax , ,a2b2max ,a2b2max ,2a2 a b  a  a   1 2a2,a 3 2  1   1 1 max ,2a2 32,a ，故当ab 时， h 有最小值为 32 ，正确. a   3 2 3 2  1 1  ,a  a 3 2 故答案为（2）（3）（4） 【点评】本题考查了不等式的综合应用，意在考查学生对于不等式的 应用能力. 18． e2 【分析】根据题意，把 f x max  ex2,ex2  写成分段函数，即可求其最 小值. 【解析】当x2时， g(x)e|x2| ex2,h(x)e|x2| ex2， 所以h(x) g(x)， 当2x0 时， g(x)e|x2| ex2,h(x)e|x2| ex2 ，所以h(x) g(x)， 当0x2时， g(x)e|x2| ex2,h(x)e|x2| ex2 ，所以h(x)g(x)． 当2 x 时， g(x)e|x2| ex2,h(x)e|x2| ex2 ，所以h(x)g(x)，  ex2,x0 综上可知 f x ， ex2,x 0 第 29 页 共 90 页所以 f x的最小值为 f 0e2. 【点评】本题主要考查了指数函数的性质，分段函数求最值，属于难 题. 19． 3 2 1 1  【分析】首先，设max , ,a2b2m，从而得到关于 m 的限制条件， a b  然后，得到 m 的最小值． 1 1  【解析】设max , ,a2b2m， a b  a、b0， 1 1 m ，m ， ma2b2， a b 1 1 2 即a ，b ，可得a2b2  ， m m m2 2 m ， m2 m 3 2 ， 即有 m 的最小值为 3 2 ， 故答案为 ． 3 2 【点评】本题考查新定义的理解和运用，注意不等式的性质的应用， 属于难题． 20．58 【解析】不妨设 A  A  A 0. 1 2 n 当n3时，由cX2X 及条件，知 2A1 2A2 2An 2A1 A2 An 2A1 A2 An . 而上式左端大于 2A1 2An ； 右端小于或等于 2A1 A2 An 2An ，故 A 1 A 2 A n  A 1 1. 又上式左端小于 2A1 1，故 A 1 A 2 A n  A 1 1，矛盾. 第 30 页 共 90 页于是，n2且 2A1 2A2 2A1 A2 2A1 A2 . 由韦恩图知其等价于A  A . 2 1 令 A a， A bab，则a1b12006217593459. 1 2 故a59158. 当a58，b33时取到最小值. 21． 2 【分析】利用平方作差法，结合已知条件利用不等式的基本性质得到 x2y5  2x1，进而max  2x1, x2y5  x2y5 ，结合已知条件利用 不等式的基本性质得到x2y50，进而得到max  2x1, x2y5 的最小 值. 【解析】 x2y5 2 2x1 2 3x2y6x2y4， 1 x1 ∵  ，∴3x3,x1,y1,2y2， 1 y1 ∴3x2y632610,x2y412410， ∴3x2y6x2y40， ∴ x2y5 2 2x1 2 0 ，∴ x2y5 2  2x1 2， ∴ x2y5  2x1， ∴max  2x1, x2y5  x2y5 ∵y1,∴2y2，结合x1，得x2y51252 ∴ x2y5 x2y52（当x1,y1时取得等号）， ∴max  2x1, x2y5 的最小值为 2. 故答案为：2 第 31 页 共 90 页3 22． 4 【解析】试题分析：由已知M(x,y) x2 y1，M(x,y) y2x1，则 2M  x2 y1 y2x1 1 1 3 3  (x2 y1)(y2x1)  x2x y2 y2  (x )2 (y )2   ，则 2 2 2 2 3 1 1 3 3 M(x,y) ．又当x ,y 时，M(x,y) ，所以M(x,y)的最小值为 ． 4 2 2 4 4 考点：新定义，绝对值的性质． 【名师点睛】本题考查新定义，关键是由新定义概念得M(x,y) x2 y1， M(x,y) y2x1，接着由绝对值的性质得 2M  x2 y1 y2x1  (x2 y1)(y2x1) ，再由配方法可放缩出 M 的一 个下界，要注意这个下界是不是最小值，还要需要能取特殊的x,y值 进行检验，否则可能出错． 23．①②④ 【分析】首先根据函数性质确定函数 f x的解析式，再画出函数Fx 的解析式，结合选项，即可判断. 【解析】由条件可知，f 0ab=0，当x趋向正无穷时，y趋向 b，所 以b=2， x 1 则 a=2 ，即 f x=2  2 ， 2 x 令 f x=gx，即2   1  2=2 x2，得x=1， 2 如图，画出函数Fx=max  f x,gx的图象， 第 32 页 共 90 页函数Fx是偶函数，在区间,2单调递减，当x=0时，函数取得最大 值 2， 1 Fx ，无实数根，故①②④正确，③错误. 2 故答案为：①②④. 24．5  3 2k3 2 ,k 1, 【解析】由结论 1，可得dM,B   k ，则 min max1,k  2k3,k 1, max  dM,B  5 k0 min 25． 1 【分析】分别求出 f xgx，f xgx的解集，即可得出函数Mx的 解析式，再根据一次函数和二次函数的图象作图即可，即可求出函数 的最小值，从而可得出答案. 【解析】解：当x3x12，即 x2x20 ， 即1x2时，Mxx3， 当当x3x12， x2x20 ， 即x2或x1时，Mxx12，   x3,x1,2  所以Mx ，  x12 ,x,12, 函数图象如图所示： 第 33 页 共 90 页由图可得，函数Mx在,1，1,2上递减，在2,上递增， 所以Mx M 2231. min 故答案为： 1. 26． 213 2 【分析】由已知在同一坐标系中分别画出 f x x24 与 f x x1的图 1 2 象，数形结合确定最低点位置，再联立方程组求解即可． 【解析】在同一直角坐标系中分别画出 f x x24 与 f x x1的图象 1 2 如图， 两个函数的图象有四个交点 A，B，C，D．由图可知，B 为函数 f xmax  x24,x1  图象的最低点，联立方程组   y4x2 ，解得 x 1 21 yx1 2 或 1 21（舍去）， x 2 所以 f xmax  x24,x1  的最小值为 1 21 1  213 ． 2 2 第 34 页 共 90 页故答案为： 213． 2 27．①④ 【分析】把 f xmaxsinx,cosx根据题意写成分段函数的形式，画出函 数的部分图像，根据图像即可判断值域、函数值的正负、周期性、对 称轴.  π 5π  sinx,x  2kπ, 2kπ   4 4  【解析】由题意得，函数 f xmaxsinx,cosx  ,kZ ，   3π π  cosx,x 2kπ, 2kπ    4 4  如图，作出函数 f x在2π,4π的图像.  3π 5π 由图可知：函数 f x为周期函数，最小正周期为 2π ，   ,  为其中  4 4  一个周期.  3π 5π 在  , 内，    4 4  ①当x0时，函数 f x有最大值 cos01 ， 5π 当x 时，函数 f x有最小值 sin 5π  2 ， 4 4 2  2  所以函数 f x的值域为  ,1 正确；  2  3π ②当 0xπ 时， f x0，所以当2kπx 2kπkZ时， f x0错误； 2 ③函数 f x的最小正周期为 2π ，所以π是函数 f x的一个周期错误； π 5π ④函数 f x关于x 2kπkZ和x 2kπkZ对称， 4 4 π 所以函数 f x图像的对称轴为x kπkZ正确. 4 故答案为：①④ 第 35 页 共 90 页28．2 【分析】将y用x表示，写出分段函数的表达式，利用函数的单调性 求最小值即可求解. 【解析】由2x2xy2x(1y)，因为x,y0， 1 2 1 1 由  2可得y ，因为y 0，所以x ， x y1 2x1 2 所以当0 y1，即x1时，2x2xy， 1 当y1，即  x1时，2x2xy， 2 2x,x1  1 所以M max2x,2xy 1 ，因为y ， 2xy,  x1 2x1  2 2x,x1  所以M  2x 1 ，  ,  x1 2x1 2 当x1时，M 2x2， 1 2x 2x11 1 当  x1时，M   1 单调递减， 2 2x1 2x1 2x1 1 1 所以M 1 1 2 ， 2x1 211 所以 M 的最小值为 2， 故答案为:2. 29．[1.+∞） 【分析】作出F(x)的图象,结合图象即可得F(x)的值域. 【解析】解：因为当x3时， f(x)3x, 令3xlog x，解得 x2 ， 2 当x3时， f(x)x3, 因为 f(5)2,g(5)log 52 f(5) , 2 11 5 f(5.5)2.5,g(5.5)log log 25  2.5， 2 2 2 2 第 36 页 共 90 页所以x (5,5.5)，使得x 3log x ， 0 0 2 0 3x,x2  所以F(x)log x,2xx ， 2 0  x3,xx 0 画出F(x)的图象如图， 由图易知，F(x)的最小值为F21, ∴F(x)的值域为[1，+∞）. 故答案为：[1，+∞）. 30． 2 【分析】作出函数 f x x3 ，gx2x图像，进而结合题意，数形结 合求解即可. 【解析】解：如图，作出函数 f x x3 ，gx2x图像， 所以，图像实线图像即为函数Fx的图像， 由图可知，当x1时，Fx有最小值 2 所以，Fx的最小值为 2 故答案为： 2 第 37 页 共 90 页31． 0,2  【分析】比较 f(x)与g(x)的大小，求得max{f(x),g(x)}，令h(x)max{f(x),g(x)}， 求得h(x)的最小值为 2aa2，由 2aa2 0 即可得出答案． 【解析】 x22ax2a(2xa2)x2(2a2)xa(a2)(xa)[x(a2)] ， 当xa或xa2时， f(x)g(x)；当a xa2时， f(x) g(x)， x22ax2a,x a或 x a2 故maxf (x),g(x) ， 2xa2,a xa2 令h(x)max{f(x),g(x)}， 当xa或xa2时， h(x) x2 2ax2a(xa)2 2aa2 2aa2； 当a xa2时， h(x)2xa2，单调递增，则当xa时，h(x)取最小值 2aa2， 所以h(x)的最小值为 2aa2， 若max{f(x),g(x)}0恒成立，则 2aa2 0 ，解得0a2． 故答案为：[0,2]． 32． 1,4  【分析】作差法比较两个函数的大小，得出M(x)的解析式求值域. 【解析】令 F(x) g(x) f(x)x12x3x2x1 解F(x)0得，x<2或x1，此时， M(x) g(x)x12； 解F(x)0得，2x1，此时，M(x) f(x) x3. x12 ,3 x2 所以，M(x) x3,2 x1 第 38 页 共 90 页显然，M(x)在x3,2上单调递减，最大值为M(3)4，最小值为 M(2)1，值域为[1,4]； M(x)在x[2,1]上单调递增，最大值为M(1)4，最小值为M(2)1，值 域为[1,4]. 综上可得，当x[3,1]时，M(x)的值域为[1,4]. 故答案为：[1,4]. 33． 6 【分析】根据a29b2  2 a29b2 6a ，分 1 6a， 1 6a讨论求解. b b a a 【解析】解：因为a29b2  2 a29b2 6a ，当且仅当a3b时，等号成立； b b 当 1 6a，即 a 6 时，hmax   1 , a29b2  a29b2 6a 6 ， a 6 a b  b 当 1 6a，即 0a 6 时，hmax   1 , a29b2  6， a 6 a b  综上： 的最小值是 ， h 6 故答案为： 6 34．5 13 2 【分析】先通过比较求出函数的解析式，再各段求出最小值即可. 【解析】解：令 x22x x1 ，解得 x 3 13或 x 3 13， 2 2  3 13 3 13 x22x,x 或x 则Mxmax  f x,g x   2 2 ，  3 13 3 13 x1, x   2 2 当 x 3 13或 x 3 13时，Mx  M    3 13    5 13 ， 2 2 min  2  2 当3 13 x 3 13时，函数没有最小值但大于5 13 ， 2 2 2 第 39 页 共 90 页综上：函数的最小值为5 13 . 2 故答案为：5 13 . 2 35．-1 【分析】利用导数研究g(x)的单调性并确定其值域，由二次函数性质 确定 f(x)值域，根据题设定义求 A、B，即可得结果. 【解析】由二次函数性质知： f x 0,，（f 1）0，（f 0）1， x1 x 而g(x) ，则g(x) ， ex ex 所以(,0)上g(x)0，g(x)递增，(0,)上g(x)0，g(x)递减， 当x趋向负无穷时g(x)也趋向负无穷，当x趋向正无穷时g(x)趋向 0， 而g01，g（1）0， 所以g(x)(,1]， 则可得，M（x） （f 1）g（1）0，A0，m（x）g（0） （f 0）1，B1，故 AB1. 故答案为：-1 36．16 【分析】令 f xgx，可得xa2或xa2，由题易知H x的最小值 1 A44a ，H x的最大值 B124a ，则可求出答案. 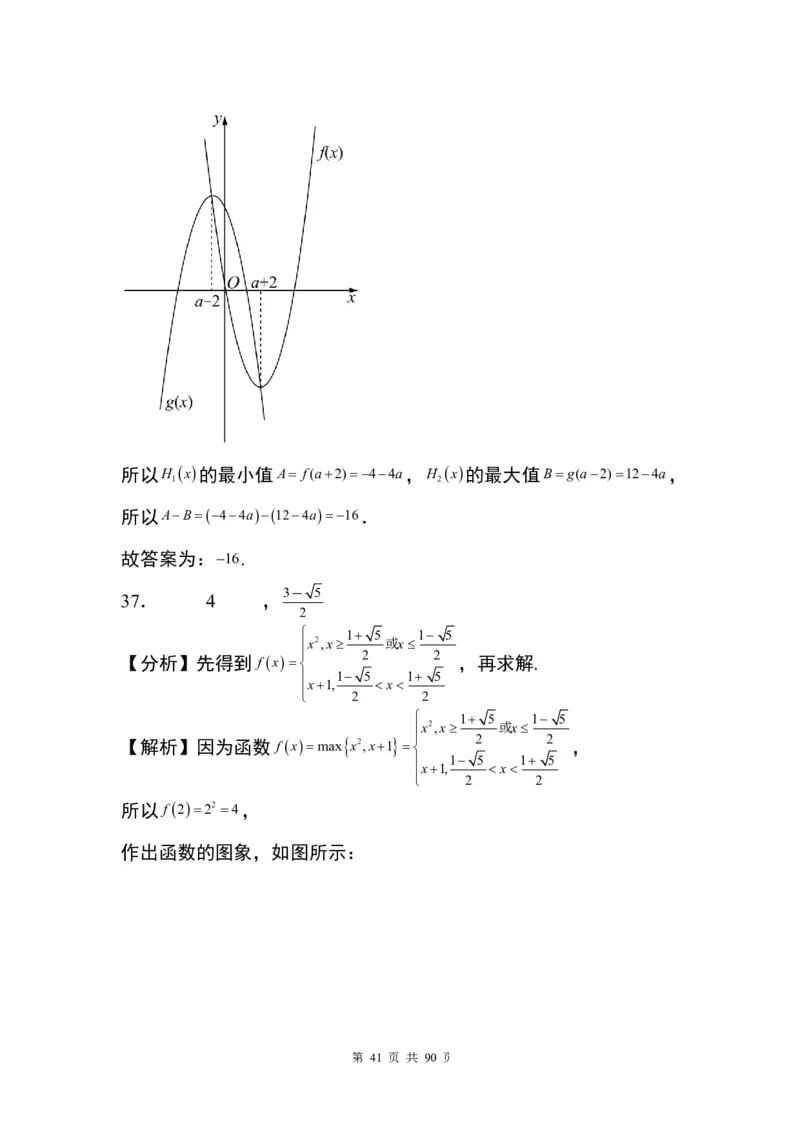2 【解析】 f x xa2  2 44a ， gx xa2  2 124a ， 令 f xgx，得xa2或xa2． 因为H xmax  f x,g x，H xmin  f x,g x， 1 2 第 40 页 共 90 页所以H x的最小值A f(a2)44a，H x的最大值Bg(a2)124a， 1 2 所以AB44a124a16． 故答案为：16. 37． 4 ，3- 5 2  1 5 1 5 x2,x 或x 【分析】先得到 f x    2 2 ，再求解.  1 5 1 5 x1, x   2 2  1 5 1 5 x2,x 或x 【解析】因为函数 f xmax  x2,x1     2 2 ，  1 5 1 5 x1, x   2 2 所以 f 222 4， 作出函数的图象，如图所示： 第 41 页 共 90 页由图象知，当 x 1 5 时， f(x)的最小值为3- 5， 2 2 故答案为： 4，3- 5 2 38．1 【分析】结合图象可得答案. 【解析】 如图，函数ylog x,y3x 在同一坐标系中， 2 且log 2321，所以M(x)在 x2 时有最小值，即M(2)1. 2 故答案为：1. 39．3 【分析】令 f xx,gxx24x，进而根据题意作出函数图像，数形结 合求解即可. 【解析】解：令 f xx,gxx24x， 解方程 f xgx得函数图像的交点横坐标为x 0,x 3， 1 2 第 42 页 共 90 页所以当 x0 或x3时， f xgx，当0x3时， f xgx， 所以min  x,x24x     x24x,x,03, ， x,x0,3 故令hxmin  x,x24x ，即hx   x24x,x,03, ， x,x0,3 所以作出hx的图像如图， 所以根据图象，当 x0 时，max  min  x,x24x  h33 . 故答案为：3 9 7 40． 5 3  x  x 【分析】分别令 f xmin2x1,3x,2  ，gxmax2x1,3x,2  ，进  2  2 而作出函数图象，利用函数图象数形结合求解即可得答案.  x 【解析】解：令 f xmin2x1,3x,2  ，作出图形如图 1（实线部分），  2  x 由函数图象可知， f xmin2x1,3x,2  在点 A 处取得最大值，  2  x y2 2 9 所以联立  2 解得A ,  ，  y2x1 5 5  x 9 所以 f xmin2x1,3x,2  的最大值为  2 5 第 43 页 共 90 页 x 令gxmax2x1,3x,2  ， 作出图形如图 2（实线部分），  2  x 由函数图象可知，gxmax2x1,3x,2  在点 B 处取得最小值，  2 y3x 2 7 所以联立  解得B ,  ， y2x1 3 3  x 7 所以gxmax2x1,3x,2  的最小值为  2 3 9 7 故答案为： ； 5 3 41．1 【分析】根据题干中max函数的定义，可以得到所求函数为分段函数， 求出每一段的最小值，取其中的最小值即可 第 44 页 共 90 页【解析】令x2x1 x2 得：x3或x1，由题意可得： x2x1,x3  max  x2x1, x2   x2,3x1 ，画出函数对应的图像如下：  x2x1,x1 由图可得：当x1时，max  x2x1, x2 最小，代入解析式可得：最小 值为 1 故答案为：1 42．3. 【分析】将函数 y2x,yx23x5 的图像画在一个坐标系中，根据题 干知取该图中靠上的部分就是 f(x)max{x2,x23x5} 的图像，在这个图 像中找到最低点，最低点的纵坐标就是函数的最小值. 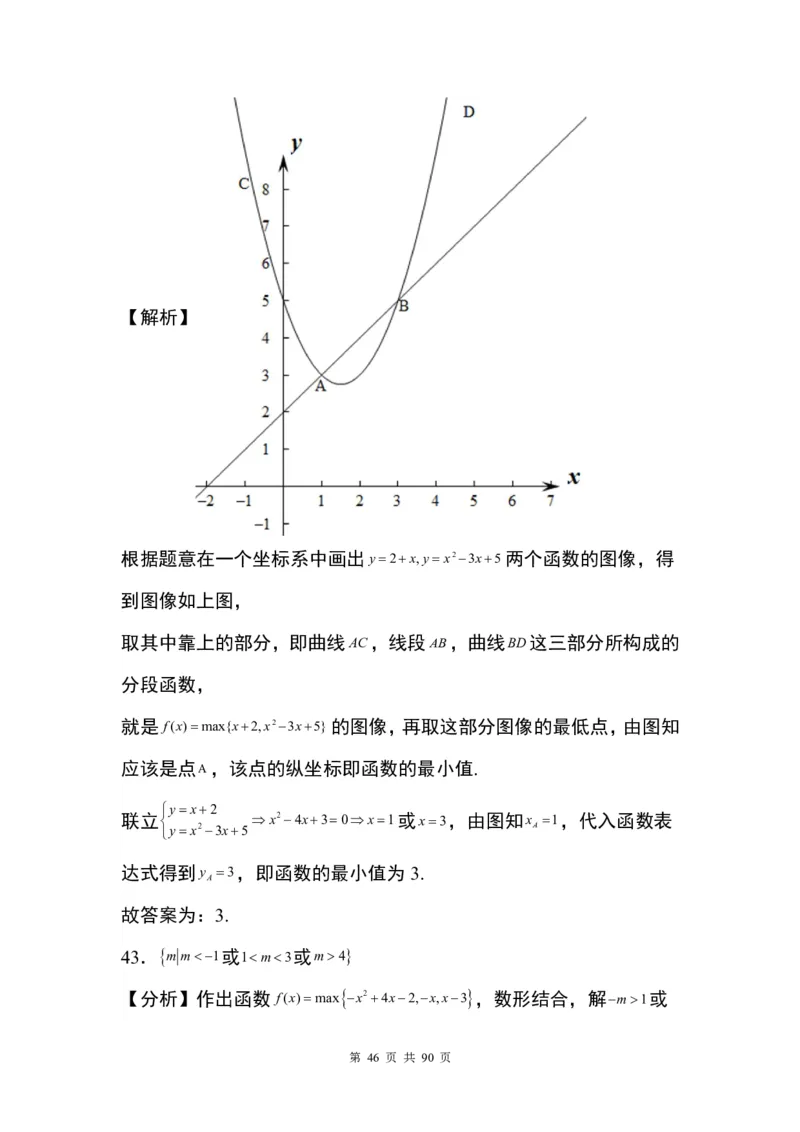第 45 页 共 90 页【解析】 根据题意在一个坐标系中画出 y2x,yx23x5 两个函数的图像，得 到图像如上图， 取其中靠上的部分，即曲线AC，线段 AB ，曲线 BD 这三部分所构成的 分段函数， 就是 f(x)max{x2,x23x5} 的图像，再取这部分图像的最低点，由图知 应该是点 A ，该点的纵坐标即函数的最小值. yx2 联立  x24x30 x1或x3，由图知x 1，代入函数表 yx23x5 A 达式得到y 3，即函数的最小值为 3. A 故答案为：3. 43． m m1或1m3或m4 【分析】作出函数 f(x)max  x24x2,x,x3 ，数形结合，解m1或 第 46 页 共 90 页m24m21 或m31即可得答案. 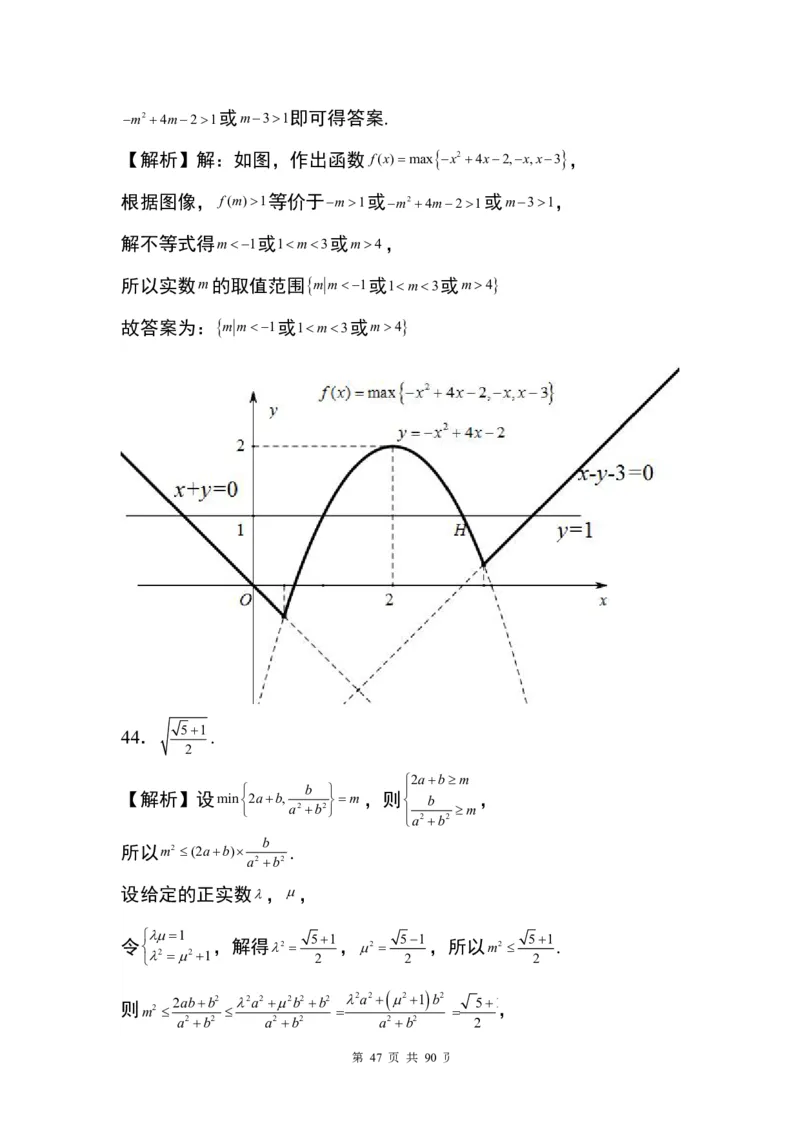【解析】解：如图，作出函数 f(x)max  x24x2,x,x3 ， 根据图像， f(m)1等价于m1或 m24m21 或m31， 解不等式得m1或1m3或m4， 所以实数m的取值范围 m m1或1m3或m4 故答案为： m m1或1m3或m4 44． 51 . 2 2abm  b   【解析】设min2ab, m ，则  b ，  a2b2  m a2b2 b 所以m2 (2ab) . a2b2 设给定的正实数，， 令   1 ，解得 2  51，2  51，所以 m2  51 . 2 21 2 2 2 则 2abb2 2a2 2b2 b2 2a2  21  b2 51， m2     a2b2 a2b2 a2b2 2 第 47 页 共 90 页2 51 当且仅当a ，b 时等号均成立， 2 51 51 2 51 51 故m的最大值为 51 , 2 故答案为： 51 . 2 1 4 45． 4 9 【分析】设 a,b,c0,a c ，然后分bmin{a,b,c}，cmin{a,b,c}讨论，再验 证得解min{a,b,c}的最大值；显然 b24ac 0 ，分amax{a,b,c}和bmax{a,b,c} 讨论可得max{a,b,c}的最小值. 【解析】设 a,b,c0,a c ， 若bmin{a,b,c}，则 c2 b2 4ac 4c2，矛盾； 1 若cmin{a,b,c}，则 b2 4ac 4c2 ，则b 2c，于是1abc 4c，解得c ， 4 此时取 f(x) 1 x22x1 ，此时函数零点为x=1，满足条件，故min{a,b,c} 4 1 的最大值为 ； 4 由题 b24ac 0 ， 若amax{a,b,c}（c同理可得），则 b2 4ac 4bc ，则b 4c,a b 4c， 1 8 则1abc4c4cc9c ，则c ，ab1c ， 9 9 4 4 a ，则max{a,b,c}的最小值是 ； 9 9 4 16 4 若bmax{a,b,c}，假设b ，则4acb2  ，则ac ， 9 81 81 5 1 1 而ac1b ，所以(ac)2 (ac)24ac ，则ac （设ac）， 9 9 3 5 1  4 4 所以 acac 9 3 4 ，则ab 矛盾，所以b ， a   9 9 2 2 9 此时 f(x) 1 4x24x1 ，零点x 1 满足条件， 9 2 第 48 页 共 90 页1 若b0，则min{a,b,c}b0  ，max{a,b,c}b； 4 1 4 综上，min{a,b,c}的最大值是 ，max{a,b,c}的最小值是 . 4 9 1 4 故答案为： ； . 4 9 46．3 【分析】在同一坐标系作出 yx24,yx2,yx3 的图象，然后根据 f x的函数定义得到其函数图象，由图象可求解出 f x的最小值. 【解析】在同一坐标系作出 yx24,yx2,yx3 的图象如下图： 根据取最大值函数的定义可知 f x的图象如下图所示： 根据 f x的图象可知， f x的最小值在 yx2 4, yx2 的一个交点处 取到， 令 x24x2 ，解得x=1或 x2 （舍）， 所以 f x 1243 ， min 第 49 页 共 90 页故答案为：3. 【点评】思路点睛：求解形如ymax  f x,gx（或ymin  f x,gx） 的函数的最小值（或最大值）的步骤： （1）根据 f xgx，先求解出两个图象交点的横坐标； （2）根据 f x,gx图象的相对位置对图象进行取舍，由此得到 ymax  f x,gx（或ymin  f x,gx）的函数图象； （3）直接根据函数图象确定出最大值（或最小值）. 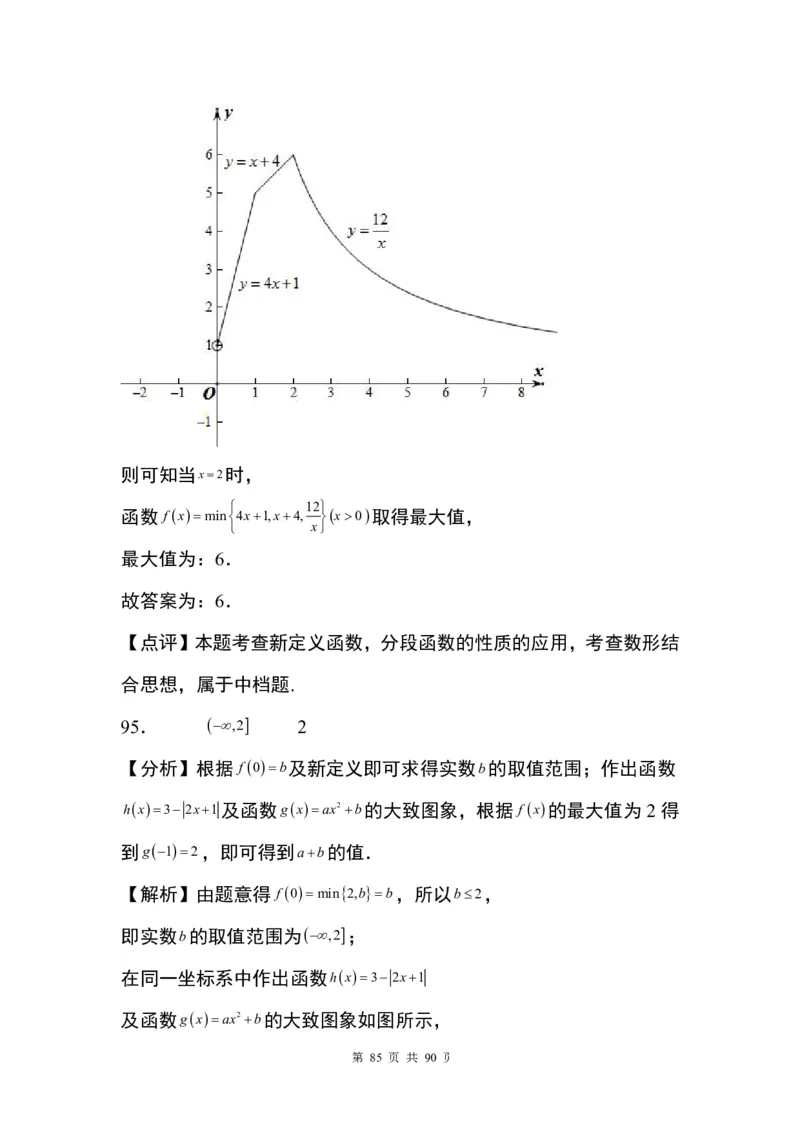47．4 【分析】由定义确定 的解析式，然后由函数的性质得结论． M 【解析】 y2x是增函数，y2x3是增函数，y6x是减函数， x2时， 2x 2x2x3 ， 0 x2 时， 2x 22x3 ， x0 时， 2x 02x3 ， 所以 2x 2x3 ，所以M max  2x,2x3,6x  max{2x,6x}， 6x,x2 又 y2x与y6x的交点是(2,4)，所以M  ，它在(,2]上递减， 2x,x2 在[2,)上递增， 所以 x2 时，M 4． min 故答案为：4． 【点评】思路点睛：本题考查新定义函数，求新定义函数的最值．一 般方法是作出函数图象，由图象得出新函数的图象与解析式，从而得 出新函数性质，本题中由于有两个式子的大小关系是确定的，因此三 个式子的最值转化为两个数的最值，只要考虑这两个函数的单调性即 易得结论． 第 50 页 共 90 页 3 5  48．  , 5  5   x y,(x2y 0) 【分析】原题等价于z 满足 x2 y2 1 区域部分，根据图 2xy,(x2y0) 形可以求出. 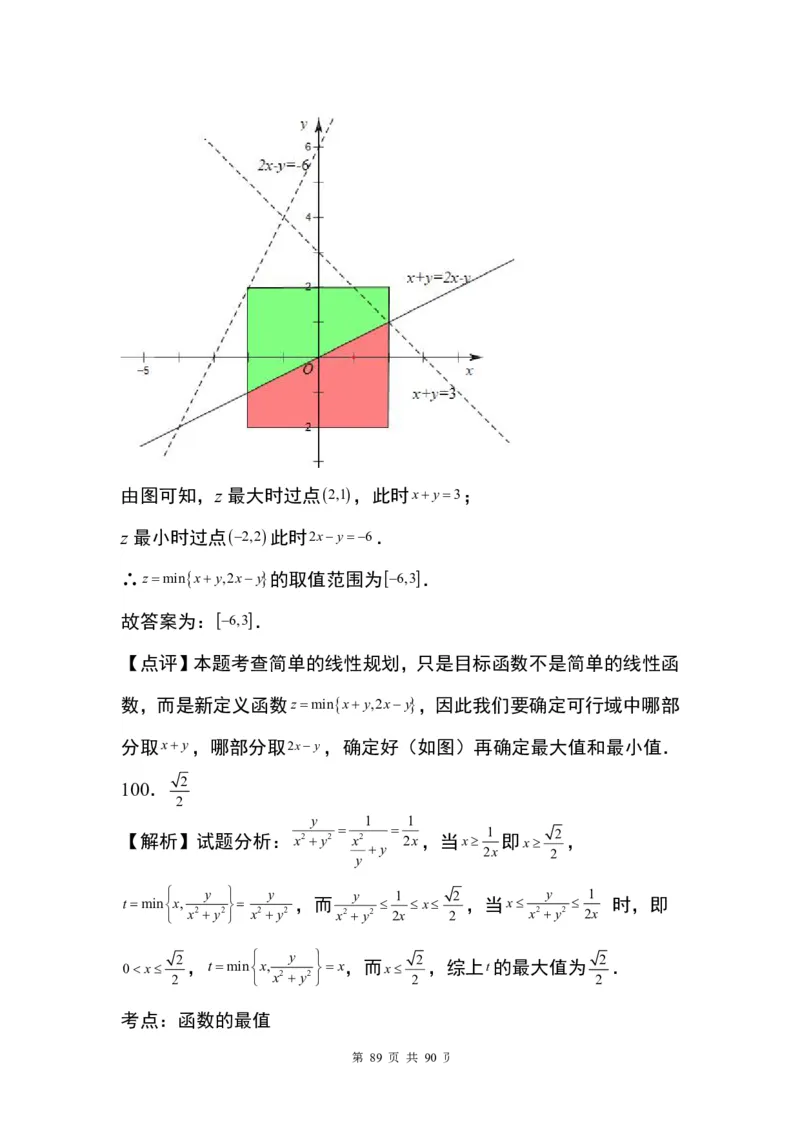【解析】(x+y)-(2x-y)=-x+2y，  x y,(x2y 0) 设方程x2y0对应的直线为 AB，z  ， 2xy,(x2y0) 直线为 AB 将约束条件 x2 y2 1 所确定的平面区域分为两部分，令 z = x+y，点(x,y)在半圆 ACB 上及其内部， 1 如图求得- 3 5 z 2 ； 5 1 令z =2x- y，点(x，y)在半圆 ADB 上及其内部(除 AB 边)，求得 2 - 3 5 z 5 ， 5 2 如图， 第 51 页 共 90 页 3 5  综上可知，z 的取值范围为  , 5.  5   3 5  故答案为：  , 5.  5  【点评】本题考查不等式比较大小，考查不等式表示的平面区域，利 用数形结合解决是有效途径. 49．2 【分析】本道题是一道数形结合题型，通过绘图，结合图形理解，发 现gx必过0,2点，代入，即可． 2 2  T=  4 【解析】令kxsin x，mxx22x2，可知kx周期为 w  ， 2 2 b 2 故关于 x=1 对称，而mx也是关于x  1对称，故 f x关于x1 2a 21 对称，在1,1上，kx递增，而mx递减，mx递增,故 f x kxmx 递增，在1,3 上，kx递减，mx递增，mx递减,故 f x kxmx递 减，当x0, f x2，故0,2在 f x上,绘制出hx的图像.实线为hx的 图像. 第 52 页 共 90 页而hxmin  f x,gx ,而hx最大值为 2，所以0,2必为 f x,gx的交点， 故0,2也在gx xt 上,所以代入gx的解析式中，得到 0t 2，而t0， 所以 t=2. 【点评】本题以新定义为背景，考查函数的图象与性质，考查数形结 合的思想方法，解题关键抓住函数 f x的图象与性质,属于中档题. 50． 3 32 5 4 【分析】先表示出 f x的解析式，然后作出 f x的图象，根据图象求 3  解出最大值；结合图象分析值域为 ,2 时定义域的情况，由此确定出   4  m,n的取值情况，即可求nm的最大值. 【解析】当x23x3 x33时，解得x1或x3，  x3 3,x,13, 所以 f x ， x23x3,x1,3 作出 f x的图象如下图所示： 第 53 页 共 90 页由图象可知：当x3时， f x有最大值，所以 f x  f 33； max 当 f x 3 时，解得x 3 或 3 或21； 4 4 2 4 当 f x2时， x 3 5或 x4 ， 2 由图象可知：当m   3 , 3  ， n 3 5 时， f x的值域为   3 ,2   ，此时nm 4 2 2 4  的最大值为3 5 3 32 5 ；   2 4 4 当m4,n 21 时， f x的值域为   3 ,2   ，此时 nm 5  32 5， 4 4  4 4 由上可知，nm的最大值为32 5， 4 故答案为：3；32 5 . 4 【点评】思路点睛：本题考查取最小值函数的应用，处理这一类函数 时，图象法是首选方法，通过数形结合的思想能高效的将问题简化. 常见的图象应用的命题角度有：（1）确定方程根的数目；（2）求参数 范围；（3）解不等式；（4）研究函数性质. 51． 10, 【分析】设gxx2ax3a5，hx x 2，分析可知函数gx至少有一 个零点，可得出0 ，求出a的取值范围，然后对实数a的取值范围进 行分类讨论，根据题意可得出关于实数a的不等式，综合可求得实数a 的取值范围. 【解析】设gxx2ax3a5，hx x 2，由 x 20可得x2. 第 54 页 共 90 页要使得函数 f x至少有3个零点，则函数gx至少有一个零点，则 a212a200 ， 解得a2或a10. ①当a2时，gx x22x1，作出函数gx、hx的图象如下图所示： 此时函数 f x只有两个零点，不合乎题意； ②当a2时，设函数gx的两个零点分别为x、x x x ， 1 2 1 2 要使得函数 f x至少有3个零点，则x 2， 2 a  2 所以， 2 ，解得a；  g245a50 ③当a10时，gxx210x25，作出函数gx、hx的图象如下图所示： 由图可知，函数 f x的零点个数为3，合乎题意； ④当a10时，设函数gx的两个零点分别为x 、x x x ， 3 4 3 4 要使得函数 f x至少有3个零点，则x 2， 3 第 55 页 共 90 页a  2 可得 2 ，解得 a4 ，此时a10.  g24a50 综上所述，实数a的取值范围是 10,. 故答案为： 10,. 【点评】方法点睛：已知函数有零点（方程有根）求参数值（取值范 围）常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参 数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解 决； （3）数形结合法：先对解析式变形，进而构造两个函数，然后在同 一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.  1   1 52．   ,00,   2   2 【分析】根据题意求出 f(x)解析式，然后画出 f(x)的图象，再由对任意 xR ，都有 f(x2) f(x)，可得将 f(x)的图象向右平移 2 个单位后，图 象在y f(x)的非下方，结合图象得 4t2(4t2)2 ，从而可求得结果. 【解析】因为函数 f(x)是定义域为 R 的奇函数，所以 f(0)0， x2 x x 当x0时，由   2t2，得 x 2t2， t2 2 2  x  2t2,x 2t2 x2 x x    2 所以 f(x)min  , 2t 2 ， t2 2 2  x2  x ,0 x 2t2 t2 2 因为 f(x)是定义域为 R 的奇函数， 第 56 页 共 90 页 x  2t2,x 2t2   2 所以当 x0 时， f(x) ，   x2  x , 2t2 x0  t2 2 当 x 2t2时，由 f(x)0，得 x4t2， 当 x 2t2时，由 f(x)0，得 x4t2， 所以 f(x)的图象如下图， 因为对任意xR ，都有 f(x2) f(x)， 所以将 f(x)的图象向右平移 2 个单位后，图象在y f(x)的非下方， 1 1 所以 4t2(4t2)2 且 t0 ，解得 t ，且 t0 ，即实数 t 的取值范围是 2 2  1   1   ,00,  ，  2   2  1   1 故答案为：   ,00,   2   2 【点评】关键点点睛：此题考查函数奇偶性的应用，考查分段函数， 考查不等式恒成立问题，解题的关键是根据题意求出函数析式，画出 图象，结合函数图象求解，考查数形结合的思想，属于较难题. 1 53．1 20202 1 【解析】解析：最大值为1 ． 20202 a i S  min i ,x 1a ,x 1 x x x 记 1i2020 1 i a i k1 k 0 ，则a i  x i x i1 ，故S  i x i1 1 x i1，即 k i i k1 x 1S  i1 ，对i1,2,3,,2020, x i 求和，并结合算术-几何平均不等式， 第 57 页 共 90 页1 有 2020(1S) 2  020 x i12020   x 0   2020  2020  2020 ， i1 x i x 2020  20202 20202 1 故S 1 ，等号当 a (20202)i (20202)i1(i1,2,3,,2020) 时取到． 20202 i 1 所以原式的最大值为1 ． 20202 1 故答案为：1 . 20202 54．1 2 b 1 1 1 【解析】根据均值不等式得到  ，考虑a 和a 两种情况， a24b2 4a 4a 4a 计算最大值得到答案. b 1 1 1    【解析】a24b2 a2 a2 4a ， 4b 2 4b b b 1 1  b  b 1 1 当a ，即a 时，hmina,    ， 4a 2  a24b2 a24b2 4a 2 1 1 a ，b 时等号成立； 2 4 1 1  b  1 当a ，即a 时，hmina,  . 4a 2  a24b2 2 综上所述：h 的最大值是1 . 2 故答案为：1 . 2 【点评】本题考查了利用均值不等式求最值，意在考查学生的计算能 力和转化能力，分类讨论是解题的关键. 55． 2 . 8 2x 【分析】根据取小定义， f(x)g(x) 2g(x)，则有 x28 1 1 1 2 g(x)    8 8 4 2 8 ， f(x)情况相同，即可得解. x 2 x x x 【解析】由题意可得：当 f(x)g(x)时，有： minf(x),g(x)g(x)， 第 58 页 共 90 页2x 那么 f(x)g(x) 2g(x)， x28 1 1 1 2 g(x)    即当x0时， 8 8 4 2 8 ， x 2 x x x 当x=0时，g(x)0，故 g(x) 2 ， 8 当 f(x) g(x)，同理可得 f(x) 2 ， 8 x 显然，当 f(x) g(x) ， x28 f(x)和g(x)都可取到最大值 2 ， 8 综上可得：min｛f(x)，g(x)｝的最大值为 2 . 8 【点评】本题考查了取小新定义，考查了基本不等式求最值，同时考 查了推理运算能力，属于较难题. 56．1 2 【分析】min  8x,8xy,8y1，花括号内三个数的底数相同，则对其指数进 1 行比较，当x为最小时，得到x ，并求出最小值 8x的最大值，然后 3 1 讨论当0 x 时，分别研究当xy最小，和y1最小时，对应的范围， 3 从而得到每种情况下的最大值，并对三中情况进行判断，从而得到结 果. 【解析】x、y∈（0，1）时，min  8x,8xy,8y1 可知花括号内三个数的底数相同，则对其指数进行比较， xxy y2x ①当x为最小时，  ，得 x y1 y1x 1 所以1x2x ，即x ， 3 此时 min  8x,8xy,8y1 8x 8  1 3  1 ； 2 1 当0 x ，则y1或者xy为最小， 3 第 59 页 共 90 页1x ②当y1为最小时，y1 xy，则y ， 2 1 1 1x 3 1 y1 1 1 2 2 3 此时 min  8x,8xy,8y1 8y18  1 3  1 ， 2 1x ③当xy为最小时，xy y1，则y ， 2 1x 1 x 1 xyx     2  2 2 3 此时 min  8x,8xy,8y1 8xy 8  1 3  1 ， 2 所以，综上所述，min  8x,8xy,8y1的最大值为1 ， 2 故答案为1 . 2 【点评】本题考查运用函数思想解决问题，考查了函数的值域，不等 式的性质，对抽象思维要求较高，属于难题. 3 5 1 57． ,    4 3 【解析】用a、b、c分别表示BC、CA、 AB 的长度，不妨设abc. 接下来求a的取值范围. 1 当ABC为正三角形时，符合题意，此时，a取得最大值 . 3 下面求a的最小值： 令cxa，b ya.则x y1. 注意到，此时ABC不为正三角形.故x1. 由三角形三边关系有abc y x1. 2S 2S 2S 1 1 1 x 设ABC的面积为 S.则由题设条件有       y . c b a b a c x1 综上， x1 x x 3 5 . x1 2 x 1 注意到，1x y1x  x1 3. x1 x1 第 60 页 共 90 页1 令 f x x1 3. x1 当1x2时，1x y12x5. 当x2时， f x取最小值 5，并在区间2,上单调递增. 因为 x 3 5 ，所以， f x f    3 5   3 5 5. 2  2  又a1xy1，则a 1  3 5 . 3 5 4 当3 5 a 52 时，可令 b 1 5 a ，c1ab； 4 2 1 1a 当 52a 时，可令bc . 3 2 不难验证，此时题设条件均可得到满足. 综上，所求a的取值范围是3 5 a 1 . 4 3 1 58． /0.5 2 ab 【分析】根据给定条件，借助基本不等式求出 的最大值即得. a2 4b2 b b 【解析】令hmin{a, }，a0,b0，于是0ha，0h ， a24b2 a24b2 ab b 则h2  ，当且仅当a 时取等号， a24b2 a24b2 ab 1 1 1    而a24b2 a 4b a 4b 4，当且仅当a  4b ，即 a2b 时取等号，  2  b a b a b a b 1 1 1 因此当a ，且a2b，即a ,b 时，h  ， a24b2 2 4 max 2 所以min{a, b }的最大值为1 . a24b2 2 故答案为：1 2 b 【点评】思路点睛：令hmin{a, }，由此建立不等式，再利用不 a24b2 等式性质变形，借助基本不等式求解. 8 59． 3 【分析】设gx3x 1，h  x   x2  2x  1，求出h1 g12，结合函数 第 61 页 共 90 页的单调性作出函数的图象，结合图象，即可得出 m2 ， a12b3.根 2 1 1  4b a1  据“1”的代换，推得      4 ，结合基本不等式，即可 a1 b 3 a1 b  得出答案. 【解析】设gx3x 1，h  x   x2  2x  1， 根据指数函数的性质可知，函数gx3x 1在 R 上单调递增，且 g13112； 根据二次函数的性质可知，函数h  x   x2  2x  1在,1上单调递增， 在1,上单调递减，且h112212 g1. 作出函数的图象， 可知 f xmin  3x 1,x22x1 的最大值为 A 点的纵坐标，即h12， 所以 m2 ，a2b2，则 a12b3. 又因为a,b0， 所以， 2 1 1 2 1 1  4b a1  1  4b a1  8 a1  b  3  a1  b   a1 2b 3  a1  b 4   3    2 a1  b 4    3 . 4b a1 1 3 当且仅当  ，且a2b2，即a ，b 时等号成立. a1 b 2 4 2 1 8 所以，  的最小值为 . a1 b 3 8 故答案为： . 3 60．1 第 62 页 共 90 页【分析】根据题意作出函数的图象，进而求出函数的最大值. 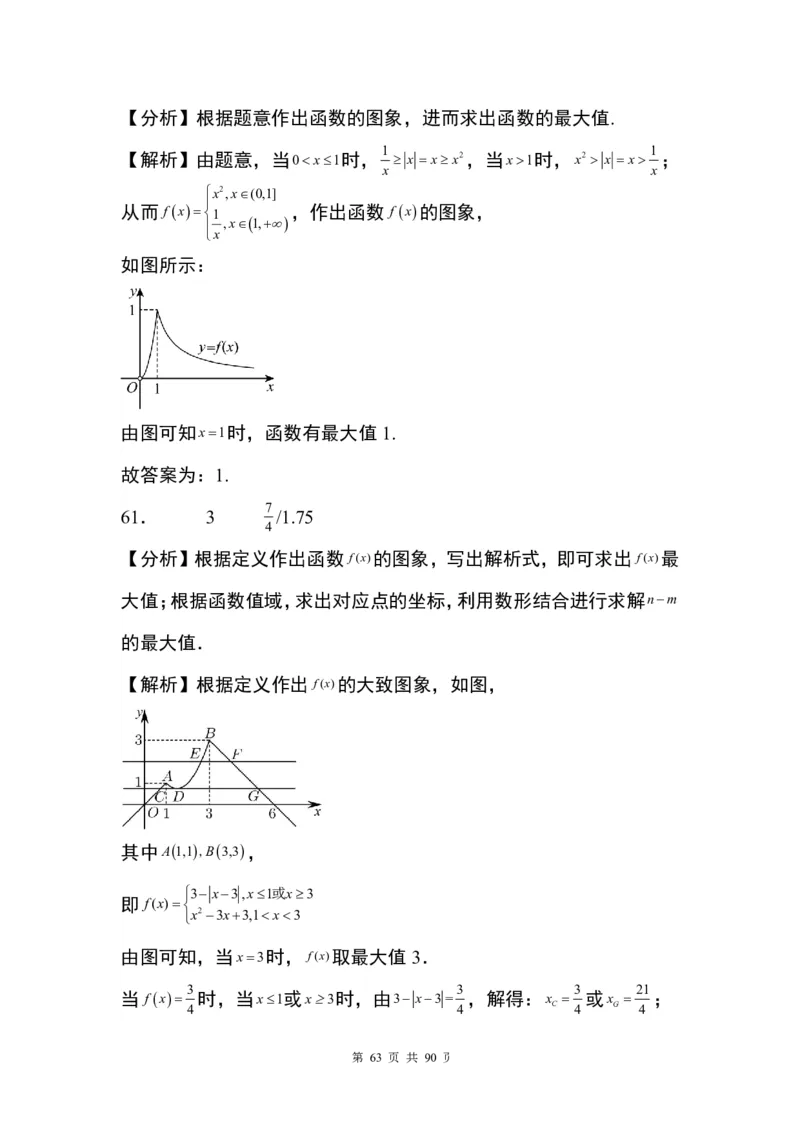1 1 【解析】由题意，当0x1时，  x  x x2，当x1时，x2  x  x ； x x x2,x(0,1]  从而 f x1 ，作出函数 f x的图象，  ,x1, x 如图所示： 由图可知x1时，函数有最大值 1. 故答案为：1. 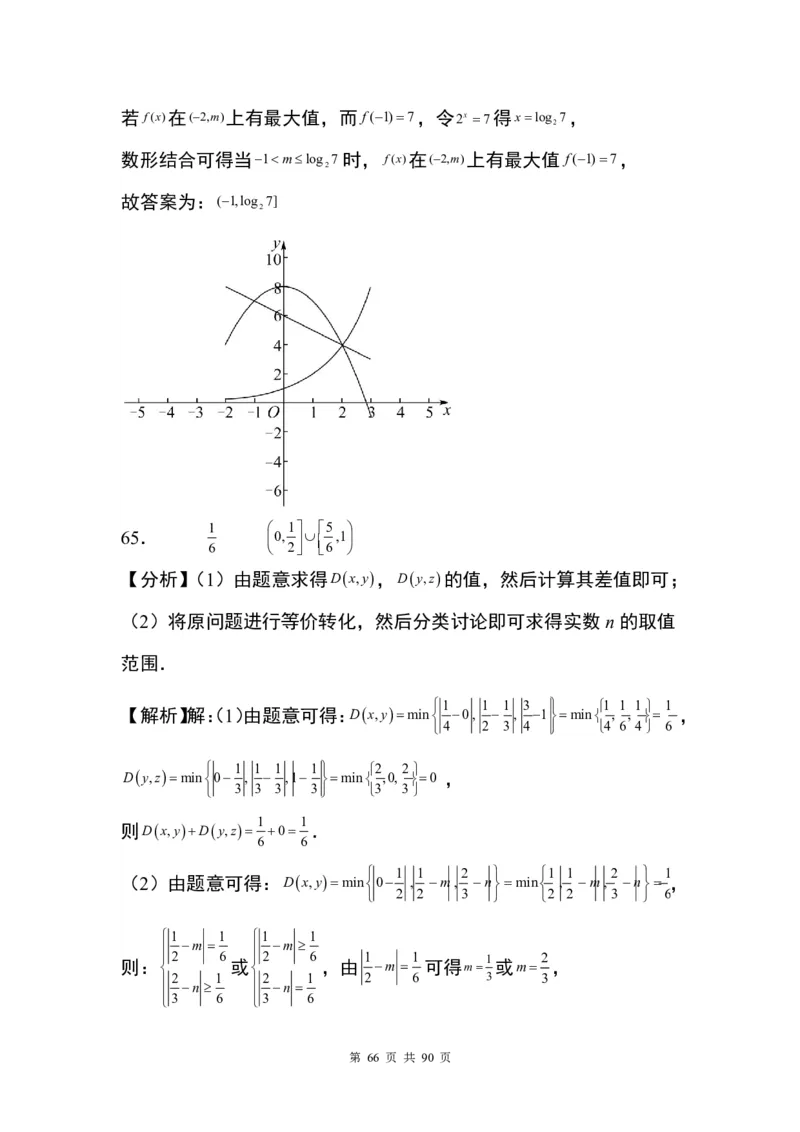7 61． 3 /1.75 4 【分析】根据定义作出函数 f(x)的图象，写出解析式，即可求出 f(x)最 大值；根据函数值域，求出对应点的坐标，利用数形结合进行求解nm 的最大值． 【解析】根据定义作出 f(x)的大致图象，如图， 其中A1,1,B3,3， 3 x3,x1或x3 即 f(x) x23x3,1x3 由图可知，当x3时， f(x)取最大值 3． 3 3 3 21 当 f x 时，当x1或x3时，由3x3= ，解得：x  或x  ； 4 4 C 4 G 4 第 63 页 共 90 页7 7 5 当 f x 时，当1x3时，由x23x3 ，解得：x  ． 4 4 E 2 3 7 由图可知，若函数 f x在区间 m,n 上的值域为 , ，则nm最大值为   4 4 5 3 7 x x =  = ． E C 2 4 4 7 故答案为：3， ． 4 62．3 【分析】①由大角对大边，结合倍角正余弦公式及充分、必要性的关 系判断；②由幂函数求参数 m，注意验证区间单调性；③由弦化切化 简求值即可；④根据函数定义，由正余弦函数的性质比较大小写出 f x的分段形式，进而确定其值域. 【解析】①当 AB ，则ab，故00， 所以0