文档内容
2023-2024学年南京师大附中高三年级寒假模拟测试
数 学 学 科 参 考 答 案
第 I卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要
求的.
1 2 3 4 5 6 7 8
C D C C D D B B
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选
对的得6分,部分选对得部分分,有错选得0分.
9 10 11
ACD ACD AD
第 II 卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
5 2
12. 13. 7 14. 8−
6 2
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(1)由题意可知 lgx−1 <1⇒−10,设E(x,y ),F(x ,y ),P(m,0),则x +x =
24k2
,xx =
36k2−3
.
1 1 2 2 1 2 3+4k2 1 2 3+4k2
∠APE=∠OPF ,
y y
k(x −3)(x −m)+k(x −3)(x −m)
∴k +k = 1 + 2 = 1 2 2 1
PE PF x −m x −m (x −m)(x −m)
1 2 1 2
72k2−6 24k2
=k⋅
2x
1
x
2
−(3+m)(x
1
+x
2
)+6m
=k⋅
3+4k2 −(3+m)⋅ 3+4k2 +6m
(x −m)(x −m) (x −m)(x −m)
1 2 1 2
72k2−6−72k2−24mk2+18m+24mk2
=k⋅
(x −m)(x −m)⋅ ( 3+4k2)
=0.
1 2
1
∴18m−6=0,∴m= .
3
存在P点满足条件.
1
∴P点坐标为 ,0.
3
18.(1)因为点N 为线段AD的中点,且EA=ED,
所以AD⊥EN,
因为EF∥AB,且四边形ABCD为正方形,故AD⊥AB,
所以AD⊥EF ,而ENEF =E,EN,EF ⊂平面EFN,
故AD⊥平面EFN,又FN ⊂平面EFN,
所以AD⊥FN;
(2)设正方形ABCD的中心为O,分别取AB,BC,EF的中点为P,Q,S,
设点H为线段AD的中点,由(1)知E,F,H,Q四点共面,且AD⊥平面EFH ,
连接OS,OS⊂平面EFH ,故AD⊥OS,
又AD⊂平面ABCD,故平面ABCD⊥平面EHQF,
且平面ABCD∩平面EHQF =HQ,
学科网(北京)股份有限公司由题意可知四边形EHQF为等腰梯形,故OS ⊥HQ,
OS⊂平面EHQF,故OS ⊥平面ABCD,
故以O为坐标原点,OP,OQ,OS为x,y,z轴建立空间直角坐标系,
因为AB=4,则A(2,−2,0),B(2,2,0),C(−2,2,0),D(−2,−2,0),又AB=2EF,故EF =2,
设EF到底面ABCD的距离为h,
四边形ABFE,CDEF为两个全等的等腰梯形,且EF∥AB,
故E(0,−1,h),F(0,1,h),又EA=ED=FB=FC =3,
故 22+12+h2 =3,∴h=2,则E(0,−1,2),F(0,1,2),
AE=(−2,1,2),AD=(−4,0,0),BF =(−2,−1,2),BA=(0,−4,0),
设AN =λAD,λ∈[ 0,1 ] ,∴BN =BA+AN =BA+λAD=(−4λ,−4,0),
设平面BFN的一个法向量为n=(x,y,z),
n⋅BF =−2x−y+2z=0
则 ,令x=2,∴n=(2,−2λ,2−λ),
n⋅BN =−4λx−4y=0
设平面ADE的一个法向量为m=(a,b,c),
m⋅AD=−4a=0
则 ,令c=1,∴m=(0,−2,1),
m⋅AE=−2a+b+2c=0
2
2
λ+
故 m⋅n 3λ+2 3 3 ,
cosn,m = = =
m⋅ n 5× 5λ2−4λ+8 5 5λ2−4λ+8
3 m2
2 2 5 cosn,m=
令m=λ+ 3 ,m∈ 3 , 3 ,则 5 5m2− 32 m+ 116 ,
3 9
3 1
1 3 3 cosn,m=
令t = m ,t∈ 5 , 2 ,则 5 116 t2− 32 t+5 ,
9 3
学科网(北京)股份有限公司116 32 3 3
令 f (t)= t2− t+5,则 f (t)在 , 上单调递增,
9 3 5 2
故当t= 3 时, f (t) = f 3 = 81 ,当t= 3 时, f (t) = f 3 =18,
5 min 5 25 2 max 2
10 5
故cosn,m∈ , ,
10 3
10 5
即平面BFN和平面ADE的夹角的余弦值得取值范围为 , .
10 3
x2
(2x)2 (2y)2 −y2 =1
19.(1)由条件得 − =1 ,得C : 9 ;
2
9 4
4
(2)∵C 、C 关于原点“伸缩变换”,对C 作变换(x,y)→(λx,λy)(λ>0),得到C
λ2x2
+
λ2y2
=1,
2 1 1 2 16 4
2
y= x(x≥0)
2 4 3 2 6
解方程组 得点A的坐标为
,
;
x2 y2 3 3
+ =1
16
4
2
y= x(x≥0)
2 4 3 2 6
解方程组 得B点的坐标为
,
;
λ2x2 λ2y2 3λ 3λ
+ =1
16 4
2 2
4 3 4 3 2 6 2 6 2 2λ−1
AB = − + − = = 2,
3λ 3 3λ 3 λ
2
化简后得3λ2−8λ+4=0,解得λ=2,λ = ,
1 2 3
x2 x2 y2
因此椭圆C 的方程为 +y2 =1或 + =1.
2
4 36 9
2p
(3)对C :y2 =2p x作变换(x,y)→(λx,λy)得抛物线C :(λy)2 =2pλx,得y2 = n x,
n n n n n+1 n n n λ
n
p p 1
又∵y2 =2p x,∴p = n ,即 n+1 = =2n,
n+1 n+1 λ p λ
n n n
p 2 ⋅ p 3 ⋅ p 4 ⋅⋅⋅⋅⋅ p n−1 ⋅ p n =2⋅22⋅23⋅⋅⋅⋅⋅⋅2n−1,则 p n =21+2+3+⋅⋅⋅+(n−1) =2 1 2 n(n−1) ,
p p p p p p
1 2 3 n−2 n−1 1
∵p 1 =1,∴ p =2 1 2 n(n−1) .
n
20.(1)X 可取值10,20,30,,,Y可取值10,20,,1000,
k
当X =k时,摸球次数为 ,没有抽中新皮肤的概率为1− p ,
10 1
学科网(北京)股份有限公司故 P(X =k)=(1− p ) 1 k 0 −1 p , k ∈N*,
1 1 10
(1− p ) 1 k 0 −1 p , k ∈N*,k ≤990
P(Y =k)= 2 2 10 .
(1− p 2 )99 ,k =1000
n
(2)令A=∑t(1− p )t−1,
1
t=1
n
则(1− p )A=∑t(1− p )t,故p A=1+(1− p )+(1− p )2+(1− p )n−1−n(1− p )n,
1 1 1 1 1 1 1
t=1
1−(1− p )n
整理得到p A= 1 −n(1− p )n,
1 p 1
1
所以 A= 1−(1− p 1 )n − n(1− p 1 )n ,
p2 p
1 1
k
若玩家按方案一抽卡,花费k元时抽到皮肤,则抽取次数为 ,
10
而 P(X =s)= p (1− p ) 1 s 0 −1,其中 s ∈N*,s≤k.
1 1 10
k k
则 E(X)=∑ 10 s(1− p ) 1 s 0 −1 p =10p ∑ 10 s (1− p ) 1 s 0 −1
1 1 1 10 1
s=1 s=1
k
=10 1−(1− p 1 ) 10 −k(1− p ) 1 k 0 ,
p 1
1
因为玩家按方案一抽卡次数无限制,
k k
且当n→+∞时, k(1− p ) 10 →0 ,(1− p ) 10 →0 ,
1 1
10
所以E(X)=
.
p
1
(3)p =2p =0.02,即p =0.02,p =0.01,
1 2 1 2
10
由(2)可得故E(X)= =500;
0.02
若玩家按方案二抽卡,则Y可取值10,20,,1000,
i
且 P(Y =i)=0.01×0.9910 −1,其中i=10,20,,990,
P(Y =1000)=0.9999,
99
故E(Y)=1000×0.9999+10∑( k×0.01×0.99k−1)
,
k=1
学科网(北京)股份有限公司99
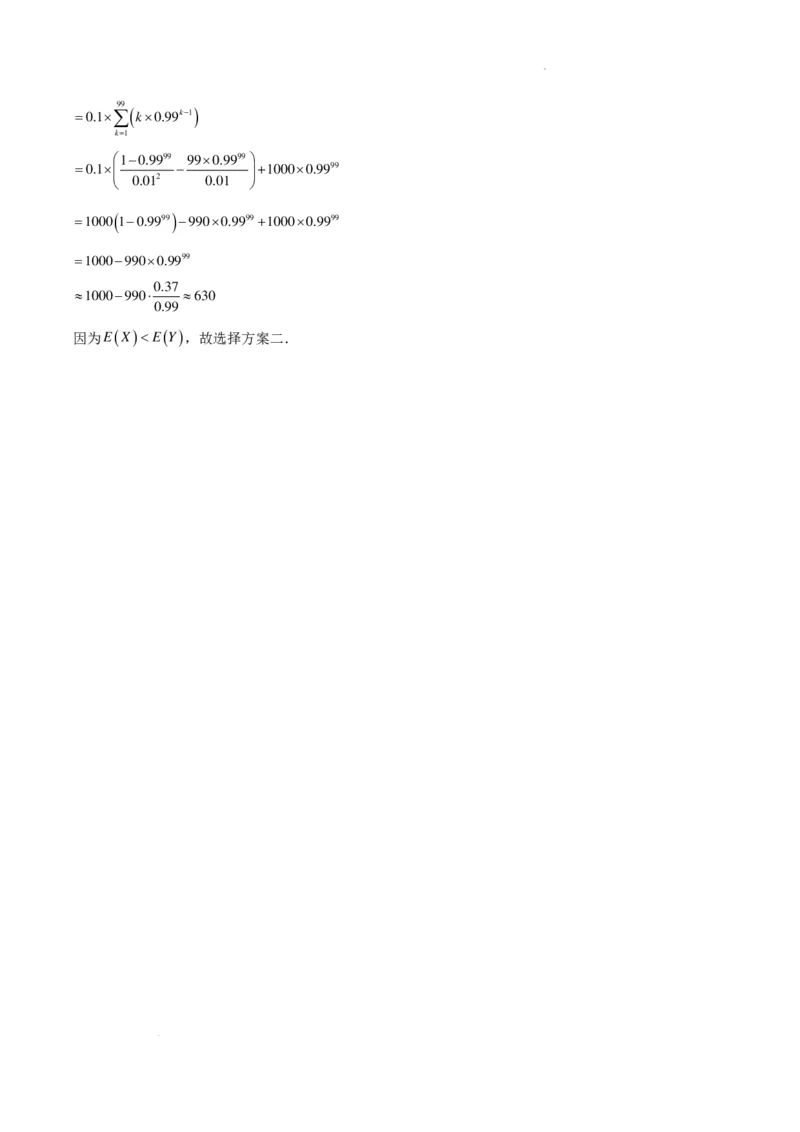
=0.1×∑( k×0.99k−1)
k=1
1−0.9999 99×0.9999
=0.1× − +1000×0.9999
0.012 0.01
=1000 ( 1−0.9999) −990×0.9999+1000×0.9999
=1000−990×0.9999
0.37
≈1000−990⋅ ≈630
0.99
因为E(X)