南京市高三六校联考数学答案_2024-2025高三（6-6月题库）_2025年02月试卷_0214江苏南京六校联合体2025届高三下学期2月调研_江苏南京六校联合体2025届高三下学期2月调研数学试卷+答案

2024-2025 学年第二学期六校联合体 2 月学情调研测试
高三数学
一、选择题：本题共 8 小题，每小题 5 分，共 40 分.在每小题给出的四个选
项中，只有一项是符合题目要求的.
1i
1.复数z 满足 i（i为虚数单位），则复数z 的共轭复数z ＝（ ）
z
A．1－i B．－1－i C．1＋i D．－1＋i
【答案】C
    
2.已知向量a （1，0），b  (x,1)，若b(b 2a)  0，则x （ ）
A.2 B.1 C.1 D.2
【答案】C
3．有4辆车停放5个并排车位，货车甲车体较宽，停靠时需要占两个车位，并且乙车与货车甲相邻停
放，则共有多少种停放方法？ （ ）
A．8 B．12 C．16 D．10
【答案】B
4. 设等差数列  a  的前n项和为S ，若S 63S ,a a 12，则  a  的公差为（ ）
n n 12 3 3 12 n
A. 1 B. 2 C. 3 D. 4
【答案】B
 1
5.已知函数 f(x) sin(x )cosx在区间  0，t  上的最小值为 ，则t的最大值为（ ）
6 2
  5 4
A. B. C. D.
6 3 6 3
【答案】D
6.已知点P为直线l:x y20上的一点，过点P作圆C:  x1 2  y1 2 1的切线PA，切点
为A，则 PCA的最大值为 （ ）
2    3 5 7
A. B. C. D.
4 4 4 4
【答案】A
 
f x
7. 定义在R上的奇函数 f  x  在  0, 上单调递增，且 f  1 0，则不等式 0的
4x1172x 4
解集为（ ）A.
2,1 

 2,
B.
,2 

1,0 


1,2

C.
2,1 


0


 2,
D.
2，1 


0,1


 2,
【答案】D
x2 y2
8.双曲线  1(ba0)，F 为双曲线焦点，O为坐标原点，若直线
l
交双曲线于两点A、B，满
a2 b2
足OAOB，若点O到直线l的距离不小于b，则离心率取值范围是（ ）
A．  1，3

B．  

2，, 1 5   C．  2，, 3

D．   1 5 ，, 3  
 2   2 
【答案】C
二、多项选择题：本题共 3 小题，每小题 6 分，共 18 分.在每小题给出的选
项中，有多项符合题目要求.全部选对的得 6 分，有选错的得 0 分，部分选对
的得部分分.
9．一个袋中有大小､形状完全相同的3个小球，颜色分别为红､黄､蓝，从袋中先后无放回地取出2个
球，记“第一次取到红球”为事件A，“第二次取到黄球”为事件B，则
1 － 1
A．P(B)＝ B．P(B|A)＝
3 3
1
C．P(A|B)＝ D．A，B相互独立
2
【答案】AC
10．在棱长为2 3的正方体ABCD—A B C D 中，点E，F分别是棱BC，CC 的中点，下列结论正确
1 1 1 1 1
的有
π
A．直线EF与A B所成的角为
1
4
27
B．经过A，E，F三点的截面面积为
2
  
C．若点P满足BP＝cos2θ·BC＋sin2θ·BB
1
，其中θ∈R，则三棱锥D—A
1
C
1
P体积为定值
D．以B 为球心，4为半径作一个球，则该球面与三棱锥B —ABC表面相交的交线长为3π
1 1
【答案】BCD
11. 定义在  0, 上的函数 f  x  满足 f  x1  f  x x，当0 x1时， f  x  x x1，
则（ ）
A. 当2 x3时， f  x  x23x6B.对任意正实数k, f  x  在区间  k,k1  内恰有一个极大值点
2nn2
C. 当n为正整数时， f  n 
2
193 401
D. 若 f  x  在区间  0,k  内有4个极大值点，则k的取值范围是  , 
 64 100
【答案】ACD
三、填空题：本题共 3 小题，每小题 5 分，共 15 分.
n
 1 
12．在  x   ，nN的展开式中，只有第五项的二项式系数最大，则展开式中x的系数为
 2x
________．【答案】7
 1   1   1 
13．已知等比数列a 中，a 1,a 2，能使不等式a  a  a  0成
n 2024 2025  1 a   2 a   m a 
1 2 m
立最小正整数m=_______________．【答案】4048
14.已知抛物线x2 4y的焦点为F ，直线l过点F 交抛物线于A,B两点，且 AF 4 FB ．直线l、l 分
1 2
别过点A,B，且与y轴平行，在直线l、l 上分别取点M、N（M、N 均在点A,B的上方），分别作ABN
1 2
8 3
和BAM 的角平分线且相交于P点，则PAB的周长为 ．【答案】8
3
四、解答题：本题共 5 小题，共 77 分.解答应写出文字说明、证明过程或演
算步骤.
15．（满分13分）
π
在△ABC中，BC＝3 2，∠BAC＝ ．
3
（1）若AC＝2 3，求sinC；
（2）D为边BC上的点且满足AD平分∠BAC，AD＝ 3，求△ABC的面积．
解析：
    
2 2
（1）法1：由余弦定理可知 3 2  c2  2 3 22 3ccos
3
c2 2 3c6  0
c  33，又c  0,---------------------------------3分
c  33c 3 2
由正弦定理知：  ，
sinC 
sin
3
2  6
sinC  ---------------------------------6分
4
AC 3 2 2
法2：因AC  2 3由正弦定理知：  ，sinB  --------------------2分
sinB  2
sin
3
 
AC  BC,B  A ，B  -------------------4分
3 4
sinC sin(A B) sin AcosBcosAsinB
3 2 1 2 2  6
=     --------------------6分
2 2 2 2 4
  
2
（2）由条件知： 由余弦定理可知 3 2  c2 b2 2bccos
3
18 c2 b2 bc ， 18（bc）2 3bc ① -----------------8分
S  S S
ABC ABD ACD
1 1 1
 ABACsinBAC  ABADsinBAD ADACsinDAC
2 2 2
1 3 1 3 1 3
bc   3b   3c
2 2 2 2 2 2
bc bc ②--------------------10分
由①②得bc  6--------------------12分
1 1 3 3 3
S  bcsin A 6  --------------------13分
ABC
2 2 2 216．（满分15分）
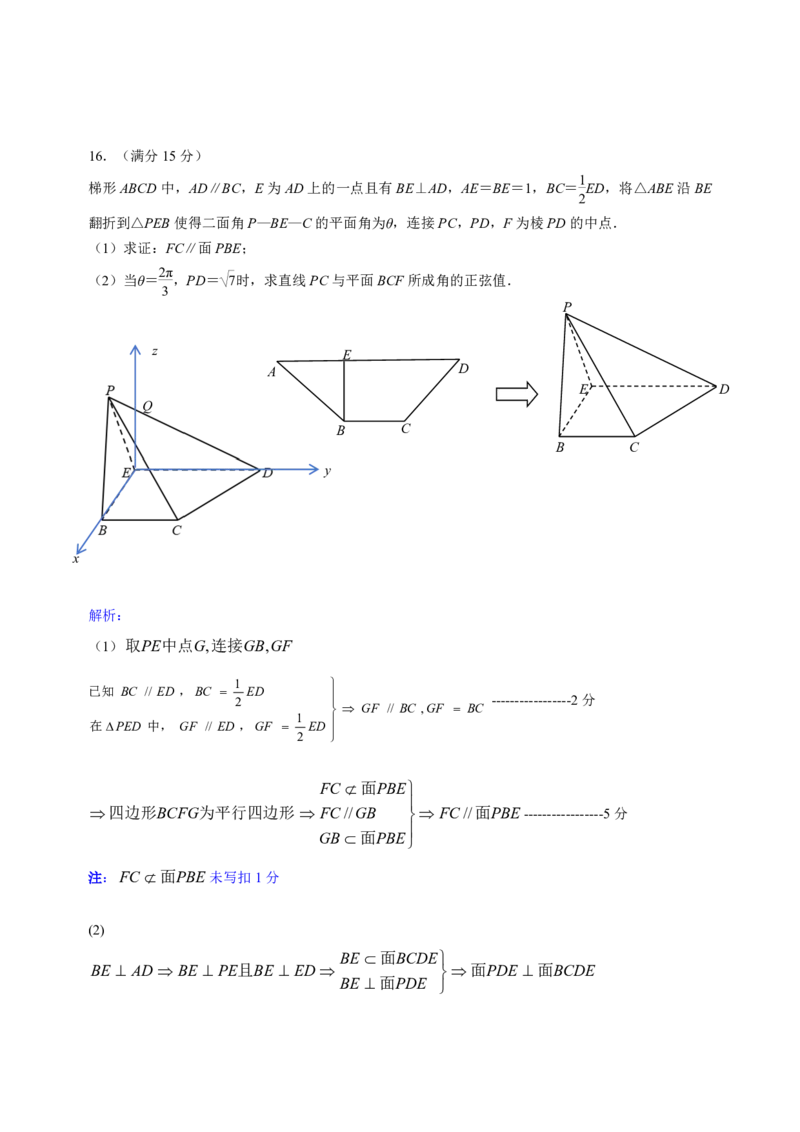
1
梯形ABCD中，AD∥BC，E为AD上的一点且有BE⊥AD，AE＝BE＝1，BC＝ ED，将△ABE沿BE
2
翻折到△PEB使得二面角P—BE—C的平面角为θ，连接PC，PD，F为棱PD的中点．
（1）求证：FC∥面PBE；
2π
（2）当θ＝ ，PD＝ 7时，求直线PC与平面BCF所成角的正弦值．
3
P
z
E
A D
E D
Q
B C
B C
y
x
解析：
（1）取PE中点G,连接GB,GF
1 
已知 BC // ED ，BC  ED
2
 -----------------2分
  GF // BC ,GF  BC
在PED 中， GF // ED ，GF  1 ED 
2

FC 面PBE

四边形BCFG为平行四边形  FC//GB  FC//面PBE-----------------5分

GB 面PBE
注：FC 面PBE未写扣1分
(2)
BE 面BCDE
BE  AD  BE  PE且BE  ED  面PDE 面BCDE
BE 面PDE 在平面PDE内，过点E作EQ  ED交PD于点Q，
DE 面PDE面BCDE
EQ 面BCDE
 
以EB,ED,EQ 为正交基底建立如图坐标系----------------7分
1 3 3 3
P(0, , ),D(0,2,0),F(0, , )
2 2 4 4
B(1,0,0),C(1,1,0)
3 3 3 3
PC  (1, , ),BC  (0.1,0),BF  (1, , ),----------------10分
2 2 4 4
设n  (x,y,z)为面BCF的法向量
y  0
  nBC  0 
则    3  n  ( 3,0,4)----------------12分
 nBF  0  x z  0
 4
 3 57
cos n,PC   ----------------14分
2 19 38
57
sin ----------------15分
38
17．（满分15分）
某运动会有两种不同价格的开幕式门票，某人花a元预定该运动会开幕式门票一张，另外还预定了乒
乓球、羽毛球比赛门票各一张，根据相关规定，从所有预定者中随机抽取相应数量的人，这些人称为
预定成功者，他们可以直接购买门票，另外，对于开幕式门票，有自动降级规定，即当这个人预定的a
元门票未成功时，系统自动使他进入b元开幕式门票的预定.假设获得a元开幕式门票的概率是0.2，
若未成功，仍有0.3的概率获得b元开幕式门票的机会，获得乒乓球、羽毛球门票概率均是0.5，且获
得每张门票之间互不影响.
（1）求这个人可以获得该运动会开幕式门票的概率；
 
（2）假设这个人获得门票总张数是X ，求X 的分布列及数学期望E X ．
17．解：（1）记“获得a元开幕式门票”为事件A，“获得b元开幕式门票”为事件B，“获得开幕式
门票”为事件C ……………………1分
－
则P(A)＝0.2，P(B)＝0.3，P(A)＝0.8－ － 11
P(C)＝P(A)＋P(AB)＝P(A)＋P(A)P(B)＝0.2＋0.8×0.3＝0.44＝ ……………………3分
25
∴这个人可以获得亚运会开幕式门票的概率为0.44
（2）X∈{0，1，2，3}
7
P(X＝0)＝(1－0.44)×0.5×0.5＝0.14＝
50
39
P(X＝1)＝(1－0.44)×0.5×0.5×2＋0.44×0.5×0.5＝0.39＝
100
9
P(X＝2)＝(1－0.44)×0.5×0.5＋0.44×0.5×0.5×2＝0.36＝
25
11
P(X＝3)＝0.44×0.5×0.5＝0.11＝ ……………………12分
100
∴X的分布为
X 0 1 2 3
P 0.14 0.39 0.36 0.11
……………………13分
36
E(X)＝0×0.14＋1×0.39＋2×0.36＋3×0.11＝1.44＝ ……………………15分
25
18．（满分17分）
已知 f(x)3x2sinxklnx．

（1）当k 0时，求曲线 f  x  在x 处的切线方程；
2
（2）当k 1时，讨论函数 f(x)的极值点个数；
（3）若存在t，t R (t t )， f(et 1) f(et 2)，求证：t t 2lnk ．
1 2 1 2 1 2
【答案】
【小问1详解】
当k 0时， f  x 3x2sinx，因为 f x 32cosx，

所以切线的斜率为 f   3， ..........................................................2分
 2
 3 
又因为切点为 ，2，
 2 2 

所以曲线 f  x  在x 处的切线方程为 y3x2 ......................................3分
2
【小问2详解】
1
当k 1时， f (x)3x2sin xln x，则 f(x) 32cosx ，
x
当x1时， ，
f(x) 22cosx  0故 f(x)在
 1,
上单调递增，不存在极值点； ......................................4分
1 1
当0 x 1时， f(x)32cosx ，则 f(x)2sinx 0总成立，
x x2
1 1
故函数 f(x)在(0,1)上单调递增，且 f (1)  22cos1 0， f   2cos 0，
3 3
1 
所以存在唯一x   ,1，使得 f x 0， ......................................6分
0 3  0
所以当0 x x 时， fx0， f(x)单调递减；当x  x1时， fx0， f(x)单调递增；
0 0
故在
0,1
上存在唯一极小值点，
综上，当k 1时，函数 f(x)的极值点有且仅有一个． ......................................8分
【小问3详解】
令et 1 x，et 2 x ．
1 2
由 f(x ) f(x )知3x 2sinx klnx 3x 2sinx klnx ，......................................9分
1 2 1 1 1 2 2 2
整理得，3(x x )2(sinx sinx )k(lnx lnx )（*），
1 2 1 2 1 2
不妨令g(x)xsinx(x0)，则g(x)1cosx0，故g(x)在(0,)上单调递增，
当0 x  x 时，有g(x ) g(x )，即x sinx  x sinx ，
1 2 1 2 1 1 2 2
那么sinx sinx x x ，
1 2 1 2
x x
因此，（*）即转化为k  1 2 ， ......................................11分
lnx lnx
1 2
x x x x x
接下来证明 1 2  x x (0 x  x )，等价于证明ln 1  1  2 ，
lnx lnx 1 2 1 2 x x x
1 2 2 2 1
x x x x
即ln 1  1  2 0，所以不妨令 1 m（0m1），
x x x x
2 2 1 2
1 2 1 (m1)2
建构新函数(m) 2lnmm ，(m) 1  0，
m m m2 m2
则(m)在(0,1)上单调递减， ......................................13分x x x
所以(m)(1)0，故ln 1  1  2
x x x
2 2 1
x x
即 1 2  x x (0 x  x )得证， ......................................15分
lnx lnx 1 2 1 2
1 2
由不等式的传递性知 xx k，即 x x  k2，即et 1 et 2  k2 ．.................................16分
1 2 1 2
所以et 1 t 2  k2 ，得证t t  2lnk . ......................................17分
1 2
19．（满分17分）
已知P为圆O：x2  y2 4上一动点，过点P分别作x轴，y轴的垂线，垂足分别为M，N，连接NM
并延长至点Q，使得 MQ  2 ，点Q的轨迹记为曲线C．
(1) 求曲线C的方程；
1
(2)设曲线C的左顶点为T，当直线l与曲线C交于不同的A,B两点， 连结AT,BT,k k   ，
AT BT 2
证明：直线l过定点；
 
(3)若过右焦点F 的直线l与曲线C交于不同的A,B两点，且F BAF ，当[2,3]时，求直线l在y
2 2 2
轴上的截距的取值范围．
解:（1）设Qx,y，P(x ,y )，则M(x ,0),N(0,y )，
0 0 0 0
   x
由题意知 MN 4，所以QM MN，得(x 0 x,y)(x 0 ,y 0 )，所以  x 0  2 ，............2分
 y y
0
x2 y2 x2 y2
因为x2 y2 4，得  1，故曲线C的方程为  1．............4分
0 0 16 4 16 4
x2 y2
设 直 线 l:ykxm ， Ax 1 ,y 1 ,Bx 2 ,y 2  ， 联 立 方 程 组  16  4 1 ， 消 去 y 得

ykxm
 14k2 x2 8kmx4m2 160，所以 x x  8km ， xx  4m216 ，
1 2 14k2 1 2 14k2
64k2m2 4  14k2 4m2 16  16  16k2 4m2 0 ............5分
又T4,0,所以
y y kx m kx m kx mx 4kx mx 4
k k  1  2  1  2  1 2 2 1 
AT BT x 4 x 4 x 4 x 4 x 4x 4
1 2 1 2 1 24m216  8km 
2kx 1 x 2 4kmx 1 x 2 8m  2k 14k2 4km  14k2   8m  2m8k  1 ，
xx 4x x 16 4m216  8km  m28km16k2 2
1 2 1 2 4 16
14k2 14k2 
............7分
化简得，m28km16k24m16k 0，即m4k24m4k0，
解得m4k或m4k4。 ..........................9分
当m4k 时，直线1过定点4,0与点T 重合，舍去
当m4k4时，直线1过定点4,4 .........................10分
x2 y2
（3）设 直 线 l:xty2 3 ， Ax 1 ,y 1 ,Bx 2 ,y 2  ， 联 立 方 程 组  16  4 1 ， 消 去 x 得 ，

xty2 3
4 3t 4
t2y24 3ty40，所以 y  y  ①， y y  ② ..........................11分
1 2 t24 1 2 t24
 
由QBQA得y y ③，
2 1
由①③可得， 4 3t ， 4 3t ，
y  y 
1  t24 1 2  t24 1
代入②化简得，12t2   t24 12， ..........................13分
即
12t2

12

221

1
2，由
[2,3]得 1
2
1
，
4
，
t24      2 3  
12t2 1 4 1  23 1  23   23
即   ，  ，解得   2，  ，即 - ， 2 2，  ， .....................15分
t24 2 3 t2  4  t  2   2 
从而直线l在 y 轴上的截距为 2 3  69，-2 62 6，69 ..........................17分
   
t