文档内容
八一路校区高二数学第一次月考测试
一、单选题
1. 若函数 在 处可导,且 ,则 ( )
A. B. C. 1 D. 2
2. 甲、乙、丙、丁、戊、己六人站成一排合影留念,则甲、乙两人中间恰好有两人的站法有( )
.
A 36种 B. 72种 C. 144种 D. 288种
3. 拉格朗日中值定理是微分学中 基的本定理之一,定理内容是:如果函数 在闭区间 上的图象
连续不间断,在开区间 内的导数为 ,那么在区间 内至少存在一点c,使得
成立,其中c叫做 在 上的“拉格朗日中值点”.根据这个定理,
可得函数 在 上的“拉格朗日中值点”的个数为( ).
A. 3 B. 2 C. 1 D. 0
4. 函数 的大致图象是( )
A. B.
C D.
.
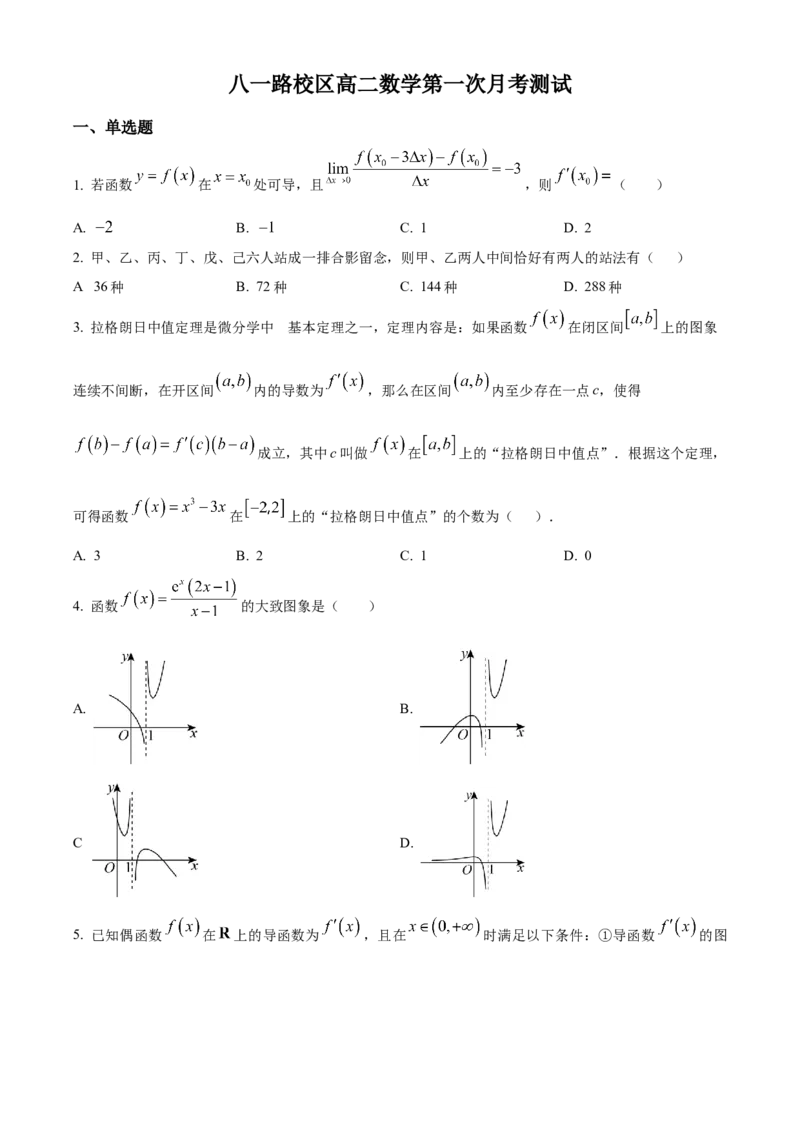
5. 已知偶函数 在 上的导函数为 ,且在 时满足以下条件:①导函数 的图象如图所示;② 唯一的零点是1.则 的解集为( )
A. B.
C. D.
6. 已知函数 ,则 (
)
A. 2024 B. C. 2025 D. 2026
7. 在 上的导函数为 ,则下列不等式成立的是( )
A. B.
C. D.
8. 已知 对 恒成立,则实数 的取值范围是( )
A. B. C. D.
二、多选题
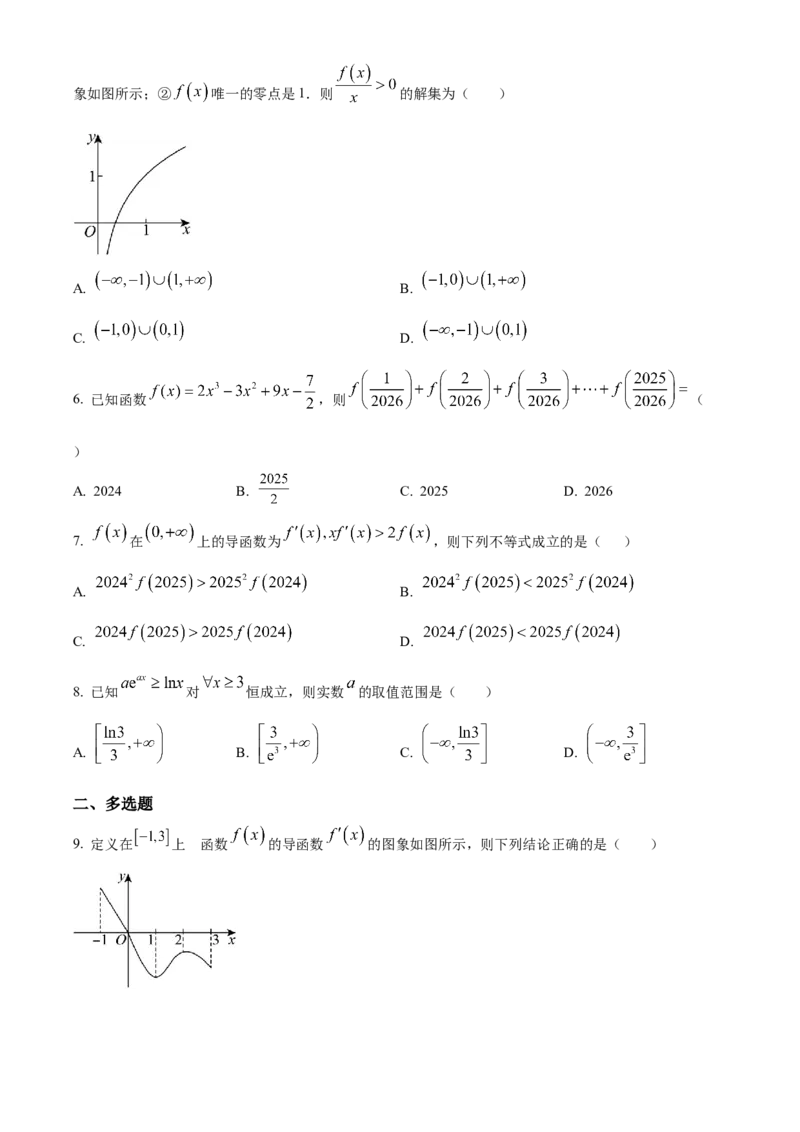
9. 定义在 上 函的数 的导函数 的图象如图所示,则下列结论正确的是( )A. 函数 在 上单调递减 B. 函数 在 上单调递减
C. 函数 在 处取得极小值 D. 函数 在 处取得极大值
10. 设函数 ,则( )
A. 函数 有两个极值点
B. 函数 有两个零点
C. 直线 是曲线 的切线
D. 点 是曲线 的对称中心
11. 设函数 ,则( )
A. 当 时, 是 的极大值点
B. 当 时, 有三个零点
C. 存在a,使得点 为曲线 的对称中心
D. 存在a,b,使得 为曲线 的对称轴
三、填空题
12. 函数 在 处有极值10,则实数 _________.
13. 若函数 在区间 上有单调递增区间,则实数 的取值范围是______.
14. 对于函数 ,若对任意的 ,存在唯一的 使得
,则实数 的取值范围是__________.
四、解答题
15. 4名男生和3名女生站成一排.(1)甲不在中间也不在两端的站法有多少种?
(2)男生甲和男生乙不相邻,女生甲和女生乙相邻,排在一起的站法有多少种?
(3)甲、乙、丙三人从左到右顺序一定的站法有多少种?
16. 已知函数 .
(1)若 ,求曲线 在点 处的切线方程;
(2)证明:当 时, .
17. 已知函数 ,其中 .
(1)若 的图象在 处的切线经过点 ,求a的值;
(2)讨论 的单调性.
18. 已知函数 .
(1)求函数 的单调区间;
(2)求证:函数 的图象在x轴上方.
19. 已知函数 .
(1)求 的单调区间;
(2)若 在区间 内有最小值,求 的取值范围;
(3)若关于 的方程 有两个不同的解 , ,求证: .