文档内容
抚州市 2024—2025 学年度上学期学生学业质量监测
高二数学试题卷
说明:1.本卷共有4大题,19个小题,全卷满分150分,考试时间120分钟.
2.本卷分为试题卷和答题卡,答案要求写在答题卡上,不得在试题卷上作答,否则不给分.
3.所有考试结束3天后,考生可凭准考证号登录智学网(www.zhixue.com)查询考试成绩,
密码与准考证号相同.
一、单项选择题:共8小题,每小题5分,共40分.在每小题给出的选项中,仅有一项符合题
目要求.
1. 已知直线 , ,若 ,则 ( )
A. 0 B. 1 C. D. 2
2. 圆心为 且过点 的圆的标准方程为( )
A. B.
C. D.
3. 设 为椭圆 的两个焦点,点 在 上,若 ,则 (
)
A. 1 B. 2 C. 4 D. 5
.
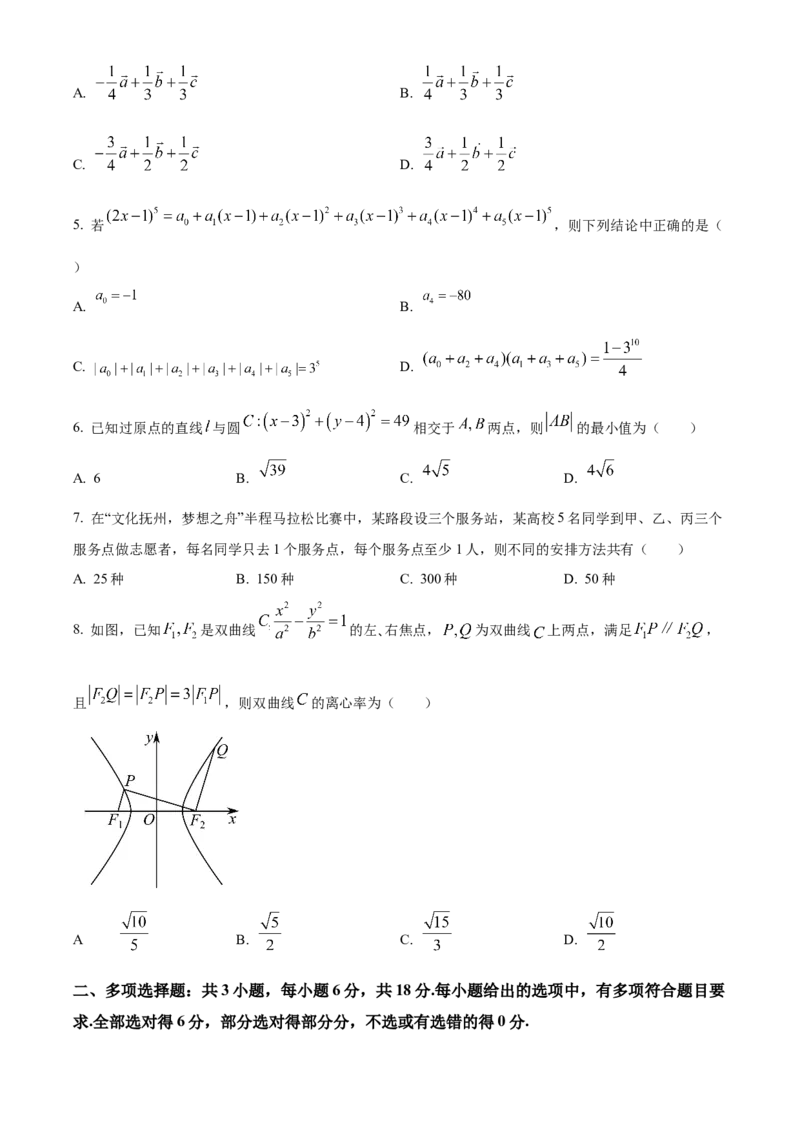
4 如图,三棱锥 中, , , ,且 , ,则
( )A. B.
C. D.
5. 若 ,则下列结论中正确的是(
)
A. B.
C. D.
6. 已知过原点的直线 与圆 相交于 两点,则 的最小值为( )
A. 6 B. C. D.
7. 在“文化抚州,梦想之舟”半程马拉松比赛中,某路段设三个服务站,某高校5名同学到甲、乙、丙三个
服务点做志愿者,每名同学只去1个服务点,每个服务点至少1人,则不同的安排方法共有( )
A. 25种 B. 150种 C. 300种 D. 50种
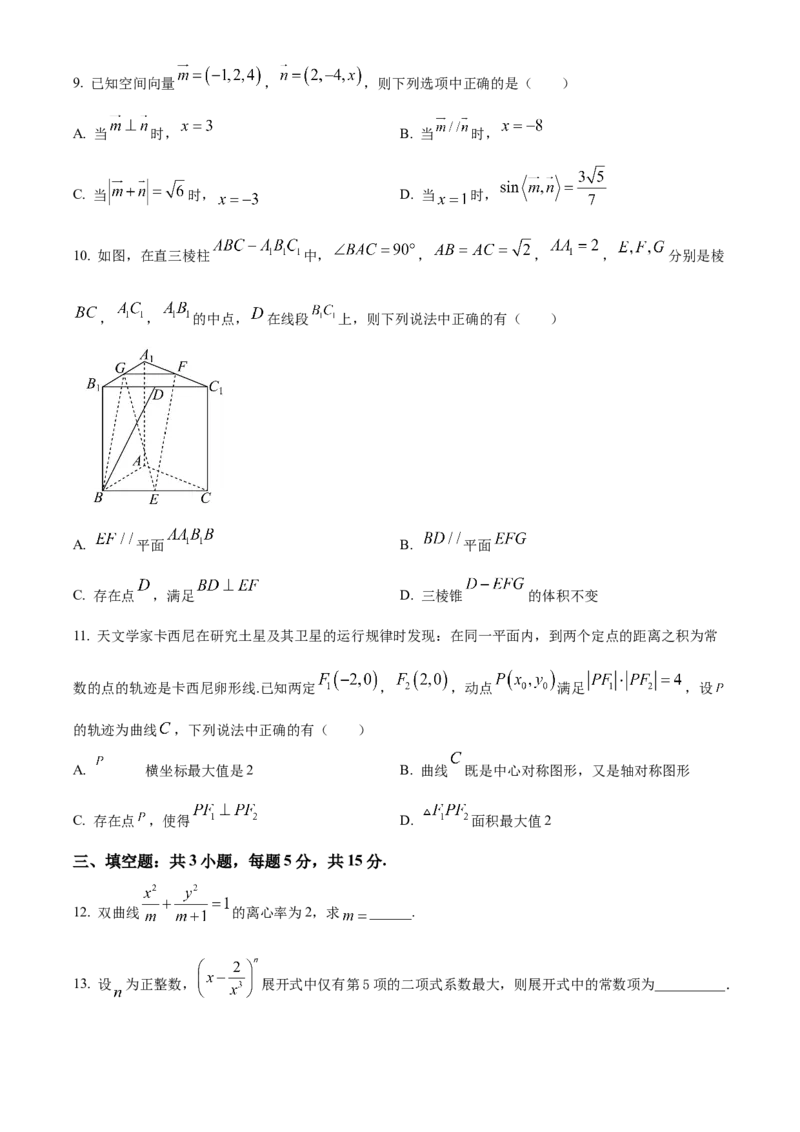
8. 如图,已知 是双曲线 的左、右焦点, 为双曲线 上两点,满足 ,
且 ,则双曲线 的离心率为( )
.
A B. C. D.
二、多项选择题:共3小题,每小题6分,共18分.每小题给出的选项中,有多项符合题目要
求.全部选对得6分,部分选对得部分分,不选或有选错的得0分.9. 已知空间向量 , ,则下列选项中正确的是( )
A. 当 时, B. 当 时,
C. 当 时, D. 当 时,
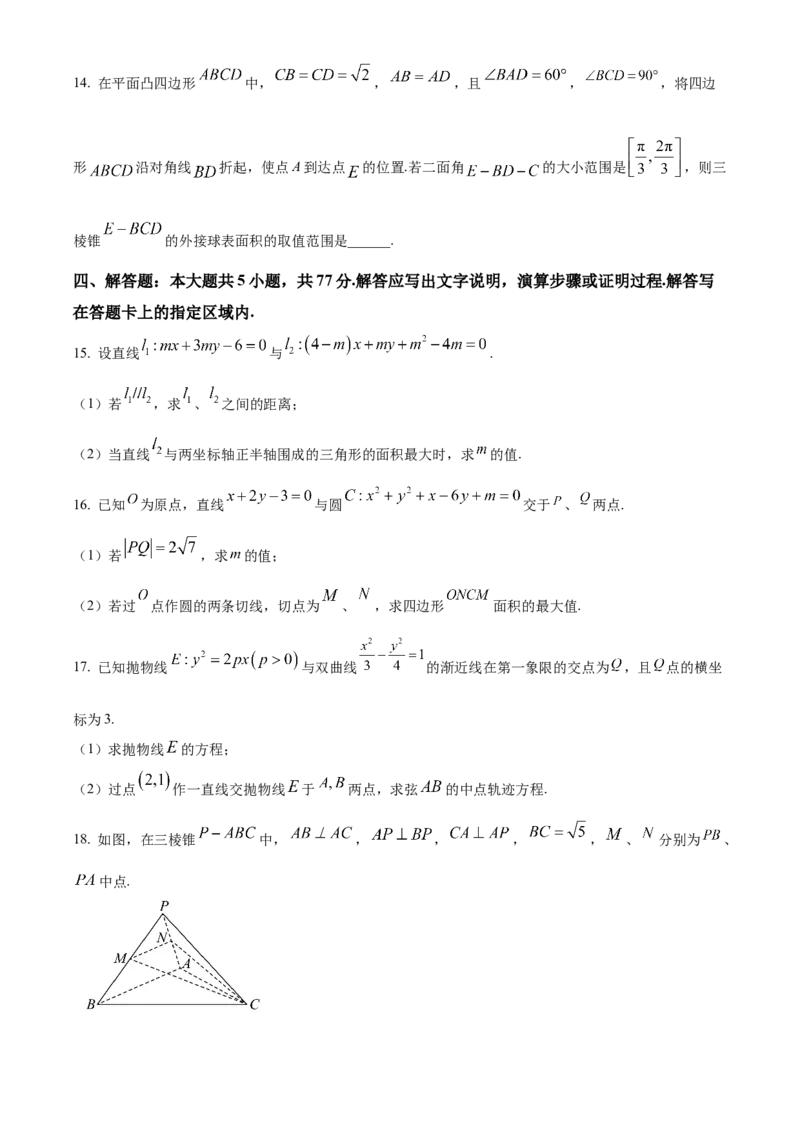
10. 如图,在直三棱柱 中, , , , 分别是棱
, , 的中点, 在线段 上,则下列说法中正确的有( )
A. 平面 B. 平面
C. 存在点 ,满足 D. 三棱锥 的体积不变
11. 天文学家卡西尼在研究土星及其卫星的运行规律时发现:在同一平面内,到两个定点的距离之积为常
数的点的轨迹是卡西尼卵形线.已知两定 , ,动点 满足 ,设
的轨迹为曲线 ,下列说法中正确的有( )
的
A. 横坐标最大值是2 B. 曲线 既是中心对称图形,又是轴对称图形
C. 存在点 ,使得 D. 面积最大值2
三、填空题:共3小题,每题5分,共15分.
12. 双曲线 的离心率为2,求 ______.
13. 设 为正整数, 展开式中仅有第5项的二项式系数最大,则展开式中的常数项为__________.14. 在平面凸四边形 中, , ,且 , ,将四边
形 沿对角线 折起,使点A到达点 的位置.若二面角 的大小范围是 ,则三
棱锥 的外接球表面积的取值范围是______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明,演算步骤或证明过程.解答写
在答题卡上的指定区域内.
15. 设直线 与 .
(1)若 ,求 、 之间的距离;
(2)当直线 与两坐标轴正半轴围成的三角形的面积最大时,求 的值.
16. 已知 为原点,直线 与圆 交于 、 两点.
(1)若 ,求 的值;
(2)若过 点作圆的两条切线,切点为 、 ,求四边形 面积的最大值.
17. 已知抛物线 与双曲线 的渐近线在第一象限的交点为 ,且 点的横坐
标为3.
(1)求抛物线 的方程;
(2)过点 作一直线交抛物线 于 两点,求弦 的中点轨迹方程.
18. 如图,在三棱锥 中, , , , , 、 分别为 、
中点.(1)证明: ;
(2)证明:平面 与平面 的交线 平面 ;
(3)若 ,二面角 的正切值为2,求 的长.
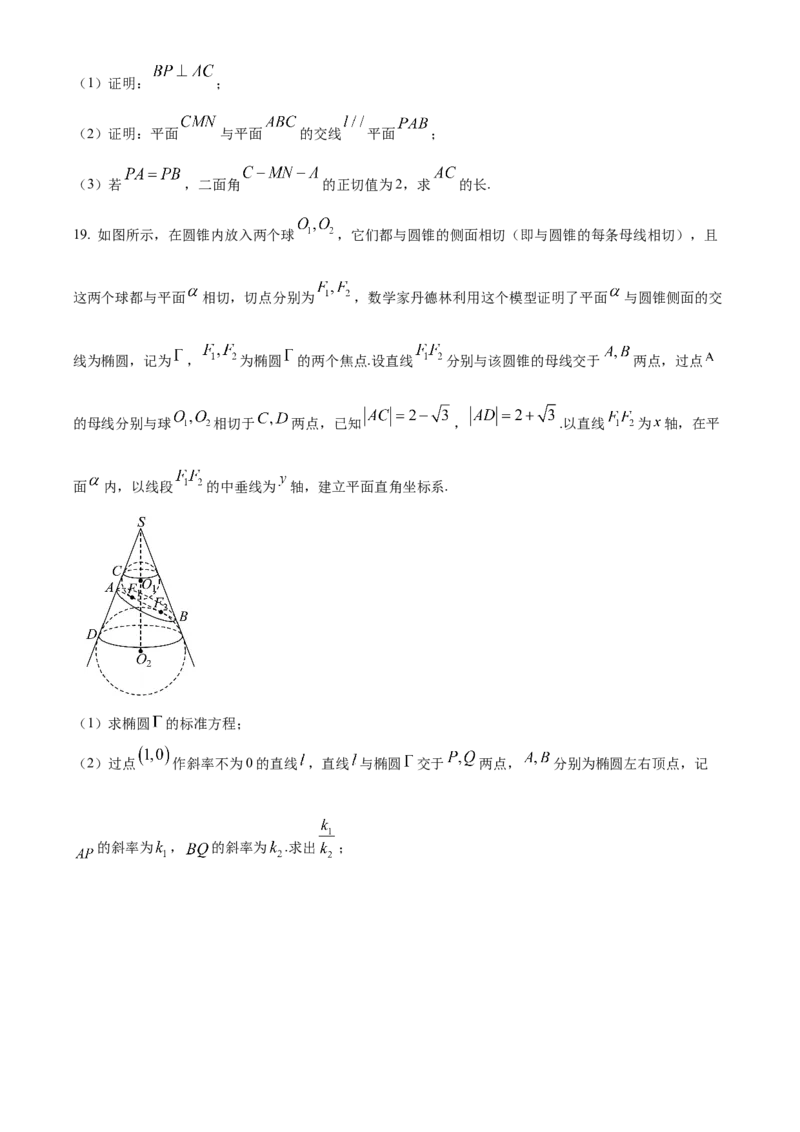
19. 如图所示,在圆锥内放入两个球 ,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且
这两个球都与平面 相切,切点分别为 ,数学家丹德林利用这个模型证明了平面 与圆锥侧面的交
线为椭圆,记为 , 为椭圆 的两个焦点.设直线 分别与该圆锥的母线交于 两点,过点
的母线分别与球 相切于 两点,已知 , .以直线 为 轴,在平
面 内,以线段 的中垂线为 轴,建立平面直角坐标系.
(1)求椭圆 的标准方程;
(2)过点 作斜率不为0的直线 ,直线 与椭圆 交于 两点, 分别为椭圆左右顶点,记
的斜率为 , 的斜率为 .求出 ;