文档内容
山西大学附中
2024 2025学年第一学期高三开学考试
~~
数 学 试 题
考查时间:120分钟 满分:150分
一.选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.设集合 , ,若 ,则 ( )
A. B. C. D.
2.若复数 满足 (其中 是虚数单位),则 的虚部是( )
A.1 B.-1 C. D.
3.已知函数 的部分图像如图所示,则 的解析式可能是( )
A. B.
C. D.
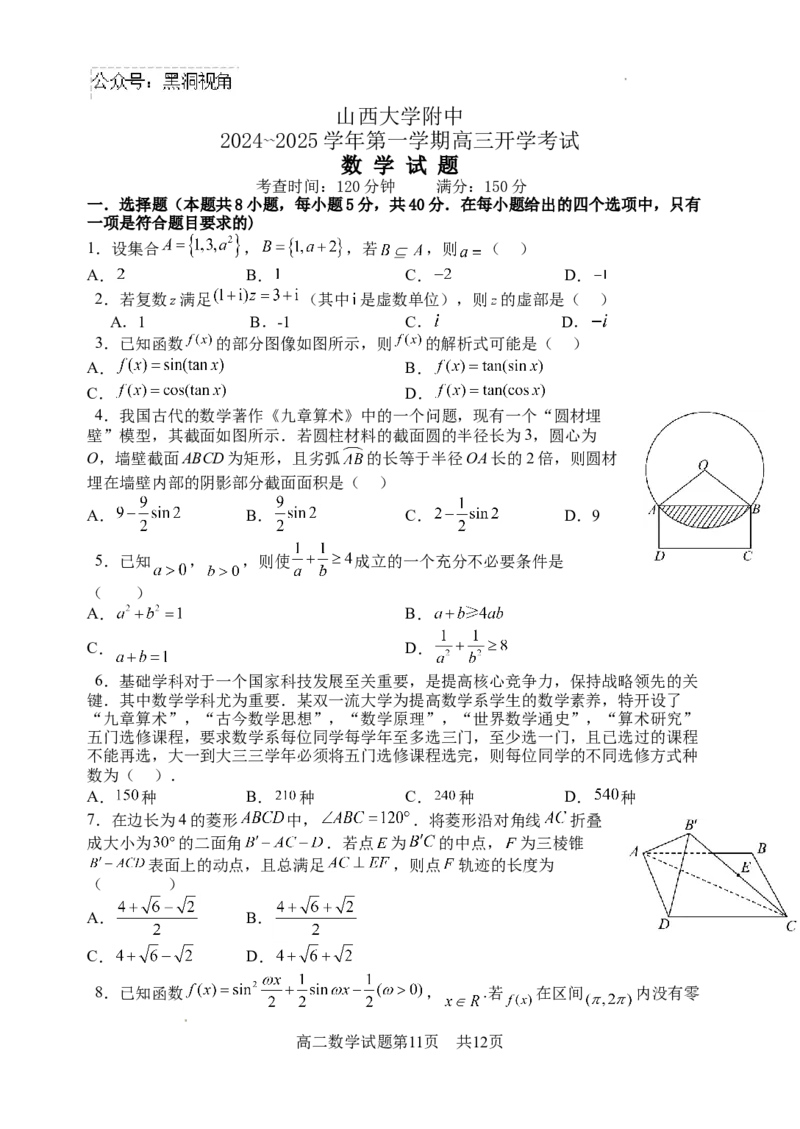
4.我国古代的数学著作《九章算术》中的一个问题,现有一个“圆材埋
壁”模型,其截面如图所示.若圆柱材料的截面圆的半径长为3,圆心为
O,墙壁截面ABCD为矩形,且劣弧 的长等于半径OA长的2倍,则圆材
埋在墙壁内部的阴影部分截面面积是( )
A. B. C. D.9
5.已知 , ,则使 成立的一个充分不必要条件是
( )
A. B.
C. D.
6.基础学科对于一个国家科技发展至关重要,是提高核心竞争力,保持战略领先的关
键.其中数学学科尤为重要.某双一流大学为提高数学系学生的数学素养,特开设了
“九章算术”,“古今数学思想”,“数学原理”,“世界数学通史”,“算术研究”
五门选修课程,要求数学系每位同学每学年至多选三门,至少选一门,且已选过的课程
不能再选,大一到大三三学年必须将五门选修课程选完,则每位同学的不同选修方式种
数为( ).
A. 种 B. 种 C. 种 D. 种
7.在边长为4的菱形 中, .将菱形沿对角线 折叠
成大小为 的二面角 .若点 为 的中点, 为三棱锥
表面上的动点,且总满足 ,则点 轨迹的长度为
( )
A. B.
C. D.
8.已知函数 , .若 在区间 内没有零
高二数学试题第11页 共12页
学科网(北京)股份有限公司点,则 的取值范围是
A. B. C. D.
二.选择题:(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有
多项符合题目要求.全部选对得6分,部分选对得3分,有选错得0分)
9.已知向量 , 不共线,向量 平分 与 的夹角,则下列结论一定正确的是( )
A. B.
C.向量 , 在 上的投影向量相等 D.
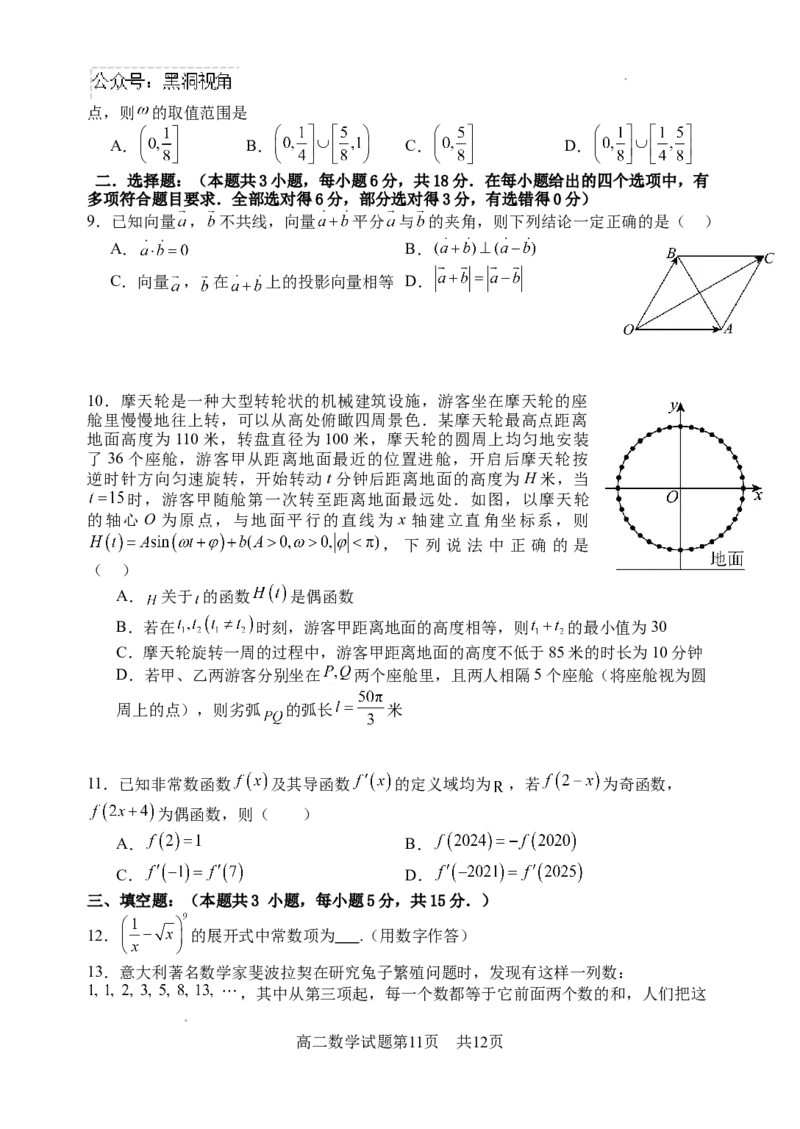
10.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座
舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离
地面高度为110米,转盘直径为100米,摩天轮的圆周上均匀地安装
了36个座舱,游客甲从距离地面最近的位置进舱,开启后摩天轮按
逆时针方向匀速旋转,开始转动t分钟后距离地面的高度为H米,当
时,游客甲随舱第一次转至距离地面最远处.如图,以摩天轮
的轴心 O 为原点,与地面平行的直线为 x 轴建立直角坐标系,则
, 下 列 说 法 中 正 确 的 是
( )
A. 关于 的函数 是偶函数
B.若在 时刻,游客甲距离地面的高度相等,则 的最小值为30
C.摩天轮旋转一周的过程中,游客甲距离地面的高度不低于85米的时长为10分钟
D.若甲、乙两游客分别坐在 两个座舱里,且两人相隔5个座舱(将座舱视为圆
周上的点),则劣弧 的弧长 米
11.已知非常数函数 及其导函数 的定义域均为 ,若 为奇函数,
为偶函数,则( )
A. B.
C. D.
三、填空题:(本题共3 小题,每小题5分,共15分.)
12. 的展开式中常数项为 .(用数字作答)
13.意大利著名数学家斐波拉契在研究兔子繁殖问题时,发现有这样一列数:
,其中从第三项起,每一个数都等于它前面两个数的和,人们把这
高二数学试题第11页 共12页
学科网(北京)股份有限公司样的一列数组成的数列 称为“斐波拉契数列”.那么 是斐波拉契
数列中的第 项.
14.已知函数 ,则方程
恰好有6个不同的解,则实数 的取值范围为 .
四、解答题:(本题共5小题,共77分.解答应写出文字说明,证
明过程或演算步骤.)
15.(本题13分)已知递增的等比数列 的前 项和为 ,且
.
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
16.如图,在四棱锥 中,底面 是平行四边形, 分别为 上的
点,且 .
(1)证明: 平面 ;
(2)若 平面 为 的中点, ,求
二面角 的正切值.
17.在直角坐标系 中,抛物线 与直线 交于 两点.
(1)若 点的横坐标为4,求抛物线在 点处的切线方程;
(2)探究 轴上是否存在点 ,使得当 变动时,总有 ?若存在,求出
点坐标;若不存在,请说明理由.
高二数学试题第11页 共12页
学科网(北京)股份有限公司18.已知函数 ,若将 的图像上的所有点向右平
移 个单位,再把所得图像上所有点的横坐标缩短为原来的 倍(纵坐标不变),得到
函数 的图像.
(1)求函数 的周期和对称轴方程;
(2)若方程 在 上的零点从小到大依次为 , , ,求
的值;
(3)若方程 在 上的解为 ,求 .
19.在平面直角坐标系中,如果将函数 的图象绕坐标原点逆时针旋转
后,所得曲线仍然是某个函数的图象,则称 为“ 旋转函数”.
(1)判断函数 是否为“ 旋转函数”,并说明理由;
(2)已知函数 是“ 旋转函数”,求 的最大值;
(3)若函数 是“ 旋转函数”,求 的取值范围.
高二数学试题第11页 共12页
学科网(北京)股份有限公司山西大学附中
2024 2025学年第一学期高三开学考试
~~
数 学 试 题
考查时间:120分钟 满分:150分
一.选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.设集合 , ,若 ,则 ( )
A. B. C. D.
【答案】A
【详解】由 ,得 ,即 ,此时 ,
由 ,得 ,而 ,所以 .
2.若复数 满足 (其中 是虚数单位),则 的虚部是( )
A.1 B.-1 C. D.
【答案】B
【详解】依题意, , 的虚部是 .
3.已知函数 的部分图像如图所示,则 的解析式可能是
( )
A. B.
C. D.
【答案】D
【详解】观察图象可知函数为偶函数,
对于A, ,为奇函数,排除;
对于B, ,为奇函数,排除;
同理,C、D选项为偶函数,而对于C项,其定义域为 ,不是R,舍去,
故D正确.故选:D
4.我国古代的数学著作《九章算术》中的一个问题,现有一个“圆材埋壁”
模型,其截面如图所示.若圆柱材料的截面圆的半径长为3,圆心为O,墙
壁截面ABCD为矩形,且劣弧 的长等于半径OA长的2倍,则圆材埋在墙
壁内部的阴影部分截面面积是( )
A. B. C. D.9
【答案】A
【详解】由题意得 ,劣弧 ,故扇形 的面积为
,设圆心角为 ,则 ,故 ,
故圆材埋在墙壁内部的阴影部分截面面积为 .
高二数学试题第11页 共12页
学科网(北京)股份有限公司5.已知 , ,则使 成立的一个充分不必要条件是( )
A. B.
C. D.
【答案】C
【详解】对于A,令 ,显然有 ,而 ,A不是;
对于B,当 , 时, ,B不是;
对于C,当 , 时,由 ,得 ,
当且仅当 时取等号,反之取 ,满足 ,而 不成立,
因此 是 成立的一个充分不必要条件,C是;
对于D,令 ,不等式 成立,而 ,D不是.故选:C
6.基础学科对于一个国家科技发展至关重要,是提高核心竞争力,保持战略领先的关键.
其中数学学科尤为重要.某双一流大学为提高数学系学生的数学素养,特开设了“九章
算术”,“古今数学思想”,“数学原理”,“世界数学通史”,“算术研究”五门选
修课程,要求数学系每位同学每学年至多选三门,至少选一门,且已选过的课程不能再
选,大一到大三三学年必须将五门选修课程选完,则每位同学的不同选修方式种数为(
).
A. 种 B. 种 C. 种 D. 种
【答案】A
【详解】先将五门课程分成三组,再安排到三个学年中,则共有
种选修方式
高二数学试题第11页 共12页
学科网(北京)股份有限公司7.在边长为4的菱形 中, .将菱形沿对角线 折叠
成大小为 的二面角 .若点 为 的中点, 为三棱锥
表面上的动点,且总满足 ,则点 轨迹的长度为
( )
A. B.
C. D.
【答案】A
【详解】连接 、 ,交于点 ,连接 , 为菱形, ,
所以 , , ,所以 为二面角 的平面角,
于是 ,又因为 ,
所以 ,
取 中点 ,取 中点 ,连接 、 、 ,所以 、 ,
所以 、 , , 相交,所以 平面 ,
所以在三棱锥 表面上,满足 的点 轨迹为 ,
因为 , , ,
所以 的周长为 ,
所以点 轨迹的长度为 .
8.已知函数 , .若 在区间 内没有零点,
则 的取值范围是
A. B. C. D.
【答案】D
【详解】由题设有 ,
令 ,则有 即 .
因为 在区间 内没有零点,故存在整数 ,使得 ,
高二数学试题第11页 共12页
学科网(北京)股份有限公司即 ,因为 ,所以 且 ,故 或 ,
所以 或
高二数学试题第11页 共12页
学科网(北京)股份有限公司二.选择题:(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有
多项符合题目要求.全部选对得6分,部分选对得3分,有选错得0分)
9.已知向量 , 不共线,向量 平分 与 的夹角,则下列结论一定正确的是( )
A. B.
C.向量 , 在 上的投影向量相等 D.
【答案】BC
【详解】作向量 ,在 中, , ,
由向量 平分 与 的夹角,得 是菱形,即 ,
对于A, 与 不一定垂直,A错误;
对于B, ,即 ,B正确;
对于C, 在 上的投影向量 ,
在 上的投影向量 ,C正确;
对于D,由选项A知, 不一定为0,则 与 不一定相等,D错误.
10.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座
舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离
地面高度为110米,转盘直径为100米,摩天轮的圆周上均匀地安装
了36个座舱,游客甲从距离地面最近的位置进舱,开启后摩天轮按
逆时针方向匀速旋转,开始转动t分钟后距离地面的高度为H米,当
时,游客甲随舱第一次转至距离地面最远处.如图,以摩天轮
的轴心 O 为原点,与地面平行的直线为 x 轴建立直角坐标系,则
, 下 列 说 法 中 正 确 的 是
( )
A. 关于 的函数 是偶函数
B.若在 时刻,游客甲距离地面的高度相等,则 的最小值为30
C.摩天轮旋转一周的过程中,游客甲距离地面的高度不低于85米的时长为10分钟
D.若甲、乙两游客分别坐在 两个座舱里,且两人相隔5个座舱(将座舱视为圆
周上的点),则劣弧 的弧长 米
【答案】BCD
【详解】对A,由题意, ,
所以 ,当 时,可得 ,所以 ,
故 ,所以 是非奇非偶函数,故A错误;
高二数学试题第11页 共12页
学科网(北京)股份有限公司对B,由题意 ,即 ,
即 ,所以 ,或 ,
,即 或 , ,故B正确;
对C,由题意 ,即 ,即 ,
所以 , ,解得 .
所以摩天轮旋转一周的过程中,游客甲距离地面的高度不低于85米的时长为10分钟,C正确;
对D,因为摩天轮的圆周上均匀地安装着36个座舱,
故每个座舱与中心连线所成的扇形的圆心角为 ,
因为 两个座舱相隔5个座舱,所以劣弧 对应的圆心角是 ,
故 (m).故D正确.
11.已知非常数函数 及其导函数 的定义域均为 ,若 为奇函数,
为偶函数,则( )
A. B.
C. D.
【答案】BCD
【详解】因为非常数函数 及其导函数 的定义域均为 ,
若 为奇函数,则 ,则 的图象关于点 对称,且
,故A错误;
因为 为偶函数,所以 ,即 ,
则 ,又 ,所以 ,
所以 ,即 ,所以 ,
故 的周期为8,所以 , ,在 中,令
,得 ,所以 ,故B正确;
对 两边同时求导,得 ,
所以导函数 的周期为8,所以 ,故C正确;
由 周期 ,得 , ,对 两边同
时求导,得 ,令 ,得 ,
所以 ,故D正确.
高二数学试题第11页 共12页
学科网(北京)股份有限公司三、填空题:(本题共3 小题,每小题5分,共15分.)
12. 的展开式中常数项为 .(用数字作答)
【答案】84
【详解】根据通项公式 ,
令 ,解得 ,所以 ,
13.意大利著名数学家斐波拉契在研究兔子繁殖问题时,发现有这样一列数:
,其中从第三项起,每一个数都等于它前面两个数的和,人们把这
样的一列数组成的数列 称为“斐波拉契数列”.那么 是斐波拉契
数列中的第 项.
【答案】2024
【详解】由已知
, .即 是斐波拉契数列
中的第2024项.
14.已知函数 ,则方程
恰好有6个不同的解,则实数 的取值范围为 .
【答案】
【详解】令 , ,
作出 图象,作出 图像,
时, 有两根,设为 , ,则 , ,即
,此时有2个根, ,此时有2个根,共4个
根,不满足条件.
时, ,解得 或 或6,即 ,无解,
,2解, ,2解,共4个解,不满足条件.
时, ,有四个根,设为 , , , ,
高二数学试题第11页 共12页
学科网(北京)股份有限公司其中 , , , ,即 ,无解,
,无解, ,2解, ,2解,共4个解,不满足条件.
时, 有4个根,0,2, , ( ), ,1解,
,1解, ,2解, ,2解,共6解,满足条件.
时, ,有3个根,设为 , , ,
其中 , , ,即 有2解, 有2解,
有2解,共6解,满足条件.
时, ,有两根 和3, 有2个根,
有2个根,共4个根,不满足条件,综上 .
故答案为 .
四、解答题:(本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.)
15.(本题13分)已知递增的等比数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
【答案】(1) (2)
【详解】(1)设等比数列 公比为 ,由题 ,…………2分
解得 ,…………4分 故 .…………5分
(2) ,…………7分
所以 ,
…………9分
高二数学试题第11页 共12页
学科网(北京)股份有限公司,…………11分
.…………13分
高二数学试题第11页 共12页
学科网(北京)股份有限公司16.如图,在四棱锥 中,底面 是平行四边形, 分别为 上的
点,且 .
(1)证明: 平面 ;
(2)若 平面 为 的中点, ,求
二面角 的正切值.
【答案】(1)证明见解析 (2)
【详解】证明:方法1:如图,在 上取一点 ,使得 ,连接 , , ,
因为底面 是平行四边形,所以 ,所以 ,
因为 , ,所以四边形 是平行四边形,所以 ,
因为 平面 , 平面 ,所以 平面 ,…………2分
又因为 ,所以 ,所以 ,
因为 平面 , 平面 ,所以 平面 ,…………4分
又因为 , 平面 ,所以平面 平面 ,…………5分
因为 平面 ,所以 平面 .…………6分
方法2:利用线线平行证明,也可酌情给分
在 上取一点 ,使得 ,连接
证明出四边形 为平行四边形…………4分
得出 …………5分,证明 平面 .…………6分
(2)当 为 中点, , ,易知 , 为 中点,
又因为 平面 ,所以 两两垂直,…………8分
则以 为坐标原点, 所在直线为 轴建立空间直角坐标系,如(1)图,
设 ,则 , , , ,
所以 , , .
设平面 的一个法向量为 ,
则 ,令 ,得 ,……10分
设平面 的一个法向量为 ,
则 ,令 ,得 ,……12分
所以 ,…………14分
高二数学试题第11页 共12页
学科网(北京)股份有限公司故二面角 的正弦值为 ,正切值为 .故二面角
的正切值为 .…………15分
17.在直角坐标系 中,抛物线 与直线 交于 两点.
(1)若 点的横坐标为4,求抛物线在 点处的切线方程;
(2)探究 轴上是否存在点 ,使得当 变动时,总有 ?若存在,求出
点坐标;若不存在,请说明理由.
【答案】(1) (2)存在;
【详解】(1)由已知,得 ,…………2分
因为 ,所以 ,斜率 ,…………4分
因此,切线方程为 ,即 .…………6分
(2)存在符合题意的点 ,理由如下:…………7分
设点 为符合题意的点, ,直线 的斜率分别为 .
联立方程 ,得 ,…………8分
因为 ,则 ,可得 ,…………10分
从而 ……12分
,……14分
因为 不恒为0,可知当且仅当 时,恒有 ,
则直线 与直线 的倾斜角互补,故 ,
所以点 符合题意.…………15分
注意:
1. 本题是利用点 位置证明 ,如果证明逻辑有误,扣1分.
2. 此处也可以带入 消去仍得到相同的式子
18.已知函数 ,若将 的图像上的所有点向右平
移 个单位,再把所得图像上所有点的横坐标缩短为原来的 倍(纵坐标不变),得到
函数 的图像.
高二数学试题第11页 共12页
学科网(北京)股份有限公司(1)求函数 的周期和对称轴方程;
(2)若方程 在 上的零点从小到大依次为 , , ,求
的值;
(3)若方程 在 上的解为 ,求 .
【详解】(1) ,…3
分
,…………4分
令 ,得 ∴对称轴方程 ;…………5分
(2)由题意可得 …………7分,
由方程 由,可得 ,因为 ,则
,令 ,则 ,所以 , ,……9分
设 ,直线 与函数 在 上的图象四个交
点,
点 、 关于直线 对称,点 、 关于直线 对称,
点 、 关于直线 对称,
所以 , , ,即 ,…………10分
即 ,解得 ;…………11分
(3) 方程 在 上的解为 ,
∴ 为方程 在 上的两解,不妨设 ,
当 时, , , ,
, , , ,……
12分
, ,…… 13分
高二数学试题第11页 共12页
学科网(北京)股份有限公司, ,…………15分
, ,∴ .
…………17分
高二数学试题第11页 共12页
学科网(北京)股份有限公司19.在平面直角坐标系中,如果将函数 的图象绕坐标原点逆时针旋转
后,所得曲线仍然是某个函数的图象,则称 为“ 旋转函数”.
(1)判断函数 是否为“ 旋转函数”,并说明理由;
(2)已知函数 是“ 旋转函数”,求 的最大值;
(3)若函数 是“ 旋转函数”,求 的取值范围.
【答案】(1)不是,理由见解析 (2) (3)
【详解】(1)函数 不是“ 旋转函数”,因为 逆时针旋转 后与 轴重合,
当 时,有无数个 与之对应,与函数的概念矛盾,…… 2分
因此函数 不是“ 旋转函数”.…… 4分
(2)由题意可得函数 与函数 最多有1个交点,…… 5分
且 ,所以 最多有一个根,
即 最多有一个根,
因此函数 与函数 R 最多有1个交点,
即函数 在 上单调,…… 6分
因为 ,且 ,
所以 ,所以 ,…… 8分
即 , ,即 的最大值为 .…… 10分
(3)由题意可得函数 与函数 最多有1个交点,
即 ,
即函数 与函数 最多有1个交点,
即函数 在 上单调,…… 12分
,当 时, 所以 ,… 13
高二数学试题第11页 共12页
学科网(北京)股份有限公司分
令 ,则 ,… 14分
因为 在 上单调减,且 ,
所以存在 ,使 ,即 ,…15分
所以 在 单调递增, 单调递减,… 16分
所以 ,即 ..…… 17分
高二数学试题第11页 共12页
学科网(北京)股份有限公司