文档内容
数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的)
1. 已知集合 ,则下图中阴影部分所表示的集合为( )
A. B.
C. D.
2. 已知 ,则 ( )
A. 10 B. 2 C. D. 4
.
3 已知 , , ,则( )
A. B. C. D.
4. 已知向量 , , ,则实数k的值为( )
A. B. C. D. 1
5. 已知函数 是幂函数,且在 上单调递减,若 ,且
,则 的值( )
A. 恒大于0 B. 恒小于0
C. 等于0 D. 无法判断
第1页/共6页
学科网(北京)股份有限公司6. 若命题“对任意的 , 恒成立”为假命题,则m的取值范围为( )
A. B.
C. D.
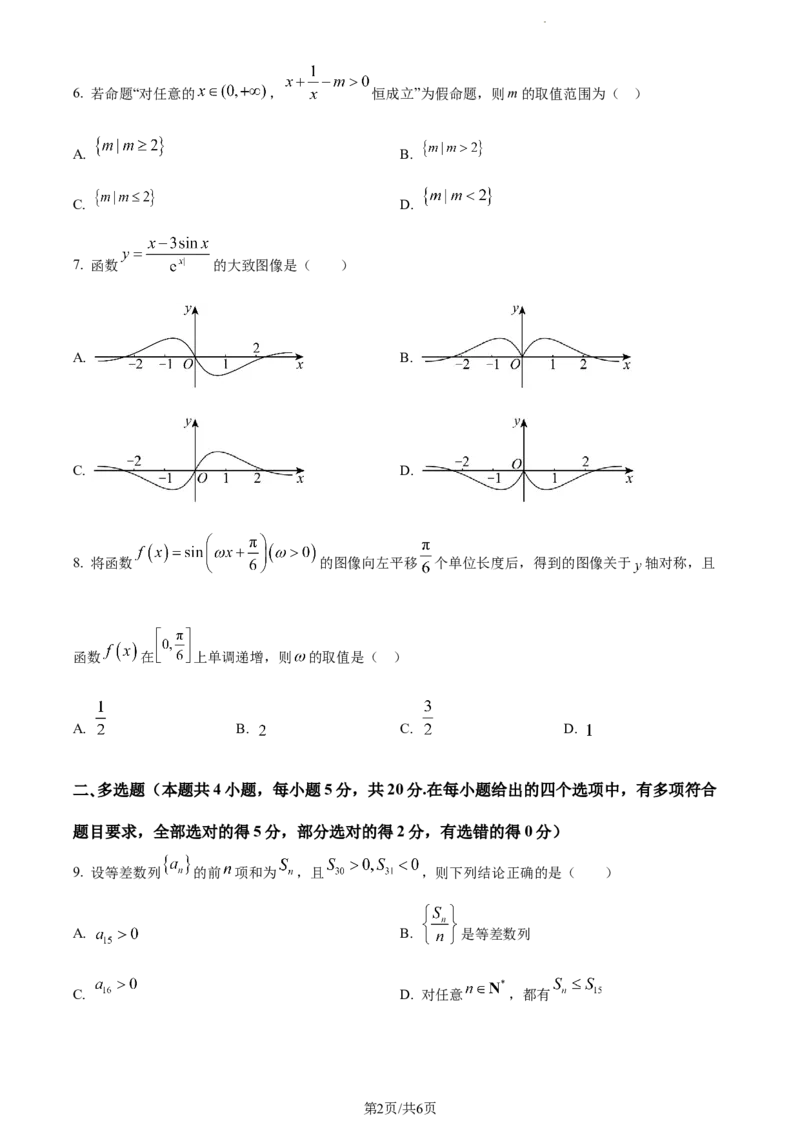
7. 函数 的大致图像是( )
A. B.
C. D.
8. 将函数 的图像向左平移 个单位长度后,得到的图像关于 轴对称,且
函数 在 上单调递增,则 的取值是( )
A. B. C. D.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合
题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分)
9. 设等差数列 的前 项和为 ,且 ,则下列结论正确的是( )
A. B. 是等差数列
C. D. 对任意 ,都有
第2页/共6页
学科网(北京)股份有限公司10. 设 是定义在 上的奇函数,且 在 上单调递减, ,则( )
A. 在 上单调递增
B.
C. 不等式 的解集为
D. 的图象与 轴只有3个交点
11. 已知函数 ,若关于 方程 有四个不等实根 、 、 、
的
,则下列结论正确的是( )
A. B.
C. D. 的最小值为
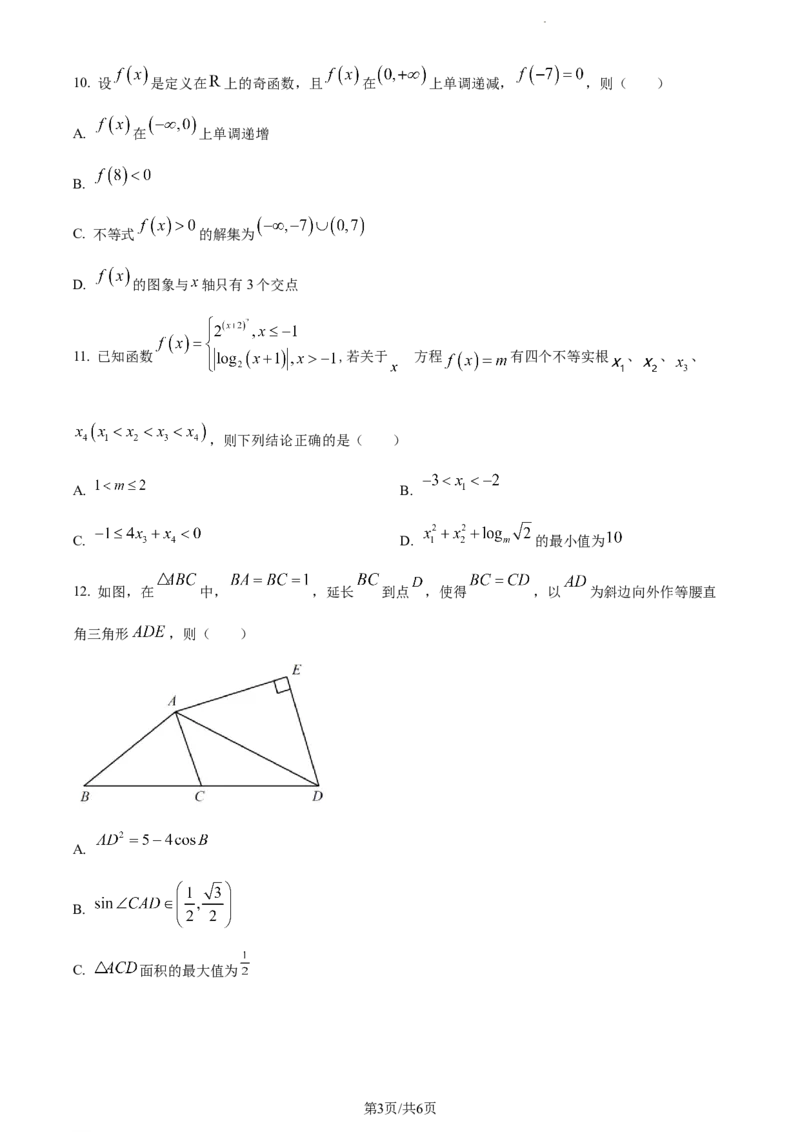
12. 如图,在 中, ,延长 到点 ,使得 ,以 为斜边向外作等腰直
角三角形 ,则( )
A.
B.
C. 面积的最大值为
第3页/共6页
学科网(北京)股份有限公司D. 四边形 面积的最大值为
第II卷(非选择题共90分)
三、填空题(本题共4小题,每小题5分,共20分)
13. 已知函数 是 上的单调递增函数,则实数 的取值范围是__________.
14. 已知函数 ,若 , ,且 ,则 的最小值为
______.
15. 已知 ,且 ,则 的最小值是______
16. 已知函数 , 的定义域均为 , 为奇函数, 为偶函数, ,
,则 ________.
四、解答题(本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17. 已知数列 的前n项和为 ,且 .
(1)求 ;
(2)若 ,求数列 的前n项和 .
的
18. 已知 ,且 图象过点 ,又 .
(1)若 成立,求 的取值范围;
(2)若对于任意 ,不等式 恒成立,求实数 的取值范围.
第4页/共6页
学科网(北京)股份有限公司19. 已知向量 , ,函数 (其中 ),函
数 的图象的一条对称轴是直线 .
(1)求 的值;
(2)若 且 ,求 值.
的
20. 在锐角三角形 中,内角 的对边分别为 ,且 .
(1)求角 的大小;
(2)若 ,求 面积的取值范围.
21. 为了改善湖泊的水质,某市环保部门于2021年年终在该湖泊中投入一些浮萍,这些浮萍在水中的繁殖
速度越来越快,2022年2月底测得浮萍覆盖面积为 ,2022年3月底测得浮萍覆盖面积为 ,
浮萍覆盖面积 (单位: )与 2022 年的月份 (单位:月)的关系有两个函数模型
与 可供选择.
(1)分别求出两个函数模型的解析式;
(2)若2021年年终测得浮萍覆盖面积为 ,从上述两个函数模型中选择更合适的一个模型,试估算
至少到哪一年的几月底浮萍覆盖面积能超过 ?(参考数据: )
22. 已知 是等差数列, .
(1)求 的通项公式和 .
(2)已知 为等比数列,对于任意 ,若 ,则 ,
(Ⅰ)当 时,求证: ;
第5页/共6页
学科网(北京)股份有限公司的
(Ⅱ)求 通项公式及其前 项和.
第6页/共6页
学科网(北京)股份有限公司